Reproductive suppression follows threats to child survival
Abstract
Natural selection presumably conserved mechanisms that allow females to block or terminate gestation when environmental circumstances threaten the survival of offspring. One example of this adaptive reproductive suppression, the Bruce effect, has been identified in several species, both in the laboratory and in the wild. Although descriptive epidemiology reports low fertility among women experiencing stressful circumstances, attempts to detect a Bruce effect in humans have been rare and limited. We contribute to this limited work by examining the relationship between the odds of child death and the sex ratio at birth in Sweden for the years 1751–1840. We find evidence of a generalized Bruce effect in humans in that unexpected changes in child mortality predict opposite unexpected changes in the secondary sex ratio in the following year, even after adjusting for period life expectancy. Our analysis broadens the scope of the Bruce effect literature to include humans, suggesting that women, through noncognitive decisional biology, adjust reproductive strategies and investments in response to changing environmental conditions.
Introduction
Given potential fitness advantages, natural selection likely produced mechanisms that allow females from several species to suppress reproduction when environmental circumstances threaten the survival of either themselves (Trivers & Willard, 1973) or their offspring (Labov, 1981; Beehner & Lu, 2013). Early noted examples of reproductive suppression included the ‘Bruce effect’ named after the researcher who observed that the presence of unfamiliar males coincided with termination of pregnancy among recently mated female laboratory mice (Bruce, 1959). Further research reported a Bruce effect in wild rodents (Mallory & Clulow, 1977), geladas (Roberts et al., 2012) and lions (Packer & Pusey, 1983). Commonly cited adaptive benefits of the Bruce effect include avoidance of infanticide (Rulicke et al., 2006; Beehner & Lu, 2013) by newly arrived males, who may eliminate offspring not their own (Elwood & Kennedy, 1990). Suppressing reproduction in these circumstances presumably improves a female's fitness by averting investment of her time and energy in offspring with relatively low chances of surviving to reproductive age.
Reports of reproductive suppression among several species in response to a wide array of threats to offspring survival suggest that circumstances beyond the presence of new males may induce the Bruce effect (Becker & Hurst, 2008; Beehner & Lu, 2013). Such threats include infanticide by male or female conspecifics (Schwagmeyer, 1979; Labov, 1981; Wasser & Norton, 1993; Ebensperger, 1998), risk of predation (de Catanzaro, 1988) and other stressors (de Catanzaro & Macniven, 1992). Pregnancy termination has been observed in voles (Schadler, 1981; Storey & Snow, 1990), horses (Bartoš et al., 2015), domestic dogs (Bartoš et al., 2016) and other primates (Colmenares & Gomendio, 1988; Beehner et al., 2005, 2006; Roberts et al., 2012) confronted with environmental or social threats to offspring survival. Taken together, these reports suggest that the Bruce effect prevents investment in offspring with low probability of survival (Ebensperger, 1998; Palombit, 2015). Thus, we define the Bruce effect in humans as spontaneous abortion induced by threats to child survival.
Descriptive literature separate from that invoking the Bruce effect has reported reproductive suppression among women in environments that threaten the survival of infants and children. Much descriptive epidemiology reports, for example, that pregnant women subjected to stressors exhibit lower fertility (Hjollund et al., 1999; Gibbs et al., 2013) and higher risk of spontaneous abortion than other women (Neugebauer et al., 1996; Wainstock et al., 2013). Evidence suggests that these pregnancy losses are not random, but rather serve to minimize investment in foetuses least likely to survive through reproductive life (Stearns, 1987; Haig, 2008).
Historically, male infants, especially male twins, have required the highest maternal investment to thrive (Maršál et al., 1996; Mace & Sear, 1997; Loos et al., 2001) and have had the highest likelihood of infant and child mortality (Wells, 2000; Drevenstedt et al., 2008). Indeed, male infants have been the age by sex group of humans most likely to die before completion of reproductive life for every year and every society with reliable life table data (Human Mortality Database, University of California). If present in humans, the Bruce effect should, therefore, target male more than female gestations and produce lower sex ratios at birth when the environment threatens survival of frail offspring. Consistent with this argument, decreases in the secondary sex ratio have been observed following economic recessions (Catalano et al., 2010), political instability (Zorn et al., 2002; Kemkes, 2006), natural disasters (Fukuda et al., 1998; Suzuki et al., 2016), threatening weather (Catalano et al., 2008; Helle et al., 2008) and terrorist attacks (Catalano et al., 2006). As predicted by the Bruce effect, the literature further reports that males from low sex ratio birth cohorts live longer than other males (Catalano & Bruckner, 2006b), yield more grandchildren for their mothers (Bruckner et al., 2015) and have higher Bayley cognitive scores of early development than males from higher sex ratio cohorts (Bruckner & Nobles, 2013). This increased performance of males results from the culling of low-performing males from the birth cohort via selection in utero.
Combining the Bruce effect literature with the human research on spontaneous abortion suggests that mechanisms conserved by natural selection to protect maternal fitness may include selection in utero against less fit males, particularly twins, when death among children exceeds endemic levels. A test of this suggestion reported relatively low ratios of Norwegian male twins to male singletons following the Oslo massacre, in which a deranged gunman murdered 77 persons, primarily youths (Catalano et al., 2016). While offering findings consistent with a Bruce effect in humans, this analysis focused on a very rare and extremely provocative event (i.e. intentional mass murder of children) and a narrow indicator of selection in utero (i.e. male twin ratio). Here, we inspect historical Swedish data, which provide the longest dependable record of human births and child mortality, to detect evidence of a generalized Bruce effect in the ratio of male to female live births (i.e. the secondary sex ratio). We use child mortality above statistically expected levels as the proximate signal that suppressing reproduction would benefit a female's fitness. We, therefore, hypothesize that the secondary sex ratio should fall below expected values when the odds of death among children rise above expected values.
Testing our hypothesis requires that we specify how long after unexpectedly many child deaths we expect to detect signals of suppressed male births. Our test, as described below, uses annual Swedish data for the 90 years beginning with 1751 and ending 1840. We cannot know the monthly distribution of child deaths or of conceptions over any of those years. Only a disproportionate share of both in the first 4 months of most of those years would, however, lead to the strongest signal of reproductive suppression appearing in the same year as child deaths. We know of no reason to assume these disproportionate distributions. The lack of evidence for ‘high first third’ distributions, and because evidence suggests that Bruce effect mechanisms may work at conception (James, 2004, 2010) as well as later in gestation (Fukuda et al., 1998; Suzuki et al., 2016), we anticipate that the strongest signal of suppressed male reproduction would appear in the year after unexpected increases in the likelihood of child death.
We anticipate the argument that an inverse association between the odds of child death and the secondary sex ratio could arise from pathologic shocks to the population that increase death rates over the lifespan and induce spontaneous abortion as morbidity rises among persons of reproductive age. The literature refers to this rival hypothesis as the Trivers–Willard effect after seminal work that argued the capacity of parents to invest in offspring would affect the secondary sex ratio (Trivers & Willard, 1973). The Trivers–Willard effect predicts that populations weakened by environmental stressors will produce fewer of whichever sex requires greater investment to rear to reproductive age (Cameron, 2004; Rosenfeld & Roberts, 2004; Roche et al., 2006). Among humans, males require more parental investment thereby leading to the hypothesis that stressed populations will exhibit relatively low secondary sex ratios. We define the Trivers–Willard effect in humans as spontaneous abortion induced by poor maternal health.
The Trivers–Willard effect differs from the Bruce effect in that the former ensues from threats to parents whereas the latter follows from threats to offspring. The logic of the Bruce effect stands without reference to parental health whereas the Trivers–Willard effect requires poor parental condition. We contend with this rival hypothesis by including in our test equation, as a covariate, period life expectancy for the population, which essentially measures the average age at death in a given year and, inversely, the level of morbidity in the population. As with child death, we expect that period life expectancy in year t−1 would correlate with the secondary sex ratio in year t.
Materials and methods
Data
We extracted data for our tests from the Human Mortality Database (Human Mortality Database, University of California). This database includes life table and mortality data from countries with dependable – as judged by demographers unconnected with this study – and virtually complete vital statistics. Among countries with vital statistics that meet the standards for inclusion in the Human Mortality Database, Sweden's statistics start earliest at 1751. These early and continuous data provide an opportunity to test our hypothesis with the longest available mortality and natality data. Our test ends with the cohort born in 1840 because outmigration of reproductive aged Swedes accelerated to relatively high levels in the ensuing decade and persisted well into the 20th century implying that temporal variation in our variables could, after 1840, arise from biasing changes in the composition of the population (SCB, 1999).
Variables
We constructed our independent variable, the odds of child death, as the annual ratio of Swedes aged 1–9 who died to those of the same age who survived the year. We excluded infants from children to avoid confounding our test with the reported high infant mortality among males from high sex ratio birth cohorts (Bruckner & Catalano, 2007). We specified our dependent variable, the secondary sex ratio, as the annual odds of a male live birth. We also specified period life expectancy, that is the average age at death, for the population as a covariate.
Analyses
Observational tests of association since Galton's seminal work in the late 19th century essentially measure the extent to which variables move away from their statistically expected values in the same cases (Stigler, 1989). ‘Cases’ in our tests include 90 years (i.e. 1751 through 1840) characterized by the Swedish secondary sex ratio and the odds of death among 1- through 9-year-old Swedes. The Bruce effect predicts that the sex ratio in year t will correlate inversely with the degree to which the odds of child death differs from expected values in year t−1.
Tests of association typically assume normal and independent distribution of variables. These assumptions allow specifying the expected value of a variable as its mean. Variables measured over time, however, often violate these assumptions by exhibiting ‘autocorrelation’ in the form of secular trends, cycles or the tendency to remain elevated or depressed, or to oscillate, after high or low values. The expected value of an autocorrelated series is not its mean but rather the value predicted by autocorrelation. Researchers dating to Fisher (Fisher, 1921) have solved this problem by identifying a model that fits observed autocorrelation in a series and using the values it estimates as the expected values. We used the most mature and widely disseminated type of such modelling to arrive at the expected values of our data. The method, devised by Box and Jenkins (Box & Jenkins, 1976), identifies which of a very large family of models best fits measurements made serially in time or space. Metaphorically, the modelling procedure assumes that the measurements passed through an unobserved ‘filter’ that imposed patterns upon them. The procedure identifies mathematical ‘signatures’ to narrow the likely filters to a few and then applies estimates of ‘fit’ to arrive at the most likely candidate. The differences between the values predicted by the model and the observed series, or model residuals, approximate the values that passed through the filter. These ‘unexpected’ values meet the assumptions of traditional tests of association because they are independent of each other (i.e. exhibit no autocorrelation), their expected value equals their mean (i.e. 0), and they exhibit constant variability over time.
The Box and Jenkins approach attributes autocorrelation to integration as well as to ‘autoregressive’ and ‘moving average’ parameters. Integration describes secular trends and seasonality. Autoregressive parameters best describe patterns that persist for relatively long periods, whereas moving average parameters parsimoniously describes less persistent patterns.
Our test proceeded through the following steps.
- We regressed the secondary sex ratio in Sweden for the years 1751 through 1840 on period life expectancy for those years. We specified period life expectancy in year t−1 for reasons described above.
- We used Box & Jenkins (1976) methods to detect and model autocorrelation in the residuals of the regression estimated in Step 1. Steps 1 and 2 ‘adjust’ the secondary sex ratio for its association with the period life expectancy and for autocorrelation.
- We used Box-Jenkins methods to detect and model autocorrelation in the odds of child (i.e. ages 1 through 9) death for the same years. The residuals of the model estimate the degree to which odds of a child death in any year exceeded or fell below values expected from autocorrelation.
- We estimated eqn 1 below formed by adding, as a predictor variable, the residuals of the Box-Jenkins model estimated in Step 3 (i.e. that for the odds of child death) to the model developed in Step 2 for the secondary sex ratio. We specified the child death residuals in the same calendar year (i.e. year t) as the sex ratio as well as in the prior two years (i.e. years t−1 and t−2). The Bruce effect predicts that the coefficient for year t−1 will be significantly (P < 0.05, one-tailed test) < 0. We include year t and t−2 in the equation as falsification tests because our argument implies they should not yield significant coefficients.
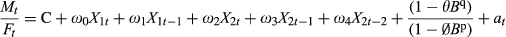 (1)
(1)Mt is the number of male births in year t. Ft is the number of female births in year t. C is constant. ω0 to ω4 are effect parameters. X1t is period life expectancy for year t. X2t is the residual of the best fitting Box-Jenkins model, estimated in step 3 above, of the odds of child death in year t. θ is the moving average parameter of the Box-Jenkins model.  is the autoregressive parameter of the Box-Jenkins model. Bp is the ‘backshift operator’ or value of a at year t−q or of
is the autoregressive parameter of the Box-Jenkins model. Bp is the ‘backshift operator’ or value of a at year t−q or of  at year t−p. at is the residual of the model at year t.
at year t−p. at is the residual of the model at year t.
Results
Table 1 shows the mean, standard deviation and range of the time series used in our tests. Table 2 shows the results of the first 2 steps and step 3 of our test. The first model in Table 2 (i.e. that produced by steps 1 and 2 above) adjusts the sex ratio for period life expectancy the year earlier and for autocorrelation. The estimated parameter for period life expectancy suggests that period life expectancy in year t−1 predicts the sex ratio in year t positively, but not significantly (i.e. P > 0.05; one-tailed test). We, however, carry the variable into the test equation because it may significantly confound the association between the sex ratio and the child death rate.
| Mean | Standard deviation | Range | |
|---|---|---|---|
| Secondary sex ratio | 1.0459 | 0.0075 | 1.0211–1.0624 |
| Odds of child death | 0.0246 | 0.0092 | 0.0111–0.0772 |
| Period life expectancy at birth | 37.6551 | 17.96 | 47.12 |
| Predictor | Coefficient | Standard error |
|---|---|---|
| Secondary sex ratio | ||
| Mean | 1.0443b | 0.0070 |
| Period life expectancy | 0.0001 | 0.0002 |
| Autoregressive parameter at B5 | −0.1849a | 0.1093 |
| Odds of child death | ||
| Mean | 0.0234b | 0.0021 |
| Moving average parameter at B11 | −0.3024b | 0.1100 |
| Autoregressive parameter at B | −0.2813b | 0.1099 |
| Autoregressive parameter at B6 | −0.2798b | 0.1079 |
- a P < 0.05, one-tailed test.
- b P < 0.01, one-tailed test.
The autoregressive parameter at B5 in the first model in Table 2 implies that, after adjusting the sex ratio for its association with period life expectancy, the series exhibited a dampening sine wave with a period of 5 years. A post hoc explanation of this autocorrelation would be entirely speculative and akin to ‘explaining’ the counterfactual in a clinical trial (i.e. the appearance of cases in the control group).
The second model in Table 2 (i.e. the product of step 3 in the analyses) shows that modelling the odds of child death required autoregressive parameters at B and B6. The parameter at B implies that high or low values in year t carried into subsequent years although diminished in size. The autoregressive at B6 suggests a dampening sine wave with a period of 6 years. The odds of child death also showed a moving average parameter at B11. This parameter suggests that any high or low values of in the series ‘echoed’ with a similar but diminished value 11 years later but not farther into the future. Again, any post hoc explanation of this autocorrelation would be entirely speculative.
Figures 1 and 2 show the results from the first 2 steps and step 3 as graphs. The graphs plot the observed and expected (from the models shown in Table 2) values of the secondary sex ratio and odds of child death.
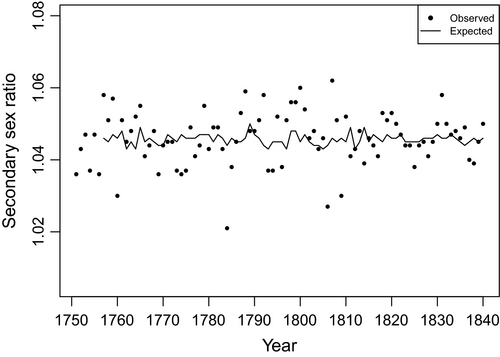
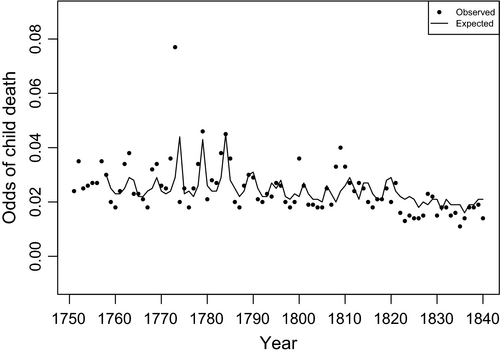
Table 3 shows the results of estimating our test equation (i.e. eqn 1 above). Consistent with the Bruce effect, the coefficient (i.e. −0.3856; SE = 0.1753; T76 = −2.20; P = 0.0154) for unexpected changes in the odds of child death in year t−1 significantly (P < 0.05, one-tailed test) and inversely predicts sex ratios in year t. Also consistent with our expectations, the coefficients for year t (i.e. −0.1020; SE = 0.0943; T76 = −1.08; P = 0.1418) and t−2 (i.e. −0.1782; SE = 0.1134; T76 = −1.57; P = 0.0603), although negatively signed, did not differ from 0 (P < 0.05, one-tailed test). Period life expectancy did not appear to confound the association between the secondary sex ratio and child death a year earlier.
| Predictor | Coefficient | Standard error |
|---|---|---|
| Mean | 1.0569a | 0.0129 |
| Period life expectancy | −0.0003 | 0.0003 |
| Unexpected odds of child death | ||
| Same year | −0.1020 | 0.0943 |
| Year earlier | −0.3856a | 0.1753 |
| Two years earlier | −0.1782 | 0.1134 |
| Autoregressive parameter at B6 | −0.2844a | 0.1076 |
- a P < 0.01, one-tailed test.
We anticipated at least four questions regarding the sensitivity of our results to circumstances we imposed on the test. First, would the odds of child death predict the sex ratio if we did not adjust either for autocorrelation? We estimated eqn 1 above with all three variables in their observed values and without adjusting the residuals for autocorrelation. The results appear consistent with the Bruce effect in that the coefficient for odds of child death at year t−1 (i.e. −0.4132) was negatively signed and exceeded that for both variables measured in the same year (i.e. −0.0008) and that with the odds of child death specified 2 years before the sex ratio (i.e. 0.0017). These coefficients provide an approximation of the association between the sex ratio and odds of child death if a reader assumes a causal relationship induced any autocorrelation these variables share. We cannot, however, estimate confidence intervals from the SE (i.e. 0.0948, 0.2024 and 0.0905, respectively) for these coefficients because the residuals of the regression exhibited autocorrelation.
Second, would the odds of child death unadjusted for autocorrelation predict the sex ratio? We estimated eqn 1 again but left the odds of child death in its original values. We can infer confidence intervals for these estimations because the residuals of the model will exhibit no autocorrelation. The results supported the Bruce effect in that the coefficient for odds of child death at year t−1 (i.e. −0.3679; SE 0.1901) remained negatively signed and significantly (i.e. P < 0.05; one-tailed test) < 0. This finding implies that the differences of the odds of child death from its mean (i.e. the intuitive expected value), like its differences from values expected from autocorrelation (i.e. the true statistically expected value), predict the secondary sex ratio.
Third, would the odds of child death predict the sex ratio if we did not adjust the later for period life expectancy? We repeated the steps listed above with the exception that step 1 did not include adjusting for period life expectancy. The results continued to support the Bruce effect in that the coefficient for odds of child death at year t−1 (i.e. −0.2595; SE 0.0906) remained negatively signed and significantly (i.e. P < 0.01; one-tailed test) < 0. Coefficients for child death at year t (i.e. −0.0757; SE 0.0886) and year t−2 (i.e. −0.1188; SE 0.0888) did not differ from 0.
Fourth, could the high rate of child death, caused by the famine of 1773, account for our findings? We addressed this question in two ways. First, we applied the methods of Chang, Tiao, and Chen (Chang et al., 1988) to detect and remove outliers in the residuals of the Box-Jenkins model for child death, estimated in step 3 of our test and repeated step 4. The results did not change in that the coefficient for odds of child death (i.e. −0.4399; SE 0.1970), adjusted for autocorrelation and outliers, at year t−1 remained significantly < 0. Second, we created a binary variable scored 1 for 1773 and 0 for all other test years and added it to the test equation described in step 4 above. Estimating this equation produced the same results as the original test in that the coefficient for odds of child death (i.e. −0.3740; SE 0.1773), adjusted for autocorrelation, at year t−1 remained significantly < 0.
We provide context for the results of our primary test in several ways. First, Fig. 3 shows the scatter plot, and best fitting line, between the adjusted (i.e. for period life expectancy and autocorrelation via steps 1 and 2) sex ratio at year t and the adjusted (i.e. for autocorrelation via step 3) odds of child death at year t−1.
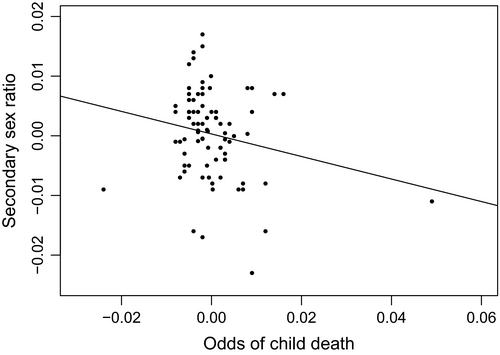
Second, we attribute variance ‘explained’ by our test equation to its components. Autocorrelation and period life expectancy accounted, as estimated by model 1 in Table 2, for 2.8% of the variance in the sex ratio. Our test equation, shown in Table 3, increased variance explained to 17%. Removing the parameters with nonsignificant contributions (i.e. period life expectancy and odds of child death in year t and year t−2) reduced the explained variance to 12%.
Third, we estimate the decreases in the annual sex ratio that may have arisen from the Bruce effect. The sex ratio ranged from 1.021 to 1.062 over the 90-year test period. Unexpected odds of child death ranged from 0.0002 to 0.0485 in the 31 ‘Bruce effect’ years in which the odds exceeded expectations. This circumstance implies that the Bruce effect hardly affected the observed sex ratio when the odds of child death changed least from expected (i.e. 0.0002 × −0.3856 = −7.712e-5) but induced a more noticeable −0.019 decrease when the child death increased most from expected (i.e. 0.0485 × −0.3856 = −0.019).
Discussion
We provide evidence consistent with a Bruce effect in humans by detecting the hypothesized association between unexpected child mortality and the secondary sex ratio in the following year. Our findings support the presence of reproductive suppression following risks to offspring. These findings should add impetus to broadening the scope of the Bruce effect literature to include humans.
Our findings imply that, consistent with the argument for reproductive suppression and the facts concerning the frailty of human males, the Bruce effect affects males more than females. The animal literature does not, to our knowledge, report the sex ratio of cohorts culled via a Bruce effect, nor does it describe differential effects on male vs. female gestations.
Connecting our findings to the human sex ratio literature suggests two hypotheses that future research should test. First, males from ‘Bruce effect’ cohorts should live longer (Catalano & Bruckner, 2006a, b; Catalano et al., 2008) than those from other cohorts because the weakest among them will have been culled. Second, males from Bruce effect cohorts should have more reproductive success than those from other cohorts (Bruckner et al., 2015). Future research should test these hypotheses. Although the current animal literature rarely examines the life course of survivors from cohorts subjected to the Bruce effect (Huck et al., 1986; Wasser & Norton, 1993), such work should require less time and raise fewer ethical objections than similar work among humans.
Although our analysis provided no support for the Trivers–Willard effect, we note that period life expectancy is a crude and imperfect measure of maternal condition and thus may not fully capture the effect of poor maternal health on reproductive suppression. It remains possible that both the Bruce effect and the Trivers–Willard effect operate in humans, either simultaneously or at different times, and they may have either independent or interactive effects. Future work should examine the Trivers–Willard effect using more precise measures of maternal stress or maternal health and should examine the interactive effects of threats to parents and threats to offspring in predicting reproductive suppression.
The annual birth data used in our analyses do not allow us to identify ‘critical periods’ in gestation when the detection of threat to offspring most likely triggers the Bruce effect. The Bruce effect may either, or both, block conception (James, 2008) or induce spontaneous abortion (Catalano et al., 2005; Catalano & Bruckner, 2006b; Bruckner et al., 2010, 2016). Blocked conception or early termination would seem least costly and would minimize the interval before the female can again attempt reproduction. The earlier the termination, however, the greater the uncertainty regarding the post-natal environment. Natural selection, therefore, may have conserved whatever mechanisms allowed women to abort throughout gestation.
Our analysis builds on previous research into the Bruce effect in humans by operationalizing environmental risk to offspring with a continuous and unambiguous indicator – the odds of child death – rather than with an environmental event the ongoing effect of which on the well-being of children remains unclear (Catalano et al., 2016). In addition, our use of child mortality as the most proximate indicator of environmental risk summarizes signals that may include nutritional, social, temperature and pathogenic risk, among others. If a generalized Bruce effect occurs in human populations, and if the Bruce effect serves to avoid offspring death, then it should be most evident in response to child mortality.
Both energetic (Bercovitch & Strum, 1993; Williams et al., 2001; Tardif et al., 2004; Beehner et al., 2006; Lujan et al., 2006) and social (Colmenares & Gomendio, 1988; Bercovitch & Strum, 1993; Wasser et al., 1998; van Noordwijk & van Schaik, 1999; Sapolsky, 2005; Marashi & Rülicke, 2012; Roberts et al., 2012) threats can induce the Bruce effect in animals. These environmental cues likely interact and are integrated by noncognitive, autonomic mechanisms, to determine an adaptive reproductive response (Wingfield & Sapolsky, 2003; Williams et al., 2007). In the case of humans, this complexity inevitably raises issues of fairness and equity. Women with access to more protective resources may be less susceptible to the Bruce effect. The likelihood of child morbidity and mortality differs by race and socioeconomic status (Bauman et al., 2006; Braveman & Barclay, 2009; Lu et al., 2010) implying that the experience and impact of the Bruce effect will do likewise. The application of the Bruce effect to humans would suggest that some fraction of the excess spontaneous abortion and preterm birth observed among, for example, women residing in violent environments, might not arise from ‘disease’ within the women or their foetuses, but rather from adaptive responses conserved across several species by natural selection.
The biologic mechanisms through which females detect signals of environmental risk, and how that detection affects reproduction, remain largely unknown and likely vary across species. In rodents, pheromones may mediate the Bruce effect, whereas the stress response may translate environmental threat to spontaneous abortion in primates (Beehner & Lu, 2013). We suspect that cognition allows humans to perceive and interpret threats in the environment, and that cognitive processes influence reproduction through stress mechanisms communicated via the hypothalamic pituitary adrenal (HPA) axis. Indeed, natural selection may have conserved the stress response, at least in part, due to its role in the Bruce effect and reproductive suppression.
An unmeasured factor could have led to the death of both children and foetuses in our data. That factor, however, would have had to act differently on male and female foetuses and not affect period life expectancy. It, moreover, could exhibit no autocorrelation in the form of trends, cycles or regression to the mean. We know of no plausible phenomenon that meets these criteria.
Our findings support the importance of viewing human reproduction through an evolutionary lens. Humans, like other species, have evolved and maintained mechanisms that adjust reproductive strategies in response to changing environmental conditions. These mechanisms may include noncognitive decisional biology that anticipates, estimates and compares the costs and benefits of investing in gestation (Wasser & Barash, 1983; Beehner & Lu, 2013).
Acknowledgment
This research was supported by the Robert Wood Johnson Health and Society Scholars Program.
Competing interest
We have no competing interests.
References
Data deposited at Human Mortality Database: doi: Data available via Human Mortality Database (www.mortality.org).




