In an uncertain economic environment, the ability of firms to adapt their production levels to unforeseen market demand is critical for their investment, financing and trade credit policies. This paper focuses on the impact of production flexibility on trade credit values and maturity in the presence of uncertain demand. We develop a continuous-time real options framework where a buyer firm with capacity constraints orders input goods on credit from a supplier. The supplier optimally chooses the trade credit maturity, considering its influence on the buyer's optimal quantities and default timing. We distinguish between flexible firms, capable of suspending production during adverse conditions, and rigid firms, constrained to constant full-scale production. Our findings reveal that production flexibility positively affects trade credit values and maturity. Flexible firms invest in larger capacity, default later and order larger quantities, resulting in higher trade credit values. Suppliers extend longer maturities to flexible firms, reflecting their higher creditworthiness and the positive effects of extended trade credit on their installed capacity. Furthermore, we explore extensions to our framework, including switching costs, entry timing, interactions between debt and trade credit and a non-cooperative bargaining game.

1 INTRODUCTION

In highly uncertain economic environments, the ability to adjust operating variables such as the level of production to cope with unpredictable changes in market conditions is essential. This operational or production flexibility has been extensively analyzed in the real options literature (e.g., Dixit & Pindyck, 1994; Trigeorgis, 1996). Several firms exploit operational flexibility in various business contexts. For example, in the automotive and electronics industries, Japanese producers such as Toyota and Sony have shown resilience by being able to halt production in response to adverse conditions caused by the tsunami that hit the country on March 11, 2011 causing interruptions in electricity supply.1 More recently, in the context of the recent rise in energy costs, several energy-intensive firms in industries such as steel and nonferrous metals have been forced to temporarily stop production. For example, ArcelorMittal had to carry out “short and selective stoppages” in several factories in Europe, while in Spain Sidenor stopped production at its largest plant for 20 days, and Fertiberia shut down one of its plants during October 2021.2 Production or volume flexibility has been shown to influence a firm's investment timing, capacity and capital structure decisions (Hagspiel et al., 2016; Rithcken & Wu, 2021).3

However, production flexibility's impact on firm value is not limited to a firm's investment and debt financing decisions. A firm's ability to adjust production level may affect its relationships with suppliers and the trade credit provided. Firms rely greatly on trade credit, especially in developing countries with poorly developed financial markets and weak financial institutions (Fisman & Love, 2003). Moreover, empirical evidence shows that trade credit is the largest single source of short-term financing (Petersen & Rajan, 1997) even in a well-developed market as the United States. Additionally, it is a key financing source not only for small and medium enterprises, but also for large ones. Yang & Birge (2018) report accounts payable 3.3 times larger than bank loans for US nonfinancial firms and document that for large public retailers in North America, accounts payable represent one third of their liabilities.

In this paper, we analyze the effect of production flexibility on trade credit values and maturity. We develop a continuous time real options framework in which the demand shock in the downstream market follows a geometric Brownian motion. We consider a buyer firm with capacity constraints that orders input goods on credit from a supplier. Given the short-term nature and roll-over character of trade credit, we build on Leland (1994, 1998) models of finite debt used in the capital structure literature to model short-term trade credit. In our benchmark model, we consider a Stackelberg leader–follower game where the supplier optimally chooses the trade credit maturity to extend to the buyer, internalizing how the choice of maturity will influence the buyer's optimal quantity and default threshold. The buyer firm acting as a follower selects optimally its capacity and quantities to be ordered from the supplier, as well as the default timing.

To analyze the impact of production flexibility on trade credit we consider two cases for the buyer firm. On the one hand, we have a flexible firm that has the possibility to temporarily suspend operations when the price drops below the marginal cost (idle mode). If market conditions improve, the firm retakes full-scale production (active mode). However, if market conditions further deteriorate the firm defaults at an endogenous threshold. On the other hand, we model a rigid firm that is restricted to always produce at full capacity and has the option to default when the demand shock drops to an optimally chosen threshold. Figure 1 shows how the flexible and rigid make decisions as revenue uncertainty unfolds in our model based on an illustrative example of the evolution of revenues.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Illustration of operating policies for flexible and rigid firm. This figure illustrates the operating policies of a flexible firm and a rigid firm. The state variable (final price of goods sold) is denoted by ${x}_t$ . For the flexible firm, production takes place as long as ${x}_t$ exceeds $w$ (prices above variable production costs), and is temporarily suspended when ${x}_t$ falls below $w$ . The flexible firm defaults when ${x}_t$ hits ${x}_{Bf}\$ from above for the first time, where ${x}_{Bf}$ represents the bankruptcy threshold for the flexible firm. The rigid firm has no flexibility and operates until it defaults when ${x}_t$ hits ${x}_{Br}\$ from above for the first time, where ${x}_{Br}$ represents the bankruptcy threshold for the rigid firm.

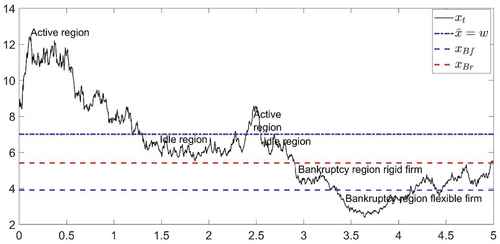
Our study demonstrates that operational flexibility significantly influences trade credit value and maturity. We find that higher operational flexibility leads to an increase in trade credit value driven by distinct channels. First, flexible firms can mitigate operational losses by temporarily suspending production, leading to increased investments in larger capacity, which improves trade credit value. Second, trade credit is higher for flexible firms because they default later compared to rigid counterparts, reflecting higher shareholder willingness to sustain them. This result aligns with the work of Petersen & Rajan (1997), highlighting that higher credit-quality buyers secure more extensive trade credit access. In line with Ritchken & Wu (2021) who found higher debt leverage for rigid firms, we observe, however, higher trade leverage ratios for rigid firms. This is attributed to the fact that the value of flexible firms increases at a greater rate compared to trade credit values, resulting in lower leverage ratios for these firms.4

Regarding trade credit maturity, we find that a supplier extends longer maturities to a flexible firm compared to the rigid one. This result is broadly in line with the evidence in Klapper et al. (2012), who find that the most creditworthy buyers obtain longer trade credit maturities. We also provide a number of new empirical predictions about production flexibility's impact on trade credit values and maturities, showing that operational flexibility is more important in industries with less intense competition between suppliers (higher prices of suppliers), in downstream markets with higher capacity constraints, for lower recovery rates in the event of bankruptcy for suppliers, for lower gross profit margins and lower capacity-holding costs of buyer firms.

We consider several extensions of our main setup. First, we consider the effects of switching costs and hysteresis, that is, the zone of inaction for the buyer firm between moving from idle to active (operational) mode and vice versa. We find that the trade credit horizon provided by the supplier has no impact on the hysteresis zone, however, higher levels of switching costs widen the hysteresis zone and decrease the trade credit value and order quantities. Second, we analyze the entry timing of firms by including the optimal timing of the option to invest for the buyer firm. We show that for a given trade credit maturity, the flexible firm postpones investment compared to the rigid firm and invests in higher capacity. Third, we consider interactions between debt financing and trade credit. We show that debt leverage decreases with the use of trade credit, as the purchase of goods from the supplier secures the firm tax shields through the tax deductibility of purchased products. In addition, covenant restrictions imposed by banks cause trade creditors to reduce trade credit maturity. Finally, we consider an alternative design of the Stackelberg leader–follower game based on a non-cooperative Nash bargaining game between the buyer and the supplier. In this setup, we show that the supplier provides longer trade credit maturities when the buyer has higher market power, in line with empirical evidence (e.g., Ellingsen et al., 2016; Fabbri & Klapper, 2016; Giannetti et al., 2011; Klapper et al., 2012). Comparing the Stackelberg solution with the Nash solution, we find that the Nash bargaining game results in higher ordered quantities and trade credit maturities compared to the Stackelberg leader–follower game. Overall, the realistic features included in these extensions yield fresh insights and enhance our understanding of firms’ decisions within the supply chain under conditions of uncertainty.

Related literature. We next summarize our contributions in relation to the literature. To the best of our knowledge, this is the first paper that bridges the literature on operational flexibility with that on trade credit. Trade credit has been modeled within a real options framework in Koussis & Silaghi (2020) and in Silaghi & Moraux (2022), however, none of these papers considers the effect of operational flexibility and its impact on trade credit value and maturity. On the other hand, papers that do incorporate operational flexibility, such as Hagspiel et al. (2016) and Sarkar (2018), focus on investment decisions and do not consider trade credit. We methodologically extend the former settings by incorporating operational flexibility for the buyer firms, while extending the latter settings by introducing trade credit. In our setting, operational flexibility not only enables a firm to reduce risks (e.g., as shown in Chod et al., 2010), but also enhances the provision of trade credit for flexible firms.

We also contribute to the literature on corporate debt and capital structure (contingent claim pricing), following Leland (1994) and subsequent research. The most closely related paper to ours in this strand of the literature is Ritchken & Wu (2021), who introduce corporate debt in the framework of Hagspiel et al. (2016) and analyze the impact of production flexibility on leverage and capital structure. Additionally, Charalambides & Koussis (2018) examine a flexible firm's option for debt rescheduling during periods of low demand. Our framework differs in several respects from these models that primarily focus on corporate debt, as we focus on trade credit and our model reflects the specific attributes of trade credit. First, while a primary determinant of corporate debt usage is its tax advantage through the tax deductibility of interest payments, trade credit implies no direct tax benefits, as the most common trade credit terms, that is, net terms, are basically interest-free loans that do not imply any interest payments. In an extension of our basic setup, we demonstrate, however, that firms may employ trade credit to boost their purchases and indirectly generate tax benefits through the tax deductibility of purchased goods. Considering trade credit along with debt allows us to highlight the role of trade credit in creating indirect tax advantages through higher purchases, which are significant enough to reduce the need for debt leverage. Consequently, we contribute to this literature by providing a potential explanation for the incapacity of capital structure models to elucidate the low leverage ratios observed in practice (e.g., Strebulaev & Yang, 2013). Moreover, unlike Iancu et al. (2017), who emphasize the positive function of debt covenants in mitigating risk-shifting incentives in inventory management, we show that debt covenants increase firm's riskiness, leading to earlier defaults. Trade creditors in turn react to these covenants by requesting earlier payment. This debt holder–supplier conflict aligns with the evidence presented in Zhang (2019). Second, unlike corporate debt, the value of trade credit depends on order quantities. Therefore, in a trade credit setting, it is important to consider how the supplier internalizes the trade credit maturity choice's effect on the capacity choices of the buyer firm. Third, while most previous papers study perpetual debt, we focus on finite maturity debt, given the short-term and roll-over nature of trade credit. This allows us to explore the impact of operational flexibility on trade credit maturity.

Finally, we contribute to the trade credit literature in finance and economics that focuses on the comparative assessment of trade credit and bank debt. Numerous theories have attempted to explain why trade credit is provided by suppliers rather than banks. Several papers motivate the use of trade credit as a way to reduce transaction costs (Emery, 1984; Ferris, 1981). Other studies, including Biais & Gollier (1997), Burkart & Ellingsen (2004), Cuñat (2007) and Giannetti et al. (2011), highlight suppliers’ informational advantage over banks. Other works argue that trade credit is offered as a warranty of product quality to solve information asymmetries between buyers and sellers (Lee & Stowe, 1993; Long et al., 1993; Ng et al., 1999). Brennan et al. (1988) explain trade credit as a price discrimination tool in response to imperfect market competition. Another explanation of trade credit is the bargaining power of buyers and suppliers as indicated by Klapper et al. (2012) and Fabbri & Klapper (2016). Finally, trade credit use is justified as a tool to promote sales (Schwartz, 1974). Similar to Schwartz (1974), our approach highlights the role of trade credit as a means for suppliers to boost future sales, providing a theoretical rationale for the observed prevalence of trade credit, as documented by Long et al. (1993) and Petersen & Rajan (1997). In our model, the supplier chooses the optimal trade credit maturity that maximizes its value by internalizing the effect on buyer's capacity and default timing, balancing the role of boosting sales against delayed payments. Importantly, our setting considers the operational flexibility of the buyer firm, an aspect that has been overlooked in the finance and economics literature. As for a flexible firm the positive effects of extending trade credit are higher (a flexible firm orders higher quantities and postpones default), the supplier will extend larger maturities to a flexible firm compared to the rigid one. Furthermore, in line with the substantial role attributed to the bargaining power of supply chain members in the trade credit literature (Fabbri & Klapper, 2016; Klapper et al., 2012), our theoretical setup explores various configurations of bargaining power among the supply chain partners, including a Stackelberg leader–follower game and a non-cooperative Nash bargaining game with varying degrees of bargaining power.

The rest of the paper is organized as follows. Section 2 presents the model setup and the valuation for trade credit and buyer firm values for the two cases of a flexible and rigid firm. Section 3 presents numerical results and sensitivity analysis. In Section 4, we consider several extensions to our framework that include switching costs, entry timing, interactions of trade credit with debt and Nash bargaining. Finally, Section 5 concludes.

2 THE MODEL

2.1 Model setup

A buyer firm produces a final good using as an input an intermediate good that it buys from the supplier firm. Τhe price of the good sold in the downstream market is p per unit of goods sold and given by the iso-elastic inverse demand function

p = x{Q}^\varepsilon

, where

- 1 &lt; \varepsilon &lt; 0

is a measure of price sensitivity and x represents the demand shock. The elasticity of demand is defined as

( {\frac{1}{{| \varepsilon |}}} )

and a higher

| \varepsilon |

implies a more inelastic demand. Following previous literature (Aguerrevere, 2009; Dixit & Pindyck, 1994; Dobbs, 2004; Silaghi & Sarkar, 2021), we assume that the demand shock in the downstream market x follows a geometric Brownian motion:

\begin{equation}\ \frac{{dx}}{x} = \ \mu dt + \sigma dZ\ ,\end{equation}

(1)

where

\mu

is the expected rate of change,

\sigma

is the volatility and

dZ

is a standard increment of a Weiner process.

Both firms (buyer and supplier) are risk neutral, thus they maximize expected profits. We denote by r the risk-free interest rate, and have that r > μ such that there is a rate of return shortfall δ = r—μ. A higher δ (while keeping r constant) captures a lower rate of growth of the good's price in the downstream market. The buyer optimally chooses the quantity of goods to produce and order from the supplier by solving an optimal capacity problem (see, e.g., Hagspiel et al., 2016; Huberts et al., 2015; Nishihara et al., 2019). For simplicity, we assume a one to one relation between the input and the output good. The buyer firm needs to incur a one-time investment cost ${{\kappa}}{Q}^\eta$ at time t = 0 to install capacity, where $Q$ represents the capacity, ${Q}^\eta$ is the amount of capital required to produce at that capacity (with $\eta > 1)$ and κ is the cost of capital per unit (in dollars). The capacity size fixes the production level and also the order quantity. However, price shocks described by Equation (1) create uncertainty in the revenue level (xQ) of the firm. Unlike Hagspiel et al. (2016), we do not explore the possibility of producing below capacity for either the rigid or the flexible firm. Rather, we capture flexibility by allowing our flexible firm to temporarily shut down production at an endogenously determined optimal price level. This type of flexibility is important in many settings including, among others, manufacturing (see Adkins & Paxson, 2012) and the airline industry (Hu & Zhang, 2015). The option to shut-down and restart was introduced in the real options literature for the analysis of mines by Brennan and Schwartz (1985).

The buyer firm faces both fixed costs of production ${C}_b$ , as well as variable costs w. Fixed costs include two components: C_b = c_f + c_h Q, where ${c}_h$ is the cost of holding one unit of capacity. We will initially assume ${c}_h = 0$ , so that there are no capacity holding costs. We then elaborate on the effect of capacity holding costs in a later section. Additionally, the buyer procures from the supplier the input goods obtained on trade credit, thus it has to incur the trade credit payments. The supplier continuously provides a quantity of goods Q to the buyer.

The initial debt principal is ${P}_SQ$ , where ${P}_S$ defines the price per unit of goods charged. In line with previous literature, we assume an exogenous price for the input good, as price discrimination is often forbidden or can lead to a price war because it is observable by competitors. Discriminating through trade credit maturity is a less aggressive and more flexible instrument (Fabbri & Klapper, 2016). We follow Leland's (1994, 1998) framework for finite debt to model trade credit. That is, we assume that at any instant of time a constant fraction m of the debt matures and the buyer reimburses a fraction payment m of the value of goods, that is, $m{P}_sQ$ of the goods are repaid. Therefore, the outstanding balance of trade credit at any instant of time t > 0 gets reduced by ${e}^{ - mt}$ . As Leland (1994, 1998) shows, the average maturity of repayment is given by 1/m. Moreover, the credit is continuously renewed, that is, each time a fraction of the credit is reimbursed by the buyer, the supplier provides a new credit identical and of equal size to the one repaid, so that trade credit is fully rolled over. This is consistent with the roll-over character of short-term financing in general and of trade credit in particular (see Amberg et al., 2020; Auboin & Engemann, 2014; Ferrando & Wolski, 2018; Garcia-Appendini, 2011). This also implies that the total outstanding amount of trade credit remains constant, that is, we have a stationary trade credit structure. Similarly, Dangl & Zechner (2021), Diamond & He (2014) and Leland (1994, 1998) have a stationary structure for corporate debt. Unlike the capital structure literature where the amount of debt is determined by the firm by balancing the tax benefits of debt against the bankruptcy costs, in our framework trade credit carries no interest tax shield. Instead, the buyer firm uses trade credit to establish a business relationship with a supplier for the provision of input quantities.

Finally, the buyer firm has the option to default. Following Diamond & He (2014) and Leland (1994, 1998), we assume that the equity holders have access to funds to cover potential losses at refinancing points. Default occurs when buyer value falls to zero and the buyer has no incentives to inject new funds into the firm. Formally, default takes place when the demand shock drops to an endogenously determined trigger, ${x}_B$ . At this point the buyer stops payments to the supplier. We assume that in the event of bankruptcy, the supplier receives the recovery value ${V}_B = b{P}_SQ$ , that is, the supplier recovers a fraction of the total value of outstanding trade credit due. Our assumption follows a large line of structural models (e.g., see Hull & White, 1995; Longstaff & Schwartz, 1995 and subsequent work). In fact, many empirical studies have focused on estimating recovery values based on the principal amount of loan recovered at bankruptcy (see, e.g., Altman et al., 2004 for a review). In our base-case analysis we assume $b = 0$ (no recovery in bankruptcy) in line with suppliers’ low priority in case of default.5 We study the impact of b in a later section.

We now analyze two different scenarios. First, we consider a rigid buyer firm with no operational flexibility that always produces at full capacity. Second, we analyze a flexible firm that can temporarily shut down when market conditions deteriorate, limiting losses. A rigid firm has the option to switch between a full-scale operating mode and an absorbing state where the firm defaults at the default threshold ${x}_B$ . A flexible firm on the other hand has the options to switch between a full-scale operating mode (active mode), an idle mode and an absorbing state where the firm declares bankruptcy. The possibility to temporarily shut down is similar to mothballing discussed in Dixit & Pindyck (1994), however, we also incorporate trade credit. In a related paper, Charalambides & Koussis (2018) considered debt rescheduling when temporarily shutting down. We assume initially that switching between the active and idle mode is costless. The firm switches from the active mode to the idle mode when the demand shock reaches from above the switching threshold $\bar{x} = \ w$ , that is, the price drops below variable costs. While being in this operating mode, the firm has the option to resume full-scale operations when the demand shock increases and reaches $\bar{x}$ . On the contrary, if the demand shock falls further, the firm may default, thus ${x}_B < \bar{x}$ .6 We incorporate switching costs in the analysis in Subsection 4.1.

2.2 Inflexible case

2.2.1 Trade credit value under inflexible case

Following Dangl & Zechner (2021), Diamond & He (2014) and Leland (1994, 1998), the value of trade credit

D( x )

follows the following second-order ordinary differential equation:

\begin{equation}r{D}_r\ \left( x \right) = \frac{{{\sigma }^2}}{2}\ {x}^2{D}_r^{^{\prime\prime}}\left( x \right) + \left( {r - \delta } \right)x{D}_r^{\prime}\left( x \right) + m\left( {{P}_SQ\ - {D}_r\left( x \right)} \right).\end{equation}

(2)

At each instant of time a fraction $m\ dt$ of credit matures. The buyer firm thus makes the principal repayment of $m{P}_SQ\ dt$ . At the same time, credit with an identical amount is issued, so the supplier provides a new credit of $m{D}_r\ dt$ . Combining the two amounts we obtain the change in trade credit value due to debt retirement given by the last term on the right-hand side of the previous equation.

The solution is given by:

\begin{equation}{D}_r\ \left( x \right) = \left( {\frac{{m{P}_SQ}}{{r + m}}} \right)\ + A_1^D{x}^{{\gamma }_1} + A_2^D{x}^{{\gamma }_2}.\end{equation}

(3)

The interpretation is intuitive. The first term represents the risk-free value of credit, while the additional terms capture the adjustments needed due to buyer's default option.

{\gamma }_1

and

{\gamma }_2

are the solutions of the following fundamental quadratic equation:

q\ = \frac{1}{2}\ {\sigma }^2\gamma ( {\gamma - 1} ) + ( {r - \delta } )\gamma - ( {r + m} ) = 0

, and are given by the following equations:

\begin{equation}\ {\gamma }_1 = \frac{1}{2}\ - \frac{{\left( {r - \delta } \right)}}{{\sigma ^2}} + \sqrt {{{\left( {\frac{{\left( {r - {{\delta}}} \right)}}{{{\sigma }^2}} - \frac{1}{2}} \right)}}^2 + \frac{{2\left( {r + m} \right)}}{{{\sigma }^2}}} &gt; 1\ ,\end{equation}

(4a)

\begin{equation}\ {\gamma }_2 = \frac{1}{2}\ - \frac{{\left( {r - {{\delta}}} \right)}}{{\sigma ^2}} - \sqrt {{{\left( {\frac{{\left( {r - {{\delta}}} \right)}}{{{\sigma }^2}} - \frac{1}{2}} \right)}}^2 + \frac{{2\left( {r + m} \right)}}{{{\sigma }^2}}} &lt; 0.\end{equation}

(4b)

Parameters

A_1^D

and

A_2^D

are constants to be determined by the following boundary conditions:

\begin{equation}\mathop {{\mathrm{lim}}}\limits_{x \to \infty } {D}_r\left( x \right) = \frac{{m{P}_SQ\ }}{{r + m}}\ ,\end{equation}

(5)

\begin{equation}{D}_r\ \left( {{x}_{Br}} \right) = {V}_B\ .\end{equation}

(6)

Extremely profitable buyers never default, and the default-free trade credit value is $\frac{{m{P}_SQ\ }}{{r + m}}$ , as in Equation (5). On the other hand, Equation (6) indicates that the buyer defaults when $x = {x}_{Br}\$ and the supplier receives the recovery value ${V}_B = \ b{P}_S{\mathrm{Q}}$ .

Solving Equation (2) with boundary conditions (5) and (6) we obtain that:

\begin{equation}\ A_1^D = 0,\end{equation}

(7a)

\begin{equation}\ A_2^D = \left( {{V}_B - \frac{{m{P}_SQ\ }}{{r + m}}} \right)\ \ x_{Br}^{ - \gamma _2}.\end{equation}

(7b)

This leads to the following solution for the value of trade credit:

\begin{equation}{D}_r\ \left( x \right) = \frac{{m{P}_SQ}}{{r + m}}\ + \left( {{V}_B - \frac{{m{P}_SQ\ }}{{r + m}}} \right){\left( {\frac{x}{{{x}_{Br}}}} \right)}^{\gamma _2}\ .\end{equation}

(8)

2.2.2 Buyer value under inflexible case

Following a similar reasoning, the rigid buyer value

{B}_r( x )

satisfies the following second-order ordinary differential equation:

\begin{equation}r{B}_r\ \left( x \right) = \frac{{{\sigma }^2}}{2}\ {x}^2{B}_r^{^{\prime\prime}}\left( x \right) + \left( {r - \delta } \right)x{B}_r^{\prime}\left( x \right) + \left( {x{Q}^{\varepsilon + 1} - wQ - {C}_b} \right) - m\left( {{P}_sQ\ - {D}_r\left( x \right)} \right).\end{equation}

(9)

The last two terms of Equation (9) represent the cash flows of the inflexible buyer firm. The first of these two terms captures the profits of the buyer comprising revenues equal to price $x{Q}^\varepsilon$ times quantity $Q$ net of variable costs $wQ$ and fixed costs ${C}_b$ , while the second one represents the rollover gains/losses of paying the principal, that is, the price of goods, $m{P}_SQ$ , and receiving the trade credit proceeds, $m{D}_r$ .

The solution of the above equation is given by:

\begin{equation}{B}_r\ \left( x \right) = \left( {\frac{{x{Q}^{\varepsilon + 1}}}{\delta } - \frac{{wQ + {C}_b}}{r}} \right)\ - {D}_r\left( x \right) + A_1{x}^{{\beta }_1} + A_2{x}^{{\beta }_2},\end{equation}

(10)

where

{D}_r( x )

is given in Equation (8) and the exponents

{\beta }_1

and

{\beta }_2

are given by:

\begin{equation}{\beta }_1 = \frac{1}{2}\ - \frac{{\left( {r - \delta } \right)}}{{{\sigma }^2}} + \sqrt {{{\left( {\frac{{\left( {r - {{\delta}}} \right)}}{{{\sigma }^2}} - \frac{1}{2}} \right)}}^2 + \frac{{2r}}{{{\sigma }^2}}} &gt; 1{\mathrm{\ ,}}\end{equation}

(11a)

\begin{equation}{\beta }_2 = \frac{1}{2}\ - \frac{{\left( {r - {{\delta}}} \right)}}{{{\sigma }^2}} - \sqrt {{{\left( {\frac{{\left( {r - {{\delta}}} \right)}}{{{\sigma }^2}} - \frac{1}{2}} \right)}}^2 + \frac{{2r}}{{{\sigma }^2}}} &lt; 0.\end{equation}

(11b)

The particular solution (first two terms in Equation 10) captures the perpetuity value of the buyer accounting for revenues, operating costs and repayment of credit, while the additional terms capture the buyer's default option. We provide details on the derivation of the particular solution in Appendix A. The constant terms A₁ and

A_2

are determined by applying the following boundary conditions:

\begin{equation}\mathop {{\mathrm{lim}}}\limits_{x \to \infty } {B}_r\ \left( x \right) = \left( {\frac{{x{Q}^{\varepsilon + 1}}}{\delta } - \frac{{wQ + {C}_b}}{r}} \right)\ - \frac{{m{P}_SQ}}{{r + m}},\end{equation}

(12a)

\begin{equation}{B}_r\left( {{x}_{Br}} \right) = 0.\end{equation}

(12b)

The first condition (12a) implies that the buyer's value is the present value of net cash flows (first term) minus the (risk-free) value of credit in the absence of default risk. Condition (12b) implies that the buyer's value in the event of bankruptcy becomes zero. We thus obtain the following solution for the rigid buyer value:

\begin{equation}{B}_r\ \left( x \right) = \left( {\frac{{x{Q}^{\varepsilon + 1}}}{\delta } - \frac{{wQ + {C}_b}}{r}} \right)\ - {D}_r\left( x \right) + \left( {{V}_B - \frac{{{x}_{Br}{Q}^{\varepsilon + 1}}}{\delta } + \frac{{wQ + {C}_b}}{r}} \right)\ {\left( {\frac{x}{{{x}_{Br}}}} \right)}^{{\beta }_2}.\end{equation}

(13)

The optimal default threshold is obtained by applying the following smooth pasting condition:

\begin{equation}\frac{{\partial {B}_r}}{{\partial x}}\ {|}_{x\ = {x}_{Br}\ \left( Q \right)} = 0.\end{equation}

(14)

Applying this smooth pasting condition, we obtain the following default threshold:

\begin{equation}{x}_{Br}\left( Q \right)\ = \frac{\delta }{{{Q}^{\varepsilon + 1}\left( {1 - {\beta }_2} \right)}}\ \left[ {{\gamma }_2\left( {{V}_B - \frac{{m{P}_SQ}}{{r + m}}} \right) - {\beta }_2\left( {{V}_B + \frac{{wQ + {C}_b\ }}{r}} \right)} \right].\end{equation}

(15)

The buyer also chooses the optimal capacity/quantity at time zero. The optimal

Q

maximizes

{B}_r( {{x}_0} )

net of capacity installment costs and therefore satisfies:

\begin{equation} \ \frac{\partial \left({B}_{r}\left({x}_{0}\right)-\kappa {Q}^{\eta}\right)}{\partial Q}=0. \end{equation}

(16)

This condition results in a nonlinear implicit equation (see Appendix A) that has no closed-form solution. Given the nonlinearity of this equation, this maximization problem is solved numerically. We run a dense grid search of Q choices for the buyer. Among the grid of Q choices created we then select the choice that maximizes the rigid buyer firm value.

2.3 Flexible case

2.3.1 Trade credit value under flexible case

Although the buyer firm has operational flexibility and can temporarily shut down, we follow Ritchken & Wu (2021), who model corporate debt and assume that the firm continues to make debt/trade credit payments in idle mode. This would be the case for example if the supplier imposes contract clauses similar to debt covenants (e.g., see Iancu et al., 2017) and thus does not resume credit if payments are interrupted. Thus, trade credit value will be derived in a similar fashion as in the inflexible case:

\begin{equation}{D}_f\ \left( x \right) = \frac{{m{P}_SQ}}{{r + m}}\ - \left( {{V}_B - \frac{{m{P}_SQ\ }}{{r + m}}} \right){\left( {\frac{x}{{{x}_{Bf}}}} \right)}^{\gamma _2}\ {\mathrm{.}}\end{equation}

(17)

However, the value of trade credit for the flexible firm ${D}_f( x )$ will generally be different than the inflexible one ${D}_r( x )$ because the optimal quantity and the default threshold chosen by the buyer might be different, as well as the optimal maturity selected by the supplier.

By focusing on the case where the buyer continues to make payments in idle mode we highlight the positive effect of operating flexibility on trade credit (i.e., by reducing supplier's risk exposure). This differs from Iancu et al. (2017) who focus on risk-shifting incentives of flexibility in replenishing or liquidating inventory, which hurt suppliers and result in increased borrowing costs. They demonstrate, however, that simple financial covenants can limit these agency conflicts between the buyer and its suppliers, and hence our focus on the positive effects of flexibility.

2.3.2 Buyer value under flexible case

When the buyer firm has operational flexibility and can temporarily shut down, buyer value will have two operating regions:

\begin{equation}{B}_1\ \left( x \right) = \frac{{x{Q}^{\varepsilon + 1}}}{\delta }\ - \frac{{wQ}}{r} - \frac{{{C}_b}}{r} - {D}_f\left( x \right) + {A}_3{x}^{{\beta }_2},\;x &gt; \overline {x\ } ,\end{equation}

(18a)

\begin{equation}{B}_0\ \left( x \right) = \ - \frac{{{C}_b}}{r} - {D}_f\left( x \right) + {A}_4{x}^{{\beta }_1} + {A}_5{x}^{{\beta }_2},\;\ x \le \bar{x}.\end{equation}

(18b)

Equation (18a) applies to the active mode, while Equation (18b) corresponds to the idle mode. The firm switches from active to idle more or vice versa when the price reaches the variable cost, that is, the threshold

\overline {x\ } = \ w

.7 The first four terms in Equation (18a) capture the discounted value of the cash flows net of variable costs, fixed costs and trade credit payments. The last term in this equation captures the buyer's option to switch to idle mode. Similarly, the first two terms in Equation (18b) capture the net cash flows of the buyer, while the third term adjusts for the option to switch to full-scale production, and the last term adjusts for the option to default. The constants

{A}_{\mathit{3}}

{A}_{\mathit{4}}

and

{A}_{\mathit{5}}

, and the optimal threshold

{x}_{Bf}

are determined from the following value matching and smooth pasting conditions:

\begin{equation}{B}_0\ \left( {\bar{x}} \right) = {B}_1\ \left( {\bar{x}} \right),\end{equation}

(19a)

\begin{equation}{B}_0\ \left( {{x}_{Bf}} \right) = \ 0,\end{equation}

(19b)

\begin{equation}B_0^{\prime}\ \left( {\bar{x}} \right) = B_1^{\prime}\ \left( {\bar{x}} \right),\end{equation}

(20a)

\begin{equation}B_0^{\prime}\ \left( {{x}_{Bf}} \right) = \ 0.\end{equation}

(20b)

The buyer switches from the active to the idle mode (and vice versa) when the demand shock drops (raises) to $\bar{x}$ (Equation 19a). The buyer function value needs to be continuously differentiable at this point (Equation 20a). When the demand shock drops to ${x}_{Bf}$ , the buyer firm defaults and its value becomes zero (Equation 19b). As the default threshold is optimally chosen, the smooth pasting condition applies (Equation 20b).

The expressions of the constants

{A}_{\mathit{3}}

{A}_{\mathit{4}}

and

{A}_{\mathit{5}}

are relegated to Appendix A. The optimal default threshold is the implicit solution of the following equation:

\begin{equation}{\beta }_1{A}_4x_{Bf}^{{\beta }_1 - 1} + {\beta }_2{A}_5x_{Bf}^{{\beta }_1 - 1} - \frac{{{\gamma }_2}}{{{x}_{Bf}}}\ \left( {{V}_B - \frac{{m{P}_SQ}}{{r + m}}} \right) = 0.\end{equation}

(21)

Finally, the buyer optimally chooses the quantity to produce at time zero:

\begin{equation} \ \frac{\partial \left({B}_{1}\left({x}_{0}\right)-\kappa {Q}^{\eta}\right)}{\partial Q}=0. \end{equation}

(22)

This condition results in a nonlinear implicit equation that has no closed-form solution. We thus solve it numerically by performing a dense grid search for Q choices, among which we select the one that maximizes the flexible buyer firm value net of the capacity cost. Additionally, we always ensure that the flexible buyer starts operations at full capacity, not in idle mode by setting ${x}_0$ sufficiently high.8

2.4 Interactions between the buyer and the supplier

In this section, we describe the interactions between the buyer and the supplier. Following Koussis & Silaghi (2020), we assume that for a given trade credit maturity, the buyer optimally selects capacity

Q

(the quantity of goods ordered from the supplier), and the default threshold that maximize buyer value. The supplier internalizes how his choice of trade credit maturity influences the buyer's optimal choices of

Q

and

{x}_B

, and optimally selects the trade credit maturity that maximizes trade credit value. These interactions are formally described in the following maximization problem:

\begin{equation} \def\eqcellsep{&}\begin{array}{@{}*{1}{c}@{}} {{\mathrm{MAX}}\;D\left( x \right)}\\ {\left( {\frac{1}{m}} \right)} \end{array} \end{equation}

(23)

\begin{equation*} \def\eqcellsep{&}\begin{array}{@{}*{1}{c}@{}} {{\mathrm{s}}{\mathrm{.t}}{\mathrm{.\ MAX\ }}B\left( x \right)}\\ {Q,{x}_B} \end{array} .\end{equation*}

Given the nonlinearity of the equations involved, this maximization problem is solved numerically. We run a dense grid search of (1/m) choices for the supplier subject to the optimal solutions $Q$ and ${x}_B$ that maximize the buyer's value. Among the grid of (1/m) choices created we then select the choice that maximizes the trade credit value. We do this for both the rigid and flexible case and compare the results to understand the effect of flexibility on trade credit values and maturity.

3 NUMERICAL RESULTS

We consider the following base case parameters: $r = 0.05$ , $\delta = 0.03$ , ${c}_f = 30$ , ${c}_h = 0$ , $w = 7$ , ${P}_S = 5$ , $\sigma = 0.15$ , $x = 8.5$ , $k = 5$ , $\eta = 2$ , b = 0. Our base parameters used for r, δ and σ are in line with other real options models (e.g., Hackbarth & Mauer, 2011; Mauer & Sarkar, 2005).9 Our base case value for η is the same as in Nishihara et al. (2019), while our base case parameters for x and ${c}_f$ were chosen alongside κ and η that define optimal order quantity levels to allow the buyer to operate with positive value. Note that ${c}_h$ is assumed initially to be zero to see more clearly the impact of initial capacity choices (we perform sensitivity subsequently on ${c}_h$ ). We assume initially no recovery at default (b = 0) which is a reasonable assumption as suppliers typically have low priority when buyer firm defaults compared to other claimants. The variable cost w is chosen to allow for a reasonable, albeit not significantly high gross profit margin (x-w) which is commensurate with assumptions used in other related studies (e.g., Hagspiel et al., 2016). We have no empirical benchmark for ${P}_S$ and we provide sensitivity results that reveal the impact of supplier pricing on trade credit duration levels, trade credit quantities and buyer and trade credit values.

In all figures, we vary m with increments of 0.1 and consider a minimum maturity (1/m) of 0.1 and maximum maturity (1/m) of 1 year. Unless otherwise stated, Q is optimally chosen by the buyer firm, where we use increments for Q search of 0.01. In the panels showing the trade credit values we illustrate with vertical lines (blue for the flexible firm and red for the rigid firm) the optimal trade credit duration that maximizes trade credit value. Moreover, in Table 1 we summarize the results for the optimal trade credit maturity selected by the supplier.

TABLE 1. A comparison of the flexible and rigid firm solutions.

	Buyer (Net)	Trade	Q	Maturity (1/m)	Maturity (in days)	x_B	Lev
Flexible
Base case	485.388	71.654	14.51	0.25	91	4.308	0.13
High σ (σ = 0.35)	1242.501	89.915	18.33	0.385	140	1.837	0.07
Low P_s (P_s = 3)	524.995	44.017	14.77	0.133	49	4.069	0.08
High η (η = 2.2)	124.186	41.14	8.34	0.27	99	5.151	0.25
Higher b (b = 0.2)	492.934	71.98	14.54	0.2	73	4.208	0.13
Low w (w = 5)	1020.352	88.796	17.93	0.192	70	3.656	0.08
High c_h (c_h= 0.5)	358.516	66.303	13.44	0.27	99	4.665	0.16
Rigid
Base case	433.275	68.39	13.83	0.222	81	4.805	0.14
High σ (σ = 0.35)	1016.144	81.565	16.55	0.286	104	2.701	0.07
Low P_s (P_s = 3)	471.671	42.001	14.09	0.128	47	4.606	0.08
High η (η = 2.2)	105.992	39.773	8.04	0.213	78	5.496	0.27
Higher b (b = 0.2)	439.798	68.718	13.86	0.169	62	4.75	0.14
Low w (w = 5)	1003.619	87.991	17.75	0.172	63	3.854	0.08
High c_h (c_h= 0.5)	322.228	63.553	12.87	0.25	91	5.041	0.16

Note: We consider the following base case parameters: $r\ = \ 0.05$ , $\delta \ = \ 0.03$ , ${c}_f = \ 30$ , ${c}_h = \ 0$ , $w\ = \ 7$ , ${P}_S = \ 5$ , $\sigma \ = \ 0.15$ , $x\ = \ 8.5$ , $k\ = \ 5$ , $\eta \ = \ 2$ , $b=0$ , $\varepsilon =0$ . Buyer (Net) denotes buyer value net of capacity cost. Q is optimally chosen by the buyer firm. The increment for Q search is 0.01. We vary m with increments of 0.1 and minimum (1/m = 0.1) and maximum maturity (1/m) of 1 year. The optimal maturity (trade credit horizon) is chosen by the supplier firm by maximizing trade credit value. Maturity (days) is calculated by multiplying (1/m) with 365 and rounded to the integer. x_B denotes the bankruptcy threshold. Lev. shows leverage ratio defined as trade credit relative to the sum of net of capacity value of buyer plus trade credit.

3.1 Baseline results

Figure 2 shows our base case results. In the first panel, we observe that extensions of trade credit duration improve the value for both the rigid and flexible firm, albeit the impact of longer trade credit horizons on the value of the flexible firm is more significant. This is reflected in the quantity choices of the two firms where the flexible firm chooses higher quantities for all credit duration levels compared to the rigid firm, however, the differences between the two firms are increasing at higher durations. This result is in line with the findings of Hagspiel et al. (2016) who show that optimal capacity is larger for a flexible firm. We also observe that in terms of default thresholds the flexible firm delays default more compared to the rigid firm and the differences become more significant for longer horizons. This result is in line with the results of Ritchken & Wu (2021) who focus on optimal capital structure decisions of flexible compared to inflexible firms. However, while Ritchken & Wu (2021) find that the flexible firm uses less debt (a lower optimal coupon), we find that the flexible firm uses more trade credit. The reason is that lower default risk in our setting results in higher order quantities, which increases trade credit values. Thus, when comparing trade credit values, we observe that the flexible firm has a higher trade credit value compared to the rigid one.

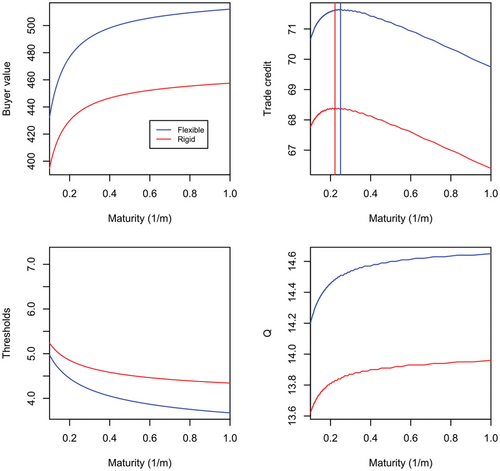
As we focus on finite debt, our model allows us to derive novel results regarding the impact of flexibility on trade credit maturity. Interestingly, our analysis reveals that trade credit value has a hump shape for both the flexible and rigid firm that results in an optimal trade credit horizon. This is driven by the trade-offs involved in the supplier's choice of increasing the duration of credit. Koussis & Silaghi (2020) analyze the case of an inflexible firm and show that for the short horizons typical for trade credit (i.e., less than 1 year) and a fixed Q, $\frac{{\partial D}}{{\partial m}} > 0\$ and thus the supplier would always prefer to increase m, that is, reduce maturity, so as to receive the payment as early as possible. However, increasing credit duration allows the buyer to order more (Q increases) and results in delayed default and thus an extended period where the supplier trades with the buyer. This effect improves the supplier value, that is, it can be shown that $\frac{{\partial D}}{{\partial Q}} > 0$ (see Koussis & Silaghi, 2020). The interaction of these two opposite effects determines the optimal credit duration. In this paper, we show that the impact of extending credit duration on order quantities and default is more significant for the flexible firm, hence the optimal trade duration provided by the supplier is generally longer for the flexible firm. Table 1 summarizes the results for the base case optimal solution for the flexible and rigid firm, respectively.

Based on the analysis above, we summarize the following first result:

Result 1 (Flexible vs. rigid firm trade credit and duration). A flexible firm obtains higher order quantities, has higher trade credit value and obtains a larger duration of credit compared to the inflexible firm.

In Table 1, the base case shows that buyer value is enhanced under the flexible case compared to the rigid one, reflecting the extra value of operating flexibility of the flexible firm over the rigid firm and also the larger quantity and order duration that the flexible firm enjoys from the supplier. From Table 1, we observe that under the base case the flexible buyer obtains 5% more trade credit and order quantities compared to its rigid counterpart. The flexible firm also obtains longer trade credit durations from the supplier firm (about 91 days compared to 81 for rigid). Finally, the flexible firm defaults later than the rigid firm.

It is important to emphasize that extensions of trade credit duration may not be achieved (for either the flexible or rigid case) if the buyer firm free rides on trade credit extensions by ordering more from other suppliers (e.g., see Chod et al., 2019). This effect is not considered here, however, our analysis is consistent because in untabulated results we show that when the supplier does not anticipate changes in order quantities (Q is fixed irrespective of trade credit horizon) then the supplier does not extend credit duration (asks for immediate payment).

Previous literature on the effect of operational flexibility on capital structure (Ritchken & Wu, 2021) also shows the effect of operational flexibility on leverage ratios, not only on debt levels. In particular, they find that leverage ratios are higher for inflexible compared to flexible firms. In Figure 3, we examine trade credit leverage defined as the ratio of trade credit over the sum of trade credit and buyer value.

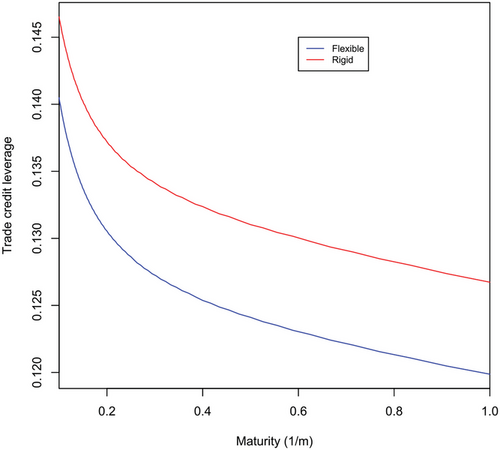
Consistently with this work, and despite the fact that trade credit is larger for flexible firms, we find the following result.

Result 2 (Trade credit leverage). Trade credit leverage ratio is higher for the inflexible compared to the flexible firm irrespective of the trade credit maturity level provided by the supplier.

Result 2 is due to the fact that flexibility increases the buyer firm value more than it increases its trade credit value. The figure also shows that the trade credit leverage ratio differences widen for longer trade credit maturities. The trade credit leverage ratios obtained are in line with empirical evidence. According to Rajan & Zingales (1995), accounts payable constituted around 15% of the total book value for the average nonfinancial firm in 1991. Table 1 shows that the resulting leverage ratios for the flexible and rigid firm arising from the supplier's choice of the optimal credit duration are 12.5% and 13.6%, respectively.

Harris (2015) finds that increases in financial flexibility are associated with higher levels of trade credit. Our model predicts that operational flexibility is also positively related to trade credit levels. We are not aware of empirical studies on the relationship between operational flexibility and trade credit duration. Our results are broadly in line with the findings of Klapper et al. (2012), who document longer trade credit maturities for more credit worthy (flexible) buyers. MacKay (2003) finds that flexible firms have lower leverage ratios and shorter maturities for corporate debt. However, he does not analyze trade credit.

3.2 Sensitivity analysis

We now provide some sensitivity analysis of our baseline results with respect to important parameters of the model that provides further insights on how flexibility affects trade credit duration and order quantities.

Figure 4 shows that a higher volatility of downstream demand results in buyer firms (both inflexible and flexible) choosing higher order quantities for all trade credit horizons compared to the case of lower volatility (see Figure 2). Thus, we find that higher volatility improves both trade credit (supplier) and buyer values. This may appear surprising at first, however, it highlights the real option effect of volatility where buyer firms hold a valuable limited liability option (default option). In addition to the limited liability option, the flexible's firm operating flexibility option increases further for higher volatility. We find that these more valuable real options occurring under higher volatility create an incentive for the supplier firm to extend trade credit duration more for the flexible firm because this can marginally lead to a more significant improvement in order quantity.

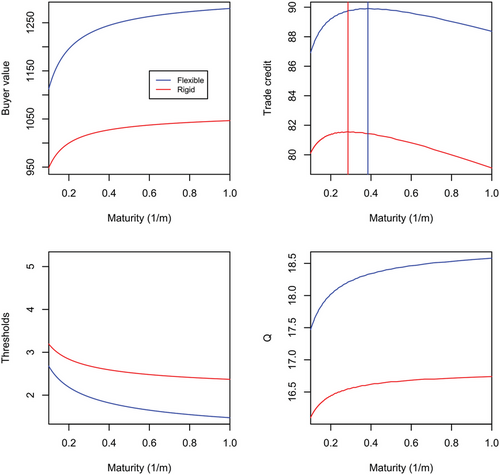
From Table 1 that summarizes the optimal solutions based on the supplier's choice of trade credit maturity we observe that higher volatility allows the flexible buyer firm to obtain a more significant increase in trade credit (10% vs. 5% compared to the base case) and a more significant increase in ordered quantities (11% vs. 5%) compared to the rigid firm. The supplier firm extends longer durations and provides higher quantities to the flexible firm under higher volatility of demand by exploiting the more significant upside potential while the downside risk is limited by the flexible firm's ability to truncate losses in the idle mode and its further delay of default (see x_B decline in Table 1). Finally, we observe, as expected, that with higher volatility trade credit leverage is lower for both the flexible and rigid firm. This reflects the more significant increase in buyer's (equity) value that arises from higher real option value compared to trade credit values increases under higher volatility.

We summarize the following main result regarding volatility.

Result 3 (Volatility effect). When downstream demand volatility is higher, the optimal order quantity, trade credit and duration increase and the duration of credit becomes higher for the flexible firm compared to the inflexible firm.

Result 3 provides important predictions relating to the value of credit and the provision of credit in different industries. In industries where downstream volatility is higher (e.g., technology products) we expect to see higher installed capacities by buyer firms and longer durations provided by supplier firms. For example, Tesla installed a significant capacity for the production of electric cars when demand for electric cars remained highly uncertain (see Randall, 2021). This high upside potential that can benefit suppliers is reflected in the new deal that Panasonic struck with Tesla relating the provision of battery for its electric cars (see Yifan, 2021). Although the agreement details are not revealed, the two parties revealed that Tesla now enjoys better terms from its supplier.

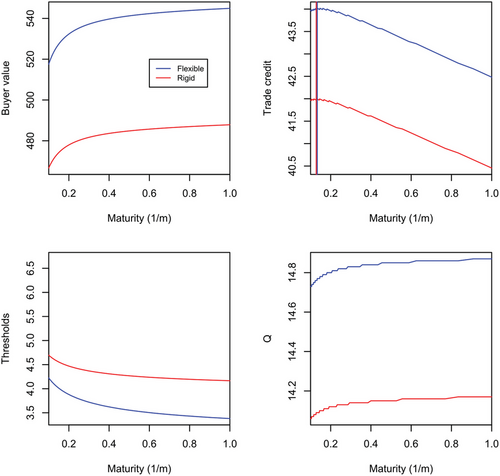
Figure 5 provides sensitivity with respect to prices P_S per unit of credit charged by the supplier. In this case we observe that for lower prices the order quantities increase relative to the base case (see Figure 1), however, the impact of extending trade credit duration on optimal selected Q becomes of less importance. Indeed, optimal Q becomes flat with respect to the trade credit duration for lower prices P_S. The same happens for the default thresholds that appear relatively flatter with respect to the trade credit duration. As for lower prices charged the buyer naturally orders higher quantities, the supplier does not need to extend such a high trade credit maturity to incentivize the buyer to order higher quantities. This results in a shortening of the credit horizon for both the flexible and rigid firm. Thus, the optimal trade durations differences between the flexible and rigid firm are of less importance (see Table 1 for the resulting optimal solutions under this case).

We summarize the following result:

Result 4 (Supplier prices). The lower the prices per unit of credit charged by the supplier the higher the order quantity for both the flexible and rigid firm and the shorter the duration of credit provided to both the flexible and rigid firm.

Our findings in Result 4 relating the effect of prices charged by suppliers P_S highlight that in industries with less intense competition between suppliers (higher prices P_S charged) for provided credit, for example, for markets of specialized inputs in technology products, trade credit duration may be a more effective mechanism for suppliers to affect order quantities of the buyer firms. On the contrary, when supplier firms face intense competition resulting in lower prices or face cash flow concerns such as in Molina and Preve (2012), the optimal policy is to reduce trade credit and trade credit duration.

Figure 6 explores the impact of higher capacity constraints (η). For brevity we do not show the sensitivity results with respect to per unit cost of capital, k that has similar implications. We observe that a longer credit duration by the supplier can have a less significant positive impact on order quantities for the rigid buyer when it faces more severe capacity constraints (a higher η). The optimal duration of credit is thus slightly lower for a higher η for the rigid firm. Although higher capacity constraints also have a negative impact for the flexible firm, we observe an extension of trade credit duration for the flexible firm because this helps the supplier retain quantities at the largest possible level. Table 1 summarizes the numerical solutions that confirm the above results showing that the difference between the flexible and rigid credit duration is 21 days (99 vs. 78) compared to 10 days under the base case (91 vs. 81). We summarize the following finding.

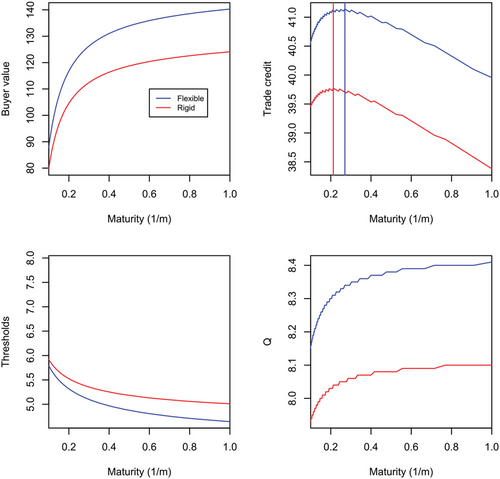
Result 5 (Capacity constraints). With more significant capacity constraints we observe a larger difference between extending duration for the flexible versus the inflexible firm.

Figure 7 explores the impact of a higher recovery rate of supplier value in the event of default (b). When recovery rates are higher, the buyer orders higher quantities and postpones default. This results in an increase in trade credit value. However, the impact of extending trade credit maturity on optimal order quantities becomes less important. Thus, the trade credit value is maximized at shorter credit durations (see also Table 1).

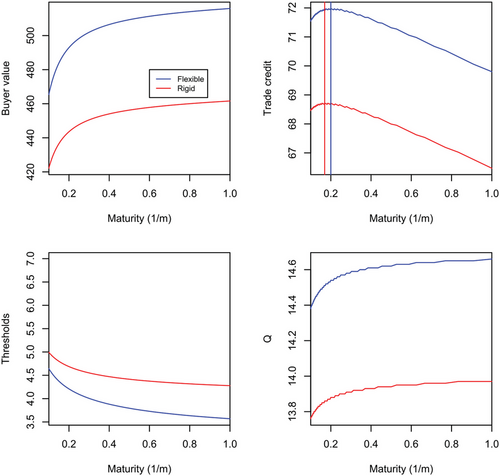
Result 6 (Recovery value). As recovery becomes more significant trade credit value increases and the supplier will optimally select shorter maturities irrespective of flexibility levels.

The positive effect of recovery values on trade credit is consistent with evidence in Costello (2013), who shows that an improvement in suppliers’ rights to the liquidation value of collateral results in an increase in the amount of credit. This is also broadly in line with Petersen & Rajan's (1997) results who find higher levels of trade credit value when buyers have higher credit ratings (as it is reasonable to assume that higher recovery values would improve ratings).

Figure 8 shows the impact of lowering the variable production costs w. We observe that extensions in trade credit duration create a significant impact on firms’ values, however, the marginal impact appears more important for short maturities. This results in a shortening of the trade credit maturity for both the flexible and rigid firm as can be seen from Table 1.

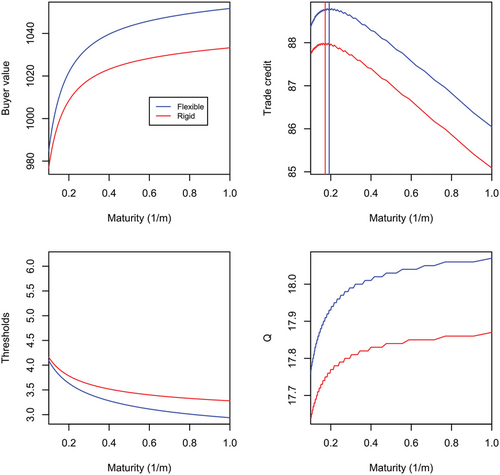
Hence, we summarize the following:

Result 7 (Profit margin of the buyer firm). When profit margins of the buyer increase (w gets lower), the optimal credit duration is shorter for both the flexible and rigid firm and their differences become less important.

In untabulated results, we observe a similar effect when we analyze a higher x that has a similar effect on gross profit (operating) margins.

Figure 9 shows the impact of higher capacity holding cost (h). A higher holding cost of capacity reduces installed capacity and order quantities for both the flexible and rigid buyer firms. Extending trade credit duration mitigates the impact on order quantities and we thus observe that the supplier firm will extend credit duration (see Table 1).

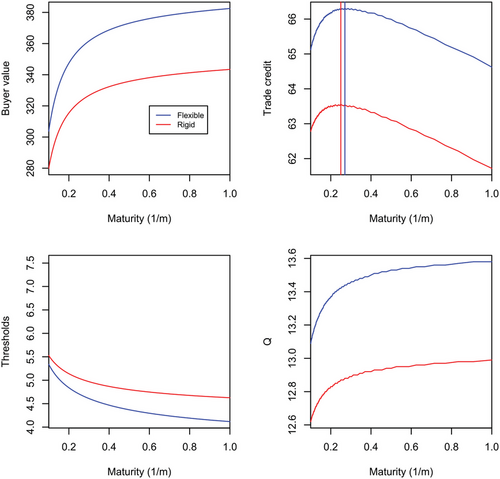
The capacity holding cost is a fixed cost that will be incurred by both the flexible and rigid firm, thus despite the flexible firm's ability to truncate variable costs in the idle mode this cost will still need to be incurred by the flexible firm. We thus observe:

Result 8 (Higher capacity holding cost). The maturity differences in the trade credit horizon become less significant between the rigid and flexible firm the higher the capacity holding costs.

In Table 2, we discuss the effect of demand elasticity. To show the implications of our results for different type of products, note that the elasticity of demand is usually defined as $\frac{1}{{| \varepsilon |}}$ showing the percentage reduction in quantity for a percentage increase in price. Thus, the higher the absolute value of ε the more inelastic the demand. This reflects the case of a necessity product where a given change in prices brings smaller changes in quantities. The results imply then that for more inelastic demand products buyers install lower capacity and suppliers provide longer credit horizons. These effects hold for both the flexible and rigid firms. However, we observe that the extension of credit difference between flexible and rigid firms becomes more pronounced for very inelastic products. We summarize the following result regarding the effect of elasticity of demand on trade credit maturity.

TABLE 2. Flexible and rigid firm solutions: The effect of elasticity of demand.

	Buyer (Net)	Trade	Q	Maturity (1/m)	Maturity (in days)	x_B	Lev	Price
Flexible
Base case	485.388	71.654	14.51	0.250	91	4.308	0.125	8.50
ε = −0.02	312.266	62.305	12.65	0.303	111	4.622	0.166	8.08
ε = −0.04	175.649	53.894	10.96	0.333	122	5.039	0.235	7.72
ε = −0.06	74.354	46.183	9.44	0.417	152	5.442	0.383	7.43
Rigid
Base case	433.275	68.390	13.83	0.222	81	4.805	0.136	8.50
ε = −0.02	265.301	58.780	11.9	0.244	89	5.167	0.181	8.09
ε = −0.04	142.616	50.363	10.23	0.303	111	5.499	0.261	7.75
ε = −0.06	48.590	42.844	8.72	0.313	114	5.942	0.469	7.46

Note: We consider the following base case parameters: $r\ = \ 0.05$ , $\delta \ = \ 0.03$ , ${c}_f = \ 30$ , ${c}_h = \ 0$ , $w\ = \ 7$ , ${P}_S = \ 5$ , $\sigma \ = \ 0.15$ , $x\ = \ 8.5$ , $k\ = \ 5$ , $\eta \ = \ 2$ , $b=0$ . Buyer (Net) denotes buyer value net of capacity cost. Q is optimally chosen by the buyer firm. The increment for Q search is 0.01. We vary m with increments of 0.1 and minimum (1/m = 0.1) and maximum maturity (1/m) of 1 year. The optimal maturity (trade credit horizon) is chosen by the supplier firm by maximizing trade credit value. Maturity (days) is calculated by multiplying (1/m) with 365 and rounded to the integer. x_B denotes the bankruptcy threshold. Lev. shows leverage ratio defined as trade credit relative to the sum of net of capacity value of buyer plus trade credit.

Result 9 (Elasticity of demand). The maturity differences in the trade credit horizon become more significant between the rigid and flexible firm for more inelastic products.

4 EXTENSIONS

In this section, we extend the benchmark model to account for several alternative modeling assumptions and extensions. First, we include switching costs into the framework for the flexible firm when switching from active to idle mode and the reverse. Second, we extend the benchmark model to account for the optimal entry timing of firms. Third, we consider debt financing together with trade credit and analyze their interaction. Finally, we model a non-cooperative Nash bargaining game between the buyer and supplier, as an alternative to the Stackelberg leader–follower game.

4.1 Switching costs

So far, we have assumed that the flexible firm can switch between the active and the idle mode without any costs. We now introduce switching costs into the framework. Our analysis in this section extends other real options models with switching costs by adding finite horizon trade credit (e.g., Dixit & Pindyck, 1994, ch.7; Charalambides & Koussis, 2018). Switching costs from idle to active mode may reflect costs related to restoring operations and re-establishing customer royalty and brand-name while costs from active to idle mode may reflect legally binding termination payments, for example, compensation for terminating contracts to workers (see Charalambides & Koussis, 2018). We have the following adjustments to the previous framework. The flexible firm starts production at $x > {x}_H$ and then may temporarily stop production when the demand shock reaches the threshold ${x}_L$ . When switching to this lower region, the buyer firm needs to incur a switching cost ${\varepsilon }_{10}$ . While being in this operating mode, the firm has the option to resume full-scale operations when the demand shock increases and reaches ${x}_H$ (from below). In this case, the firm starts producing at full capacity again, and incurs a switching cost ${\varepsilon }_{01}$ . On the contrary, if the demand shock falls further, the firm may default, thus ${x}_B < {x}_L < {x}_H$ .10 The zone between ${x}_H$ and ${x}_L\$ is the hysteresis zone in the presence of trade credit because within that region the firm remains active if previously in the active mode or idle if previously in the idle mode (e.g., see Dixit & Pindyck, 1994, chapter 7, for the simpler cases without trade credit). This is intuitive because the firm postpones entering a different mode to avoid incurring the switching costs involved. Compared to the framework without switching costs, the switching thresholds satisfy ${x}_L < w < {x}_H$ . The mathematical details of the model including boundary conditions and buyer value are provided in Appendix B.

In Figure 10, we investigate a case with positive switching costs ${\varepsilon }_{10} = {\varepsilon }_{01} = 20$ . Indeed, the results show that when switching costs are positive there is a hysteresis zone created due to the difference between ${x}_H$ and ${x}_L$ . The firm enters the idle mode once $x$ first crosses ${x}_L$ from above. If $x$ crosses ${x}_L\$ again from below, the firm remains in the idle mode until ${x}_H$ is now reached from below.

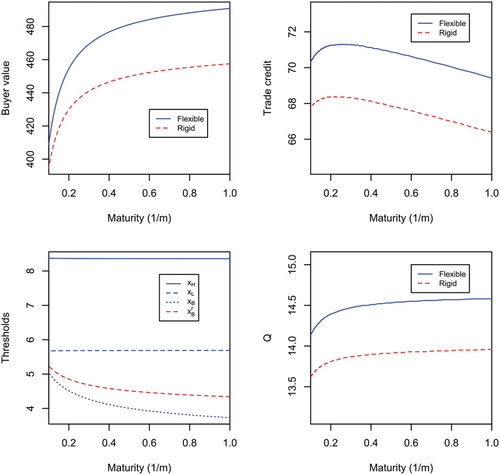
We summarize the following result:

Result 10a (Fixed switching costs with varying trade credit horizon). The operating policies of the firm regarding the utilization of operating flexibility remain unchanged irrespective of the trade horizon, that is, $\ {x}_H$ and ${x}_L$ do not depend on m. The flexible firm in the presence of switching costs only adjusts the default trigger as the trade credit horizon is altered similarly to the changes taking place for the fully flexible firm.

Compared to the fully flexible firm (no switching costs), the flexible firm with positive switching costs has slightly lower order quantities and trade credit. The differences between the flexible firm with positive switching costs and the rigid firm thus remain (albeit become smaller).

Figure 11 shows sensitivity results of the model with switching costs in the special case where the switching costs are zero ( ${\varepsilon }_{01} = {\varepsilon }_{10} = 0$ ). The results confirm that in the case that switching costs are zero we obtain an identical solution to the flexible model because the optimal switching threshold is ${x}_H = {x}_L = w$ . We thus obtain the solutions of the fully flexible firm of the previous section.

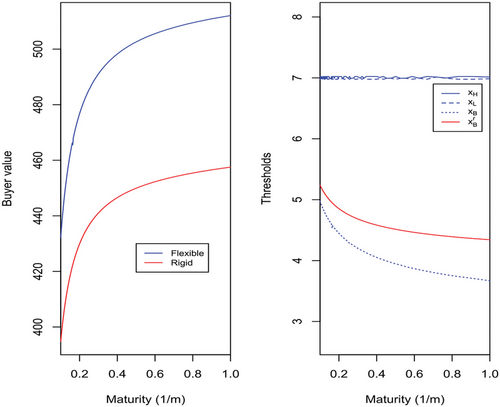
Figure 12 explores the effect of varying the switching costs for a given trade credit maturity.11 We summarize the following result.

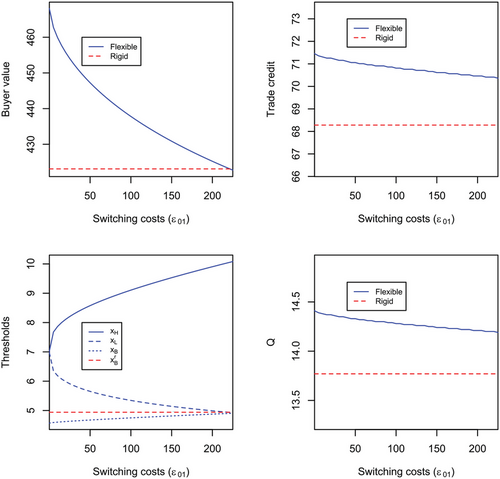
Result 10b (The effect of switching costs for given trade credit horizon). At higher switching costs the hysteresis zone widens, the value of trade credit and order quantities decreases and the flexible firm value decreases and converges to the rigid firm value.

Result 10b summarizes the findings relating the effect of switching costs. First, as the level of switching costs increases the hysteresis zone widens. This is intuitive because with higher switching costs the flexible firm postpones switching modes to avoid incurring the higher switching cost level. Second, higher switching costs decrease the value of trade credit and order quantities. However, note that the flexible firm retains higher trade credit and quantities even when switching costs are high. Third, we observe that the flexible firm value converges to the rigid firm value for a certain high level of switching costs. Notice that at that point of convergence of the flexible firm value to the rigid firm value, the idle threshold for the flexible firm converges to the default threshold.12

4.2 Entry timing of firms

In this section, we consider a rigid or flexible firm's optimal timing to enter the market at a threshold ${x}_I$ . Post entry, the rigid firm's trade credit and buyer values are those described in Subsection 2.2. For the flexible firm, we focus on the case with no switching costs, and hence post entry values are those provided in Subsection 2.3.2. Note that at the timing of entry, the flexible firm could enter either the idle or active mode. However, it is reasonable to assume that the firm starts in active mode because starting in idle mode, the firm incurs the capacity investment cost and also needs to incur the per-period operational cost ${C}_b$ without generating any revenue. Therefore, investment can only take place in the full capacity region (active mode). When demand is so low that the firm suspends production (idle mode), it is better for the firm to wait, thus no investment takes place, as the firm saves on investment expenses.13

Following standard steps in real options setting (e.g., see Dixit & Pindyck, 1994), the value of the option to enter the market

{B}_I( x )

(for either the rigid or flexible firm) satisfies the following second-order ordinary differential equation:

\begin{equation}r{B}_I\ \left( x \right) = \frac{{{\sigma }^2}}{2}\ {x}^2{B}_I^{^{\prime\prime}}\left( x \right) + \left( {r - \delta } \right)x{B}_I^{\prime}\left( x \right)\end{equation}

(24)

The general solution of the above claim

{B}_I( x )

can be expressed as a linear combination of two independent solutions (see Dixit & Pindyck, 1994, p. 142):

\begin{equation}{B}_I\ \left( x \right) = A_1\ {x}^{\beta _1} + A_2{x}^{\beta _2}\ .\end{equation}

(25)

For the flexible firm, the boundary conditions that need to be satisfied for the option to invest are the following:

\begin{equation}B_I^f\left( 0 \right) = 0,\end{equation}

(26)

\begin{equation}B_I^f\ \left( {{x}_I} \right) = {B}_1\ \left( {{x}_I} \right) - k{Q}^\eta .\end{equation}

(27)

Note that

{B}_1( {{x}_I} )

is the value of the flexible firm given by Equation (18a). Using the boundary condition in Equation (26) we obtain that

{A}_2 = 0

and using (27) we obtain that

{A}_1 = ( {{B}_1( {{x}_I} ) - k{Q}^\eta } )\ {( {\frac{1}{{{x}_I}}} )}^{{\beta }_1}

. Thus, the value of the investment option of the flexible firm, denoted as

B_I^f( x )

\begin{equation}B_I^f\ \left( x \right) = \left( {{B}_1\left( {{x}_I} \right) - k{Q}^\eta \ } \right)\ {\left( {\frac{x}{{{x}_I}}} \right)}^{{\beta }_1}.\end{equation}

(28)

To determine the optimal timing

{x}_I

we need to solve the following:

\begin{equation}B_I^{f\prime }\left( {{x}_I} \right) = B_1^{\prime}\left( {{x}_I} \right).\end{equation}

(29)

To optimize the quantity level, we run a numerical search for various $Q$ levels that satisfies (29) and choose the one that maximizes buyer's firm value in (28).

Using a similar reasoning as above, the rigid firm value with optimal timing to invest is given by:

\begin{equation}B_I^r\ \left( x \right) = \left( {{B}_r\left( {{x}_I} \right) - k{Q}^\eta \ } \right)\ {\left( {\frac{x}{{{x}_I}}} \right)}^{{\beta }_1}.\end{equation}

(30)

To determine the optimal timing

{x}_I

we use:

\begin{equation}B_I^{r\prime }\left( {{x}_I} \right) = B_r^\prime \left( {{x}_I} \right).\end{equation}

(31)

And to optimize the quantity level we run a numerical search for various $Q$ levels that satisfies (31) and choose the one that maximizes buyer's firm value in (30).

Table 3 discusses a numerical exercise comparing the flexible and rigid firms’ decisions regarding the timing of entry. For the sensitivity results, we assume a lower volatility of 8%, compared to that of the base case (which was of 15%), to allow for a more reasonable entry level. It is well-known in this setting of capacity choice, starting with Dangl (1999) (see also the discussion in Hagspiel et al., 2016), that investment thresholds explode quite rapidly with increasing volatility levels. The lower volatility level is also in line with our model's assumption of operating at full capacity upon entry, as shown in Hagspiel et al. (2016). Indeed, lower volatility makes it more likely that flexible firms enter at full capacity. For sensitivity analysis, we also assume a common trade credit maturity offered by the supplier firm for both the rigid and flexible firms of 90 days.14

TABLE 3. A comparison of entry decision of the flexible and rigid firm.

	Buyer (Option)	Q	Maturity (1/m)	Maturity (in days)	x_I	x_B
Flexible
	2845.396	316	0.247	90	95.170	5.428
Rigid
	2737.183	250	0.247	90	79.347	4.444

Note: We consider the following base case parameters: $r\ = \ 0.05$ , $\delta \ = \ 0.03$ , ${c}_f = \ 30$ , ${c}_h = \ 0$ , $w\ = \ 7$ , ${P}_S = \ 5$ , $\sigma \ = \ 0.08$ , $x\ = \ 8.5$ , $k\ = \ 5$ , $\eta \ = \ 2$ , $b=0$ , $\varepsilon =0$ . Buyer (Net) denotes buyer value net of capacity cost. Q is optimally chosen by the buyer firm. The increment for Q search is 1 unit. We set m = 0.247 the implied maturity in days is about 90 days where maturity (days) is calculated by multiplying (1/m) with 365 and rounded to the integer. x_B denotes the bankruptcy threshold.

The results indicate that the flexible firm delays investment more compared to the rigid firm. This allows the flexible firm to install higher capacity, which is in line with our previous findings that the flexible firm can operate at higher quantities. Our framework extends of the model of Hagspiel et al. (2016) by incorporating trade credit. In line with them, we find that the flexible firm delays more investment than the inflexible firm and installs higher capacity.

Result 11 (Entry timing of flexible and rigid firm for given trade credit horizon). The flexible firm delays investment more compared to the rigid firm and installs higher capacity upon entry to the market.

In addition to the above, we find that the flexible firm's default rate is set at slightly higher levels than the rigid firm, but accounting for the relatively higher value of revenues upon entry makes the flexible firm less likely to default. Finally, we note that accounting for the timing of entry to the market shows that a flexible firm can have a 4% markup on its value compared to a rigid firm counterpart.

4.3 Interactions of trade credit with debt

A recent literature points to the importance of jointly analyzing trade credit and debt both for understanding default risk (e.g., Cathcart et al., 2020; McGuinness et al., 2018; Molina & Preve, 2012) and for jointly determining the level of debt and trade credit, considering their interactions (e.g., see Shenoy & Willliams, 2017). In this section, we thus extend our model to incorporate interactions between debt financing and trade credit. We focus on the rigid firm and provide some insights on the impact of flexibility at the end of the section.

Assume that in addition to trade credit, the firm considers issuing long-term debt with coupon

R

. To introduce the incentives for the firm to use debt for tax shield purposes we introduce corporate taxes

\tau

on corporate profits. Define

{x}_D

as the bankruptcy threshold that is optimally chosen by the buyer firm. Following the stricter covenant requirements placed by lenders compared to trade creditors, we assume that debt holders have priority over trade creditors over the firm's assets in the event of bankruptcy (Zhang, 2019). Thus, in the event of bankruptcy, debt holders recover the minimum of the fraction

{b}_D

of unlevered assets or the remaining (perpetual) value of coupons, that is, at bankruptcy they recover:

\begin{equation}{L}_{r\ }\ \left( {{x}_D} \right) = {\mathrm{\ min}}\left( {{b}_D{V}_D,\frac{R}{r}} \right),\end{equation}

(32)

where

{b}_D

captures proportional recovery value of unlevered assets in the event bankruptcy, and

{V}_D\

represents the value of unlevered assets (see Equation 34).15 Thus, following Leland (1994), the value of debt

{L}_r( x )

is a contingent claim on the firm's cash flows and its value is given by:

\begin{equation}{L}_r\ \left( x \right) = \ \frac{R}{r} + \left( {{L}_{r\ }\left( {{x}_D} \right) - \frac{R}{r}} \right){\left( {\frac{x}{{{x}_D}}} \right)}^{{\beta }_2},\end{equation}

(33)

where

{\beta }_2

was given in Equation (11a). Following the capital structure literature, we assume that debt holders recover a fraction

{b}_D

of the value of unlevered assets

{V}_D

defined as:

\begin{equation}{V}_D = {\mathrm{max}}\left( {\left( {\frac{{{x}_D{Q}^{\varepsilon + 1}}}{\delta } - \frac{{wQ + {C}_sQ + {C}_b}}{r}} \right)\left( {1 - \tau } \right),0} \right).\end{equation}

(34)

Note that in (34), we introduce the per unit operating cost ${C}_s$ for the firm to be able to obtain goods after default (assumed now to be paid in cash with no credit).16 To avoid negative liquidation values, note that if ${V}_D < 0$ debt holders’ recovery is zero.

Trade creditors’ recovery value in the event of default is as follows:

\begin{equation}{D}_r\ \left( {{x}_D} \right) = {b}_D\ {V}_D - {L}_r\left( {{x}_D} \right).\end{equation}

(35)

Combined with (32) that describes the recovery value of debt holders, (35) implies that ${D}_r\ ( {{x}_D} ) = 0\$ when ${L}_{r\ }\ ( {{x}_D} ) = {b}_D\ {V}_D$ . Under this scenario all assets are obtained by debt holders and trade creditors receive zero. On the other hand, with sufficient recovery value to repay debt holders, that is, when ${L}_{r\ }\ ( {{x}_D} ) = \frac{R}{r}\$ in (32) we obtain ${D}_r\ ( {{x}_D} ) = {b}_D{V}_D - \frac{R}{r} > 0.$

Like before we assume trade creditors can choose the maturity of debt repayment in an effort to obtain the highest trade credit value. Following similar steps as in Section 2, trade credit value is given by:

\begin{equation}{D}_r\ \left( x \right) = \frac{{m{P}_SQ}}{{r + m}}\ + \left( {{D}_r\left( {{x}_D} \right) - \frac{{m{P}_SQ\ }}{{r + m}}} \right){\left( {\frac{x}{{{x}_D}}} \right)}^{{\gamma }_2}\ .\end{equation}

(36)

In comparison with Equation (8) derived earlier with no debt, now ${D}_r( {{x}_D} )$ includes the recovery value of trade creditors assuming that debt holders have priority in the event of default.

4.3.1 Buyer value and interactions of debt and trade credit

The rigid buyer value

{B}_r( x )\

satisfies the following second-order ordinary differential equation:

\begin{equation}r{B}_r\ \left( x \right) = \frac{{{\sigma }^2}}{2}\ {x}^2{B}_r^{^{\prime\prime}}\left( x \right) + \left( {r - \delta } \right)x{B}_r^{\prime}\left( x \right) + \left( {x{Q}^{\varepsilon + 1} - wQ - {C}_b - R} \right)\left( {1 - \tau } \right) + \tau {P}_sQ - m\left( {{P}_sQ\ - {D}_r\left( x \right)} \right).\end{equation}

(37)

Note that compared to Section 2 we are now subtracting the coupon payment from the firm's cash flows and also considering taxes. Note the additional tax savings the firm obtains from purchased goods each period (term

\tau {P}_sQ

).17 The buyer value can then be obtained as follows:

\begin{equation} \def\eqcellsep{&}\begin{array}{l} {B}_r\ \left( x \right) = \left( {\frac{{x{Q}^{\varepsilon + 1}}}{\delta } - \frac{{wQ + {C}_b + R}}{r}} \right)\ \left( {1 - \tau } \right) + \frac{{\tau {P}_sQ}}{r} - {D}_r\left( x \right) + {D}_r\left( {{x}_D} \right){\left( {\frac{x}{{{x}_D}}} \right)}^{{\beta }_2}\\ + \left( {\frac{{wQ + {C}_b + R}}{r} - \frac{{{x}_D{Q}^{\varepsilon + 1}}}{\delta }} \right)\left( {1 - \tau } \right){\left( {\frac{x}{{{x}_D}}} \right)}^{{\beta }_2} - \frac{{\tau {P}_sQ}}{r}\;{\left( {\frac{x}{{{x}_D}}} \right)}^{{\beta }_2}. \end{array} \end{equation}

(38)

{x}_D

is obtained by applying the following smooth pasting condition (see Appendix C for its analytical expression):

\begin{equation}\frac{{\partial {B}_r}}{{\partial x}}\ {|}_{x\ = {x}_D\ } = \ 0.\end{equation}

(39)

The total firm value of the buyer at

t\ = \ 0

includes the proceeds from debt and it is hence optimized by the buyer firm by choosing the optimal coupon

R\

and capacity

Q

\begin{equation}{F}_r\ \left( x \right) = \mathop {{\mathrm{argmax}}}\limits_{R,Q} ({B}_r\left( x \right) + {L}_r\left( x \right) - {{\kappa}}{Q}^\eta )\ .\end{equation}

(40)

Given the nonlinearity of firm value, the above maximization problem is solved numerically. For different values of $R$ we run a dense grid search of Q choices for the buyer. Among the grid of Q choices created we then select the choice that maximizes the firm value (40). We then repeat the process for different $R$ and among all solutions we select the ( $R,Q)$ pair that provides the maximum firm value.

Table 4 provides some sensitivity results of the above setting. Our base case parameters are like before, assuming a tax rate τ = 0.25. In our base case, debt leverage (debt proportion relative to net firm value plus trade credit) stands at 18%. This relatively low ratio contrasts with the high leverage ratios found in the capital structure literature and is driven by trade credit's indirect tax benefits, that is, the tax deductibility of purchased products (see Equation 38, the term $\frac{{\tau {P}_sQ}}{r}$ ). These results highlight the importance of accounting for debt-trade credit interactions (e.g., see Shenoy & Williams, 2017). Our model explains the empirically observed low debt leverage ratios (Strebulaev & Yang, 2013), attributed to debt-trade credit interactions, complementing explanations by Ju et al. (2005), such as dynamic financing considerations and finite debt maturity. Furthermore, our analysis reveals that, even in the presence of debt, trade credit constitutes approximately 14% of financing in the base case (ranging from 11% to 14% across parameters), aligning with evidence from Petersen and Rajan (1997) and Molina & Preve (2012).

TABLE 4. Interactions of trade credit with debt.

	Firm (Net)	Buyer	Debt	Trade	Q	Maturity (1/m)	Maturity (in days)	x_D	Optimal coupon	Debt lev.	Trade lev.
Base case	385.189	1108.857	78.977	62.604	12.67	0.238	87	4.59	5	0.18	0.14
No debt	376.285	1171.345	0	62.29	12.61	0.244	89	4.41	0	0.00	0.14
Higher σ	534.131	1181.748	227.547	64.917	13.23	0.37	135	3.7	19	0.38	0.11
Covenant	186.746	883.181	83.566	62.135	12.49	0.1	37	6.20	5^a	0.34	0.25

Note: We consider the rigid firm with the following base case parameters: $r\ = \ 0.05$ , $\delta \ = \ 0.03$ , ${c}_f = \ 30$ , ${c}_h = \ 0$ , $w\ = \ 7$ , ${P}_S = \ 5$ , ${C}_S = \ 0.25,$ $\sigma \ = \ 0.15$ , $x\ = \ 8.5$ , $k\ = \ 5$ , $\eta \ = \ 2$ , ${b}_D = \ 0.5,$ $b=0$ , $\varepsilon =0,$ $\tau =0.25$ . Firm (Net) denotes firm (buyer value plus debt) net of capacity cost. Q is optimally chosen by the buyer firm by optimizing firm value. The increment for Q search is 0.01. We vary m with increments of 0.1 and minimum (1/m = 0.1) and maximum maturity (1/m) of 1 year. The optimal maturity (trade credit horizon) is chosen by the supplier firm by maximizing trade credit value. Maturity (days) is calculated by multiplying (1/m) with 365 and rounded to the integer. X_D denotes the bankruptcy threshold. Optimal coupon was chosen based on increments of 1 unit. Higher σ case is with σ = 0.25. No debt case uses base case parameters assuming zero coupon. Covenant case uses base case parameters with an imposed covenant for positive worth of recovery of asset value ${b}_D{V}_D$ being 40% of the par value of debt (i.e., 40% of coupon/r).
^a In this case the coupon is not optimized but set equal to the base case to provide a comparison of the covenant case with the base case with no covenant restriction.

Result 12 (Interactions of debt with trade credit). Trade credit reduces debt leverage due to the tax-deductibility of purchased products, which improves with increased trade credit.

For comparison, we illustrate in Table 4 the case with no debt in the presence of corporate taxes. We can see that the firm's buyer value decreases, forgoing some tax benefits. Reduced tax benefits modestly impact installed capacity, partly compensated by a slight extension of trade credit. This suggests that debt's overall impact on trade credit remains limited due to the relatively small proportion of optimal debt financing.

Additionally, we illustrate the sensitivity with respect to volatility. Our results challenge the conventional notion of lower debt leverage with increased volatility. Instead, they reveal that higher volatility may increase debt leverage due to higher real option upside potential, benefiting all stakeholders. Debt increases as the buyer firm expands capacity and suppliers extend credit duration, both effects contributing to enhancing debt capacity.

Result 13 (The effect of volatility in the presence of debt and trade credit). Higher volatility increases trade credit and debt values, as well as credit duration.

Although many banks and debt holders enjoy covenant protection, only a small proportion of trade creditors do (Costello, 2013). Consequently, we explore agency conflicts between debt holders and trade creditors when debt holders impose positive net worth covenants. These covenants require debt holders to recover a specified portion of debt par value in default (see, e.g., Zhang, 2019). To obtain the default threshold ${x}_D$ in the case of debt with a covenant restriction, we solve for ${x}_D$ satisfying the following positive net worth restriction on recovery value at default: ${b}_D{V}_D\ ( {{x}_D} ) = \ rec\frac{R}{r}$ , where $rec$ denotes the required recovery of par at default by debt holders. To facilitate comparisons with previous studies, we assume a recovery rate of 40% similar to that used in Correia et al. (2018), Ericsson et al. (2015) and Lovreta & Silaghi (2020), among others, which is also consistent with the average historical recovery rate on senior unsecured bonds of 37.4% as reported by Moody's (2015).

Our results (see last panel of Table 4) demonstrate that positive net worth covenants significantly constrain buyer value. With these covenants, the buyer defaults earlier due to covenant violations, compared to the endogenous default timing optimally chosen by the buyer in the absence of covenants. This is in line with evidence showing that technical defaults due to covenant violations occur frequently (Dichev & Skinner, 2002). Despite the higher default threshold, debt value remains similar to the base case due to the higher recovery value for debt holders. Earlier default coupled with zero recovery for trade creditors (see Equation 35) results in a significant downward adjustment of trade credit maturity with the supplier requesting early payment of credit. This prediction of our model is in line with Zhang (2019) demonstrating a debt holder–supplier conflict channel. Based on this analysis we summarize the following results:

Result 14a (The effect of covenants on buyer value). Debt covenant restrictions significantly reduce buyer value.

Result 14b (The effect of covenants on trade credit). Debt covenant restrictions cause earlier default and significantly reduce trade credit maturity.

Our analysis focuses on rigid firms, however, we can draw some implications for flexible firms based on insights from our earlier analysis. Our benchmark model has revealed (see earlier sections) that flexible firms order higher quantities and have greater trade credit values. We hence conjecture that trade credit may crowd out debt more significantly for flexible firms. Their incentives to leverage trade credit for tax benefits and quantity enhancement are thus expected to lead flexible firms having lower debt ratios, aligning with findings by Ritchken & Wu (2021).

4.4 The non-cooperative Nash bargaining game

In this section, we consider an alternative design of trade credit terms, assuming that the interaction between the supplier and buyer firm follows a non-cooperative Nash bargaining game instead of a Stackelberg leader–follower game. Considering the non-cooperative Nash bargaining game is important in order to understand how the bargaining power of the members of the supply chain and their potential threat of not entering a trade agreement affect the values of each party in the supply chain, the produced quantities as well as the resulting trade credit maturity.

For tractability, we focus on the case with no operational flexibility for the buyer and provide implications for the flexible buyer case based on the insights from our previous analysis. For simplicity, we assume that supplier value, $S( x ),$ is equivalent to trade credit value, that is, $S( x )\ = \ D( x )$ given by Equation (18) for the rigid firm.18

The outcome of the Nash bargaining game depends on the parties’ threat points and on their relative bargaining power. The threat points reflect the status quo between the negotiating parties. This status quo represents the utility gained by the parties if the bargaining breaks down (Binmore et al., 1986). Let ${\Gamma}_{S}$ and ${\Gamma}_{B}$ be the status quo of the supplier and the buyer, respectively, which reflects the external value each party obtains if the bargaining breaks down. For example, the buyer might internalize procurement to its own subsidiaries $\mathit{(}{\Gamma}_{B}>0)$ or may face significant disruptions that will stop production $({\Gamma}_{B}=\ 0)$ . Relatedly, the supplier might have the potential for alternative customers $({\Gamma}_{S}>0)$ or could lose the business entirely if it does not grant trade credit $({\Gamma}_{S}=\ 0)$ . On the other hand, the bargaining power of each party will depend on their market power, size and the competition they are facing (Fabbri & Klapper, 2016; Klapper et al., 2012). Let ${\eta }_B$ denote the buyer's bargaining power and ${\eta }_S = \ 1 - {\eta }_B$ , the one of the supplier. Define the total network value net of capacity cost to be $N\ ( {m,Q} ) = \ B( {m,Q} ) + S( {m,Q} ) - k{Q}^\eta$ .

Under the Nash bargaining game, the buyer obtains

{B}^{net}\ ( {m,Q\ } ) = B( {m,Q} ) - k{Q}^\eta = \ {\theta }^*\ N( {m,Q} )

in negotiation, while the supplier gets

S\ ( {m,Q} ) = \ (1 - {\theta }^*)N( {m,Q} )

, where

{\theta }^*

is a parameter that reflects the sharing rule and depends on the bargaining power,

{\eta }_B

and on the status quo of the parties,

{\Gamma}_{S}

and

{\Gamma}_{B}

. The Nash solution is then characterized by:

\begin{equation}\ {\theta }^* = \ {\mathrm{arg}}\mathop {{\mathrm{max}}}\limits_\theta {\left\{ {\theta N\left( {m,Q} \right) - {{{\Gamma}}}_B} \right\}}^{{\eta }_B\ }{\left\{ {\left( {1 - \theta } \right)N\left( {m,Q} \right) - {{{\Gamma}}}_S} \right\}}^{1 - {\eta }_B\ }.\end{equation}

(41)

The solution of this game results in the following sharing rule

{\theta }^*

obtained by the buyer firm:

\begin{equation}\ {\theta }^* = {\eta }_B\ - \frac{{{\eta }_B{{{\Gamma}}}_S - \left( {1 - {\eta }_B} \right){{{\Gamma}}}_B}}{{N\left( {m,Q} \right)}}.\end{equation}

(42)

Note that for ${\Gamma}_{S}={\Gamma}_{B}=0$ , we get ${\theta }^* = {\eta }_B\$ , that is, when the parties’ status quo is zero, the total network value is split according to the bargaining power of the parties.

The optimal sharing rule implies a Nash equilibrium relationship between the quantities

Q

and the trade credit maturity

1/m

. Focusing on the buyer's stake that is equal to

{B}^{net}\ ( {m,Q\ } ) = B( {m,Q} ) - k{Q}^\eta = \ {\theta }^*\ N( {m,Q} )

, and plugging in the expressions for the optimal sharing rule

{\theta }^*

and for the network value

N( {m,Q} )

, we obtain the following relationship:

\begin{equation}{\eta }_B\ S\left( {m,Q} \right) - \left( {1 - {\eta }_B} \right)B\left( {m,Q} \right) + \left( {1 - {\eta }_B} \right)\ k\ {Q}^\eta = {\eta }_B\ {{{\Gamma}}}_S - \left( {1 - {\eta }_B} \right){{{\Gamma}}}_B.\end{equation}

(43)

There is an infinite number of pairs (m,Q) satisfying this relationship. Among these pairs, the optimal one is the one that maximizes network value. In Table 5, we illustrate the optimal pairs (m,Q) that maximize network value, for different values of buyer bargaining power ${\eta }_B$ varying between 0.2 and 0.8, assuming ${{\Gamma}}_{S}={{\Gamma}}_{B}\ =\ 0.$ 19 The optimal default threshold, the values for the buyer, supplier and total network value are also presented.

TABLE 5. Nash bargaining solutions with varying buyer market power (

{{\bm{\eta }}}_{\bm{B}}

Panel A: Nash bargaining game
η_B	Maturity (1/m)	Maturity (in days)	Q	x_B	Buyer (Net)	Supplier	Network
0.2	0.313	114	23.037	4.298	28.353	113.410	141.763
0.4	0.323	118	22.530	4.300	73.907	110.861	184.769
0.6	0.345	126	21.500	4.304	158.516	105.677	264.193
0.8	0.476	174	18.258	4.308	356.639	89.160	445.799

Panel B: Comparison with Stackelberg game
Maturity (1/m)	Maturity (in days)	Q	x_B	Buyer (Net)	Supplier	Network
0.222	81	13.830	4.805	433.275	68.390	501.665

Note: We consider the following base case parameters: $r\ = \ 0.05$ , $\delta \ = \ 0.03$ , ${c}_f = \ 30$ , ${c}_h = \ 0$ , $w\ = \ 7$ , ${P}_S = \ 5$ , $\sigma \ = \ 0.15$ , $x\ = \ 8.5$ , $k\ = \ 5$ , $\eta \ = \ 2$ , $b=0$ . In Panel A, Q and m are optimally chosen to maximize network value among the pairs that satisfy equation (x4). The increment for Q search is 0.01. We vary m with increments of 0.1 and minimum (1/m = 0.1) and maximum maturity (1/m) of 1 year. Maturity (days) is calculated by multiplying (1/m) with 365 and rounded to the integer. x_B denotes the bankruptcy threshold. Buyer (Net) denotes buyer value net of capacity cost. In Panel B, we provide the optimal pair $( {{m}^*,{Q}^*} )$ resulting from the Stackelberg game, where the optimal maturity was chosen by the supplier firm and the optimal quantity was chosen by the buyer.

As expected, Table 5, Panel A, shows that the higher the buyer market power, the larger the buyer value and the smaller the supplier value. Moreover, with higher market power of the buyer, the buyer orders a smaller quantity and defaults slightly sooner, while network value increases. Intuitively, when the buyer has more market power it has more power to internalize the costly capacity decision, thus installs a lower capacity (avoiding costly excess capacity). In addition, Table 5 shows that the supplier extends larger trade credit maturities when the buyer has higher market power. This result is in line with empirical evidence by Ellingsen et al. (2016), Fabbri & Klapper (2016), Giannetti et al. (2011) and Klapper et al. (2012), who find that contracts to the largest buyers, buyers with a larger share of the supplier's sales or with more suppliers entail longer maturities (net days). We summarize the following result relating the effect of the impact of market power:

Result 15 (The effect of market power on buyer, supplier and network value and on trade maturity). For higher levels of buyer market power, buyer value grows larger while supplier value diminishes, and network value increases. With higher buyer market power, suppliers extend longer trade credit durations.

We now compare the Nash bargaining model with our benchmark model based on a Stackelberg game in which the supplier being the leader chooses $m$ subject to the buyer choosing $Q$ . Compared to the optimal pair $( {{m}^*,{Q}^*} )$ that solves the Stackelberg game (see panel B), we can see that the Nash bargaining game results in higher trade credit maturities and higher quantities. Intuitively, in the Stackelberg game, quantities are decided by the buyer firm that totally internalizes the costly capacity installation decision, thus resulting in lower quantities compared to the Nash bargaining game. Regarding trade credit maturity, this is optimally decided by the supplier in the Stackelberg game, hence resulting in lower maturities compared to the Nash bargaining game, where maturities increase with buyer bargaining power. We summarize the following result relating the comparison of the Nash bargaining game with the Stackelberg game of the benchmark model:

Result 16 (Comparison of the Nash bargaining game with Stackelberg game). The Nash bargaining game leads to higher trade credit maturities and quantities compared to the Stackelberg game's optimal values.

Finally, we provide some implications for the flexible firm. First, just like in the case of inflexibility, we expect that when the flexible firm has more bargaining power, it can better internalize capacity costs and, thus, adjust capacity downward, which will be beneficial for the overall network value. From our earlier analysis (see result 1), we found, however, that a flexible firm obtains higher order quantities than the inflexible one. Thus, we anticipate that the downward adjustment of capacity will be smaller for the flexible firm compared to the inflexible one when the buyer has higher bargaining power. We also showed earlier that the flexible buyer firm defaults later than the inflexible firm (see Table 1). Therefore, with more market power, the degree of acceleration of default would be less significant for the flexible buyer compared to the case of the inflexible firm. Finally, we determined that the flexible buyer firm obtains a longer trade credit duration from the supplier (result 1). Thus, we expect that when the flexible buyer firm has more bargaining power, the extension of the duration it would obtain will be more significant than that of the inflexible firm.

5 CONCLUSIONS

This paper investigates the effect of operational flexibility on trade credit values, order quantities and trade credit maturity. We find that firms that have the ability to temporarily shut down will order higher quantities and have larger trade credit values. Moreover, suppliers will extend larger trade credit maturities to flexible firms. Our analysis shows however, that trade credit as a proportion of buyer firm value is higher for the inflexible firm because flexible firm's value increases more rapidly than the associated increase in trade credit. This result may be useful for empirical researchers usually focusing on ratios rather than levels.

We provide a number of predictions such as that the effect of flexibility on trade credit and credit durations is more significant in more uncertain environments, in industries with less intense competition between suppliers and in downstream markets with higher capacity constraints, lower recovery rates, lower gross profit margins or lower capacity holding costs.

We extend the basic setup to account for several important issues such as switching costs, entry timing of firms, interactions of debt with trade credit or Nash bargaining between parties. When introducing switching costs for the flexible firm switching between idle and active mode, we find a hysteresis (inaction) zone where the buyer firm does not switch modes to avoid incurring the switching costs. This zone of inaction is not affected by trade credit horizon provided by the supplier, however, higher levels of switching costs widen the zone of inaction and decrease the value of trade credit and order quantity. Regarding the entry timing of firms, we show that, for a given trade credit horizon, the flexible firm delays investment more than the rigid firm and invests in higher capacity. When trade credit interacts with standard debt, we show that trade credit reduces debt leverage due to the tax-deductibility of purchased products. Moreover, in the presence of debt covenants causing earlier default, trade credit maturity is significantly reduced. Finally, under non-cooperative Nash bargaining, buyers with higher bargaining power obtain longer trade credit maturities, in line with empirical evidence. Moreover, the Nash bargaining game leads to higher trade credit maturities and quantities compared to the Stackelberg game's optimal values.

There are some factors that we have overlooked in our analysis and provide the basis for future extensions. First, although our analysis provides for some adjustments in production, it would be interesting to investigate how the framework can be adjusted to incorporate capacity utilization, so that production can be upscaled and downscaled in relation to demand. Second, we have assumed a single buyer and supplier and it would thus be interesting to investigate competitive interactions in the supplier or/and the buyer markets. Finally, we analyze a single product sold by the buyer firm while in many cases firms operate and manage multiple products.

ACKNOWLEDGMENTS

Florina Silaghi is a Serra Húnter Fellow and gratefully acknowledges financial support through Project PID2020-114460GB-C31 from the Spanish Ministry of Science and Innovation and from the Ramón Areces Foundation. The authors would like to express their gratitude to Elettra Agliardi and Zvi Wiener for valuable insights, as well as other participants in the 2021 Annual Real Options Conference, 2021 International Risk Management Conference, and 2022 Annual Scientific Conference of Romanian Academic Economists from abroad for comments and suggestions. We would also like to thank two anonymous referees for their constructive input. The usual disclaimer applies.

APPENDIX A: DETAILS ON THE DERIVATION OF BUYER'S VALUE

In this appendix, we provide details on our derivation of the buyer value for both the inflexible and the flexible cases.

Inflexible buyer value

To derive the particular solution in Equation (10) of the buyer, we proceed by applying the solution:

\begin{equation}B\ \left( x \right) = \ B + {C}_0x + {C}_1{x}^{{\gamma }_2}\end{equation}

(A1)

that satisfies differential Equation (9) obtaining the following solutions for

{C}_0

{C}_1

and B:

\begin{equation}B\ = \ \frac{m}{r}\frac{{m{P}_SQ}}{{r + m}} - \frac{{m{P}_SQ + wQ + {C}_b}}{r},\ \ {C}_0 = \frac{{{Q}^{\varepsilon + 1}}}{\delta },\;{C}_1 = - A_2^D.\end{equation}

(A2)

We note that to derive ${C}_1$ we have used the fact that $m\ = \ - ( {r - ( {r - \delta } ){\gamma }_2 - \frac{1}{2}{\gamma }_2( {{\gamma }_2 - 1} ){\sigma }^2} )$ which simplifies the presentation of the solution. Note also that unlike the standard particular solution, the term ${C}_1{x}^{{\gamma }_2}\$ in (A1) is used to capture trade credit value in the differential Equation (9) (which as seen in Equation (8) depends on ${\gamma }_2$ term).

Replacing solutions of constants

{C}_0,\ {C}_1

and B from (A2) back in (A1) and noting that

\begin{equation}\frac{{m{P}_SQ}}{r} - \frac{m}{r}\ \frac{{m{P}_SQ}}{{r + m}} = \frac{{m{P}_SQ}}{{r + m}}\ ,\end{equation}

(A3)

one can verify first two terms in Equation (10).

Next, we note that as

{\beta }_1 &gt; 0\

applying (12a) to Equation (10) implies that:

\begin{equation}\ A_1 = \ 0.\end{equation}

(A4)

Applying the boundary condition (12b) to Equation (10), we obtain that:

\begin{equation*}{A}_2 = - \left[ {\left( {\frac{{{x}_{Br}{Q}^{\varepsilon + 1}}}{\delta } - \frac{{m{P}_SQ + wQ + {C}_b}}{r}} \right) + \frac{m}{r}\frac{{m{P}_SQ}}{{r + m}} - \left( {{V}_B - \frac{{m{P}_SQ}}{{r + m}}} \right)} \right]{({x}_{Br})}^{ - {\beta }_2}.\end{equation*}

Using (A3), we can further simplify

A_2\

and we obtain that:

\begin{equation}{A}_2 = - \left[ {\left( {\frac{{{x}_{Br}{Q}^{\varepsilon + 1}}}{\delta } - \frac{{wQ + {C}_b}}{r}} \right) - {V}_B} \right]{({x}_{Br})}^{ - {\beta }_2}.\end{equation}

(A5)

Replacing (A4) and (A5) into Equation (10) together with the particular derived above, we thus derive the final solution for the buyer value in Equation (13).

The optimal quantity ordered by the buyer maximizes buyer value. From Equation (16), we obtain the implicit equation for

Q

\begin{equation*} \def\eqcellsep{&}\begin{array}{l} \frac{{\left( {\varepsilon + 1} \right){Q}^\varepsilon x}}{\delta } - \frac{w}{r} - \frac{{m{P}_S}}{{r + m}} - \left( {b{P}_S - \frac{{m{P}_S}}{{r + m}}} \right)\ {\left( {\frac{x}{{{x}_{Br}\left( Q \right)}}} \right)}^{{\gamma }_2}\\ + \frac{{{\gamma }_2}}{{{x}_{Br}\left( Q \right)}}\left( {b{P}_SQ - \frac{{m{P}_SQ}}{{r + m}}} \right)\ {\left( {\frac{x}{{{x}_{Br}\left( Q \right)}}} \right)}^{{\gamma }_2}\frac{{\partial {x}_{Br}\left( Q \right)}}{{\partial Q}}\\ + \left[ {b{P}_S - \frac{{\left( {\varepsilon + 1} \right){Q}^\varepsilon {x}_{Br}\left( Q \right)}}{\delta } - \frac{{{Q}^{\varepsilon + 1}}}{\delta }\frac{{\partial {x}_{Br}\left( Q \right)}}{{\partial Q}} + \frac{w}{r}} \right]\ \\ {\left( {\frac{x}{{{x}_{Br}\left( Q \right)}}} \right)}^{{\beta }_2} - \frac{{{\beta }_2}}{{{x}_{Br}\left( Q \right)}}\left[ {b{P}_SQ - \frac{{{x}_{Br}\left( Q \right){Q}^{\varepsilon + 1}}}{\delta } + \frac{{wQ + {C}_b}}{r}} \right]\ {\left( {\frac{x}{{{x}_{Br}\left( Q \right)}}} \right)}^{{\beta }_2}\frac{{\partial {x}_{Br}\left( Q \right)}}{{\partial Q}} - {\mathrm{\kappa \ }}\eta {Q}^{\eta - 1} = \ 0, \end{array} \end{equation*}

where we have used the fact that recovery value is given by

{V}_B = \ b{P}_SQ

Flexible buyer value

The constants

{A}_3

{A}_4

{A}_5

determined from the boundary conditions are given by the following expressions:

\begin{equation*}\ {A}_4 = \frac{1}{{{\beta }_2 - {\beta }_1}}\ \frac{1}{{{{\bar{x}}}^{{\beta }_1}}}\left( {\frac{{\left( {{\beta }_2 - 1} \right)\bar{x}{Q}^{\varepsilon + 1}}}{\delta } - \frac{{{\beta }_2wQ}}{r}} \right),\end{equation*}

\begin{equation*}\ {A}_5 = x_{Bf}^{ - {\beta }_2}\ \left( {\frac{{{C}_b}}{r} + {V}_B - {A}_4x_{Bf}^{{\beta }_1}} \right),\end{equation*}

\begin{equation*}\ {A}_3 = {A}_5\ + \frac{{\frac{{\left( {{\beta }_1 - 1} \right)\bar{x}{Q}^{\varepsilon + 1}}}{\delta } - \frac{{{\beta }_1wQ}}{r}}}{{\left( {{\beta }_2 - {\beta }_1} \right){{\bar{x}}}^{{\beta }_2}}}.\end{equation*}

APPENDIX B: FLEXIBLE BUYER VALUE WITH SWITCHING COSTS

The buyer value has two operating regions:

\begin{equation}{B}_1\ \left( x \right) = \frac{{x{Q}^{\varepsilon + 1}}}{\delta }\ - \frac{{wQ}}{r} - \frac{{{C}_b}}{r} - {D}_f\left( x \right) + {A}_3{x}^{{\beta }_2},\;x &gt; {x}_H,\end{equation}

(A6a)

\begin{equation}{B}_0\ \left( x \right) = \ - \frac{{{C}_b}}{r} - {D}_f\left( x \right) + {A}_4{x}^{{\beta }_1} + {A}_5{x}^{{\beta }_2},\;\ x \le {x}_L,\end{equation}

(A6b)

where

{D}_f\ ( x ) = \frac{{m{P}_SQ}}{{r + m}}\ - ( {{V}_B - \frac{{m{P}_SQ\ }}{{r + m}}} ){( {\frac{x}{{{x}_{Bf}}}} )}^{\gamma _2}

. The constants

{\mathrm{A}}_3

{\mathrm{A}}_4

and

{\mathrm{A}}_5

, and the optimal thresholds

{x}_H

\ {x}_L

and

{x}_{Bf}

are determined from the following value matching and smooth pasting conditions:

\begin{equation}{B}_0\ \left( {{x}_H} \right) = {B}_1\ \left( {{x}_H} \right) - {\varepsilon }_{01},\end{equation}

(A7a)

\begin{equation}{B}_1\ \left( {{x}_L} \right) = {B}_0\ \left( {{x}_L} \right) - {\varepsilon }_{10},\end{equation}

(A7b)

\begin{equation}{B}_0\ \left( {{x}_{Bf}} \right) = \ 0,\end{equation}

(A7c)

\begin{equation}B_0^{\prime}\ \left( {{x}_H} \right) = B_1^{\prime}\ \left( {{x}_H} \right),\end{equation}

(A8a)

\begin{equation}B_1^{\prime}\ \left( {{x}_L} \right) = B_0^{\prime}\ \left( {{x}_L} \right),\end{equation}

(A8b)

\begin{equation}B_0^{\prime}\ \left( {{x}_B} \right) = \ 0.\end{equation}

(A8c)

The expressions of the constants

{A}_{\mathit{3}}

{A}_{\mathit{4}}

and

{A}_{\mathit{5}}

are given by:

\begin{equation*}{A}_4 = \frac{{x_H^{1 - {\beta }_1}}}{{{\beta }_1}}\ \frac{{{Q}^{\varepsilon + 1}}}{\delta }\left( {1 + \frac{{x_L^{1 - {\beta }_1} - x_H^{1 - {\beta }_1}}}{{x_H^{{\beta }_2 - {\beta }_1} - x_L^{{\beta }_2 - {\beta }_1}}}x_H^{{\beta }_2 - 1}} \right),\end{equation*}

\begin{equation*}{A}_5 = - \frac{{{\beta }_1}}{{{\beta }_2}}{A}_4x_{Bf}^{{\beta }_1 - {\beta }_2} - \left( {{V}_B - \frac{{m{P}_SQ\ }}{{r + m}}} \right)\frac{{{\gamma }_2}}{{{\beta }_2}}x_{Bf}^{ - {\beta }_2},\end{equation*}

\begin{equation*}{A}_3 = {A}_5 + \frac{{{Q}^{\varepsilon + 1}}}{{\delta {\beta }_2}}\frac{{x_L^{1 - {\beta }_1} - x_H^{1 - {\beta }_1}}}{{x_H^{{\beta }_2 - {\beta }_1} - x_L^{{\beta }_2 - {\beta }_1}}}.\end{equation*}

The optimal thresholds are the implicit solutions of the following equations:

\begin{equation*}{A}_4x_H^{{\beta }_1} + \left( {{A}_5 - {A}_3} \right)x_H^{{\beta }_2} + {\epsilon }_{01} = \left( {\frac{{{x}_H{Q}^{\varepsilon + 1}}}{\delta } - \frac{{wQ}}{r}} \right),\end{equation*}

\begin{equation*}{A}_4x_L^{{\beta }_1} + \left( {{A}_5 - {A}_3} \right)x_L^{{\beta }_2} - {\epsilon }_{01} = \left( {\frac{{{x}_L{Q}^{\varepsilon + 1}}}{\delta } - \frac{{wQ}}{r}} \right),\end{equation*}

\begin{equation*}{A}_4x_{Bf}^{{\beta }_1} + {A}_5x_{Bf}^{{\beta }_2} = \frac{{{C}_b}}{r} + {V}_B.\end{equation*}

APPENDIX C: ANALYTICAL DERIVATION OF x_D IN THE PRESENCE OF DEBT IN SUBSECTION 4.3

{L}_{r\ }( {{x}_D} )

implies a minimum and this affects

\ {D}_r( {{x}_D} )

, we will have two solutions.

Case 1: If $\min ( {{b}_D{V}_D,\frac{R}{r}} ) = {b}_D\ {V}_D,$ then ${D}_r\ ( {{x}_D} ) = \ 0$ . Note that for this to be the case it must be that ${b}_D{V}_D < \frac{R}{r}$ which implies a condition on ${x}_D$ , namely:
$\begin{equation}{x}_D < \left( {\frac{R}{{r{b}_D\left( {1 - \tau } \right)\ }} + \frac{{wQ + {C}_SQ + {C}_b\ }}{r}} \right)\frac{\delta }{{{Q}^{\varepsilon + 1}}}\end{equation}$ (A9)

that will have to be satisfied by the solution.

Applying the smooth pasting condition, we get following solution in this case:

\begin{equation*}{x}_D\left( Q \right)\ = \frac{\delta }{{{Q}^{\varepsilon + 1}\left( {1 - {\beta }_2} \right)\left( {1 - \tau } \right)}}\ \left[ { - {\gamma }_2\frac{{m{P}_SQ}}{{r + m}} - {\beta }_2\left( {\frac{{wQ + {C}_b + R\ }}{r}\left( {1 - \tau } \right) - \tau \frac{{{P}_SQ}}{r}} \right)} \right],\end{equation*}

which has to satisfy inequality (A9).

Case 2: If $\min ( {{b}_D{V}_D,\frac{R}{r}} ) = \frac{R}{r}\$ then ${D}_r\ ( {{x}_D} ) = {b}_D\ {V}_D - \frac{R}{r}$ . Note that for this to be the case it must be that ${b}_D{V}_D > \frac{R}{r}$ which implies a condition on ${x}_D$ , namely:
$\begin{equation}{x}_D > \left( {\frac{R}{{r{b}_D\left( {1 - \tau } \right)\ }} + \frac{{wQ + {C}_SQ + {C}_b\ }}{r}} \right)\frac{\delta }{{{Q}^{\varepsilon + 1}}}\end{equation}$ (A10)

that will have to be satisfied by the solution.

Applying the smooth pasting condition, we get the following solution in this case:

\begin{equation*} \def\eqcellsep{&}\begin{array}{l} {x}_D\left( Q \right)\ = \frac{\delta }{{{Q}^{\varepsilon + 1}\left( {1 - {\beta }_2 + \left( {{\beta }_2 - {\gamma }_2} \right){b}_D} \right)\left( {1 - \tau } \right)}}\\ \ \left[ { - {\gamma }_2\frac{{m{P}_SQ}}{{r + m}} + \frac{{wQ + {C}_b + R\ }}{r}\left( {1 - \tau } \right)\left( {\left( {{\beta }_2 - {\gamma }_2} \right){b}_D - {\beta }_2} \right) + {\beta }_2\tau \frac{{{P}_SQ}}{r} + \left( {{\beta }_2 - {\gamma }_2} \right)\frac{R}{r}} \right], \end{array} \end{equation*}

which has to satisfy inequality (A10).

Although case 2 is theoretically plausible, our numerical results show that it is never reached.

Open Research

DATA AVAILABILITY STATEMENT

Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.

REFERENCES

Adkins, R., & Paxson, D. (2012). Real input-output energy-switching options. The Journal of Energy Markets, 5(3), 3.
10.21314/JEM.2012.076
Google Scholar
Aguerrevere, F. L. (2003). Equilibrium investment strategies and output price behavior: A real-options approach. The Review of Financial Studies, 16, 1239–1272.
10.1093/rfs/hhg041
Web of Science® Google Scholar
Aguerrevere, F. L. (2009). Real options, product market competition, and asset returns. The Journal of Finance, 64, 957–983.
10.1111/j.1540-6261.2009.01454.x
Web of Science® Google Scholar
Altman, E., Resti, A., & Sironi, A. (2004). Default recovery rates in credit risk modelling: a review of the literature and empirical evidence. Economic Notes, 33(2), 183–208.
10.1111/j.0391-5026.2004.00129.x
Google Scholar
Amberg, N., Jacobson, T., von Schedvin, E., & Townsend, R. (2021). Curbing shocks to corporate liquidity: The role of trade credit. Journal of Political Economy, 129(1), 182–242.
10.1086/711403
Web of Science® Google Scholar
Auboin, M., & Engemann, M. (2014). Testing the trade credit and trade link: Evidence from data on export credit insurance. Review of World Economics, 150, 715–743.
10.1007/s10290-014-0195-4
Web of Science® Google Scholar
Biais, B., & Gollier, C. (1997). Trade credit and credit rationing. The Review of Financial Studies, 10(4), 903–937.
10.1093/rfs/10.4.903
Web of Science® Google Scholar
Binmore, K., Rubinstein, A., & Wolinsky, A. (1986). The Nash bargaining solution in economic modelling. RAND Journal of Economics, 17, 176–188.
10.2307/2555382
Web of Science® Google Scholar
Brennan, M., Maksimovic, V., & Zechner, J. (1988). Vendor financing. Journal of Finance, 43(5), 1127–1141.
10.1111/j.1540-6261.1988.tb03960.x
Web of Science® Google Scholar
Brennan, M. J., & Schwartz, E. S. (1985). Evaluating natural resource investments. Journal of business, 135–157.
10.1086/296288
Web of Science® Google Scholar
Burkart, M., & Ellingsen, T. (2004). In-kind finance: A theory of trade credit. American Economic Review, 94(3), 569–590.
10.1257/0002828041464579
Web of Science® Google Scholar
Cathcart, L., Dufour, A., Rossi, L., & Varotto, S. (2020). The differential impact of leverage on the default risk of small and large firms. Journal of Corporate Finance, 60, 101541.
10.1016/j.jcorpfin.2019.101541
Web of Science® Google Scholar
Charalambides, M., & Koussis, N. (2018). A stochastic model with interacting managerial operating options and debt rescheduling. European Journal of Operational Research, 267, 236–249.
10.1016/j.ejor.2017.11.004
Web of Science® Google Scholar
Chod, J., Lyandres, E., & Yang, S. A. (2019). Trade credit and supplier competition. Journal of Financial Economics, 131(2), 484–505.
10.1016/j.jfineco.2018.08.008
Web of Science® Google Scholar
Chod, J., Rudi, N., & Van Mieghem, J. A. (2010). Operational flexibility and financial hedging: Complements or substitutes? Management Science, 56(6), 1030–1045.
10.1287/mnsc.1090.1137
Web of Science® Google Scholar
Correia, M., Kang, J., & Richardson, S. (2018). Asset volatility. Review of Accounting Studies, 23, 37–94.
10.1007/s11142-017-9431-1
Web of Science® Google Scholar
Costello, A. M. (2013). Mitigating incentive conflicts in inter-firm relationships: Evidence from long-term supply contracts. Journal of Accounting and Economics, 56(1), 19–39.
10.1016/j.jacceco.2013.02.001
Web of Science® Google Scholar
Cuñat, V. (2007). Trade credit: Suppliers as debt collectors and insurance providers. Review of Financial Studies, 20(2), 491–527.
10.1093/rfs/hhl015
Web of Science® Google Scholar
Dangl, T. (1999). Investment and capacity choice under uncertain demand. European Journal of Operational Research, 117(3), 415–428.
10.1016/S0377-2217(98)00274-4
Web of Science® Google Scholar
Dangl, T., & Zechner, J. (2021). Debt maturity and the dynamics of leverage. The Review of Financial Studies, 34(12), 5796–5840.
10.1093/rfs/hhaa148
Web of Science® Google Scholar
Deloitte. (2019). IFRS 9 financial instruments: Applying the expected credit loss model to trade receivables using a provision matrix. https://www2.deloitte.com/cy/en/pages/risk/articles/ifrs-9-financial-instruments.html
Google Scholar
Desai, M., Foley, C., & Hines, J. (2016). Trade credit and taxes. Review of Economics and Statistics, 98(1), 132–139.
10.1162/REST_a_00534
Web of Science® Google Scholar
Diamond, D. W., & He, Z. (2014). A theory of debt maturity: the long and short of debt overhang. The Journal of Finance, 69(2), 719–762.
10.1111/jofi.12118
Web of Science® Google Scholar
Dichev, I. D., & Skinner, D. J. (2002). Large–sample evidence on the debt covenant hypothesis. Journal of accounting research, 40(4), 1091–1123.
10.1111/1475-679X.00083
Web of Science® Google Scholar
Dixit, A., & Pindyck, R. (1994). Investment under uncertainty. Princeton University Press.
10.1515/9781400830176
Google Scholar
Dobbs, I. M. (2004). Intertemporal price cap regulation under uncertainty. The Economic Journal, 114, 421–440.
10.1111/j.1468-0297.2004.00215.x
Web of Science® Google Scholar
Ellingsen, T., Jacobson, T., & von Schedvin, E. (2016). Trade credit: Contract-level evidence contradicts current theories. Sveriges Riksbank Research Paper Series.
Google Scholar
Emery, G. W. (1984). A pure financial explanation for trade credit. Journal of Financial and Quantitative Analysis, 19(3), 271–285.
10.2307/2331090
Web of Science® Google Scholar
Ericsson, J., Reneby, J., & Wang, H. (2015). Can structural models price default risk? Evidence from bond and credit derivative markets. Quarterly Journal of Finance, 5(3), 1–32.
10.1142/S201013921550007X
Google Scholar
Fabbri, D., & Klapper, L. (2016). Bargaining power and trade credit. Journal of Corporate Finance, 41(C), 66–80.
10.1016/j.jcorpfin.2016.07.001
Google Scholar
Ferrando, A., & Wolski, M. (2018). Investment of financially distressed firms: The role of trade credit. EIB Working Papers, No. 2018/04.
Google Scholar
Ferris, J. S. (1981). A transactions theory of trade credit use. Quarterly Journal of Economics, 96(2), 243–270.
10.2307/1882390
Web of Science® Google Scholar
Fisman, R., & Love, I. (2003). Trade credit, financial intermediary development, and industry growth. The Journal of Finance, 58(1), 353–374.
10.1111/1540-6261.00527
Web of Science® Google Scholar
García-Appendini, E. (2011). Supplier certification and trade credit. Working Paper series, Bocconi University-IGIER.
Google Scholar
Giannetti, M., Burkart, M., & Ellingsen, T. (2011). What you sell is what you lend? Explaining trade credit contracts. Review of Financial Studies, 24(4), 1261–1298.
10.1093/rfs/hhn096
Web of Science® Google Scholar
Hackbarth, D., & Mauer, D. C. (2011). Optimal priority structure, capital structure, and investment. The Review of Financial Studies, 25(3), 747–796.
10.1093/rfs/hhr129
Web of Science® Google Scholar
Hagspiel, V., Huisman, K., & Kort, P. (2016). Volume flexibility and capacity investment under demand uncertainty. International Journal of Production Economics, 178, 95–108.
10.1016/j.ijpe.2016.05.007
Web of Science® Google Scholar
Harris, C. (2015). Trade credit and financial flexibility. Banking & Finance Review, 7(1), 47–57.
Google Scholar
Hu, Q., & Zhang, A. (2015). Real option analysis of aircraft acquisition: A case study. Journal of Air Transport Management, 46, 19–29.
10.1016/j.jairtraman.2015.03.010
Web of Science® Google Scholar
Huberts, N. F., Huisman, K. J., Kort, P. M., & Lavrutich, M. N. (2015). Capacity choice in (strategic) real options models: A survey. Dynamic Games and Applications, 5(4), 424–439.
10.1007/s13235-015-0162-2
Web of Science® Google Scholar
Hull, J., & White, A. (1995). The impact of default risk on the prices of options and other derivative securities. Journal of Banking & Finance, 19(2), 299–322.
10.1016/0378-4266(94)00050-D
Web of Science® Google Scholar
Iancu, D. A., Trichakis, N., & Tsoukalas, G. (2017). Is operating flexibility harmful under debt. Management Science, 63(6), 1730–1761.
10.1287/mnsc.2015.2415
Web of Science® Google Scholar
Ju, N., Parrino, R., Poteshman, A. M., & Weisbach, M. S. (2005). Horses and rabbits? Trade-off theory and optimal capital structure. Journal of Financial and Quantitative analysis, 40(2), 259–281.
10.1017/S0022109000002301
Web of Science® Google Scholar
Koussis, N., & Silaghi, F. (2020). Trade credit duration and optimal order quantities under buyer capacity constraints. Working Paper.
Google Scholar
Klapper, L., Laeven, L., & Rajan, R. (2012). Trade credit contracts. The Review of Financial Studies, 25(3), 838–867.
10.1093/rfs/hhr122
Web of Science® Google Scholar
Lee, Y. W., & Stowe, J. D. (1993). Product risk, asymmetric information, and trade credit. Journal of Financial and Quantitative Analysis, 28(2), 285–300.
10.2307/2331291
Web of Science® Google Scholar
Leland, H. (1994). Bond prices, yield spreads, and optimal capital structure with default risk (No. RPF-240). University of California at Berkeley.
Google Scholar
Leland, H. E. (1998). Agency costs, risk management, and capital structure. The Journal of Finance, 53(4), 1213–1243.
10.1111/0022-1082.00051
Web of Science® Google Scholar
Long, M. S., Malitz, I. B., & Ravid, A. (1993). Trade credit, quality guarantees, and product marketability. Financial Management, 22(4), 117–127.
10.2307/3665582
Web of Science® Google Scholar
Longstaff, F. A., & Schwartz, E. S. (1995). A simple approach to valuing risky fixed and floating rate debt. The Journal of Finance, 50(3), 789–819.
10.1111/j.1540-6261.1995.tb04037.x
Web of Science® Google Scholar
Lovreta, L., & Silaghi, F. (2020). The surface of implied firm's asset volatility. Journal of Banking & Finance, 112, 105253.
10.1016/j.jbankfin.2017.11.008
Web of Science® Google Scholar
MacKay, P. (2003). Real flexibility and financial structure: An empirical analysis. Review of Financial Studies, 16, 1131–1165.
10.1093/rfs/hhg022
Web of Science® Google Scholar
Mauer, D. C., & Sarkar, S. (2005). Real options, agency conflicts, and optimal capital structure. Journal of Banking & Finance, 29(6), 1405–1428.
10.1016/j.jbankfin.2004.05.036
Web of Science® Google Scholar
McGuinness, G., Hogan, T., & Powell, R. (2018). European trade credit use and SME survival. Journal of Corporate Finance, 49, 81–103.
10.1016/j.jcorpfin.2017.12.005
Web of Science® Google Scholar
Molina, C. A., & Preve, L. A. (2012). An empirical analysis of the effect of financial distress on trade credit. Financial Management, 41(1), 187–205.
10.1111/j.1755-053X.2012.01182.x
Web of Science® Google Scholar
Moody's. (2015). Annual default study: Corporate default and recovery rates, 1920–2014. Moody's Investors Service.
Google Scholar
Ng, C., Smith, J., & Smith, R. (1999). Evidence on the determinants of credit terms used in interfirm trade. Journal of Finance, 54(3), 1109–1129.
10.1111/0022-1082.00138
Web of Science® Google Scholar
Nishihara, M., Sarkar, S., & Zhang, C. (2019). Agency cost of debt overhang with optimal investment timing and size. Journal of Business, Finance & Accounting, 46(5–6), 784–809.
10.1111/jbfa.12379
Web of Science® Google Scholar
Petersen, M. A., & Rajan, R. G. (1997). Trade credit: Theories and evidence. The Review of Financial Studies, 10(3), 661–691.
10.1093/rfs/10.3.661
Web of Science® Google Scholar
Rajan, R., & Zingales, L. (1995). What do we know about capital structure? Some evidence from international data. Journal of Finance, 50(5), 1421–1460.
10.1111/j.1540-6261.1995.tb05184.x
Web of Science® Google Scholar
Randall, C. (2021). Tesla upgrades Shanghai Gigafactory production capacities. https://www.electrive.com/2021/11/26/tesla-upgrades-shanghai-gigafactory-production-capacities/
Google Scholar
Reinartz, S. J., & Schmid, T. (2016). Production flexibility, product markets, and capital structure decisions. The Review of Financial Studies, 29(6), 1501–1548.
10.1093/rfs/hhv126
Web of Science® Google Scholar
Ritchken, P., & Wu, Q. (2021). Capacity investment, production flexibility, and capital structure. Production and Operations Management, 30(12), 4593–4613.
10.1111/poms.13253
Web of Science® Google Scholar
Sarkar, S. (2018). Optimal DOL (degree of operating leverage) with investment and production flexibility. International Journal of Production Economics, 202, 172–181.
10.1016/j.ijpe.2018.05.022
Web of Science® Google Scholar
Schwartz, R. (1974). An economic model of trade credit. Journal of Financial and Quantitative Analysis, 9(4), 643–657.
10.2307/2329765
Web of Science® Google Scholar
Shenoy, J., & Williams, R. (2017). Trade credit and the joint effects of supplier and customer financial characteristics. Journal of Financial Intermediation, 29, 68–80.
10.1016/j.jfi.2015.09.001
Web of Science® Google Scholar
Silaghi, F., & Moraux, F. (2022). Trade credit contracts: Design and regulation, European Journal of Operational Research, 296(3), 980–992.
10.1016/j.ejor.2021.04.036
Web of Science® Google Scholar
Silaghi, F., & Sarkar, S. (2021). Agency problems in public-private partnerships investment projects. European Journal of Operational Research, 290(39), 1174–1191.
10.1016/j.ejor.2020.08.050
Google Scholar
Strebulaev, I. A., & Yang, B. (2013). The mystery of zero-leverage firms. Journal of Financial Economics, 109(1), 1–23.
10.1016/j.jfineco.2013.02.001
Web of Science® Google Scholar
Trigeorgis, L. (1996). Real options: Managerial flexibility and strategy in resource allocation. MIT press.
Google Scholar
Yang, A., & Birge, J. (2018). Trade credit, risk sharing, and inventory financing portfolios. Management Science, 64(8), 3667–3689.
10.1287/mnsc.2017.2799
Web of Science® Google Scholar
Yifan, Y., (2021). Tesla strikes new Panasonic battery deal as sales and shares soar. https://asia.nikkei.com/Business/Technology/Tesla-strikes-new-Panasonic-battery-deal-as-sales-and-shares-soar
Google Scholar
Zhang, Z. (2019). Bank interventions and trade credit: Evidence from debt covenant violations. Journal of Financial and Quantitative Analysis, 54(5), 2179–2207.
10.1017/S0022109018001163
Web of Science® Google Scholar

1 https://www.economist.com/finance-and-economics/2011/03/17/the-cost-of-calamity
2 https://thecorner.eu/news-spain/spain-economy/spanish-industry-starts-to-grind-to-a-halt-due-to-the-price-of-energy-the-most-expensive-in-europe/98786/.
3 Throughout the paper, we use interchangeably the terms “operational flexibility,” “volume flexibility” or “production flexibility” to refer to firms’ ability to adjust operating variables to cope with unpredictable changes in market conditions.
4 Data comparing flexible with rigid firms’ trade credit “leverage” ratios are not readily available because much of the focus of the literature is on debt (capital structure decisions). MacKay (2003) finds that firms that can easily adjust their production use less financial leverage, and less public debt. Reinartz and Schmid (2016) focus on energy utilities and show that more flexible firms have higher leverage ratios attributing this to lower costs of financial distress and higher tax benefits of debt.
5 Longstaff and Schwartz (1995) summarize the empirical evidence that suggests an average write-down of unsecured debt that can exceed 80% (see p. 794). Although these write-down rates may not fully reflect risks of collecting receivables in the event of default, they are reflective of the high rates of trade credit. In principle, under the international accounting standard IFR9 firms need to recognize their expected credit losses using a provision matrix that is based on historical experience (see, e.g., Deloitte (2019) report on the subject).
6 Theoretically, it is also possible that ${x}_B > \bar{x}$ if ${P}_S$ is sufficiently high. In this case, the firm never shuts down temporarily and operational flexibility is not used. Therefore, the appropriate firm value is given by the value of the rigid firm. In our analysis below, we focus on the case where ${x}_B < \bar{x}$ , that is, the flexible firm defaults at a value where the firm is operating in the idle mode.
7 With no switching costs the switching threshold is simply given by the variable costs (as in Ritchken & Wu, 2021). In Subsection 4.1, we extend the framework to include switching costs and show that when switching costs tend to zero the switching thresholds tend to the variable cost, w.
8 Intuitively, it would only make sense for the firm to start operations in active mode, not in idle mode to save costs. Rithcken and Wu (2020) show that that it is optimal for the firm to invest at a threshold above the switching threshold. We model investment timing in Subsection 4.2.
9 Mauer and Sarkar (2005) use r = 0.05, δ = 0.02 and $\sigma = 0.25$ , while Hackbarth and Mauer (2011) use r = 0.06, δ = 0.05 and $\sigma = 0.25$ . Our use of a lower volatility level reflects product markets with a moderate effect of variations in the target market size, disposable income, tastes and prices of substitute products (see, for instance, Aguerrevere, 2003, 2009). We consider higher volatility that is more reflective of industries with a larger variation such as luxury or technology products in our sensitivity results.
10 Theoretically, it is also possible that ${x}_B > {x}_L$ if ${P}_S$ is sufficiently high. In this case, the firm never reduces scale temporarily and operational flexibility is not used. Therefore, the appropriate firm value is given by the value of the rigid firm. In our analysis below, we focus on the case where ${x}_B < {x}_L$ , that is, the flexible firm defaults at a value where the firm is operating in idle mode.
11 As our goal is to investigate the effect of switching costs, without loss of generality we fix the rollover parameter m = 6 which fixes the trade credit maturity to (1/m) equal to 2 months across all sensitivities. Qualitatively similar results are obtained if we fix the trade horizon at a different level.
12 In the figure we vary only the switching costs from idle to active mode. When we vary both switching costs, we observe a similar widening of the hysteresis zone and a similar effect of switching costs on trade credit and quantities (albeit this is triggered at lower switching costs levels because both switching costs are varied).
13 Similarly, in Hagspiel et al. (2016) the flexible firm can only invest in active mode, and not in idle mode. In active mode, the firm can invest such that right after the moment of investment it operates either below or at full capacity, as they allow for varying utilization rates of capacity. As our focus is on modeling entry decisions in the presence of trade credit, to keep the model tractable we assume only two regions (either active mode operating at full capacity or idle mode).
14 In additional nontabulated sensitivity analysis, our findings reveal that, in the context of high demand levels triggering investment, both flexible and rigid firms result in supplier requesting early payment tilting solutions to short maturity. This outcome is mostly driven by the extensive delay of investment inherent in these frameworks and yields no particularly new insights. We have thus opted to study the entry timing and capacity of the flexible and rigid firm for a fixed maturity horizon.
15 For consistency with the previous sections, we define a recovery value parameter instead of proportional bankruptcy costs as typically in the capital structure literature. Recovery defined above is simply one minus the proportional bankruptcy costs incurred.
16 Note that ${C}_S$ and ${P}_S$ are not directly comparable, as ${C}_S$ is a flow of operating costs while ${P}_S$ is like a principal payment. We set ${C}_S = 0.25$ because ${C}_S/r$ implies a similar reduction in buyer value as $\frac{{m{P}_S}}{{r + m}}$ for the low trade credit maturities $1/m$ (high enough $m)\$ used in practice.
17 Note that the firm receives the full amount ${P}_sQ$ on credit. As this is part of the cost of goods sold that is tax deductible, this implies a tax benefit related to purchases from supplier of $\tau {P}_sQ$ per period. The rollover of credit involves the repayment of trade credit with payments $m{P}_sQ$ that have no additional tax implications because taxes have already been considered at the time of purchase under accrual accounting (see Desai et al., 2016). Thus, although trade credit is an interest free loan that does not provide interest tax shield, the purchase of goods from the supplier (on credit or in cash) provides the firm tax shields through the tax deductibility of purchased products.
18 One could incorporate a per unit cost for the supplier, ${C}_S,$ which could imply that supplier value is $S( x ) = D( x ) - \frac{{{C}_SQ}}{r} + \frac{{{C}_SQ}}{r}\ {( {\frac{x}{{{x}_B}}} )}^{{\beta }_2}$ . However, incorporating this per unit costs would simply scale down supplier's value. Without loss of generality, and as in the previous extension, we thus assume in our simulations that ${C}_S = 0$ . We have also conducted sensitivity results assuming ${C}_S > 0$ without changing the insights we provide below.
19 Our implications are robust to different choice of ${\Gamma}_{S}$ and ${\Gamma}_{B}$ . Our sensitivity analysis of varying ${\Gamma}_{S}$ and ${\Gamma}_{B}$ has shown they have the same directional effects as the effects of ${\eta}_{S}$ and ${\eta}_{B}$ respectively.

Citing Literature

Volume51, Issue9-10

October-November 2024

Pages 2371-2409

Production flexibility and trade credit under revenue uncertainty

Abstract

1 INTRODUCTION

2 THE MODEL

2.1 Model setup

2.2 Inflexible case

2.2.1 Trade credit value under inflexible case

2.2.2 Buyer value under inflexible case

2.3 Flexible case

2.3.1 Trade credit value under flexible case

2.3.2 Buyer value under flexible case

2.4 Interactions between the buyer and the supplier

3 NUMERICAL RESULTS

3.1 Baseline results

3.2 Sensitivity analysis

4 EXTENSIONS

4.1 Switching costs

4.2 Entry timing of firms

4.3 Interactions of trade credit with debt

4.3.1 Buyer value and interactions of debt and trade credit

4.4 The non-cooperative Nash bargaining game

5 CONCLUSIONS

ACKNOWLEDGMENTS

APPENDIX A: DETAILS ON THE DERIVATION OF BUYER'S VALUE

Inflexible buyer value

Flexible buyer value

APPENDIX B: FLEXIBLE BUYER VALUE WITH SWITCHING COSTS

APPENDIX C: ANALYTICAL DERIVATION OF x_D IN THE PRESENCE OF DEBT IN SUBSECTION 4.3

Open Research

DATA AVAILABILITY STATEMENT

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Production flexibility and trade credit under revenue uncertainty

Abstract

1 INTRODUCTION

2 THE MODEL

2.1 Model setup

2.2 Inflexible case

2.2.1 Trade credit value under inflexible case

2.2.2 Buyer value under inflexible case

2.3 Flexible case

2.3.1 Trade credit value under flexible case

2.3.2 Buyer value under flexible case

2.4 Interactions between the buyer and the supplier

3 NUMERICAL RESULTS

3.1 Baseline results

3.2 Sensitivity analysis

4 EXTENSIONS

4.1 Switching costs

4.2 Entry timing of firms

4.3 Interactions of trade credit with debt

4.3.1 Buyer value and interactions of debt and trade credit

4.4 The non-cooperative Nash bargaining game

5 CONCLUSIONS

ACKNOWLEDGMENTS

APPENDIX A: DETAILS ON THE DERIVATION OF BUYER'S VALUE

Inflexible buyer value

Flexible buyer value

APPENDIX B: FLEXIBLE BUYER VALUE WITH SWITCHING COSTS

APPENDIX C: ANALYTICAL DERIVATION OF xD IN THE PRESENCE OF DEBT IN SUBSECTION 4.3

Open Research

DATA AVAILABILITY STATEMENT

REFERENCES

Citing Literature

Figures

References

Related

Information

APPENDIX C: ANALYTICAL DERIVATION OF x_D IN THE PRESENCE OF DEBT IN SUBSECTION 4.3