Unexpected management forecasts and future stock returns
Abstract
This study investigates the effect of managerial discretion regarding initial earnings forecasts on future stock returns for Japanese firms. We estimate the unexpected portion of initial management earnings forecasts (“unexpected forecasts”) based on the findings of fundamental analysis research and define it as a proxy for forecast management. Using this measure, we find that firms with higher unexpected forecasts are related to negative abnormal returns over the subsequent 12 months. By contrast, the expected portion of earnings forecasts is not related to future abnormal returns. These results suggest that the market tends to appropriately price the credible portion of management forecasts, while overpricing the less credible portion. Further analysis reveals that the relationship between unexpected forecasts and future returns is (1) distinct from accruals anomaly, notably (2) in the 6-month return window, (3) in the first half of the sample period (especially in 2005 and 2006), (4) in extreme unexpected forecast news and (5) in a poor information environment. This study extends the literature by focusing on a more desirable research setting in Japan, compared to other studies, to explore management forecasts and present new implications for the market pricing of management earnings forecasts.
1 INTRODUCTION
Many studies document that management earnings forecasts are useful for stock market investors (Ajinkya & Gift, 1984; Frost, 1997; Hutton et al., 2003; Jennings, 1987; Patell, 1976; Penman, 1980; Rogers & Stocken, 2005; Skinner, 1994; Waymire, 1984). Some also reveal that management forecasts are systematically upwardly biased, suggesting that managers may be incentivized to bias their initial earnings forecasts (Iwasaki et al., 2023; Kato et al., 2009; Rogers & Stocken, 2005). This study investigates the effect of managerial discretion over initial earnings forecasts on future stock return. In other words, we investigate whether investors can see through forecast management at the initial forecast announcement date.
We use a new measure to evaluate the forecast management at the forecast announcement date drawn from Iwasaki et al. (2023) and Kitagawa and Shuto (2021). They develop a prediction model based on the findings of fundamental analysis research (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993) to decompose the forecast change in earnings by managers (“forecast innovations”)1 into expected and unexpected portions (“expected forecasts” and “unexpected forecasts,” respectively). We adopt unexpected forecasts as the proxy for the forecast management, and examine whether stock investors fully anticipate the implications of forecast management.
We use a sample of Japanese firms because their reporting practice for management forecasts has features that are useful to our study (Iwasaki et al., 2023; Kato et al., 2009). First, most listed firms report point management forecasts conforming with the recommendations of the Tokyo Stock Exchange (TSE). Second, listed companies are obliged to report their main accounting earnings for the current year and their earnings forecasts for these items for the next year simultaneously. These factors are expected to mitigate sample selection bias and measurement error of the variables, which provides a useful setting to test our hypothesis.
This study seeks to better understand the economic consequences of bias in management earnings forecasts. Market participants use management forecast announcements, especially in Japan, as a crucial source of latest information. For example, previous studies reveal that stock price reactions around the announcement date are more pronounced for forecast earnings than for actual earnings (Conroy et al., 1998; Darrough & Harris, 1991). Recent studies document that forecast-based earnings benchmarks at the earnings announcement, that is, forecast innovations, have incremental information content beyond actual earnings surprise measures around the announcement date (Asano, 2009; Iwasaki et al., 2023; Kato et al., 2009).
The significant economic consequences may induce Japanese managers to manage their earnings forecasts. Iwasaki et al. (2023) adopt unexpected forecasts as a proxy for forecast management and provide evidence that Japanese firm managers are likely to manage their earnings forecasts to obtain higher stock returns on the earnings announcement date.2 Moreover, Iwasaki et al. (2023) find that firms with upward forecast management are more likely to miss their earnings forecasts at fiscal year-end and to revise their forecasts downward to meet their earnings forecasts during the same period. These findings imply that management earnings forecasts containing a high unexpected portion are less credible than those containing a low unexpected portion. Despite the practical importance of management earnings forecasts as a significant source of decision making, research on how unexpected forecast management affects future stock performance is scarce. Ng et al. (2013) analyze management forecasts under voluntary disclosure in the United States and provide evidence that more credible forecasts are associated with a larger reaction around management forecasts and a smaller post-management forecast drift, suggesting that the credibility of management forecasts can remedy the market's mispricing of management forecasts. However, the relationship between the credibility of management forecasts and future stock returns in situations in which the former are extensively disclosed, such as in Japan, remains unclear. Exploring the relationship between management forecast bias and future stock price could enhance the understanding of stock market efficiency and help investors use management earnings forecasts more efficiently.
Thus, this study investigates whether investors fully comprehend the implications of unexpected forecasts for the credibility of management earnings forecasts. Specifically, we examine the relationship between unexpected forecasts and future returns. We predict that investors have difficulty in evaluating the credibility of management forecasts because these depend heavily on firms’ private information. Hence, we hypothesize that investors naively fail to anticipate the lower credibility of higher unexpected forecasts (i.e., overpriced unexpected forecasts) at the initial forecast announcement dates, and thus, a negative relationship between unexpected forecasts and future abnormal stock returns will occur.
Our hedge-portfolio test, which comprises a portfolio long in firms in the most negative decile and short in firms in the most positive decile of unexpected forecasts, yields an abnormal return of 5.5% over 12 months. By contrast, we find that a hedge-portfolio test based on expected forecasts does not yield significant positive abnormal returns over 12 months. We conduct regression analysis and find that unexpected forecasts are negatively associated with future returns. These results suggest that the market tends to appropriately price the credible portion of management forecasts while overpricing the less credible portion.
This study includes several additional analyses to verify the validity of our results. First, we investigate whether the relationship between unexpected forecasts and future returns is distinct from an accruals anomaly (Collins & Hribar, 2000; Richardson et al., 2005; Sloan, 1996; Xie, 2001). The theoretical background of the relationship between unexpected forecasts and future returns is similar to that of a discretionary accruals anomaly. This is because both are caused by managerial discretion that results in a bias in earnings. Importantly, the Japanese listed firms report realized earnings and management forecast simultaneously, suggesting that the measurement periods of discretionary accruals and unexpected forecast anomalies are the same. Therefore, our main findings may be explained with reference to the accruals anomaly. After controlling for discretionary accruals, we find that unexpected forecasts are negatively associated with future returns suggesting that the mentioned anomalies are distinct.
Second, we focus on an alternative explanation for our results based on risk pricing in efficient markets by investigating abnormal stock returns over the short window around subsequent announcements of management forecast revisions. Our results reveal a significant positive relationship between unexpected forecasts and short-window returns around subsequent forecast revision announcement dates. This implies that abnormal stock returns earned through a trading strategy based on unexpected forecasts are less likely to be caused by incorrectly measured risk.
Third, we provide a deeper understanding of the mispricing hypothesis. Specifically, the unexpected forecasts anomaly is observed only in the subsamples with low sophisticated investors (i.e., institutional and foreign investors) ownership. Moreover, the unexpected forecasts anomaly is more distinct in the first half of the sample period (especially in 2005 and 2006) compared to the second half, suggesting the existence of the learning effect. These are consistent with market mispricing.
Fourth, we investigate the relationship between unexpected forecasts and future outcomes and find that firms with higher unexpected forecasts are more likely to miss their earnings forecasts. Accordingly, our argument that earnings forecasts containing higher unexpected forecasts are less credible is generally validated. Finally, we provide some evidence through additional analyses. First, we find no significant relationship between Ng et al.’s (2013) measure of unexpected forecasts and future returns. Second, we examine the effect of outliers and find that extreme unexpected forecast news increases investor mispricing. Third, the good information environment attenuates investors’ mispricing of unexpected forecasts. Fourth, we confirm that our results are robust to the standard error bias highlighted by Chen et al. (2023). Finally, our results are robust to controlling for insider ownership and scale effects.
This study contributes to the literature in several ways. First, we reveal the economic consequences of unexpected forecasts management. Previous studies demonstrate that while management forecasts have information contents (Kato et al., 2009), managers opportunistically report their earnings forecasts and their forecast management is related to subsequent forecast revisions and errors (Iwasaki et al., 2023). We extend these studies by showing that investors do not fully understand the implications of forecast management and price corrections occur after the issuance of initial earnings forecasts.
We extend Ng et al.’s (2013) research by focusing on a more desirable research setting in Japan and present different implications for the market pricing of management earnings forecasts. In contrast to Ng et al. (2013), who focus on US firms with voluntary disclosure of management forecasts, we focus on the Japanese setting, in which managerial forecast earnings are almost compulsorily disclosed. When firms that disclose managerial forecasts in the United States have unique characteristics (e.g., strong incentives to disclose high-quality information or an excellent information environment), interpreting the results becomes difficult owing to the problem of self-selection bias (see Section 2 for details). Ng et al. (2013) establish that the market underreacts more to less credible forecasts, while we provide evidence suggesting that the market in Japan overprices more to unexpected (less reliable) forecasts at the announcement and results in a subsequent correction. In other words, it implies that while the US market can determine the credibility of management forecasts at the announcement to a certain degree, the Japanese market cannot accurately discern the credibility of management forecasts. The reason for these different results may be that, in addition to the differences in institutional backgrounds between the United States and Japan, we directly estimate the unexpected portion of management earnings forecasts. Ng et al. (2013) use several proxy variables for management, but do not directly estimate the unexpected portion of management forecasts. Thus, investors may not see through the unexpected forecasts appropriately.
Second, our study contributes to the literature on fundamental analysis. Existing literature documents that the fundamental signals available from financial statements are related to future earnings and stock returns (Abarbanell & Bushee, 1997, 1998; Mohanram, 2005; Ou & Penman, 1989; Piotroski, 2000; Wahlen & Wieland, 2011). We extend these studies by providing further evidence that unexpected management forecasts estimated using the fundamental signals presented in Abarbanell and Bushee (1997, 1998) are also useful for predicting future returns.
Finally, we reveal that the relationship between unexpected forecasts and future returns is not explained by the accruals anomaly. More importantly, we demonstrate the usefulness of the investing strategy based on unexpected forecasts and (discretionary) accruals. Studies reveal the efficacy of combining two investing strategies such as book-to-market ratio and F-score (Piotroski, 2000; Piotroski & So, 2012), momentum and F-score (Ahmed & Safdar, 2018; Chen et al., 2016), sales growth and F-score (Ahmed & Safdar, 2017), F-score or G-score (Mohanram, 2005) and V/P ratio (Frankel & Lee, 1998; Li & Mohanram, 2019). In line with these studies, we demonstrate that an investing strategy based on unexpected forecasts and (discretionary) accruals earns larger returns than an individual strategy.
The remainder of this paper is organized as follows. Section 2 summarizes the literature and develops our research hypotheses. Section 3 explains the variable measurements used and the research design for testing our hypotheses. Section 4 outlines the sample selection procedure and describes the descriptive statistics. Section 5 reports the empirical results of the relationship between unexpected forecasts and future performance. Section 6 summarizes the results of the additional analyses. Finally, Section 7 concludes with a summary.
2 HYPOTHESIS DEVELOPMENT
2.1 Management forecasts practice in Japan
-
Listed companies are expected to release point forecasts of annual earnings on each annual earnings announcement date and revisions of these forecasts on interim earnings announcement dates. Thus, managers provide initial forecasts for year t when year t – 1 earnings are announced, and revisions (including confirmations) when interim earnings are announced.
-
Managers are expected to provide forecasts for sales, operating income, earnings before extraordinary items and taxes, net income, earnings per share and dividend per share.
-
Forecasts must be updated if there are “significant” revisions in management estimates, defined as either changes in sales estimates of 10% (or more), or in earnings estimates of 30% (or more; the “Significance Rule”), or both. In contrast to the initial forecasts encouraged by the stock exchange listing rules, these revisions are required under the Act (Securities Listing Regulations, Rule 405, Paragraphs 1 and 3).
These management earnings forecast practices in Japan differ from those in the United States and offer a useful research setting for our analysis. First, management forecast disclosure is effectively mandated in Japan (Kato et al., 2009; Iwasaki et al., 2023). Although management forecasts expected by the TSE comprise a voluntary disclosure without legal backing, almost all firms provide such forecasts in accordance with the TSE's recommendation.3 Owing to the comprehensive availability of observables, studies using Japanese firms are free from self-selection bias (Ishida et al., 2021; Iwasaki et al., 2023; Kato et al., 2009). This is a clear difference from those examining US firms with voluntary disclosure of management forecasts and is a major benefit of focusing on Japanese firms.4
Second, listed companies are obliged to simultaneously report the main accounting items of the current year and the management forecasts of these items on annual earnings announcement dates. Hence, we can form all the portfolios for the hedge-portfolio strategy based on unexpected forecasts at the beginning of each fiscal year, which can reduce any bias caused by differences in issue dates.5
Finally, while many US firms tend to provide range-estimated forecasts, Japanese listed companies provide point-estimated forecasts.6,7 Some studies provide evidence that range forecasts can introduce a measurement error problem (Ciconte et al., 2014; Jensen & Plumlee, 2020).8 However, point-estimated forecasts in Japanese management forecasts practice do not introduce such bias. Thus, the Japanese system provides a useful setting in which to investigate the effects of management earnings forecasts on future stock returns.
2.2 Literature on the relationship between unexpected forecasts and future earnings
The credibility of management earnings forecasts has been a central concern in accounting research, because managers have an incentive to bias them (Rogers & Stocken, 2005). Several studies investigate the credibility of management earnings forecasts by identifying the determinants of their systematic bias (Frost, 1997; Kato et al., 2009; Ota, 2006; Rogers & Stocken, 2005). In general, they explore the determinants of earnings forecasts errors at fiscal year-end to evaluate the credibility of management earnings forecasts.9 Kasznik (1999) examines management earnings forecasts in terms of earnings management, and demonstrates that managers tend to use discretionary accruals and revise forecasts downward to meet their own forecast earnings.
Kato et al. (2009) and Iwasaki et al. (2023) are more relevant for our study because they focus on the initial management earnings forecasts for a sample of Japanese firms. Managers in Japanese firms are likely to have an incentive to manage their earnings forecasts because, as indicated by previous market-oriented research, market participants use management forecast announcements as a crucial source of new information. Several recent studies reveal that forecast innovations, the forecast-based earnings benchmark at the earnings announcement, contain incremental information content beyond actual earnings surprise measures around the announcement date (Asano, 2009; Iwasaki et al., 2023; Kato et al., 2009). Further, many studies provide evidence that stock price reactions around the announcement date are more pronounced for forecast earnings than for actual earnings (Conroy et al., 1998; Darrough & Harris, 1991). Finally, an analysis based on Ohlson's (2001) valuation framework shows that management forecasts have the highest correlation with and incremental explanatory power for stock prices (Ota, 2010). These results suggest that management earnings forecasts have higher information content than actual annual earnings in the Japanese stock market and may induce Japanese managers to manage their earnings forecasts.10
Consistent with this view, Kato et al. (2009) suggest that initial management earnings forecasts for a fiscal year are systematically upward biased, and managers revise their forecasts downward during the fiscal year to meet their forecasts. Iwasaki et al. (2023) measure the unexpected portion of initial management forecasts and reveal that managers control their initial earnings forecasts to meet forecast innovations. Iwasaki et al. (2023) also document that firms with higher unexpected forecasts tend to revise their forecasts downward after issuing initial forecasts.
2.3 Hypothesis on the relationship between unexpected forecasts and future returns
We extend previous studies showing that firms with higher unexpected forecasts are more likely to miss their forecasts and revise them downward (Iwasaki et al., 2023). We examine whether markets fully understand the implications of such behavior for the credibility of management earnings forecasts. Many studies have indicated that management earnings forecasts are positively associated with current stock returns, attributable to the ability of earnings forecasts to summarize value relevant information (Ajinkya & Gift, 1984; Frost, 1997; Hutton et al., 2003; Jennings, 1987; Patell, 1976; Penman, 1980; Rogers & Stocken, 2005; Skinner, 1994; Waymire, 1984). Regarding Japanese firms, some studies have revealed that stock price reactions around announcement dates are more pronounced for management earnings forecasts for year t + 1 than for actual annual earnings for year t. That is, management earnings forecasts have higher information content than actual annual earnings around the announcement date in the Japanese stock market (Conroy et al., 1998; Darrough & Harris, 1991; Ota, 2010). Furthermore, Kato et al. (2009) indicate that forecast innovations are associated with announcement period stock returns after controlling for both an earnings surprise and a dividend surprise measure. Finally, forecast revisions subsequent to the initial forecasts also have a significantly positive association with announcement period stock returns, indicating that the revisions’ announcements can surprise investors (Gotoh, 1997; Kato et al., 2009). Taken together, these results suggest that management earnings forecasts have information content because they influence stock prices.
However, the effect of management earnings forecasts on future returns has been largely ignored. Ng et al. (2013), who examine the effect of the credibility of management forecasts on post-management forecasts drift in return, are an exception.11 In particular, they document an underreaction to management forecasts news at the announcement and a significant post-management forecasts drift in return. They also find that more credible forecasts are associated with a larger reaction around the management forecasts and a smaller post-management forecast drift in return. The results suggest that the market overly discounts less credible forecasts, resulting in a greater underreaction and a subsequent correction. In other words, this implies that the market can determine the credibility of management forecasts at the announcement to a certain degree.
Although Ng et al. (2013) present interesting evidence, as already noted, it may contain problems associated with focusing on management forecasts, which is a voluntary disclosure. For example, the results may be difficult to interpret if there is a characteristic that firms issuing management forecasts have incentive to provide higher quality financial reporting. Therefore, the relationship between the credibility of management forecasts and future stock returns is not fully explored.
We can assume two contrary predictions about the consequences of unexpected forecasts. If investors anticipate the implication of unexpected forecasts for the credibility of management earnings forecasts, we can predict that these are not associated with future abnormal returns. In other words, managers would not be able to raise stock prices by discretionarily increasing earnings forecasts. This is because investors are likely to properly discount low-quality earnings forecasts. However, if investors naively fail to understand the implications of the lower credibility of unexpected forecasts, these forecasts will have a negative association with future abnormal returns. Specifically, if investors naively ignore the current unexpected forecasts expected to cause forecast errors and revisions, they will be surprised by bad performance announcements in subsequent periods, leading to negative abnormal returns in later periods.
Considering Japan's institutional background, we expect the latter explanation (mispricing hypothesis) to be valid. First, the disclosure of management forecasts is effectively mandated in Japan and is a crucial source of information for investors (Conroy et al., 1998; Darrough & Harris, 1991; Ota, 2010). Therefore, managers have a strong incentive to manipulate their earnings forecasts. However, even though disclosure is semi-mandatory, management forecasts are not audited. Furthermore, previous studies argue that litigation costs in Japan are lower than those in the United States, which induces managers of Japanese firms to conduct forecast management more aggressively (Iwasaki et al., 2023; Kato et al., 2009). Therefore, while there are regulations that encourage the disclosure of management forecasts, there is no institutional system that guarantees the reliability of management earnings forecasts.
Second, analysts’ earnings forecasts can help explain the objectivity of management forecasts, but there are differences in the information environment for analysts between Japan and the United States. Compared to the US market, analyst coverage of firms is relatively low in Japan, and analyst forecasts are not issued as often as in the United States (Nara & Noma, 2013a). There is also evidence that Japanese investors respond more to management forecasts than to analysts’ forecasts (Ota, 2010). In addition, previous studies on Japanese firms provide evidence that analysts revise their own forecasts in line with management forecasts when they are released (Nara & Noma, 2013b; Ota & Kondo, 2011). Therefore, there are relatively few indices to evaluate the objectivity of management forecasts in Japan.
Finally, the mispricing hypothesis is similar to the theoretical explanation of the accruals anomaly (Collins & Hribar, 2000; Richardson et al., 2005; Sloan, 1996; Xie, 2001). Studies reveal that investors overestimate the persistence of accruals that are components of actual earnings and, thus, overprice these accruals. In addition to evidence from the US market, studies indicate that the accruals anomaly exists in the Japanese stock market (Kubota et al., 2010; Leippold & Lohre, 2012; Pincus et al., 2007).12 Given the evidence of accrual mispricing in the Japanese stock market, we predict that the mispricing hypothesis will also apply to the relationship between unexpected forecasts and future abnormal returns. This is because unexpected management for initial forecasts is less perceptible and more difficult for investors to detect than earnings management. Investors may be able to detect earnings management by analyzing accounting items in financial statements, but it will be more difficult for them to see through the forecasts management because these depend heavily on a firm's private information. Thus, we predict a negative relationship between unexpected forecasts and future returns and propose the following hypothesis:
Hypothesis 1.: Unexpected forecasts are negatively related to future returns.
3 RESEARCH DESIGN
3.1 Variable measurement
where
CEARNt = (net income for year t – net income for year t – 1)/total assets at the end of year t – 1. CHGEARNt-1 = (net income for year t – 1 – net income for year t – 2)/total assets at the end of year t – 1. AB fundamental signalst-1 = fundamental signals for the current fiscal year t proposed by Lev and Thiagarajan (1993) and Abarbanell and Bushee (1997). Detailed definitions of the variables are summarized in the Appendix. HISTBIASt-1 = 2-year average of the absolute value of the forecast error based on initial forecast. The forecast error based on initial forecast for year t – 1 = (actual earnings for year t – 1 – management earnings forecast released at the same time as actual earnings for year t – 2)/total assets at the end of year t – 1. ABSERRORt-1 = absolute value of the forecast error based on last forecasts. The forecast error based on last forecast for year t – 1 = (actual earnings for year t – 1 – the latest management forecasts for year t – 1)/total assets at the end of year t – 1. NUMREVt-1 = number of revisions during year t – 1. BONDt-1 = 10-year government bond yield for year t – 1. CHGGDPt-1 = annual growth rate of nominal GDP for year t – 1.
Our estimation model is based primarily on the first-order serial correlation model for changes in annual earnings in accordance with the findings of previous studies on earnings persistence (Bernard & Thomas, 1990; Brown & Kennelly, 1972; Freeman & Tse, 1989). Thus, we include the current change in net income (CHGEARNt) as an independent variable.15
Furthermore, we include nine fundamental signals variables empirically supported by previous fundamental analysis research (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993) to improve the model's explanatory power. The fundamental signals include changes in inventory (INVt-1), accounts receivables (ARt-1), capital expenditures (CAPXt-1), gross margin (GMt-1), selling and administrative expenses (S&At-1), effective tax rate (ETRt-1), total accruals (CTACt-1),16 audit qualification dummy (AQt-1) and sales revenue per employee (LFt-1). Detailed definitions of each fundamental signal are provided in the Appendix. Lev and Thiagarajan (1993) indicate that these signals are significantly associated with contemporaneous stock returns, whereas Abarbanell and Bushee (1997) demonstrate that the association between signals and contemporaneous returns can be explained by their ability to predict future earnings. Following Lev and Thiagarajan (1993) and Abarbanell and Bushee (1997), fundamental signals variables are defined as having a negative association with future performance. Thus, these variables are expected to have a negative association with CEARNt.17
Furthermore, we control for two factors: manager bias and future macroeconomic expectations. First, we use the 2-year average of the absolute value of the forecast error based on initial forecast (HISTBIASt-1) to capture the historical manager forecast bias. Second, we add the absolute value of the forecast error on last forecasts (ABSERRORt-1) and the number of revisions (NUMREVt-1) as control variables. Next, we add the 10-year government bond yield (BONDt-1) to control for future macroeconomic expectations. Finally, we add the annual growth rate of nominal GDP (CHGGDPt-1) as a proxy for future GDP change.
FIt for year t is measured by the management forecasts for year t + 1 less the actual earnings for year t. Both EFt and FIt are divided by total assets at the end of year t – 1. A larger UFt implies more upward forecast management.21
3.2 Forecast management and future returns
To test our hypothesis, we first conduct an analysis using a hedge-portfolio test method commonly used for testing mispricing of accounting information (Frankel & Lee, 1998; Sloan, 1996; Xie, 2001). Specifically, we group firms into portfolio deciles each year based on their ranking of unexpected forecasts and form a hedge portfolio that takes a long position in the most negative unexpected forecasts decile and a short position in the most positive. We investigate the hedge portfolio returns beginning 4 months after the fiscal year-end and running to the 6th and 12th month for evidence of price correction.22 Hedge portfolio returns are calculated using 6- and 12-month size-adjusted buy-and-hold returns, as defined below. If investors overprice unexpected forecasts in the portfolio formation year, as our hypothesis suggests, the hedge portfolio returns in subsequent years will be positive because of investors’ delayed price response to information about the credibility of management forecasts.
where
BHAR6mt+1 (BHAR12mt+1) = size-adjusted abnormal return calculated as the firms’ buy-and-hold return beginning at the start of the 4 months after the fiscal year-end t and ending at the end of the third month after the interim (fiscal) year-end t + 1, minus the buy-and-hold return on a size-matched portfolio over the same period. UFt = forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1. AB fundamental signalst = fundamental signals for current fiscal year t proposed by Lev and Thiagarajan (1993) and Abarbanell and Bushee (1997). Carhart four factorst = risk factors for current fiscal year t proposed by Carhart (1997).
Our primary concern with the independent variable is the unexpected forecasts (UFt), as described in Subsection 3.1.23 The negative coefficient of UFt signifies that investors do not fully understand and overestimate the credibility of unexpected forecasts, consistent with our hypothesis. Conversely, if investors anticipate the implication of unexpected forecasts for the credibility of management forecasts, we expect that UFt is not significantly associated with BHAR6mt+1 and BHAR12mt+1. Furthermore, to examine the effect of expected forecasts on future stock returns, we include EFt as an independent variable and predict that there is no significant association between EFt and BHAR6mt+1 and BHAR12mt+1.
Moreover, we control for several variables that explain future firm performance. First, we include nine fundamental signals for the current fiscal year t (AB fundamental signalst), as defined in Subsection 3.1. (INVt, ARt, CAPXt, GMt, S&At, ETRt, CTACt, AQt and LFt). As previously described, these variables are expected to have a negative association with future earnings. Thus, we expect that all these variables will be negatively related to future forecast errors and revisions.
Furthermore, we control for Carhart's (1997) risk factors (Carhart four factorst) of market beta (BETAt), firm size (SIZEt), book-to-market ratio (BMt) and momentum effect (MOMENTt). BETAt is calculated with a market model using monthly returns over the 60-month period ending in the current fiscal year t. SIZEt is the natural log of the market value of equity at the end of year t, and BMt corresponds to the book value of equity at the end of year t divided by the market value of equity at the end of year t. MOMENTt is the monthly buy-and-hold stock return over fiscal year t. These variables are expected to represent unknown risk factors and are positively correlated to future expected returns (Carhart, 1997; Fama & French, 1993). The expected signs of the coefficients on BETAt, BMt and MOMENTt are positive, and SIZEt is negative. Finally, we control for year- and industry-fixed effects.
4 SAMPLE SELECTION AND DESCRIPTIVE STATISTICS
4.1 Sample selection procedure
Our sample selection procedure is summarized in Table 1. The necessary data on financial statements, management forecasts and stock price are all obtained from the Nikkei NEEDS Financial QUEST database. After excluding financial institutions (banks, securities companies, insurance companies and credit and leasing financial institutions), we identify listed companies that report consolidated financial statements for the calendar years 2003 to 2019. Our initial sample comprises 56,673 firm-year observations. For this sample period, we delete firm-year observations as follows: (1) whose fiscal year does not end in March, (2) those with changing fiscal year-ends, (3) with missing data needed to calculate forecast innovations, errors and revisions and (4) with missing financial statements and stock data needed for our analyses. These criteria yield a final sample size of 29,326 firm-year observations. The untabulated results reveal that about 99.6% of observations (56,472 of 56,673) in our initial sample include forecast data. This indicates that most Japanese firms issue forecast information, and is consistent with the findings of studies that have argued that Japanese forecasting practices are effectively mandated (Iwasaki et al., 2023; Kato et al., 2009).
| Criteria | Firm-years |
|---|---|
| Firm-years with data on consolidated financial statements during 2003−2019a | 56,673 |
| Less: | |
| Fiscal year does not end in March | (16,750) |
| Changing in accounting month within firm-years necessary for our analyses | (136) |
| Missing data for calculating forecast innovations, current and future forecast errors | (5221) |
| Missing financial statements and stock data necessary for our analyses | (5240) |
| Final sample | 29,326 |
- Note: The data necessary for this study are available from the Nikkei NEEDS Financial QUEST. The industry is based on the Nikkei industry classification code (Nikkei gyousyu chu-bunrui). The financial statements data are acquired from consolidated financial statements.
- a Excluding financial institutions (banks, securities companies and insurance companies) and other financial institutions (credit and leasing).
4.2 Descriptive statistics
Descriptive statistics for our sample are provided in Table 2. To avoid outlier effects, we winsorize all sequential variables at 1% and 99%. While the average of unexpected forecasts (UFt), the variable of our primary concern, is 0.015, the average of expected forecasts (EFt) is −0.006. The untabulated results reveal that the mean value of scaled management forecast is 0.033. That is, on average, approximately 45% of initial management earnings forecasts are composed of unexpected forecasts.
| Mean | p25 | P50 | P75 | SD | Skewness | Kurtosis | N | |
|---|---|---|---|---|---|---|---|---|
| BHAR6mt+1 | 0.007 | −0.125 | −0.015 | 0.104 | 0.218 | 1.378 | 7.898 | 29,326 |
| BHAR12mt+1 | −0.002 | −0.189 | −0.039 | 0.128 | 0.321 | 1.522 | 8.637 | 29,326 |
| FIt | 0.009 | −0.002 | 0.003 | 0.011 | 0.033 | 3.486 | 22.253 | 29,326 |
| UFt | 0.015 | −0.005 | 0.007 | 0.026 | 0.036 | 1.534 | 8.642 | 29,326 |
| EFt | −0.006 | −0.014 | −0.002 | 0.008 | 0.027 | −0.504 | 5.336 | 29,326 |
| INVt | 0.021 | −0.107 | 0.005 | 0.118 | 0.288 | 1.555 | 10.902 | 29,326 |
| ARt | −0.001 | −0.082 | −0.006 | 0.070 | 0.175 | 0.538 | 7.539 | 29,326 |
| CAPXt | −0.106 | −1.841 | 0.247 | 2.488 | 18.959 | −5.630 | 130.404 | 29,326 |
| GMt | −0.011 | −0.061 | −0.004 | 0.050 | 0.160 | −1.296 | 15.733 | 29,326 |
| S&At | −0.006 | −0.058 | −0.004 | 0.048 | 0.112 | −0.250 | 5.998 | 29,326 |
| ETRt | 0.003 | −0.001 | 0.000 | 0.002 | 0.016 | 3.358 | 26.549 | 29,326 |
| CTACt | 0.002 | −0.034 | 0.001 | 0.036 | 0.073 | 0.140 | 5.956 | 29,326 |
| AQt | 0.012 | 0.000 | 0.000 | 0.000 | 0.110 | 8.897 | 80.158 | 29,326 |
| LFt | −0.011 | −0.066 | −0.009 | 0.050 | 0.129 | −0.482 | 6.571 | 29,326 |
| BETAt | 9.976 | 8.726 | 9.773 | 11.028 | 1.696 | 0.507 | 2.874 | 29,326 |
| SIZEt | 1.280 | 0.704 | 1.107 | 1.658 | 0.806 | 1.457 | 6.408 | 29,326 |
| BMt | 0.011 | −0.200 | −0.036 | 0.147 | 0.363 | 1.795 | 9.998 | 29,326 |
| MOMENTt | 0.007 | −0.125 | −0.015 | 0.104 | 0.218 | 1.378 | 7.898 | 29,326 |
- Note: BHAR6mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 6 months beginning at the start of the 4 months after fiscal year-end. BHAR12mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 12 months beginning at the start of the 4 months after fiscal year-end. FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. UFt = forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1. EFt = Expected forecasts/total assets at the end of year t – 1. INVt = Δ Inventory in year t – Δ Sales in year t. The variable is merchandise and finished goods when available, total inventory otherwise. ARt = Δ Accounts receivable in year t – Δ Sales in year t. The variable is accounts receivable when available, accounts and notes receivable otherwise. CAPXt = Δ Industry capital expenditure in year t – Δ Firm capital expenditure in year t. Industry capital expenditure = aggregating capital expenditure for all firms with the same the Nikkei medium classification industry code. Firm capital expenditure = change in gross property, plant and equipment for a firm. GMt = Δ Sales in year t – Δ Gross margin in year t. S&At = Δ Selling and administrative expenses in year t – Δ Sales in year t. ETRt = Average effective tax rate from year t – 4 to year t – 1 – effective tax rate in year t. Effective tax rate = income taxes/income before income taxes. Each variable is acquired from the parent-only financial statement. CTACt = (total accruals for year t minus total accruals for year t – 1)/total assets at the end of year t. Total accruals are calculated as follows. Total accruals = (change in current assets – change in cash and deposits) – (change in current liabilities – change in financing items) – (change in allowance for doubtful debts + change in provision for retirement benefits or provision for retirement allowance + change in provision for directors’ retirement benefits + change in other long-term provision + depreciation). Financing items = change in short-term loans payable + change in commercial papers + change in current portion of long-term loans payable + change in current portion of straight bonds and convertible bonds. AQt = Dummy variable set to 0 if auditor's opinion in year t is unqualified, and 1 if auditor's opinion is qualified, or other.
- LFt = (sales revenue per employee for year t – 1 – sales revenue per employee for year t)/sales revenue per employee for year t – 1. Sales revenue per employee = sales/the number of employees at year-end. BETAt = Historical beta calculated using monthly returns over the 60-month period ending at the current fiscal year-end t. SIZEt = Natural log of market value of equity at the end of year t. BMt = Book value of equity at the end of year t/market value of equity at the end of year t. MOMENTt = Monthly buy-and-hold stock return over fiscal year t. The definitions of all of the fundamental signals except for ETR and CTAC (i.e., INV, AR, CAPX, GM, S&A, AQ and LF) are taken from Lev and Thiagarajan (1993). The Δ operator represents a percentage change in the percentage change in the variable based on 2-year average expectation model, which is the same as that of previous studies (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993). For example, ΔSales in year t = {Salest − E(Salest)}/E(Salest), where E(Salest) = (Salest-1 + Salest-2)/2. All other variables with Δ operator are calculated utilizing the same procedure.
The Pearson and Spearman rank-order correlation matrix among the variables used in our regression analyses is reported in Table 3. Consistent with our hypothesis, we find that UFt is significantly and negatively associated with BHAR6mt+1 and BHAR12mt+1. These results indicate that investors overprice unexpected forecasts and that firms with higher unexpected forecasts are more likely to earn lower future returns in year t + 1.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | (13) | (14) | (15) | (16) | (17) | (18) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (1) BHAR6mt+1 | 0.66 | −0.04 | −0.02 | −0.02 | −0.01 | 0.02 | 0.01 | −0.01 | −0.01 | 0.01 | −0.01 | −0.04 | 0.00 | −0.03 | 0.01 | 0.04 | 0.01 | |
| (2) BHAR12mt+1 | 0.64 | −0.03 | −0.04 | 0.01 | −0.02 | 0.01 | 0.01 | 0.01 | −0.01 | 0.01 | −0.01 | −0.05 | 0.00 | −0.02 | 0.04 | 0.01 | −0.02 | |
| (3) FIt | −0.05 | −0.03 | 0.59 | 0.10 | 0.04 | 0.01 | −0.02 | 0.17 | 0.12 | 0.00 | −0.04 | 0.07 | 0.08 | 0.04 | −0.10 | −0.07 | −0.09 | |
| (4) UFt | −0.06 | −0.04 | 0.70 | −0.60 | 0.01 | −0.06 | 0.00 | 0.08 | 0.13 | 0.07 | −0.01 | 0.15 | 0.17 | −0.03 | −0.13 | 0.03 | 0.03 | |
| (5) EFt | 0.02 | 0.03 | 0.27 | −0.49 | 0.00 | 0.07 | −0.02 | 0.07 | −0.02 | −0.08 | −0.05 | −0.14 | −0.12 | 0.07 | 0.01 | −0.09 | −0.16 | |
| (6) INVt | −0.02 | −0.02 | 0.03 | 0.02 | 0.01 | 0.09 | 0.00 | 0.08 | 0.19 | −0.04 | 0.08 | −0.03 | 0.20 | 0.00 | 0.01 | 0.02 | −0.06 | |
| (7) ARt | 0.01 | 0.00 | −0.01 | −0.03 | 0.03 | 0.09 | 0.03 | −0.03 | 0.05 | −0.01 | 0.14 | −0.05 | 0.07 | −0.03 | 0.02 | −0.01 | 0.02 | |
| (8) CAPXt | 0.00 | 0.01 | 0.00 | 0.05 | −0.07 | 0.00 | −0.01 | −0.02 | −0.02 | 0.02 | 0.01 | −0.03 | −0.01 | 0.01 | 0.00 | −0.01 | 0.02 | |
| (9) GMt | −0.01 | 0.01 | 0.19 | 0.11 | 0.08 | 0.05 | −0.05 | −0.02 | −0.15 | −0.06 | −0.06 | −0.01 | 0.04 | −0.01 | −0.05 | 0.09 | −0.23 | |
| (10) S&At | −0.02 | −0.01 | 0.15 | 0.17 | −0.06 | 0.17 | 0.07 | −0.01 | −0.05 | −0.06 | −0.05 | 0.02 | 0.53 | −0.04 | −0.05 | 0.12 | −0.18 | |
| (11) ETRt | 0.01 | 0.00 | 0.00 | 0.08 | −0.10 | −0.04 | −0.01 | 0.01 | −0.09 | −0.06 | 0.03 | 0.01 | −0.05 | 0.04 | −0.04 | 0.00 | 0.04 | |
| (12) CTACt | −0.01 | −0.02 | −0.06 | −0.01 | −0.06 | 0.09 | 0.14 | 0.01 | −0.09 | −0.06 | 0.06 | 0.00 | −0.03 | 0.01 | 0.01 | −0.02 | 0.04 | |
| (13) AQt | −0.03 | −0.04 | 0.07 | 0.18 | −0.15 | −0.02 | −0.04 | −0.01 | 0.00 | 0.02 | 0.03 | 0.00 | 0.00 | −0.01 | −0.02 | 0.01 | 0.01 | |
| (14) LFt | −0.01 | 0.00 | 0.07 | 0.18 | −0.15 | 0.18 | 0.11 | 0.00 | 0.09 | 0.55 | −0.06 | −0.04 | 0.00 | −0.03 | −0.05 | 0.12 | −0.16 | |
| (15) BETAt | 0.01 | 0.02 | 0.09 | 0.02 | 0.09 | 0.01 | −0.02 | 0.02 | −0.03 | −0.04 | 0.05 | 0.01 | −0.01 | −0.04 | 0.15 | −0.14 | 0.02 | |
| (16) SIZEt | −0.01 | 0.00 | −0.16 | −0.16 | 0.01 | 0.00 | 0.01 | 0.00 | −0.03 | −0.04 | −0.04 | 0.01 | −0.02 | −0.03 | 0.13 | −0.48 | 0.16 | |
| (17) BMt | 0.02 | 0.01 | −0.02 | 0.08 | −0.13 | −0.02 | −0.03 | −0.01 | 0.08 | 0.11 | −0.01 | −0.03 | 0.03 | 0.11 | −0.13 | −0.48 | −0.23 | |
| (18) MOMENTt | 0.00 | −0.03 | −0.10 | 0.01 | −0.13 | −0.03 | 0.03 | 0.03 | −0.22 | −0.17 | 0.06 | 0.05 | 0.01 | −0.13 | 0.09 | 0.13 | −0.22 |
- Note: Spearman (Pearson) correlations are above (below) the diagonal. BHAR6mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 6 months beginning at the start of the 4 months after fiscal year-end. BHAR12mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 12 months beginning at the start of the 4 months after fiscal year-end. FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. UFt = Forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1. EFt = Expected forecasts/total assets at the end of year t – 1. INVt = Δ Inventory in year t – Δ Sales in year t. The variable is merchandise and finished goods when available, total inventory otherwise. ARt = Δ Accounts receivable in year t – Δ Sales in year t. The variable is accounts receivable when available, accounts and notes receivable otherwise. CAPXt = Δ Industry capital expenditure in year t – Δ Firm capital expenditure in year t. Industry capital expenditure = aggregating capital expenditure for all firms with the same Nikkei medium classification industry code. Firm capital expenditure = change in gross property, plant and equipment for a firm. GMt = Δ Sales in year t – Δ Gross margin in year t. S&At = Δ Selling and administrative expenses in year t – Δ Sales in year t. ETRt = Average effective tax rate from year t – 4 to year t – 1 – effective tax rate in year t. Effective tax rate = income taxes/income before income taxes. Each variable is acquired from the parent-only financial statement. CTACt = (total accruals for year t minus total accruals for year t – 1)/total assets at the end of year t. Total accruals are calculated as follows. Total accruals = (change in current assets – change in cash and deposits) – (change in current liabilities – change in financing items) – (change in allowance for doubtful debts + change in provision for retirement benefits or provision for retirement allowance + change in provision for directors’ retirement benefits + change in other long-term provision + depreciation). Financing items = change in short-term loans payable + change in commercial papers + change in current portion of long-term loans payable + change in current portion of straight bonds and convertible bonds. AQt = Dummy variable set to 0 if auditor's opinion in year t is unqualified, 1 if auditor's opinion is qualified or other. LFt = (sales revenue per employee for year t – 1 – sales revenue per employee for year t)/sales revenue per employee for year t – 1. Sales revenue per employee = sales/the number of employees at year-end. BETAt = Historical beta calculated using monthly returns over the 60-month period ending at the current fiscal year-end t. SIZEt = Natural log of market value of equity at the end of year t. BMt = Book value of equity at the end of year t/market value of equity at the end of year t. MOMENTt = Monthly buy-and-hold stock return over fiscal year t. The definitions of all of the fundamental signals except for ETR and CTAC (i.e., INV, AR, CAPX, GM, S&A, AQ and LF) are taken from Lev and Thiagarajan (1993). The Δ operator represents a percentage change in the percentage change in the variable based on 2-year average expectation model, which is the same as that of previous studies (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993). For example, ΔSales in year t = {Salest − E(Salest)}/E(Salest), where E(Salest) = (Salest-1 + Salest-2)/2. All other variables with Δ operator are calculated utilizing the same procedure. Bold indicates statistically significant values at less than 0.1 level of significance using a two-tailed t-test.
5 MAIN RESULTS
5.1 Portfolio test
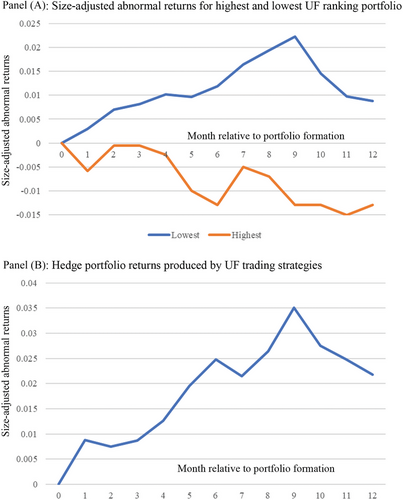
The average size-adjusted abnormal return for each unexpected forecasts decile and for the hedge portfolio based on UFt are summarized in Table 4. While the size-adjusted returns for the most positive unexpected forecasts decile are all negative in 6 (−0.013) and 12 months (−0.013); those for the most negative unexpected forecasts decile are all positive in 6 (0.012) and 12 months (0.009). The size-adjusted abnormal returns for the highest-minus-lowest hedge portfolio are 0.025 (t-value = 3.662) in 6 months and 0.022 (t-value = 2.152) in 12 months.24 These results are consistent with the market's overestimation of the credibility of unexpected forecasts and its overpricing in year t.
| Portfolio | Ranked by UF | Ranked by EF | ||
|---|---|---|---|---|
| Ranking | 6 months | 12 months | 6 months | 12 months |
| Lowest (–) | 0.012 | 0.009 | 0.003 | −0.013 |
| 2 | 0.012 | 0.001 | 0.010 | 0.001 |
| 3 | 0.007 | −0.007 | 0.002 | −0.007 |
| 4 | 0.010 | −0.007 | 0.015 | 0.002 |
| 5 | 0.014 | 0.005 | 0.008 | −0.002 |
| 6 | 0.008 | −0.004 | 0.011 | −0.004 |
| 7 | 0.009 | −0.011 | 0.008 | −0.001 |
| 8 | 0.005 | 0.000 | 0.013 | 0.009 |
| 9 | 0.011 | 0.005 | 0.006 | −0.005 |
| Highest (+) | −0.013 | −0.013 | −0.001 | −0.002 |
| Hedge | 0.025*** | 0.022** | 0.004 | −0.011 |
| (t-Value) | (3.662) | (2.152) | (0.585) | (−1.102) |
| N | 29,326 | 29,326 | 29,326 | 29,326 |
- Note: UFt = Forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1. EFt = Expected forecasts/total assets at the end of year t – 1. Size-adjusted abnormal returns are calculated as the buy-and-hold return on the security (including dividends) beginning at the start of the 4 months after fiscal year-end t and ending at the end of the indicated months (i.e., 6 and 12) less the buy-and-hold return on a size-matched portfolio over the same period.
- *** and ** = Statistically significant at the 0.01 and 0.05 levels using a two-tailed t-test, respectively.
To compare these results, we form a hedge portfolio based on expected forecasts (EFt). The size-adjusted abnormal returns for the highest-minus-lowest hedge portfolio ranked by EFt are 0.004 (t-value = 0.585) and −0.011 (t-value = −1.102). Thus, the size-adjusted abnormal returns for the expected forecasts-based hedge portfolio are not significantly positive, inconsistent with the results of the hedge portfolio based on unexpected forecasts.
To further illustrate the pattern of returns in relation to forecast management, the size-adjusted abnormal returns over 12 months starting 4 months after the fiscal year-end for the highest and lowest portfolios are plotted in Panel A of Figure 1 and the hedge portfolio in Panel B. In Panel A, we observe a generally upward (downward) trend in abnormal returns for the lowest (highest) portfolio. The graph in Panel B reveals that the hedge portfolio returns are consistently positive throughout the analytical period, with a clear upward trend. Note that in Panel B, the hedge portfolio returns have a rapid upward trend until month 10 (i.e., 0.035), but they drop significantly thereafter. This is because realized earnings are announced in month 10 in the Kessan Tanshin as described in footnote 22. This graphical evidence conforms to the statistical findings in Table 4.
5.2 Regression analyses
The results of the regression analysis of Model (4) are reported in Table 5. We find that unexpected forecasts are significantly and negatively associated with size-adjusted abnormal returns in year t + 1. The coefficients of UFt, −0.313 and −0.357, are significantly negative (t-values = −2.600 and −1.858), when the dependent variable is BHAR6mt+1 and BHAR12mt+1, respectively. However, the coefficient of EFt is not significant, implying that expected forecasts are not significantly associated with the size-adjusted abnormal return in year t + 1 and, thus, the market does not misprice expected forecasts.
| Model (4) | |||||
|---|---|---|---|---|---|
| Dependent variable | BHAR6mt+1 | BHAR12mt+1 | |||
| Independent variables | Exp. sign | Coefficient | t-Value | Coefficient | t-Value |
| Constant | (?) | −0.007 | (−0.177) | −0.113** | (−2.023) |
| UFt | (–) | −0.313*** | (−2.600) | −0.357* | (−1.858) |
| EFt | (?) | −0.140 | (−0.823) | 0.000 | (−0.001) |
| INVt | (–) | −0.011 | (−1.115) | −0.020 | (−1.524) |
| ARt | (–) | 0.020 | (1.219) | 0.021 | (0.910) |
| CAPXt | (–) | −0.000 | (−0.421) | −0.000 | (−0.129) |
| GMt | (–) | 0.006 | (0.271) | 0.033 | (1.446) |
| S&At | (–) | −0.009 | (−0.273) | −0.009 | (−0.277) |
| ETRt | (–) | 0.081 | (0.870) | 0.060 | (0.618) |
| CTACt | (–) | −0.035* | (−1.785) | −0.057 | (−1.639) |
| AQt | (–) | −0.006 | (−1.515) | 0.009* | (1.973) |
| LFt | (–) | 0.005 | (0.205) | 0.003 | (0.086) |
| BETAt | (+) | 0.007 | (0.249) | 0.009 | (0.371) |
| SIZEt | (–) | −0.002 | (−0.852) | 0.004 | (1.375) |
| BMt | (+) | 0.013*** | (2.947) | 0.028*** | (3.773) |
| MOMENTt | (+) | 0.003 | (0.179) | −0.015 | (−1.113) |
| Year dummies | Yes | Yes | |||
| Industry dummies | Yes | Yes | |||
| Adj. R2 | 0.018 | 0.031 | |||
| N | 29,326 | 29,326 | |||
- Note: BHAR6mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 6 months beginning at the start of the 4 months after fiscal year-end. BHAR12mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 12 months beginning at the start of the 4 months after fiscal year-end. FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. UFt = Forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1. EFt = Expected forecasts/total assets at the end of year t – 1. INVt = Δ Inventory in year t – Δ Sales in year t. The Inventory variable is merchandise and finished goods when available, total inventory otherwise. ARt = Δ Accounts receivable in year t – Δ Sales in year t. The variable is accounts receivable when available, accounts and notes receivable otherwise. CAPXt = Δ Industry capital expenditure in year t – Δ Firm capital expenditure in year t. Industry capital expenditure = aggregating capital expenditure for all firms with the same the Nikkei medium classification industry code. Firm capital expenditure = change in gross property, plant and equipment for a firm. GMt = Δ Sales in year t – Δ Gross margin in year t. S&At = Δ Selling and administrative expenses in year t – Δ Sales in year t. ETRt = Average effective tax rate from year t – 4 to year t – 1 – effective tax rate in year t. Effective tax rate = income taxes/income before income taxes. Each variable is acquired from the parent-only financial statement. CTACt = (total accruals for year t minus total accruals for year t – 1)/total assets at the end of year t. Total accruals are calculated as follows. Total accruals = (change in current assets – change in cash and deposits) – (change in current liabilities – change in financing items) – (change in allowance for doubtful debts + change in provision for retirement benefits or provision for retirement allowance + change in provision for directors’ retirement benefits + change in other long-term provision + depreciation). Financing items = change in short-term loans payable + change in commercial papers + change in current portion of long-term loans payable + change in current portion of straight bonds and convertible bonds. AQt = Dummy variable set to 0 if auditor's opinion in year t is unqualified, 1 if auditor's opinion is qualified or other. LFt = (sales revenue per employee for year t – 1 – sales revenue per employee for year t)/sales revenue per employee for year t – 1. Sales revenue per employee = sales/the number of employees at year-end. BETAt = Historical beta calculated using monthly returns over the 60-month period ending at the current fiscal year-end t. SIZEt = Natural log of market value of equity at the end of year t. BMt = Book value of equity at the end of year t/market value of equity at the end of year t. MOMENTt = Monthly buy-and-hold stock return over fiscal year t. The definitions of all of the fundamental signals except for ETR and CTAC (i.e., INV, AR, CAPX, GM, S&A, AQ and LF) are taken from Lev and Thiagarajan (1993). The Δ operator represents a percentage change in the percentage change in the variable based on 2-year average expectation model, which is the same as that of previous studies (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993). For example, ΔSales in year t = {Salest − E(Salest)}/E(Salest), where E(Salest) = (Salest-1 + Salest-2)/2. All other variables with Δ operator are calculated as the same procedure. All variables are winsorized at 1% by year. t-Statistics are corrected for heteroskedasticity, and cross-sectional and time-series correlation using a two-way cluster at the firm and year level proposed by Petersen (2009).
- ***, ** and * = Statistically significant at the 0.01, 0.05 and 0.1 levels using a two-tailed t-test, respectively.
With respect to the control variable, INVt, CAPXt, S&At, CTACt, AQt, BETAt and BMt have their expected signs, but only CTACt, AQt and BMt are statistically significant at the conventional levels. These findings are consistent with the portfolio results in Table 4. Overall, the results in this section suggest that investors cannot fully anticipate the implications of unexpected forecasts for their credibility and thus overprice unexpected forecasts in the portfolio formation year, consistent with our hypothesis.
6 ADDITIONAL ANALYSES
6.1 Relationship between unexpected forecasts and discretionary accruals anomalies
We investigate whether the relationship between unexpected forecasts and future returns is distinct from the accruals anomaly. The theoretical background on the relationship between them is similar to that on the accruals anomaly because both are caused by managerial discretion and bias. As previously stated, Iwasaki et al. (2023) reveal that managers in Japan engage in forecast management in considering stock market reaction. Consistent with their findings, several studies demonstrate that managers issue more optimistic forecasts when they have incentive to inflate stock prices (e.g., stock issuance) (Lang & Lundholm, 2000; Rogers & Stocken, 2005). Meanwhile, other studies provide evidence that managers also conduct earnings management in response to stock market reaction. For example, managers are likely to engage in upward (downward) earnings management before stock issuance (e.g., Erickson & Wang, 1999; Rangan, 1998; Teoh et al., 1998). These results suggest that managerial opportunism affects both the reversal of accruals and credibility of management forecasts, causing both accruals and unexpected forecasts anomalies in our study.
Otherwise, if managers are optimistic (pessimistic) about future prospects, both management forecasts and accruals will be positive (negative). For example, managers will report smaller loan loss provisions (therefore more positive accruals) and more positive earnings forecasts when they have optimistic future prospects and vice versa. Consistent with this argument, Gong et al. (2009) and Xu (2010) provide evidence that management earnings forecasts are optimistic (pessimistic) when accruals are more positive (negative). This suggests that managerial bias also affects both the reversal of accruals and credibility of management forecasts, causing accruals and unexpected forecasts anomalies. Importantly, the Japanese listed firms report realized earnings and management forecast simultaneously, suggesting that the measurement periods of accruals and unexpected forecast anomalies are the same. Therefore, these arguments lead to the prediction that our main findings may simply reflect accruals anomaly.
The regression results of Model (5) are reported in Table 6. The coefficients of DACt are significantly negative, indicating the existence of discretionary accruals anomaly in the Japanese stock market.26 Importantly, the coefficients of UFt in both columns remain significantly negative even after controlling for the effect of DACt. Therefore, we conclude that the relationship between unexpected forecasts and the subsequent size-adjusted abnormal returns is not fully explained by the effects of the accruals anomaly.
| Model (5) | |||||
|---|---|---|---|---|---|
| Dependent variable | BHAR6mt+1 | BHAR12mt+1 | |||
| Independent variables | Exp. sign | Coefficient | t-Value | Coefficient | t-Value |
| Constant | (?) | −0.007 | (−0.171) | −0.112 | (−2.015) |
| UFt | (–) | −0.324*** | (−2.648) | −0.374* | (−1.928) |
| EFt | (?) | −0.135 | (−0.802) | 0.008 | (0.032) |
| DACt | (–) | −0.112** | (−2.490) | −0.176*** | (−2.629) |
| INVt | (–) | −0.009 | (−0.870) | −0.017 | (−1.287) |
| ARt | (–) | 0.025 | (1.419) | 0.029 | (1.177) |
| CAPXt | (–) | −0.000 | (−0.413) | −0.000 | (−0.122) |
| GMt | (–) | 0.006 | (0.284) | 0.034 | (1.466) |
| S&At | (–) | −0.011 | (−0.360) | −0.014 | (−0.403) |
| ETRt | (–) | 0.076 | (0.824) | 0.052 | (0.556) |
| CTACt | (–) | −0.006 | (−0.248) | −0.011 | (−0.361) |
| AQt | (–) | −0.006 | (−1.464) | 0.010** | (2.094) |
| LFt | (–) | 0.002 | (0.095) | −0.001 | (−0.021) |
| BETAt | (+) | 0.007 | (0.252) | 0.009 | (0.377) |
| SIZEt | (–) | −0.002 | (−0.862) | 0.004 | (1.359) |
| BMt | (+) | 0.013*** | (2.931) | 0.028*** | (3.760) |
| MOMENTt | (+) | 0.002 | (0.144) | −0.016 | (−1.190) |
| Year dummies | Yes | Yes | |||
| Industry dummies | Yes | Yes | |||
| Adj. R2 | 0.018 | 0.031 | |||
| N | 29,326 | 29,326 | |||
- Note: BHAR6mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 6 months beginning at the start of the 4 months after fiscal year-end. BHAR12mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 12 months beginning at the start of the 4 months after fiscal year-end. FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. UFt = Forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1. EFt = Expected forecasts/total assets at the end of year t – 1. DACt = Discretionary accruals for year t estimated using the model in Dechow et al. (1995). INVt = Δ Inventory in year t – Δ Sales in year t. The Inventory variable is merchandise and finished goods when available, total inventory otherwise. ARt = Δ Accounts receivable in year t – Δ Sales in year t. The variable is accounts receivable when available, accounts and notes receivable otherwise. CAPXt = Δ Industry capital expenditure in year t – Δ Firm capital expenditure in year t. Industry capital expenditure = aggregating capital expenditure for all firms with the same the Nikkei medium classification industry code. Firm capital expenditure = change in gross property, plant and equipment for a firm. GMt = Δ Sales in year t – Δ Gross margin in year t. S&At = Δ Selling and administrative expenses in year t – Δ Sales in year t. ETRt = Average effective tax rate from year t – 4 to year t – 1 – effective tax rate in year t. Effective tax rate = income taxes/income before income taxes. Each variable is acquired from the parent-only financial statement. CTACt = (total accruals for year t minus total accruals for year t – 1)/total assets at the end of year t. Total accruals are calculated as follows. Total accruals = (change in current assets – change in cash and deposits) – (change in current liabilities – change in financing items) – (change in allowance for doubtful debts + change in provision for retirement benefits or provision for retirement allowance + change in provision for directors’ retirement benefits + change in other long-term provision + depreciation). Financing items = change in short-term loans payable + change in commercial papers + change in current portion of long-term loans payable + change in current portion of straight bonds and convertible bonds. AQt = Dummy variable set to 0 if auditor's opinion in year t is unqualified, 1 if auditor's opinion is qualified or other. LFt = (sales revenue per employee for year t – 1 – sales revenue per employee for year t)/sales revenue per employee for year t – 1. Sales revenue per employee = sales/the number of employees at year-end. BETAt = Historical beta calculated using monthly returns over the 60-month period ending at the current fiscal year-end t. SIZEt = Natural log of market value of equity at the end of year t. BMt = Book value of equity at the end of year t/market value of equity at the end of year t. MOMENTt = Monthly buy-and-hold stock return over fiscal year t. The definitions of all of the fundamental signals except for ETR and CTAC (i.e., INV, AR, CAPX, GM, S&A, AQ and LF) are taken from Lev and Thiagarajan (1993). The Δ operator represents a percentage change in the percentage change in the variable based on 2-year average expectation model, which is the same as that of previous studies (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993). For example, ΔSales in year t = {Salest − E(Salest)}/E(Salest), where E(Salest) = (Salest-1 + Salest-2)/2. All other variables with Δ operator are calculated utilizing the same procedure. All variables are winsorized at 1% by year. t-Statistics are corrected for heteroskedasticity, and cross-sectional and time-series correlation using a two-way cluster at the firm and year level proposed by Petersen (2009).
- ***, ** and * = Statistically significant at the 0.01, 0.05 and 0.1 levels using a two-tailed t-test, respectively.
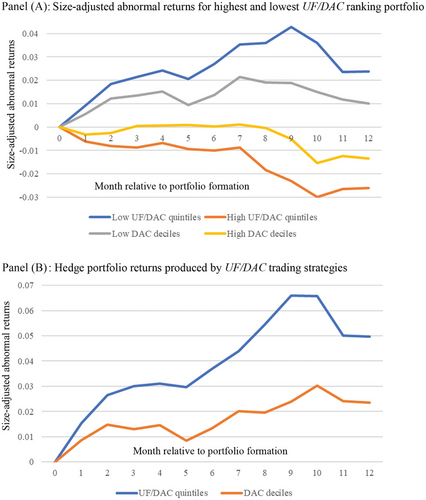
The size-adjusted abnormal returns produced by UF and DAC quintile portfolios are plotted in Figure 2. We also plot the abnormal returns by DAC decile portfolio (Xie, 2001) in comparison. Panel A reveals an upward (downward) trend in abnormal returns for the lowest (highest) UF and DAC quintile portfolio and Panel B shows that the hedge portfolio returns are consistently positive throughout the sample period.27 The abnormal returns by the UF and DAC portfolio are larger than those by the DAC decile portfolio. Specifically, the hedge portfolio returns by the UF and DAC portfolio earn 5.0% while those by the DAC decile portfolio earn 2.3%. This evidence is in line with the findings in Table 6.
6.2 Risk hypothesis
In this section, we conduct additional analyses (risk hypothesis) concerning the alternative explanations for our main findings. Our finding that unexpected forecasts are negatively associated with subsequent size-adjusted abnormal returns is consistent with our hypothesis (i.e., the mispricing hypothesis) that investors do not accurately measure the credibility of initial management forecasts and, thus, overprice unexpected forecasts. However, the efficient market hypothesis posits an alternative explanation based on the risk compensation notion that changes in the risk information contained in unexpected forecasts may cause the significant relationship between unexpected forecasts and future stock returns. To address this issue, we observe the market reaction to forecast revisions (FRRETt+1) by the UFt portfolio in Table 4, where, FRRETt+1 is the sum of size-adjusted buy-and-hold returns over the 3-day window (days from “0” to “+2”) surrounding management forecast revisions announced for year t + 1.28 The definition of the size-matched portfolio used to calculate the expected stock returns is the same as that described in Subsection 3.2. Firms that do not revise their forecasts during the period are excluded from the sample.29 As a result, our sample consists of 29,148 firm-year observations.
On the one hand, if investors overestimate the implications of unexpected forecasts for the credibility of management forecasts, the announcements of subsequent forecast revisions will be a surprise for investors and cause them to modify their misvaluations of the initial management forecasts. Therefore, under the mispricing hypothesis, we expect UFt to have a negative association with FRRETt+1. On the other, if the risk hypothesis is supported, we expect that UFt will not have a significant correlation with FRRETt+1.
The results are summarized in Table 7. Firms in a higher (lower) UFt portfolio experience lower (higher) abnormal returns around the forecast revision announcement day, which is consistent with the mispricing hypothesis. A comparative analysis of the magnitudes of the hedge portfolio returns in Tables 4 and 7 indicates that the abnormal returns earned by the hedge portfolio based on unexpected forecasts are concentrated in the days around the announcement of subsequent forecast revisions. Specifically, approximately 45.5% ( = 0.010/0.022) of the hedge portfolio return is clustered in 3 days, even though the announcement period windows employed in Table 7 contain less than 10% of the total trading days in Table 4. 30 These results are consistent with the mispricing hypothesis, rather than the risk hypothesis, presented in our main analysis.
| Portfolio | Ranked by UFt |
|---|---|
| Ranking | FRRET t+1 |
| Lowest (–) | 0.003 |
| 2 | 0.003 |
| 3 | 0.000 |
| 4 | 0.001 |
| 5 | 0.002 |
| 6 | −0.001 |
| 7 | −0.004 |
| 8 | −0.003 |
| 9 | −0.005 |
| Highest (+) | −0.007 |
| Hedge | 0.010* |
| (t-value) | (1.836) |
| N | 29,148 |
- Note: FRRETt+1 = Sum of the size-adjusted abnormal return around subsequent forecast revision announcement. Stock returns around the announcement are measured as the compounded stock returns earned over the 3-day window surrounding each announcement (days from “0” to “+2”) minus the compounded value-weighted return on a size-matched portfolio earned over the same window. UFt = Forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1.
- * = Statistically significant at the 0.1 level using a two-tailed t-test.
6.3 Exploring the mispricing hypothesis
First, we investigate the effect of investor sophistication on the relationship between unexpected forecasts and future returns. If this relationship is caused by investor mispricing, it will be weaker for firms with a higher proportion of sophisticated investor ownership. For example, Collins et al. (2003) find that the accruals anomaly is weaker in firms with a higher level of institutional ownership. Therefore, we divide the sample into two subsamples based on the sophisticated investors ownership and re-estimate Model (4) for each subsample. Here, we define sophisticated investors ownership as the proportion of domestic institutional investor shareholdings (INSTt) and that of foreign investor shareholdings (FOREIGNt). We obtain the data on institutional and foreign ownership from the NEEDS-Cges (Corporate governance evaluation system) database of Nikkei Media Marketing, Inc.
The results are presented in Table 8. There is a significant association between unexpected forecasts and future returns only in the subsamples with low institutional and foreign investor shareholdings. This suggests that sophisticated investors make investment decisions considering unexpected management forecasts.
| Panel A: Low ownership subsample (below median) | |||||
|---|---|---|---|---|---|
| Model (4) | Model (4) | ||||
| Divided by INSTt | Divided by FOREIGNt | ||||
| Dependent variable | BHAR12mt+1 | BHAR12mt+1 | |||
| Independent variables | Exp. sign | Coefficient | t-Value | Coefficient | t-Value |
| Constant | (?) | −0.028 | (−0.883) | 0.000 | (0.016) |
| UFt | (–) | −0.362** | (−2.553) | −0.426*** | (−3.169) |
| EFt | (?) | 0.073 | (0.306) | 0.234 | (1.349) |
| Control variables | Yes | Yes | |||
| Year dummies | Yes | Yes | |||
| Industry dummies | Yes | Yes | |||
| Adj. R2 | 0.035 | 0.035 | |||
| N | 12,983 | 12,986 | |||
| Panel B: High ownership subsample (above median) | |||||
|---|---|---|---|---|---|
| Model (4) | Model (4) | ||||
| Divided by INSTt | Divided by FOREIGNt | ||||
| Dependent variable | BHAR12mt+1 | BHAR12mt+1 | |||
| Independent variables | Exp. sign | Coefficient | t-Value | Coefficient | t-Value |
| Constant | (?) | −0.119** | (−2.083) | 0.049 | (0.927) |
| UFt | (–) | −0.650 | (−1.562) | −0.533 | (−1.617) |
| EFt | (?) | 0.399 | (1.296) | 0.188 | (0.531) |
| Control variables | Yes | Yes | |||
| Year dummies | Yes | Yes | |||
| Industry dummies | Yes | Yes | |||
| Adj. R2 | 0.030 | 0.032 | |||
| N | 12,972 | 12,981 | |||
- Note: BHAR12mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 12 months beginning at the start of the 4 months after fiscal year-end. INSTt = Proportion of total shares owned by domestic institutional investors at the end of year t. This is defined as the sum of trust account shareholding ratio and life insurance separate account shareholding ratio. FOREIGNt = Proportion of total shares owned by foreign investors at the end of year t. FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. UFt = Forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1. EFt = Expected forecasts/total assets at the end of year t – 1. INVt = Δ Inventory in year t – Δ Sales in year t. The Inventory variable is merchandise and finished goods when available, total inventory otherwise. ARt = Δ Accounts receivable in year t – Δ Sales in year t. The variable is accounts receivable when available, accounts and notes receivable otherwise. CAPXt = Δ Industry capital expenditure in year t – Δ Firm capital expenditure in year t. Industry capital expenditure = aggregating capital expenditure for all firms with the same the Nikkei medium classification industry code. Firm capital expenditure = change in gross property, plant and equipment for a firm. GMt = Δ Sales in year t – Δ Gross margin in year t. S&At = Δ Selling and administrative expenses in year t – Δ Sales in year t. ETRt = Average effective tax rate from year t – 4 to year t – 1 – effective tax rate in year t. Effective tax rate = income taxes/income before income taxes. Each variable is acquired from the parent-only financial statement. CTACt = (total accruals for year t minus total accruals for year t – 1)/total assets at the end of year t. Total accruals are calculated as follows. Total accruals = (change in current assets – change in cash and deposits) – (change in current liabilities – change in financing items) – (change in allowance for doubtful debts + change in provision for retirement benefits or provision for retirement allowance + change in provision for directors’ retirement benefits + change in other long-term provision + depreciation). Financing items = change in short-term loans payable + change in commercial papers + change in current portion of long-term loans payable + change in current portion of straight bonds and convertible bonds. AQt = Dummy variable set to 0 if auditor's opinion in year t is unqualified, 1 if auditor's opinion is qualified or other. LFt = (sales revenue per employee for year t – 1 – sales revenue per employee for year t)/sales revenue per employee for year t – 1. Sales revenue per employee = sales/the number of employees at year-end. BETAt = Historical beta calculated using monthly returns over the 60-month period ending at the current fiscal year-end t. SIZEt = Natural log of market value of equity at the end of year t. BMt = Book value of equity at the end of year t/market value of equity at the end of year t. MOMENTt = Monthly buy-and-hold stock return over fiscal year t. The definitions of all of the fundamental signals except for ETR and CTAC (i.e., INV, AR, CAPX, GM, S&A, AQ and LF) are taken from Lev and Thiagarajan (1993). The Δ operator represents a percentage change in the percentage change in the variable based on 2-year average expectation model, which is the same as that of previous studies (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993). For example, ΔSales in year t = {Salest − E(Salest)}/E(Salest), where E(Salest) = (Salest-1 + Salest-2)/2. All other variables with Δ operator are calculated utilizing the same procedure. All variables are winsorized at 1% by year. t-Statistics are corrected for heteroskedasticity, and cross-sectional and time-series correlation using a two-way cluster at the firm and year level proposed by Petersen (2009).
- *** and ** = Statistically significant at the 0.01 and 0.05 levels using a two-tailed t-test, respectively.
Second, we investigate the learning effect of management forecast credibility. If the relationship between unexpected forecasts and future returns is caused by investor mispricing, it will diminish over time because investors seeking arbitrage opportunities learn about it and arbitrage it away (Green et al., 2011; Lev & Nissim, 2006). Furthermore, advances in statistical techniques such as machine learning may have reduced arbitrage opportunities for investors. To address this issue, we calculate hedge portfolio returns by year and observe the time-series trends in Figure 3. The average hedge portfolio return is greater in positive years than in negative years. Specifically, the 6-month (12-month) hedge portfolio return is positive in 14 of the 17 periods (9 of 17 periods), with an average hedge return of 3.3% (7.2%) in positive years and −1.8% (−4.0%) in negative years. In particular, the lowest 6-month hedge portfolio return is −2.2% in 2010, where it does not appear that the trading strategy ever generates statistically significant negative returns in any given year.
More importantly, positive hedge returns are observed in the first half of the sample period, whereas relatively fewer hedge returns are observed in the second half. Large positive returns are observed especially in 2005 and 2006.31 To analyze this trend in more depth, we divide our sample into the first and second half periods (2003–2010 and 2011–2019, respectively) and observe hedge returns. According to the Figure 3, positive hedge returns (3.5% for 6 months and 5.5% for 12 months) are observed in the first half of the period (2003–2010), while hedge returns (1.5% for 6 months and −1.1% for 12 months) are relatively low in the later period (2011–2019). Further, we implement the regression analysis performed in our main analysis for a sample segmented into the first and second halves of the sample period (2003–2010 and 2011–2019, respectively). The untabulated results reveal that the results obtained in the main analysis are primarily due to the first half of the sample period (coefficients of UF are −0.448 and −0.524 when using 6- and 12-month returns, t-values are −2.872 and −2.336, respectively). These results are consistent with the scenario on investor learning, or the fact that investors are more likely to use machine learning and statistical methods to minimize mispricing.
6.4 Unexpected forecasts and future outcomes
The results are summarized in Table 9. The coefficient of UF is significantly negative as expected, but we also find that the coefficient of EF is significantly negative, which is not consistent with our prediction. However, the results of the F-test indicate that the magnitude of the coefficient of UF is significantly larger than that of the coefficient of EF. This suggests that firms with higher unexpected forecasts are more likely to miss their earnings forecasts. Therefore, we conclude that our argument is generally validated: earnings forecasts containing higher unexpected forecasts are less credible.
| Model (6) | |||
|---|---|---|---|
| Dependent variable | ERRORt+1 | ||
| Independent variables | Exp. sign | Coefficient | t-Value |
| Constant | (?) | −0.017*** | (−3.865) |
| UFt | (–) | −0.286*** | (−6.945) |
| EFt | (?) | −0.095** | (−1.989) |
| INVt | (–) | −0.002** | (−2.178) |
| ARt | (–) | 0.005 | (1.549) |
| CAPXt | (–) | 0.000* | (1.687) |
| GMt | (–) | −0.009** | (−2.477) |
| S&At | (–) | −0.014*** | (−3.152) |
| ETRt | (–) | −0.038 | (−1.636) |
| CTACt | (–) | −0.006 | (−1.566) |
| AQt | (–) | −0.004*** | (−7.029) |
| LFt | (–) | −0.001 | (−0.227) |
| BETAt | (+) | −0.004** | (−2.221) |
| SIZEt | (–) | 0.002*** | (5.179) |
| BMt | (+) | 0.001** | (1.983) |
| MOMENTt | (+) | 0.008*** | (5.009) |
| Year dummies | Yes | ||
| Industry dummies | Yes | ||
| Adj. R2 | 0.031 | ||
| N | 29,326 | ||
| Result of F-test | F-value | Prob. > F | |
| UFt = EFt | 15.670 | 0.000 | |
- Note: ERRORt+1 = (actual earnings for year t + 1 – initial management forecasts for year t + 1)/total assets at the end of year t – 1. FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. UFt = Forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1. EFt = Expected forecasts/total assets at the end of year t – 1. INVt = Δ Inventory in year t – Δ Sales in year t. The Inventory variable is merchandise and finished goods when available, total inventory otherwise. ARt = Δ Accounts receivable in year t – Δ Sales in year t. The variable is accounts receivable when available, accounts and notes receivable otherwise. CAPXt = Δ Industry capital expenditure in year t – Δ Firm capital expenditure in year t. Industry capital expenditure = aggregating capital expenditure for all firms with the same the Nikkei medium classification industry code. Firm capital expenditure = change in gross property, plant and equipment for a firm. GMt = Δ Sales in year t – Δ Gross margin in year t. S&At = Δ Selling and administrative expenses in year t – Δ Sales in year t. ETRt = Average effective tax rate from year t – 4 to year t – 1 – effective tax rate in year t. Effective tax rate = income taxes/income before income taxes. Each variable is acquired from the parent-only financial statement. CTACt = (total accruals for year t minus total accruals for year t – 1)/total assets at the end of year t. Total accruals are calculated as follows. Total accruals = (change in current assets – change in cash and deposits) – (change in current liabilities – change in financing items) – (change in allowance for doubtful debts + change in provision for retirement benefits or provision for retirement allowance + change in provision for directors’ retirement benefits + change in other long-term provision + depreciation). Financing items = change in short-term loans payable + change in commercial papers + change in current portion of long-term loans payable + change in current portion of straight bonds and convertible bonds. AQt = Dummy variable set to 0 if auditor's opinion in year t is unqualified, 1 if auditor's opinion is qualified or other. LFt = (sales revenue per employee for year t – 1 – sales revenue per employee for year t)/sales revenue per employee for year t – 1. Sales revenue per employee = sales/the number of employees at year-end. BETAt = Historical beta calculated using monthly returns over the 60-month period ending at the current fiscal year-end t. SIZEt = Natural log of market value of equity at the end of year t. BMt = Book value of equity at the end of year t/market value of equity at the end of year t. MOMENTt = Monthly buy-and-hold stock return over fiscal year t. The definitions of all of the fundamental signals except for ETR and CTAC (i.e., INV, AR, CAPX, GM, S&A, AQ and LF) are taken from Lev and Thiagarajan (1993). The Δ operator represents a percentage change in the percentage change in the variable based on the 2-year average expectation model, which is the same as that of previous studies (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993). For example, ΔSales in year t = {Salest − E(Salest)}/E(Salest), where E(Salest) = (Salest-1 + Salest-2)/2. All other variables with Δ operator are calculated utilizing the same procedure. All variables are winsorized at 1% by year. t-Statistics are corrected for heteroskedasticity, and cross-sectional and time-series correlation using a two-way cluster at the firm and year level are proposed by Petersen (2009).
- ***, ** and * = Statistically significant at the 0.01, 0.05 and 0.1 levels using a two-tailed t-test, respectively.
6.5 Other additional analyses
Finally, we conduct four additional analyses to ensure the validity of our results. First, we use an alternative measure of unexpected forecasts. We measure management forecast surprises using analyst forecasts (AFSURPt) based on Ng et al. (2013). Here, AFSURPt is defined as the management forecasts for year t + 1 minus the latest analyst forecasts for year t + 1 divided by total assets at the end of year t – 1. We obtain data of analyst forecasts from Datastream of Refinitiv. Owing to the low analyst following in Japan, the sample size is reduced to 3897 firm-year observations.
The analysis results are reported in Table 10. There is no significant relationship between AFSURPt and future returns (BHAR6mt+1 and BHAR12mt+1). This suggests that the forecast surprises based on analysts’ earnings forecasts are efficiently incorporated into stock prices. The results also suggest that the unexpected forecasts in our main analysis contain information about future performance that is not reflected in the forecast surprises based on analysts’ earnings forecasts.
| Model (7) | |||||
|---|---|---|---|---|---|
| Dependent variable | BHAR6mt+1 | BHAR12mt+1 | |||
| Independent variables | Exp. sign | Coefficient | t-Value | Coefficient | t-Value |
| Constant | (?) | −0.075 | (−1.188) | 0.071 | (0.789) |
| AFSURPt | (–) | 0.008 | (0.039) | 0.211 | (0.847) |
| INVt | (–) | −0.044*** | (−3.063) | −0.076** | (−2.250) |
| ARt | (–) | 0.027 | (0.778) | 0.040 | (0.665) |
| CAPXt | (–) | −0.000 | (−1.453) | −0.000 | (−0.355) |
| GMt | (–) | −0.003 | (−0.059) | 0.065 | (1.257) |
| S&At | (–) | 0.057 | (1.454) | 0.094 | (1.521) |
| ETRt | (–) | 0.161 | (0.502) | 0.049 | (0.078) |
| CTACt | (–) | −0.174*** | (−3.781) | −0.206* | (−1.797) |
| AQt | (–) | 0.057* | (1.868) | −0.022 | (−0.302) |
| LFt | (–) | 0.021 | (0.532) | 0.028 | (0.488) |
| BETAt | (+) | 0.011 | (0.417) | 0.012 | (0.400) |
| SIZEt | (–) | 0.002 | (0.581) | −0.003 | (−0.587) |
| BMt | (+) | 0.020 | (0.817) | 0.005 | (0.149) |
| MOMENTt | (+) | −0.017 | (−0.529) | −0.032 | (−0.865) |
| Year dummies | Yes | Yes | |||
| Industry dummies | Yes | Yes | |||
| Adj. R2 | 0.043 | 0.038 | |||
| N | 3897 | 3897 | |||
- Note: BHAR6mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 6 months beginning at the start of the 4 months after fiscal year-end. BHAR12mt+1 = Size-adjusted return calculated as the buy-and-hold return on the security (including dividends) for 12 months beginning at the start of the 4 months after fiscal year-end. AFSURPt = (management forecasts for year t + 1 minus the latest analyst forecasts for year t + 1)/total assets at the end of year t – 1. INVt = Δ Inventory in year t – Δ Sales in year t. The Inventory variable is merchandise and finished goods when available, total inventory otherwise. ARt = Δ Accounts receivable in year t – Δ Sales in year t. The variable is accounts receivable when available, accounts and notes receivable otherwise. CAPXt = Δ Industry capital expenditure in year t – Δ Firm capital expenditure in year t. Industry capital expenditure = aggregating capital expenditure for all firms with the same Nikkei medium classification industry code. Firm capital expenditure = change in gross property, plant and equipment for a firm. GMt = Δ Sales in year t – Δ Gross margin in year t. S&At = Δ Selling and administrative expenses in year t – Δ Sales in year t. ETRt = Average effective tax rate from year t – 4 to year t – 1 – effective tax rate in year t. Effective tax rate = income taxes/income before income taxes. Each variable is acquired from the parent-only financial statement. CTACt = (total accruals for year t minus total accruals for year t – 1)/total assets at the end of year t. Total accruals are calculated as follows. Total accruals = (change in current assets – change in cash and deposits) – (change in current liabilities – change in financing items) – (change in allowance for doubtful debts + change in provision for retirement benefits or provision for retirement allowance + change in provision for directors’ retirement benefits + change in other long-term provision + depreciation). Financing items = change in short-term loans payable + change in commercial papers + change in current portion of long-term loans payable + change in current portion of straight bonds and convertible bonds. AQt = Dummy variable set to 0 if auditor's opinion in year t is unqualified, 1 if auditor's opinion is qualified or other. LFt = (sales revenue per employee for year t – 1 – sales revenue per employee for year t)/sales revenue per employee for year t – 1. Sales revenue per employee = sales/the number of employees at year-end. BETAt = Historical beta calculated using monthly returns over the 60-month period ending at the current fiscal year-end t. SIZEt = Natural log of market value of equity at the end of year t. BMt = Book value of equity at the end of year t/market value of equity at the end of year t. MOMENTt = Monthly buy-and-hold stock return over fiscal year t. The definitions of all of the fundamental signals except for ETR and CTAC (i.e., INV, AR, CAPX, GM, S&A, AQ and LF) are taken from Lev and Thiagarajan (1993). The Δ operator represents a percentage change in the percentage change in the variable based on 2-year average expectation model, which is the same as that of prior studies (Abarbanell & Bushee, 1997; Lev & Thiagarajan, 1993). For example, ΔSales in year t = {Salest − E(Salest)}/E(Salest), where E(Salest) = (Salest-1 + Salest-2)/2. All other variables with Δ operator are calculated utilizing the same procedure. All variables are winsorized at 1% by year. t-Statistics are corrected for heteroskedasticity, and cross-sectional and time-series correlation using a two-way cluster at the firm and year level proposed by Petersen (2009).
- ***, ** and * = Statistically significant at the 0.01, 0.05 and 0.1 levels using a two-tailed t-test, respectively.
In the second analysis, we investigate the effect of outliers on the unexpected forecast anomaly. The literature emphasizes the importance of performing robustness checks when we test economic or behavioral explanations for accounting-related mispricing (Kraft et al., 2006). Specifically, we examine whether our results hold when we eliminate the top and bottom 0% (i.e., no outlier treatment), 1%, 5% and 10%.
According to the results in Table 11, the smaller the number of observations to be eliminated, the larger the hedge returns. The hedge portfolio returns are 2.5% and 1.7% for 6 and 12 months, respectively, when we do not eliminate outliers in Panel A, and they are 0.7% and 0.1% for 6 and 12 months, respectively, when we eliminate the top and bottom 10% in Panel D. These results suggest that the significant association between unexpected forecasts and future returns mainly arises from unexpected forecasts with relatively large absolute values. The result that investors misprice more for relatively large absolute values is not contradictory to the mispricing hypothesis.
| Panel A: No outlier processing | ||||
|---|---|---|---|---|
| Decile | Ranked by UF | Ranked by EF | ||
| Portfolio | 6 months | 12 months | 6 months | 12 months |
| Lowest (–) | 0.019 | 0.028 | 0.011 | −0.002 |
| 2 | 0.020 | 0.012 | 0.013 | 0.004 |
| 3 | 0.011 | 0.000 | 0.004 | −0.003 |
| 4 | 0.011 | −0.006 | 0.017 | 0.004 |
| 5 | 0.015 | 0.007 | 0.010 | 0.004 |
| 6 | 0.010 | 0.000 | 0.014 | 0.002 |
| 7 | 0.012 | −0.005 | 0.011 | 0.007 |
| 8 | 0.007 | 0.002 | 0.018 | 0.018 |
| 9 | 0.017 | 0.015 | 0.010 | 0.005 |
| Highest (+) | −0.006 | 0.010 | 0.007 | 0.024 |
| Hedge | 0.025*** | 0.017* | 0.004 | −0.026* |
| (t-value) | (2.950) | (1.652) | (0.501) | (−1.818) |
| Panel B: Cut the top and bottom 1% | ||||
|---|---|---|---|---|
| Decile | Ranked by UF | Ranked by EF | ||
| Portfolio | 6 months | 12 months | 6 months | 12 months |
| Lowest (–) | 0.005 | −0.004 | −0.005 | −0.021 |
| 2 | 0.003 | −0.015 | 0.007 | −0.005 |
| 3 | 0.003 | −0.012 | −0.003 | −0.013 |
| 4 | 0.010 | −0.007 | 0.013 | 0.000 |
| 5 | 0.012 | 0.001 | 0.007 | −0.005 |
| 6 | 0.004 | −0.008 | 0.009 | −0.012 |
| 7 | 0.005 | −0.016 | 0.004 | −0.007 |
| 8 | 0.001 | −0.005 | 0.008 | 0.000 |
| 9 | 0.006 | −0.009 | 0.003 | −0.015 |
| Highest (+) | −0.015 | −0.018 | −0.006 | −0.016 |
| Hedge | 0.020*** | 0.014* | 0.001 | −0.005 |
| (t-value) | (3.439) | (1.661) | (0.087) | (−0.550) |
| Panel C: Cut the top and bottom 5% | ||||
|---|---|---|---|---|
| Decile | Ranked by UF | Ranked by EF | ||
| Portfolio | 6 months | 12 months | 6 months | 12 months |
| Lowest (–) | −0.004 | −0.028 | −0.011 | −0.037 |
| 2 | −0.008 | −0.027 | 0.000 | −0.022 |
| 3 | −0.003 | −0.025 | −0.008 | −0.028 |
| 4 | 0.001 | −0.021 | 0.004 | −0.012 |
| 5 | 0.003 | −0.021 | −0.003 | −0.022 |
| 6 | −0.001 | −0.022 | −0.003 | −0.023 |
| 7 | −0.004 | −0.024 | −0.001 | −0.023 |
| 8 | −0.005 | −0.023 | −0.001 | −0.019 |
| 9 | −0.003 | −0.025 | −0.009 | −0.025 |
| Highest (+) | −0.020 | −0.028 | −0.011 | −0.031 |
| Hedge | 0.016*** | −0.000 | 0.000 | −0.006 |
| (t-value) | (3.605) | (−0.026) | (0.004) | (−1.013) |
| Panel D: Cut the top and bottom 10% | ||||
|---|---|---|---|---|
| Decile | Ranked by UE | Ranked by EF | ||
| Portfolio | 6 months | 12 months | 6 months | 12 months |
| Lowest (–) | −0.013 | −0.034 | −0.014 | −0.041 |
| 2 | −0.014 | −0.032 | −0.004 | −0.026 |
| 3 | −0.007 | −0.033 | −0.010 | −0.038 |
| 4 | −0.007 | −0.031 | −0.001 | −0.027 |
| 5 | −0.004 | −0.031 | −0.006 | −0.029 |
| 6 | −0.006 | −0.032 | −0.009 | −0.035 |
| 7 | −0.007 | −0.034 | −0.009 | −0.033 |
| 8 | −0.007 | −0.032 | −0.006 | −0.029 |
| 9 | −0.005 | −0.033 | −0.014 | −0.035 |
| Highest (+) | −0.020 | −0.035 | −0.017 | −0.035 |
| Hedge | 0.007* | 0.001 | 0.003 | −0.005 |
| (t-value) | (1.851) | (0.209) | (0.808) | (−1.027) |
- Note: UFt = forecast innovation (FIt) minus expected forecasts (EFt). FIt = (management forecasts for year t + 1 minus actual net income for year t)/total assets at the end of year t – 1. EFt = expected forecasts/total assets at the end of year t – 1. Size-adjusted abnormal returns are calculated as the buy-and-hold return on the security (including dividends) beginning at the start of the 4 months after fiscal year-end t and ending at the end of the indicated months (i.e., 6 and 12) less than the buy-and-hold return on a size-matched portfolio over the same period.
- *** and * = Statistically significant at the 0.01 and 0.1 levels using a two-tailed t-test, respectively.
Third, we explore the determinants of our main results. Specifically, we develop 10 variables regarding (1) industry uncertainty (i.e., industry return and sales volatility), (2) the characteristics of managers (i.e., managerial overconfidence, tenure and turnover risk) and (3) the information environment (i.e., analyst coverage)32 and add them and the intersection terms between UF and those variables to Model (4). We then examine whether the coefficients of the intersection terms are significant.
The untabulated results reveal the following three main points. First, the coefficients of the intersection term between UF and industry uncertainty variables are all insignificant, suggesting that industry uncertainty does not drive our main results. Second, managerial characteristics, that is, managerial overconfidence, tenure and turnover risk do not affect the relationship between UF and future returns. Finally, our analyses reveal that analyst coverage weakens the relationship between UF and future returns. Specifically, the coefficients of the intersection term between UF and the analyst coverage dummy are significantly positive at less than the 0.05 level. In summary, we conclude that the information environment is a determinant of unexpected forecasts anomaly.
Fourth, we conduct a robustness check with bootstrapping. Chen et al. (2023) indicate that uncertainty associated with coefficient estimates in the first-stage regression causes underestimation bias in the standard errors associated with all of the second-stage regressors. Additionally, they reveal that bootstrapping mitigates this problem. As our main analysis could face this issue,33 we conduct a robustness check with clustered bootstrap as recommended by Chen et al. (2023).34
The untabulated results indicate that standard errors (t-values) in bootstrapping are larger (lower) than those in the ordinary least squares (OLS) estimation, suggesting that OLS may have an underestimation problem with standard errors, as highlighted by Chen et al. (2023) point out. However, the coefficients of UF in both columns remain significantly negative (t-values using BHAR6m and BHAR12m as dependent variables are −2.289 and −1.799, respectively). Therefore, we conclude that the results of the main analysis are robust even after considering the effects of standard error bias.
Fifth, we control for the effects of firm size and inside ownership on future stock returns. We add the fraction of shares owned by directors (MO) as a control variable in the regression model and reexamine the relationship between unexpected forecasts and future stock returns. Kato et al. (2009) find that optimistic initial forecasts are more pronounced for firms with relatively high levels of insider ownership, and less pronounced for larger firms. The untabulated results indicate that the coefficient of UF remains significantly negative, suggesting that firms with higher unexpected forecasts earn negative abnormal returns after controlling for the effect of inside ownership.
Finally, we investigate the small firm effect on our main results. This study controls for the size effect because SIZE (the natural log of the market value of equity) is included in the regression models. However, to further examine the small firm effect, we divide the full sample into (1) a small firms group and (2) a nonsmall firms group and estimate Model (4) for each subsample. We define the small firms group as those whose market value is below the 10th percentile in each year. The untabulated results indicate that in both subsamples, the coefficients of UF are significantly negative at less than the 0.1 level. This result suggests that our main results do not derive from the small firm effect. Thus, our results are robust to the analyses controlling for the effects of small firms and inside ownership.
7 CONCLUSION
This study investigates the effect of managerial discretion over initial earnings forecasts on future stock returns. By estimating the unexpected portion of initial management earnings forecasts based on the findings of fundamental analysis research, we examine whether stock investors fully anticipate the implication of unexpected forecasts for the credibility of management earnings forecasts. Our hedge-portfolio test, with a portfolio long in firms in the most negative decile and short in firms in the most positive decile of unexpected forecasts, yields consistently positive hedge returns over the subsequent 6 and 12 months. By contrast, a hedge-portfolio test based on expected forecasts does not yield significant positive abnormal returns. These suggest that investors overreact to unexpected forecasts and that the overreaction is corrected as new information on actual earnings becomes available.
Further, as an additional analysis, we examine whether the relationship between unexpected forecasts and future returns are distinctive from the discretionary accruals anomaly. The results reveal that unexpected forecasts are negatively related to future returns after controlling for discretionary accruals. Thus, we conclude that the relationship between unexpected forecasts and future returns is distinct from discretionary accruals anomaly. Additionally, we also find that the relationship is more pronounced for (1) a 6-month return window, (2) the first half of the sample period (especially in years 2005 and 2006), (3) extreme unexpected news and (4) a poor information environment.
Unlike the United States, disclosure of management forecasts is effectively mandatory in Japan. As a result, management forecasts are available at the time of earnings announcements for almost all listed companies in the Japanese market. Investors can systematically analyze these, and thus consider management forecasts an important source of information for decision making (Iwasaki et al., 2023; Kato et al., 2009). However, as management has the discretion to determine the forecast values and these forecasts are not legally audited, investors may be misled by unreliable forecasts and may overreact to unexpected forecasts. Further exploration of the validity of this interpretation is the subject of future research.
Moreover, based on its limitations, this study raises several avenues for future research. First, although we measure unexpected forecasts using the findings of the fundamental analysis, future research may develop a better proxy for them. Second, we conduct additional analyses to verify our mispricing hypothesis, but it is difficult to completely consider all the unknown risk factors. Future research could examine other dimensions or forms of market mispricing. Finally, although we focus on the Japanese market, researchers could investigate whether our findings can be generalized to other markets. In particular, whether the results differ between the United States, where management earnings forecasts are disclosed voluntarily, and Japan, where they are semi-mandatory, will be interesting to discern.
ACKNOWLEDGMENTS
The authors sincerely appreciate the comments from Andrew Stark (editor) and the anonymous referee. The authors also appreciate the comments received from Gary Chen (discussant) and participants at the American Accounting Associations 2014 Annual Meeting, Atlanta and the Tokyo Accounting Workshop at the University of Tokyo. The authors also appreciate the helpful comments and suggestions received from Eli Bartov, Patricia Dechow, Baruch Lev, Shyam Sunder, Douglas J. Skinner and X. Frank Zhang. All errors are the responsibility of the authors.
APPENDIX: DEFINITIONS OF FUNDAMENTAL SIGNALS
| Signal | Measurement |
|---|---|
| Inventory (INVt-1) | Δ Inventory in year t – 1 – Δ Sales in year t – 1.a The variable is merchandise and finished goods when available; otherwise, it is total inventory. |
| Accounts receivables (ARt-1) | Δ Accounts receivable in year t – 1 – Δ Sales in year t – 1. The variable is accounts receivable when available; otherwise, it is accounts and notes receivable. |
| Capital expenditures (CAPXt-1) | Δ Industry capital expenditure in year t – 1 – Δ Firm capital expenditure in year t – 1. Industry capital expenditure = aggregating capital expenditure for all firms with the same Nikkei medium classification industry code. Firm capital expenditure = change in gross property, plant and equipment for a firm. |
| Gross margin (GMt-1) | Δ Sales in year t – 1 – Δ Gross margin in year t – 1. |
| Selling and administrative expenses (S&At-1) | Δ Selling and administrative expenses in year t – 1 – Δ Sales in year t – 1. |
| Effective tax rate (ETRt-1) | Average effective tax rate from year t – 5 to year t – 2 – effective tax rate in year t – 1. Effective tax rate = income taxes/income before income taxes. Each variable was acquired from the parent-only financial statement. |
| Change in total accruals (CTACt-1) | (total accruals for year t – 1 minus total accruals for year t – 2)/total assets at the end of year t – 1.b |
| Audit qualification (AQt-1) | Dummy variable set to 0 if auditor's opinion in year t – 1 is unqualified, and 1 if auditor's opinion is qualified or other. |
| Labor force (LFt-1) | (sales revenue per employee for year t – 2 – sales revenue per employee for year t – 1)/sales revenue per employee for year t – 2. Sales revenue per employee = sales/the number of employees at year-end. |
- aΔ operator represents the percentage change in the variable based on a 2-year average expectation model, which is the same as in Lev and Thiagarajan (1993) and Abarbanell and Bushee (1997). For example, ΔSales in year t – 1 = {Salest-1 − E(Salest-1)}/E(Salest-1), where E(Salest-1) = (Salest-2 + Salest-3)/2. All the other variables with the Δ operator are calculated using the same procedure.
- bTotal accruals are calculated as follows. Total accruals = (change in current assets – change in cash and deposits) – (change in current liabilities – change in financing items) – (change in allowance for doubtful debts + change in provision for retirement benefits or provision for retirement allowance + change in provision for directors’ retirement benefits + change in other long-term provision + depreciation). Financing items = change in short-term loans payable + change in commercial papers + change in current portion of long-term loans payable + change in current portion of straight and convertible bonds.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are publicly available.
REFERENCES
- 1 The forecast innovation for year t is measured as the management forecasts for year t + 1 minus the actual earnings for year t (Iwasaki et al., 2023; Kato et al., 2009).
- 2 For instance, on May 11, 2012, Panasonic Corporation reported 2013 management earnings forecasts of 5 billion JPY that represents an 882 billion JPY increase over the current year (Nihon Keizai Shimbun, May 12, 2012). Its positive forecasts caused the stock price to increase from 570 to 578 (approximately 1.4%) at the press release date. However, on October 31, 2012, Panasonic revised its earnings forecasts downward to 765 billion in losses from 5 billion in profits. As a result, its stock price dropped from 514 to 414 (approximately 19.5%) by the press release date (Nihon Keizai Shimbun, November 1, 2012). This case suggests that managers are likely to report optimistic initial earnings forecasts and that investors appear to overvalue them.
- 3 For example, Kato et al. (2009) document that 93.7% of their sample (38,068 of 40,647) report management forecasts within a sample period between 1997 and 2007, and Iwasaki et al. (2023) indicate that approximately 95% of observations (28,615 of 30,192) issue their forecasts within a sample period between 1997 and 2009. These findings suggest that management forecast disclosure in Japan is effectively mandated.
- 4 Although most studies examining US firms address sample selection bias by using statistical designs such as Heckman's two-stage estimation (e.g., Feng & Li, 2014; Feng et al., 2009; Gong et al., 2011; Hui et al., 2009; Shivakumar et al., 2011; Xu, 2010; Zhang, 2012), some studies show the difficulty of mitigating the bias perfectly even if the statistical procedures are used (e.g., Lennox et al., 2012).
- 5 The difference in the issue dates refers to two differences observed in the US firms: one is the difference in the announcement dates of firms’ actual earnings and management forecasts, and the other is the difference in those of management forecasts among firms. These differences affect the measurements of forecasts error or forecasts horizon and may introduce bias in the analysis. On the other hand, in the case of Japanese firms, actual earnings and management forecasts are disclosed at the same time, and firms with the same fiscal month issue their management forecasts at almost the same time. Therefore, the analysis for Japanese firms does not suffer from such problems.
- 6 For example, Kasznik (1999) establishes that the percentages of point- and range-estimated forecasts are 54.7% and 45.3%, respectively, from 1987 to 1991. More recently, Kwak et al. (2012) indicate that, of the 8483 management earnings forecasts between 1997 and 2009, the point, range and other forms of forecasts are 20.7%, 72.7% and 6.6%, respectively.
- 7 In Japan, only the dividend per share is sometimes reported by a range estimate (Gotoh, 1997; Ota, 2010).
- 8 For example, Ciconte et al. (2014) find that managers place significantly more weight on the upper bound of forecast ranges, suggesting that using midpoint estimates introduces bias into management forecast errors.
- 9 Hirst et al.’s (2008) literature review reports useful details on the determinants of management earnings forecasts. They summarize the factors operating when managers decide to issue a forecast and classify them into two broad categories: (1) forecast environment, the features of the legal, regulatory, analyst and investor environments and (2) forecaster characteristics, the information asymmetry, pre-commitment to disclosure, firm-specific litigation, managerial incentives, prior forecasting behavior and proprietary costs.
- 10 Iwasaki et al. (2023) identify two additional factors to explain why Japanese managers have a strong incentive to manage earnings forecasts. First, the costs of management forecasts at the announcement date are expected to be lower than those of other management methods (i.e., earnings management or forecast revisions) to beat the earnings benchmark. This is because (1) managers have no restriction on the continuous use of forecast management while accruals-based earnings management is restricted owing to the effect of accruals reversion, and (2) manipulation for initial forecasts is likely to be less perceivable and more difficult to detect. Second, litigation costs in Japan are relatively low compared to those in Western countries (West, 2001; Ginsburg & Hoetker, 2006), which induces managers to conduct forecasts management (Kato et al., 2009).
- 11 Other related studies include Xu (2009), Das et al. (2012) and Hurwitz (2018). They examine the relationship between management forecast characteristics and future returns. However, Ng et al. (2013) is closer to our study in that it examines the effect of earnings forecast credibility on market pricing.
- 12 Asano (2002), Enomoto (2003) and Okumura (2003) also provide evidence suggesting the existence of the accruals anomaly in Japan.
- 13 Studies such as Fama and French (2006) and Hou et al. (2012) present alternative earnings expectation models. However, we adopt the model that is similar to Iwasaki et al. (2023) because we must estimate the expected value of the change in earnings to estimate unexpected forecasts. The expectation models of Fama and French (2006) and Hou et al. (2012) are developed to estimate the expected value of the level of earnings.
- 14 Iwasaki et al. (2023) and Kitagawa and Shuto (2021) adopt an estimation model similar to that used by Matsumoto (2002), which estimates the expected portion of analysts’ forecasts. Specifically, Matsumoto (2002) estimates the expected analysts’ forecasts by modeling the seasonal change in earnings as a function of (1) the previous quarter's seasonal change in earnings and (2) cumulative excess return of year t. Iwasaki et al. (2023) extend this model by adding fundamental signals variables. We estimate the model similar to Iwasaki et al. (2023) for each year. Each sequential variable is winsorized at 1 and 99 percentiles by year.
- 15 Following Abarbanell and Bushee (1997), we adopt total assets at the end of year t – 1 as the denominator of CHGROAt-1. The authors also calculate 1-year ahead earnings changes (ΔEPSt+1) and current year's earnings changes (CHGEPSt), both of which are deflated by stock price at the end of year t – 1.
- 16 Regarding earnings quality measures, Abarbanell and Bushee (1997) use a dummy variable set to “1” if a firm adopts LIFO and “0” otherwise. We adopt CTAC instead of the LIFO measure because total accruals are expected to capture earnings quality more accurately than a single accounting procedure could.
- 17 Other than fundamental signals, Iwasaki et al. (2023) include firm-specific daily excess (market-adjusted) returns that are cumulated from 3 days after the year t – 2 earnings announcement to 20 days before the year t – 1 earnings announcement (CRET) to control for additional value-relevant information (other than fundamental signals) that managers might use to forecast earnings. We do not add the CRET but add some alternative variables in our estimation model. As an additional analysis, we estimate the unexpected forecast using a model that includes CRET. However, the results are consistent with those of the non-CRET model presented later.
- 18 Untabulated results from estimating Equation (1) reveal that the average coefficients for CHGEARN, INV, CAPX, GM, S&A, TAC, AQ and LF are negative, which is consistent Abarbanell and Bushee's (1997, 1998) results. Additionally, the average coefficients of HISTBIAS and BOND are positive and those of ABSERROR, NUMREV, and CHGGDP are negative. Furthermore, the mean value of adjusted R-square for model (1) is approximately 19%, suggesting that our model has reasonable explanatory power.
- 19 In the regression of an analysis covering 2006–2008, we cannot estimate the parameter of AQ because all AQ observations are “0” (i.e., all observations are unqualified opinions). Therefore, we exclude AQ from the regression model covering 2006–2008.
- 20 The estimate of managers’ expected forecasts should use only data that would be available to managers in making their forecasts. Thus, we use parameter estimates from the previous firm-year to determine expected forecasts (EF). This procedure is also crucial in terms of strategic feasibility for the securities investment.
- 21 As a result of our estimation procedure, management earnings forecasts are classified into forecast innovation and net income; forecast innovations are then classified into unexpected and expected forecasts as follows (Iwasaki et al., 2023, fig. 1, panel B):
Our sample comprised firms whose fiscal years end on March 31; their earnings (presented in the summary of financial results referred to as Kessan-Tanshin) are generally announced by mid-May to comply with the requirement of the TSE. The financial statements are disclosed in June (at the latest), so that the required shareholders’ general meeting can be held by the end of June (Kubota et al., 2010, p. 138). Therefore, we formed ranked portfolios on July 1.
Management earnings forecasts for year t + 1 (MF) (issued concurrently with net income for year t) Forecast innovations for year t (FI) Net income for year t Unexpected forecasts for year t (UF) Expected forecasts for year t (EF) Net income for year t - 22 We also conduct analyses in which the unexpected forecasts variable is defined as a decile rank variable, but the results are consistent with those of our study.
- 23 In addition to subsequent 12-month size-adjusted buy-and-hold returns, we also believe that the result on the subsequent 6-month size-adjusted buy-and-hold returns is important. As explained in Subsection 2.1, managers are expected to provide forecast revisions (including confirmation) when subsequent interim earnings are announced. Investors who fail to see through the unexpected forecasts at the earnings announcement date may learn the consequences of unexpected forecasts through forecast revisions in the interim earnings report. The analysis of the relationship between the subsequent 6-month returns and unexpected forecasts is expected to capture this effect.
- 24 Nondiscretionary accruals are estimated cross-sectionally for each industry in a given year using the Nikkei industry classification code (Nikkei gyousyu chu-bunrui). Total accruals = (change in current assets – change in cash and deposits) – (change in current liabilities – change in financing items) – (change in allowance for doubtful debts + change in provision for retirement benefits or provision for retirement allowance + change in provision for directors’ retirement benefits + change in other long-term provision + depreciation). Financing items = change in short-term loans payable + change in commercial papers + change in current portion of long-term loans payable + change in current portion of straight bonds and convertible bonds.
- 25 These results are consistent with those of previous studies on the accruals anomaly in Japan (e.g., Kubota et al., 2010; Leippold & Lohre, 2012; Pincus et al., 2007).
- 26 We divide the firms into five groups based on UF quintiles by year and further sort each group into five portfolios based on DAC by year. Firms whose UF and DAC are both in the highest (lowest) quintile are included in the highest (lowest) UF and DAC quintile portfolio.
- 27 If firms revise their forecasts once, FRRETt+1 corresponds to the size-adjusted abnormal return surrounding the management forecast revision announcement date. If firms revise their forecasts more than once, FRRETt+1 is defined as the sum of the size-adjusted abnormal return surrounding each management forecast revision announcement date.
- 28 If firms do not revise their forecasts during the period, investors may have information about the credibility of the initial management forecasts through the earnings announcement at the fiscal year-end. As an additional analysis, we define the FRRETt+1 of firms that do not revise their forecasts as the size-adjusted abnormal return around earnings announcement (days from “0” to “+2”) for the next year and add them to the sample. We thereby confirm the robustness of our findings.
- 29 In our sample, management forecast revisions per fiscal year occur approximately 2.09 times on average and eight times at most. Therefore, the announcement period windows are 6.27 days on average and 24 days at most.
- 30 The 6-month (12-month) hedge portfolio return when only 2005 and 2006 are included in the sample is 6.8% (19.2%). By contrast, that when 2005 and 2006 were excluded from the sample was 1.8% (–0.3%). One possible reason for the notably large hedge portfolio returns in 2005 and 2006 may be that accounting standards for impairment were introduced in this period, making it difficult for investors to forecast net income.
- 31 The definitions of the 10 variables are as follows. Variables for industry uncertainty: (1) dummy variable set to 1 if the industry return volatility for the last 12 months is above the median, and 0 otherwise; (2) dummy variable set to 1 if the industry return volatility for the last 12 months is above the third quartile, and 0 otherwise; (3) dummy variable set to 1 if industry sales volatility for the last 5 years is above the median, and 0 otherwise; (4) dummy variable set to 1 if industry sales volatility for the last 5 years is above the third quartile, and 0 otherwise. Variables for the characteristics of managers: (5) dummy variable set to 1 if the industry-adjusted capital expenditure is above the median, and 0 otherwise; (6) dummy variable set to 1 if the industry-adjusted capital expenditure is above the third quartile, and 0 otherwise; (7) dummy variable set to 1 if managers have a tenure of at least 4 years, and 0 otherwise; (8) dummy variable set to 1 if the industry-adjusted return during the manager's tenure (the last 36 months) is below the median, and 0 otherwise; (9) dummy variable set to 1 if the industry-adjusted return during the manager's tenure (the last 36 months) is in the first quartile, and 0 otherwise. Variables for the information environment: (10) dummy variable set to 1 if there is analyst coverage, and 0 otherwise.
- 32 We estimate the predicted value (EF) of the first-stage regression to create the main variable (UF). Because our main regression model (i.e., Model (4)) includes not only UF but also EF, which corresponds to the predicted value Chen et al. (2023) indicate as problematic, our main result may also face standard error bias. Specifically, as EF faces uncertainty associated with the first-step regression parameters, it causes underestimation bias of standard errors associated with all independent variables (including the main variable: UF) in the second-stage regression (i.e., Model (4)), leading to incorrect inferences in our main regression analysis.
- 33 The steps of the analysis are as follows: (1) Randomly draw with replacement a bootstrap sample clustered from the sample used in the first-step regression (i.e., Model (1) in our manuscript) along a firm dimension. (2) Estimate Model (1) using the bootstrap sample. (3) Use the coefficient estimates derived from the bootstrap sample in the year t – 1 and actual data in year t to obtain expected forecasts (EF). (4) Estimate unexpected forecasts (UF) by subtracting the expected forecasts (EF) for year t from the forecast innovations (FI) for year t. (5) Estimate the second-step regression (i.e., Model (4)) using the bootstrap sample and the generated variables (i.e., UF and EF), and store the coefficient estimates. (6) Repeat this process 1000 times. (7) Use the standard deviations of the collected coefficient estimates as the bootstrapped standard errors.
- 34 The steps of the analysis are as follows: (1) Randomly draw with replacement a bootstrap sample clustered from the sample used in the first-step regression (i.e., Model (1) in our manuscript) along a firm dimension. (2) Estimate Model (1) using the bootstrap sample. (3) Use the coefficient estimates derived from the bootstrap sample in the year t – 1 and actual data in year t to obtain expected forecasts (EF). (4) Estimate unexpected forecasts (UF) by subtracting the expected forecasts (EF) for year t from the forecast innovations (FI) for year t. (5) Estimate the second-step regression (i.e., Model (4)) using the bootstrap sample and the generated variables (i.e., UF and EF), and store the coefficient estimates. (6) Repeat this process 1000 times. (7) Use the standard deviations of the collected coefficient estimates as the bootstrapped standard errors.




