Distracted institutions, information asymmetry and stock price stability
Abstract
We study the interplay between stock price stability and the information environment following periods of institutional distraction. Using a large panel dataset over the years 1982–2016, we find that the level of ownership by distracted institutions significantly explains crash risk independent of additional determinants identified in prior research. Distraction has a pronounced effect on crash risk among firms that are subject to greater information opacity. Furthermore, we identify a causal impact of institutional distraction on the quality of the information environment that persists over the year following the distraction period. This heightened information asymmetry impedes investors’ ability to process information, leading investors to overreact to bad news.
1 INTRODUCTION
Institutional shareholders are important corporate monitors who play a critical role in the stability of stock prices and the information environment surrounding firms. In 1970, institutions held approximately 18% of the corporate equity market. As of 2018, this percentage increased to 64%.1 This institutional shareholder class has considerable heterogeneity, with constituents that include insurance companies, banks, mutual funds, pensions and hedge funds. The importance of institutional shareholders to price stability and the quality of the information environment surrounding firms lies in their ability to intervene when firm management behaves poorly. These institutions may intervene directly by communication and the exercise of voting rights or indirectly by trading economically large quantities of a firm's shares. However, monitoring and intervention can only take place if institutional shareholders are paying attention.
A well-developed line of research identifies a positive association between institutional monitoring, corporate governance and firm value (Appel et al., 2016; Boone & White, 2015; X. Chen et al., 2007; Harford et al., 2018; Shleifer & Vishny, 1986). However, institutional monitoring intensity varies with factors that include the weight of the firm in the institutional investors’ portfolio, the investment horizon of the institution and the attention devoted to other investments in the institution's portfolio (An & Zhang, 2013; Borochin & Yang, 2017; X. Chen et al., 2007; Kempf et al., 2017). Consequently, institutional investors may not distribute their attention equally across their holdings, resulting in suboptimal managerial decisions that lead to a decrease in firm value (Kempf et al., 2017; Ward et al., 2018).
In this study, we focus on the interplay between stock price stability and the information environment surrounding the firm subsequent to the institutional investor distraction period. As shown by Kempf et al. (2017), such periods of distraction are associated with poor firm operating performance and the announcement of value-decreasing merger transactions. Kempf et al. (2017) suggest these periods afford managers the opportunity to take actions that maximize their private benefits at the expense of shareholders. Our findings demonstrate that distraction leads to greater information asymmetry and, consequently, an increasing potential for stock price crashes in subsequent periods relative to the distraction period.
Institutional monitoring plays a critical corporate governance role. In the distraction context, lapses in institutional monitoring impair the quality of the information environment surrounding the firm. Within this environment, the eventual release of bad news causes the stock price to crash (Habib et al., 2018). Following prior literature, we gauge crash risk with the skewness of the return distribution. Based on a panel of US firms over the years 1982 to 2016, we find a positive and statistically significant association between institutional shareholder distraction and stock price crash risk that is robust to a variety of alternative measures of distraction. Our results illustrate that the level of negative return skew nearly doubles (relative to the sample mean) in the year following the period where the firm's institutional shareholders are distracted. Alternatively, when we use a stock crash indicator variable as the dependent variable, a one standard deviation increase in institutional distraction increases the probability of a stock price crash by approximately 2.2% in the subsequent year.
Information opacity likely intensifies the association between institutional distraction and the severity of price crash risk. The importance of institutional monitoring stems from their ability to collect and process information about the firm. For example, Devos et al. (2015) document stronger market reactions to analyst signals for subsets of firms with a lower balance of public to private information. Therefore, to the extent that institutional monitoring should be more important for less transparent firms, we anticipate a stronger association between institutional distraction and firm crash risk among these firms. Our results support this conjecture. Using a principal component-based index to measure opacity, we find that the association between institutional distraction and crash risk is strongest among firms in the highest opacity tercile. A one standard deviation increase in institutional distraction increases negative return skew by 1.6 times (relative to the subset mean) for firms in the highest tercile of information opacity. Conversely, crash risk is unaffected by the level of institutional distraction for firms in the lowest tercile of information opacity. As a result, the institutional monitoring role becomes increasingly important for firms that are less transparent to outside investors.
In addition, prior research associates information asymmetry with stock price crashes (Hutton et al., 2009; Jin & Myers, 2006; Kothari et al., 2009). In particular, Boone and White (2015) show institutional monitoring reduces information asymmetry of the firms they own. Based on these findings, we anticipate that reduced monitoring associated with institutional distraction gives rise to an increase in information asymmetry. We employ a matched firm approach to examine this premise, where control firms differ from distraction sample firms only by their levels of institutional distraction. We find that firms with greater levels of institutional distraction experience higher levels of information asymmetry during the following year. Our analysis encompasses multiple information asymmetry measures including stock price synchronicity, idiosyncratic volatility, bid-ask spread (BAS) and analyst forecast error. Our estimates suggest that firms with higher (top tercile) institutional distraction experience economically significant increases in these asymmetry measures ranging from 3% to 14% over the subsequent year. Taken together, our results suggest that information asymmetry is a channel through which distraction leads to greater subsequent stock price instability.
Finally, we assess investor reaction to bad news following periods of institutional distraction. Greater information asymmetry increases the resources required by investors to access new information. Consequently, greater information asymmetry diminishes investors’ ability to price bad news efficiently. For example, empirical work by Ben-Rephael et al. (2017) and Schmidt (2019) link contemporaneous periods of institutional distraction with the inefficient pricing of new information. Moreover, greater information asymmetry affords managers the opportunity to withhold bad news. To test this premise, we examine if the extent of institutional distraction at the beginning of the year influences the market reaction to negative earnings announcements during the year: that is, if greater distraction precedes periods of greater information asymmetry, investors should be more likely to overreact to the announcements. Our evidence demonstrates that the magnitude of “missed earnings” is greatest among firms with the highest institutional distraction at the beginning of the year. Further, the magnitudes of abnormal stock return and trading turnover, as well as subsequent return drift, associated with the negative news are increasing in institutional distraction. Specifically, a one standard deviation increase in institutional distraction decreases the buy-and-hold abnormal return (BHAR) over the [−1, 1] window surrounding the earnings announcement by 35 basis points and increases abnormal trading volume by roughly 30% over the same period. In addition, we identify a persistent negative return drift to these earnings as our estimates demonstrate a one standard deviation increase in institutional distraction is associated with a 104 basis point decrease in BHAR over the [2, 40] window. These results are consistent with the informational implications of institutional distraction, where distraction hinders investors’ ability to price new information efficiently.
We contribute to the institutional monitoring and crash risk literature in the following ways. First, our findings extend the results of Kempf et al. (2017) by showing that the implications of distracted institutions extend beyond the period in which distraction takes place—the focal point of their study. Additionally, we identify pronounced effects of institutional distraction among firms that have characteristics consistent with greater information asymmetry. These findings support the notion in Kempf et al. (2017) that firms with distracted institutional investors have greater agency problems that afford managers the opportunity to act in their own self-interest.
Second, we show that institutional distraction is a determinant of firm crash risk apart from a growing set of explanatory variables identified by the extant crash risk literature. These determinants typically focus on aspects of firm transparency, firm monitoring and characteristics of the firm's management. For example, work by Hutton et al. (2009), Kim et al. (2011b), and Kim and Zhang (2016) demonstrate that limited transparency, as proxied by factors that include a firm's use of opaque accounting tactics, allows firms to withhold bad news thereby leading to higher firm crash risk. Other studies focus on specific chief executive officer (CEO) characteristics (P. C. Andreou et al., 2017), the compensation structure of management (Kim et al., 2011a; Chowdhury et al., 2020), and board characteristics (P. C. Andreou et al., 2016). Of particular relevance to our study, An and Zhang (2013) and Callen and Fang (2013) rely solely on the investment horizon of a firm's institutional shareholders and find that greater ownership by institutions with a short-term horizon leads to greater crash risk. Our findings are robust to the inclusion of these existing crash risk determinants and highlight an additional mechanism through which institutional monitoring affects firm crash risk. Our findings show that lapses in monitoring lead to higher crash risk, even for firms whose investors share a long-term investment horizon and have large portfolio allocations. In addition, distraction has a particularly pronounced effect on crash risk among firms that are subject to greater information asymmetry.
Third, we provide evidence of a causal association between institutional distraction and measures of information asymmetry surrounding the firm subsequent to the distraction period. To our knowledge, our study is the first to document a causal association between institutional distraction and the degree of information asymmetry during the following year. Prior work by Xiang et al. (2020) and Ni et al. (2020) documents a positive association between institutional distraction and firm crash risk. Xiang et al. (2020) use a sample of Chinese listed companies in the Shanghai Stock Exchange during 2011–2017 period to demonstrate a positive relation between institutional distraction and crash risk, particularly among state-owned entities. Using a sample of US firms, Ni et al. (2020) focus on persistent institutional distraction by averaging distraction events annually. In contrast to these studies, we focus on distraction measured in the quarter prior to the crash risk measurement period, allowing us to provide a robust causal association. Most important, Xiang et al. (2020) and Ni et al. (2020) do not identify the channel through which institutional distraction increases crash risk. Periods of institutional distraction cause higher information asymmetry as managers hoard bad news. Because investors cannot price this news, the market price diverges from its intrinsic value. The eventual revealing of bad news provokes downward pressure on price (i.e., crash risk) in direct proportion to the level of asymmetry associated with distraction.
Finally, our findings contribute to the interpretation in extant work about how negative news withheld by the managers becomes available to investors. Jin and Myers (2006) propose that managers withhold negative information until it becomes impossible to hide any longer, leading to a sudden release of negative news. Alternatively, Hong and Stein (1999), J. Chen et al. (2001) and Hong and Stein (2003) suggest that some negative information becomes available to investors prior to the crash. Using high-frequency data, recent work by C. K. Andreou et al. (2021) demonstrates that increases in financial distress risk take place over a brief period prior to the stock price crash, implying that negative firm-specific information is incrementally dispersed to the market. Our findings regarding higher turnover and prolonged negative return draft are consistent with the gradual release of negative firm-specific information.
2 RESEARCH DESIGN AND SAMPLE DATA
2.1 Measuring stock price crash risk
2.2 Measuring institutional distraction
The ID measure estimates the exposure of firm f’s institutional investors to significant distracting events in other industries. Following Kempf et al. (2017), a distraction is a firm in an industry whose quarterly return is either the highest or the lowest among the 12 Fama and French industries. Therefore, the degree to which an institution is distracted is increasing in the portion of their portfolio allocated to these firms. The intuition behind this measure is that “a given investor i is more likely to be distracted if there is an attention-grabbing event in another industry, and if that industry is important in investor i’s portfolio.” (Kempf et al., 2017, p.1668). For robustness, we also construct an above median ID indicator variable that equals one if ID is above the median in the given year and zero otherwise. Additionally, we split our sample into quintiles each year based on the value of the continuous ID variable. We construct ID Quintile 2 through ID Quintile 5 indicator variables that are equal to one if the firm's level of distraction in year t has a quintile portfolio placement of 2 through 5, respectively, and zero otherwise.
2.3 Empirical specification
Following prior work (e.g., Chang et al., 2017; Hutton et al., 2009; Kim et al., 2011a, 2011b), we control for firm characteristics including the lagged value of firm i’s negative conditional skewness (), detrended turnover (Turnover), standard deviation of weekly returns, average weekly return, size (Log of Market Capitalization), book-to-market ratio, book leverage and firm profitability (Return on Assets). Additionally, we control for research and development expenses (R&D to Total Assets) and acquisitions (Acquisition Indicator) by using an indicator variable that is one if the firm announces an acquisition in the current year. Kempf et al. (2017) provide evidence that firms having high distraction in quarter t–1 are more likely to announce an acquisition in quarter t. As such, Acquisition Indicator controls for the negative return reaction typically associated with an acquisition announcement. With the exception of the Acquisition Indicator, we construct control variables using data from calendar year t–1.5 We measure all stock price data as of December of calendar year t–1. Additionally, we cluster-adjust the standard errors of the coefficient estimates by firm (White, 1980) and include year and industry fixed effects using the Fama and French 48 industries.
We extend our baseline regression specification to account for the growing set of characteristics shown to be associated with crash risk in the extant literature. These extended models include the firm's transient institutional ownership, dedicated institutional ownership and overall institutional ownership (An & Zang, 2013). Additionally, we control for stock liquidity with logged Amihud Illiquidity measured over calendar year t–1 (Amihud, 2002; Chang et al., 2017). Based on prior work, we add measures of transparency, including the firm's long-run effective tax rate (Kim et al., 2011b), accounting conservatism (Kim & Zhang, 2016) and discretionary accruals (Hutton et al., 2009).
In addition to institutional shareholder monitoring, board of director and executive characteristics may also affect crash risk. For example, P. C. Andreou et al. (2016) and Cao et al. (2019) show that board characteristics, such as the proportion of outside directors, the board size and director experience, can affect crash risk. Moreover, Kim et al. (2011a), P. C. Andreou et al. (2016, 2017), Chowdhury et al. (2020) and Al Mamun et al. (2020) show various CEO characteristics (e.g., compensation structure, duality, age and experience) can influence the degree of crash risk. To control for these board- and CEO-related characteristics, we include the CEO's age and tenure with the firm, whether she is chair of the board (CEO Duality), her compensation structure (Equity/Option Compensation), the CEO's pay slice (CEO Pay Slice) and whether the firm is part of an industry with greater tournament incentives (Industry Tournament Incentives). Table A1 provides variable definitions and calculations.
2.4 Sample selection and descriptive statistics
Our empirical analyses use data from multiple sources. We obtain stock price and accounting data from CRSP and Compustat. We obtain institutional ownership data required for our computation of distraction from the Thomson-Reuters Institutional Holdings (13F) database. We obtain other variables used in our multivariate analyses pertaining to executive compensation, merger events and analyst estimates from the ExecuComp, Thomson Reuters SDC and IBES databases, respectively. Our final sample consists of 47,098 firm-year observations over the years 1982 to 2016. Following J. Chen et al. (2001), our sample includes firms with a share code of 10 and 11 in CRSP and those with a fully populated set of control variables required for our baseline crash risk model specified by equation (3). To maintain consistency with Kempf et al. (2017), we exclude firms with market capitalizations in the lowest quintile of all the New York Stock Exchange (NYSE) stocks at the end of each calendar year. Our final sample includes 47,098 firm-year observations.
Table 1 provides summary statistics of the variables we use throughout the study. In line with summary statistics provided by Kempf et al. (2017), the distraction (ID) measure has a mean (standard deviation) of 0.18 (0.07), respectively. In line with the findings of related crash risk studies (e.g., An & Zhang, 2013; P. C. Andreou et al., 2017; Callen & Fang, 2013; Kim et al., 2011a, 2011b), NCSKEW has a mean 0.04 and is highly dispersed based on the standard deviation of 0.85. The alternative crash risk indicator (CRASH) demonstrates that roughly 18% of firm-year observations in our sample experience a stock price crash in a given year (i.e., mean CRASH is 0.18). We provide the frequency of firm stock price crashes over the year 1982 to 2016 in Table A2. Similar to prior studies (e.g., P. C. Andreou et al., 2017; Kim et al., 2011a, 2011b), the average yearly percentage of firms that have a stock price crash is 17.25% with an increasing trend in the percentage of firms experiencing a price crash over time. The remaining variables in Table 1 consist of control variables we use throughout our multivariate tests. Because we exclude the smallest quintile of firms from our analyses, these statistics demonstrate that firms in our sample are larger and more profitable with significant institutional ownership.
| Variable | N | Mean | STD | 25th | Median | 75th |
|---|---|---|---|---|---|---|
| Institutional Distraction (ID) | 47,098 | 0.18 | 0.07 | 0.13 | 0.19 | 0.23 |
| Above Median ID by Year | 47,098 | 0.50 | 0.50 | 0.00 | 0.00 | 1.00 |
| NCSKEW | 47,098 | 0.04 | 0.85 | −0.39 | 0.00 | 0.41 |
| CRASH | 47,098 | 0.18 | 0.38 | 0.00 | 0.00 | 0.00 |
| COUNT | 47,098 | 0.01 | 0.59 | 0.00 | 0.00 | 0.00 |
| DUVOL | 47,098 | 0.02 | 0.53 | −0.31 | 0.00 | 0.33 |
| Turnover | 47,098 | 0.01 | 0.10 | −0.01 | 0.00 | 0.02 |
| Weekly Return Standard Deviation | 47,098 | 4.37 | 2.42 | 2.79 | 3.82 | 5.33 |
| Average Weekly Return | 47,098 | −0.12 | 0.19 | −0.14 | −0.07 | −0.04 |
| Log of Market Capitalization | 47,098 | 14.03 | 1.47 | 12.97 | 13.86 | 14.89 |
| Book-to-Market Ratio | 47,098 | 0.62 | 0.49 | 0.31 | 0.52 | 0.81 |
| Book Leverage | 47,098 | 0.30 | 0.23 | 0.09 | 0.29 | 0.44 |
| Return on Assets | 47,098 | 0.15 | 0.16 | 0.08 | 0.14 | 0.21 |
| R&D to Total Assets | 47,098 | 0.03 | 0.08 | 0.00 | 0.00 | 0.02 |
| Acquisition Indicator | 47,098 | 0.13 | 0.34 | 0.00 | 0.00 | 0.00 |
| Transient Institutional Ownership (%) | 47,098 | 0.13 | 0.11 | 0.05 | 0.11 | 0.19 |
| Dedicated Institutional Ownership (%) | 47,098 | 0.08 | 0.10 | 0.00 | 0.05 | 0.11 |
| Institutional Ownership (%) | 47,098 | 0.57 | 0.25 | 0.38 | 0.58 | 0.76 |
| Log of Amihud Illiquidity | 47,098 | −5.35 | 2.33 | −6.98 | −5.43 | −3.69 |
| Long Run Effective Tax Rate | 47,098 | 0.14 | 0.18 | 0.00 | 0.02 | 0.28 |
| Accounting Conservatism | 46,833 | 0.05 | 0.15 | 0.00 | 0.07 | 0.13 |
| Discretionary Accruals | 31,121 | 0.25 | 0.34 | 0.08 | 0.15 | 0.29 |
| Log of CEO Age | 23,404 | 4.02 | 0.13 | 3.93 | 4.03 | 4.11 |
| Log of CEO Tenure | 24,233 | 1.44 | 1.03 | 0.69 | 1.61 | 2.20 |
| CEO Duality | 24,233 | 0.59 | 0.49 | 0.00 | 1.00 | 1.00 |
| Log of CEO Equity Compensation | 24,233 | 8.69 | 2.61 | 7.74 | 8.93 | 10.13 |
| Log of CEO Option Compensation | 24,232 | 6.66 | 3.65 | 5.35 | 7.87 | 9.25 |
| CEO Pay Slice | 24,233 | 0.39 | 0.12 | 0.32 | 0.39 | 0.46 |
| Log of Industry Tournament Incentives | 22,621 | 9.34 | 1.02 | 8.80 | 9.45 | 9.97 |
| Analyst Coverage | 47,098 | 12.50 | 10.12 | 5.00 | 10.00 | 18.00 |
| Firm Age (in quarters) | 47,087 | 86.65 | 73.57 | 31.00 | 67.00 | 118.00 |
| Synchronicity | 45,928 | −1.08 | 1.28 | −1.78 | −0.93 | −0.19 |
| Idiosyncratic Volatility | 46,102 | 0.02 | 0.01 | 0.01 | 0.02 | 0.03 |
| Bid Ask Spread (BAS) | 45,882 | 0.01 | 0.01 | 0.00 | 0.01 | 0.01 |
| Analyst Absolute Annual Forecast Error | 40,458 | 0.21 | 0.89 | 0.01 | 0.04 | 0.11 |
| Price Informativeness (Theta Measure) | 43,520 | 0.00 | 0.32 | −0.18 | 0.00 | 0.19 |
- Note: Table 1 provides summary statistics of variables used in the multivariate analyses. The sample period spans from 1982 to 2016. Table A1 provides variable definitions.
3 RESULTS
3.1 Base model specifications
We compute the average level of skew within each of our distraction quintile portfolios to gain an intuitive perspective of the relation between institutional distraction and firm crash risk and plot these statistics in Figure 1. As shown in the figure, there is an upward trend in negative skewness moving from the first to the fifth quantiles of institutional distraction. Crash risk is greatest among firms in the highest quintile distraction portfolio, where the negative conditional return skew of these firms is roughly 248% greater versus firms in the low distraction portfolio (0.078 vs. 0.032). Figure 1 provides preliminary evidence that indicates greater institutional distraction is associated with greater crash risk.
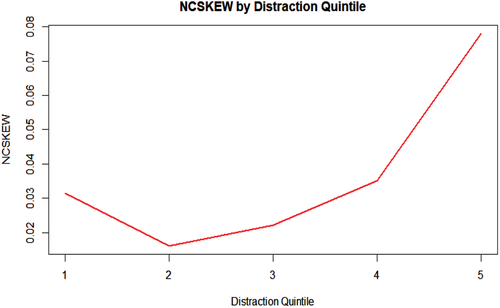
NCSKEW by distraction quintile. This figure plots the average NCSKEW within institutional distraction quintile portfolios. For each year, we sort firms into quintiles based on the firm's level of institutional distraction and compute the average NCSKEW across quintiles
We next turn to a multivariate setting and estimate our baseline model as specified by equation (3). We report these results in Table 2. In Model 1, we use the continuous ID variable (measured as of the fourth quarter of year t–1) as the main explanatory variable of interest. As Table 2 illustrates, the ID coefficient estimate of 1.0422 is statistically significant at the 1% level, consistent with the premise that greater distraction leads to greater negative return skew. The ID estimate implies that a one standard deviation increase in institutional distraction corresponds to a 0.073 magnitude increase in skewness, which is approximately twice the NCSKEW sample mean. Putting this into the context of prior findings, J. Chen et al. (2001) find that a one standard deviation increase in market-to-book leads to a 0.018 magnitude increase in skewness, and Chang et al. (2017) find that a one standard deviation increase in liquidity corresponds with a 0.047 increase in return skewness.
| (1) | (2) | (3) | |
|---|---|---|---|
| Dependent variable | NCSKEW | NCSKEW | NCSKEW |
| ID | 1.0422*** | ||
| (4.49) | |||
| Above Median (ID) Indicator | 0.0160** | ||
| (2.05) | |||
| ID Quintile 2 | −0.0146 | ||
| (−1.19) | |||
| ID Quintile 3 | −0.0069 | ||
| (−0.55) | |||
| ID Quintile 4 | −0.0032 | ||
| (−0.26) | |||
| ID Quintile 5 | 0.0240* | ||
| (1.93) | |||
| Lag NCSKEW | 0.0428*** | 0.0431*** | 0.0431*** |
| (7.15) | (7.19) | (7.19) | |
| Turnover | 0.1734*** | 0.1742*** | 0.1723*** |
| (3.15) | (3.16) | (3.13) | |
| Weekly Return Standard Deviation | 0.0467*** | 0.0479*** | 0.0475*** |
| (7.43) | (7.71) | (7.61) | |
| Average Weekly Return | 0.3549*** | 0.3552*** | 0.3541*** |
| (4.30) | (4.39) | (4.36) | |
| Log of Market Capitalization | 0.0330*** | 0.0338*** | 0.0342*** |
| (9.59) | (9.83) | (9.92) | |
| Book-to-Market Ratio | −0.0723*** | −0.0732*** | −0.0724*** |
| (−6.93) | (−7.01) | (−6.94) | |
| Book Leverage | −0.0398* | −0.0418** | −0.0403* |
| (−1.88) | (−1.97) | (−1.90) | |
| Return on Assets | 0.2739*** | 0.2759*** | 0.2759*** |
| (7.86) | (7.91) | (7.92) | |
| R&D to Total Assets | 0.3208*** | 0.3231*** | 0.3201*** |
| (4.22) | (4.25) | (4.21) | |
| Acquisition Indicator | 0.0165 | 0.0176 | 0.0171 |
| (1.45) | (1.55) | (1.50) | |
| Intercept | −0.8715*** | −0.7808*** | −0.7767*** |
| (−8.69) | (−7.96) | (−7.90) | |
| Year Fixed Effects | YES | YES | YES |
| Industry Fixed Effects | YES | YES | YES |
| No. Obs. | 47,098 | 47,098 | 47,098 |
| Adjusted R2 | 0.035 | 0.035 | 0.035 |
- Note: Table 2 provides coefficient estimates of ID over the fourth quarter in year t−1 and additional control variables using calendar year t NCSKEW as the dependent variable. The regressions are at the firm-year level and we measure all independent variables as of calendar year t−1. In Model 2, the independent variable of interest is an indicator variable that is one if ID is above the median in the given year. In Model 3, ID Quintile 2–ID Quintile 5 are indicator variables that are one if the firm's level of distraction in fourth quarter year t−1 has a quintile portfolio placement of 2 through 5, respectively. We include year fixed effects and industry fixed effects using the Fama and French 48 industries and cluster the robust standard errors at the firm level.
- ***, ** and * denotes statistical significance at the 1%, 5% and 10% levels, respectively.
To ensure that our continuous ID result is robust to potential outliers, the second version of our baseline model uses ID Above Median Indicator as the main variable of interest. As illustrated in Table 2, Model 2, the ID Above Median Indicator estimate is 0.016 and is statistically significant at the 5% level. The coefficient estimate implies that above-median institutional distraction in the fourth quarter of calendar year t−1 is associated with negative return skew during the subsequent year t by approximately 43.8% from the sample mean.
Finally, our third baseline model specification uses ID Quintile 2-ID Quintile 5 indicator variables. Table 2, Model 3, reports coefficients estimates of −0.0146, −0.0069, −0.0032 and 0.0240, respectively. The coefficient estimates increase monotonically from the low to high distraction quintiles, where the ID Quintile 5 estimate is statistically significant at the 10% level. In addition, we conduct a number of robustness tests using our baseline model. First, we estimate the model using negative conditional skewness computed with the expanded market model employed by Hutton et al. (2009). Additionally, we exclude observations from the recent financial crisis (i.e., years 2006–2008), as these years were prone to more stock price crashes. The results of these tests are qualitatively similar to those illustrated in Table 2, Models 1–3; we provide these results in Table A3. We also estimate our baseline model using the crash variables CRASH, COUNT, and DUVOL. As Table A4 illustrates, institutional distraction continues to be positively associated with crash risk. For example, the marginal effect of the CRASH indicator in Model 1 is 0.3276, suggesting a one standard deviation increase in institutional distraction (i.e., 0.698) increases the probability of a stock price crash by 2.29%. In Model 2, using a linear probability model, a one standard deviation increase in distraction increases the probability by approximately 2.15%. Finally, we examine our baseline model results using firm fixed effects (Table A5, Model 1) and with two-way standard error clustering by firm and year (Table A5, Model 2). Institutional distraction continues to have a positive and statistically significant relation with crash risk in each of these models. Viewed collectively, these results are consistent with our hypothesis and the findings of prior research that institutional distraction is positively associated with the degree of stock price crash in the subsequent year.
3.2 Additional control variables
The firm- and market-level control variables in our baseline crash risk model are consistent with the traditional specification used in the crash risk literature. However, omitted variables identified in recent work may potentially bias our results. Therefore, we add additional measures that recent crash risk research identifies as relevant in order to avoid omitted variable bias in our baseline ID results. Table 3, Models 1–6, provide ID estimates using the extended baseline specifications. In Model 1, we include measures of the composition of a firm's institutional ownership to our baseline model. An and Zhang (2013) and Callen and Fang (2013) demonstrate that higher institutional ownership leads to greater crash risk and that the investment horizon of these institutions plays a role in the magnitude of the association. Therefore, we include overall institutional ownership, percentage ownership by transient institutions (i.e., short-term investment horizon) and percentage ownership by dedicated institutions (i.e., longer-term investment horizon). We follow Bushee's (1998, 2001) classifications of transient and dedicated institutional investment horizons.6 Consistent with prior findings, the estimates in Model 1 show that transient institutions primarily drive the positive association between institutional ownership and crash risk. Conversely, greater monitoring diligence by dedicated institutions mitigates crash risk. However, despite the statistical significance of these institutional characteristics, distraction continues to significantly affect crash risk based on the coefficient estimate of 0.8567 (p = 0.01).
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| Dependent variable | NCSKEW | NCSKEW | NCSKEW | NCSKEW | NCSKEW | NCSKEW |
| ID | 0.8567*** | 0.9614*** | 1.0168*** | 1.0700*** | 0.9176** | 0.7865** |
| (3.66) | (4.13) | (4.38) | (3.30) | (2.47) | (2.10) | |
| Transient Institutional Ownership | 0.5320*** | |||||
| (7.58) | ||||||
| Dedicated Institutional Ownership | −0.1139** | |||||
| (−2.14) | ||||||
| Institutional Ownership | 0.1062*** | |||||
| (3.04) | ||||||
| Log of Amihud Illiquidity | −0.0263*** | |||||
| (−5.39) | ||||||
| Long Run Effective Tax Rate | −0.0744** | |||||
| (−2.52) | ||||||
| Accounting Conservatism | 0.0263 | |||||
| (1.12) | ||||||
| Discretionary Accruals | 0.0534** | |||||
| (2.05) | ||||||
| Log of CEO Age | −0.0244 | |||||
| (−0.47) | ||||||
| Log of CEO Tenure | −0.0034 | |||||
| (−0.55) | ||||||
| CEO Duality | −0.0007 | |||||
| (−0.05) | ||||||
| Log of CEO Equity Compensation | −0.0015 | |||||
| (−0.62) | ||||||
| Log of CEO Option Compensation | 0.0019 | |||||
| (1.03) | ||||||
| CEO Pay Slice | 0.1026** | |||||
| (1.99) | ||||||
| Log of Industry Tournament Incentives | −0.0008 | |||||
| (−0.10) | ||||||
| Firm Controls | YES | YES | YES | YES | YES | YES |
| Year Fixed Effects | YES | YES | YES | YES | YES | YES |
| Industry Fixed Effects | YES | YES | YES | YES | YES | YES |
| No. Obs. | 47,098 | 47,098 | 47,098 | 30,926 | 23,404 | 22,620 |
| Adjusted R2 | 0.040 | 0.036 | 0.036 | 0.027 | 0.026 | 0.026 |
- Note: Table 3 provides coefficient estimates using calendar year t NCSKEW as the dependent variable. The regressions are at the firm-year level and we measure all independent variables as of calendar year t−1. We measure ID over the fourth quarter in year t−1. In Models 1–6, we control for firm/CEO characteristics including the level and type of institutional ownership, illiquidity, tax avoidance, accounting transparency, CEO characteristics and CEO compensation structure. We include year fixed effects and industry fixed effects using the Fama and French 48 industries and cluster the robust standard errors at the firm level.
- ***, ** and * denotes statistical significance at the 1%, 5% and 10% percent levels, respectively.
Prior research demonstrates that liquidity is a mechanism by which transient institutions increase firm crash risk. For example, Chang et al. (2017) show more liquid firms have greater crash risk, arguing transient institutions are better able to sell when firms release bad news. In Table 3, Model 2, we add logged Amihud Illiquidity (2002) to the baseline model. Consistent with the findings of Chang et al. (2017), Amihud Illiquidity has a negative and statistically significant coefficient. However, the economic and statistical significance of institutional distraction is unaffected: the ID measure coefficient estimate is 0.9614 (p = 0.01).
In Table 3, Models 3 and 4, we use three alternative proxies of accounting transparency including the firm's long-run tax rate, level of conservatism, and use of discretionary accruals. The loadings on these variables are generally consistent with prior research. For example, in Model 3, the long-run effective tax rate is negatively associated with crash risk, consistent with management extracting fewer rents and reducing their hoarding of bad news (Kim et al., 2011a). Similarly, following the premise that less financial statement transparency allows for greater bad new hoarding by management (Hutton et al., 2009), discretionary accruals are positively associated with crash risk However, these additional controls collectively do not qualitatively affect the statistical and economic significance of the ID measure, which remains consistent with the baseline models.
Table 3, Models 5 and 6, consider managerial and executive compensation characteristics. In Model 5, we include the age of the CEO, the tenure of the CEO with the firm and whether the CEO holds the position of chair of the board. Younger, less experienced CEOs and CEO's having a dual CEO-board chair role have each been shown to increase firm crash risk, likely driven by greater risk incentives (Al Mamun et al., 2020; P. C. Andreou et al., 2016,2017). Relatedly, risk-taking is associated with the structure of CEO compensation. For example, Kim et al. (2011a) and P. C. Andreou et al. (2016) provide evidence that option-based compensation is directly associated with firm crash risk. Further, the relative pay of the CEO within the firm and to other CEOs in the same industry has been shown to affect crash risk (Chowdhury et al., 2020; Kim et al., 2016). For example, CEOs in high tournament incentive industries more aptly disclose bad news to maintain a long-term sustainable image in external labor markets (Chowdhury et al., 2020). In Model 6, we add four CEO compensation variables. The market values of a CEO's equity holdings in the firm (CEO Equity Compensation) and option-based compensation (CEO Option Compensation) control for incentives associated with equity-linked compensation. In a similar vein, we include two measures of the relative magnitude of the CEO's compensation, including the percentage of the CEO's total compensation relative to the top five executives of the firm (CEO Pay Slice), and the difference between the total compensation of the second-highest-paid CEO in the same Fama and French 48 industry (Industry Tournament Incentives).7
Institutional distraction continues to be positively associated with firm crash risk in Models 5 and 6, and the ID estimates of 0.918 and 0.787, respectively, are significant at the 5% levels. Many of the managerial and compensation characteristic variables have coefficients of the expected sign, but few are statistically significant. Among the additional controls, the CEO pay slice is significantly associated with crash risk. Overall, the results in Table 3 demonstrate that the association between institutional investor distraction and crash risk is robust to the consideration of a wide range of predictors employed in the crash risk literature.
3.3 Information asymmetry and crash risk
We investigate whether information opacity plays a moderating role in the association between distraction and the severity of price crash risk. We segment our sample into terciles at the end of each year based on firm characteristics identified in extant research as indicative of greater opacity (e.g., Baik et al., 2018; Jiang et al., 2005; Piotroski & Roulstone, 2004; Zhang, 2006). Segmenting our sample in this manner allows us to distinguish the quality of each firm's information environment. The firm characteristics we use include low (high) market capitalization, low (high) analyst coverage, low (high) firm age, low (high) institutional ownership, low (high) book-to-market ratio and a high (low) composite index of these five measures. We estimate our baseline model and test whether the difference in the institutional distraction coefficients is statistically significant within the top and bottom tercile portfolios.
Table 4 provides subsample regression results along with Chow test chi-square statistics and p-values for the differences in ID coefficients across terciles in the bottom row. The estimates illustrate a pronounced effect of institutional distraction on firm crash risk for firms with higher degrees of opacity. For each opacity measure, the ID coefficient estimate is positive and statistically significant at the 5% level or lower for the high opacity subsample. We create an opacity index using the alternative measures. We assign tercile rankings using each opacity characteristic. We place firms into the high (low) opacity portfolio if they are in the top (bottom) tercile in at least three of the five individual characteristic rankings. The results in Table 4 provide evidence that institutional distraction has a significantly stronger effect in the high opacity subset. In Model 11, the ID estimate in the high opacity index subset is 1.441 (p = 0.01). Based on this estimate, a one standard deviation increase in institutional distraction is associated with negative return skewness that is approximately 1.6 times greater than the sample mean during the subsequent year.8 Conversely, the ID coefficient estimate is statistically insignificant in Model 12, indicating that institutional distraction is unrelated to crash risk among firms in the low opacity tercile. Taken together, the results of Table 4 support the notion that lapses in monitoring are particularly costly for firms with lower quality information environments.9
| Firm size | Analyst coverage | Firm age | Institutional ownership | Book-to-market ratio | Opacity index | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| High | Low | High | Low | High | Low | High | Low | High | Low | High | Low | |
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | (9) | (10) | (11) | (12) | |
| ID | 0.2840 | 1.1182*** | −0.6820 | 1.6273*** | 0.8786 | 1.5359*** | 0.8387 | 1.1354*** | 0.4979 | 0.8014** | 1.4413*** | −0.7283 |
| (0.48) | (3.63) | (−1.15) | (4.92) | (1.63) | (4.38) | (1.59) | (3.74) | (1.22) | (2.03) | (4.45) | (−1.01) | |
| Lag NCSKEW | 0.0410*** | 0.0293*** | 0.0421*** | 0.0424*** | 0.0395*** | 0.0257** | 0.0387*** | 0.0532*** | 0.0337*** | 0.0568*** | 0.0326*** | 0.0419*** |
| (3.72) | (3.09) | (3.92) | (4.02) | (3.89) | (2.52) | (3.62) | (5.39) | (3.45) | (5.06) | (2.82) | (3.65) | |
| Turnover | −0.0355 | 0.3033*** | 0.0349 | 0.1877 | 0.1339 | 0.1998*** | 0.0575 | 0.0999 | 0.1838 | 0.2347** | 0.1402 | −0.0030 |
| (−0.36) | (3.12) | (0.53) | (1.52) | (1.11) | (3.01) | (0.69) | (1.14) | (1.55) | (2.56) | (1.49) | (−0.03) | |
| Weekly Return Standard Dev. | 0.0317*** | 0.0456*** | 0.0265*** | 0.0413*** | 0.0356*** | 0.0466*** | 0.0560*** | 0.0234*** | 0.0187** | 0.0595*** | 0.0352*** | 0.0229** |
| (3.35) | (5.42) | (2.73) | (4.78) | (3.41) | (4.45) | (5.64) | (2.83) | (2.17) | (6.14) | (3.67) | (2.00) | |
| Average Weekly Return | 0.2230*** | 0.3763*** | 0.2063** | 0.2712*** | 0.3482** | 0.3408*** | 0.3078*** | 0.1496 | 0.1138 | 0.5627*** | 0.2363** | 0.1443 |
| (2.59) | (3.74) | (2.38) | (2.83) | (2.51) | (2.83) | (2.89) | (1.61) | (1.12) | (5.21) | (2.19) | (1.21) | |
| Log of Market Capitalization | 0.0144** | 0.1191*** | 0.0160** | 0.0594*** | 0.0338*** | 0.0453*** | 0.0108 | 0.0443*** | 0.0341*** | 0.0228*** | 0.0822*** | 0.0146** |
| (2.03) | (8.64) | (2.40) | (5.86) | (6.07) | (5.86) | (1.46) | (7.56) | (5.98) | (3.69) | (6.56) | (2.00) | |
| Book-to-Market Ratio | −0.0868*** | −0.0402*** | −0.0860*** | −0.0696*** | −0.0512*** | −0.0713*** | −0.0795*** | −0.0640*** | −0.0157 | −0.3394*** | −0.0628*** | −0.0835*** |
| (−3.94) | (−2.90) | (−4.65) | (−3.75) | (−2.91) | (−3.93) | (−4.50) | (−4.01) | (−1.10) | (−3.75) | (−3.36) | (−4.61) | |
| Book Leverage | 0.0149 | −0.1028*** | −0.0066 | −0.0024 | −0.0448 | −0.0842** | −0.0850** | −0.0322 | 0.0325 | −0.1248*** | −0.1121*** | −0.0030 |
| (0.41) | (−3.04) | (−0.17) | (−0.07) | (−1.06) | (−2.52) | (−2.24) | (−0.90) | (0.77) | (−3.71) | (−3.07) | (−0.07) | |
| Return on Assets | 0.2886*** | 0.2640*** | 0.2528*** | 0.2560*** | 0.3197*** | 0.2881*** | 0.1580** | 0.2515*** | 0.1854* | 0.1576*** | 0.2696*** | 0.2053* |
| (3.49) | (5.65) | (3.17) | (4.72) | (2.94) | (6.49) | (2.13) | (5.30) | (1.88) | (3.53) | (5.69) | (1.96) | |
| R&D to Total Assets | 0.2661 | 0.2683** | 0.2345 | 0.2563** | −0.1068 | 0.2604*** | 0.1582 | 0.3128*** | 1.0340*** | 0.0906 | 0.3223*** | 0.1788 |
| (1.62) | (2.33) | (1.27) | (2.20) | (−0.32) | (2.67) | (1.00) | (2.73) | (3.71) | (1.02) | (2.92) | (0.69) | |
| Acquisition Indicator | 0.0540*** | 0.0141 | 0.0110 | 0.0289 | 0.0402** | −0.0027 | 0.0079 | 0.0301 | 0.0244 | −0.0006 | 0.0260 | 0.0371* |
| (2.96) | (0.74) | (0.57) | (1.40) | (2.02) | (−0.14) | (0.38) | (1.59) | (1.21) | (−0.03) | (1.19) | (1.79) | |
| Intercept | −0.4293** | −2.0736*** | −0.0704 | −1.2492*** | −0.8842*** | −1.0211*** | −0.8622*** | −1.0525*** | −0.7894*** | −0.8061*** | −1.5581*** | −0.3981 |
| (−2.31) | (−9.90) | (−0.24) | (−6.51) | (−5.81) | (−5.75) | (−4.92) | (−7.09) | (−4.09) | (−3.89) | (−7.59) | (−1.16) | |
| Year Fixed Effects | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| Industry Fixed Effects | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES | YES |
| No. Obs. | 15,730 | 15,683 | 14,747 | 15,195 | 15,589 | 15,403 | 15,730 | 15,683 | 15,730 | 15,684 | 11,943 | 12,685 |
| Adjusted R2 | 0.029 | 0.048 | 0.030 | 0.043 | 0.035 | 0.039 | 0.027 | 0.042 | 0.037 | 0.033 | 0.052 | 0.027 |
| Low–High ID Coefficient | 0.8342 | 2.3093*** | 0.6573 | 0.2967 | 0.3035 | 2.1696*** | ||||||
| (1.61) | (11.59) | (1.05) | (0.29) | (0.24) | (7.50) | |||||||
- Note: Table 4 provides coefficient estimates using calendar year t NCSKEW as the dependent variable. We segment the sample into terciles based on firm opacity characteristics including market capitalization, analyst coverage, firm age, institutional ownership, book-to-market ratio and a composite opacity index. We classify firms in the high (low) opacity index portfolio if they are in the top (bottom) tercile in at least three of the five individual characteristic rankings. We measure each opacity measure as of the end of year t−1. Each model includes year and industry fixed effects using the Fama and French 48 definitions. We use robust standard errors to compute t-statistics and cluster standard errors by firm. The final row of the table includes the difference in ID coefficients and Chow test chi-square statistics to test whether the difference between the ID coefficients within the high and low opacity groups is statistically different from zero.
- ***, ** and * denotes statistical significance at the 1%, 5% and 10% levels, respectively.
3.4 Institutional distraction and subsequent information environments
The dependent variable in equation (4) is an indicator variable that equals one if the firm's institutional distraction is in the top tercile at the end of calendar year t–1 and zero otherwise. This model provides the probability that a firm will have high levels of institutional distraction at the end of year t–1. The firm-level covariates are market capitalization (), book-to-market ratio (), stock return during year t–1 (), analyst coverage based on the number of analysts issuing at least one annual forecast for the year (), institutional ownership () and a measure of price informativeness () suggested by Llorente et al. (2002) that is based on stock return autocorrelation conditional on trading volume.
We examine the balancing properties of the covariates used to estimate the propensity scores. We find that one-to-one and radius matching provide the highest quality samples with no statistically significant differences in means among covariates and minor differences among the size and book-to-market covariates using the remaining matching methods.10 At the end of each year, we form a matched sample using the propensity score from equation (4). Specifically, we sort the cross-section of firms into terciles based on their level of institutional distraction as of the fourth quarter of calendar year t–1. We match each firm in the high tercile distraction portfolio to a corresponding firm in the bottom tercile portfolio having the closest propensity score.
As Tucker (2010) notes, there is no single best-matching PSM approach. Therefore, we employ nearest-neighbor, radius and kernel methodologies. The nearest-neighbor approach with replacement picks a single control firm according to the closest propensity score. Radius matching searches for matches with propensity scores within a predefined radius of the sample firms’ propensity scores. We use small (large) calipers of 0.005 (0.03) to identify sets of matches, respectively. Finally, kernel matching uses the entire sample of control firms as matches, where each unit's weight is in proportion to its closeness to the treated observation. These processes identify firms that share similar characteristics but differ only on their level of institutional distraction.
We examine differences in four alternative measures of year t+1 information asymmetry used in previous studies between treated and matched firms. First, stock return synchronicity reflects the relative balance of market and firm-specific information following the methodology of Durnev et al. (2003) and related work. A line of work in the synchronicity literature attributes lower return synchronicity with less informative stock price (e.g., Devos et al., 2015). Second, we calculate each firm's idiosyncratic volatility using the standard deviation of each firm's daily residuals from a Carhart four-factor model estimated over year t+1. Higher levels of idiosyncratic volatility are associated with greater information asymmetry in prior research (e.g., Kelly, 2014; Krishnaswami & Subramaniam, 1999; Lee & Liu, 2011). Third, we calculate a daily BAS estimate using daily high and low prices following the methodology developed by Corwin and Schultz (2012, eq. 12). Corwin and Schultz show that this BAS estimator outperforms alternative low-frequency spread estimators. Mean BAS is the mean of the BAS measure over a 225-day window following the fiscal year date for a given firm-year. Fourth, we use each firm's annual absolute forecast error. Following Loh and Stulz (2018), we compute forecast error as the absolute value of the difference between actual annual earnings and the consensus analyst forecast, scaled by actual earnings. Table A1 provides more detail pertaining to the construction of each measure.
Table 5 provides the average treatment effect on the treated, that is, the average difference in the outcome (asymmetry) variable between the treated and propensity score-matched control firms. Our results suggest that firms with institutional distraction experience relatively higher information asymmetry in the following year. The treated (distraction) sample has traits that are consistent with higher levels of information asymmetry: lower levels of stock price synchronicity (panel A), greater idiosyncratic return volatility (panel B), greater BASs (panel C) and greater analyst forecast error (panel D). The mean differences from the matched sample are statistically significant using nearly all matching methods and are economically significant, with increases ranging from 3% to 14%. Taken together, Table 5 provides evidence of a causal link between institutional distraction and subsequent levels of information asymmetry, providing the channel through which distraction hinders investors’ ability to price new information and thereby leading to a heightened likelihood of a stock price crash.
| Panel A: Stock price synchronicity | ||||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Treated | Match | ATET | T-statistic | |
| 1 to 1 match | −1.0760 | −1.045 | −0.031 | (−1.55) |
| Radius matching (0.005) | −1.0760 | −1.034 | −0.422*** | (−2.71) |
| Radius matching (0.03) | −1.0760 | −1.044 | −0.032** | (−2.05) |
| Kernel matching | −1.0760 | −1.050 | −0.026* | (−1.67) |
| Panel B: Idiosyncratic volatility | ||||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Treated | Match | ATET | T-statistic | |
| 1 to 1 match | 0.0230 | 0.0210 | 0.002*** | (12.15) |
| Radius matching (0.005) | 0.0230 | 0.0210 | 0.002*** | (16.03) |
| Radius matching (0.03) | 0.0230 | 0.0210 | 0.002*** | (15.66) |
| Kernel matching | 0.0230 | 0.0210 | 0.002*** | (15.49) |
| Panel C: BAS | ||||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Treated | Match | ATET | T-statistic | |
| 1 to 1 match | 0.0089 | 0.0082 | 0.0008*** | (4.31) |
| Radius matching (0.005) | 0.0089 | 0.0083 | 0.0007*** | (6.20) |
| Radius matching (0.03) | 0.0089 | 0.0083 | 0.0007*** | (6.02) |
| Kernel matching | 0.0089 | 0.0083 | 0.0007*** | (5.87) |
| Panel D: Analyst absolute annual forecast error | ||||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Treated | Match | ATET | T-statistic | |
| 1 to 1 match | 0.2150 | 0.1910 | 0.024* | (1.81) |
| Radius matching (0.005) | 0.2150 | 0.1880 | 0.027*** | (2.69) |
| Radius matching (0.03) | 0.2150 | 0.1880 | 0.027*** | (2.66) |
| Kernel matching | 0.2150 | 0.1880 | 0.027*** | (2.62) |
- Note: We estimate propensity scores at the end of t−1 using each firm's institutional distraction as the dependent variable and covariates including logged market capitalization, book-to-market ratio, stock return during the calendar year, analyst coverage, institutional ownership and information-based trading captured by the theta measure described by Llorente et al. (2002). We sort firms into terciles based on the firm's level of institutional distraction and match firms in the top and bottom tercile portfolios according to the closest propensity score. We assess the difference in the respective information asymmetry measure between the treated and matched samples in year t. Panels A–D show results of information asymmetry proxies that include return synchronicity, idiosyncratic volatility, BAS and analysts’ absolute annual forecast error. In each panel, columns 1 and 2 display sample averages, column 3 displays the average treatment effect on the treated (ATET) and column 4 provides the ATET t–statistic.
- ***, ** and * denotes statistical significance at the 1%, 5% and 10% levels, respectively.
3.5 Institutional distraction and reaction to negative news
Higher information asymmetry following periods of institutional distraction suggests greater difficulty for investors to process bad news. Consequently, a firm's crash risk increases. We explore the implications of this premise by examining the market reaction to an earnings “miss” during the year following the distraction period. We focus on negative earnings announcements for two reasons. First, crashes only occur with negative news; second, an earnings miss is unambiguously negative because the consensus analyst estimate is a widely accepted benchmark for the market's expectation.
We compare actual quarterly earnings with the respective consensus quarterly forecast of analysts. We classify earnings as negative if the firm's actual earnings are lower than the consensus expectation of covering analysts. To compute analyst consensus, we use each analyst's final forecast prior to the firm's quarterly earnings announcement. We obtain quarterly earnings estimate data from the Thomson Reuters institutional brokers' estimate system (I/B/E/S) database. Table 6 provides summary statistics regarding the relation between institutional distraction and subsequent earnings performance.
| Panel A: Distraction portfolio negative earnings percentage | ||
|---|---|---|
| N | Negative earnings percentage | |
| Overall | 158,773 | 0.3732 |
| Low distraction | 31,749 | 0.3820 |
| 2 | 31,757 | 0.3735 |
| 3 | 31,766 | 0.3764 |
| 4 | 31,755 | 0.3678 |
| High distraction | 31,746 | 0.3663 |
| Panel B: Negative earnings sample–quarterly consensus analyst forecast error | ||||||
|---|---|---|---|---|---|---|
| N | Mean | STD | 25th | Median | 75th | |
| Overall sample | 59,253 | −0.4338 | 0.8971 | −0.4141 | −0.1164 | −0.0345 |
| Low distraction | 12,129 | −0.4434 | 0.9004 | −0.4375 | −0.1250 | −0.0385 |
| 2 | 11,861 | −0.4259 | 0.8955 | −0.4000 | −0.1125 | −0.0337 |
| 3 | 11,956 | −0.4064 | 0.8430 | −0.3753 | −0.1064 | −0.0313 |
| 4 | 11,680 | −0.4229 | 0.9154 | −0.3885 | −0.1083 | −0.0313 |
| High distraction | 11,627 | −0.4710 | 0.9288 | −0.4740 | −0.1330 | −0.0385 |
| Panel C: Negative earnings sample-BHAR [−1, 1] | ||||||
|---|---|---|---|---|---|---|
| N | Mean | STD | 25th | Median | 75th | |
| Low distraction | 12,129 | −0.0186 | 0.0742 | −0.0456 | −0.0123 | 0.0145 |
| 2 | 11,861 | −0.0197 | 0.0694 | −0.0462 | −0.0127 | 0.0136 |
| 3 | 11,956 | −0.0185 | 0.0701 | −0.0441 | −0.0123 | 0.0141 |
| 4 | 11,680 | −0.0196 | 0.0763 | −0.0465 | −0.0125 | 0.0138 |
| High distraction | 11,627 | −0.0221 | 0.0827 | −0.0498 | −0.0134 | 0.0151 |
| Panel D: Negative earnings sample–high versus low distraction forecast error and BHAR [−1, 1] | |||
|---|---|---|---|
| High | Low | High-low | |
| Earnings forecast error | −0.4710 | −0.4434 | −0.0276** |
| (−2.33) | |||
| BHAR | −0.0221 | −0.0186 | −0.0035*** |
| (−1.83) | |||
- Note: We compute each firm's consensus analyst earnings per share (EPS) forecast using quarterly earnings estimate data in the Thomson Reuters I/B/E/S database. We use each analyst's final forecast prior to the firm's earnings announcement to compute the consensus forecast. Firms have “negative earnings” if the actual EPS is less than the consensus forecast. We compute the buy-and-hold abnormal return (BHAR) in the [−1,1] window around the earnings announcement date provided in I/B/E/S and using the CRSP value-weighted index as a benchmark. Panel A displays the percentage of firms having negative earnings across quintile distraction portfolios. Panel B provides forecast error summary statistics for firms with negative earnings announcements. Panel C provides BHAR statistics for negative earnings announcements within each quintile distraction portfolio. Panel D displays the results from the difference in means tests between the low and high quintile distraction portfolios for analyst forecast error and negative earnings announcement BHAR.
- ***, ** and * denotes statistical significance at the 1%, 5% and 10% levels, respectively.
In Table 6, panel A, we provide summary statistics for the total percentage of negative earnings in our sample, as well as the percentage of negative earnings in each distraction quantile portfolio.11 Interestingly, the percentage of negative earnings is lowest in the high distraction quantile but does not vary significantly from the first (low distraction) quantile to the fifth (high distraction) quantile of distraction. Thus, firms with distracted institutional shareholders do not have a greater likelihood of missing earnings.
The magnitude of deviation from analysts’ consensus forecast, however, does vary based on the degree of institutional distraction. We measure analyst forecast error as the difference between actual quarterly earnings per share (EPS) and the consensus analyst forecast for that quarter, divided by the absolute value of actual EPS (e.g., Loh & Stultz, 2018) and winsorize the tails at the 1% level. Using the quarterly forecast error to measure the extent of negative news, the magnitude of negative earnings is the largest among firms in the highest distraction portfolio. In panel B of Table 6, the average forecast error of firms in the high distraction portfolio is −0.4710 versus −0.4434 for firms in the low distraction portfolio. The difference in forecast error of −0.0276 is statistically significant at the 5% level as illustrated in panel D of Table 6. These results are consistent with the premise that firms with distracted institutional shareholders withhold more bad news.
Next, we investigate the market response to negative earnings announcements. We compare the cumulated BHAR for the [−1, 1] window surrounding the earnings announcement date provided in I/B/E/S and using the CRSP value-weighted index as a benchmark.12 Table 6, panel C, provides BHAR statistics for negative earnings announcements within each distraction portfolio. As shown in Table 6, panel C, firms in the high distraction portfolio have the largest negative BHAR of −2.21%, whereas firms in the low distraction portfolio have an average BHAR of −1.86%. The difference in BHAR of −0.35% is statistically significant at the 1% level, consistent with our hypothesis of a pronounced negative response to bad news for firms with greater ex-ante institutional distraction.
To gain a broader perspective of the market's reaction to and ability to process negative news, we use three alternative measures of the market's response to negative news. These include the [−1, 1] window BHAR, [−1, 1] window abnormal turnover and [2, 40] window BHAR. We compute abnormal turnover as the average daily turnover during the [ −1, 1] day window, scaled by the average daily turnover during the [−50,−10] day window relative to the earnings announcement. The two former measures assess the immediate market reaction, while the latter measure provides a longer-term assessment of the market's ability to process the negative news. Table A1 provides additional details about the construction of these measures.
For consistency, we use the alternative continuous and binary specifications of ID employed above, where we measure distraction in the most recent fourth-quarter prior to quarter t earnings. Given the mechanical relation between the magnitude of the negative return reaction and the magnitude with which the firm misses analysts’ expectations, it is critical to control for the magnitude of the earnings miss. Therefore, we include the absolute value of the analyst forecast error () for firm i’s earnings in quarter t. Finally, we also control for additional firm characteristics, including firm i’s market capitalization and book-to-market ratio, each measured at the end of the most recent year prior to quarter t. We include stock performance over the prior 12 months, the average monthly stock illiquidity over the prior year and firm i’s profitability using prior-year return on assets. Last, we include firm i’s institutional ownership as of the most recent fiscal year-end. Consistent with our prior multivariate tests in Table 3, we cluster standard errors by firm and include year and industry fixed effects using Fama and French 48 industry definitions.
We provide estimates using equation (5) in Table 7, Models 1–3, using [−1, 1] BHAR as the dependent variable and alternative measures of distraction. Models 1 through 3 illustrates that distraction is negatively associated with [−1, 1] BHAR at the 1%. This effect is economically significant; the −0.1179 ID estimate in Model 1 implies that a one standard deviation increase in institutional distraction at the end of the prior year is associated with an 84 basis point average decrease in [−1, 1] BHAR.13 This negative association persists in Models 2 and 3. For example, in Model 3, the highest ID quintile coefficient estimate of −0.0038 is statistically significant at the 1% level, implying that [−1, 1] BHAR is 38 basis points lower for firms in the highest institutional distraction quantile.
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| BHAR [−1, 1] | BHAR [−1, 1] | BHAR [−1, 1] | Abnormal turnover [−1, 1] | Abnormal turnover [−1, 1] | Abnormal turnover [−1, 1] | |
| ID | −0.1179*** | 2.9210*** | ||||
| (−4.43) | (4.64) | |||||
| Above Median (ID) Indicator | −0.0020*** | 0.0497*** | ||||
| (−3.23) | (3.52) | |||||
| ID Quintile 2 | −0.0015 | −0.0246 | ||||
| (−1.58) | (−1.12) | |||||
| ID Quintile 3 | −0.0003 | −0.0336 | ||||
| (−0.30) | (−1.60) | |||||
| ID Quintile 4 | −0.0018* | 0.0184 | ||||
| (−1.81) | (0.82) | |||||
| ID Quintile 5 | −0.0038*** | 0.0670*** | ||||
| (−3.65) | (2.72) | |||||
| Abs. Value of Forecast Error | −0.0040*** | −0.0041*** | −0.0041*** | 0.0597*** | 0.0604*** | 0.0598*** |
| (−10.08) | (−10.15) | (−10.09) | (7.73) | (7.80) | (7.73) | |
| Book-to-Market | −0.0002 | −0.0001 | −0.0001 | −0.1122*** | −0.1154*** | −0.1134*** |
| (−0.20) | (−0.08) | (−0.12) | (−5.27) | (−5.37) | (−5.29) | |
| Log of Market Capitalization | 0.0047*** | 0.0049*** | 0.0049*** | −0.0872*** | −0.0931*** | −0.0915*** |
| (6.95) | (7.28) | (7.21) | (−5.97) | (−6.40) | (−6.29) | |
| Prior Stock Performance | −0.0022** | −0.0024** | −0.0023** | 0.0923*** | 0.0955*** | 0.0948*** |
| (−2.34) | (−2.49) | (−2.46) | (3.98) | (4.10) | (4.09) | |
| Log of Amihud Illiquidity | 0.0018*** | 0.0020*** | 0.0020*** | −0.0258** | −0.0309*** | −0.0306*** |
| (3.60) | (4.01) | (3.92) | (−2.16) | (−2.62) | (−2.59) | |
| Return on Assets | −0.0108*** | −0.0106*** | −0.0107*** | 0.5673*** | 0.5616*** | 0.5648*** |
| (−3.32) | (−3.23) | (−3.26) | (10.21) | (10.07) | (10.13) | |
| Institutional Ownership | −0.0008 | −0.0004 | −0.0006 | 0.4667*** | 0.4576*** | 0.4621*** |
| (−0.38) | (−0.21) | (−0.27) | (9.72) | (9.55) | (9.63) | |
| Intercept | −0.0090 | −0.0410*** | −0.0398*** | 0.3358 | 1.1287*** | 1.1375*** |
| (−0.68) | (−3.46) | (−3.45) | (1.13) | (4.46) | (4.50) | |
| Year Fixed Effects | YES | YES | YES | YES | YES | YES |
| Industry Fixed Effects | YES | YES | YES | YES | YES | YES |
| No. Obs. | 59,253 | 59,253 | 59,253 | 59,253 | 59,253 | 59,253 |
| Adjusted R2 | 0.031 | 0.030 | 0.030 | 0.047 | 0.047 | 0.047 |
- Note: We compute BHAR as described in Table 6. Daily turnover is trading volume divided by shares outstanding. Abnormal turnover is the average daily turnover during the [−1,1] window scaled by the average daily turnover during the [−50,−10] window relative to the earnings announcement date. The absolute value of the analyst forecast error controls for the relative magnitude of missed earnings. We measure the remaining independent variables as of calendar year t−1. We include year fixed effects and industry fixed effects using the Fama and French 48 industries and cluster the robust standard errors at the firm level.
- ***, ** and * denotes statistical significance at the 1%, 5% and 10% levels, respectively.
In Table 7, Models 4–7, we use cumulated abnormal turnover over the [−1, 1] window as the dependent variable. Karpoff (1986) argues that investors’ willingness to trade arises from dispersion in prior expectations and idiosyncratic interpretation of information events. In a similar vein, Kandel and Pearson (1995) assert that trading activity is stimulated when investors share, but interpret differently, the same public information. Consistent with this view, the ID coefficient of 2.921 in Model 4 is statistically significant at the 1% level and indicates that a one standard deviation increase in ID is associated with a 29.20% increase in [−1, 1] abnormal turnover.14 The estimates for the alternative ID measures further demonstrate that distraction is directly associated with abnormal turnover associated with negative news, providing additional support for the notion that information asymmetry is higher among firms with more distraction.
The results of Table 7 suggest that greater distraction inhibits the ability of market participants to efficiently process negative news and are in line with the findings of Devos et al. (2015) who provide evidence that the magnitude of price reactions in response to new information is associated with the quality of the underlying information environment. Indeed, these results suggest that investors in firms with higher ex-ante institutional distraction may overreact to missed earnings, where greater information asymmetry likely causes investors to require more time to process negative news. Because we control for the extent the firm misses earnings, the investor distraction coefficients in Table 7 suggest a more negative return reaction for the same relative magnitude of earnings miss. In this scenario, high distraction firms could experience positive return drift following the earnings announcement, thereby correcting the initial overreaction. Alternatively, high distraction firms that miss earnings may continue to divulge negative news that managers withheld during the distraction period. In this scenario, high distraction firms would have a greater negative return drift.
We examine these two alternative possibilities in Table 8, using the [2, 40] BHAR following the quarterly earnings miss as the dependent variable. Consistent with the latter explanation, we find greater negative return drift among high distraction firms. Models 1 and 2 of Table 8 provide evidence that ID is negatively associated with [2, 40] BHAR, at the 1% level using continuous ID and at the 5% level using the above-median ID indicator variable. Furthermore, these effects are economically significant. The results in Model 1 indicate that a one standard deviation increase in ID results in a 104 basis point decrease in [2, 40] BHAR. Finally, Model 3 of Table 8 demonstrates that the highest ID quintile is associated with the largest negative return reaction. Overall, the results in Tables 7 and 8 collectively suggest that stock prices of firms with high institutional distraction are less efficient, resulting in stronger reactions to bad news and subsequent post-announcement drift.
| (1) | (2) | (3) | |
|---|---|---|---|
| BHAR [2, 40] | BHAR [2, 40] | BHAR [2, 40] | |
| ID | −0.1458*** | ||
| (−2.92) | |||
| Above Median (ID) Indicator | −0.0025** | ||
| (−1.99) | |||
| ID Quintile 2 | −0.0006 | ||
| (−0.31) | |||
| ID Quintile 3 | 0.0007 | ||
| −0.35 | |||
| ID Quintile 4 | −0.0006 | ||
| (−0.31) | |||
| ID Quintile 5 | −0.0040* | ||
| (−1.91) | |||
| Abs. Value of Forecast Error | −0.0024*** | −0.0024*** | −0.0024*** |
| (−3.17) | (−3.22) | (−3.17) | |
| Book-to-Market | 0.0128*** | 0.0130*** | 0.0129*** |
| −2.68 | −2.71 | −2.69 | |
| Log of Market Capitalization | −0.0001 | 0.0002 | 0.0001 |
| (−0.06) | −0.14 | −0.09 | |
| Prior Stock Performance | −0.0064*** | −0.0066*** | −0.0066*** |
| (−3.06) | (−3.13) | (−3.11) | |
| Log of Amihud Illiquidity | 0.0005 | 0.0008 | 0.0007 |
| −0.49 | −0.73 | −0.71 | |
| Return on Assets | 0.0055 | 0.0057 | 0.0056 |
| −0.46 | −0.48 | −0.47 | |
| Institutional Ownership | 0.0229*** | 0.0234*** | 0.0232*** |
| −5.39 | −5.49 | −5.45 | |
| Intercept | −0.0498 | −0.0894* | −0.0892* |
| (−0.94) | (−1.70) | (−1.72) | |
| Year Fixed Effects | YES | YES | YES |
| Industry Fixed Effects | YES | YES | YES |
| No. Obs. | 59,248 | 59,248 | 59,248 |
| Adjusted R2 | 0.021 | 0.020 | 0.020 |
- Note: The sample includes firms with quarterly EPS less than analyst consensus. Models 1–3 use [2, 40] window BHAR following the quarterly earnings announcements occurring in year t as the dependent variable. The absolute value of the analyst forecast error controls for the relative magnitude of missed earnings. We include year fixed effects and industry fixed effects using the Fama and French 48 industries and cluster the robust standard errors at the firm level.
- ***, ** and * denotes statistical significance at the 1%, 5% and 10% levels, respectively.
4 CONCLUSION
The developing crash risk literature argues that distracted institutional investors are unable to devote sufficient attention to managerial behavior, possibly leading to greater agency problems. Consistent with the findings of related work, we identify a significant positive relation between institutional shareholder distraction and crash risk that extends beyond the period in which distraction takes place.
While our initial results complement the findings of extant research, we extend this literature by highlighting the underlying roles of information opacity and asymmetry not only as a determinant of crash risk severity but also as an effect of distraction. First, our findings suggest that firm characteristics associated with a more opaque information environment exacerbate the severity of crashes associated with distraction. In other words, distraction affords managers of firms with impaired information environments greater opportunity to withhold bad news that, when released in subsequent periods, causes a firm's stock price to crash. Second, our results identify a causal effect of distraction on information asymmetry, giving rise to the channel whereby the risk of a crash is in direct proportion to the level of asymmetry associated with distraction. We build on the latter insight in subsequent analyses, where we demonstrate that heightened information asymmetry impedes investors’ ability to process information, thereby leading investors to overreact to bad news.
ACKNOWLEDGMENTS
We are grateful to Steven Young, the editor, and an anonymous reviewer for their helpful and constructive comments that improved our manuscript. We thank seminar participants for their valuable comments and discussion at the 2019 International Risk Management Conference and Southern Finance Association Meeting 2019. All remaining errors are our own.
APPENDIX A
| Institutional Distraction (ID) | The measure of a firm's institutional distraction as of the fourth quarter of the calendar year. This variable is constructed following Kempf, et al. (2017). It is a firm-level measure capturing the degree to which its institutional owners are distracted from monitoring the firm. Greater ID signals greater distraction |
| CRASH | An indicator variable that is one if the firm has at least one crash during the calendar year. Crashes are determined using each firm's weekly returns during the calendar year, following Hutton et al. (2009) and Kim et al. (2011a, 2011b). A firm has a crash if the firm-specific component of a weekly return is 3.20 standard deviations below the mean firm-specific weekly return in the respective calendar year |
| NCSKEW | The annual measure of the negative conditional skewness of a firm's weekly firm-specific return. This measure is constructed following Kim et al. (2011a, 2011b) and An and Zhang (2013). Specifically, we compute NCSKEW for firm j of year t as NCSKEWjt = –[n(n–1)3/2 ∑(wjk)3] / [(n–1)(n–2)(∑(wjk)2)3/2], where wjk denotes the firm-specific weekly return for firm j in week k and n denotes the number of weeks in year t |
| COUNT | Number of crashes in a calendar year minus the number of jumps in a calendar year. A firm has a crash (jump) if the firm-specific component a weekly return is 3.20 standard deviations below (above) the mean firm-specific weekly return in the respective calendar year |
| DUVOL | The measure of down-to-up volatility calculated as the log of the ratio of the standard deviation of firm-specific return on up weeks to that on down weeks. See J. Chen et al. (2001) and An and Zhang (2013) |
| Turnover | Measures the detrended turnover, which is calculated as the difference between average monthly turnover in calendar year t–1 and the average monthly turnover in year t–2 |
| Weekly return standard deviation | The standard deviation of the firm's weekly firm-specific returns over the calendar year multiplied by 100 |
| Average Weekly Return | The average of a firm's weekly firm-specific return over the calendar year multiplied by 100 |
| Log of Market Capitalization | The natural log of a firm's market cap at the end of the calendar year |
| Book-to-market ratio | The firm's book-to-market ratio computed following Fama and French (2008) and using a firm's most recent annual financial statements. We winsorize this variable at the 1% level |
| Book leverage | The firm's book leverage computed using a firm's most recent annual financial statements. We winsorize this variable at the 1% level |
| Return on Assets | The firm's return on assets using a firm's most recent financial statements. We winsorize this variable at the 1% level |
| Acquisition Indicator | An indicator variable that is one if the firm announces an acquisition during the calendar year in which crash risk is measured. Merger data is taken from the Thomson Reuters SDC merger database |
| Transient Institutional Ownership | The total shares of a firm owned by transient institutional shareholders, scaled by total shares outstanding. This measure is computed each December and using the institutional shareholder classifications provided by Bushee (1998) |
| Dedicated Institutional Ownership | The total shares of a firm owned by dedicated institutional shareholders, scaled by total shares outstanding. This measure is computed each December and using the institutional shareholder classifications provided by Bushee (1998) |
| Institutional Ownership | The percentage of a firm's shares owned by institutional shareholders as of December. Institutional shareholder data is obtained from the Thomson Reuters 13F database |
| Log of Amihud Illiquidity | The measure of Amihud Illiquidity over the calendar year. Following Amihud (2002), we calculate illiquidity for each stock and in each month as , where N is the number of non-zero trading days in the respective month, Rt is the return on day t, and VOLDt is dollar volume on day t. We then average the monthly illiquidity over the calendar year and take the natural log for our final measure to be used in our multivariate tests |
| Long Run Effective Tax Rate | The firm's long-run effective tax rate computed as in Kim et al. (2011b). This variable is the sum of income tax paid over the previous 5 years (Compustat item #317), divided by the sum of a firm's pre-tax income (Compustat #170) less special items (Compustat #17). We winsorize the resulting measure at zero and one |
| Accounting Conservatism | Measures a firm's conditional accounting conservatism in the respective year. We use 5-year rolling regressions that includes a combination of a firm's stock performance, market value, market-to-book ratio and debt to equity ratio. Refer to Kim and Zhang (2016) for details regarding the computation each firm's measure |
| Discretionary Accruals | The measure of transparency used in Hutton et al. (2009). Opaque is the prior 3 year's moving sum of the absolute value of discretionary accruals, where we measure discretionary accruals using a modified Jones model (Jones, 1991). Data for this measure is not available before 1990. Therefore, our sample period covers the years 1990 to 2015 when using this measure |
| Log of CEO Age | The natural log of the age of a firm's CEO reported in the ExecuComp database |
| Log of CEO Tenure | The natural log of the tenure of a firm's CEO reported in the ExecuComp database |
| CEO Duality | An indicator variable that is one if the firm's CEO also has the role of chairman of the board. We obtain this data from the ExecuComp database |
| Log of CEO Equity Base Compensation | The natural log of the market value of the shares held by the CEO. We obtain this data from the ExecuComp database |
| Log of CEO Option Compensation | The natural log of the intrinsic value of the vested and unvested in the money options held by the CEO. We obtain this data from the ExecuComp database |
| CEO Pay Slice | The percentage of the sum of total compensation of a firm's top five executives that is designated to the CEO. We use each executive's total compensation (TDC1) reported in the ExecuComp database. Refer to Bebchuk et al. (2011) for further details |
| Log of Industry Tournament Incentives | The natural log of the difference in total compensation (TDC1) of the executive under consideration from the second-highest-paid executive in the same size-adjusted industry. We compute this variable by year and use industry classifications determined by the Fama and French 48 industry classifications. If the difference is negative, we set these to zero. Refer to Coles et al. (2018) and Chowdhury et al. (2020) for further details |
| Analyst Coverage | The number of analysts issuing at least one annual earnings forecast in the respective year |
| Firm Age (in quarters) | The number of quarters since the firm was first covered in CRSP |
| Stock Price Synchronicity | The annual measure of firm return synchronicity. Following Durnev et al. (2003), we compute a firm's stock price synchronicity as the R2 from a regression of a stock's weekly returns over the respective year, regressed onto the weekly returns of the market and the return of a portfolio of firms having the same two-digit sic code. The final synchronicity of the firms is computed as the log transform of the model R2 |
| Idiosyncratic Volatility | Following Ang, Hodrick, Xing, and Zhang (2006), we estimate idiosyncratic volatility as the standard deviation of each firm's daily residuals from a Carhart (1997) four-factor model estimated over the calendar year |
| Bid-Ask Spread (BAS) | We measure BAS following Corwin and Schultz (2012). Specifically, we compute each firm's BAS as the average 2-day BAS over the respective year |
| Absolute Quarterly Analyst Forecast Error | The consensus forecast error of quarterly earnings estimate data in the Thomson Reuters I/B/E/S database. We compute forecast error for each firm using the consensus analyst earnings per share (EPS) forecast. We use each analyst's final forecast prior to the firm's quarterly earnings announcement to compute the consensus forecast. Forecast error is the difference between actual EPS and the consensus forecast, divided by the absolute value of the firm's actual EPS. We winsorize forecast each quarter at the 1% level and use the absolute value of this measure in our multivariate tests |
| Absolute Annual Analyst forecast Error | The consensus forecast error of annual earnings estimate data in the Thomson Reuters I/B/E/S database. We compute forecast error for each firm using the consensus analyst EPS forecast. We use each analyst's final forecast prior to the firm's annual earnings announcement to compute the consensus forecast. Forecast error is the difference between actual EPS and the consensus forecast, divided by the absolute value of the firm's actual EPS. Following Loh and Stulz (2018), if the absolute value of a firm's actual earnings is less than 0.1, we scale forecast error by 0.1. We winsorize forecast error each year at the 1% level and use the absolute value of this measure in our multivariate tests |
| Llorente Measure of Price Informativeness | This is a proxy for stock price informativeness, measured following Llorente et al. (2002). Each firm-year, we estimate the regression . In this regression, re contemporaneous and lagged weekly stock returns and is lagged log turnover detrended by subtracting the moving average of logged turnover over the prior 26 weeks. The key estimate is the coefficient of the interaction term, , which reflects the amount of information-based trading during year y. Higher values of signal a higher degree of information-based trading, as these stocks will exhibit positive return autocorrelation in periods when the volume is higher |
- Note: This table provides a detailed description of the variables used in the multivariate analyses.
| (1) | (2) | (3) | |
|---|---|---|---|
| Year | Crash events | Total observations | Percent crash |
| 1982 | 65 | 749 | 8.68% |
| 1983 | 61 | 709 | 8.60% |
| 1984 | 165 | 1068 | 15.45% |
| 1985 | 116 | 1052 | 11.03% |
| 1986 | 108 | 1087 | 9.94% |
| 1987 | 94 | 1143 | 8.22% |
| 1988 | 128 | 1097 | 11.67% |
| 1989 | 166 | 1192 | 13.93% |
| 1990 | 235 | 1362 | 17.25% |
| 1991 | 182 | 1392 | 13.08% |
| 1992 | 199 | 1426 | 13.96% |
| 1993 | 252 | 1410 | 17.87% |
| 1994 | 246 | 1606 | 15.32% |
| 1995 | 194 | 1392 | 13.94% |
| 1996 | 190 | 1559 | 12.19% |
| 1997 | 285 | 1791 | 15.91% |
| 1998 | 282 | 1720 | 16.40% |
| 1999 | 260 | 1699 | 15.30% |
| 2000 | 274 | 1584 | 17.30% |
| 2001 | 334 | 1642 | 20.34% |
| 2002 | 352 | 1538 | 22.89% |
| 2003 | 285 | 1526 | 18.68% |
| 2004 | 287 | 1530 | 18.76% |
| 2005 | 259 | 1225 | 21.14% |
| 2006 | 265 | 1258 | 21.07% |
| 2007 | 215 | 1369 | 15.71% |
| 2008 | 289 | 1208 | 23.92% |
| 2009 | 278 | 1465 | 18.98% |
| 2010 | 247 | 1289 | 19.16% |
| 2011 | 312 | 1412 | 22.10% |
| 2012 | 308 | 1199 | 25.69% |
| 2013 | 267 | 1233 | 21.66% |
| 2014 | 332 | 1226 | 27.08% |
| 2015 | 311 | 1393 | 22.33% |
| 2016 | 436 | 1547 | 28.18% |
| AVERAGE | 237 | 1346 | 17.25% |
- Note: This table illustrates the yearly percentage of firms that have a stock price crash. Following Kim et al. (2011a), stock price crashes are events where the firm-specific component of a firm's weekly return is 3.20 standard deviations below the mean firm-specific weekly return in the respective calendar year. The sample includes firms having a share code of 10 and 11 and excludes microcap firms (i.e., if the market capitalization of the firm is below the 20th percentile market capitalization breakpoint computed using all NYSE listed firms with CRSP share codes of 10 or 11).
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| NCSKEW | NCSKEW | NCSKEW | NCSKEW | NCSKEW | NCSKEW | |
| ID | 0.9939*** | 1.1866*** | ||||
| (4.41) | (5.04) | |||||
| Above Median (ID) Indicator | 0.0139* | 0.0185** | ||||
| (1.82) | (2.32) | |||||
| ID Quintile 2 | −0.0065 | −0.0068 | ||||
| (−0.53) | (−0.54) | |||||
| ID Quintile 3 | 0.0011 | −0.0023 | ||||
| (0.09) | (−0.18) | |||||
| ID Quintile 4 | 0.0019 | 0.0033 | ||||
| (0.16) | (0.26) | |||||
| ID Quintile 5 | 0.0270** | 0.0294** | ||||
| (2.23) | (2.29) | |||||
| Lag NCSKEW | 0.0389*** | 0.0391*** | 0.0391*** | 0.0474*** | 0.0477*** | 0.0477*** |
| (6.64) | (6.66) | (6.66) | (7.48) | (7.52) | (7.52) | |
| Turnover | 0.1561*** | 0.1568*** | 0.1554*** | 0.1380** | 0.1400** | 0.1379** |
| (3.32) | (3.34) | (3.31) | (2.51) | (2.54) | (2.51) | |
| Weekly Return Standard Deviation | 0.0433*** | 0.0445*** | 0.0440*** | 0.0442*** | 0.0458*** | 0.0454*** |
| (8.24) | (8.57) | (8.44) | (6.76) | (7.10) | (7.00) | |
| Average Weekly Return | 0.3082*** | 0.3085*** | 0.3078*** | 0.3420*** | 0.3436*** | 0.3426*** |
| (5.10) | (5.22) | (5.18) | (3.94) | (4.05) | (4.02) | |
| Log of Market Capitalization | 0.0271*** | 0.0279*** | 0.0280*** | 0.0355*** | 0.0364*** | 0.0368*** |
| (7.97) | (8.22) | (8.24) | (9.99) | (10.24) | (10.32) | |
| Book-to-Market Ratio | −0.0537*** | −0.0546*** | −0.0540*** | −0.0792*** | −0.0803*** | −0.0795*** |
| (−5.37) | (−5.45) | (−5.39) | (−6.80) | (−6.88) | (−6.81) | |
| Book Leverage | −0.0582*** | −0.0600*** | −0.0589*** | −0.0400* | −0.0425* | −0.0411* |
| (−2.84) | (−2.93) | (−2.87) | (−1.81) | (−1.92) | (−1.86) | |
| Return on Assets | 0.2518*** | 0.2538*** | 0.2537*** | 0.2683*** | 0.2713*** | 0.2711*** |
| (7.46) | (7.51) | (7.51) | (7.40) | (7.48) | (7.47) | |
| R&D to Total Assets | 0.2871*** | 0.2889*** | 0.2882*** | 0.3380*** | 0.3410*** | 0.3393*** |
| (3.87) | (3.90) | (3.89) | (4.31) | (4.35) | (4.33) | |
| Acquisition Indicator | 0.0096 | 0.0106 | 0.0102 | 0.0144 | 0.0159 | 0.0154 |
| (0.87) | (0.96) | (0.92) | (1.22) | (1.35) | (1.31) | |
| Intercept | −0.6882*** | −0.6018*** | −0.6001*** | −0.9103*** | −0.8074*** | −0.8068*** |
| (−6.82) | (−6.09) | (−6.06) | (−9.05) | (−8.19) | (−8.17) | |
| Year Fixed Effects | YES | YES | YES | YES | YES | YES |
| Industry Fixed Effects | YES | YES | YES | YES | YES | YES |
| No. Obs. | 47,098 | 47,098 | 47,098 | 43,056 | 43,056 | 43,056 |
| Adjusted R2 | 0.027 | 0.027 | 0.027 | 0.036 | 0.036 | 0.036 |
- Note: In Models 1–3, we compute NCSKEW following Hutton et al. (2009) using models that incorporate lead and lag industry returns in addition to the lead and lag market returns used by Kim et al. (2011a). In Models 1–3, the sample covers 1982 to 2016. In Models 4–6, we follow the model specification of Table 2 but eliminate firm-years within the financial crisis period 2006–2008. We include year fixed effects and industry fixed effects using the Fama and French 48 industries and cluster the robust standard errors at the firm level.
- ***, ** and * denotes statistical significance at the 1%, 5% and 10% levels, respectively.
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| CRASH | CRASH | COUNT | DUVOL | |
| ID | 2.3361*** | 0.3079*** | 0.4761*** | 0.6891*** |
| (3.04) | (2.71) | (2.84) | (4.83) | |
| Lag Crash Indicator | 0.1684*** | 0.0260*** | ||
| (5.39) | (5.22) | |||
| Lag NCSKEW | 0.0219*** | 0.0233*** | ||
| (5.58) | (6.63) | |||
| Turnover | 0.2402* | 0.0405** | 0.0834*** | 0.1082*** |
| (1.89) | (2.04) | (2.63) | (3.36) | |
| Weekly Return Standard Deviation | 0.0891*** | 0.0112*** | 0.0189*** | 0.0282*** |
| (5.21) | (5.19) | (4.81) | (6.83) | |
| Average Weekly Return | 0.8298*** | 0.0912*** | 0.1611*** | 0.2010*** |
| (3.71) | (3.76) | (3.24) | (3.51) | |
| Log of Market Capitalization | −0.0234** | −0.0029* | 0.0187*** | 0.0204*** |
| (−2.00) | (−1.82) | (7.74) | (9.32) | |
| Book-to-Market Ratio | −0.1292*** | −0.0161*** | −0.0421*** | −0.0493*** |
| (−3.67) | (−3.88) | (−6.00) | (−7.51) | |
| Book Leverage | 0.0062 | −0.0006 | −0.0127 | −0.0218* |
| (0.10) | (−0.06) | (−0.90) | (−1.69) | |
| Return on Assets | 0.6138*** | 0.0921*** | 0.1687*** | 0.1828*** |
| (6.34) | (6.17) | (7.39) | (8.58) | |
| R&D to Total Assets | 0.6081*** | 0.1053*** | 0.1744*** | 0.1979*** |
| (3.22) | (3.13) | (3.39) | (4.35) | |
| Acquisition Indicator | −0.0176 | −0.0019 | 0.0054 | 0.0045 |
| (−0.47) | (−0.36) | (0.66) | (0.64) | |
| Intercept | −3.0220*** | 0.0016 | −0.5090*** | −0.5231*** |
| (−8.90) | (0.04) | (−8.33) | (−7.30) | |
| Year Fixed Effects | YES | YES | YES | YES |
| Industry Fixed Effects | YES | YES | YES | YES |
| No. Obs. | 47,098 | 47,098 | 47,098 | 47,098 |
| R2 | 0.034 | 0.029 | 0.019 | 0.042 |
- Note: We measure the CRASH, COUNT and DUVOL dependent variables as of calendar year t. Model 1 provides logistic regression estimates, and Models 2–4 provide OLS estimates. We include year fixed effects and industry fixed effects using the Fama and French 48 industries and cluster the robust standard errors at the firm level.
- ***, ** and * denotes statistical significance at the 1%, 5% and 10% levels, respectively.
| (1) | (2) | |
|---|---|---|
| Dependent variable | NCSKEW | NCSKEW |
| ID | 0.5196* | 1.0174* |
| (1.82) | (1.71) | |
| Lag NCSKEW | −0.0448*** | 0.0482*** |
| (−8.20) | (7.40) | |
| Turnover | 0.1704*** | 0.1748*** |
| (3.50) | (2.65) | |
| Weekly Return Standard Deviation | 0.0132** | 0.0436*** |
| (2.12) | (4.48) | |
| Average Weekly Return | 0.1281* | 0.3212*** |
| (1.92) | (3.05) | |
| Log of Market Capitalization | 0.1677*** | 0.0321*** |
| (19.47) | (5.74) | |
| Book-to-Market Ratio | −0.0343*** | −0.0610*** |
| (−2.59) | (−4.83) | |
| Book Leverage | 0.0947*** | −0.0498* |
| (2.97) | (−1.95) | |
| Return on Assets | 0.2389*** | 0.2890*** |
| (4.84) | (6.13) | |
| R&D to Total Assets | 0.2918*** | 0.3554*** |
| (2.62) | (3.39) | |
| Acquisition Indicator | 0.0056 | 0.0148 |
| (0.44) | (1.40) | |
| Intercept | −2.2777*** | −0.6416*** |
| (−14.68) | (−6.43) | |
| Year Fixed Effects | YES | YES |
| Industry Fixed Effects | YES | YES |
| Firm Fixed Effects | YES | NO |
| Firm x Year Clustering | NO | YES |
| No. Obs. | 47,098 | 47,098 |
| Adjusted R2 | 0.100 | 0.031 |
- Note: In Model 1, we include year fixed effects, industry fixed effects using the Fama and French 48 industry definitions and firm fixed effects. In Model 2, we include year fixed effects, industry fixed effects and two-way clustering of standard errors by firm and year. We display t-statistics below coefficient estimates.
- Statistical significance at the 1%, 5% and 10% levels is denoted by ***, ** and *.
REFERENCES
- 1 We obtain these statistics from the Federal Reserve's Flow of Funds report, Table L.223. This data is available at https://www.federalreserve.gov/releases/z1/20160609/data.htm.
- 2 We consider additional expanded market models that include leading and lagged weekly returns from the value-weighted industry index of the same two-digit standard industrial classification (SIC) code as a given firm (Hutton et al., 2009). Our main result is unchanged when using this alternative market model. We provide these results in Table A3.
- 3 CRASH, COUNT, and DUVOL denote the additional measures of crash risk. CRASH is a binary measure equal to one if the firm has at least one crash during the calendar year and zero otherwise. Following Kim et al. (2011a), we determine crashes using each firm's weekly returns during the calendar year. A firm has a crash if the firm-specific weekly return is 3.2 standard deviations below the mean firm-specific weekly return in the respective calendar year. COUNT is the number of crashes in a calendar year minus the number of jumps in a calendar year. A firm has a crash (jump) if the firm-specific weekly return is 3.2 standard deviations below (above) the mean firm-specific weekly return in the respective calendar year. DUVOL is the measure of down-to-up volatility calculated as the log of the ratio of the standard deviation of firm-specific return on up weeks to that on down weeks (see An & Zhang, 2013); J. Chen et al., 2001). We provide results of our baseline model specification using these additional crash measures in Table A4.
- 4 We thank Elisabeth Kempf for making their data available at https://sites.google.com/site/elikempf/research.
- 5 For example, if a firm has a fiscal year-end (FYE) date of March 31, 2017, then we use FYE 2017 financial statement data for calendar year 2017. Alternatively, if a firm has an FYE date of September 31, 2017, then we use FYE 2017 statement data for calendar year 2018.
- 6 We thank Brain Bushee for making the classifications available on his website.
- 7 We reach the same conclusions using size-adjusted measures of Industry Tournament Incentives, following Coles, Li, and Wang (2018) and Chowdhury et al. (2020). These results are available upon request.
- 8 The increase in negative return skewness is calculated by multiplying the ID coefficient by its sample standard deviation (0.074) and dividing by the sample mean of NCSKEW (0.065). These univariate statistics are based on the high opacity tercile.
- 9 We conduct these tests using alternative measure of information asymmetry that include CEO age, a firm's risk of bankruptcy as measured by Altman's Z-score and measures of industry competition and concentration. We continue to find the effects of institutional distraction take place primarily in the high information asymmetry groups. These results are available upon request.
- 10 These results are untabulated for brevity but are available upon request.
- 11 As before, we rank firms into quintiles each year based on their respective ID for the fourth quarter.
- 12 The results of our univariate and multivariate return tests are consistent when we use other return windows that include [−3, +3] and [−5, +5]. These results are available upon request.
- 13 We obtain this estimate by multiplying the ID coefficient by 0.071 sample standard deviation.
- 14 We multiply the ID coefficient estimate by the 0.071 standard deviation and divide by mean abnormal turnover (0.71).




