Quantitative Structure-property Relationship Studies on Amino Acid Conjugates of Jasmonic Acid as Defense Signaling Molecules
Supported by the National Natural Science Foundation of China (30500339) and the Natural Science Foundation Program of Zhejiang Province (Y407308).
Abstract
Jasmonates and related compounds, including amino acid conjugates of jasmonic acid, have regulatory functions in the signaling pathway for plant developmental processes and responses to the complex equilibrium of biotic and abiotic stress. But the molecular details of the signaling mechanism are still poorly understood. Statistically significant quantitative structure-property relationship models (r2 > 0.990) constructed by genetic function approximation and molecular field analysis were generated for the purpose of deriving structural requirements for lipophilicity of amino acid conjugates of jasmonic acid. The best models derived in the present study provide some valuable academic information in terms of the 2/3D-descriptors influencing the lipophilicity, which may contribute to further understanding the mechanism of exogenous application of jasmonates in their signaling pathway and designing novel analogs of jasmonic acid as ecological pesticides.
Plants have evolved highly effective and complex octadecanoid signaling pathways known as “signal transduction” to coordinate responses to the developmental processes and the complex equilibrium of biotic and abiotic stress (Tamogami and Kodama 1998; Pauw and Memelink 2005; Chini et al. 2007; Delker et al. 2007; Xu and Dong 2008). Small signaling molecules, such as jasmonates, auxins, gibberellins, abscisic acid and brassinosteroids, are involved in these actions, functioning as plant growth regulators and making them essential for plant survival in nature (Walter et al. 2007; Vandenbussche and Van Der Straeten 2007; Xu and Dong 2008).
Considerable quantities of published literature concerning jasmonates have been reported (Beale and Ward 1998; Wu and Pan 1998; Liu et al. 2002; Turner et al. 2002; Wang et al. 2002; Maksymiec et al. 2005; Liu and Wang 2006; Chehab et al. 2007; Hause et al. 2007; Jiang et al. 2007; Wasternack 2007; Xu and Dong 2008) since (-) methyl jasmonate (JA-Me) and its free acid, (-)-jasmonic acid (JA) were first isolated in 1962 and 1971 (Beale and Ward 1998). Jasmonates and related compounds have various biological activities including a broad range of defense-related regulators of plant responses to environmental stress and biotic challenges (Miersch et al. 1999; Liu et al. 2002; Howe 2004; Halitschke and Baldwin 2005; Mithofer et al. 2005; Schaller et al. 2005; Liu and Wang 2006; Chen et al. 2007;Chini et al. 2007; Shan et al. 2007; Thines et al. 2007; Xu and Dong 2008), such as ozone exposure, wounding, water deficit, UV light, pathogen, insect attack, and pest attack. They are also involved in many aspects of plant developmental processes (Beale and Ward 1998; Wang et al. 2002; Chini et al. 2007; Shan et al. 2007; Thines et al. 2007) including root growth, production of viable pollen, seed germination, tuberization, fruit ripening, tendril coiling, leaf abscission, and senescence. Naturally occurring amino acid conjugates of jasmonic acid have been discovered to exhibit the same abilities as signaling compound in the elicitation process as shown by JA (Kramell et al. 1995; Tamogami et al. 1997), which can induce specific abundant defensive proteins named jasmonate-inducible proteins (JIPs) in barley leaf tissue and proteinase inhibitors (PINs) in tomato and potato (Herrmann et al. 1987; Miersch et al. 1999) and also induce the activity of a key enzyme named naringenin 7-O-methyltransferase (NOMT) for biosynthesis of antimicrobial secondary metabolites known as phytoalexins in rice plants (Farmer and Ryan 1990). Based on their significance on plants, they are highlighted in the research field of plant physiology and plant molecular biology.
Although a large number of studies exist on the biological effects of jasmonates and related compounds, the molecular details of their signaling mechanism at the biochemical level are largely unknown (Chini et al. 2007; Thines et al. 2007; Walter et al. 2007). Many synthetic analogs have only been tested in a few systems; therefore, interpretation of the data does entail some difficulties in fully understanding their mechanism (Beale and Ward 1998). Recently, it has been suggested that the capability of plants to manage events is related to the natural workings of jasmonates in the form of direct or indirect penetration of their cells (Farmer 2007). Thus, lipophilicity is essential for the signaling abilities of jasmonates during exogenous application of those compounds. Lipophilicity, usually expressed as the logarithm of n-octanol/water partition coefficient (logP) (Šoškić and Magnus 2007), plays an important role in ligand- receptor interactions and simplifies the estimate of the binding free energy of ligands (Marisa et al. 2008). It is also one of the major factors that influence the transport, absorption, and distribution of chemicals in biological systems (Bartalis and Halaweish 2005). Although jasmonates and related compounds are important to plants, no systematic structure-property studies have been available until now. The aim of the present study was to obtain some statistically significant 2D/3D- quantitative structure-property relationship (QSPR) models for the reported 59 amino acid conjugates of jasmonic acid. The results in the present research should contribute to further understanding the mechanism of exogenous application of jasmonates in their signaling pathway and also provide some academic guidelines to design novel analogs of jasmonic acid as an ecological pesticide.
Results
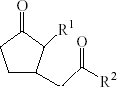
Amino acid conjugates of jasmonic acid and their lipophilicity
To obtain the structural requirements for lipophilicity (logP) of amino acid conjugates of jasmonic acid, the structures of 59 amino acid conjugates of jasmonic acid were collected from the literature (Katsin et al. 1977; Bohlmann et al. 1984; Kramell et al. 1988, 1995, 1997, 1999; Schneider et al. 1989; Meyer et al. 1991; Tamogami et al. 1997; Miersch et al. 1999; Jikumaru et al. 2004; Staswick and Tiryaki 2004; Guranowski et al. 2007), and their lipophilicity in the form of n-octanol/water partition coefficient (logP) (Table 1) were automatically calculated in the Cerius2 version 4.10, since experimental logP value was unavailable (Liu and So 2001). Some researchers have evaluated the experimental logP and calculated logP of structural dependence in the majority of tested software products and the calculated results were in good correlation with that determined experimentally (Mrkvičková et al. 2008), indicating that logP in this study can represent the actual logP of compounds in some sense.
 |
- aMolecules in training set; bMolecules in test set; cResidual = calculated logP − predicted logP.
Molecules were then rationally divided into a training set and test set (Table 1), maintaining the structure and property diversity in both sets for subsequent QSPR models development. A molecule structurally very similar to the training set molecules will be predicted well because it captures common features.
2D-QSPR models
Different sets of 2D-QSPR equations with several descriptors were generated using the genetic function approximation (GFA) method. A brute force approach was first used to investigate the number of descriptors necessary and adequate for the QSPR equation. As the number of descriptors in the equation increased one by one, the effect of added new terms was evaluated using cross-validated r2(r2CV) as the limiting factor for the number of descriptors to be used in the model (Chen et al. 2008; Nair and Sobhia 2008; Li et al. 2008c, 2009). As shown in Table 2, adding the number of descriptors in the equation does increase the r2CV value of the best model, but r2CV and conventional r2 increase a little when the number of descriptors ranges from 4 to 5. Based on our experiments, adding the additional descriptor S_sssCH does not improve the values of Friedman's lack of fit (LOF) and F-Test compared with the model with four descriptors. Thus, the number of descriptors was restricted to four for the final model. The models with varying number of descriptors for amino acid conjugates of jasmonic acid are shown in Table 2. The selection of best model was based on the values of conventional r2 (square of the correlation coefficient for the training set of compounds), LOF, F-Test, r2CV (cross-validated r2), r2BS (bootstrap correlation coefficient), and predicted sum of deviation squares (PRESS) (Li et al. 2008a).
| Descriptor | Equation | LOF | r 2 | r 2adj | F-test | LSE | r | r 2 BS | r 2 CV |
|---|---|---|---|---|---|---|---|---|---|
| 1 | logP =−3.317 84 + 0.841 82(Dipole-mag) | 1.287 | 0.608 | 0.599 | 71.220 | 1.131 | 0.779 | 0.608 | 0.577 |
| 2 | logP = 43.615 3 − 35.416 3 (Density) − 0.350 636(S_ssO) | 0.598 | 0.863 | 0.854 | 92.477 | 0.395 | 0.929 | 0.863 | 0.843 |
| 3 | logP =−5.107 75 − 0.704 588(S_ssO) − 1.039 53(Hond Donor) + 0.022 301(Area) | 0.311 | 0.929 | 0.924 | 191.116 | 0.205 | 0.964 | 0.929 | 0.913 |
| 4 | logP = 23.912 − 26.422 7(Density) + 0.000 551(Apol) − 0.580 903(S_ssO) − 0.738 634(Hond Donor) | 0.042 | 0.990 | 0.989 | 1 059.542 | 0.029 | 0.995 | 0.990 | 0.987 |
| 5 | logP = 22.442 5 − 0.713 654(Hond Donor) − 0.581 729 (S_ssO) − 24.824 5(Density) + 0.000 548(Apol) + 0.178 096(S_sssCH) | 0.049 | 0.992 | 0.989 | 1 039.828 | 0.023 | 0.996 | 0.992 | 0.989 |
- LOF, Friedman's lack of fit test; LSE, least square error.
The statistically significant 2D-QSPR model is shown below. A summary of good GFA method-derived models generated with four descriptors are shown in Table 3.
| No. | Equation | LOF | r 2 | r 2adj | F-test | LSE | r |
|---|---|---|---|---|---|---|---|
| 1 | logP = 23.912 − 26.422 7(Density) + 0.000 551(Apol) − 0.580 903(S_ssO) − 0.738 634(Hond Donor) | 0.042 | 0.990 | 0.989 | 1 059.542 | 0.029 | 0.995 |
| 2 | logP = 12.617 7 − 0.617 997(S_ssO) + 0.023 956(Vm) − 16.283 4(Density) − 0.825 239(Hond Donor) | 0.099 | 0.976 | 0.974 | 440.432 | 0.069 | 0.988 |
| 3 | logP = 27.194 7 − 0.624 233(S_ssO) + 0.001 577 (Wiener) − 0.811 461(Hond Donor) − 25.226 2 (Density) | 0.104 | 0.975 | 0.973 | 419.789 | 0.072 | 0.987 |
| 4 | logP =−2.558 96 − 0.591 104(S_ssO) + 0.021 268(Area) − 0.797 97(Hond Donor) − 0.617 348 (Hond Acceptor) | 0.105 | 0.975 | 0.972 | 416.099 | 0.073 | 0.987 |
| 5 | logP = 10.388 6 − 0.636 564(S_ssO) − 0.880 269 (Hond Donor) + 0.019 317(Area) − 14.467 1 (Density) | 0.110 | 0.974 | 0.971 | 395.253 | 0.076 | 0.987 |
| 6 | logP =−1.904 5 − 0.569 714(S_ssO) + 0.026 174(Vm) − 0.651 011(Hond Acceptor) − 0.740 543 (Hond Donor) | 0.129 | 0.969 | 0.966 | 334.266 | 0.090 | 0.984 |
| 7 | logP =−3.783 33 + 0.019 968(Area) − 0.878 941 (Hond Donor) − 0.699 587(S_ssO) + 0.616 766 (S_dssC) | 0.145 | 0.965 | 0.962 | 297.314 | 0.101 | 0.982 |
| 8 | logP =−3.238 04 − 0.686 571(S_ssO) + 0.024 588(Vm) − 0.821 794(Hond Donor) + 0.686 469(S_dssC) | 0.151 | 0.964 | 0.960 | 283.778 | 0.105 | 0.982 |
| 9 | logP =−2.353 85 − 0.962 775(Hond Donor) + 0.022 493 (Area) − 0.621 075(S_ssO) − 0.084 95(S_dO) | 0.155 | 0.963 | 0.959 | 277.032 | 0.108 | 0.981 |
| 10 | logP =−1.544 34 − 0.596 066(S_ssO) − 0.095 799 (S_dO) + 0.028 08(Vm) − 0.908 262(Hond Donor) | 0.165 | 0.960 | 0.957 | 260.017 | 0.114 | 0.980 |
- LOF, Friedman's lack of fit test; LSE, least square error.
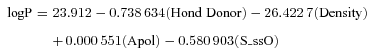
The leave-one-out (LOO) test and randomization tests were used to determine reliability and significance of generated models. From the cross-validation test r2CV of 0.987 indicated that the results obtained were not by chance correlation. The randomization tests (Deswal and Roy 2006; Chen et al. 2008; Li et al. 2008a, 2008c, 2009) were carried out at 90% (nine trials), 95% (19 trials), 98% (49 trials) and 99% (99 trials) confidence levels and carried out by repeatedly permuting the dependent variable set. The results of randomization tests (Table 4) showed that none of the permuted datasets produced the random r comparable to non-random r of 0.995, suggesting that the value obtained for the original GFA method-derived model was significant. The derived best 2D-QSPR model thus was robust and used for predicting the properties of the test set (Table 1). Some compounds in the test set gained poor predicted logP values, partly as a result of the low r2pred value of the above model. The inter-correlation of the descriptors in the above model was taken into account and the descriptors were found to be reasonably orthogonal (Table 5).
| Randomization test | ||||
|---|---|---|---|---|
| Confidence level | 90% | 95% | 98% | 99% |
| Total trials | 9 | 19 | 49 | 99 |
| r from non-random | 0.995 | 0.995 | 0.995 | 0.995 |
| Random r's < non-random | 9 | 19 | 49 | 99 |
| Random r's > non-random | 0 | 0 | 0 | 0 |
| Mean of r from random trial | 0.489 | 0.525 | 0.527 | 0.519 |
| Standard deviation of random trials | 0.071 | 0.090 | 0.079 | 0.077 |
| Standard deviation from non-random r to mean | 7.128 | 5.214 | 5.929 | 6.205 |
| logP | Apol | Hond Donor | S_ssO | Density | |
|---|---|---|---|---|---|
| logP | 1 | ||||
| Apol | −0.077 | 1 | |||
| Hond Donor | −0.026 | −0.019 | 1 | ||
| S_ssO | −0.685 | 0.413 | −0.515 | 1 | |
| Density | −0.572 | 0.262 | 0.181 | 0.161 | 1 |
3D-QSPR models
Molecular field analysis (MFA) samples the steric and electrostatic fields surrounding a set of ligands and constructs 3D-QSPR models by correlating the corresponding properties in form of logP with the 3D field values computed using atomic coordinates of binding molecules and interaction energies.

The reasonable values of correlation coefficient r2 of 0.922 and cross-validated r2 of 0.841 indicate that this model could explain satisfactorily the variances of logP. The robust and highly predictive ability of the models was reflected insufficiently only by the cross-validation test; thus, the external predictive power of the model was evaluated with the test set molecules (Equbal et al. 2008). The predictive power of the model is calculated by r2pred= (SD − PRESS)/SD (Chen et al. 2008; Li et al. 2008c, 2009), where SD is the sum of squared deviations between the logP of each molecule and the mean logP of the molecules in the training set and PRESS is the sum of squared deviations between the predicted and calculated logP values for each molecule in the test set. The high r2pred value of 0.905 for the test set accounted for good predictive ability, which was also used for predicting logP of the test set (Table 1).
Discussion
Interpretation of model-1
According to model-1, the calculated logP of amino acid conjugates of jasmonic acid is influenced by structural descriptors (Hond Donor and Density), electronic descriptor (Apol) and E-State-keys (S_ssO), which can also be approved by the usage of descriptors during generation of QSPR models (Figure 1). Among these descriptors, small changes of the molecular density can greatly change logP; thus, Density is an important parameter for amino acid conjugates of jasmonic acid involved in penetration of plant cells. S_ssO is the descriptor of the E-state indices and represents the atomic type of –O– in alkanes or cycloalkanes. The E-state indices encode information about both the topological environment and the electronic interaction of an atom due to all other atoms in the molecule (Hall and Kier 1995). S_ssO with negative coefficient indicates its importance to the lipophilicity (logP) of compounds. The number of hydrogen-bond donors (Hond Donor) with negative coefficient indicates that hydrogen-bonding interactions are important for amino acid conjugates of jasmonic acid to penetrate the plant cells. The sum of atomic polarizabilities (Apol) with small positive coefficient reveals that it contributes less to logP than other descriptors in the model-1, which describes the molecule's ability to polarize in a magnetic field.
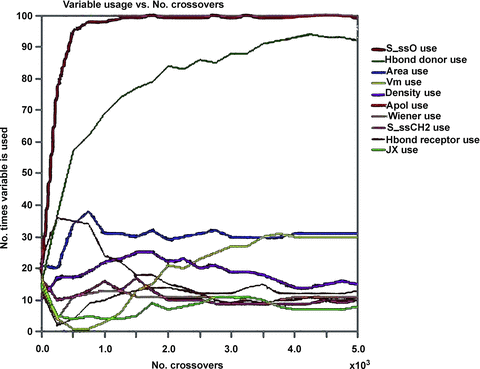
Descriptor usage during generating 2D-quantitative structure-property relationship (2D-QSPR) models by the genetic function approximation (GFA) method.
Interpretation of model-2
The numbers associated with the descriptors specify their location in the 3D-grid around the aligned molecules is shown in Figure 2. The model-2 explains 92.2% of variances of logP. The good r2CV and r2pred values indicate a better predictive credibility compared with the corresponding GFA model. Model-2 contains seven methyl (CH3) probes and four proton (H+) probes. As shown in Figure 2, the appearance of CH3/573 and CH3/580 in the region of C7 indicate that bulky substituents are unfavored to the logP. The other probes distributing in the area of C3 indicate that both steric and electrostatic substituents are important to logP.
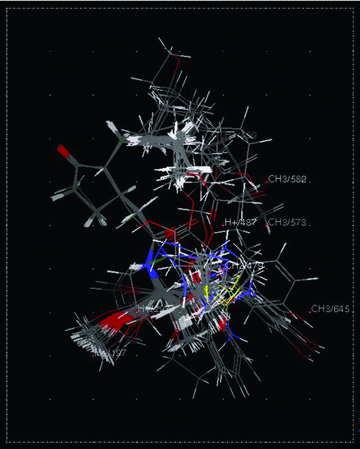
Stereo view of aligned molecules in the training set and test set within the 3D point grid of the 3D-model-2 is shown. H+ represents electrostatic interaction, while CH3 represents steric interaction.
Materials and Methods
Molecular modeling
The molecular geometrical structures of 59 amino acid conjugates of jasmonic acid were subjected to an energy minimization procedure of UFF-VALBOND1.1 (Rappe et al. 1992) after structural construction and partial atomic charges were assigned using the Gasteiger method (Gasteiger and Marsili 1980) in the Cerius2 Builder option. All of the structures were subsequently energy minimized until a root mean square derivation 0.001 kcal/mol was achieved and used in the present study.
2D-QSPR modeling
The 2D-QSPR analysis was carried out by genetic function approximation (GFA). GFA is a formalism that deals with statistical analysis and correlation between property (biological activity) and selected relevant physicochemical descriptors. It is genetically involved in the combination of Fried machs multivariate adaptive regression splines (MARS) and Holland's genetic algorithm (GA) (Rogers and Hopfinger 1994; Shi et al. 1998; Leonard and Roy 2008). Hundreds of candidate models are created and tested during evolution, but only the superior models survive, and then are used as “parents” for the creation of the next generation of candidate models. And it also provides an error measure called the lack of fit (LOF) score (Nair and Sobhia 2008) that automatically penalizes models with too many features. The length of equation was initially fixed to five terms including a constant for the training set. After some initial runs for observation, GFA crossovers of 5 000 and smoothness value of 1.0 were set (other default settings were maintained) to obtain a reasonable convergence. Cross-validated r2(r2CV) was calculated using the cross-validated test option. Before generating the 2D-QSPR model, the correlation matrix of about 141 descriptors was considered and the descriptors with value over 0.7 were removed for reducing the crossover on each other and also for improving the correlation with properties. A complete list of remaining descriptors used in subsequent QSPR analysis is shown in Table 6.
| Number | Descriptor | Family | Description |
|---|---|---|---|
| 1 | RadOfGyration | Spacial | Radius of gyration |
| 2 | PMI-mag | Spacial | Principal moment of inertia |
| 3 | Area | Spacial | Molecular surface area |
| 4 | Density | Spacial | Molecular density |
| 5 | Vm | Spacial | Molecular volume |
| 6 | Sr | Electronic | Superdelocalizability |
| 7 | LUMO | Electronic | Lowest unoccupied molecular orbital energy |
| 8 | HOMO | Electronic | Highest occupied molecular orbital energy |
| 9 | Dipole-mag | Electronic | Dipole moment magnitude |
| 10 | Apol | Electronic | Sum of atomic polarizabilities |
| 11 | Chiral centers | Structural | Number of chiral centers |
| 12 | Rotlbonds | Structural | Number of rotatable bonds |
| 13 | Hond Donor | Structural | Number of hydrogen-bond donors |
| 14 | Hond Acceptor | Structural | Number of hydrogen-bond acceptors |
| 15 | JX | Topological | Balaban indices |
| 16 | PHI | Topological | Molecular flexibility index |
| 17 | Wiener | Topological | Wiener index |
| 18 | logZ | Topological | Logarithm of Hosoya index |
| 19 | Energy | Conformation | Energy of the selected conformation |
| 20a | S_sCH3 | E-State-keys | Atomic-type –CH3 |
| 21a | S_ssCH2 | E-State-keys | Atomic-type –CH2– |
| 22a | S_dsCH | E-State-keys | Atomic-type = CH– |
| 23a | S_aaCH | E-State-keys | Atomic-type aCHa |
| 24a | S_sssCH | E-State-keys | Atomic-type –CH< |
| 25a | S_tsC | E-State-keys | Atomic-type ≡C– |
| 26a | S_dssC | E-State-keys | Atomic-type = C< |
| 27a | S_ssNH | E-State-keys | Atomic-type –NH– |
| 28a | S_sOH | E-State-keys | Atomic-type –OH |
| 29a | S_dO | E-State-keys | Atomic-type = O |
| 30a | S_ssO | E-State-keys | Atomic-type –O– |
- aIn the E-state keys symbols, S stands for the sum of the E-state values for a given atom type in a molecule. The set of bonds to a skeletal atom is given by a string of lower case letters: s (single), d (double), t (triple) and a (aromatic). JX, Balaban indices; PHI, Molecular flexibility index.
3D-QSPR modeling
Molecular field analysis (MFA) was used to derive the 3D-QSPR model in the present study. MFA is an effective method for evaluating the interaction energy between a probe molecule and a set of aligned target molecules at a series of points defined by a rectangular grid, especially for the analysis of datasets with available activity data but unknown 3D receptor site structure (Hirashima et al. 2003; Equbal et al. 2008; Chen et al. 2008; Li et al. 2008b, 2009). The interaction energy values measured for each point of 3D-grids are computed using atomic coordinates of binding molecules and can be used in structure-property relationships.
In the present study, the core substructure search (CSS) method coupled with root mean square (RMS) alignment method (Chen et al. 2008; Li et al. 2008b, 2009) was used to rigidly align all of the structures in the analogous series based on a defined substructure of cyclopentanone. So that common features are discernable from any other random arrangement of orientations and the sum of squares of the distances between all atoms to be superimposed are functionally minimized. The consensus RMS is 0.1781. Stereo-view of aligned molecules in training set and test set is shown in Figure 2.
The molecular fields of the molecules were calculated using CH3 and H+ as probes once they were aligned. The fields were computed at each point of a regularly spaced grid of 2 Å and were energy truncated ± 30.000 kcal/mol. The total grid points generated were 792 and 10% of all new significant descriptors with highest variance were automatically set as independent X variables for the latter 3D-QSPR modeling. Regression analysis was carried out using the genetic partial least squares (G/PLS) (Chen et al. 2008; Equbal et al. 2008; Li et al. 2008b, 2009) method consisting of over 5 000 generations and a population size of 100. The length of the equation was fixed at 15 terms containing constant. The 3D-QSPR models were done with a cross-validation test by clicking cross-validated test buttons in the validate control panel.
(Handling editor: Dao-Xin Xie)




