Kinematic Analysis of Leaf Growth in Grasses: A Comment on Spatial and Temporal Quantitative Analysis of Cell Division and Elongation Rate in Growing Wheat Leaves under Saline Conditions
Hu and Schmidhalter (2008) conducted a study with wheat seedlings growing in saline and non-stressed (control) conditions with the aim of identifying and quantifying the cellular basis for the reduction in leaf growth. We applaud their goals as salinity is an important issue for plant ecology and food production; however, we have concerns about the methodology used and the subsequent conclusions that are drawn.
Hu and Schmidhalter measured independently the leaf elongation rate and the epidermal cell length distribution in the growth zone of leaf 4, and used these data to investigate the spatial distribution of cell division rates and the kinetics of cell elongation in the abaxial epidermis. They reported that the saline treatment significantly reduced leaf elongation rate by about 18% and final epidermal cell length by about 12%. Based on these data, and using established methods, we calculate a 6% reduction in the cell production rate due to salinity (see below). In contrast, they reported that the saline treatment significantly reduced the cell division rate by approximately 30% in the zone of most active meristematic activity and that overall cell production (the integral of cell division rate throughout the meristem) was reduced by approximately 24% (see maximum cell flux in their figure 6). This implied that cell production was impaired more by saline conditions than cell elongation. We have looked carefully at the methodology used and the data presented and find that their conclusion is in error.
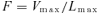 (1)
(1)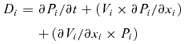 (2)
(2)Equation 2 shows that the calculation of the cell division rate distribution requires knowledge of the cell length and velocity of displacement distributions within the “cell division” region. Hu and Schmidhalter did not measure the velocity of displacement distribution in this region, but estimated it from the cell length data (their equation 1: Vi=Vmax×Li/Lmax). This approach is valid for the “elongation-only” region of the leaf growth zone, where velocity of displacement is proportional to cell length. But it is invalid in the cell division zone, where cell length depends on two processes, cell elongation and cell division (Green 1976; Silk 1992). Cell division rates cannot be estimated with the continuity equation if independent measurements of displacement velocity and cell length distribution are not available.
Cell division in a file of cells begins when an initial divides to form two daughter cells. The initial in tall fescue (Festuca arundinacea Schreb.) is often about 20 μm long and expands up to about 50 μm long to divide and form two cells each about 25 μm long, one of which remains as the initial. Both increase in length, again to about 50 μm then divide with the proximal one staying at the base as the initial where it continues to enlarge, divide and enlarge again. The daughter cells that are produced also enlarge, divide and so on, such that there are several cells in the file that are dividing, enlarging and dividing again (MacAdam et al. 1989; Skinner and Nelson 1994). At the distal end of the cell division region the cell enlarges, but does not divide and enters the cell elongation region. Thus, cell lengths in the cell division region do not increase in a permanent manner and the cell length stays within the range given by the minimal cell length (recently divided cell) and maximal cell length (mitotic cell). So, while active expansion growth occurs inside the meristem, this is not mirrored in the cell length distribution in this region.
Hu and Schmidhalter did not address the condition, that independent measurements of displacement velocity and cell length in the meristem are required for estimation of cell division rates. But they recognized that the equation relating velocity to cell length (their equation 1) “might underestimate the velocity of displacement in the cell division zone” and generated “adjusted curves of Vdi between the leaf base and about 5 mm above the leaf base”. This adjustment, “obtained by fitting five-parameter Weibull curves”, seems an arbitrary procedure and effectively produced the erroneous rate and distribution of cell division. Without the adjustment, the velocity of displacement data (calculated with their equation 1) would have yielded cell division rates equal to zero everywhere in the meristem. Furthermore, the magnitude and distribution of cell division rates obtained by the adjustment were also unrealistic. In addition, and most importantly, the curve adjustment procedure invalidated the subsequent analyses.
As a result, it remains unclear if the slight decrease in the cell production rate was due to a decrease in the cell division rate or to a reduction in the number of meristematic cells in the division zone. Other parameters calculated with the erroneous adjusted velocity data (Figure 2) were also faulty and include the relative elemental growth rate (Figure 3), duration of cell growth (Figure 4), cell division rate (Figure 5), and cell flux (Figure 6). Accordingly, the conclusions drawn from the calculations are also incorrect and some of the data are contradictory. For example, the cell production rate in the control treatment (see maximum cell flux in Figure 6) can not under any circumstance be 30 cells/h, since the final cell length was 1.14 mm and leaf elongation rate was 2.73 mm/h. If it was real, then the leaf elongation rate must have been 34.2 mm/h, more than 12 times the measured rate.
Moreover, their analysis suggests that epidermal cell division continued to the end of the growth zone (cell flux increased until the end of the growth zone in Figure 6). This contrasts with all other studies in leaves of Poaceae (including studies of wheat and its ancestors), which show that epidermal cell division is restricted to the basal 5% to 25% of the leaf growth zone (MacAdam et al. 1989; Beemster et al. 1996; Masle 2000; Fiorani et al. 2000; Bultynck et al. 2003; Kavanova et al. 2006, 2008).
Clearly, a different approach is needed to estimate the velocity and elemental growth rate distribution in the cell division-region of the leaf growth zone. In roots or hypocotyls, on which marks can be observed directly and continuously, velocity data have been derived from observational records (e.g. streak photographs, image sequence analysis) of displacement of natural or artificial marks on the surface of the tissue in the meristematic regions (Erickson and Sax 1956; Walter et al. 2002; van der Weele et al. 2003). But, such measurements cannot be made in a non-destructive way in the leaf growth zone of Poaceae, since it is enclosed by the sheaths of older leaves and is therefore not directly accessible.
At present, aside from cell-length profiles in the elongation-only region, the only available alternative technique for the derivation of growth velocities in the leaf growth zone of grasses is the marking of the growth zone by pinning through the surrounding sheaths and measuring the pin-hole displacement after a short time interval (Schnyder et al. 1987; Bernstein et al. 1993; Ben-Haj-Salah and Tardieu 1995) or by following ink marks placed on the growth zone after removal of the surrounding sheaths (Volenec and Nelson 1981; Schnyder et al. 1987). In principle, the pinning method can also be used to determine the velocity distribution in the cell division zone of the leaf, which is necessary for calculation of cell division distribution using the continuity equation. But since the velocity is slow the time interval for accuracy becomes a challenge. In contrast with the anatomical method, however, the marking methods do not depend on the steady-state condition. This also means that the anatomical and marking methods will give different growth rate distributions, if the steady-state condition is not satisfied.
Hu and Schmidhalter disregarded the pinning method. They argued that it causes artefacts in the growth rate distribution, stating “in studies of stressed plants, the reduction in leaf elongation rate caused by pricking will confound drawing accurate conclusions of the effects of stresses (e.g. drought, salinity, temperature) on the spatial distribution of leaf elongation” and more particularly they write that “the pinning method results in a smaller size of the growth zone …”. However, Hu and Schmidhalter did not present direct evidence for their statement. Also, their concern is not new and has been addressed in several studies. Schnyder et al. (1987) demonstrated that although leaf elongation rate was substantially reduced for several hours after pinning the relative distribution of growth was not affected. Moreover, in leaves of Lolium perenne L. during the phase of near-constant leaf elongation, the spatial distribution of relative elemental growth rates obtained from pinning corresponded well with that derived from the anatomical record (Schnyder et al. 1990). These studies indicated that the relative effect of pinning on local growth rate was uniform over the growth zone and could be therefore corrected by applying a correction coefficient (Schnyder et al. 1987; Ben-Haj-Salah and Tardieu 1995).
Using a two-pinhole method, Hu and Schmidhalter (2000) confirmed that the relative reduction in tissue expansion due to the pinning did not differ along the whole growth zone. Of interest is whether there is an interaction between the effect of saline conditions and pinning, but Hu and Schmidhalter did not examine this. Nevertheless, they noted that the growth rate distributions obtained in their study (which used the anatomical method) differed from that obtained in their former investigations (which used the pinning method) and suggested that artefacts by the pinning method were responsible for the difference. In view of the above, we deem it more likely that the differences were associated with other factors, including the described errors in the derivation of the growth rate distribution from the anatomical data, size effects on growth zone dimensions (Kavanova et al. 2005), or experimental variation.
A disadvantage of the pinning method is its limited spatial resolution, which reduces its usefulness in studies of cell division in short meristems, such as that of wheat leaves. However, the method was successfully used with maize leaves (Granier et al. 2000; Assuero et al. 2004) (the work by Granier et al. 2000 also demonstrated a close correspondence between the activity of p34cdc2 kinase, involved in the progression of the cell cycle, and the cell division rate assessed by the continuity equation that was based on pinning and cell number data). Unfortunately, at present there seems to be no better alternative method to assess directly the distributions of growth rates in the cell division region of grass leaves. Therefore, studies of cell division in leaves of Poaceae have generally used different approaches. Since the information on growth rates in the meristem is so difficult to obtain, these alternative approaches all depended on the measurement of some cell division marker (see below). These studies can be grouped in two categories: (i) those that assessed average division rates of cells in the meristem (e.g. Fiorani et al. 2000; Kavanova et al. 2006) and (ii) the ones that also resolved the spatial distribution of cell division rates in the meristem (Beemster et al. 1996).
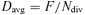 (3)
(3)The only way by which the spatial distribution of cell division rates can be determined without knowledge of cell length and growth rate distribution is by the use of a direct quantitative indicator of cell division. Thus, Beemster et al. (1996) analyzed the spatial distribution of freshly deposited cell walls in the meristem of wheat leaves and estimated the spatial distribution of cell division rate by dividing the number of freshly deposited cell walls by the number of cells in certain intervals along the division zone. In view of the difficulties associated with the assessment of growth rates in the meristems of grass leaves (which are, as discussed above, necessary for quantifying the spatial distribution of cell division rate from cell length profiles), the development of improved and alternative methodologies for the direct quantification of cell division activity in grass leaf meristems is a commendable goal. Such advances may come from the use of alternative microscopic markers (e.g. phragmoplast as an unambiguous marker for cytokinesis) or from work with reporter lines for cell cycle activity, which has already been useful in developmental and growth studies in dicots (Donnelly et al. 1999, West et al. 2004).
(Handling editor: Jinxing Lin)




