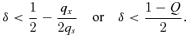EFFECTS OF REPRODUCTIVE COMPENSATION, GAMETE DISCOUNTING AND REPRODUCTIVE ASSURANCE ON MATING-SYSTEM DIVERSITY IN HERMAPHRODITES
Abstract
Hermaphroditism allows considerable scope for contributing genes to subsequent generations through various mixtures of selfed and outcrossed offspring. The fitness consequences of different family compositions determine the evolutionarily stable mating strategy and depend on the interplay of genetic features, the nature of mating, and factors that govern offspring development. This theoretical article considers the relative contributions of these influences and their interacting effects on mating-system evolution, given a fixed genetic load within a population. Strong inbreeding depression after offspring gain independence selects for exclusive outcrossing, regardless of the intensity of predispersal inbreeding depression, unless insufficient mating limits offspring production. The extent to which selfing evolves under weak postdispersal inbreeding depression depends on predispersal inbreeding depression and the opportunity for resource limitation of offspring production. Mixed selfing and outcrossing is an evolutionarily stable strategy (ESS) if selfed zygotes survive poorly, but selfed offspring survive well, and maternal individuals produce enough “extra” eggs that deaths of unviable outcrossed embryos do not impact offspring production (reproductive compensation). Mixed mating can also be an ESS, despite weak lifetime inbreeding depression, if self-mating reduces the number of male gametes available for outcrossing (male-gamete discounting). Reproductive compensation and male-gamete discounting act largely independently on mating-system evolution. ESS mating systems always involve either complete fertilization or fertilization of enough eggs to induce resource competition among embryos, so although reproductive assurance is adaptive with insufficient mating, it is never an ESS. Our results illustrate the theoretical importance of different constraints on offspring production (availability of male gametes, egg production, and maternal resources) for both the course and outcome of mating-system evolution, whereas unequal competition between selfed and outcrossed embryos has limited effect. These results also underscore the significance of heterogeneity in the nature and intensity of inbreeding depression during the life cycle for the evolution of hermaphrodite mating systems.
Hermaphroditic organisms exhibit diverse mating systems, ranging from complete selfing to exclusive outcrossing (Goodwillie et al. 2005; Jarne and Auld 2006). Two opposing genetic features have long been recognized as key influences on this continuum. Each selfed offspring contributes two copies of maternal alleles to the next generation in contrast to one copy for outcrossed offspring, which strongly favors selfing (Fisher 1941). This genetic-transmission advantage is offset in populations with appreciable genetic load by poor performance of selfed offspring, whose high homozygosity increases the chance of expression of deleterious recessive traits compared to more heterozygous, outcrossed offspring (Charlesworth and Charlesworth 1999). Consideration of these two factors alone leads to the expectation that complete selfing evolves in diploids when selfed offspring are at least half as fit as outcrossed offspring, on average, otherwise selection favors complete outcrossing (Nagylaki 1976; Lloyd 1979; Lande and Schemske 1985). These contrasting outcomes represent the extremes of the mating-system continuum, but do not explain the common occurrence of mixed mating, the production of combinations of selfed and outcrossed offspring (Goodwillie et al. 2005; Jarne and Auld 2006). Consequently, additional processes that modulate the genetic aspects of mating and contribute to mixed mating have received considerable recent attention (reviewed by Goodwillie et al. 2005).
Mixed mating can be adaptive only if it provides a compromise that capitalizes on the contrasting advantages of selfed and outcrossed offspring. Three mating processes that can promote mixed mating illustrate such compromises. First, reproductive assurance, or increased fecundity caused by autonomous selfing when outcrossing opportunities are limited, can be favored even though the resulting offspring may be genetically inferior to outcrossed progeny (Lloyd 1979; Goodwillie et al. 2005; Jarne and Auld 2006). Second, gamete discounting, which occurs when the use of gametes in self-mating that otherwise could have been involved in outcrossing (Nagylaki 1976; Lloyd 1992), erodes the benefits of selfing, selecting for some outcrossing when selfing is genetically advantageous (Holsinger 1991; Johnston 1998; Porcher and Lande 2005a). The third process, reproductive compensation, occurs when individuals produce more eggs (ovules) than the number of offspring that they can provision. These “extra” eggs reduce the fecundity cost of offspring deaths during development (Minchella and Loverde 1981) resulting from predispersal (early-acting) inbreeding depression, and thereby increase the production of offspring of sufficient genetic quality to reach independence. Such compensation for embryo deaths mitigates the disadvantages of self-mating in populations with high genetic load (Porcher and Lande 2005b; Harder and Routley 2006).
These three processes may be the most common mechanisms responsible for mixed mating by hermaphrodites. Hermaphrodites tend to have limited mobility and often fail to realize their reproductive potential (Ashman et al. 2004; Jarne and Auld 2006). Reproductive assurance alleviates this shortcoming (Eckert et al. 2006), if low fecundity results from insufficient, rather than poor-quality, mating. Indeed, reproductive assurance is the most commonly invoked adaptive explanation for mixed mating (Lloyd 1992; Goodwillie et al. 2005; Jarne and Auld 2006). In contrast, male-gamete discounting is recognized as a common nonadaptive explanation for mixed mating (Lloyd 1992; Goodwillie et al. 2005; Jarne and Auld 2006). In particular, for plants, self-pollination between flowers on the same individual involves the same interactions with pollen vectors as cross-pollination, so the resulting pollen discounting has been interpreted as an inevitable consequence of outcrossing (Lloyd 1992). The contribution of reproductive compensation to the incidence of mixed mating is less appreciated, because its influence on mating-system evolution has been recognized only recently (Porcher and Lande 2005; Harder and Routley 2006). Nevertheless, this mechanism may be widespread. For example, a survey of seed production following excess cross-pollination for 65 plant species found that only 60% of ovules become seeds (Harder and Routley 2006), suggesting that plants typically produce considerably more ovules than they can mature into seeds.
Despite their significance in the evolution of hermaphroditic mating systems, the relative importance and possible interacting effects of inbreeding depression, reproductive assurance, gamete discounting, and reproductive compensation have not been examined. All mating-system theory considers inbreeding depression explicitly, but the implications of variation in inbreeding depression during the life cycle have received little attention (but see Porcher and Lande 2005 a, b; Harder and Routley 2006). In particular, because recessive lethal traits tend to be expressed earlier than less deleterious traits (Husband and Schemske 1996; Charlesworth and Charlesworth 1999), inbreeding depression may affect selfed offspring more strongly when they depend on parental resources than after they are independent. Mating-system theory also implicitly incorporates female-gamete discounting, or a trade-off between the production of selfed and outcrossed offspring, but this trade-off may have been represented incompletely, because mating-system theory seldom considers consumption of maternal resources by developing offspring (although see Porcher and Lande 2005b; Harder and Routley 2006). Within a framework of nonspecific inbreeding depression and a simple trade-off in the production of selfed versus outcrossed offspring (and perhaps insufficient mating), mating-system theory usually considers the consequences of only one other influence on reproduction (reviewed for plants by Goodwillie et al. 2005). Porcher and Lande (2005 a, b) provided the most complete analyses for plant reproduction; however, they considered pollen discounting and reproductive compensation separately and focused on the consequences of different selfing rates for the evolution of genetic load, so the converse problem focusing on mating-system evolution has not been explored fully.
In this article, we consider the theoretical joint effects of inbreeding depression, reproductive assurance, gamete discounting, and reproductive compensation on the evolution of hermaphroditic mating systems, specifically those of angiosperms. We begin by examining the deterministic influence of reproductive compensation on mating-system evolution when selfing does not alter male outcrossing opportunities, individuals produce many female gametes, and selfed and outcrossed embryos compete equally for maternal resources. We then consider more realistic situations of limited female reproductive potential, stochastic offspring production, and an advantage of outcrossed embryos over selfed embryos during competition for maternal resources. Finally, we return to the deterministic model and allow male-gamete discounting. Although our analysis incorporates features specific to plant mating, the conclusions should apply generally to hermaphroditic organisms.
Mating Models
To explore the consequences of reproductive compensation and male-gamete discounting for mating-system evolution, we model plants that produce P pollen grains and O ovules and consider the entire reproductive cycle from pollination to seedling establishment (Fig. 1; see Table 1 for definitions of additional parameters and variables). We assume that ovule and pollen production per individual remain constant during mating-system evolution, leaving sex-allocation implications for subsequent examination. Mating outcomes within a population depend on the fates of pollen, so we define a plant's phenotype as its contributions of pollen to self-pollination and potential pollen export. Because male-gamete discounting occurs during mating, we focus on selfing that occurs simultaneously with outcrossing. Reproductive assurance can enhance fecundity if insufficient pollen import limits seed production. The plants we model have enough resources to mature only a fraction, m, of their ovules into seeds, so they produce (1 −m)O compensatory ovules that can fail after fertilization for various reasons (e.g., genetic death, predation, maternal choice) without affecting maximal seed production. For simplicity, we assume a fixed genetic load in the population, which is not unreasonable given that reproductive compensation allows deleterious alleles to persist in populations, despite the purging effect of inbreeding depression (Charlesworth 1994; Hastings 2001; Porcher and Lande 2005b). This outcome results because compensation allows heterozygous parents to perpetuate recessive lethal alleles by producing more (viable) heterozygous offspring than they would have if compensation had not absorbed genetic deaths of homozygous embryos. Given the preceding assumptions, we seek the evolutionarily stable mating system for which any possible variant phenotype realizes lower or equal fitness to the resident phenotype.
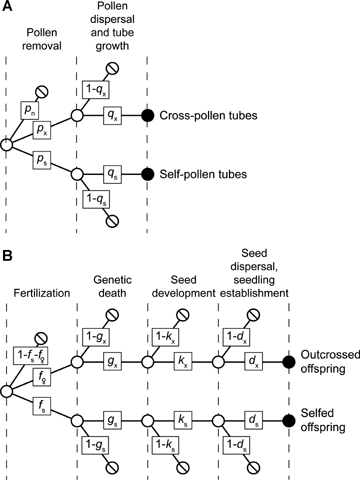
The fates of (A) pollen and (B) ovules considered in the mating-system models. Labeled parameters indicate transition probabilities between consecutive states.  indicates loss of pollen grains or ovules from the reproductive process,
indicates loss of pollen grains or ovules from the reproductive process,  indicates a transitory state, and
indicates a transitory state, and indicates successful entry of pollen tubes into ovaries (A), or seed production (B).
indicates successful entry of pollen tubes into ovaries (A), or seed production (B).
| Parameter or variable | Definition |
|---|---|
| c s and cx | weights that determine the relative success of selfed and outcrossed embryos, respectively, in competition for maternal resources |
| D | ds/dx |
| δ, δe, and δd | total, predispersal and postdispersal inbreeding depression, respectively |
| f ♂ | relative siring success, or the number of ovules fertilized by a plant on other plants, relative to its own ovule production |
| G | gs/gx |
| k | proportion of the embryos that survived genetic death that subsequently develop into seeds, when selfed and outcrossed embryos compete equally for maternal resources (i.e., k=ks=kx) |
| K | ks/kx |
| m | proportion of ovules that can mature into seeds, given the available maternal resources |
| Ms | m/gs |
| Mx | m/gx |
| Ns and Nx | numbers of self- and cross-fertilized embryos, respectively |
| O | ovule production |
| P | pollen production |
| p and p′ | two-element vectors that summarize the proportions of pollen involved in self-pollination and export for the resident and invading phenotypes, respectively; p= (ps, px) and p′= (ps′, px′) |
| p nmin | the minimum possible proportion of pollen that is not available for either self-pollination or export |
| Q | qx/qs |
| S | number of self-fertilized embryos |
| t | proportion of a plant's seeds that is self-fertilized (maternal outcrossing rate) |
| W | absolute fitness per ovule |
BASIC MODEL OF DETERMINISTIC MATING WITH MANY OVULES AND EQUAL RESOURCE COMPETITION
Our deterministic model considers plants that produce many pollen grains and many ovules per ovary, so the related results are asymptotically true. Suppose that during pollination proportions ps and px of a plant's pollen grains leave its anthers and have the potential to fertilize the plant's own ovules and those on other plants, respectively. The remaining proportion of pollen pn= 1 −ps−pe stays in the anthers (removal failure) and/or is lost without being carried away by a pollen vector (removal loss) and cannot contribute to the plant's fitness (Fig. 1A; see Harder and Routley 2006). We refer to the common resident phenotype as p= (ps, px) and the phenotype of a solitary invader as p′= (ps′, px′). Various processes either claim pollen as it moves between anthers and stigmas or cause pollen-tube attrition (see Harder and Routley 2006), so only proportions qs and qx of the potential self- and cross-pollen contribute to the pollen tubes that enter an ovary and can participate in fertilizing ovules (Fig. 1A). Thus, ovaries of plants that allocate proportion ps of their pollen to self-pollination receive qspsP self-pollen tubes. Correspondingly, all ovaries receive an average of qxpxP cross-pollen tubes, regardless of phenotype, because the invader is so rare that it contributes a trivial fraction of the total cross-pollination in the population. Note that the latter outcome occurs regardless of the dispersion of cross-pollen among recipient plants. Specifically, if each donor contributes qxpxP pollen tubes to ovaries of n neighboring plants, each recipient will receive qxpxP/n pollen tubes from each of its n neighbors for a total of nqxpxP/n=qxpxP pollen tubes.
 ((1a))
((1a)) ((1b))
((1b))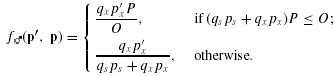 ((1c))
((1c))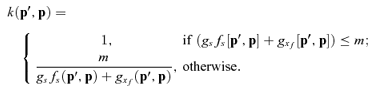 (2)
(2)This characterization identifies three possible limits on seed production. In general, seed production is fertilization-limited if too few embryos survive genetic death to compete for maternal resources, gs fs(p′, p) +gx f♀(p′, p) < m. However, fertilization limitation arises from either of two causes, so when it occurs we describe seed production as being pollen-limited if, in addition, some ovules remain unfertilized, fs(p′, p) +f♀(p′, p) < 1 (Fig. 2A, light gray area), or ovule-limited if fertilization is complete, fs(p′, p) +f♀(p′, p) = 1 (Fig. 2A, heavy line). Alternatively, seed production is resource-limited when more embryos survive genetic death than can mature given the available maternal resources, gs fs(p′, p) +gx f♀(p′, p) ≥m, regardless of the limit on fertilization (Fig. 2A, dark gray area). (This condition illustrates that m < 1 is necessary for resource limitation, but it is not a sufficient condition, as implied by Porcher and Lande[2005b: c < 1 in their notation].)
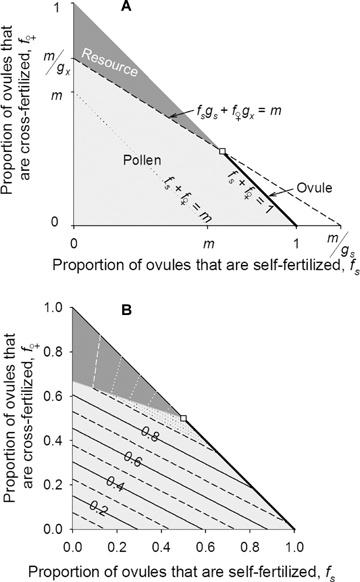
Combinations of self- (fs) and cross-fertilized ovules (f♀) under which seed production is limited by pollen receipt (light gray area), ovule production (heavy line), and maternal resource availability (dark gray area) when gs < m < gx. Because of the ovule-production constraint (fs+f♀≤ 1), only combinations of self- and cross-fertilization in the shaded areas are possible. In panel A, the dashed line illustrates the transition between pollen and resource limitation, fsgs+f♀gx=m, and the dotted line depicts the limit on seed production if no embryos died during development imposed by the availability of maternal resources (fs+f♀=m). In panel B, alternating solid and dashed lines indicate isoclines of relative fitness (w=W/Wmax) in increments of w= 0.1 and dotted isoclines depict increments of w= 0.02. The transition between resource and ovule limitation (white square: eq. 4) is the ESS mating system in panel B when self-pollination does not reduce pollen export and gs= 0.3, gx= 0.9, ds= 0.7, dx= 0.9, and m= 0.6.

Proportions ds and dx of the selfed and outcrossed seeds, respectively, disperse, establish, and become reproductive adults (Fig. 1B; ds≤dx). Consequently, postdispersal (late-acting) inbreeding depression equals δd= 1 − (ds/dx) = 1 −D, where D=ds/dx. Furthermore, total inbreeding depression experienced by self-fertilized embryos is δ= 1 −GKD. Note that although total zygote survival equals the product of pre- and postdispersal survival, total inbreeding depression is not the product of its pre- and postdispersal components (i.e., δ≠δeδd).
 (3)
(3)Phenotype p* is a local evolutionarily stable strategy (ESS) if no alternative phenotype realizes greater fitness when all resident plants exhibit p*, or W(p′, p*) ≤W(p*, p*) for all possible invader phenotypes p′ near p* (Lawlor and Maynard Smith 1976). Phenotype p* is also a continuously stable strategy (CSS) if a population with a resident phenotype similar to p* can be invaded by a phenotype that is even more similar to p* (Eshel 1983). We seek phenotypes that are both ESS and CSS, as they will be favored by natural selection. In addition to the analytic derivations of p* presented in the Appendix, we investigated evolutionary dynamics toward p* by numerically evaluating the gradient of W with respect to px and ps, given the constraint that px+ps≤ 1 −pn.
We derived all analytic results by considering absolute transition probabilities (e.g., qs, qx, gs, gx: see Appendix); however, most outcomes depend on the ratios of transition probabilities for selfing and outcrossing (e.g., Q and G), rather than their absolute values. Therefore, we present the results in terms of relative transition probabilities whenever possible. Note that Q=qx/qs is an outcrossing:selfing ratio, whereas D, G, and K are selfing:outcrossing ratios; see Table 1.
EFFECTS OF FINITE OVULE NUMBER AND UNEQUAL RESOURCE COMPETITION
We used a stochastic simulation model to consider the effects of two factors that could modify the results of our analytic model. First, most plant species produce relatively few ovules per ovary, a situation in which stochasticity during fertilization and seed development could influence average reproductive performance by competing phenotypes. This effect could occur because both ovule fertilization (eq. 1) and competition among embryos for maternal resources (eq. 2) are decelerating, nonlinear processes, so variation in input (i.e., numbers of pollen tubes and embryos, respectively) reduces mean seed production compared to that expected for the mean input (Jensen's inequality: see Smallwood 1996). The effect of such nonlinear averaging is greatest with large coefficients of variation, which for binomial processes like fertilization and competition occurs when few trials are involved (e.g., for fertilizations  , where φ is the probability of fertilization per ovule). The second factor that could influence our results involves unequal survival of selfed and outcrossed embryos (i.e., ks < kx) owing to inbreeding depression or maternal choice.
, where φ is the probability of fertilization per ovule). The second factor that could influence our results involves unequal survival of selfed and outcrossed embryos (i.e., ks < kx) owing to inbreeding depression or maternal choice.
Our simulation model determined the optimal mating system in the absence of pollen discounting for specific combinations of gs and gx, given complete fertilization. Specifically, we considered ovaries with O= 40 ovules, of which only 20 could develop into seeds (i.e., m= 0.5). During a simulation, S ovules were self-fertilized and the remaining 40-S ovules were cross-fertilized, so fertilization was not pollen-limited (fs+f♀= 1). If fewer than mO= 20 embryos survived genetic death, they all developed into seeds. If more than 20 embryos survived, seed production was resource-limited and 20 embryos were selected to develop into seeds by a weighted lottery, with selfed and outcrossed embryos assigned weights of cs and cx, respectively, where cs≤cx. Specifically, if Ns selfed and Nx outcrossed embryos remained when the next embryo was to be selected for the development into a seed, a selfed embryo was chosen randomly with probability csNs/(csNs+cxNx), otherwise an outcrossed embryo was chosen. Finally, selfed and outcrossed seeds became adult offspring with probabilities ds and dx, respectively. Fitness during a single simulation was calculated as twice the number of surviving selfed offspring plus the number of surviving outcrossed offspring. We calculated the mean (expected) fitness resulting from self-fertilization of S ovules for 50,000 stochastic simulations for a given combination of gs and gx. This process was repeated for S= 0, 1,…, 40 selfed ovules and the value of S associated with the maximum fitness was identified as the optimum mating system.
Results
ESS MATING SYSTEM WITH NO POLLEN DISCOUNTING AND MANY OVULES
The effects of reproductive compensation on mating-system evolution are appreciated most easily by considering situations in which self-pollination does not discount the pollen available for export (i.e., px=px′= a fixed positive constant) and all fertilized ovules compete equally for maternal resources (i.e., ks=kx, so K= 1). The absence of pollen discounting has several implications. First, as all plants are assumed to export an equal proportion of pollen, all plants must receive an equal amount of imported pollen. As a result, any fitness difference between the resident and invading phenotypes depends only on the self- and cross-fertilization of a plant's own seeds. In particular, increased self-pollination alters the mating system only by diluting the proportion of ovules fertilized by imported pollen. Consequently, mating outcomes are not frequency dependent and the ESS can be found simply by maximizing the sum of the selfing and female components of fitness given in equation (3) (see Appendix). Second, in the absence of a trade-off with pollen export, increased self-pollination must reduce pollen that otherwise would not be removed from flowers or would be lost during pollen removal (i.e., pn= 1 −ps−px). As the incidence of cross-pollination, px, is assumed to be a positive constant, exclusive selfing (i.e., ps= 1) is impossible and instead “complete selfing” is said to occur when pn= 0 and ps= 1 −px. However, results presented in the Appendix indicate that when “complete selfing” is favored selection also favors a reduction in the fixed value of px. Thus for such cases, we assume subsequent evolution of px and eventual evolution of exclusive selfing ( f*s= 1).
As a pollen-limited mating system never maximizes fitness (see Appendix), we focus on situations that result in complete ovule fertilization (i.e., fs+f♀= 1). With no pollen discounting, the optimal mating system depends on a hierarchy of dichotomous criteria, which progressively incorporate more influences on female fertility (Fig. 3). First, exclusive outcrossing ( f*s= 0) is favored if postdispersal inbreeding depression is so strong that selfed seeds are less than half as likely to become reproductive adults than outcrossed seeds (D < 0.5: i.e., δ > 1 −G/2 in Fig. 4A). This outcome occurs regardless of the relative success of selfed and outcrossed embryos during seed development. Previous models of mating-system evolution have not identified this condition, because it is subsumed by a more rigorous outcrossing threshold (δ > 0.5) in the absence of reproductive compensation (Porcher and Lande 2005b considered only D= 0.75 in their compensation model).

Summary of conditions favoring alternative mating systems when self-pollination does not reduce the fixed incidence of pollen export.

Relations of alternate ESS mating systems to inbreeding depression from ovule fertilization to offspring establishment (δ) and the proportion of ovules that could mature into seeds, given available maternal resources (m) when (A) self-pollination does not reduce pollen export, or (B) self-pollination causes pollen discounting. These results incorporate the assumption that selfed and outcrossed embryos compete equally for maternal resources (i.e., ks=kx) when seed production is resource-limited. Broken lines indicate ESS female selfing rates of t= 0.1 (dotted lines), 0.25 (dash-dotted lines), 0.5 (short-dashed lines), and 0.75 (long dash, short dash line). Note that δ= 1 − (G/2) is equivalent to dx= 2ds.
Unlike the previous case, a diversity of mating systems is possible when selfed seeds have relatively high postdispersal survival (D > 0.5: Fig. 4A for δ < 1 −G/2, and 3, 5). Exclusive self-fertilization (f*s= 1) is favored if self-fertilized zygotes are at least half as likely to join the next generation as outcrossed zygotes (GD > 0.5: i.e., δ < 0.5). Because selection of exclusive selfing in this situation occurs regardless of the details of ovule production (m), it is also predicted by mating-system models that ignore resource competition (Lloyd 1979; Lande and Schemske 1985; Charlesworth et al. 1990; Jarne and Charlesworth 1993).

Optimal mating strategies for all possible combinations of the proportions of selfed and outcrossed embryos that survive genetic death (gs and gx, respectively), when half of an ovary's ovules can be developed into seeds (m= 0.5) and 2ds > dx. (A) Results from the analytic model for many ovules when all ovules compete equally for maternal resources. (B and C) Optimal number of self-fertilized ovules when ovaries contain 40 ovules and (B) all embryos compete equally for maternal resources, or (C) outcrossed embryos are 10-fold better competitors than selfed embryos (cx= 10 and cs= 1), as identified by numerical simulation. Note that combinations above the diagonal are not possible, because we assume that gs≤gx. “Complete” selfing ( f*s= fsmax) is favored in light-gray areas, whereas exclusive outcrossing is optimal in dark-gray areas. In (A), mixed mating is favored in the unshaded area below the diagonal, with the optimal proportion of self-fertilized ovules ( f*s) indicated by contours. In (B and C), indicates optimal self-fertilization of 1–19 ovules (i.e., 0 ≤ f*s≤ 0.5), + indicates optimal self-fertilization of 20 ovules (i.e., f*s= 0.5), ^indicates optimal self-fertilization of 21–39 ovules (i.e., 0.5 ≤ f*s≤ 1), and the dashed line delimits the mixed-mating boundary expected with many ovules. In all cases, ds= 0.33 and dx= 0.5.
 (4)
(4)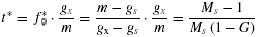 (5)
(5)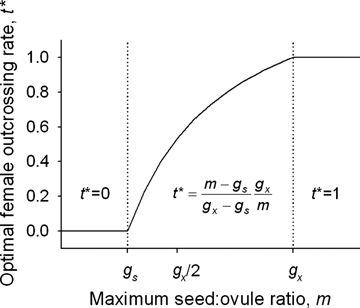
The relation of the optimal maternal outcrossing rate (t*) to the maximum proportion of ovules that can develop into seeds (m) with no pollen discounting, ovule fertilization is not pollen-limited, and the ESS mating system occurs at the transition between resource and ovule limitation. Based on equation (5).
Examination of fitness isoclines close to the maximum reveals that the three limits on seed production differ in their fitness consequences. For example, consider the situation that favors mixed mating, for which the optimal mating system lies at the intersection between pollen, ovule, and resource limitation (Fig. 2B). The dashed line in Figure 2B closest to the optimal mating system illustrates combinations of self- and cross-fertilization for which fitness is 90% of the maximum possible. This line is closest to the optimum in the area of the figure that represents pollen limitation, next closest in the direction of ovule limitation and farthest in the direction of resource limitation. Consequently, pollen limitation results in the steepest fitness gradient, whereas resource limitation results in a shallow gradient, so selection should act more strongly to alleviate pollen limitation and least strongly to counteract resource limitation, with intermediate selection against ovule limitation. These results expose two conclusions. First, the intense selection under pollen limitation places a premium on reproductive assurance; however, increased selfing to provide this assurance rarely produces the ESS mating system. Second, in the absence of pollen limitation (i.e., fs+f♀= 1) deviations from the optimal mating system toward more cross-fertilization, which aggravates resource limitation, should be more common than elevated self-fertilization, which intensifies ovule limitation.
ESS MATING SYSTEM WITH NO POLLEN DISCOUNTING AND FEW OVULES
Stochasticity in embryo survival resulting from the production of a finite number of ovules slightly increases the range of conditions that favor exclusive outcrossing, rather than mixed mating (compare Fig. 5A, B). Given both stochasticity in the incidence of genetic deaths and the greater survival of outcrossed embryos than selfed embryos (gx > gs), a slight increase in cross-fertilization reduces the chance that too few ovules will survive genetic death to consume the available maternal resources. This bet-hedging against ovule limitation also reduces the range of conditions under which self-fertilization of 50–100% of ovules is optimal (compare isocline for f*s= 0.5 in Fig. 5A, B). In general, the transition between pure outcrossing and mixed mating was difficult to assess accurately (Fig. 5B), because a range of selfing fractions, fs, near the optimum often resulted in nearly equivalent fitness. This result is consistent with the shallow gradient in fitness associated with an increase in cross-fertilization from the optimum observed with the analytic model (Fig. 2B).
Whether self- and cross-fertilized embryos compete equally or unequally for maternal resources also has little effect on the optimal mating system, even for ovaries with few ovules (compare Fig. 5B, C). Indeed, a tenfold competitive advantage for outcrossed ovules (cx/cs= 10) expanded the conditions favoring outcrossing only slightly, even in the presence of stochasticity.
ESS MATING SYSTEM WITH COMPLETE POLLEN DISCOUNTING AND MANY OVULES
We now consider the consequences of complete pollen discounting, for which each pollen grain involved in self-pollination reduces the pollen available for export. This model assumes that a fixed minimum proportion of pollen is not removed from anthers or lost during removal, pnmin, so px= 1 −ps−pnmin when pollen vectors remove all the pollen available for export. Because plants of different phenotypes now contribute unequal numbers of cross-pollen tubes to ovaries, a plant's paternal success now depends on the pollination strategies of other plants in the population. The resulting frequency dependence complicates identification of the ESS (see Appendix).
Pollen discounting allows a broader range of ESSs and mating-system evolution need not follow a direct trajectory to the ESS. The vectors in Figure 7A–C depict the direction and strength of selection (log transformed) for different pollen allocations (ps, px) given the three combinations of reproductive compensation and inbreeding depression indicated in Figure 7D. The long vectors for conditions that cause pollen limitation (white areas) illustrate that in such situations selection strongly favors some self-pollination for reproductive assurance. Note in particular that the selection vectors associated with reproductive assurance rarely point toward the ESS, so that alleviating pollen limitation of fertilization takes (short-term) precedence over offspring quality. In contrast, when seed production is not pollen-limited the direction of selection on pollen allocation depends on whether the current allocation and the ESS invoke the same constraint on seed production. If so, selection acts first to commit all possible pollen to pollination (e.g., Fig. 7C, dark gray area) and then to “tune” the mating system along the px+ps≤ 1 −pnmin constraint. If instead the ESS involves a different limitation than currently prevails, selection usually first shifts pollen allocation to the transition between resource and ovule limitation (e.g., Fig. 7C, light gray area), then increases the pollen involved in pollination along this transition, and finally moves allocation along the 1 −pnmin constraint. Thus, the trajectory followed during mating-system evolution is guided by the various constraints on pollination, fertilization, and seed production. We now focus on the ESSs under different conditions (see Appendix), which always involve complete fertilization (i.e., fs+f♀= 1; Fig. 7A–C).

Selection gradients for mating-system evolution in the presence of complete pollen discounting for the conditions identified in panel D. Each vector indicates the direction and relative strength of selection on a ln-scale when all plants with the resident phenotype allocate proportion ps of their pollen to self-pollination and proportion px to export, and pnmin= 0. Resident strategies are indicated by the circle at each vector's origin. The selection gradient is given by the vector (∂W/∂ps, ∂W/∂px)/W, where W is defined in equation (3). In panels A–C seed production is limited by ovules (light gray area), resources (dark gray area), and pollen (white area).
Complete pollen discounting greatly expands the range of conditions that favor some outcrossing (compare Fig. 4A, B). Indeed, exclusive selfing is never an ESS mating system with complete pollen discounting (Fig. 4B) if fertilization is not pollen-limited (also see Holsinger 1991). This outcome arises because once stigmas receive enough pollen to fertilize all ovules, increased allocation of pollen to self-pollination both intensifies competition between a plant's own pollen grains for access to its own ovules and reduces potential siring opportunities on other plants. The synergistic impacts of local mate competition and pollen discounting on siring success are sufficient to counteract the twofold genetic benefit of self-fertilization, even in the absence of inbreeding depression.
Compared to the nondiscounting case, the inbreeding-depression threshold that favors exclusive outcrossing now depends on the relative success of self- and cross-pollen, decreasing by qx/2qs (=Q/2: compare Fig. 4A, B). This change is probably relatively small for self-compatible species, as a pollen grain with export potential has a much smaller chance of entering an ovary than a potential self-pollen grain (i.e., qx≪qs). Thus, although the details of pollination and pollen-tube growth influence the evolution of exclusive outcrossing, their effects are limited compared to those caused by postfertilization differences between selfing and outcrossing. Note that even when conditions favor exclusive outcrossing, some self-pollination is advantageous if it alleviates pollen limitation (Fig. 7A).
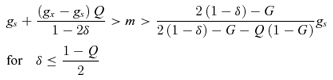 ((6a))
((6a)) ((6b))
((6b)) (7)
(7)| Limitation on seed production under ESS | Proportion of pollen allocated to self−pollination (p*s) | Proportion of ovules that are self-fertilized ( f*s) | Proportion of outcrossed seeds (t*) |
|---|---|---|---|
| Resources |  |
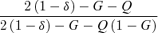 |
 |
| Transition | 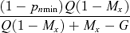 |
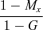 |
 |
| Ovules | 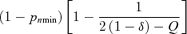 |
 |
 |
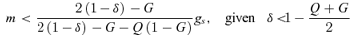 (8)
(8)Discussion
The models described above provide a general framework for investigating the evolution of hermaphroditic mating systems and synthesize the results of many previous analyses. Our models provide additional support for claims since Darwin (1876) that selfing often persists in populations when it provides reproductive assurance (reviewed by Eckert et al. 2006), as the strongest selection identified by our models occurred when too few ovules (eggs) were fertilized to maximize offspring production (2, 7). We also found the well-known dichotomy between selfing and outcrossing (e.g., Lloyd 1979; Lande and Schemske 1985) when selfing does not affect male outcrossing and ovule (egg) production does not exceed an individual's resource capacity to produce offspring (along top axis of Fig. 4A). Male-gamete discounting and production of compensatory ovules (eggs) modify this outcome differently and largely independently. On one hand, male-gamete discounting promotes some outcrossing to convert local mate competition for self-fertilization into outcrossing opportunities when weak inbreeding depression otherwise favors selfing (Fig. 4B: Holsinger 1991; Johnston 1998; Porcher and Lande 2005a). On the other hand, production of “extra” eggs (m < 1) can allow individuals to benefit from the genetic-transmission advantage of selfing when strong predispersal inbreeding depression would otherwise favor outcrossing (Fig. 4: Porcher and Lande 2005b).
Our models also expose new insights on mating-system evolution and identify specific conditions favoring particular ESS outcomes. Significantly, these models illustrate that the prevailing constraint on offspring production governs the course of mating-system evolution (Fig. 7) and the ultimate ESS (Table 2, Fig. 2B). The overall ESS mating system never involves pollen limitation (2, 7), so mixed mating associated with reproductive assurance always represents a suboptimal solution to insufficient outcrossing. Furthermore, the widespread observations of pollen limitation among angiosperms (reviewed by Ashman et al. 2004) seem enigmatic from an evolutionary perspective, unless they represent common misinterpretation of the effects of poor-quality pollen, rather than insufficient pollen (see Harder and Routley 2006; Aizen and Harder 2007).
Given that selection strongly promotes sufficient mating to fertilize all female gametes, or at least more than can mature into independent offspring given available maternal resources (2, 6), mating-system evolution should typically occur in a context of ovule- and/or resource limitation. Most previous mating-system models assumed complete fertilization and ignored resource limitation, so they implicitly involved ovule limitation. As we have defined it, ovule limitation of seed production occurs when all ovules are fertilized, but too few embryos survive genetic death to compete for maternal resources. If most embryos survive, then mating-system evolution can do little to improve seed production, although it may increase the proportion of selfed offspring that contribute two gene copies to the next generation. In this case, ovule limitation should also favor reallocation of resources from potential seed production to increased ovule production. In contrast, poor embryo survival implies extensive fertilization by poor-quality pollen, which should select for floral mechanisms that promote high-quality pollination. In most mating-system models, including those presented here (e.g., 2, 7), this response involves selection for increased outcrossing. In contrast, resource limitation occurs only when a parent produces more female gametes than can mature into offspring (i.e., m < 1: Fig. 2A), which intrinsically allows compensation for deaths caused by predispersal inbreeding depression. Consequently, resource limitation favors selfing when postdispersal inbreeding depression is weak (Fig. 3), because competition among developing embryos can exclude valuable selfed embryos that contain only maternal genes and have survived predispersal inbreeding depression. These contrasting effects of ovule and resource limitation create opportunities for mixed mating to be an ESS, if the occurrence of one limitation or the other depends on the proportions of outcrossed and selfed embryos.
Our models indicate universal and distinct roles for the relative, intrinsic performance of selfed and outcrossed embryos (G) and seeds (D) in mating-system evolution (Table 2, 3, 4). The genetic consequences of self-fertilization for reduced offspring performance have been recognized as significant influences on mating-system evolution since Darwin's assertion that “nature abhors perpetual self-fertilisation” (1876, p. 8); however, the contrasting natures of predispersal inbreeding depression (1 −G) and postdispersal inbreeding depression (1 −D) have been appreciated only recently (Husband and Schemske 1996; Charlesworth and Charlesworth 1999) and the implications of this contrast remain to be explored fully. Our analyses reveal that intense postdispersal inbreeding depression (D < 0.5) by itself is sufficient to select for exclusive outcrossing (Fig. 3: Fig. 4A, δ > 1 −G/2: Fig. 4B, δ > 1 −[Q+G]/2). Consequently, self-incompatibility should be especially prevalent in species subject to strong postdispersal inbreeding depression. More diverse mating systems are possible with weak postdispersal inbreeding depression (D > 0.5). Thus, mating-system evolution depends fundamentally on the dynamics of inbreeding during the life cycle.
Temporal variation in the severity of inbreeding depression is an essential feature of the adaptive role of reproductive compensation, which influences mating-system evolution primarily when selfed zygotes survive poorly compared to outcrossed zygotes (GD < 0.5), but selfed seeds realize high relative survival (D > 0.5: 3, 4). In this situation, production of extra female gametes allows a heterozygous maternal hermaphrodite to produce families comprised of both outcrossed offspring with relatively good predispersal survival and the small proportion of selfed offspring that are heterozygous for early acting lethal alleles and also have relatively good postdispersal survival. As angiosperms commonly produce more ovules than they can mature (Harder and Routley 2006) and predispersal inbreeding depression is often much stronger than postdispersal inbreeding depression (Husband and Schemske 1996), reproductive compensation may frequently contribute to adaptive mixed mating.
When self-mating discounts outcrossing opportunities, the relative success of male gametes involved in self- versus cross-mating (Q=qx/qs) also influences mating-system evolution (Table 2, Fig. 4). This parameter incorporates both the dispersal of male gametes and their survival in female reproductive tracts. It influences mating-system evolution by determining the relative impacts on paternal success of local mate competition for self-fertilization and pollen discounting. In the absence of male-gamete discounting, increased self-mating augments an individual's genetic contributions to its own offspring without affecting its contributions to offspring produced by other individuals, so the resulting aggravation of local mate competition bears no siring costs. In contrast, when self-mating reduces outcross siring opportunities, a specific male gamete may have a higher probability of fertilizing an egg on another individual than of succeeding in local mate competition to fertilize a sibling egg. We argued above that Q is probably quite small for angiosperms with granular pollen, because of the vagaries of pollen dispersal; however, this term may be larger for plants with more efficient pollen transfer (e.g., orchids: Harder and Johnson in press) and hermaphroditic animals with internal fertilization. In general, large Q elevates the ESS proportion of outcrossed offspring (Fig. 4B), because of the greater probability that a male gamete diverted from self-mating actually contributes to cross-fertilization.
In contrast to male-gamete performance and the intrinsic performance of embryos and seeds, the relative competitive ability of selfed embryos during competition for maternal resources (K) had little impact on the ESS mating system in our stochastic model (Fig. 5) and is probably a general outcome. This insensitivity results for several reasons. When exclusive selfing or outcrossing is favored, the presence of only one class of embryos precludes competition among classes. When the ESS mixed-mating system involves either ovule limitation, or the transition between ovule and resource limitation, the optimal number of embryos surviving genetic deaths is less than or equal to the maximum number that can be developed, given the available resources. Consequently, all surviving ovules should develop, regardless of their relative competitive ability. The possible exception to a limited impact of relative competitive ability could occur when the ESS mating system involves resource limitation. However, we expect this situation to occur rarely and to be transient for two reasons. First, resource-limited mixed mating is favored primarily when individuals produce more female gametes than are needed to compensate for all genetic deaths, even with exclusive selfing (i.e., m < gs). Such profligate production of female gametes should be countered by selection to redistribute maternal resources to offspring development. Second, mixed-mating ESSs that involve resource limitation also involve predominant self-fertilization and Porcher and Lande (2005b) concluded that “high selfing rates purge most embryonic lethals …, regardless of the opportunity for compensation” (p. 680). Thus, regardless of the ESS mating system, the relative competitive abilities of selfed and outcrossed embryos seem unlikely to play a major role in the evolution of hermaphrodite mating systems, as long as self- and cross-fertilization occur simultaneously.
Our models demonstrate that the complete spectrum of hermaphrodite mating systems could arise as evolutionary stable strategies in contrasting mating environments. Clearly, many circumstances could cause deviations from the ESS mating system, especially insufficient pollination, which favors reproductive assurance (Fig. 7). Nevertheless, all of the requirements for adaptive mixed mating incorporated in our models are probably common features of reproduction by hermaphrodites, including: male-gamete discounting (e.g., Harder and Barrett 1995); production of compensatory female gametes (Harder and Routley 2006); and heterogeneity in the nature of inbreeding depression during the life cycle, with lethal traits expressed early when homozygous (Husband and Schemske 1996; Charlesworth and Charlesworth 1999). Thus, the diversity of hermaphrodite mating systems (Goodwillie et al. 2005; Jarne and Auld 2006) may often bear the imprint of selection that maximizes genetic contributions to the next generation, rather than simply the sloppiness of mating, or convenient remedies for insufficient fertilization.
Associate Editor: T. Meagher
ACKNOWLEDGMENTS
We thank S. C. H. Barrett for discussions of mating-system evolution, and S. C. H. Barrett, M. Burd, C. G. Eckert, and B.C. Husband for comments on an early version of the manuscript. This research was funded by the Natural Sciences and Engineering Research Council of Canada (LDH and MBR) and the G8 Chair in Wildlife Ecology, The University of Calgary (SAR).
Appendix
In this appendix, we derive the ESS allocations of pollen to self-pollination and export, first in the absence of pollen discounting and then with complete pollen discounting. The solutions are asymptotically true for large numbers of ovules per ovary. In all cases, selfed and outcrossed embryos are assumed to compete equally for maternal resources. We also assume that if a plant exports pollen it must also import pollen, and that fertilization is not pollen-limited for any potential phenotype (i.e., fs+f♀= 1, where fs and f♀ are defined by eqs. 1a and 1b, respectively, or [qsps′+qxpx′]P > O), because selection acts most strongly against incomplete fertilization (see 2, 7).
ESS MATING SYSTEM WITH NO POLLEN DISCOUNTING
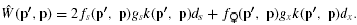
Case 1: (0 < gs < gx < m < 1)

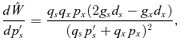

Case 2: (0 < m < gs < gx < 1)

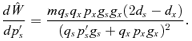

Case 3: (0 < gs < m < gx < 1)

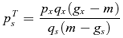


ESS MATING SYSTEM WITH COMPLETE POLLEN DISCOUNTING



 ((A1))
((A1))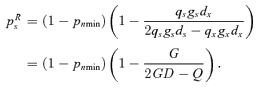
Some calculus shows that the second partial derivative of W with respect to p′s is strictly negative when ps=psR, implying pRs is a local fitness maximum. Thus, pRs is the ESS if it lies within the range of self-pollination that results in resource limitation, namely 0 < pRs < pTs.

 ((A2))
((A2))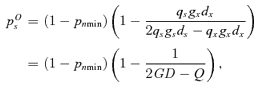
 ((A3))
((A3))The ESS in this situation is determined by both the value of pTs with respect to pOs and pRs and whether pTs, pOs, or pRs are positive or negative. The assumption that gs≤gx implies that pOs≤pRs < 1, which leads to three possible situations describing the relative relations between pTs, pOs, and pRs. From above, we know that pRs is the ESS if pRs < pTs, or pOs is the ESS if pTs < pOs. To determine the evolutionary outcome otherwise note that if pOs < pTs and ps > pTs, then seed production is ovule-limited and selection will favor reduced ps. Also note, if pTs < pRs and ps < pTs, then seed production is resource-limited and selection will favor enhanced ps. Hence, as the fitness function is piecewise continuous, if pOs < pTs < pRs, ps will evolve to pTs if it is nonnegative. As the ESS must be positive, to determine the evolutionary outcome, we must consider the following three possible cases regarding the signs of pOs and pRs.
Case A: pOs < pRs < 0
 ((A4))
((A4))Case B: pOs≤ 0 ≤pRs


Case C: 0 < pOs < pRs