ASYMMETRIES IN PHYLOGENETIC DIVERSIFICATION AND CHARACTER CHANGE CAN BE UNTANGLED
Abstract
The analysis of diversification and character evolution using phylogenetic data attracts increasing interest from biologists. Recent statistical developments have resulted in a variety of tools for the inference of macroevolutionary processes in a phylogenetic context. In a recent paper Maddison (2006 Evolution, 60: 1743–1746) pointed out that uncareful use of some of these tools could lead to misleading conclusions on diversification or character evolution, and thus to difficulties in distinguishing both phenomena. I here present guidelines for the analyses of macroevolutionary data that may help to avoid these problems. The proper use of recently developed statistical methods may help to untangle diversification and character change, and so will allow us to address important evolutionary questions.
The last 20 years have witnessed a remarkable change in paradigm for evolutionists: the variation in speciation and extinction rates (i.e., the tempo of evolution), and the variation in the rates of character change (the mode of evolution) are now ideally studied with molecular phylogenies and data collected on recent species. These issues, traditionally called macroevolution, were the domain of paleontologists during several decades (Simpson 1953), whereas molecular data were used to address microevolutionary mechanisms (to have an idea of this changing paradigm, compare the two editions of the same book by Futuyma 1986, 1998).
In a recent paper, Maddison (2006) used simulated data following two scenarios to bring attention to some limits of this new paradigm. In the first scenario, some clades were simulated starting from the root, and a character evolved along the tree: two states were allowed (0 and 1) with a constant probability of change between them. The speciation rate was related to the state of the character so that species in state 1 split at a higher rate than those in state 0. Maddison showed that the estimates of the ratio of character transition rates were correlated with the ratio of the speciation rates. In the second scenario, Maddison used a similar setting except that the speciation rate was constant, but the rates of transition of the character in one direction were four times higher than in the other. He, then, showed that the analysis of diversification led to infer, more frequently than by chance, that the speciation rate was different between the states of the character.
Maddison (2006) concludes that, if simple data analyses are done, biased diversification with respect to a character may lead to wrong conclusions on the evolution of this character. On the other hand, biased character evolution may lead to false association of this character to biased diversification. In other words, this raises the question whether we may be able to untangle differential evolution of character from differential diversification. The question may be framed in more specific terms from Maddison's simulation study: if a character state is observed to be relatively rare in a clade, can we distinguish whether this state is associated with a low speciation rate, or evolution toward this state occurs at a low rate? (Or both?)
This issue is of great importance because, if we can answer positively, we could point which effect most contributes to the generation of diversity. Heterogeneous diversification rates and heterogeneous character change rates are likely linked to different evolutionary mechanisms. Character states with a high transition rate may be the result of counter-selection, developmental instability, or low plasticity of the character. On the other hand, a high speciation rate related to a character state may be the result of its adaptative value, or its association with the rate of reproductive isolation.
My aim in the present article is to show that appropriate data analysis methods can separate the effects of biased character change and biased diversification. This suggests that heterogeneous character evolution and heterogeneous diversification rates can be untangled in future analyses of macroevolutionary data. I point to some recommendations for data analyses in macroevolutionary studies with recent species, as well as further needs for future research in this area.
Methods
ANALYSIS OF CHARACTER CHANGE
Maddison (2006) showed that the maximum-likelihood estimates of the ratio of character transition rates were correlated with the actual ratio in speciation rates. One may be tempted to interpret a high ratio of character transition rates as evidence for a strong bias in character change, thus concluding that rates are actually different. However, Maddison did not address the issue of testing whether these rates are significantly different. Indeed, looking at parameter estimates is not the ideal way to assess the validity of an hypothesis. The results from Maddison's analyses illustrate that these parameter estimates can be strongly biased when a wrong model is used, not that they are significantly different.
(1)
(2)
, on its standard error, se
, can be used as an indication of the shape of the likelihood. This ratio is in fact a formulation of the Wald test that, under the null hypothesis that r is equal to zero, follows a standard normal distribution (see Rao 1973)
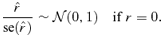
The LRT and the Wald test can thus be used to test the same hypothesis, but the latter is rarely used because it has generally poorer statistical performance than the LRT, particularly for small sample sizes (Agresti 1990; McCulloch and Searle 2001). However, both tests are expected to give the same results for large sample sizes (Rao 1973; McCulloch and Searle 2001).
I propose the following rule of thumb: when this ratio is less than 2, it is likely that the model under consideration is not appropriate. A justification for this rule is that, under the assumption that the maximum-likelihood estimates are normally distributed, (a standard assumption of the likelihood theory of estimation), then a 95% confidence interval may be calculated with 
. Consequently, if 
then zero is included in this interval suggesting the presence of a flat likelihood function. The method should be used as follows. First, perform the LRT comparing both models. If this test is significant, then examine the ratios of the rate estimates of model 2 on their standard errors: if one of them is less than 2, then it is likely that the LRT is biased and the null hypothesis is true.
ANALYSIS OF DIVERSIFICATION
Maddison (2006) inferred differences in speciation rates by comparing the number of species between sister clades that are different with respect to the character, but all species within each clade have the same character state. This method does not use all available information as it considers only a subset of the nodes of the tree, and it ignores branch lengths. Several methods have been proposed to analyze diversification that essentially differ in the type of data under consideration (see reviews in Sanderson and Donoghue 1996; Mooers and Heard 1997; Pagel 1999). For instance, some methods consider tree topology and balance (e.g., Aldous 2001), whereas others consider the distribution of branch lengths (e.g., Pybus and Harvey 2000). When the topology and branch lengths of the analyzed phylogeny are available, it is possible to refine the analyses and use more elaborate methods. Recent developments have been done in the inference of diversification, particularly the Yule model with covariates, which takes full account of all phylogenetic information (tree topology and branch lengths) to infer the effects of species traits on speciation rates (Paradis 2005). In this model the speciation rate depends on a linear combination of some variables measured on each species. This approach is similar to a standard linear regression where the mean of the response is given by a linear combination of variables. Consequently, a wide variety of models may be fitted to the same phylogenetic and species traits data. The latter could be continuous and/or discrete.
. The same criterion proposed above for the analysis of character was applied as well.DATA SIMULATION
I simulated some data with known parameters to assess the statistical performance of the methods described above. The idea was to generate some datasets in which the majority of the species are in a state due to, either different speciation rates, or different rates of character change, or both. The data were then analyzed to assess whether the two processes can be untangled. The simulations were started from the root of the tree, that is the initial bifurcation. At each time-step, each species present in the clade had a given probability (λ) to split into two, and a probability (p) to change the state of its character x. When a species split, the daughter species inherited its value of x. Both λ and p depend on x, and so are hereafter denoted λ0, p0, λ1, and p1, where the subscript indicates the value of x. Two of these parameters were fixed for all simulations: λ0= 10−4 and p0= 5 × 10−5. Three different combinations of parameters were used for λ1 and p1: (1) λ1= 5λ0, p1=p0, (2) λ1=λ0, p1=p0/10, and (3) λ1= 2.5λ0, p1=p0/4.
These settings correspond to the three plausible biological scenarios leading to the abundance of a trait in a clade: (1) this trait is associated with a high speciation rate, (2) species without this trait tend to evolve toward acquiring it, and (3) a mixture of both processes. The parameter values were chosen so that ca. 90% of species had x= 1 at the end of the simulation. These were found analytically in setting (2), because speciation was homogeneous, using the matrix exponentiation explained above, and the fact that the expected number of species after t time-steps is given by 2eλt (Kendall 1948). It was obviously unnecessary to consider here the null setting λ1=λ0 and p1=p0 because this would yield 50% of species in each state, and so little difficulty for data analysis. The first setting is similar to Maddison's (2006) first scenario, whereas the second setting is close to his second one: the difference is that he used a ratio of 4 instead of 10.
The time-step of the simulations was transformed in time unit equal to 0.001. Giving a probability of change of 5 × 10−5 for t= 0.001, we can find by back-transformation with the matrix exponentiation and interpolation that the actual parameter of the first setting was r≈ 0.05. All simulations were run until 100 species were present. This was replicated 100 times for each possible initial state at the root (0 or 1) and each combination of the parameters. The trees and values for x at the end of the simulation were saved (the files are available from the author). All simulations were programmed in R version 2.4.0 (R Development Core Team 2006). The data were analyzed as if they were real data: the procedures described above were applied to all replicates using R's standard looping functions. Both LRTs and Wald tests were computed, as well as the proportion of cases in which the tests agreed in rejecting the null hypothesis. The analyses of character change and of diversification were done with the package APE (Paradis et al. 2004).
Results
The results were slightly affected by the state of the root as it changed slightly the proportion of species in state 1 at the end of the simulation: 83.8% and 91.6%, for a root in state 0 or 1, respectively (data pooled over all simulations). This proportion had in fact a skewed distribution when calculated for each replicate; the corresponding medians were thus slightly larger: 85% (range: 28–99) and 92% (63–99). For simplicity, the results below are presented for the two series of simulations pooled because they were overall consistent.
ANALYSIS OF CHARACTER CHANGE
The proportions of replicates where the LRT comparing models 1 and 2 was significant at the 5% level were 0.18, 0.405, and 0.175 for the three scenarios of equal rate of change, strong, and moderate biases, respectively (Table 1). On the other hand, the Wald test had relatively poor performance as the rejection rate of the null hypothesis was almost the same whatever the scenario (ca. 0.25). After examining the standard errors of the parameter estimates, the proportions of cases where the LRT was significant and the ratios 
and 
were greater than 2 were lowered to 0.055, 0.26, and 0.1. Only the first one was not significantly different from 0.05 (two-sided exact binomial test: P= 0.744, P < 0.0001, and P= 0.003, respectively).
| p 1 | λ1 | Character change | Diversification | ||||
|---|---|---|---|---|---|---|---|
| LRT | Wald | Both | LRT | Wald | Both | ||
| p 0 | 5λ0 | 0.18* | 0.265* | 0.055* | 0.415 | 0.53 | 0.415 |
| 0.1p0 | λ0 | 0.405 | 0.31 | 0.26 | 0.01* | 0.01* | 0.01* |
| 0.25p0 | 2.5λ0 | 0.175 | 0.235 | 0.1 | 0.13 | 0.23 | 0.13 |
Figure 1 gives a summary of the distributions of the estimates under both models for the three settings. As observed by Maddison (2006), a few cases resulted in extremely dispersed estimates, so I focused on the median and first and third quartiles. In the first setting, the median of the estimator 
was very close to the true value (0.049, instead of 0.05). Remarkably, the dispersion of all parameter estimates and their standard errors were smaller when model 2 was true.
Distribution summaries of the estimates of the rates of character change and their standard errors. The dots indicate the median, and the error bars the first and third quartiles. The panels correspond to the three simulated scenarios.
The reconstruction of ancestral states is also informative. Under model 2 nearly all nodes (except the most terminal ones) had a relative likelihood of 0.5 for each state, meaning that these reconstructions were in fact indeterminate under this model. Under model 1 most nodes were estimated to be in state 1 with a high probability (relative likelihood greater than 0.9): this was particularly the case for the root even if the actual state was 0 (Fig. 2). Thus the models failed to estimate correctly the ancestral states of the simulated character.
For each simulated dataset, the relative likelihood that the root was in state x= 0 was calculated under both models of character change. This series of histograms shows the distribution of these values for each combination of parameters (as rows) and each actual initial state of the root (as pairs of columns). A value close to zero implies that the root state was inferred to be x= 1, a value close to one implies it was x= 0, and a value close to 0.5 implies that the inference of the root state was indeterminate by this model.
ANALYSIS OF DIVERSIFICATION
The simulated trees and phenotypic values were analyzed with the Yule model with covariates testing for the effect of x on λ. The method requires us to reconstruct the values of x at the nodes of the tree: this was done with a simple parsimony criterion. The branch lengths were back-transformed to the original time scale of the simulations prior to analysis to ease the fitting procedure. The proportion of significant LRT were 0.415, 0.01, and 0.13. All these proportions are significantly different from 0.05 (two-sided exact binomial test: P≤ 0.005 in all cases). The Wald test gave similar results, but with slightly larger rejection rates of the null hypothesis. However, in all cases in which the LRT was significant the Wald test was as well (Table 1). It is interesting to note that although the estimated ancestral states were inaccurate, the test was able to reject the null hypothesis in more than 5% of the cases, and so is robust, at least partially, to inexact ancestral character estimation (at least in the present situation).
Discussion
The combined use of the LRT and Wald test here revealed an interesting contrast between analyses. In the analysis of character change, the proposed criterion derived from the Wald test helped to keep the type I error rate at a reasonable value. In the analysis of diversification, the LRT performed well and there is, in the present scenarios, no need to use the proposed criterion. How to explain this difference? There are three possible, nonexclusive explanations of the relatively poor performance of the models of character change. First, the departures from the Markovian assumptions may be too strong so that the models considered here are too “ill-defined” for the present data. Second, the maximization of the likelihood functions of these models is not straightforward as it requires iterative calculations of likelihoods along the nodes of the tree that may be difficult for current optimization methods. By contrast, the likelihood function of the Yule model with covariates is a linear function of the parameters (Paradis 2005). Third, the current formulation of the model of character change may not be adequate for likelihood maximization, and a reparameterization resulting in a linear combination of parameters might be more appropriate.
Mooers and Schluter (1999) were cautious about the approximation of the LRT with a chi-square distribution, and recommended using conservative values to assess the increase in likelihood when fitting model 2. They also called for more work to verify the validity of this approximation. In the present study, I observed in some cases a difficulty to fit the models that required to repeat the fitting procedure with different starting values. Some further study is needed to assess whether this is due to the inadequacy of these models, or a failure of our current algorithms of likelihood maximization.
All simulations were run with parameter values that gave equal number of species, and similar frequencies of the states of x. So the differences in the results of the tests were due to the internal structure of the data, not to the prevalence of species with x= 1. The Yule model with covariates will tend to be accepted when shorter branches are associated with a character state. Such an association may be significant even if a state is at low frequency. Another interesting property of the Yule model with covariates revealed here is that it is robust to inexact estimation of ancestral states. This is likely to be important giving difficulties in reconstructing ancestral states (see below).
The simulations strongly suggest that the methods considered here are statistically consistent: they had greater power to reject the null hypothesis when the difference between the parameters were larger. Mooers and Schluter (1999) suggested that most datasets are too small to yield enough statistical power to reject model 1. Interestingly, most datasets they considered have many fewer than 100 species. With the increasing size of biological databases, and the advent of supertree techniques (e.g., Agnarsson et al. 2006; Beck et al. 2006; Bininda-Emonds et al. 2007), we are likely to have now the possibility to fit more complex models of character change.
A possible limitation of the current Markovian models of character change is the assumption of equilibrium (Nosil and Mooers 2005). When this is violated, and this is certainly true in real situations, then our methods will lose some power. However, the simulations presented here suggest that this is apparently a question of degree. Although the method loses some power, it remains statistically consistent. In a more general context, the statistical consistency of data analysis methods is important in the face of confounding factors in realistic situations. The critical point is that the methods can still detect significant effects even when their assumptions are not met. An important confounding factor not considered here is extinction and the variation of its rate. If extinction rate is related with a species character, then this will likely result in biases for both methods considered here because this character will be associated with long branches in the tree. With respect to the Yule model with covariates, a previous simulation study showed that random extinction resulted in a loss of statistical power but the method remained statistically consistent (Paradis 2005).
The present article considered separate analyses of character change and diversification with currently available methods. From a statistical point of view, this can be viewed as each analysis was conditioned on the other: the analysis of character change was done assuming constant and homogeneous diversification, whereas the analysis of diversification was done assuming given reconstruction of the ancestral states. An interesting perspective would be to develop a joint analysis of these processes. Because each analysis is done by maximum likelihood, it is possible to combine both likelihood functions in a joint likelihood function that would be maximized over all parameters (r and λ). It remains to be seen whether this would increase the statistical performance of our methods.
ESTIMATION OF ANCESTRAL STATES
The results of the analyses of character change show that the inferred state at the root is likely to be misleading (see also Mooers and Schluter 1999, Fig. 1B). This failure to estimate correctly the state at the root is due to the assumption of equilibrium common to most Markovian models. A consequence of this assumption is that whatever the initial state, the probability to be in any state is given by its relative transition rate. For model 1, these probabilities are 0.5 because the transition rates are equal. This is concretely visualized by calculating etQ whose values tend to 0.5 when t increases. Consequently, if one state is rare this implies that the initial state (i.e., the root) was in the other state, and so the system is in transition toward its equilibrium.
On the other hand, it was observed that the estimates of the rate of change were nearly unbiased. This suggests that, although we are able to correctly assess how frequently a character changed, our estimates of its ancestral states may not be meaningful. This is an important issue because there is more interest in ancestral states than on rates of change (e.g., Webster and Purvis 2002; Oakley 2003). This clearly needs further study because if the relative poor performance of inferring ancestral states is confirmed, this would require a revision of some previous results and ideas.
It must be pointed out that the ancestral states were estimated assuming uniform priors on the root (i.e., it could a priori be in any state). This can be relaxed, for instance, by assuming that the prior probabilities of the root are equal to the observed proportions of the states (Maddison 2006). It will be interesting to examine whether this has an effect on ancestral state estimates.
Conclusion
To conclude, I would echo Maddison's (2006) view that uncareful analyses of evolutionary data can lead to wrong conclusions. Although the modern approach to macroevolution has certainly some limitations, there are reasons to be optimistic. Future data analyses should include several tools based on model fitting, hypothesis testing, model checking, and parameter estimation. There is clearly a need to study the statistical behavior of our models in a wide range of realistic situations. There is also space for many methodological developments. One issue that still remains challenging is how extinction can be considered efficiently in these methods.
Associate Editor: A. Mooers
ACKNOWLEDGMENTS
I am grateful to W. Maddison for reading a previous version of this article, to G. Chen for clarifying some issues on the Wald test, and to three anonymous referees and A. Mooers for their constructive comments on the text. This research was supported by a project Spirales from the Institut de Recherche pour le Développement (IRD).
