AN INTERSPECIFIC TEST OF ALLEN'S RULE: EVOLUTIONARY IMPLICATIONS FOR ENDOTHERMIC SPECIES
Abstract
Ecogeographical rules provide potential to describe how organisms are morphologically constrained to climatic conditions. Allen's rule (relatively shorter appendages in colder environments) remains largely unsupported and there remains much controversy whether reduced surface area of appendages provides energetic savings sufficient to make this morphological trend truly adaptive. By showing for the first time that Allen's rule holds for closely related endothermic species, we provide persuasive support of the adaptive significance of this trend for multiple species. Our results indicate that reduction of thermoregulatory cost during the coldest part of the breeding season is the most likely mechanism driving Allen's rule for these species. Because for 54% of seabird species examined, rise in seasonal maximum temperature over 100 years will exceed that for minimum temperatures, an evolutionary mismatch will arise between selection for limb length reduction and ability to accommodate heat stress.
Ecogeographical rules, such as Bergmann's rule (Bergmann 1847) and Allen's rule (Allen 1877), that relate large-scale geographical distributions to morphological variation, offer potential to describe how organisms are restricted to the environmental conditions under which they persist. Since their formulation, parallel studies in ecology and anthropology have provided limited evidence for these relationships (e.g., Roberts 1953; Mayr 1956) although there has been a recent resurgence in interest, especially given current rapid rates of climatic change (Millien et al. 2006; Steegmann Jr. 2007). Despite being established ecological tenets, these rules have remained controversial (Scholander 1955; Mayr 1956; Irving 1957; Hamilton 1961; Millien et al. 2006; Steegmann Jr. 2007) and their true potential for describing species' distributions has not been established.
Allen's rule states that the length of appendages relative to body size is reduced in cooler parts of an endothermic species' range to reduce heat loss from appendages and consequent thermoregulatory costs (Allen 1877). Insulation, however, provides a major avenue through which endotherms adapt to thermal niches (Scholander 1955) and it is generally agreed that alternative selection pressures can explain exceptions to the rules (Mayr 1956; Hamilton 1961; Millien et al. 2006), and maybe even the rules themselves (Scholander 1955; Irving 1957; McNab 1971). Mayr (1956), however, strongly asserted that intraspecific variation in appendage size stemmed from the relative advantage conferred to individuals equally constrained by phylogeny. By logical extension, related species should show similar interspecific geographic variation in appendage size, but this has yet to be established. The most practical way to test the validity of mechanisms behind ecogeographical rules, therefore, is to amass data for multiple species and determine which mechanisms are most prevalent (e.g., Millien et al. 2006). Allen's rule, although widely cited in ecological textbooks, remains poorly supported by empirical data and the few existing validations are for single species with wide geographical ranges (Ray 1960; Johnston and Selander 1971; Griffing 1974; Stevenson 1986; Lindsay 1987; Lazenby and Smashnuk 1999). One exception, a recent study considering Allen's rule for several shorebird species, found a strong correlation between tarsometatarsus length and metabolic rate (Cartar and Morrison 2005). This study examined the heat loss consequences of height above the ground's surface, not the importance of the surface area of appendages (e.g., leg elements) for heat loss that is the formulation of Allen's rule (1877) and therefore provided support only for an extension of Allen's rule.
Robust examinations of Allen's rule for multiple species are potentially confounded by the two factors, scaling and alternative functions that prevent a similar validation of Bergmann's rule. The scaling confound may be removed by using residual limb length from a regression of limb length upon body mass. Unfortunately, limb length is still influenced by other factors, such as locomotion. One group of animals in which differential selection pressures upon limb length are minimized is the Laridae and Sternidae (gulls and terns), which have unspecialized legs, used mainly for standing or swimming (Burger and Gochfeld 1996; Gochfeld and Burger 1996), but known to be important for heat exchange (Baudinette et al. 1976). Therefore, much interspecific variation in residual limb length could arise from thermoregulatory constraints for these species. On the other hand, because gulls and terns possess several mechanisms to minimize this route of heat loss (Chatfield et al. 1953; Baudinette et al. 1976) and the general importance of extremities for heat loss is debatable (Steegmann Jr. 2007) (given physiological mechanisms to reduce blood flow to these areas [Chatfield et al. 1953]), the legs of these species should not be expected to conform to Allen's rule. This latter argument has been invoked repeatedly by eminent physiologists to invalidate ecogeographical rules (Scholander 1955; Irving 1957).
To provide a critique of Allen's rule for multiple related species, two main hypotheses are investigated: that the lengths of exposed (nonfeathered) leg elements are reduced when thermoregulatory costs are high but the length of feathered elements, insulated from heat loss, are not. If, as Allen's rule suggests and Mayr (1956) advocates, minimization of heat loss from appendages is a major selection pressure influencing appendage surface area and limiting geographical distribution, both hypotheses should be supported. If height above the substrate (Cartar and Morrison 2005) or alternative function (e.g., shorter limbs supporting greater body weight at high latitudes) influences relative leg length, feathered elements should instead be reduced in colder environments. Finally, as should be expected given known physiological adaptations (Scholander 1955; Irving 1957), if no relationship is evident for either set of leg elements then Allen's rule remains unsupported for these species.
Materials and Methods
LEG LENGTH, BREEDING LATITUDE, AND TEMPERATURE MEASUREMENT
Measurements of exposed leg bone elements (tarsometatarsus length + middle toe length; 36 species), and feathered elements (femur length + tibiotarsus length; 43 species) were collected from museum skeletons for 24 gull and 19 tern species (Table 1). Sample sizes varied from 1 to 5, median = 2 (Table 1). Body mass, M, taken from the literature (Dunning Jr. 1993) was used to control for body size. In standing birds the feathered femur takes a more horizontal incline necessary for balance and contributes less to height above the substrate than the feathered tibiotarsus. Similarly, when resting on the sea, the unfeathered tarsometatarsus is folded under the body and may be insulated from heat loss. Consequently, to distinguish between Allen's rule and competing hypotheses, we examined relationships with temperature estimates for tibiotarsus and foot (middle-toe) lengths alone, as well as the sets of exposed and feathered elements.
| Species | n | Body mass (kg) | Femur (mm) | Tibiotarsus (mm) | Tarso-metatarsus (mm) | Middle-toe (mm) | Breeding latitude (km from equator) | Breeding season | Change in maximum temperature difference 1961–2061 (°C)* | Change in minimum temperature difference 1961–2061 (°C)* |
|---|---|---|---|---|---|---|---|---|---|---|
| Creagrus furcatus | 1 | 0.687 | 47 | 83 | 53 | 47 | 167 | Annual | −1.63 | −1.69 |
| Larus argentatus | 5 | 1.135 | 57 | 108 | 63 | 48 | 6336 | Apr–Sep | −2.31 | −2.11 |
| Larus atricilla | 1 | 0.325 | 37 | 77 | 50 | 32 | 3133 | Apr–Aug | −2.58 | −2.82 |
| Larus californicus | 2 | 0.691 | 48 | 92 | 58 | 45 | 5466 | May–Aug | −3.68 | −3.87 |
| Larus canus | 2 | 0.404 | 39 | 82 | 52 | 35 | 6400 | May–Sep | −2.21 | −2.12 |
| Larus delawarensis | 3 | 0.519 | 45 | 88 | 58 | 37 | 5454 | May–Aug | −3.66 | −3.89 |
| Larus dominicanus | 1 | 0.900 | 52 | 99 | 60 | 49 | 4099 | Oct–Jan | −1.17 | −1.15 |
| Larus fuscus | 3 | 0.766 | 54 | 104 | 67 | 47 | 6463 | Apr–Aug | −2.29 | −2.07 |
| Larus genei | 2 | 0.281 | 37 | 81 | 55 | 34 | 3852 | Apr–Aug | −2.26 | −2.22 |
| Larus glaucescens | 2 | 1.010 | 62 | 116 | 71 | 5777 | May–Aug | −3.50 | −4.26 | |
| Larus glaucoides | 3 | 0.863 | 52 | 94 | 54 | 32 | 7485 | May–Aug | −3.07 | −2.77 |
| Larus heermanni | 2 | 0.500 | 41 | 81 | 52 | 5390 | Apr–Jun | −3.07 | −3.33 | |
| Larus hemprichii | 1 | 0.455 | 41 | 79 | 56 | 1463 | Jul–Nov | −2.13 | −2.19 | |
| Larus hyperboreus | 3 | 1.413 | 63 | 120 | 71 | 64 | 7623 | May–Sep | −2.07 | −1.61 |
| Larus ichthyaetus | 3 | 1.407 | 59 | 118 | 76 | 52 | 4925 | Apr–Sep | −3.52 | −4.15 |
| Larus marinus | 5 | 1.659 | 66 | 130 | 81 | 64 | 6373 | Apr–Sep | −2.40 | −2.25 |
| Larus melanocephalus | 2 | 0.256 | 39 | 85 | 53 | 34 | 5028 | May–Aug | −2.77 | −2.68 |
| Larus minutus | 2 | 0.118 | 21 | 48 | 27 | 6002 | May–Sep | −2.47 | −2.99 | |
| Larus novaehollandiae | 3 | 0.323 | 39 | 79 | 53 | 36 | 3219 | Apr–Feb | −1.13 | −1.12 |
| Larus pacificus | 1 | 1.018 | 55 | 103 | 63 | 50 | 3798 | Sep–Apr | −2.18 | −1.85 |
| Larus philadelphia | 1 | 0.212 | 27 | 58 | 34 | 26 | 6469 | Jun–Aug | −3.97 | −4.84 |
| Larus ridibundus | 3 | 0.284 | 33 | 72 | 45 | 32 | 5692 | Apr–Jul | −1.58 | −1.59 |
| Rissa tridactyla | 4 | 0.407 | 35 | 65 | 33 | 36 | 6574 | May–Aug | −1.57 | −1.52 |
| Xena sabini | 2 | 0.191 | 27 | 56 | 34 | 25 | 7758 | Jun–Aug | −1.96 | −1.82 |
| Anous stolidus | 3 | 0.198 | 25 | 43 | 24 | 28 | 658 | Annual | −3.02 | −4.33 |
| Anous tenuirostris | 1 | 0.111 | 21 | 37 | 27 | 26 | 1219 | Oct–Jan | −3.11 | −7.04 |
| Childonias hybrida | 2 | 0.088 | 23 | 39 | 20 | 17 | 1004 | May–Dec | −1.36 | −1.38 |
| Childonias niger | 2 | 0.065 | 19 | 33 | 16 | 13 | 5412 | May–Sep | −1.93 | −1.92 |
| Gygis alba | 3 | 0.111 | 21 | 30 | 13 | 19 | 521 | Annual | −1.23 | −1.22 |
| Larosterna inca | 1 | 0.180 | 30 | 50 | 23 | 22 | 1431 | Annual | −2.39 | −2.43 |
| Sterna albifrons | 1 | 0.057 | 18 | 30 | 16 | 13 | 1356 | Annual | −1.36 | −1.39 |
| Sterna anaethetus | 2 | 0.096 | 24 | 40 | 21 | 458 | Annual | −1.94 | −2.75 | |
| Sterna bengalensis | 1 | 0.204 | 29 | 52 | 26 | 20 | 52 | Jun–Jan | −2.53 | −3.30 |
| Sterna bergii | 3 | 0.342 | 34 | 56 | 27 | 23 | 537 | Apr–Jan | −1.94 | −2.77 |
| Sterna fuscata | 3 | 0.180 | 26 | 45 | 23 | 19 | 259 | Annual | −1.34 | −1.41 |
| Sterna hirundo | 4 | 0.120 | 24 | 39 | 19 | 15 | 4193 | May–Sep | −3.51 | −3.35 |
| Sterna lunata | 1 | 0.146 | 27 | 47 | 26 | 32 | 273 | Feb–Sept | −1.13 | −1.08 |
| Sterna maxima | 1 | 0.419 | 38 | 64 | 33 | 352 | Apr–Sep | −1.71 | −1.38 | |
| Sterna paradisaea | 3 | 0.110 | 23 | 36 | 15 | 14 | 6575 | Jul–Aug | −2.80 | −2.75 |
| Sterna repressa | 3 | 0.090 | 21 | 36 | 19 | 15 | 1449 | May–Aug | −1.93 | −2.00 |
| Sterna sandvicensis | 2 | 0.208 | 29 | 52 | 27 | 17 | 686 | Apr–Aug | −1.47 | −1.41 |
| Sterna striata | 2 | 0.160 | 27 | 44 | 21 | 4941 | Oct–Jan | −1.01 | −1.09 | |
| Sterna sumatrana | 2 | 0.100 | 24 | 40 | 21 | 16 | 409 | Annual | −1.51 | −1.55 |
- *Highlighted in bold where change in minimum temperature difference (Tb–Tmax) exceeds change in maximum temperature difference (Tb–Tmin).
Analyses were duplicated (three times) using, as predictors of leg length, (1) latitude (distance, in kilometers, of breeding range midpoint from equator) and estimates of the (2) minimum air temperature (Tmin) and (3) maximum temperature difference (temperature gradient between an animal and the environment: Tmaxdiff= body temp (Tb) –Tmin) experienced during the breeding season. Passive heat transfer between an animal and its environment is proportional to the temperature gradient between the animal's surface and surrounding air (McNeill Alexander 1999). Therefore, Tmaxdiff provides the most direct index of thermoregulatory costs of the three measures. Body temperature was estimated from an allometric equation (McNab 1966).
Temperature data were from 1961–1990 climate normals (New et al. 1999). Thirty-year means of the three temperature variables for each species's breeding season were interpolated to the latitudinal and longitudinal midpoint of the breeding range for each species (Burger and Gochfeld 1996; Gochfeld and Burger 1996), avoiding complications for species differing in breeding range extent. Midpoint combinations for all species were locations in which actual breeding sites existed. Temperature measurements during the breeding season for each species were used to explore climatic limitation because gulls and terns nest territorially in exposed areas (Burger and Gochfeld 1996; Gochfeld and Burger 1996) and consequently adults are highly exposed to physical environmental stresses at the point in their life cycle when energy expenditure is greatest (Bryant 1997). Thirty-year means for sea surface temperature (SST) were calculated from GISST2.2 data (Parker et al. 1995) for the same period and substituted where air temperatures were unavailable.
To explore the implications of Allen's rule under forecast climate change, future temperature estimates were derived from the HadCM3 GCM (Pope et al. 2000), using SRES scenario B2a. Mean estimates for 2061–2090 across each species' breeding season were interpolated to breeding midpoints. For each species, change in Tmaxdiff and Tmindiff (minimum temperature difference, Tb–Tmax), between 1961–1990 and 2061–2090 were calculated.
SPECIES TREATED AS INDEPENDENT DATAPOINTS
Separate general linear models (GLMs) were fitted to explore the relationship between (1) latitude, (2) Tmin and (3) Tmaxdiff, and length of exposed and feathered leg elements, with body mass as a covariate and taxonomic family (Laridae or Sternidae) as a factor, because ecological factors influencing leg length could vary considerably between families.
COMPARATIVE ANALYSIS USING INDEPENDENT CONTRASTS
To ensure phylogenetic independence in the data, standardized independent contrasts using CAIC version 2.6.9 (Purvis and Rambault 1995) were calculated and the relationship between leg length and latitude/temperature was re-examined. The Laridae phylogeny used is depicted in Figure 1 of Pons et al. (2005) and the Sternidae phylogeny is shown in Figure 2 of Bridge et al. (2005), both based on mtDNA sequence analysis. Results assuming a gradualistic model of evolution (using genetic distance as branch lengths) and a punctuational model of evolution (i.e., all branch lengths assumed to be equal length) are given. Sterna repressa was missing from the Sternidae phylogeny but was placed as the sister species to S. hirundo with equal branch length (based on table 2 of Bridge et al. (2005)).
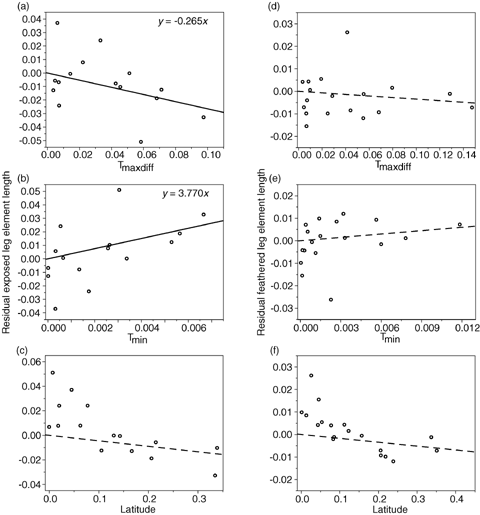
Relationship between residual exposed (a-c) and feathered (d-f) leg lengths and latitude, maximum temperature difference (Tmaxdiff), and minimum temperature (Tmin) for the Laridae from CAIC contrasts, assuming a gradualistic model of evolution. All axes are standardized contrast values. Solid lines represent significant relationships, dashed lines represent nonsignificant trends.
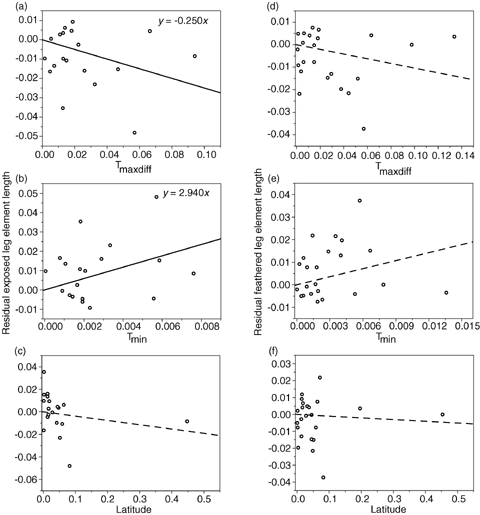
Relationship between residual exposed (a-c) and feathered (d-f) leg lengths and latitude, maximum temperature difference (Tmaxdiff), and minimum temperature (Tmin) for the Sternidae from CAIC contrasts, assuming a gradualistic model of evolution. Axes are standardized contrast values. Solid lines represent significant relationships, dashed lines represent nonsignificant trends.
| Proxy for thermoregulatory cost | Family | Body mass | Latitude or temperature |
|---|---|---|---|
| Exposed leg elements | |||
| Breeding range midpoint (km) | F 1,32=28.36, r2=0.06, P<0.001 | F 1,32=65.28, r2=0.87, P<0.001 | F 1,32=2.69, r2=0.01, P=0.111 |
| Minimum temperature | F 1,32=41.93, r2=0.07, P<0.001 | F 1,32=95.53, r2=0.87, P<0.001 | F 1,32=8.50, r2=0.01, P=0.006 (2.508) |
| Maximum temperature difference | F 1,32=42.58, r2=0.07, P<0.001 | F 1,32=93.24, r2=0.87, P<0.001 | F 1,32=8.91, r2=0.01, P=0.005 (−0.214) |
| Feathered leg elements | |||
| Breeding range midpoint (km) | F 1,39=16.63, r2=0.02, P<0.001 | F 1,39=302.07, r2=0.94, P<0.001 | F 1,39=0.05, r2=0.01, P=0.820 |
| Minimum temperature | F 1,39=22.13, r2=0.02, P<0.001 | F 1,39=317.27, r2=0.94, P<0.001 | F 1,39=1.98, r2=0.01, P=0.415 |
| Maximum temperature difference | F 1,39=19.97, r2=0.02, P<0.001 | F 1,39=317.32, r2=0.94, P<0.001 | F 1,39=0.19, r2=0.01, P=0.663 |
| Tibiotarsus | |||
| Breeding range midpoint (km) | F 1,39=27.55, r2=0.03, P<0.001 | F 1,39=216.55, r2=0.92, P<0.001 | F 1,39=0.11, r2=0.01, P=0.744 |
| Minimum temperature | F 1,39=34.69, r2=0.04, P<0.001 | F 1,39=228.00, r2=0.92, P<0.001 | F 1,39=0.61, r2=0.01, P=0.439 |
| Maximum temperature difference | F 1,39=31.88, r2=0.03, P<0.001 | F 1,39=227.90, r2=0.92, P<0.001 | F 1,39=0.16, r2=0.01, P=0.687 |
| Middle toe | |||
| Breeding range midpoint (km) | F 1,32=10.02, r2=0.04, P=0.003 | F 1,32=49.10, r2=0.85, P<0.001 | F 1,32=2.51, r2=0.01, P=0.123 |
| Minimum temperature | F 1,32=16.70, r2=0.05, P<0.001 | F 1,32=74.87, r2=0.85, P<0.001 | F 1,32=8.74, r2=0.01, P=0.006 (3.120) |
| Maximum temperature difference | F 1,32=18.50, r2=0.05, P<0.001 | F 1,32=74.77, r2=0.85, P<0.001 | F 1,32=10.42, r2=0.01, P=0.003 (−0.279) |
To remove the variation resulting from body mass (M), log10 values for leg length and M (Garland Jr. et al. 1992) were used to calculate contrasts using the CRUNCH algorithm of CAIC (Purvis and Rambault 1995). A regression of leg length contrasts against M contrasts gives an unbiased (phylogenetically independent) estimate of the relationship between these variables. A standardized value for leg length was then calculated from the regression equation (y=xα) between leg length contrasts (y) and M contrasts (x), where α is the scaling exponent. Residual (mass-independent) variation in leg length for each species (relative leg length) equaled this standardized value subtracted from the original value.
Relative leg length was tested for correlation against log10 latitude, log10Tmin, or log10Tmaxdiff using the CRUNCH algorithm. Regression analyses of contrasts generated using CAIC are performed through the origin (Purvis and Rambault 1995) but the absence of a y-intercept value is unimportant because the correlation coefficient between leg length and latitude/temperature variables using relative values still represents the true nature of the relationship (Pagel 1992; Purvis and Rambault 1995).
All data were log10 converted before analysis; Tmin was converted to Kelvin (i.e., Celsius + 273) prior to log transformation to accommodate negative values. Analyses were carried out separately for each family because controlling for phylogeny did not control for ecological differences between the families, only for effects of common ancestry. Where necessary, log10 transformed branch lengths were used in CAIC analyses to remove heterogeneity.
Results
As predicted by Allen's rule, exposed leg length was significantly negatively correlated with Tmaxdiff and positively correlated with Tmin (Table 2) and the length of feathered leg elements were not significantly related to either temperature measure or latitude (Table 2). Similarly, the length of the middle toe alone was significantly negatively correlated with Tmaxdiff and positively correlated with Tmin (Table 2) but tibiotarsus length did not correlate with either temperature measure or latitude. These results were corroborated when phylogeny was controlled for, both using a gradualistic model of evolution (Table 3, Figs. 1, 2) and a punctuational model (Table 3), except in the case of middle toe length in the Laridae, where the relationship with Tmaxdiff was not quite significant at the 0.05 level for either the gradualistic (P= 0.067) or punctuational model (P= 0.051). The statistical nonsignificance of this result was due to a single species' data: Larus glaucoides. When the outlying contrast relating to L. glaucoides was removed, relationships with Tmaxdiff were significant (P < 0.05). It is likely that because the relationship with Tmin was significant for both models of evolution (gradualistic and punctuational), the outlying nature of L. glaucoides resulted from an error in estimation of body temperature from mass, because Tmaxdiff=Tb–Tmin and L. glaucoides is a multiple subspecies complex that is likely to vary widely in body mass. These results are therefore consistent with heat loss from the legs as the mechanism behind Allen's rule in these species, but not with increased height above the substrate or the alternative function hypotheses.
| Model of evolution | Leg element | Family | Regression with Tmaxdiff | Regression with Tmin | Regression with latitude |
|---|---|---|---|---|---|
| Gradualistic | Exposed | Laridae | t=−2.47, n=19, r2=0.25, P=0.024 | t=2.91, n=19, r2=0.32, P=0.009 | t=−1.06, n=19, r2=0.06, P=0.304 |
| Sternidae | t=−2.47, n=15, r2=0.30, P=0.027 | t=2.36, n=15, r2=0.29, P=0.033 | t=−1.33, n=15, r2=0.11, P=0.204 | ||
| Feathered | Laridae | t=−1.75, n=23, r2=0.12, P=0.095 | t=2.02, n=23, r2=0.16, P=0.056 | t=−0.40, n=23, r2=0.01, P=0.691 | |
| Sternidae | t=−0.89, n=18, r2=0.05, P=0.382 | t=0.92, n=18, r2=0.05, P=0.370 | t=−1.32, n=18, r2=0.09, P=0.204 | ||
| Tibiotarsus | Laridae | t=−1.23, n=23, r2=0.06, P=0.233 | t=1.48, n=23, r2=0.09, P=0.152 | t=0.07, n=23, r2=0.01, P=0.944 | |
| Sternidae | t=−0.95, n=18, r2=0.05, P=0.355 | t=0.97, n=18, r2=0.05, P=0.347 | t=−1.45, n=18, r2=0.11, P=0.165 | ||
| Middle toe | Laridae | t=−1.95, n=19, r2=0.18, P=0.067 | t=2.55, n=19, r2=0.27, P=0.020 | t=−0.82, n=19, r2=0.04, P=0.425 | |
| Sternidae | t=−2.70, n=15, r2=0.34, P=0.017 | t=2.34, n=15, r2=0.28, P=0.035 | t=−0.88, n=15, r2=0.05, P=0.396 | ||
| Punctuational | Exposed | Laridae | t=−2.57, n=19, r2=0.27, P=0.019 | t=3.01, n=19, r2=0.34, P=0.008 | t=−1.14, n=19, r2=0.07, P=0.269 |
| Sternidae | t=−2.29, n=15, r2=0.27, P=0.038 | t=2.20, n=15, r2=0.26, P=0.045 | t=−1.17, n=15, r2=0.09, P=0.262 | ||
| Feathered | Laridae | t=−1.76, n=23, r2=0.12, P=0.092 | t=2.02, n=23, r2=0.16, P=0.056 | t=−0.44, n=23, r2=0.01, P=0.666 | |
| Sternidae | t=−0.80, n=18, r2=0.04, P=0.434 | t=0.84, n=18, r2=0.04, P=0.411 | t=−1.18, n=18, r2=0.08, P=0.252 | ||
| Tibiotarsus | Laridae | t=−1.22, n=23, r2=0.06, P=0.235 | t=1.46, n=23, r2=0.09, P=0.158 | t=0.04, n=23, r2=0.01, P=0.971 | |
| Sternidae | t=−0.85, n=18, r2=0.04, P=0.405 | t=0.90, n=18, r2=0.05, P=0.382 | t=−1.31, n=18, r2=0.09, P=0.208 | ||
| Middle toe | Laridae | t=−2.09, n=19, r2=0.20, P=0.051 | t=2.70, n=19, r2=0.29, P=0.015 | t=−0.93, n=19, r2=0.05, P=0.365 | |
| Sternidae | t=−2.65, n=15, r2=0.34, P=0.019 | t=2.29, n=15, r2=0.27, P=0.038 | t=−0.80, n=15, r2=0.04, P=0.437 |
As expected from allometric scaling, leg length correlated with body mass both when controlling for phylogeny (scaling of leg elements did not differ from the slope expected for isometry; Table 4) and treating datapoints as independent (Table 2). Using species as independent datapoints, significant differences in exposed leg lengths, feathered leg lengths, tibiotarsus length, and middle toe length existed between families in each of the three analyses, consistent with differences in their ecologies (Table 2).
| Model of evolution | Leg element | Family | Scaling equation (95% confidence intervals) | Regression |
|---|---|---|---|---|
| Gradualistic | Exposed | Laridae | y=x0.32 (0.20–0.44) | t=5.53, r2=0.63, n=19, P<0.001 |
| Sternidae | y=x0.30 (0.12–0.48) | t=3.61, r2=0.48, n=15, P=0.003 | ||
| Feathered | Laridae | y=x0.32 (0.25–0.40) | t=9.01, r2=0.79, n=23, P<0.001 | |
| Sternidae | y=x0.33 (0.27–0.39) | t=12.21, r2=0.90, n=18, P<0.001 | ||
| Tibiotarsus | Laridae | y=x0.31 (0.19–0.42) | t=7.97, r2=0.74, n=23, P<0.001 | |
| Sternidae | y=x0.32 (0.28–0.36) | t=9.73, r2=0.85, n=18, P<0.001 | ||
| Middle toe | Laridae | y=x0.40 (0.27–0.52) | t=6.66, r2=0.71, n=19, P<0.001 | |
| Sternidae | y=x0.34 (0.31–0.37) | t=3.36, r2=0.45, n=15, P=0.005 | ||
| Punctuational | Exposed | Laridae | y=x0.32 (0.27–0.37) | t=5.52, r2=0.63, n=19, P<0.001 |
| Sternidae | y=x0.29 (0.23–0.36) | t=2.94, r2=0.38, n=15, P=0.011 | ||
| Feathered | Laridae | y=x0.33 (0.29–0.37) | t=9.09, r2=0.79, n=23, P<0.001 | |
| Sternidae | y=x0.33 (0.31–0.36) | t=9.51, r2=0.84, n=18, P<0.001 | ||
| Tibiotarsus | Laridae | y=x0.31 (0.16–0.46) | t=8.03, r2=0.75, n=23, P<0.001 | |
| Sternidae | y=x0.33 (0.21–0.46) | t=7.66, r2=0.78, n=18, P<0.001 | ||
| Middle toe | Laridae | y=x0.39 (0.16–0.54) | t=7.09, r2=0.74, n=19, P<0.001 | |
| Sternidae | y=x0.32 (0.22–0.42) | t=2.81, r2=0.36, n=15, P=0.014 |
Surprisingly, exposed leg length and middle toe length did not correlate with breeding latitude (Tables 2 and 3, 1, 2). This was because the correlation between temperature estimates and latitude was weaker (Pearson correlation coefficients: Tmin,r=−0.814; Tmaxdiff, r= 0.834) than between the temperature estimates themselves (r=−0.987). Using temperature difference Tmaxdiff, the most direct measure of thermoregulatory cost, gave the strongest relationship with leg length, providing further support for heat loss from the legs as the mechanism behind Allen's rule.
Forecast climatic warming over the next 100 years has different consequences for heat loss potential during the coldest (Tmaxdiff) and warmest periods (Tmindiff) of the breeding season (Fig. 3). Fifty-four percent of the species examined (points below the line in Fig. 3; listed in bold type in Table 1) will experience changes in Tmindiff exceeding changes in Tmaxdiff.

Differences between forecast changes in heat loss potential during the coldest (Tmaxdiff) and warmest periods (Tmindiff) of the breeding season for 19 tern species (Sternidae: gray circles) and 24 gull species (Laridae: black crosses) between 1961–1990 and 2061–2090. Dotted line indicates equal changes in both temperature extremes.
Discussion
Our analyses provide the first persuasive support for Allen's rule across related species, indicating that thermoregulatory requirements can impose strong selection pressure upon the evolution of limb morphology for endothermic species. For terns and gulls, the length of exposed leg elements is correlated with thermoregulatory costs, but feathered element length is not, even though both exposed and feathered elements necessarily contribute to height above the substrate and functional support of the bird. Although in some cases feathered elements exhibited a trend similar to that for exposed elements, this relationship was never significant, even though the lengths of these two sets of leg elements should evolve simultaneously to an extent enabling structural function. The length of the foot (middle-toe) alone (the region primarily exposed to heat loss when resting on water) was also correlated with thermoregulatory costs, but tibiotarsus length (the feathered element contributing most to height in a standing bird) was not. Consequently, our results provide the first interspecific validation of Allen's rule, showing that appendage length is restricted in cold environments to reduce surface area available for heat loss from exposed skin, not to limit height above the substrate (Cartar and Morrison 2005) or support the increased body mass predicted by Bergmann's rule (Bergmann 1847). This result is surprising considering the highly effective physiological mechanisms these species possess to reduce heat loss (Chatfield et al. 1953; Baudinette et al. 1976), existing adaptive variation in insulative properties (Scholander 1955; Irving 1957), and the myriad of alternative selection pressures (e.g., McNab 1971). Additionally, because these species show geographical variation in body size (e.g., Olsen and Larrson 1995) and, for each species, the few individuals available for measurement were collected from varying locations, the existence of a strong, phylogenetically independent relationship between leg length and temperature supports the argument of Mayr (1956), that the variation described by Allen's rule results from adaptive benefits.
As expected from allometric scaling, body mass explained the majority of variation in leg length and, although the residuals from this relationship were strongly correlated with temperature, corresponding r2 values were therefore low, indicating the relative importance of body size and ambient temperature for leg length. Predictions from Allen's rule were clearly upheld for the taxa we examined, presumably because confounding factors, such as sexual dimorphism, specialist locomotory function, and alternative/specialist avenues of heat loss (e.g., counter-current systems), did not provide stronger selection pressures in these species. It seems likely that thermoregulatory requirements influence limb length in many endothermic taxa but, because of other confounds (e.g., selection for foraging or locomotion) or alternative heat loss mechanisms, this relationship may not always be detectable.
Morphological adaptation to thermoregulatory regimes appears to be a general mechanism restricting these seabirds, and presumably other long-lived endotherms, to specific climatic conditions. This mechanism directly relating species distributions to climatic conditions provides a potential validation for climatic envelope models that predict range shifts and extinctions resulting from climatic change (e.g., Thomas et al. 2004). An alternative to range-shifts, sensu Cronin and Schneider (1990), is that appendage length will evolve in tandem with climatic warming. This seems improbable, however, for long-lived seabirds that have relatively long generation times. A strong thermoregulatory coupling of limb morphology and temperature implies that these species may become poorly adapted for heat loss within their current breeding ranges as a result of forecast climatic warming. Using simple extrapolation, for over half the species examined, heat loss potential during the warmest period of the breeding season will be reduced 19 (±0.27)% more than heat loss potential during the coldest period (Fig. 3) over the next 100 years. Because heat conservation during the coolest part of the breeding season appears the most plausible mechanism driving observed variation in limb morphology (1, 2) these species will likely have more difficulty loosing heat during the warm periods. This assumes that current limb morphology represents selection caused by recent historical minimum temperatures (1961–1990): a conservative assumption, as this period exhibited the highest mean global temperatures of the last 2000 years (Houghton et al. 2001). Not all species will respond similarly to forecast temperature change, even to comparable changes in maximum temperatures, and high-latitude species have structural and physiological adaptations that may exacerbate heat-loss problems. Thermal stress has been found to have both a direct and an indirect role in the mortality of breeding seabirds (Salzman 1982; Gaston et al. 2002) but impacts of climate change mediated by food availability are currently thought to be more important (Croxall et al. 2002), possibly because of flexible thermoregulatory behavior (Lustick 1984). Given the rapidity of forecast climate change (Huntley et al. 2006), however, thermoregulatory problems for these species may become commonly observed.
Many gull and tern species are migratory (Burger and Gochfeld 1996; Gochfeld and Burger 1996). Our analyses were restricted to the breeding season because increased energetic demand (Bryant 1997) and requirement for nest guarding reduce opportunities for active heat loss (e.g., resting on the water or bathing). Consequently, conditions during migration are unlikely to be as important in constraining appendage size as they are for resident species. Allen's rule was not explored for seabird chicks, but because of developmental and phylogenetic constraints, chick morphology is likely to show similar relationships with thermoregulatory conditions.
In our examination of the mechanisms behind Allen's rule, three surrogate measures for thermoregulatory costs (latitude, minimum temperature (Tmin) and maximum temperature difference (Tmaxdiff)) were considered. Of these, Tmaxdiff showed the strongest relationship with exposed leg length. As Tmaxdiff provides the most direct index of thermoregulatory costs of the three measures, it is most probable that heat conservation during the coldest part of the breeding season is a major selection pressure behind Allen's rule in these species. Latitude proved a poor proxy for temperature estimates, exhibiting no significant relationship with leg length. Because using only latitude as a predictor would have resulted in no firm support for Allen's rule, it is crucial to incorporate more direct thermoregulatory proxies in future studies of ecogeographical rules of morphology.
Associate Editor: F. Galis
ACKNOWLEDGMENTS
RLN is supported by a Leverhulme Early Career Research Fellowship. We thank J. Cooper at the Natural History Museum, Tring, UK for access to skeletons, and E.M. Humphreys, J.M. Arnold, P. Aerts and an anonymous reviewer for helpful comments on the manuscript. Thanks also to J.-M. Pons for providing branch length data.




