ABSOLUTE FITNESS, RELATIVE FITNESS, AND UTILITY
Abstract
It is well known that (1) natural selection typically favors an allele with both a large mean fitness and a small variance in fitness; and (2) investors typically prefer a portfolio with both a large mean return and a small variance in returns. In the case of investors, this mean–variance trade-off reflects risk aversion; in the case of evolution, the mathematics is straightforward but the result is harder to intuit. In particular, it is harder to understand where, in the mathematics of natural selection, risk aversion arises. Here I present a result that suggests a simple answer to this question. Although my answer is essentially identical to one offered previously, my path to it differs somewhat from previous approaches. Some may find this new approach easier to intuit.
The purpose of this note is to explain a familiar connection between the theory of evolution and the theory of finance. It is well known that most investors should, when choosing among portfolios, pay attention to both the mean and variance in returns. For example, when choosing among risky portfolios—those that contain only assets like stocks and bonds, whose returns fluctuate unpredictably through time—investors should typically choose a portfolio that maximizes the mean per-period return on investment while minimizing the variance in per-period returns (Bodie et al. 2007, chaps. 6 and 7). Investors should not, therefore, necessarily choose that portfolio with the greatest expected return. Instead, they might well be better off choosing a portfolio with a somewhat lower expected return if it also features a much lower variance in returns.
Similarly, it is well known that when the fitnesses of alleles fluctuate through time natural selection will typically “choose” the allele that shows the best trade-off between average fitness and variance in fitness. For example, in haploid models in which the absolute fitnesses of genotypes fluctuate randomly through time (with no autocorrelation), the allele that ultimately dominates the population is the one with the greatest geometric mean absolute fitness through time (Dempster 1955; Haldane and Jayakar 1963; Gillespie 1973). Because the geometric mean is G≈μ−σ2/(2 μ), where μ is the (arithmetic) mean and σ2 is the variance in absolute fitness, the allele favored by natural selection is the one that best boosts μ while reducing σ2. Oddly, then, both selection of an optimal portfolio and selection of the best allele typically depend on the first and second moments of performance. All else being equal, smaller variances are better.
Although it is easy to derive these well-known results from population genetics (Gillespie 1973; Bulmer 1994, pp. 99–101), it is not so obvious why portfolio selection and natural selection show such similar properties. The problem is this: An investor should reduce the variance in returns only if he is risk averse (almost all investors are risk averse; more on this shortly). An unusual investor who simply wants to increase his expected total wealth—an investor who is risk neutral—should not consider the variance in returns. Instead, he should choose the investment having the greatest arithmetic mean return. The question I ask here is: Why does natural selection act as although it is risk averse? Where in the mathematics of selection does risk aversion enter?
I suggest an answer below. To see this answer, I briefly review what it means to be risk averse. I then present a simple result that shows where risk aversion arises in the mathematics of selection. I emphasize that few or no new theoretical results emerge below; in fact my key finding is essentially identical to one obtained by Gillespie (1977) (see also Frank and Slatkin [1990] and Grafen [1999, 2002]). My route to this result will, however, differ somewhat from those taken by previous authors. It is hoped that this new approach might bring greater notice to these earlier findings.
RISK AVERSION AND UTILITY
When considering tolerance of financial risk, it is convenient to distinguish among three types of investors. The first is risk averse. Such an investor is pleased to receive his first $1000 but is not quite as pleased to receive his second $1000. This investor is considered risk averse because, after receiving his first $1000, he would be more upset to lose that $1000 than pleased to make another $1000. If we plot an investor's total wealth on the x-axis versus his “satisfaction” on the y-axis, a risk-averse investor shows a curve of diminishing returns (Fig. 1). This curve is called a utility function. A risk-averse investor has a concave utility function. Given this concavity, it is easy to show (by Jensen's inequality [Ross 1999; Stearns 2000]) that, all else equal, an investor should prefer small fluctuations in wealth. This is because big increases in wealth boost utility less than big decreases in wealth lower it.
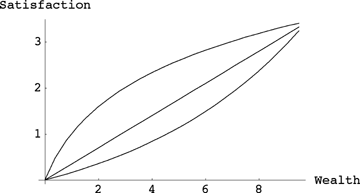
Investor satisfaction as a function of total wealth. The top curve (concave) corresponds to a risk-averse investor; the middle curve (linear) corresponds to a risk-neutral investor; the bottom curve (convex) corresponds to a risk-prone investor.
The second kind of investor is risk neutral. Such an investor is as pleased to receive his second $1000 as his first. He has a linear utility function. The third kind of investor is risk prone. Such an investor is more pleased to receive his second $1000 than his first. He has a convex utility function.
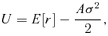 (1)
(1)When surveying risky assets, an investor should choose a portfolio that maximizes his utility. For a risk-averse investor, equation (1) shows that this requires weighting assets within a portfolio, for example, how much is invested in stocks versus bonds, in a way that increases E[r] while decreasing σ2 (Bodie et al. 2007). Note, however, that this is not the strategy that a risk-neutral investor (A= 0) should pursue. Instead, a risk-neutral investor should choose a portfolio that maximizes E[r]regardless of σ2. This maximizes the risk-neutral investor's expected return and his utility.
Returning to evolution, we can refine our question. If natural selection favors an allele that increases mean fitness while decreasing the variance in fitness, selection acts as though it were risk averse. What, then, plays the role of the concave utility function in evolution? Given, as many have suggested (Dawkins 1995; Stearns 2000), that fitness is the utility that natural selection maximizes— that is, fitness is the only thing that natural selection cares about and fitness therefore sits on the y-axis of the plot corresponding to Figure 1—what population-genetic quantity sits on the x-axis?
It is important to immediately dismiss a misleading possibility. If we consider a morphological or behavioral trait, we can trivially introduce a curve of diminishing returns between the trait and fitness. This is done routinely in the large literature on bet-hedging in behavioral ecology (e.g., Seger and Brockman 1987; Real and Ellner 1992). Such a relationship is enough to ensure that evolution acts in a risk-averse way. But this has no bearing on our problem, which is subtler. Our population-genetic result is not concerned with any morphological or behavioral trait, but with fitness only.
HAPLOID SELECTION
To see the solution to our problem, consider a simple model of haploid selection involving two genotypes, A1 and A2. Generations are discrete. Our analysis will, by analogy with a “single-period” analysis in finance, consider only one bout of selection, changing allele frequency from one generation to the next. In the current generation, A1 has frequency p and A2 has frequency q, with p+q= 1. Assigning fitnesses to these genotypes, we assume, for the moment, that fitnesses are constant. Genotype A1 has absolute fitness W1 and genotype A2 has absolute fitness W2. The mean absolute fitness of the population is 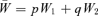 . We define the relative fitness of A1 as
. We define the relative fitness of A1 as 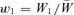 and of A2 as
and of A2 as 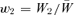 . The mean relative fitness of the population is
. The mean relative fitness of the population is  . Note that our parameterization of this selection model differs somewhat from the traditional one. In particular, we define relative fitness as relative to the mean absolute fitness of the population whereas relative fitness is often defined relative to a reference genotype (typically the fittest genotype). Our parameterization was often used by Kimura and Crow (1978) and Falconer (1981), among others. It will help to clarify our thinking.
. Note that our parameterization of this selection model differs somewhat from the traditional one. In particular, we define relative fitness as relative to the mean absolute fitness of the population whereas relative fitness is often defined relative to a reference genotype (typically the fittest genotype). Our parameterization was often used by Kimura and Crow (1978) and Falconer (1981), among others. It will help to clarify our thinking.
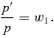 (2)
(2)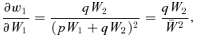 (3)
(3)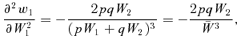 (4)
(4)
Relative fitness is a concave function of absolute fitness. In the example shown, p=q= 0.5 and W2= 0.5. It should also be noted that the extent of the concave relationship between w1 and W1 depends on p: as p gets very small the relationship becomes nearly linear (Frank and Slatkin 1990). Thus a new mutation is nearly risk neutral. For larger p, the relationship between w1 and W1 becomes more curvilinear (see eqs. 3 and 4).
Equations (3) and (4) and Figure 2 reveal something counterintuitive about natural selection: producing one more offspring affects relative fitness less than producing one fewer offspring. More exactly, producing an extra offspring improves a genotype's fitness relative to the population mean less than producing one fewer offspring worsens a genotype's fitness relative to the population mean. The latter statement is independent of the fitness scheme used above (see the Appendix). This, then, is where the curve of diminishing returns enters the mathematics of natural selection.
Given this concave function, it can be shown by Jensen's inequality that natural selection is sensitive to both the mean and variance in a genotype's absolute fitness (Gillespie 1977; Stearns 2000). In particular, it can be shown that natural selection prefers an allele that boosts mean absolute fitness while reducing the variance in absolute fitness.
COMPARISON TO PREVIOUS RESULTS AND CONCLUSIONS
Given that relative fitness is the quantity that natural selection cares about, the present approach may make the analogy between evolution and finance clearer: both feature a mean–variance trade-off because both feature concave utility functions. In finance, the concave function involves wealth versus satisfaction, whereas, in evolution, it involves absolute fitness versus relative fitness.
Gillespie (1977) derived a result that is formally equivalent to the one presented here. In particular, he showed that there is a curve of diminishing returns between the number of copies of an allele in the next generation and that allele's frequency in the next generation. Although the present result can be derived trivially from Gillespie's result, some may find the present interpretation easier to intuit. In particular, the idea of risk aversion might seem captured more naturally by a relationship between absolute and relative fitness than by a relationship between allele copy number and allele frequency. In any case, a curve of diminishing returns between absolute and relative fitness may have evolutionary implications not suggested by an analogous curve between copy number and frequency.
Frank and Slatkin (1990) also briefly described the curvilinear relationship between “reproductive success” and relative fitness. Their discussion appeared, though, in a somewhat technical paper devoted to the analysis of units of selection, that is, to partitioning variation in total reproductive success to that due to variation within individuals of a genotype and that due to correlations in success across individuals. Grafen (1999, 2002) also noted that strategies that maximize the geometric mean of the absolute number of progeny simultaneously maximize the arithmetic mean of the relative number of progeny, a closely connected point. In any case, these authors' results have not received the attention they deserve. It is hoped that the present approach will bring greater notice to their findings.
Finally, I emphasize that the analysis presented here is limited in some ways. In particular, by analogy with single-period analysis in finance, I have considered only a single bout of natural selection. Risk aversion might also arise in multibout (multiple generation) models of natural selection for reasons that are independent of those discussed here.
Associate Editor: H. Thomas
ACKNOWLEDGMENTS
I thank S. Frank, J. Fry, A. Grafen, T. Hansen, L. Orr, and D. Presgraves for helpful comments and/or discussions. I also thank I. Safdar of the Simon School of Business at the University of Rochester for teaching me some finance. This work was supported by NIH grant GM51932.
Appendix
Change in allele frequency is a function of a genotype's fitness relative to (normalized by) the population mean fitness. Our claim is that producing an extra offspring improves a genotype's fitness relative to the population mean less than producing one fewer offspring worsens a genotype's fitness relative to the population mean. We also claim that this result is independent of the fitness scheme used, that is, the unorthodox one in which a genotype's absolute fitness is normalized by the population mean absolute fitness (as above) or the orthodox one in which absolute fitness is normalized by the absolute fitness of the best genotype. I prove these claims here.
In the unorthodox fitness scheme, 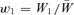 and
and 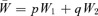 , as in the text. A genotype's fitness relative to the population mean fitness is just
, as in the text. A genotype's fitness relative to the population mean fitness is just 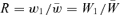 . Because
. Because 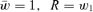 and ∂R/∂W1 and ∂2R/∂W21 are identical to equations (3) and (4) of the text, respectively. R is therefore a concave function of W1. In the orthodox fitness scheme, w1=W1/W1= 1 (where we assume genotype 1 is fittest) and w2=W2/W1. A genotype's fitness relative to the population mean is
and ∂R/∂W1 and ∂2R/∂W21 are identical to equations (3) and (4) of the text, respectively. R is therefore a concave function of W1. In the orthodox fitness scheme, w1=W1/W1= 1 (where we assume genotype 1 is fittest) and w2=W2/W1. A genotype's fitness relative to the population mean is  , which is the same as above. Thus ∂R/∂W1 and ∂2R/∂W21 are again identical to equations (3) and (4) of the text and R is a concave function of W1.
, which is the same as above. Thus ∂R/∂W1 and ∂2R/∂W21 are again identical to equations (3) and (4) of the text and R is a concave function of W1.




