THE INFLUENCE OF MATERNAL CARE IN SHAPING HUMAN SURVIVAL AND FERTILITY
Abstract
The influence of maternal care on child survival has evolved throughout human history due to variation in altriciality, allocare, and maternal behaviors. Here, we study the impact of these factors on the force of selection acting on age-specific survival and fertility (measured with elasticity analysis) in a model that incorporates the dependence of child survival on maternal survival. Results reveal life-history changes that cannot be elucidated when considering child's survival independent of maternal survival: decrease of late fertility and increase of late survival, and concomitant decrease of early and late fertility. We also show that an increase of child altriciality in early humans might explain the main human life-history traits: a high life expectancy and postreproductive life; a long juvenile period and a higher, and narrowed, fertility at the peak of the reproductive period.
Mammalian life histories follow a “slow–fast” continuum (after the effect of body size has been removed) from species with late maturity, few offspring per reproductive event and high adult survival (i.e., a long generation time) to species that reproduce early, have large litters and low adult survival (i.e., a short generation time, Harvey and Zammuto 1985; Gaillard et al. 1989; Promislow and Harvey 1990). Primates are at the slow end of this continuum. From small to large body size, primates consistently exhibit smaller litter size (one offspring, sometime two), longer life-expectancy (Charnov and Berrigan 1993), and slower postnatal growth leading to a longer juvenile period (Watts 1986) than other mammals. Humans are among the slowest primates with the exception of fertility, which is especially high at the peak of the reproductive period (in the absence of modern contraception) due to short birth spacing (see Mace 2000). Human females also exhibit senescence of fertility before a sudden cessation of reproduction (i.e., menopause). Whether this feature is shared with other primates is not fully known (Peccei 2001).
Comparative life-history analyses have been advanced by elasticity analysis. Elasticities are used in evolutionary ecology to estimate the intensity of selection exerted on life-history traits (e.g., Houle 1992; de Kroon et al. 2000) and therefore to identify which life-history components have the greater impact on fitness (e.g., Oli and Dobson 2003). This has allowed categorization of mammalian life histories along the slow–fast continuum according to the relative effect of each life-history component on fitness (Hepell et al. 2000). For species at the slow end of the continuum, juvenile survival to maturity has a greater effect on fitness than other demographic traits (Hepell et al. 2000). Every phenotypic trait that increases this probability (increase of offspring size at birth, reduction of litter size, and increased parental care) should therefore be all the more selected for. As maternal care (in terms of feeding, protection, education, and affection) is a major determinant of child survival in humans (e.g., Pavard et al. 2005), it has certainly coevolved with child survival during human evolution. Although effects of parental care on the optimal life history are the subject of increasing research interest and recent theoretical advances (Chu and Lee 2006), the way in which the relationship between maternal care and child survival has shaped the life-history patterns observed in our species (including adult survival and fertility) is still unclear.
Evolution of postnatal care has mainly been explored with optimality approaches (e.g., in humans, Lee 2003; Chu and Lee 2006). This approach searches for the optimal balance (in terms of fitness) between benefits gained through current reproduction (e.g., parental care improving offspring survival) and its costs assessed in terms of survival and/or future reproduction (extensively reviewed by Clutton-Brock 1991). The resulting optimal cost-benefit balance depends on how the relationship between parental care and offspring fitness is modeled and how the two costs of survival and future reproduction interact (Caswell 1982). In humans these trade-offs are especially difficult to measure empirically because of complex social interactions and because of their variation among populations (Gross 2005; Chu and Lee 2006). Nonetheless, optimality results inherently depend on the force of selection acting on each of the life-history components under a set of assumed trade-offs, which is measured by the selection gradients (Lande 1982; Arnold and Wade 1984). Yet, focus tends to be on equilibria rather than the force of natural selection leading up to the equilibria. Often forgotten, a change in one demographic trait (e.g., juvenile survival) will affect the force of selection on all other traits (e.g., survival and fertility at adult ages), even in the absence of trade-offs (Caswell 2007).
Understanding the influence of maternal care on the force of natural selection acting on demographic traits could therefore provide insight into the evolution of life-history strategies. Because the influence of maternal care on the human life history can be captured by the known empirical importance of maternal survival for child survival during the rearing time and up to maturity (Pavard et al. 2005, 2007), and because certain aspects regarding changes in the relationship between maternal survival and child survival during human history are known, it is possible to study the impact of these changes on the force of selection and to assess their consequences on life-history evolution.
There are indeed several key evolutionary events that may have influenced the relationship between maternal care and child survival during human history. The most influential event occurred millions of years ago in early Hominina. The simultaneous (1) acquisition of bipedalism, which compelled a reduction of pelvic channel size, and (2) increasing brain size, have together reduced the ratio between the diameter of the pelvis channel and that of the fetus' head. As a result, the gestation period coevolved to be shorter, leading to the birth of premature infants with smaller head to facilitate their delivery (see Smith and Tompkins 1995). A human birth is then followed by an extension of fetal growth during the first year of life in which children are particularly dependent on adults' care for their development. This is referred to by Portmann (1941) as “secondary altriciality” and explains why human babies mature much more slowly than those of other primates (Watts 1986, pp. 415–439). Many psychologists since Wallon (see Jalley 1981) see in this helpless period of human development the beginnings of the emergence of cognitive and social capacities specific to humans. This event should have increased the dependence of young children on maternal care, and therefore increased the impact of maternal survival on child survival soon after birth.
The second phenomenon that could have affected the importance of maternal care on child survival is allocare. In humans, caregivers other than the mother take part in child care. Because of nonmaternal breast-feeding and adoption, a motherless child at birth is not certain to die (Pavard et al. 2005). Secondary care decreases the impact of the absence of maternal care on child survival. Allocare has important consequences in many species. However, adoption remains rare in others primates (see Maestripieri 2001). Child care compensating that of the mother after her death is therefore likely to have arisen gradually during human history with the increasing complexity of social relationships. Compared to increased child altriciality described above, this phenomenon acts in the opposite way because it makes early childhood survival less dependent on maternal survival.
Finally, the third evolutionary event refers to each time mothers were able to increase late childhood survival, but not early childhood survival. This may have indeed been the case from australopithecines to Homo ergaster due to the tremendous increase in body size (McHenry and Coffing 2000), which suggests a reduction in mortality through the allometry of juvenile mortality on adult body mass. Children would have also required greater breast-feeding and nurturing to grow to larger adult body sizes (i.e., to develop), further increasing the importance of maternal care in child survival during human history. As maternal care becomes more important for the child to grow big, the increased efficiency of maternal care on child survival becomes increasingly important. Another example is the fact that a child's education provided by its mother may increase child survival at ages where education affects the ability of children to care for themselves, but not at early ages like the previous two phenomena. Events like these, where maternal care impacts child survival more when the child grows older, have likely occurred many times throughout the human history via changes in maternal behavior and technical improvements.
Each of these evolutionary phenomena can be modeled by modifying a simple function: the child's survival probability until maturity as a function of the child's age at mother's death (Pavard et al. 2007). Here we study the evolutionary consequences of these phenomena on human life history by measuring how each influences the force of natural selection on age-specific survival and fertility of adults. To accomplish this, we (1) altered the effect of mother's death on either early or late childhood survival to mimic the evolutionary scenarios described above; (2) provide the mathematical derivations to calculate elasticities of fitness to changes in age-specific survival and fertility in a model incorporating the effect of maternal care on child survival; (3) discuss the theoretical interest of the model in life-history analysis for species with high parental care, and (4) use the elasticity results to discuss how maternal care and its effect on child survival may have shaped human life history.
Methods
CHILD SURVIVAL AS A FUNCTION OF MATERNAL AGE AT CHILDBIRTH
In a previous study, Pavard et al. (2007) proposed a discrete-time model in which child survival until the age at maturity is a function of maternal survival during the rearing period. To develop this here, let us focus on a cohort of children born to mothers at age x. Hereafter, and to simplify further derivations, we consider that the first age class of children (age class 1) corresponds to age 0. The mothers of these children will die after their birth at different ages x+y− 1, where x is the mothers' age when they give birth and y− 1 is the number of years between the women's age at the birth of the child and her age at death (with y defined between 1 and ∞). Thus y is also the age that children would be when their mothers die if they survive until then, and, for simplicity, we denoted y“the child's age at mother's death.” Let us also assume that all children are similarly cared for while their mother is alive (more precisely, the care that a child receives from their mother is independent of the mother's age). Children's survival is compromised if their mother dies before they reach the mature age-class (hereafter called M, corresponding to the age at maturity M− 1) because of the subsequent lack of maternal care. If mothers die after M, children have reached maturity (y≥M) and a mother's death no longer impacts her children's survival. Let wy be the probability of survival to maturity of a child whose mother dies when the child was y years. Therefore, the function wy increases steadily with y between 1 and M (the older the child at the death of the mother, the lower the impact of this death on child survival) and asymptotically reaches a constant value at age M (wy=wM for y≥M). This function describes how a mother's death affects her child's survival until maturity and captures therefore the strength of the relationship between maternal care and child's survival.
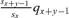 , where qx+y−1 is the probability of death between age x+y− 1 and x+y of women surviving at age x+y− 1. For example, the probability of a mother dying in the year following her child's birth (so for a child's age class y equal 1) is (sx/sx)qx. The probability ux is therefore equal to the sum over all the child's ages y (from 1 to ∞) of the product between (1) the probability of the mother dying when the child “reaches” this age y (which corresponds to age x+y− 1 of the mother) and (2) the child's probability of surviving until maturity according to the child's age at mother's death wy. It can be calculated as follows:
, where qx+y−1 is the probability of death between age x+y− 1 and x+y of women surviving at age x+y− 1. For example, the probability of a mother dying in the year following her child's birth (so for a child's age class y equal 1) is (sx/sx)qx. The probability ux is therefore equal to the sum over all the child's ages y (from 1 to ∞) of the product between (1) the probability of the mother dying when the child “reaches” this age y (which corresponds to age x+y− 1 of the mother) and (2) the child's probability of surviving until maturity according to the child's age at mother's death wy. It can be calculated as follows:
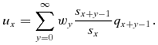 (1)
(1)In general, models of evolutionary ecology consider child survival until maturity as an average measured over all children in the population. This measure of child survival until maturity is therefore a constant independent of maternal survival 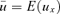 rather than a function of mother's age at childbirth ux (see Pavard et al. 2007 for calculation). In what follows, we refer to all calculations incorporating this probability
rather than a function of mother's age at childbirth ux (see Pavard et al. 2007 for calculation). In what follows, we refer to all calculations incorporating this probability  as the “reference model.”
as the “reference model.”
IMPACT OF MATERNAL CARE ON CHILD SURVIVAL UNTIL MATURITY
Pavard et al. (2005) used a large database on the pre-industrial population of French Canadians who lived in the St. Lawrence valley during the 16th and 17th centuries (early Quebec) to empirically study a child's risk of dying specifically associated with the loss of maternal care following the death of the mother at any time during the rearing period (from birth to age 15). Based on these estimates, Pavard et al. (2007) calculated a function of survival probability between ages 0 to 15 with respect to the number of years between a child's birth and death of its mother (Fig. 1, black line). This discrete function, denoted wy, is shown in Figure 1 from y= 1 (age 0) to y=M. The function wy continually climbs with y and tends to reach a maximum survival for children whose mothers remain alive during their whole childhood (wy∼ 0.7 for y≥M in the case of early Quebec but this value may vary among populations). The probability wM is the survival probability until maturity of children who are fully cared for from birth to maturity and who received the maximal maternal care. Because fathers, relatives and even the community as a whole can also be care providers, and because nonmaternal breast-feeding and adoption are frequent in human populations, the probability of reaching age M for children becoming motherless soon after their birth is not null (w1≠ 0). This phenomenon is mainly the product of human socialization that emphasizes the role of secondary caretakers (i.e., other than the mother). We call this effect “allocare.” The difference between these two values (wM−w1) is called the Net Benefit of Mother's Survival (NBMS). It is the difference in survival between a child who receives the maximum of maternal care and one who receives no maternal care.
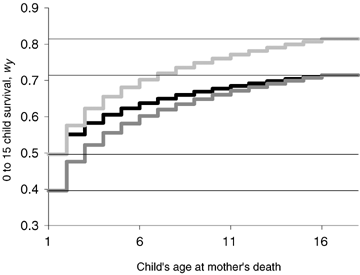
Evolutionary scenarios—Probability wy of surviving from age 0 to 15 as a function of the number of years y between the child's birth and the death of its mother. Age class y varies between 1 (age 0) and ∞. wy equals wM for y≥M, where age class M is the first mature age class (which corresponds here to an age at maturity M− 1 = 15 years). The black line corresponds to the estimates for the population of early Quebec from Pavard et al. (2005, 2007) and is the initial function [wy]i for both scenarios. The +ALT/−ALL scenario refers to a shift of wy from the black curve [wy]i to the dark gray curve [wy]f (which corresponds to a decrease by 0.1 of wy for y= 1). The +EFF scenario refers to a shift of wy from the black curve [wy]i to the light gray curve [wy]f (which corresponds to an increase by 0.1 of wy for y≥M).
CONSTRUCTION OF TWO EVOLUTIONARY SCENARIOS
To determine how the relationship between maternal care and child survival could have affected the force of selection on survival and fertility, and therefore may have shaped them over evolutionary time, we built two evolutionary scenarios. In both we modeled an increase of the importance of maternal care on child survival and therefore an increase of the NBMS on the wy function. Each evolutionary scenario considered an initial function [wy]i and a final function [wy]f; the final function showing a greater impact of mother's death on child survival than the initial function. For both scenarios, the initial function [wy]i was the one estimated for the population of early Quebec (with NBMSi∼ 0.71 − 0.49 ∼ 0.22). The two final functions [wy]f corresponding to each scenario were built from the initial one by increasing the NBMS by a quantity Q (Q=NBMSf−NBMSi= 0.1). The value NBMSi can be increased by a value Q in two opposite ways that define the two evolutionary scenarios considered in this study (see Fig. 1): either (1) a decrease of the survival of children whose mother dies soon after their birth w1 (with [w1]f=[w1]i−Q), or (2) an increase of the survival of children whose mothers survive during the whole rearing time wM (with [wy]f=[wy]i+Q for y≥M).
Although these two scenarios increase the NBMS, they differ in their evolutionary implications. The first scenario assumes a decrease in the probability of survival of a motherless child at birth but no change in that of a child whose mother remains alive during the whole childhood. This scenario models a decrease in the survival of children receiving nonmaternal care and is expected when the dependence of early childhood survival on maternal care increases. This scenario makes children more altricial at birth and is therefore relevant for modeling the emergence of human children's secondary altriciality. This first scenario is also appropriate to model a decrease in the care provided by secondary caretakers in the event of a mother's death and therefore models a reduction in allocare. A reduction in the survival of motherless children can be associated in this case with a decreasing level of allocare (see Introduction). We therefore call this the +ALT/−ALL scenario (increase of altriciality or decrease of allocare). The second scenario assumes that a motherless child's survival does not vary, but maternal care has an increasing impact on survival as the child ages: evolution increases survival of children receiving the maximum maternal care. This scenario models therefore an increase in the efficiency of maternal care on child survival as the child grows older. This can be observed as a result of changing behavior and technical advances in contemporary populations, and is particularly relevant to model the impact of education on child survival (see Introduction). We call this scenario the +EFF scenario (increase of maternal care efficiency on child survival).
CALCULATION OF THE FINITE RATE OF INCREASE λ AND ELASTICITY OF λ
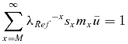 (2)
(2)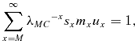 (3)
(3)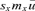 and it is expected that λRef and λMC will differ.
and it is expected that λRef and λMC will differ.The elasticity of λ to a demographic parameter is an estimate of the force of selection exerted on this parameter. Age-specific elasticities of survival or fertility are defined as the change in λ with respect to a relative change in survival or fertility at a given age. Elasticity of λ with respect to a change in survival and fertility at age z are, respectively, defined as e pz=∂lnλ/∂lnpz and e mz=∂lnλ/∂lnmz, where pz is the probability of surviving from age z to age z+ 1 and mz is the maternity rate at age z. Elasticities are the resulting effect on λ of multiplicative changes in either fertility or survival (Houle 1992).
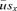 between the probability of surviving up to maturity
between the probability of surviving up to maturity  times the probability of surviving up to age x of survivors at age M, sx:
times the probability of surviving up to age x of survivors at age M, sx:
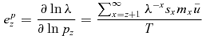 (4)
(4)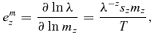 (5)
(5)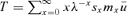 is the generation time. Because ux can vary with respect to a change in survival at age z, calculation of elasticities e pz and e mz incorporating the probability ux are more complicated in the case of the MC model:
is the generation time. Because ux can vary with respect to a change in survival at age z, calculation of elasticities e pz and e mz incorporating the probability ux are more complicated in the case of the MC model:
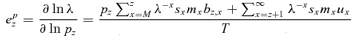 (6)
(6)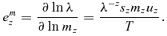 (7)
(7)For fertility, e mz follows Hamilton's derivations (1966). See the Appendix for the proof of the formula for e pz and the algebraic definition of the parameter bz,x.
ELASTICITY ANALYSES
Both scenarios +ALT/−ALL and +EFF involve two functions of the relationship between child survival until maturity and child age at maternal death (Fig. 1). An initial function [wy]i (estimated from the early Quebec population) and a final function [wy]f specific to each scenario. For each scenario, we calculated the difference in elasticities of λ to age-specific survival and fertility between the final function and the initial function for survival [e pz]f−[e pz]i and for fertility [e mz]f−[e mz]i. These differences indicate whether age-specific forces of selection on survival and fertility increased (the difference is positive) or decreased (the difference is negative) as a result of the change in the impact of maternal care on child survival modeled in each scenario. Because trade-offs are not modeled here (among maternal care, maternal survival, and maternal fertility), the force of selection is always positive in our model and an optimal life history cannot be found. However, assuming trade-offs being equal, it is reasonable to consider that a change in the force of selection on demographic traits resulting from each scenario will select for change in the magnitudes of these traits. Assuming human evolution imposed the change in the relationship between maternal care and child survival outlined in scenarios +ALT/−ALL and +EFF, the elasticity differences [e pz]f−[e pz]i and [e mz]f−[e mz]i, therefore, provide us with the expected resulting changes in adult maternal survival and fertility associated with each evolutionary scenario.
COMPARISON WITH THE REFERENCE MODEL
It is well known in evolutionary ecology that any change in offspring survival strongly impacts the force of selection on adult survival and fertility (e.g., Caswell 2001, chap. 9). As scenario +ALT/−ALL and +EFF, respectively, decrease and increase child survival until maturity for all values of y, they, respectively, decrease and increase the mean child survival until maturity  . It is therefore expected that they affect elasticities of λ, independently of the specific relationship between maternal survival and child survival modeled by the probability ux. To specify the effect of the MC model on the force of selection affecting survival and fertility, all analyses were also performed in the case of the reference model and results were compared.
. It is therefore expected that they affect elasticities of λ, independently of the specific relationship between maternal survival and child survival modeled by the probability ux. To specify the effect of the MC model on the force of selection affecting survival and fertility, all analyses were also performed in the case of the reference model and results were compared.
NUMERICAL APPLICATION
The initial function [wy]i was fitted to a logarithmic function of y from age class 1 to M, wy=a ln (y) +b (with a = 0.0787 and b= 0.4962, R2= 0.97) from estimates for the population of early Quebec (Pavard et al. 2005, 2007) and equaled wM for y > M. We also used the logarithmic function of y above to calculate the two hypothetical final functions [wy]f corresponding to scenario +ALT/−ALL ([w0]f=[w0]i− 0.1 and [wM]f=[wM]i; a= 0.11477 and b= 0.3962) and scenario +EFF ([w0]f=[w0]i and [wM]f=[wM]i+ 0.1; a = 0.11477 and b = 0.4962). In this article, we used age-specific survival and fertility estimated for the population of early Quebec (Charbonneau et al. 1987, pp. 131 and 89), but similar results are found for demographic parameters of other populations (e.g., for the Ache, Hill, and Hurtado 1996, pp. 196 and 261).
Results
For reference, we provide the elasticity values for age-specific fertility and survival for both scenario +ALT/−ALL and +EFF (Fig. 2). The elasticity differences, [e pz]f−[e pz]i and [e mz]f−[e mz]i, indicate how the evolutionary scenarios modified the force of selection on adult survival px and fertility mx. They are shown in Figure 3, for (1) survival and fertility, (2) each evolutionary scenario, and (3) the reference and the MC model.
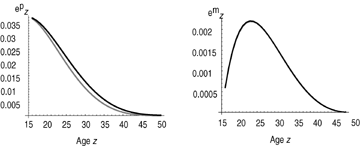
Age-specific elasticities e pz (for survival) and e mz (for fertility) corresponding to the function [wy]i estimated for the population of early Quebec; for the reference (gray curve) and MC model (black curve). A net difference in elasticities between models is visible for survival but differences are small for fertility.
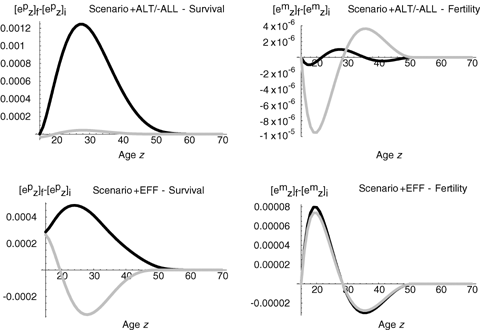
Differences in age-specific elasticities [e pz]f−[e pz]i (for survival) and [e mz]f−[e mz]i (for fertility) resulting from each evolutionary scenario (+ALT/−ALL and +EFF) and for the reference (gray curve) and MC model (black curve).
Because elasticities are scaled sensitivities, an important property of elasticities is that their overall sum across ages or stages equals 1. As a result, the more ages or stages involved, the lower each elasticity value. For example, in our study the elasticities sum to 0.963 for survival and to 0.037 for fertility (in the case of the reference model; the lower-level analyses for effects of maternal care on survival are more complicated). Because we calculated elasticities for 35 reproductive ages in the case of the reference model (from age 15 to age 50), the order of magnitude of elasticities is ∼0.963/35 ∼ 10−2 for survival and ∼0.037/35 ∼ 10−3 to 10−4 for fertility. These ranges correspond to the orders of magnitude of the original values shown in Figure 2 (elasticities vary between 0 and 0.035 for survival and between 0 and 0.002 for fertility). It is therefore expected that differences in elasticties (see Fig. 3) be at least one order of magnitude smaller than the original values (∼10−3 for survival and ∼10−4 to 10−5 for fertility). Except for the case of differences in fertility elasticities for scenario +ALT/−ALL, these orders of magnitude correspond to our estimates (see Fig. 3), and a change in elasticities corresponding to these magnitudes should be considered as evolutionarily significant.
For survival, the scenarios +ALT/−ALL and +EFF increased the force of selection on survival at all ages (until age 55, so even after menopause) in the MC model. For the reference model, the +ALT/−ALL scenario decreased the force of selection for ages lower than 20, then increased for ages higher than 20. The opposite was observed in +EFF scenario. More generally the magnitude of the increase in the force of selection for the MC model was much higher than for the reference model (up to 10 times higher for the +ALT/−ALL scenario).
For fertility, in the case of the reference model, the +ALT/−ALL scenario decreased the force of selection during the first part of the reproductive life (up to age 28) and increased them in the second part (age 28 and latter). The MC model leads to a more complicated pattern characterized by decreased force of selection on fertility at the very beginning of the reproductive life (form age 15 to 22), then an increase of the force of selection at the peak of the reproductive life (from age 22 to 36), and finally a decrease of the force of selection at the end of the reproductive life (after age 36). In the scenario +EFF no dramatic differences were observed between the reference model and the MC model.
Discussion
CAVEATS
Our estimated effect of maternal care on child survival until maturity (the function wy) was based on a highly derived, agrarian population, which we used as a baseline function for our two evolutionary scenarios: +ALT/−ALL and +EFF. Moreover, the adult survival probabilities considered in the present study are those of two contemporary populations (population of early Quebec and Ache). As shown in equation (1), a given child's survival depends on the mother's survival probability in years following childbirth, which was likely to have been much lower at the pleisiomorphic state of the hominid lineage. This state would have also exhibited lower child survival. Thus, the magnitude of the effect of maternal care on child survival may have been much larger in evolutionary history than the change in the wy function considered in each of our scenarios (i.e., [w0]f=[w0]i− 0.1 for scenario +ALT/−ALL and [wM]f=[wM]i+ 0.1 for scenario +EFF). Yet, given the large uncertainty about early hominid demography, we instead focused on qualitative changes in the force of selection resulting from maternal care in each evolutionary scenario. When demographic estimates of the wy function become available for other populations and species, future studies will be able to use our quantitative framework to estimate the impact of different maternal care scenarios (affecting child survival) on the force of selection affecting the evolution of adult survival and fertility.
A drawback of our study is that we analyzed only one aspect of the evolutionary process (natural selection). Genetic variance and covariance among traits, mutation rates, and genetic drift also influence the evolution of phenotypic traits. Because the variance–covariance matrix (i.e., the G-matrix) for age-specific survival and fertility is not known for humans, the rate at which selection affects the evolution of survival and fertility cannot be quantified (at least not with empirical data; Lande 1982; Charlesworth 1990; Steppan et al. 2002).
Finally, both evolutionary scenarios model historical events that took place over different evolutionary time scales. The emergence of secondary altriciality in humans (modeled by the +ALT/−ALL scenario), and the increased efficiency of maternal care (modeled by scenario +EFF, and related to increasing body size in the Hominina evolution), occurred millions of years ago. Since the early emergence of these characters, ample time has elapsed for even small changes in the force of selection to have significant impacts on phenotypic traits like age-specific survival and fertility (Charlesworth 1990). On the other hand, scenarios +ALT/−ALL and +EFF also model the effects of change in allocare, and change in education and childcare practices, respectively, on child survival. These events may have occurred many times throughout history and may have varied among populations. Thus, for these modeled changes in maternal care to have had a biologically significant impact on the evolution of age-specific patterns in survival and fertility, maternal care had to make a large change in the force of selection affecting these traits on a shorter evolutionary time scale.
For survival, the maternal care scenarios had a strong impact on both the qualitative and quantitative aspects of elasticities across age. A gene increasing (infinitesimally) the survival at all ages will increase the overall sum of survival elasticities by 2.3% for model +ALT/−ALL and 1.5% for +EFF, both signifying a strong impact on the force of selection. Thus, changes in maternal care behaviors could have had a strong effect on the evolution of age-specific patterns in survival over short and long evolutionary time scales (Fig. 3—survival). However, our maternal care scenarios changed fertility elasticities by amounts that were two to three orders of magnitude smaller than for survival (Fig. 3—fertility). Thus, long periods of time would have had to elapse for such changes in the force of selection to make a significant impact on evolved patterns of age-specific fertility.
LIFE-HISTORY THEORY
Life-history theory generally assumes offspring survival is independent of mother's survival (i.e., offspring survival until maturity is a mean  ). In our MC model, offspring survival, ux, is a function of mother's survival during years following childbirth. Our results show that the change in the force of selection resulting from our evolutionary scenarios can diverge between the reference model and the MC model.
). In our MC model, offspring survival, ux, is a function of mother's survival during years following childbirth. Our results show that the change in the force of selection resulting from our evolutionary scenarios can diverge between the reference model and the MC model.
First, the +ALT/−ALL scenario decreased the mean child survival until maturity  . The reference model predicts in this case a decrease of fertility during the first part of reproductive life (before age 28 in our example) and an increase of fertility during the second part (see, Fig. 2, +ALT/−ALL scenario—Fertility). In the case of the MC model, the decrease in
. The reference model predicts in this case a decrease of fertility during the first part of reproductive life (before age 28 in our example) and an increase of fertility during the second part (see, Fig. 2, +ALT/−ALL scenario—Fertility). In the case of the MC model, the decrease in  is due to a higher dependence of children's survival on maternal care and our results show a more complex pattern: a decrease of fertility at the very beginning and at the end of reproductive life, and an increase of fertility at the peak of reproductive life. Fertility appears here to be narrowed at the peak of the reproductive life. The increase of altriciality modeled by the +ALT/−ALL scenario can therefore explain complex fertility schedules that cannot be explained by the reference model.
is due to a higher dependence of children's survival on maternal care and our results show a more complex pattern: a decrease of fertility at the very beginning and at the end of reproductive life, and an increase of fertility at the peak of reproductive life. Fertility appears here to be narrowed at the peak of the reproductive life. The increase of altriciality modeled by the +ALT/−ALL scenario can therefore explain complex fertility schedules that cannot be explained by the reference model.
Second, the +EFF scenario increased the mean child survival until maturity  . According to the reference model, this leads to (1) an increase of adult survival at the very beginning of the reproductive life (before age 20 in our example), (2) a decrease of adult survival after this age, and (3) an absence of effect after menopause (see Fig. 3, +EFF scenario—survival). In the case of the MC model, the +EFF scenario implies an increase in a child's survival until maturity conditional on the mother's survival. This leads to an increase of adult survival at all ages during reproductive life and even after menopause. In the case of the +ALT/−ALL scenario, both the reference model and the MC model increase adult survival after age 20. In the MC model however, the magnitudes of the force of selection are up to 10 times higher.
. According to the reference model, this leads to (1) an increase of adult survival at the very beginning of the reproductive life (before age 20 in our example), (2) a decrease of adult survival after this age, and (3) an absence of effect after menopause (see Fig. 3, +EFF scenario—survival). In the case of the MC model, the +EFF scenario implies an increase in a child's survival until maturity conditional on the mother's survival. This leads to an increase of adult survival at all ages during reproductive life and even after menopause. In the case of the +ALT/−ALL scenario, both the reference model and the MC model increase adult survival after age 20. In the MC model however, the magnitudes of the force of selection are up to 10 times higher.
Classical life-history theory also predicts that an increase in early fertility to the detriment of late fertility should be associated with a decrease of late adult survival (e.g., Hamilton 1966). It is true for elasticity analyses (see Fig. 3, +EFF scenario—Fertility and Survival for the reference model) but also for resource allocation theories that generally assume a trade-off between survival and reproduction (e.g., Caswell 1982). By contrast, our results show that an increase of child survival conditional on maternal care can lead to increased fertility at young ages (early reproduction to the detriment of late reproduction) and increased adult survival. More generally, we provide evidence that elasticity analyses using the MC model allow association of life-history features that cannot be elucidated using classical theory (decrease of late fertility and increase of late survival; concomitantly decreased early and late fertility).
HUMAN EVOLUTION
Our results allow us to establish two main predictions concerning the shaping of humans' survival and fertility. Although these evolutionary scenarios are not mutually exclusive and might have both occurred at different periods of human history, we address them individually.
Scenario +ALT/−ALL leads to an increase in the force of selection on survival at all ages considered and to a narrowing of fertility at the peak of the reproductive period. Given this finding, the following prediction can be made concerning an increase in altriciality: any phenomenon increasing children's altriciality and therefore increasing their dependence on maternal care for survival would lead to an extension of women's life expectancy (even during the post reproductive period); a later age at sexual maturity; an increase in fertility at the peak of the reproductive period; and a decrease in fertility toward the end of the reproductive period. These four life-history features are all fundamental characteristics of human life history (Mace 2000). In comparison with other primates, human reproduction indeed exhibits a very long juvenile period, a very high fertility characterized by very short birth spacing, and a reproductive cessation in midlife. This high reproduction is moreover associated with higher adult survival. All these life-history traits can result therefore from an increase in the dependence of children's survival on maternal care as modeled in the +ALT/−ALL scenario. As evidence shows that humans are particularly altricial and that the mother is the proximal caretaker, it is likely that the increase in altriciality at the very beginning of the Hominina's history played a crucial part in shaping the human life history.
However, scenario +ALT/−ALL acts in an opposite way to an increase of care by secondary caregivers in childcare and education. Such an increase in allocare during human evolution could have counterbalanced the effect of the increase in altriciality. However, our model links child survival only to that of the mother. When the mother dies, the child's residual survival probability wy becomes invariant. It would be revealing to study what happens if child survival is also conditional on survival of secondary caregivers according to their gender and their kinship coefficients. It is likely that such models would show that the force of selection would shape life histories of secondary caretakers as they shape those of the mother. Finally, several authors argue that the higher fertility observed in humans is precisely due to the allocare provided by related females (like grandmothers, see Hawkes 2003), which reduces the cost of reproduction for the mother and allows shorter interbirth intervals. We are here confronted with a contradiction, as an increase in allocare should (1) increase fertility by decreasing the cost of reproduction, but (2) at the same time tend to decrease the force of selection on fertility (as we provide evidence that a decrease of allocare increases the force of selection on fertility). To solve this contradiction one should therefore appraise the respective strength of these two selective processes on fertility. Concerning survival, an increase of allocare tends to decrease the force of selection on maternal survival. However, if grandmothers are the main allocare providers, then maternal survival and the availability of allocare will actually be directly linked, as the potential for allocare will become far more likely as maternal survival increases. Further study should address this specific question.
Scenario +EFF increased the selection pressures on survival at all ages considered. Moreover, it increased the selection pressures on fertility before age 25 and decreased them after this age. We can therefore make the following predictions: if during human evolution an increase in maternal care led to an increase in child survival, then this increase in maternal care led in the same way to an extension of women's life expectancy, an increase in fertility at the beginning of reproductive life and to a decrease in fertility when more advanced in years. This prediction would be true if a reduction in child mortality has occurred during the course of human evolution. It is at the moment impossible to determine a phylogenetic trend in human child mortality compared to other primate species, as child survival is mainly body-size related between species and gender-related within species (Allman et al. 1998). However, it is likely that the increasing size in the Hominina lineage and the consequent need for breast-feeding and nurturing has led to an increasing relationship between maternal care and child survival (McHenry and Coffing 2000). It is also likely that technical advances in childcare practices or changes in maternal behaviors that increased childhood survival have occurred in the distant past as it occurs in contemporary populations.
Conclusion
We present a method integrating the relationship between a mother's survival and that of her children into life-history analysis. We show that this relationship may be determinant in explaining the evolution of survival and fertility for species in which the death of the mother compromises her offspring's chances to survive and in which the mother has a high risk of death before her offspring reach maturity. This relationship could explain complex life-history patterns not understandable through usual perturbation analyses without adding trade-offs between life-history traits. For example, our model can explain an increase of adult survival and fertility at the peak of the reproductive life as well as a decrease of early and late fertility. Our model may also explain differences in survival between gender not only in humans but also among primates species in which the main caregiver lives longer (Allman et al. 1998). We also show how the increase of altriciality in early humans is likely to have shaped the main human life-history features (long juvenile period, high fertility at the peak of the reproductive life, decrease of late fertility, and high adult survival). Finally, our model would also be interesting for studying life histories of others mammal species. For example, standard elasticity analyses predict that an increase of offspring's survival independent of the mothers' survival should lead to an earlier fertility and a decrease of adult survival. Standard elasticity analyses therefore predict the opposite of what is observed along the slow-fast continuum as species with higher juvenile survival, such as primates and humans, are at the slow end of the continuum and have high adult survival and low fertility. Our model, on the other hand, might explain such patterns and further study could test this prediction.
Associate Editor: D. Promislow
ACKNOWLEDGMENTS
We are grateful to A. Gagnon, J. Metcalf, J. Vaupel, H. Caswell, S. Tuljapurkar, D. Promislow, J. Holland Jones, and an anonymous reviewer for enlightening discussion and for comments on earlier drafts of this article. We acknowledge funding from the Fondation de France, the Association pour la Recherche sur le Cancer (ARC) and the Max Planck Institute for Demographic Research.
Appendix
SELECTION ON SURVIVAL
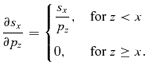
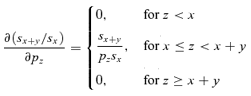
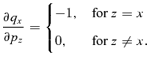
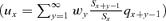 with respect to pz. The variable y can vary from 1 to ∞ such as, for some given x and z, x+y− 1 < z, x+y− 1 =z, or x+y− 1 > z. Then for y < z−x+ 1 (so y≤z−x), y=z−x+ 1 or y > z−x+ 1 (so y≥z−x+ 2). Because pz is a factor of sx+y−1/sx for x≤z < x+y− 1 and of qx+y−1 for z=x+y− 1, the derivative of (sx+y−1/sx)qx+y−1 is therefore non-null for x≤z≤x+y− 1. By differentiating bz,x for y=z−x+ 1 and y≥z−x+ 2 we obtain
with respect to pz. The variable y can vary from 1 to ∞ such as, for some given x and z, x+y− 1 < z, x+y− 1 =z, or x+y− 1 > z. Then for y < z−x+ 1 (so y≤z−x), y=z−x+ 1 or y > z−x+ 1 (so y≥z−x+ 2). Because pz is a factor of sx+y−1/sx for x≤z < x+y− 1 and of qx+y−1 for z=x+y− 1, the derivative of (sx+y−1/sx)qx+y−1 is therefore non-null for x≤z≤x+y− 1. By differentiating bz,x for y=z−x+ 1 and y≥z−x+ 2 we obtain
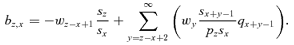
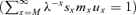 . As discussed above, pz is a factor of bz,x only if x≤z≤x+y (the survival probability until maturity of a child born to a mother at age x is influenced by a change in her mother's survival only if this change occurs after the child's birth, so after age x) and we obtain
. As discussed above, pz is a factor of bz,x only if x≤z≤x+y (the survival probability until maturity of a child born to a mother at age x is influenced by a change in her mother's survival only if this change occurs after the child's birth, so after age x) and we obtain
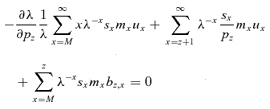 ((A1))
((A1))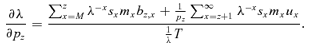 ((A2))
((A2))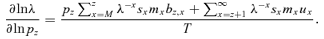 ((A3))
((A3))



