Overcoming Confirmation Bias in Causal Attribution: A Case Study of Antibiotic Resistance Risks
Abstract
When they do not use formal quantitative risk assessment methods, many scientists (like other people) make mistakes and exhibit biases in reasoning about causation, if-then relations, and evidence. Decision-related conclusions or causal explanations are reached prematurely based on narrative plausibility rather than adequate factual evidence. Then, confirming evidence is sought and emphasized, but disconfirming evidence is ignored or discounted. This tendency has serious implications for health-related public policy discussions and decisions. We provide examples occurring in antimicrobial health risk assessments, including a case study of a recently reported positive relation between virginiamycin (VM) use in poultry and risk of resistance to VM-like (streptogramin) antibiotics in humans. This finding has been used to argue that poultry consumption causes increased resistance risks, that serious health impacts may result, and therefore use of VM in poultry should be restricted. However, the original study compared healthy vegetarians to hospitalized poultry consumers. Our examination of the same data using conditional independence tests for potential causality reveals that poultry consumption acted as a surrogate for hospitalization in this study. After accounting for current hospitalization status, no evidence remains supporting a causal relationship between poultry consumption and increased streptogramin resistance. This example emphasizes both the importance and the practical possibility of analyzing and presenting quantitative risk information using data analysis techniques (such as Bayesian model averaging (BMA) and conditional independence tests) that are as free as possible from potential selection, confirmation, and modeling biases.
1. INTRODUCTION: CONFIRMATION BIAS IN CAUSAL INFERENCES
Quantitative risk assessment (QRA) of animal antibiotic use is largely about identifying and quantifying probabilistic causal relations between exposures and adverse consequences. Risk managers typically want to know by how much reducing preventable exposures would reduce adverse human health consequences such as numbers of deaths or illnesses per year. QRA offers methods to help answer such questions.
Although causal relations are crucial to effective risk management, experimental psychology and neuropsychological studies demonstrate convincingly that, without using formal quantitative methods such as QRA, most people (including scientists) are prone to flawed and biased intuitive reasoning about causality and relevance of evidence.(1) A common pattern, sometimes called “premature closure,” is that individuals and groups tend to adopt prematurely causal hypotheses and conclusions to explain observations, based on inadequate information.(2) They then tend to seek confirming evidence and to ignore or underweight disconfirming evidence for the favored causal hypothesis—the phenomenon of confirmation bias.(3,4) Experimental psychologists have also found that real-world reasoning about conditionals (if-then relations) and causality often differs from the prescriptions of formal logical analysis and modeling.(5–7)
If risk analysts fall into such “decision traps,” they may end up publishing conclusions and advocating risk management actions that are not objectively justified and that then fail to achieve their stated objectives for reducing risks.
1.1. Example: The Wason Selection Task
A famous experiment investigates how people reason about conditionals and evidence, by showing subjects four cards with letters and numbers on them, such as: A, 4, 7, and D.(8) Subjects are told that each card has a letter on one side and a number on the other. They are asked to identify the smallest subset of cards that must be turned over (revealing what is printed on their other sides) in order to decide whether the following hypothesis is correct:
-
H1: Any card that has a vowel on one side has an even number on its other side.
After some thought, most subjects correctly identify that it is necessary to turn over card A, in order to confirm whether the prediction from Hypothesis H1 is true (i.e., whether this card has an even number on its other side). But relatively few subjects spontaneously recognize that it is also necessary to turn over card 7, to verify that Hypothesis H1 is not disconfirmed by the appearance of a vowel on its other side. (Many subjects also fail to recognize that turning over cards 4 or D would be irrelevant, because nothing that appears on their reverse sides can disconfirm Hypothesis H1.) Thus, even in this logically simple situation, it is difficult for most people to pinpoint the evidence needed to decide whether a simple stated hypothesis is true.
The tendencies to seek confirming evidence, neglect disconfirming evidence, and overinterpret confirming evidence as support for a prior causal hypothesis are not confined to contrived abstract psychological experiments such as the Wason selection task. They also occur in important real-world decisions with significant financial or health consequences.(9)
1.2. Example: Attributing Antibiotic Resistance to Specific Causes
A recently published study(10) noted that “[t]he Australian government has prohibited the use of fluoroquinolones in food-producing animals” and “[a]mong locally acquired infections, only 2% of isolates (range, 0%–8% in different states) were resistant to ciprofloxacin [a fluoroquinolone].” This is lower than the estimated corresponding average resistance rates for locally acquired infections in countries that have used fluoroquinolones for animal health (e.g., 6.4% in the United States(11)). The authors interpret this difference causally: “The very low level of ciprofloxacin resistance in C. jejuni isolates likely reflects the success of Australia's policy of restricting use of fluoroquinolones in food-producing animals.”
The presented evidence is certainly consistent with this causal hypothesis, much as turning over card A and finding an even number, or turning over card 4 and finding a vowel, would be consistent with Hypothesis H1 in the Wason selection task. But more than such consistency is needed to support a causal hypothesis. For example, the same evidence may be consistent with different causal hypotheses. To support a unique causal interpretation of the data, other equally plausible or more plausible competing explanations should be eliminated.(12) Formal mathematical models of causality(13) point out that if one variable (such as fluoroquinolone (FQ) use in animals) truly causes another (such as FQ resistance in human patients), then the association between them should not be explained away by any third variable (so that conditioning on the third variable eliminates the association). Yet, this particular study did not consider that “Australia prescribes proportionally less fluoroquinolones than other developed countries due to prescribing restrictions.”(14) It did not address whether this low human use, rather than (or in addition to) low animal use, might explain the lower rate of FQ resistance in human patients in Australia. The suggested causal interpretation has therefore not been established by the data presented, even though it is consistent with them.
More generally, current widespread suspicion and concern that use of animal antibiotics increases the frequency of antibiotic-resistant illnesses in humans provides a point of departure for many published interpretations of data and discussions of risk associated with particular “bug-drug” pairs. Yet, authors seem not to be always mindful of the potential for confirmation bias and for invalid causal inferences in such settings, nor of the importance of investigating potential disconfirming evidence and plausible alternative explanations before drawing causal conclusions based on data that are consistent with alternative causal hypotheses.(15,16)
This article considers how current statistical models and methods can help to avoid potential confirmation biases (without introducing opposite preconceptions and biases) in interpreting animal antibiotic use and human health data causally. As a case study, we focus on a recent report by Kieke et al.(17) that announced a positive relation between use of virginiamycin (VM) (a member of the streptogramin class of antimicrobials) in poultry and resistance determinants or readily “inducible resistance” (discussed below) to VM-like (streptogramin) antibiotics in humans. The study concluded that “the results of the present investigation suggest that virginiamycin use in poultry contributes to human carriage of Enterococcus faecium that contains streptogramin resistance genes with readily inducible resistance.” This appears to be a causal conclusion: that virginiamycin use in animals contributes to carriage of E. faecium with antibiotic resistance potential in humans. Based on this causal interpretation, an accompanying editorial(18) called for reduced use of virginiamycin use in food animals.
The following sections examine the evidence on which this suggested causal interpretation is based. They show that the data that the authors analyzed do not justify this causal interpretation over others. Indeed, we shall see that conditional independence relations in the data(13,15,16) suggest a different causal explanation: the “readily inducible resistance” defined and reported by Kieke et al. results from selection pressures associated with the hospital environment, rather than with food animals.
The existence of alternative plausible causal interpretations for the same data raises the central challenge addressed in this article: To what extent can current statistical methods objectively determine which of several competing causal hypotheses is best supported by observed data, and how (if at all) can such data be used to identify and eliminate incorrect or unsupported explanations? QRA methods typically seek to constrain as tightly as possible the set of causal interpretations that are consistent with or implied by available data, in part by using the data to identify and eliminate incorrect explanations where possible. Yet, any claim to have done so using objective data analysis invites skepticism from those who favor the discarded causal theories. This gives particular value to methods of analysis that can produce valid conclusions using generally accepted statistical methods that can be independently replicated and verified by all parties.
The following sections seek to identify and illustrate such methods for VM and human streptogramin resistance. We first make some qualitative observations about the study design, and then turn to quantitative risk modeling. Although we focus on the specific example of virginiamycin and streptogramin resistance, we believe that data analysis and modeling methods that avoid confirmation bias in causal attribution for antibiotic resistance are crucial for sound antimicrobial risk assessment(11) and deserve wider development and application.
2. METHODS FOR AVOIDING CONFIRMATION BIAS AND TESTING ALTERNATIVE CAUSAL HYPOTHESES
2.1. Observations on Study Design: Hospitalization Provides an Alternative Possible Explanation for the Observed Resistance Data
E. faecium is a commensal bacterium commonly found in human, bird, and animal intestines. It is not normally harmful, and has been used as a probiotic dietary supplement for both humans and poultry. However, E. faecium can threaten seriously ill human patients, typically in intensive care units (ICU) of hospitals, via opportunistic infections. ICU patients with immune systems weakened by chemotherapy, organ transplants, AIDS, leukemia, or other conditions, or with surgical wounds or invasive medical devices, are at greatest risk of opportunistic E. faecium infections. E. faecium bacteria have high levels of intrinsic and acquired resistance to some antibiotics, such as penicillin and vancomycin. Vancomycin-resistant E. faecium (VREF) have become prevalent in hospitals on several continents, and other drugs such as linezolid or the streptogramin combination Synercid® (quinupriston-dalfopristin) may be used to treat these VREF cases.(37) This development has focused attention on the ongoing use of the streptogramin virginiamycin in food-producing animals.
Kieke et al.(17) compared newly admitted (36 hours or less) hospitalized patients who ate poultry (and other meats) to healthy vegetarians in four communities. They concluded that human exposure to poultry was associated with presence of quinupristin-dalfopristin (QD) resistance genes and experimentally inducible QD resistance in human fecal E. faecium. No actually QD-resistant E. faecium were found. QD is a streptogramin combination used in the human drug Synercid®, and resistance to the animal-use streptogramin drug virginiamycin confers cross-resistance to Synercid® in E. faecium.(21)“Inducible QD resistance” is not (yet) a standard outcome measure and has no widely accepted definition (although it is well recognized that some resistance genes in some species of bacteria must be switched on by external stimuli, i.e., induced in order to be expressed). Inducible QD resistance has not been shown to be a valid surrogate for clinically relevant QD resistance. The investigators generously provided us with their data,(19) enabling us to attempt to replicate and validate their results.
The study design, comparing hospitalized exposed cases to healthy inexposed controls, clearly creates a potential for uncontrolled confounding and noncausal statistical associations. As noted by Kieke et al.,(17)“confounding may have occurred, and other factors associated with vegetarian status may have contributed to the observed associations.” Qualitatively, it seems plausible that frequently hospitalized patients may be exposed to nosocomial E. faecium and other hospital-associated conditions that healthy patients, including the vegetarians in this study, are not exposed to.
Kieke et al.(17) reported that, among participants without recent antibiotic use, “[c]arriage of E. faecium with vatE[a streptogramin resistance gene] was significantly associated with both touching raw poultry and higher poultry consumption in the combined hospital patient and vegetarian group.” But this could simply reflect that hospitalized patients (many of whom had more than five physician visits in the previous year) have higher proportions of bacteria with resistance determinants than healthy subjects (i.e., vegetarians, in this study—who, of course, had little or no exposure to poultry). Interpreting the reported association as reflecting exposure to poultry rather than exposure to the hospital environment, or as a reason to “raise additional concerns regarding the continued use of virginiamycin in food animals”(17) is unjustified if hospitalization, rather than transfer from poultry, explains the observed association between poultry exposure and carriage of E. faecium with vatE. Thus, a challenge for QRA is to determine which causal hypothesis is most consistent with the data.
3. OBSERVATIONS ON CHOICE OF ENDPOINTS: POULTRY EXPOSURE IS ASSOCIATED WITH REDUCED RESISTANCE, BY SOME MEASURES
As might be expected, QD resistance prevalence is significantly higher for isolates from conventional retail poultry (56% prevalence) compared to antibiotic-free retail poultry (13%). Fortunately, resistance in poultry isolates was not observed to transfer to resistance in human isolates: “None of the human E. faecium isolates had constitutive resistance to quinupristin-dalfopristin.”(17) Antibiotic use on farms was also associated with significantly reduced E. faecium prevalence in retail poultry (48% for conventional retail poultry samples compared to 88% for antibiotic-free poultry samples).
A striking feature of the data(17) is that E. faecium was isolated from 65% of vegetarians (65 out of 100) but from less than 19% of patients (the group that consumed and handled poultry) (105 out of 567). Moreover, the fraction of “susceptible” isolates is significantly higher for hospital patients than for vegetarians (24% vs. 12%). Thus, a randomly selected member of the poultry-exposed group (i.e., hospital patients) has probability (105/567) × (1 − 24%) = 14% of having reduced (“intermediate”) QD susceptibility of E. faecium, compared to a much higher probability of (65/100) × (1 − 12%) = 57% for a randomly selected member of the nonpoultry-exposed group (i.e., vegetarians). Such calculations might be interpreted as suggesting that chicken eaters have less risk than vegetarians of carrying intermediate QD-susceptibility E. faecium. These data refer to constitutive resistance and susceptibility (i.e., exhibited with no preexposure to virginiamycin). Also, most, but not quite all, hospital patients were self-reported consumers of chicken and other meats.
These calculations show how the same data set might be interpreted to support different conclusions about the human health effects of exposure to poultry, depending on the modeler's choice of outcome measures and comparisons to perform. Clearly, more objective methods of causal analysis and interpretation are desirable.
4. QUANTITATIVE STATISTICAL METHODS AND ANALYSIS
This section considers statistical models that can potentially help to resolve ambiguities and select among rival causal interpretations using relatively objective methods (especially, conditional independence tests.)
Table I provides a checklist of potential threats to valid causal interpretations of observed statistical association (left column) and some statistical methods developed to help avoid or eliminate these threats (right column). A “threat” to valid causal interpretation of an association is a potential noncausal explanation for it. Many of the statistical techniques in the right column have extensive technical literatures that have been previously surveyed,(16) as well as implementation algorithms that are now widely available and included in standard statistical packages. In this article, therefore, we only briefly describe the main methods and software packages used to address selected threats relevant for this case study.
| Potential Problem (Possible Sources of Spurious (Noncausal) Associations in Statistical Risk Assessments) | Potential Solutions* |
|---|---|
| Modeling Biases | |
| Variable selection bias (includes selection of covariates in model) | Bootstrap variable selection, Bayesian model averaging (BMA),(22,23) cross-validation for variable selection. |
| Omitted explanatory variables (including omitted confounders and/or risk factors) | Include potential confounders in an explicit Bayesian network model;(13,15) test for unobserved latent variables. |
| Variable coding bias (i.e., how variables are coded may affect apparent risks) | Use automated variable-coding methods (e.g., classification trees(31)). Don't code/discretize continuous variables.(28,29) |
| Aggregation bias/Simpson's paradox | Test hypothesized relations at multiple levels of aggregation. Include potential confounders in Bayesian network model. |
| Multiple testing/multiple comparisons bias | Use current (step-down) procedures to adjust p-values. |
| Choice of exposure and dose metrics; choice of response effect definitions and measures | Use multiple exposure indicators (e.g., concentration and time). (Don't combine.) Define responses as survival functions and/or transition rates among observed health states. |
| “Model uncertainty”: model form selection bias and uncertainty about the correct model | Use flexible nonparametric models (smoothers, wavelets).BMA.(22,23)Report model diagnostics and sensitivity analyses. |
| Missing data values can bias results | Use data augmentation, EM algorithm, multiple imputation, Markov Chain Monte Carlo (MCMC) algorithms.(32–34) |
| Measurement and misclassification errors in explanatory variables | Bayesian measurement error models, data augmentation, EM algorithm, and other missing-data techniques.(16) |
| Unmodeled heterogeneity in individual response probabilities/parameters | Latent variable and finite mixture distribution models;(16) jump MCMC algorithms; frailty models of variability. |
| Biases in interpreting and reporting results | Report results (e.g., posterior PDFs) conditioned on data, models, assumptions, and methods. Show sensitivities. |
| Sample Selection Biases | |
| Sample selection (sample does not represent population) | Randomly sample all cohort members if possible. |
| Data set selection bias (i.e., selection of a subset of studies may affect results) | Show meta-analysis of sensitivity of conclusions to studies.Use Bayesian network models to integrate diverse data sets. |
| Health status confounding, hospital admission bias (and referral bias) | If possible, use prospective cohort design. Use population-based cases and controls. |
| Selective attrition/survival (e.g., if exposure affects attrition rates) | Use a well-specified cohort. “Include non-surviving subjects in the study through proxy interviews.” Compare counterfactual survival curves. |
| Differential follow-up loss | |
| Detection/surveillance bias | Match cases to controls (or exposed to unexposed subjects) based on cause of admission. |
| Membership bias (e.g., lifestyle bias, socioeconomic history) | In cohort studies, use multiple comparison cohorts. Hard to control in case-control studies. |
| Self-selection bias; response/volunteer bias | Achieve response rate of at least 80% by repeated efforts. Compare respondents with sample of nonrespondents. |
| Information Collection Biases | |
| Intrainterviewer bias | Blind interviewers to study hypotheses, subject classifications. |
| Interinterviewer bias | Use same interviewer for study and comparison groups. |
| Questionnaire bias | Mask study goals with dummy questions; avoid leading questions/leading response options. |
| Diagnostic suspicion biasExposure suspicion bias | Hard to prevent in case-control studies. In cohort studies, make diagnosis and exposure assessments blind to each other. |
- *Source: Reference 16 provides discussion and references for the methods listed here.
Applying this checklist to the case study(17) identifies the following potential concerns and statistical methods to address them.
4.1. Sample Self-Selection Bias
Fewer than 40% of invited hospitalized subjects agreed to participate in the study. Study participants might differ systematically from those who did not agree to participate. We could not address this potential limitation, as the data had already been collected.
4.2. Bayesian Model Averaging (BMA) Avoids Variable Selection Bias
The conclusions in the case study(17) are contingent on the validity of a regression model that selects a specific subset of predictors (including EATPOULTRY; see Table II of the study), while excluding others (such as concurrent hospitalization status). It is now well known that, in such settings, model selection bias can exaggerate estimated effects and significance levels by ignoring model uncertainty about which variables to include as predictors, implicitly assuming that the selected model has the correct predictors.(22) We examined this issue using BMA software(23) for the R statistical software environment(24) to account for uncertainty about variable selection.
| Variable | Meaning | Missing Data Count |
|---|---|---|
| TouchBeef | Subject touched beef | 3 |
| TouchPork | Subject touched pork | 4 |
| BEEFTOT_MO | Times ate beef in month prior | 4 |
| PORKTOT_MO | Times ate pork in month prior | 2 |
| EATPOULTRY | Subject self-reported eating poultry | 3 |
| POULTRYTOT_MO | Times ate poultry in month prior | 6 |
| COOKOWN_MO | Times cooked own meal in month prior | 3 |
| TOUCHPOULTRY | Subject self-reported touching poultry | 4 |
| GRADE2 | Highest grade or year of school | 1 |
| HOSP_GT1 | Had > 1 hospitalization in prior 12 months | 1 |
| ICU | Was admitted to ICU in past 12 months | 1 |
| LIVEBIRDEXP | Exposure to live turkey or chickens | 2 |
| Total | 34 |
The BMA approach assigns a posterior probability to each model in a set of plausible models (subsets of candidate variables), each with coefficients determined through standard regression procedures. It computes the posterior mean model coefficients for each variable and their standard errors. We used this information to compute posterior odds ratios and confidence intervals for each variable that account for model uncertainty. A key output of the algorithm, probne0 (probability not equal to zero), gives the probability that each variable appears (i.e., has a coefficient significantly different from zero) in a randomly selected plausible model. We also computed conditional odds ratios, that is, odds ratios conditioned on the variable appearing in a model.
4.3. Using Continuous Variables Avoids Dichotimization/Variable Coding Bias for Exposure
Kieke et al.(17) dichotomized a continuous variable (POULTRYTOT_MO), describing the number of times per month that poultry is consumed, to obtain a binary indicator of frequency of poultry consumption. Cases with poultry consumption above the median level were assigned a value of “high,” while cases below the median level were assigned a value of “low.” Vegetarians were a separate category.
Such dichotomization of a continuous predictor can bias effects estimates.(25–28) At a minimum, alternative cutpoints should be used and the results presented.(27) Royston et al.(29) state that “dichotomization of continuous data is unnecessary for statistical analysis, and in particular, should not be applied to explanatory variables in regression models.” We therefore reanalyzed the data keeping POULTYTOT_MO as a continuous variable.
4.4. Using Multiple Response Variable Definitions Avoids Results that Depend on Any Single Response Definition
The “median relative percentage of growth in the exposed group divided by that in the unexposed group” for cultured E. faecium under the experimental conditions of the case study, interpreted by Kieke et al.(17) as a “measure of association for the inducible resistance models,” has no known clinical relevance. We therefore considered several possible definitions of the response variable (see the Appendix) to determine whether the reported associations are robust to variations in definitions.
4.5. Nonparametric Methods and Multiple Alternative Regression Models Avoid Regression Model Form Selection/Misspecification Bias
The case study(17) did not provide regression diagnostics or model validation results to indicate whether the reported associations are artifacts of regression model misspecification. We therefore reanalyzed the data using nonparametric (classification tree) methods, as well as some alternative parametric (regression) models, as follows.
4.5.1. Logistic Regression Analysis of VatE Resistance Gene Data (VATE Variable)
We modified the bic.glm (BMA for generalized linear modeling) function in R to use a specialized logistic regression algorithm, logistf(30) that addresses bias and separation. Separation occurs in fitting a logistic regression model if the likelihood converges to a finite value while at least one parameter estimate diverges to (plus or minus) infinity. This can occur in small or sparse samples with highly predictive covariates. Without logistf, we found that variables such as EATPOULTRY did exhibit separation. EATPOULTRY has a value of 1 (or Yes, coded as Y in other analyses) for all but one patient in the subset of 45 E. faecium-colonized hospital patients without antibiotic use during the preceding month; for that patient, VATE= 0 (N or No). Thus, without correction, an inordinately large model weight is placed on EATPOULTRY as a predictor that separates that one VATE patient from others, but it also has an extremely large standard error.
4.5.2. Linear Regression Analysis of Induced Resistance Values (REP_V_S_P)
With induced resistance (REP_V_S_P) as the response variable, we used BMA for multivariate linear regression to develop posterior mean regression coefficients for different variables, computed by the BMA bicreg R function for linear regression analysis, as inputs to a linear predictive model for the response REP_V_S_P. From these, we computed “adjusted ratios,” similar to those in Table IV of Kieke et al.,(17) using the methodology in the Appendix. We also provided the univariate “unadjusted ratios” (we extended the ratio concept to continuous nonindicator variables by using the conditions [>0; = 0] rather than [Yes; No]).
| Variable Name | Probne 0 = Probability (%) That Variable Is a Predictor | Posterior Mean | Odds Ratio | Lower 95% Confidence Limit | Upper 95% Confidence Limit | Conditional Posterior Mean |
|---|---|---|---|---|---|---|
| Intercept | 100 | −5.4665 | NA | NA | NA | −5.4665 |
| HOSPITALIZED | 48.8 | 1.8606 | 6.43 | 2.33 | 68.93 | 3.8157 |
| AGE | 100 | 0.0376 | 1.04 | 1.01 | 1.07 | 0.0376 |
| ANYAB_BY29 | 47.5 | 0.7000 | 2.01 | 1.37 | 3.02 | 1.4743 |
| GRADE22 | 39.7 | 0.4442 | 1.56 | 1.12 | 2.19 | 1.1194 |
4.5.3. Classification Tree Analysis of VATE and REP_V_S_P
We used the nonparametric classification tree algorithm, rpart (recursive partitioning and regression trees), in the R statistical software to recursively “split” response variables (VATE or REP_V_S_P) on values of explanatory variables (or on ranges of values, for continuous and ordered-categorical variables) to “best” separate the conditional distributions of the response variables obtained by conditioning on the splits (using built-in criteria including mutual information between explanatory and response variables, and F tests). Each leaf of a classification tree has a set of corresponding cases that match the description leading to that tip of the tree. These cases have an empirical joint frequency distribution of values for all variables. Classification trees are similar to regression models in that they have a single response variable and multiple explanatory variables. However, they can complement regression models by discovering nonlinear patterns, high-order interactions, and conditional independence relations in multivariate data.(16,35) The rpart algorithm closely follows the classification approach of Breiman et al.(31) To check our results with a different implementation, we also used the commercial KnowledgeSeeker™ commercial classification tree software.
4.6. Bayesian Multiple Imputation Overcomes Biases from Missing Data
Table II summarizes missing data values in the case study data set (the “Marshfield” data set(17,19)). A total of 14 records out of 170 (one record per subject) had at least one missing value, leaving 156 complete records. The set of 110 subjects who reported no prior use of antibiotics had six records with at least one missing value, leaving 104 complete records. The subset of 45 hospitalized patients with no prior use of antibiotics had five records with at least one missing value, leaving 40 complete records.
Many standard statistics packages have a default that simply deletes cases with missing data values. But this can introduce bias and reduce statistical power.(32,33) Therefore, we used the aregImpute function of the Hmisc software package(34) for the R open-source statistical language and environment. This function performs multiple imputation (using additive regression bootstrapping and predictive mean matching) to approximate drawing predicted values from a full Bayesian predictive distribution. We used the procedure on the full set of 170 records, and also for the two subsets of 110 with no reported previous antibiotic use and 45 hospitalized patients.(17) (The SAS 9.1 software cited by Kieke et al.(17) also includes multiple imputation functions, MIANALYZE and MI, but the article does not indicate whether they were used.)
4.7. Using All Data Avoids Multiple Testing/Multiple Comparisons/Subset Selection Bias
Kieke et al.(17) analyzed a subset of subjects—those with no recent recorded antibiotic use. While this is common practice and common sense (since recent antibiotic consumption could select for antibiotic-resistant E. faecium) it does raise a statistical issue. The selection was made only after looking at the data and determining that, unlike other patients, “hospital patients without recent antibiotic use had an increased risk of carrying E. faecium isolates with vatE if they had touched raw poultry… On the basis of these findings, results are reported for participants without recent antibiotic use.” Deciding to report results on a subset of subjects because it has been found to support one's hypothesis clearly invalidates the use and interpretation of standard p-values and significance tests. It risks a strong form of confirmation bias (had the desired association held only in patients who had reported recent antibiotic use, the authors could have selected that subset instead). To address this issue, we reanalyzed the data considering all subjects, as well as the different subsets.
In summary, the statistical methods outlined here attempt to prevent confirmation bias from entering the analysis via any of the following routes.
- •
Selecting variables to support specific hypotheses, while excluding other variables (e.g., by including chicken-related variables but excluding hospital-related ones, when the two are correlated).
- •
Selecting or constructing a specific response definition (e.g., for “inducible resistance”) to support a preconceived hypothesis, while ignoring other response definitions (e.g., fraction of susceptible isolates) that do not support it.
- •
Selecting a subset of subjects to analyze (e.g., patients with no self-reported recent antibiotic use) only after determining that it will support a preexisting hypothesis (e.g., that poultry exposure is associated with a QD resistance gene).
- •
Selecting a single parametric model form (e.g., logistic regression with some continuous variables such as POULTRYTOT_MO dichotomized), when different forms or nonparametric methods might give different conclusions.
We also attempted to avoid other potential biases (not necessarily resulting from choices made by the modeler, and hence not as subject to confirmation bias), by using multiple imputation for missing data and keeping POULTRYTOT_MO as a continuous variable.
4.8. Conditional Independence Tests Can Objectively Choose Among Rival Causal Models
The preceding measures may help to limit the potential influence of confirmation bias, but they cannot necessarily discriminate among rival causal models or hypotheses for explaining any associations that still persist in the absence of confirmation bias. Fortunately, as illustrated in the next section, classification tree analysis can also be used to test for conditional independence relations among variables, and these relations, in turn, can be used to test and discriminate among rival causal hypotheses.(13,15)
According to both Model 1 and Model 2, any pair of these variables may be correlated. However, according to Model 1 (which may be loosely interpreted as implying that “Poultry exposure causes resistance”), but not according to Model 2 (loosely interpreted as “Hospitalization causes resistance”), Resistance should be conditionally independent of Hospitalized, given the value of Poultry exposure. Conversely, in Model 2, but not in Model 1, Resistance should be conditionally independent of Poultry exposure, given the value of Hospitalized. Thus, these models have quite different implications for conditional independence relations, and hence statistical methods for testing conditional independence relations can reveal which model (if either) is consistent with the data.(15)
Although this example has considered using conditional independence tests to choose between two prespecified causal models, classification tree analysis can also be used to determine conditional independence relations in the absence of any prespecified hypothesis. Assuming that the data set is large and diverse enough to correctly reveal these relations, it is then possible to mathematically identify the possible causal graph models that are consistent with these empirically determined relations.(13,15,35) This provides an approach to generating empirically driven causal theories, without any need to formulate an a priori hypothesis that can then be subject to confirmation bias.
5. RESULTS OF QUANTITATIVE RISK ASSESSMENT MODELING
5.1. Results for VatE Resistance Determinant
Table III shows the main results of the BMA logistic regression analysis for presence of the vatE resistance determinant (variable VATE), for the full set of 170 subjects with E. faecium isolates. The predictors that appear most often among the different plausible models are: AGE, ANYAB_BY29 (an indicator of recent antibiotic use), and BEEFTOT_MO (number of times beef eaten per month). Less frequent are EATPOULTRY (self-reported poultry consumption; this verifies the originally reported association(17)), COOKOWN_MO (number of times cooked own meal per month, which has a mild protective effect), and GRADE22 (high school graduates). The most significant odds ratio is for prior use of antibiotics (ANYAB_BY29). Of the others, all but COOKOWN_MO have significant odds ratios (confidence intervals do not include 1.0), but only slightly so. No individual hospital has a significant effect. (Hospital1–Hospital4 are binary indicator variables for the four hospitals that provided data for this study.)
| Variable Name | Probne 0 = Probability (%) That Variable Is a Predictor | Posterior Mean | Odds Ratio | Lower 95% Confidence Limit | Upper 95% Confidence Limit | Conditional Posterior Mean |
|---|---|---|---|---|---|---|
| Intercept | 100 | −4.7348 | NA | NA | NA | −4.7348 |
| Hospital1 | 0 | |||||
| Hospital2 | 0 | |||||
| Hospital3 | 0 | |||||
| Hospital4 | 0 | |||||
| GENDER_E | 0 | |||||
| AGE | 100 | 0.0486 | 1.0498 | 1.0253 | 1.0782 | 0.0486 |
| Alcohol | 0 | |||||
| Dr_Visits2 | 0 | |||||
| Dr_Visits3 | 0 | |||||
| Dr_Visits4 | 0 | |||||
| TouchBeef | 0 | |||||
| TouchPork | 0 | |||||
| CM_INDEX | 0 | |||||
| (a comorbidity | ||||||
| index) | ||||||
| ANYAB_BY29 | 57.2 | 0.9117 | 2.4886 | 1.5821 | 4.0140 | 1.5940 |
| BEEFTOT_MO | 27.5 | 0.0121 | 1.0122 | 1.0038 | 1.0217 | 0.0441 |
| PORKTOT_MO | 0 | |||||
| EATPOULTRY | 8.4 | 0.1776 | 1.1944 | 1.0760 | 1.3728 | 2.1266 |
| POULTRYTOT_MO | 0 | |||||
| COOKOWN_MO | 3.6 | −0.0003 | 0.9997 | 0.9993 | 1.0001 | −0.0083 |
| TOUCHPOULTRY | 0 | |||||
| GRADE22 | 3.4 | 0.0445 | 1.0455 | 1.0176 | 1.0748 | 1.3158 |
| GRADE23 | 0 | |||||
| GRADE24 | 0 | |||||
| WORK | 0 | |||||
| HOSP_GT1 | 0 | |||||
| ICU | 0 | |||||
| LIVEBIRDEXP | 0 | |||||
| (indicates exposure | ||||||
| to live birds) | ||||||
| STATE_WI | 0 | |||||
| RACE2 | 0 |
- Note: See text for discussion of the meanings of column headings.
As previously discussed, poultry consumption is strongly positively correlated with hospitalization: all but a few hospitalized cases ate poultry, while all nonhospitalized cases, being vegetarians, did not. We therefore created a single summary indicator variable, “HOSPITALIZED,” with a value of 1 for hospitalized cases, and 0 otherwise. Table IV shows the results of a BMA analysis when this hospitalization status variable is included as a predictor. (To save space, only the variables with nonzero inclusion probabilities are shown. A discussion of how all variables, including those that turned out not to be significant predictors, were defined and coded is given in a technical report available from the authors.) Now, COOKOWN_MO and EATPOULTRY (see Table II for variable definitions) drop out. Only HOSPITALIZED and ANYAB_BY29 have highly significant odds ratios. Thus, when both exposure to poultry (EATPOULTRY) and hospitalization status (HOSPITALIZED) are allowed as candidate predictors, automated variable selection via BMA identifies HOSPITALIZED, but not EATPOULTRY, as a significant predictor of presence of the vatE-resistance determinant (VATE). This is consistent with VATE being conditionally independent of EATPOULTRY, given HOSPITALIZED (i.e., with Model 2, but not Model 1, in the previous section).
To check this possibility without assuming any particular parametric regression model form (thus risking model misspecification biases), we also analyzed the full data by classification tree analysis. When HOSPITALIZED is excluded, then, similar to the BMA analysis, ANYAB_BY29, BEEFTOT_MO, and AGE are identified as significant predictors. Once prior antibiotic use (ANYAB29), AGE, and BEEFTOT_MO are accounted for (i.e., conditioned on), no poultry-related variable appears as a predictor of VATE. In other words, resistance (VATE) is conditionally independent of poultry consumption, given AGE, BEEFTOT_MO, and ANYAB29.
Importantly, the converse is not true: VATE is not conditionally independent of BEEFTOT_MO or ANYAB29, given poultry variables. For example, even after forming a tree by splitting first on EATPOULTRY and POULTRYTOT (the two poultry variables that are significantly associated with the response variable VATE), it is still the case that ANYAB29 (and BEEFTOT_MO_missing, meaning that a patient did not provide data about prior beef consumption) still enter the tree as additional splits. This asymmetry has strong implications for possible causal models.(35) It implies that EATPOULTRY cannot be a direct parent of VATE in a causal graph because its effects are fully “explained away” by the other variables with which it is correlated (BEEFTOT_MO, AGE, and ANYAB29).
When HOSPITALIZED is included in the data set, it becomes the most important predictor (first split). Fig. 1 shows the resulting tree, generated by the commercial software KnowledgeSeeker™. This tree is read as follows. Each node contains three numbers. The bottom-most number (e.g., 170 in the top node of the tree) shows the total number of cases described by that node. The middle number (e.g., 23.5%) is the percentage of cases in the node that have VATE= Y (Yes, the vatE streptogramin resistance gene was detected), and the top number (e.g., 76.4) is the percentage of cases with VATE= N (No, it was not detected). These two percentages total to 100% at each node. The set of splits between the top node and any other node describe the cases at that node. For example, “HOSPITALIZED= N” is the description for the 65 cases with 0% having VATE= Y and 100% having VATE= N. “HOSPITALIZED= Y and BEEFTOT_MO= Y” is the description of the node with four cases, all of which have VATE= Y.
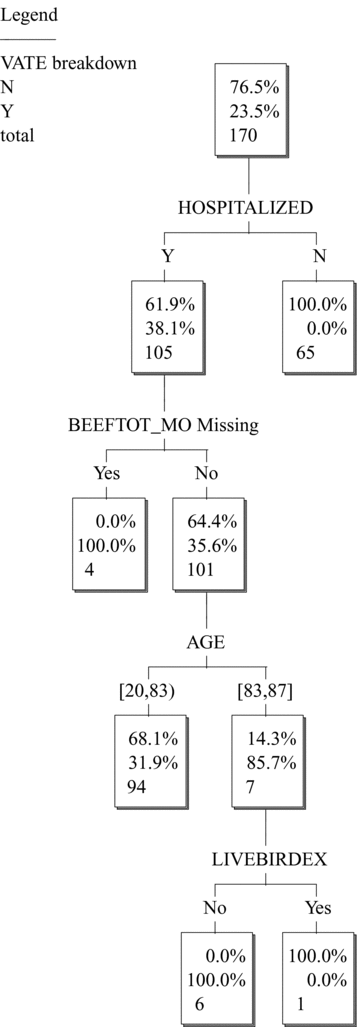
KnowledgeSeeker™ classification tree for full data set of 170 subjects with E. faecium isolates.
Classification trees are most often used to identify descriptions (i.e., conjunctions of variable values or ranges of values) that are highly predictive of or informative about the response variable.(31) However, they can also be used to reveal which variables (namely, those not in the tree) the response variable does not significantly depend on, given (i.e., after conditioning on) the subset of variables that are in the tree. This provides a statistical test for conditional independence relations in multivariate data sets—a staple of modern causal modeling.(13,15) The response variable is conditionally independent (at least within the power of the classification tree algorithm to discover) of the variables not in the tree, conditioned on the ones that are in the tree. Explanatory variables that cannot be forced out of a tree by conditioning on other variables (or, more generally, explanatory variables that the response variable cannot be made statistically independent of by conditioning on other variables) are often proposed as candidates for having a potential direct causal relation with the response variable.(13,15)
Fig. 1 shows that poultry consumption variables are not significant predictors of vatE risk after conditioning on hospitalization. In other words, conditioning on hospitalization makes VATE conditionally independent of poultry variables. However, importantly, the converse is not true. If one splits (i.e., conditions) on EATPOULTRY first, then HOSPITALIZED (and BEEFTOT_MO) still enter the tree as significant predictors (Fig. 2). Thus, their effects are not explained away by correlation with EATPOULTRY. This asymmetry shows that poultry variables appeared to be significant predictors in the case study(17) only because they acted as surrogates for hospitalization: including HOSPITALIZED directly as a predictor eliminates the poultry consumption variables as significant predictors. This goes well beyond simply stating that hospitalization and poultry consumption are strongly associated or multicollinear with each other (so that either one could act as a surrogate for the other, e.g., in multiple regression modeling with stepwise variable selection). It suggests that hospitalization is more fundamental than poultry consumption as a predictor of resistance, since including hospitalization as a predictor makes poultry variables redundant, but including poultry variables does not make hospitalization redundant.
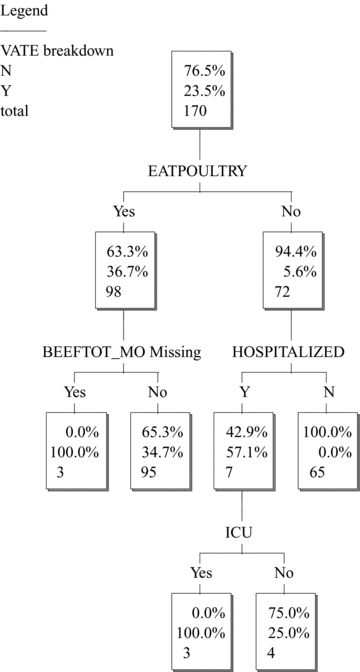
VATE is not conditionally independent of HOSPITALIZED, given EATPOULTRY.
The pattern of conditional independence relations revealed by these classification tree analyses is consistent with the causal graph in Fig. 3. It is inconsistent with any causal graph (or causal hypothesis or interpretation) in which EATPOULTRY is a parent (potential direct cause) of VATE. (“NONVEG” is a mnemonic variable introduced here to stand for “nonvegetarian.” By the study design, it is the same as HOSPITALIZED.)
A causal graph model that is consistent with conditional independence relations revealed by classification tree analysis.
5.2. Results for Inducible Resistance
Table V shows the BMA linear regression results and ratios with induced resistance (REP_V_S_P) as the response variable. Again, HOSPITALIZED and EATPOULTRY enter the model with highly significant adjusted ratios. The sum of their inclusion probabilities is close to 100% in this table, implying that they are substitutes for each other. Classification tree analysis showed that REP_V_S_P is also conditionally independent of all poultry variables after conditioning on nonpoultry variables (Fig. 4). Again, however, HOSPITALIZED still enters as an explanatory variable even after conditioning on poultry variables. This empirical finding is inconsistent with any a priori causal hypothesis that poultry consumption increases risk of inducible resistance.
| Variable Name | Probne 0 = Probability (%) That Variable Is a Predictor | Posterior Mean | Conditional Posterior Mean | Unadjusted Ratio | Adjusted Ratio | Lower 95% Confidence Limit | Upper 95% Confidence Limit |
|---|---|---|---|---|---|---|---|
| Intercept | 100 | −3.8656 | −3.8656 | NA | NA | NA | NA |
| HOSPITALIZED | 46.7 | 0.5427 | 1.1617 | 2.77 | 2.72 | 2.44 | 3.03 |
| GENDER_E | 0 | 0 | 0 | 1.42 | 1.69 | 1.45 | 1.97 |
| AGE | 28 | 0.0023 | 0.0083 | NA | NA | NA | NA |
| Alcohol | 0 | 0 | 0 | 0.82 | 0.78 | 0.65 | 0.94 |
| Dr_Visits2 | 0 | 0 | 0 | 1.01 | 1.19 | 1.00 | 1.42 |
| Dr_Visits3 | 0 | 0 | 0 | 1.51 | 1.60 | 1.35 | 1.88 |
| Dr_Visits4 | 0 | 0 | 0 | 1.47 | 1.70 | 1.36 | 2.14 |
| TouchBeef | 100 | −0.5865 | −0.5865 | 1.23 | 1.57 | 1.37 | 1.80 |
| TouchPork | 12 | 0.0376 | 0.3140 | 1.52 | 1.50 | 1.28 | 1.75 |
| CM_INDEX | 6.6 | −0.0032 | −0.0476 | 2.61 | 2.49 | 2.20 | 2.81 |
| ANYAB_BY29 | 76.4 | 0.3473 | 0.4545 | 3.69 | 2.36 | 2.08 | 2.68 |
| BEEFTOT_MO | 0 | 0 | 0 | 2.66 | 2.59 | 2.32 | 2.89 |
| PORKTOT_MO | 1.9 | −0.0005 | −0.0243 | 2.63 | 2.42 | 2.15 | 2.71 |
| EATPOULTRY | 54.4 | 0.5562 | 1.0218 | 2.77 | 2.70 | 2.42 | 3.01 |
| POULTRYTOT_MO | 0 | 0 | 0 | 2.57 | 2.69 | 2.41 | 3.00 |
| COOKOWN_MO | 0 | 0 | 0 | 0.19 | 0.42 | 0.36 | 0.50 |
| TOUCHPOULTRY | 1.4 | 0.0036 | 0.2485 | 1.23 | 1.60 | 1.39 | 1.84 |
| GRADE22 | 19.4 | 0.1316 | 0.6765 | 1.80 | 1.76 | 1.50 | 2.07 |
| GRADE23 | 14.9 | 0.1255 | 0.8403 | 0.96 | 0.86 | 0.71 | 1.04 |
| GRADE24 | 14.9 | 0.1194 | 0.7994 | 0.76 | 0.52 | 0.45 | 0.59 |
| WORK | 0 | 0 | 0 | 0.63 | 0.63 | 0.54 | 0.74 |
| HOSP_GT1 | 10.3 | −0.0265 | −0.2570 | 1.55 | 1.76 | 1.49 | 2.08 |
| ICU | 2.1 | 0.0068 | 0.3308 | 3.39 | 1.75 | 1.46 | 2.09 |
| LIVEBIRDEXP | 4 | −0.0087 | −0.2168 | 0.78 | 0.64 | 0.54 | 0.78 |
| STATE_WI | 0 | 0 | 0 | 1.20 | 1.38 | 1.17 | 1.63 |
| RACE2 | 4.3 | −0.0282 | −0.6541 | 1.16 | 1.71 | 0.81 | 3.58 |
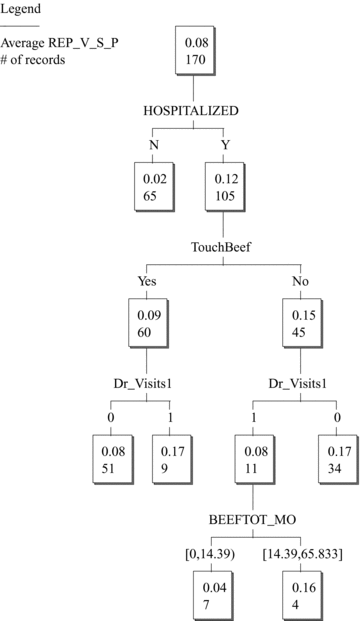
KnowledgeSeeker™ classification tree for inducible resistance. The upper number in each node is the conditional mean of REP_V_S_P.
6. DISCUSSION AND IMPLICATIONS FOR PREVIOUS CONCLUSIONS
The conditional independence relations identified in the case study data do not support a causal hypothesis that poultry consumption increases resistance risks. There was no significant relation between poultry exposure and VATE or inducible resistance after accounting for nonpoultry variables. Poultry-exposed subjects also had lower risks than other subjects for both E. faecium carriage and intermediate QD susceptibility.
The case study does not provide resistance results specifically for patients who might be harmed by QD resistance, that is, vanA VREF patients,(37) so its clinical relevance is unclear. Its conclusion(17) that “the results of the present study suggest that the FDA [draft risk assessment(36)] model may underestimate the true risk of food-borne acquisition, because streptogramin resistance genes are commonly found in human fecal E. faecium” appears to be unwarranted by the data. The data do not show that food-borne resistance occurred, or that any nonzero resistance risk or clinical harm occurred. To the contrary, they support previous risk assessment modeling predictions(38) that antibiotic-treated poultry might have lower levels of susceptible E. faecium than other poultry, while finding no evidence of QD resistance in isolates from human patients.
Similarly, the case study data do not support the stated conclusion(17) that “the presence of vatE and inducible streptogramin resistance in the endogenous fecal flora of newly hospitalized patients creates a genetic reservoir for the emergence of streptogramin-resistant, vancomycin-resistant E. faecium in the hospital environment.” First, the study did not specifically examine streptogramin-resistant, vancomycin-resistant E. faecium, so it cannot support this conclusion. Second, many of the “newly hospitalized” patients had a record of many prior visits to physicians in the past year (and an unknown amount of prior exposure to hospital bacteria). The data do not suggest that these patients are reservoirs from which resistant bacteria enter the hospital environment. To the contrary, these patients may acquire resistant bacteria from the hospital environment (selected by the use of antibiotics in hospitals).(20) Because the patients were newly admitted, resistance might not have been acquired yet on the current visit. One could speculate that it might instead have resulted from previous exposures. How plausible this is depends on details of hospitalization and exposure histories, transient colonization, and clearance that are not available in this study. We do not seek to explain further why or how hospitalization fully accounts for resistance previously attributed to poultry in this case study, but simply emphasize that it does so (1-4).) Third, vatE has not been shown to be relevant to resistance in human patients. For example, it was found in none of 167 tested isolates of E. faecalis and E. faecium from bacteremia patients.(39)
The speculation that future increased use of QD (i.e., Synercid™), combined with presence of resistance genes, “might facilitate the rapid emergence of streptogramin resistance”(17) is similarly not supported by the study data, which showed zero QD resistance despite years of QD use in hospitals. (It is also contradicted by a quantitative risk model for emergence of resistance(40).)
Our analysis shows that many nonpoultry variables also have significant unexplained associations with induced resistance, including hospital location, age, beef consumption, pork consumption, higher education, and alcohol (the latter two with protective effects). In the 45-case subset of hospitalized patients, the only significant adjusted ratio occurred for the indicator variable for college graduates. Thus, “induced resistance” ratios may not be very meaningful (e.g., they do not indicate that poultry consumption is any more of a risk factor than educational status or other nonpoultry variables) and may reflect correlations to hospitalization status more than anything else.
In summary, although several strong causal conclusions and interpretations of the case study data have previously been presented(17,18) that suggest increased human health risk from virginiamycin use in poultry, we could not reproduce these findings or conclusions using statistical methods that seek to minimize confirmation bias and dependence on a priori causal hypotheses. We believe that it would be valuable to expand the data set in the Marshfield study to include healthy poultry eaters and hospitalized nonpoultry eaters (categories currently of size 0 and 4, respectively). This would provide a better basis for analysis of resistance element transfers (if any) from poultry to humans.
7. CONCLUSIONS
When adequate data are available, as in this case study, achieving the goal of objective causal inference may be helped by the techniques we have illustrated, such as BMA, classification tree analysis, and conditional independence testing of causal assumptions and interpretations. The case study in this article illustrates that a risk assessor's choice of which predictive variables to include in a model can drive the risk attributed to specific variables, such as poultry consumption. It can make otherwise nonsignificant associations (e.g., between EATPOULTRY and VATE) appear significant by excluding correlated variables (such as HOSPITALIZED) that explain them away.
To avoid such potential biases and dependencies on modeling choices, we have illustrated how techniques such as BMA, classification trees, and conditional independence tests can be used to bypass human selection of variables, model forms, responses, subsets of subjects, and a priori causal hypotheses to test. Eliminating these human choices can reduce the opportunity for confirmation biases and increase the role and value of empirical data in revealing unexpected findings and causal relations.
In our analysis of the case study data, poultry consumption turned out to be a proxy for hospitalization. Rather than confirming prior causal interpretations that the study data “raise additional concerns regarding the continued use of virginiamycin in food animals,”(17) we found that use of antibiotics is associated with reduced prevalence of bacteria in retail meats. People who eat such meats have a lower prevalence of E. faecium and a higher proportion of QD-susceptible E. faecium than people who do not. The study data did not suggest that resistant bacteria or resistance determinants were transferred from poultry to human patients. The data are consistent with the causal hypothesis that hospitalization causes resistance (e.g., vatE presence), but are inconsistent with the alternative causal hypothesis that poultry consumption causes resistance.
The ability to use relatively objective and widely available modern statistical methods to test and decide among alternative causal models has the potential to revolutionize causal interpretations of risk assessment data. Perhaps, further development and applications of such methods will eventually help to suppress confirmation bias and increase the value of empirical data in informing understanding of the causes of antibiotic resistance and other risks.
Footnotes
ACKNOWLEDGMENTS
This work was supported in part by Phibro Animal Health, a manufacturer of virginiamycin. All research questions addressed and all aspects of the article are solely the authors'. Phibro Animal Health played no decision-making role in the research or in the reporting of results. We thank Dr. Edward Belongia for sharing the Marshfield Enterococcal Study Group's data and codebooks so that we could analyze the data in detail. Three anonymous reviewers provided detailed comments and suggestions that greatly helped to improve the exposition. Tony Cox thanks Professors Sander Greenland and Paolo Ricci for stimulating discussions of conditional independence tests and causal inference in risk analysis.
Appendix
APPENDIX: COMPUTING ADJUSTED RATIOS OF MEDIANS AND THEIR CONFIDENCE LIMITS
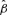(from the BMA analysis), we calculate the vector of mean response values (for induced resistance REP_V_S_P) as
((A.1))
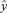into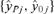 
, where 
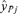is a vector of the responses, yi, i= 1, 2, 3, … n, for Xij positive (>0) and 
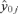is a vector of the responses, yi, where Xij was equal to 0. This is a generalization of the criteria where Xij is either “Yes” (1) or “No” (0), allowing the methodology to be applied to continuous variables as well. The “adjusted ratio” as defined in Kieke et al.(17) and further generalized for all variables, j= 1, 2, … p is then
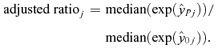((A.2))
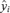, we note that the standard formula for confidence intervals on the mean response is
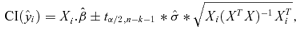((A.3))- •
Xi. is a row, i, of the data matrix, X
- •
t α/2,n−k−1 is the t-statistic at confidence level (1−α) with n−k−1 degrees of freedom, where n is the number of observations in the data set and k is the number of variables with nonzero posterior mean coefficients.
- •
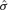is the standard error of the regression estimate =
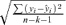, where yi= ln(REP_V_S_P) - •
(XTX)−1 is the variance-covariance matrix
- •
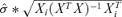is the standard deviation of the mean response for observation i.
To compute confidence limits on the adjusted ratios, we used a simulation approach. Each iteration of the simulation generates a response vector, with each vector element, i, drawn from a t-distribution (tn-k−1) with mean equal to the mean response,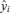 
, and standard deviation equal to the standard deviation of the mean response for 
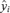as provided above. From each simulated response vector, we compute an adjusted ratio for each variable2 as in Equation (A.2) above. We ran the simulation for 10,000 iterations to generate a large distribution for each variable's ratio. The lower confidence limit we report corresponds to the 0.025 quantile of the sample distribution, while the upper confidence limit corresponds to the 0.975 quantile of the sample distribution. The distributions appear to be approximately lognormal, but we have chosen to use the sample quantiles rather than quantiles of a fitted lognormal distribution as this requires making fewer assumptions and we have a large sample to work with.
