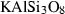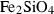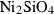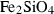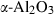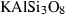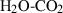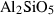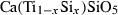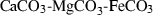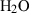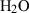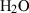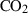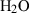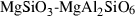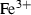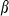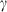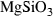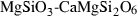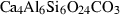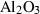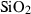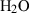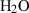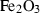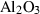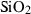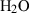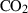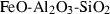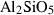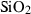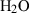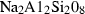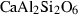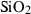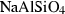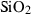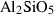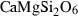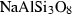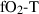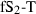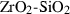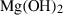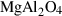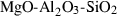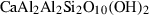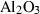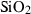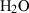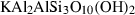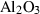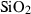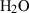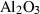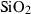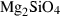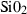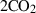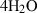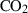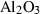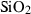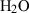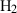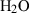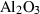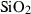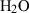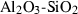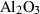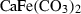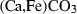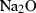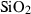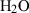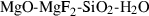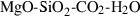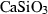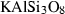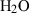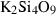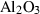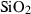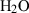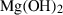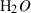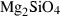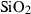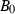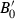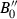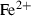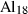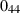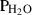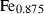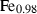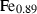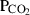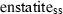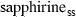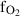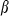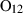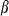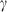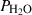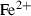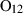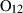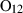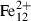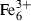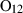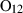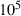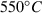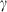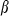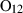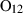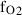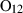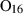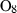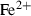An improved and extended internally consistent thermodynamic dataset for phases of petrological interest, involving a new equation of state for solids
Improvements have already been made to the dataset: for the current top-copy, please go to http://www.esc.cam.ac.uk/people/academic-staff/tim-holland, or http://www.metamorph.geo.uni-mainz.de/thermocalc/.
Abstract
The thermodynamic properties of 254 end-members, including 210 mineral end-members, 18 silicate liquid end-members and 26 aqueous fluid species are presented in a revised and updated internally consistent thermodynamic data set. The PVT properties of the data set phases are now based on a modified Tait equation of state (EOS) for the solids and the Pitzer & Sterner (1995) equation for gaseous components. Thermal expansion and compressibility are linked within the modified Tait EOS (TEOS) by a thermal pressure formulation using an Einstein temperature to model the temperature dependence of both the thermal expansion and bulk modulus in a consistent way. The new EOS has led to improved fitting of the phase equilibrium experiments. Many new end-members have been added, including several deep mantle phases and, for the first time, sulphur-bearing minerals. Silicate liquid end-members are in good agreement with both phase equilibrium experiments and measured heat of melting. The new dataset considerably enhances the capabilities for thermodynamic calculation on rocks, melts and aqueous fluids under crustal to deep mantle conditions. Implementations are already available in thermocalc to take advantage of the new data set and its methodologies, as illustrated by example calculations on sapphirine-bearing equilibria, sulphur-bearing equilibria and calculations to 300 kbar and 2000 °C to extend to lower mantle conditions.
Introduction
The need for thermodynamic data of sufficient quality to make reliable calculations on rocks continues to grow, particularly to capitalize on new methods of application of phase equilibria that involve increasingly complex solid and fluid solutions, as well as on new advances in software.
The basic philosophy from our earlier summary (Holland & Powell, 1998; hereafter referred to as HP98) is maintained. The thermodynamic data extraction involves using weighted least squares on the different types of data (calorimetric, phase equilibria, natural mineral partitioning) to determine enthalpies of formation of the end-members of the phases. Entropies, volumes, heat capacities, thermal expansions and compressibilities are not derived by regression, but are taken as known in this process. Where they are not known experimentally, they are estimated as outlined in our earlier papers. The new regression involves determination of the enthalpies of 254 end-members, of which 69 are new to the data set, with an overall fit in which 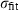 is 1.09 (
is 1.09 (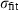 being a goodness-of-fit parameter, identical to
being a goodness-of-fit parameter, identical to 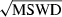 in geochronology that relates directly to the chi-squared test).
in geochronology that relates directly to the chi-squared test).
Major methodological changes from HP98 are embodied in this new data set, within the basic philosophy outlined above. They are documented below, along with minor ones that have arisen since HP98, some of which are incorporated in the currently used data set, tc-ds55.txt, from November 2003, but have not been documented properly before.
A list of the chemical compositions of the end-members considered in this study may be found in Table 1. The end-members are listed under the headings orthosilicates and ring silicates (garnet, olivine, etc.), chain silicates (pyroxene and pyroxenoid, amphibole, etc.), sheet silicates (mica, chlorite, etc.), framework silicates, oxides and hydroxides, carbonates, elements, high-pressure phases, gas species, melt species and aqueous species. The new data set itself is given in Table 2. Table 3 lists the calorimetric data used in the dataset generation. Appendix 1 gives the data sources for the thermodynamic properties, and Appendix 2 is a summary table of the experimental studies used in the data set regression. Appendix 3 provides information on minor changes since the publication of HP98. The table of all the experimentally determined mineral equilibrium brackets used in the least squares analysis and the calculated fit to them is presented in Table S1 as well as at http://www.esc.cam.ac.uk/people/academic-staff/tim-holland and http://www.metamorph.geo.uni-mainz.de/thermocalc/. This is in the form of full computer output from the data extraction program LSQDS. Table S2 contains the activity–composition relations that were used in the generation of the data set.
| Group | Abbreviation | End-member | Formula |
|---|---|---|---|
| Garnets & olivines | alm | almandine | Fe3Al2Si3O12 |
| andr | andradite | Ca3Fe2Si3O12 | |
| gr | grossular | Ca3Al2Si3O12 | |
| knor • | knorringite | Mg3Cr2Si3O12 | |
| maj • | majorite | Mg4Si4O12 | |
| py | pyrope | Mg3Al2Si3Ol2 | |
| spss | spessartine | Mn3Al2Si3O12 | |
| chum | clinohumite | Mg9Si4O16(OH)2 | |
| fa | fayalite | Fe2SiO4 | |
| fo | forsterite | Mg2SiO4 | |
| lrn | larnite | Ca2SiO4 | |
| mont | monticellite | CaMgSiO4 | |
| teph | tephroite | Mn2SiO4 | |
| Aluminosilicates | and | andalusite | Al2SiO5 |
| ky | kyanite | Al2SiO5 | |
| sill | sillimanite | Al2SiO5 | |
| amul • | Al-mullite | Al2.5Si0.5O4.75 | |
| smul • | Si-mullite | Al2SiO5 | |
| fctd | Fe-chloritoid | FeAl2SiO5(OH)2 | |
| mctd | Mg-chloritoid | MgAl2SiO5(OH)2 | |
| mnctd | Mn-chloritoid | MnAl2SiO5(OH)2 | |
| fst | Fe-staurolite | Fe 4Al18Si7.5O44(OH)4 | |
| mst | Mg-staurolite | Mg4Al18Si7.5O44(OH)4 | |
| mnst | Mn-staurolite | Mn4Al18Si7.5O44(OH)4 | |
| tpz | hydroxy-topaz | Al2SiO4(OH)2 | |
| Other orthosilicates | ak | akermanite | Ca2MgSi2O7 |
| geh | gehlenite | Ca2Al2SiO7 | |
| jgd • | julgoldite (FeFe) | Ca4Fe6Si6O21(OH)7 | |
| merw | merwinite | Ca3MgSi2O8 | |
| mpm | pumpellyite (MgAl) | Ca4MgAl5Si6O21(OH)7 | |
| fpm | pumpellyite (FeAl) | Ca4FeAl5Si6O21(OH)7 | |
| rnk | rankinite | Ca3Si2O7 | |
| sph | sphene | CaTiSiO5 | |
| spu | spurrite | Ca5Si2CO11 | |
| ty | tilleyite | Ca5Si2C2O13 | |
| zrc | zircon | ZrSiO4 | |
| Sorosilicates | cz | clinozoisite | Ca2Al3Si3O12(OH) |
| ep | epidote(ordered) | Ca2FeAl2Si3O12(OH) | |
| fep | Fe-epidote | Ca2Fe2AlSi3O12(OH) | |
| law | lawsonite | CaAl2Si2O6(OH)4 | |
| pmt • | piemontite (ordered) | Ca2MnAl2Si3Oi2(OH) | |
| zo | zoisite | Ca2Al3Si3O12(OH) | |
| vsv | vesuvianite | Ca19Mg2Al11Si18O69(OH)9 | |
| Cyclosilicates | crd | cordierite | Mg2Al4Si5O18 |
| hcrd | hydrous-cordierite | Mg2Al4Si5O17(OH)2 | |
| fcrd | Fe-cordierite | Fe2Al4Si5O18 | |
| mncrd | Mn-cordierite | Mn2Al4Si5O18 | |
| osm1 | osumilite (1) | KMg2Al5Si10O30 | |
| osm2 | osumilite (2) | KMg3Al3Si11O30 | |
| fosm | Fe-osumilite | KFe2Al5Si10O30 | |
| High-P phases | apv • | Al-perovskite | AlAlO3 |
| cpv • | Ca-perovskite | CaSiO3 | |
| cstn • | CaSi-titanite | CaSi2O5 | |
| fak • | Fe-akimotoite | FeSiO3 | |
| fpv • | Fe-perovskite | FeSiO3 | |
| frw • | Fe-ringwoodite | Fe2SiO4 | |
| fwd • | Fe-wadsleyite | Fe2SiO4 | |
| mak • | akimotoite | MgSiO3 | |
| mpv • | Mg-perovskite | MgSiO3 | |
| mrw • | Mg-ringwoodite | Mg2SiO4 | |
| mwd • | Mg-wadsleyite | Mg2SiO4 | |
| phA | phaseA | Mg7Si2O8(OH)6 | |
| Pyroxenes & pyroxenoids | acm | acmite | NaFeSi2O6 |
| caes • | Ca-eskola pyroxene | Ca0.5AlSi2O6 | |
| cats | Ca-tschermaks pyroxe | CaAl2SiO6 | |
| cen • | clino enstatite | Mg2Si2O6 | |
| di | diopside | CaMgSi2O6 | |
| en | enstatite | Mg2Si2O6 | |
| fs | ferrosilite | Fe2Si2O6 | |
| hed | hedenbergite | CaFeSi2O6 | |
| hen • | Hi-P clinoenstatite | Mg2Si2O6 | |
| jd | jadeite | NaAlSi2O6 | |
| kos • | kosmochlor | NaCrSi2O6 | |
| mgts | Mg-tschermaks pyroxe | MgAl2SiO6 | |
| pren • | protoenstatite | Mg2Si2O6 | |
| pswo | pseudowollastonite | CaSiO3 | |
| pxmn | pyroxmangite | MnSiO3 | |
| rhod | rhodonite | MnSiO3 | |
| wal • | walstromite | CaSiO3 | |
| wo | wollastonite | CaSiO3 | |
| Amphibole | anth | anthophyllite | Mg7Si8O22(OH)2 |
| cumm | cummingtonite | Mg7Si8O22(OH)2 | |
| fact | ferroactinolite | Ca2Fe5Si8O22(OH)2 | |
| fanth | Fe-anthophyllite | Fe7Si8O22(OH)2 | |
| fgl | ferroglaucophane | Na2Fe3Al2Si8O22(OH)2 | |
| gl | glaucophane | Na2Mg3Al2Si8O22(OH)2 | |
| grun | grunerite | Fe7Si8O22(OH)2 | |
| parg | pargasite | NaCa2Mg4Al3Si6O22(OH)2 | |
| rieb | riebeckite | Na2Fe5Si8O22(OH)2 | |
| tr | tremolite | Ca2Mg5Si8O22 (OH)2 | |
| ts | tschermakite | Ca2Mg3Al4Si6O22(OH)2 | |
| Other chain silicates | deer | deerite | Fe 18Si12O40(OH)10 |
| fcar | ferrocarpholite | FeAl2Si2O6(OH)4 | |
| fspr | Fe-sapphirine (221) | Fe4Al8Si2O20 | |
| mcar | magnesiocarpholite | MgAl2Si2O6(OH)4 | |
| spr4 | sapphirine (221) | Mg4Al8Si2O20 | |
| spr5 | sapphirine (351) | Mg3Al10SiO20 | |
| Micas | ann | annite | KFe3AlSi3O10(OH)2 |
| cel | celadonite | KMgAlSi4O10(OH)2 | |
| east | eastonite | KMg2Al3Si2O10(OH)2 | |
| fcel | ferroceladonite | KFeAlSi4O10(OH)2 | |
| ma | margarite | CaAl4Si2O10(OH)2 | |
| mnbi | Mn-biotite | KMn3AlSi3O10(OH)2 | |
| mu | muscovite | KAl3Si3O10(OH)2 | |
| naph | sodaphlogopite | NaMg3AlSi3O10(OH)2 | |
| pa | paragonite | NaAl3Si3O10(OH)2 | |
| phl | phlogopite | KMg3AlSi3O10(OH)2 | |
| Chlorites | afchl | Al-free chlorite | Mg6Si4O10(OH)8 |
| ames | amesite (14A) | Mg4Al4Si2O10(OH)8 | |
| clin | clinochlore (ordered) | Mg5Al2Si3O10(OH)8 | |
| daph | daphnite | Fe5Al2Si3O10(OH)8 | |
| fsud | ferrosudoite | Fe2Al4Si3O10(OH)8 | |
| mnchl | Mn-chlorite | Mn5Al2Si3O10(OH)8 | |
| sud | sudoite | Mg2Al4Si3O10(OH)8 | |
| Other sheet silicates | atg | antigorite | Mg48Si34O85(OH)62 |
| chr | chrysotile | Mg3Si2O5(OH)4 | |
| fpre • | ferri-prehnite | Ca2FeAlSi3O10(OH)2 | |
| fstp • | ferrostilpnomelane | K0.5Fe5Al2Si8O18(OH)12.5 | |
| fta | ferrotalc | Fe3Si4O10(OH)2 | |
| glt • | greenalite | Fe3Si2O5(OH)4 | |
| kao | kaolinite | Al2Si2O5(OH)4 | |
| liz • | lizardite | Mg3Si2O5(OH)4 | |
| minm • | Mg-minnesotaite | Mg3Si4O10(OH)2 | |
| minn • | minnesotaite | Fe3Si4O10(OH)2 | |
| mstp • | Mg-stilpnomelane | K0.5Mg5Al2Si8O18(OH)12.5 | |
| pre | prehnite | Ca2Al2Si3O10(OH)2 | |
| prl | pyrophyllite | Al2Si4O10(OH)2 | |
| ta | talc | Mg3Si4O10(OH)2 | |
| tap • | prl-talc | Al2Si4O10(OH)2 | |
| tats | tschermak-talc | Mg2Al2Si3O10(OH)2 | |
| Feldspars & feldspathoid | abh | albite (high) | NaAlSi3O8 |
| albite | ab | NaAlSi3O8 | |
| an | anorthite | CaAl2Si2O8 | |
| anl | analcite | NaAlSi2O5(OH)2 | |
| cg • | carnegieite (low) | NaAlSiO4 | |
| cgh • | carnegieite (high) | NaAlSiO4 | |
| kcm • | K-cymrite | KAlSi3O7(OH)2 | |
| kls | kalsilite | KAlSiO4 | |
| lc | leucite | KAlSi2O6 | |
| mic | microcline | KAlSi3O8 | |
| ne | nepheline | NaAlSiO4 | |
| san | sanidine | KAlSi3O8 | |
| Silica minerals | coe | coesite | SiO2 |
| crst | cristobalite (high) | SiO2 | |
| q | quartz | SiO2 | |
| stv | stishovite | SiO2 | |
| trd | tridymite (high) | SiO2 | |
| Other framework silicates | heu | heulandite | CaAl2Si7O12(OH)12 |
| hol • | hollandite | KAlSi3O8 | |
| lmt | laumontite | CaAl2Si4O8(OH)8 | |
| me | meionite | Ca4Al6Si6CO27 | |
| sdl • | sodalite | Na8Al6Si6O24Cl2 | |
| stlb | stilbite | CaAl2Si7O11(OH)14 | |
| wa • | Si-wadeite | K2Si4O9 | |
| wrk | wairakite | CaAl2Si4Oio(OH)4 | |
| Oxides | bdy | baddeleyite | ZrO2 |
| bix • | bixbyite | Mn2O3 | |
| cor | corundum | Al2O3 | |
| cup • | cuprite | Cu2O | |
| esk • | eskolaite | Cr2O3 | |
| fper • | ferropericlase | FeO | |
| geik | geikielite | MgTiO3 | |
| hem | hematite | Fe2O3 | |
| herc | hercynite | FeAl2O4 | |
| ilm | ilmenite | FeTiO3 | |
| lime | lime | CaO | |
| mang | manganosite | MnO | |
| mcor • | MgSi-corundum | MgSiO3 | |
| mft | magnesioferrite | MgFe2O4 | |
| mt | magnetite | Fe3O4 | |
| NiO | nickel oxide | NiO | |
| per | periclase | MgO | |
| picr • | picrochromite | MgCr2O4 | |
| pnt | pyrophanite | MnTiO3 | |
| ru | rutile | TiO2 | |
| sp | spinel | MgAl2O4 | |
| ten • | tenorite | CuO | |
| usp | ulvospinel | Fe2TiO4 | |
| Hydroxides | br | brucite | Mg(OH)2 |
| dsp | diaspore | AlO(OH) | |
| gth | goethite | FeO (OH) | |
| Carbonates | ank | ankerite | CaFe(CO3)2 |
| arag | aragonite | CaCO3 | |
| cc | calcite | CaCO3 | |
| dol | dolomite | CaMg(CO3)2 | |
| mag | magnesite | MgCO3 | |
| rhc | rhodochrosite | MnCO3 | |
| sid | siderite | FeCO3 | |
| Halides & sulphides | any • | anhydrite | CaSO4 |
| hlt • | halite | NaCl | |
| lot • | low troilite | FeS | |
| pyr • | pyrite | FeS2 | |
| syv • | sylvite | KCl | |
| tro • | troilite | FeS | |
| trot • | pyrrhotite | FeS | |
| trov • | pyrrhotite | Fe0.875S | |
| Elements | Cu • | copper | Cu |
| diam | diamond | C | |
| gph | graphite | C | |
| iron | iron | Fe | |
| Ni | nickel | Ni | |
| S • | sulphur | S | |
| Gas species | H2O | water | H2O |
| CO2 | carbon dioxide | CO2 | |
| CO | carbon monoxide | CO | |
| CH4 | methane | CH4 | |
| O2 | oxygen | O2 | |
| H2 | hydrogen | H2 | |
| S2 • | sulphur gas | S2 | |
| H2S • | Hydrogen sulphide | H2S | |
| Melt species | abL | albite liquid | NaAlSi3O8 |
| anL | anorthite liquid | CaAl2Si2O8 | |
| corL • | corundum liquid | Al2O3 | |
| diL | diopside liquid | CaMgSi2O6 | |
| enL | enstatite liquid | Mg2Si2O6 | |
| faL | fayalite liquid | Fe2SiO4 | |
| foL | forsterite liquid | Mg2SiO4 | |
| h2oL | H2O liquid | H2O | |
| hltL • | halite liquid) | NaCl | |
| kspL | K-feldspar liquid | KAlSi3O8 | |
| lcL • | leucite liquid | KAlSi2O6 | |
| limL • | CaO liquid | CaO | |
| neL • | nepheline liquid | NaAlSiO4 | |
| perL • | MgO liquid | MgO | |
| qL | quartz liquid | SiO2 | |
| silL | sillimanite liquid | Al2SiO5 | |
| syvL • | sylvite (liquid) | KCl | |
| woL • | wollastonite liquid | CaSiO3 | |
| Aqueousspecies | H+ | hydrogen ion | H+ |
| Cl− | chloride ion | Cl− | |
| OH− | hydroxyl ion | HO− | |
| Na+ | sodium ion | Na+ | |
| K+ | potassium ion | K+ | |
| Ca++ | calcium ion | Ca2+ | |
| Mg++ | magnesium ion | Mg2+ | |
| Fe++ | ferrous ion | Fe 2+ | |
| Al+++ | aluminium ion | Al3+ | |
| CO3− | carbonate ion | 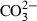 |
|
| AlOH3 | aluminium hydroxide | Al(OH)3 | |
| AlOH4− | aluminium hydroxide | 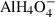 |
|
| KOH | potassium hydroxide | K(OH) | |
| HCl | hydrogen chloride | HCl | |
| KCl | potassium chloride | KCl | |
| NaCl | sodium chloride | NaCl | |
| CaCl2 | calcium chloride | CaCl2 | |
| CaCl+ | calcium chloride | CaCl+ | |
| MgCl2 | magnesium chloride | MgCl2 | |
| MgCl+ | magnesium chloride | MgCl+ | |
| FeCl2 | ferrous chloride | FeCl2 | |
| aqSi | silica (aq) | SiO2 | |
| HS−• | sulphide (aq) | HS− | |
| HSO3−• | sulphite (aq) | 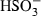 |
|
| SO42−• | sulphate (aq) | 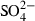 |
|
| HSO4−• | sulphate2 (aq) | 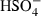 |
| Group | End-member |  |
 |
S | V |  |
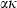 |
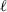 |
||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a | b | c | d | 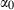 |
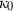 |
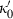 |
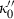 |
|||||||
| Garnet and olivine | Almandine (alm) | −5260.65 | 1.31 | 342.00 | 11.525 | 0.6773 | 0 | −3772.7 | −5.0440 | 2.12 | 1900.0 | 2.98 | −0.0016 | |
| Andradite (andr) | −5769.08 | 1.56 | 316.40 | 13.204 | 0.6386 | 0 | −4955.1 | −3.9892 | 2.86 | 1588.0 | 5.68 | −0.0036 | ||
| grossular (gr) | −6642.95 | 1.46 | 255.00 | 12.535 | 0.6260 | 0 | −5779.2 | −4.0029 | 2.20 | 1720.0 | 5.53 | −0.0032 | ||
| Knorringite (knor) | −5687.75 | 3.88 | 317.00 | 11.738 | 0.6130 | 0.3606 | −4178.0 | −3.7294 | 2.37 | 1743.0 | 4.05 | −0.0023 | ||
| Majorite (maj) | −6050.33 | 9.62 | 255.20 | 11.457 | 0.7136 | −0.0997 | −1158.2 | −6.6223 | 1.83 | 1600.0 | 4.56 | −0.0028 | ||
| Pyrope (py) | −6282.13 | 1.06 | 269.50 | 11.313 | 0.6335 | 0 | −5196.1 | −4.3152 | 2.37 | 1743.0 | 4.05 | −0.0023 | ||
| Spessartine (spss) | −5693.65 | 3.14 | 335.30 | 11.792 | 0.6469 | 0 | −4525.8 | −4.4528 | 2.27 | 1740.0 | 6.68 | −0.0038 | ||
| Clinohumite (chum) | −9609.82 | 2.49 | 443.00 | 19.785 | 1.0700 | −1.6533 | −7899.6 | −7.3739 | 2.91 | 1194.0 | 4.79 | −0.0040 | ||
| Fayalite (fa) | −1477.74 | 0.68 | 151.00 | 4.631 | 0.2011 | 1.7330 | −1960.6 | −0.9009 | 2.82 | 1256.0 | 4.68 | −0.0037 | ||
| Forsterite (fo) | −2172.57 | 0.57 | 95.10 | 4.366 | 0.2333 | 0.1494 | −603.8 | −1.8697 | 2.85 | 1285.0 | 3.84 | −0.0030 | ||
| Larnite (lrn) | −2307.04 | 0.90 | 127.60 | 5.160 | 0.2475 | −0.3206 | 0 | −2.0519 | 2.90 | 985.0 | 4.07 | −0.0041 | 1 | |
| Monticellite (mont) | −2251.31 | 0.52 | 109.50 | 5.148 | 0.2507 | −1.0433 | −797.2 | −1.9961 | 2.87 | 1134.0 | 3.87 | −0.0034 | ||
| Tephroite (teph) | −1733.95 | 1.05 | 155.90 | 4.899 | 0.2196 | 0 | −1292.7 | −1.3083 | 2.86 | 1256.0 | 4.68 | −0.0037 | ||
| Aluminosilicates | Andalusite (and) | −2588.72 | 0.68 | 92.70 | 5.153 | 0.2773 | −0.6588 | −1914.1 | −2.2656 | 1.81 | 1442.0 | 6.89 | −0.0048 | |
| Kyanite (ky) | −2593.02 | 0.67 | 83.50 | 4.414 | 0.2794 | −0.7124 | −2055.6 | −2.2894 | 1.92 | 1601.0 | 4.05 | −0.0025 | ||
| Sillimanite (sill) | −2585.85 | 0.68 | 95.40 | 4.986 | 0.2802 | −0.6900 | −1375.7 | −2.3994 | 1.12 | 1640.0 | 5.06 | −0.0031 | 2 | |
| Mullite (amul) | −2485.51 | 0.91 | 113.00 | 5.083 | 0.2448 | 0.0968 | −2533.3 | −1.6416 | 1.36 | 1740.0 | 4.00 | −0.0023 | ||
| Mullite (smul) | −2569.28 | 0.69 | 101.50 | 4.987 | 0.2802 | −0.6900 | −1375.7 | −2.3994 | 1.36 | 1740.0 | 4.00 | −0.0023 | ||
| Chloritoid (fctd) | −3208.31 | 0.80 | 167.00 | 6.980 | 0.4161 | −0.3477 | −2835.9 | −3.3603 | 2.80 | 1456.0 | 4.06 | −0.0028 | ||
| Chloritoid (mctd) | −3549.31 | 0.75 | 146.00 | 6.875 | 0.4174 | −0.3771 | −2920.6 | −3.4178 | 2.63 | 1456.0 | 4.06 | −0.0028 | ||
| Chloritoid (mnctd) | −3336.20 | 1.68 | 166.00 | 7.175 | 0.4644 | −1.2654 | −1147.2 | −4.3410 | 2.60 | 1456.0 | 4.06 | −0.0028 | ||
| Staurolite (fst) | −23 755.04 | 6.34 | 1010.00 | 44.880 | 2.8800 | −5.6595 | −10642.0 | −25.3730 | 1.83 | 1800.0 | 4.76 | −0.0026 | ||
| Staurolite (mnst) | −24 246.42 | 8.60 | 1034.00 | 45.460 | 2.8733 | −8.9064 | −12688.0 | −24.7490 | 2.09 | 1800.0 | 4.76 | −0.0026 | ||
| Staurolite (mst) | −25 124.32 | 6.28 | 910.00 | 44.260 | 2.8205 | −5.9366 | −13774.0 | −24.1260 | 1.81 | 1684.0 | 4.05 | −0.0024 | ||
| Topaz (tpz) | −2900.76 | 0.96 | 100.50 | 5.339 | 0.3877 | −0.7120 | −857.2 | −3.7442 | 1.57 | 1315.0 | 4.06 | −0.0031 | ||
| Other orthosilicates | Akermanite (ak) | −3865.63 | 0.94 | 212.50 | 9.254 | 0.3854 | 0.3209 | −247.5 | −2.8899 | 2.57 | 1420.0 | 4.06 | −0.0029 | |
| Gehlenite (geh) | −3992.26 | 1.33 | 198.50 | 9.024 | 0.4057 | −0.7099 | −1188.3 | −3.1744 | 2.23 | 1080.0 | 4.08 | −0.0038 | 2 | |
| Julgoldite (jgd) | −11 809.63 | 8.50 | 830.00 | 31.080 | 1.7954 | −3.7986 | −4455.7 | −14.8880 | 2.49 | 1615.0 | 4.05 | −0.0025 | ||
| Merwinite (merw) | −4545.87 | 1.36 | 253.10 | 9.847 | 0.4175 | 0.8117 | −2923.0 | −2.3203 | 3.19 | 1200.0 | 4.07 | −0.0034 | ||
| Pumpellyite (fpm) | −14 033.82 | 2.63 | 657.00 | 29.680 | 1.7372 | −2.4582 | −5161.1 | −14.9630 | 2.49 | 1615.0 | 4.05 | −0.0025 | ||
| Pumpellyite (mpm) | −14 386.75 | 2.41 | 629.00 | 29.550 | 1.7208 | −2.4928 | −5998.7 | −14.6203 | 2.47 | 1615.0 | 4.05 | −0.0025 | ||
| Rankinite (rnk) | −3943.92 | 1.36 | 210.00 | 9.651 | 0.3723 | −0.2893 | −2462.4 | −2.1813 | 3.28 | 950.0 | 4.09 | −0.0043 | ||
| Sphene (sph) | −2601.65 | 0.96 | 124.00 | 5.565 | 0.2279 | 0.2924 | −3539.5 | −0.8943 | 1.58 | 1017.0 | 9.85 | −0.0097 | 1 | |
| Spurrite (spu) | −5847.08 | 2.23 | 332.00 | 14.697 | 0.6141 | −0.3508 | −2493.1 | −4.1680 | 3.40 | 950.0 | 4.09 | −0.0043 | ||
| Tilleyite (ty) | −6368.39 | 2.21 | 390.00 | 17.039 | 0.7417 | −0.5345 | −1434.6 | −5.8785 | 3.41 | 950.0 | 4.09 | −0.0043 | ||
| Zircon (zrc) | −2035.05 | 1.66 | 83.03 | 3.926 | 0.2320 | −1.4405 | 0 | −2.2382 | 1.25 | 2301.0 | 4.04 | −0.0018 | ||
| Sorosilicates | Clinozoisite (cz) | −6895.42 | 1.31 | 301.00 | 13.630 | 0.6309 | 1.3693 | −6645.8 | −3.7311 | 2.33 | 1197.0 | 4.07 | −0.0034 | |
| Epidote (ep) | −6473.90 | 1.17 | 315.00 | 13.920 | 0.6133 | 2.2070 | −7160.0 | −2.9877 | 2.34 | 1340.0 | 4.00 | −0.0030 | ||
| Epidote (fep) | −6027.57 | 1.23 | 329.00 | 14.210 | 0.5847 | 3.0447 | −7674.2 | −2.2443 | 2.31 | 1513.0 | 4.00 | −0.0026 | ||
| Lawsonite (law) | −4868.61 | 0.81 | 229.00 | 10.132 | 0.6878 | 0.1566 | 375.9 | −7.1792 | 2.65 | 1229.0 | 5.45 | −0.0044 | ||
| Piemontite (pmt) | −6543.04 | 2.70 | 340.00 | 13.820 | 0.5698 | 2.7790 | −5442.9 | −2.8126 | 2.38 | 1197.0 | 4.07 | −0.0034 | ||
| Zoisite (zo) | −6896.21 | 1.31 | 298.00 | 13.575 | 0.6620 | 1.0416 | −6006.4 | −4.2607 | 3.12 | 1044.0 | 4.00 | −0.0038 | ||
| Vesuvianite (vsv) | −42 345.19 | 8.95 | 1890.00 | 85.200 | 4.4880 | −5.7952 | −22269.3 | −33.4780 | 2.75 | 1255.0 | 4.80 | −0.0038 | ||
| Cyclosilicates | Cordierite (crd) | −9163.48 | 1.51 | 404.10 | 23.322 | 0.9061 | 0 | −7902.0 | −6.2934 | 0.68 | 1290.0 | 4.10 | −0.0031 | 2 |
| Cordierite (fcrd) | −8444.02 | 1.66 | 461.00 | 23.710 | 0.9240 | 0 | −7039.4 | −6.4396 | 0.67 | 1290.0 | 4.10 | −0.0031 | 2 | |
| Cordierite (hcrd) | −9449.32 | 1.52 | 475.60 | 23.322 | 0.9802 | 0 | −7035.9 | −6.6808 | 0.67 | 1290.0 | 4.10 | −0.0031 | 2 | |
| Cordierite (mncrd) | −8693.64 | 3.60 | 473.00 | 24.027 | 0.8865 | 0 | −8840.0 | −5.5904 | 0.69 | 1290.0 | 4.10 | −0.0031 | 2 | |
| Osumilite (fosm) | −14 238.91 | 3.99 | 762.00 | 38.320 | 1.6560 | −3.4163 | −6497.7 | −14.1143 | 0.49 | 800.0 | 4.10 | −0.0051 | ||
| Osumilite (osm1) | −14 959.21 | 3.83 | 701.00 | 37.893 | 1.6258 | −3.5548 | −8063.5 | −13.4909 | 0.47 | 810.0 | 4.10 | −0.0051 | ||
| Osumilite (osm2) | −14 799.99 | 4.05 | 724.00 | 38.440 | 1.6106 | −3.4457 | −8262.1 | −13.1288 | 0.47 | 810.0 | 4.10 | −0.0051 | ||
| High-pressure phases | akimotoite (fak) | −1142.14 | 10.12 | 91.50 | 2.760 | 0.1003 | 1.3328 | −4364.9 | 0.4198 | 2.12 | 2180.0 | 4.55 | −0.0022 | |
| Akimotoite (mak) | −1490.85 | 0.62 | 59.30 | 2.635 | 0.1478 | 0.2015 | −2395.0 | −0.8018 | 2.12 | 2110.0 | 4.55 | −0.0022 | ||
| CaSi-titanite (cstn) | −2496.17 | 2.81 | 99.50 | 4.818 | 0.2056 | 0.6034 | −5517.7 | −0.3526 | 1.58 | 1782.0 | 4.00 | −0.0022 | ||
| Perovskite (apv) | −1646.76 | 1.12 | 51.80 | 2.540 | 0.1395 | 0.5890 | −2460.6 | −0.5892 | 1.80 | 2030.0 | 4.00 | −0.0020 | ||
| Perovskite (cpv) | −1541.73 | 1.80 | 73.50 | 2.745 | 0.1593 | 0 | −967.3 | −1.0754 | 1.87 | 2360.0 | 3.90 | −0.0016 | ||
| Perovskite (fpv) | −1084.64 | 8.14 | 91.00 | 2.548 | 0.1332 | 1.0830 | −3661.4 | −0.3147 | 1.87 | 2810.0 | 4.14 | −0.0016 | ||
| Perovskite (mpv) | −1443.02 | 0.69 | 62.60 | 2.445 | 0.1493 | 0.2918 | −2983.0 | −0.7991 | 1.87 | 2510.0 | 4.14 | −0.0016 | ||
| PhaseA (phA) | −7132.27 | 1.90 | 348.00 | 15.442 | 0.9640 | −1.1521 | −4517.8 | −7.7247 | 3.79 | 1450.0 | 4.06 | −0.0028 | ||
| Ringwoodite (frw) | −1471.79 | 0.76 | 140.00 | 4.203 | 0.1668 | 4.2610 | −1705.4 | −0.5414 | 2.22 | 1977.0 | 4.92 | −0.0025 | ||
| Ringwoodite (mrw) | −2127.66 | 0.78 | 90.00 | 3.949 | 0.2133 | 0.2690 | −1410.4 | −1.4959 | 2.01 | 1781.0 | 4.35 | −0.0024 | ||
| Wadsleyite (fwd) | −1467.92 | 0.97 | 146.00 | 4.321 | 0.2011 | 1.7330 | −1960.6 | −0.9009 | 2.73 | 1690.0 | 4.35 | −0.0026 | ||
| Wadsleyite (mwd) | −2138.50 | 0.76 | 93.90 | 4.051 | 0.2087 | 0.3942 | −1709.5 | −1.3028 | 2.37 | 1726.0 | 3.84 | −0.0022 | ||
| Pyroxene and pyroxenoid | Acmite (acm) | −2583.50 | 2.43 | 170.60 | 6.459 | 0.3071 | 1.6758 | −1685.5 | −2.1258 | 2.11 | 1060.0 | 4.08 | −0.0038 | |
| Ca-eskola pyroxene (caes) | −3002.01 | 1.74 | 127.00 | 6.050 | 0.3620 | −1.6944 | −175.9 | −3.5657 | 2.31 | 1192.0 | 5.19 | −0.0044 | ||
| Ca-Tschermak pyroxene (cats) | −3310.14 | 0.80 | 135.00 | 6.356 | 0.3476 | −0.6974 | −1781.6 | −2.7575 | 2.08 | 1192.0 | 5.19 | −0.0044 | 2 | |
| Clinoenstatite (cen) | −3091.12 | 0.66 | 132.00 | 6.264 | 0.3060 | −0.3793 | −3041.7 | −1.8521 | 2.11 | 1059.0 | 8.65 | −0.0082 | ||
| Clinoenstatite high-P (hen) | −3082.74 | 0.67 | 131.70 | 6.099 | 0.3562 | −0.2990 | −596.9 | −3.1853 | 2.26 | 1500.0 | 5.50 | −0.0036 | ||
| Diopside (di) | −3201.69 | 0.62 | 142.90 | 6.619 | 0.3145 | 0.0041 | −2745.9 | −2.0201 | 2.73 | 1192.0 | 5.19 | −0.0044 | ||
| Enstatite (en) | −3090.23 | 0.66 | 132.50 | 6.262 | 0.3562 | −0.2990 | −596.9 | −3.1853 | 2.27 | 1059.0 | 8.65 | −0.0082 | ||
| Ferrosilite (fs) | −2388.72 | 0.81 | 189.90 | 6.592 | 0.3987 | −0.6579 | 1290.1 | −4.0580 | 3.26 | 1010.0 | 4.08 | −0.0040 | ||
| Hedenbergite (hed) | −2841.92 | 0.94 | 175.00 | 6.795 | 0.3402 | 0.0812 | −1047.8 | −2.6467 | 2.38 | 1192.0 | 3.97 | −0.0033 | ||
| Jadeite (jd) | −3025.26 | 1.67 | 133.50 | 6.040 | 0.3194 | 0.3616 | −1173.9 | −2.4695 | 2.10 | 1281.0 | 3.81 | −0.0030 | ||
| Kosmochlore (kos) | −2746.80 | 2.46 | 149.65 | 6.309 | 0.3092 | 0.5419 | −664.6 | −2.1766 | 1.94 | 1308.0 | 3.00 | −0.0023 | ||
| Mg-Tschermak pyroxene (mgts) | −3196.61 | 0.73 | 131.00 | 6.050 | 0.3714 | −0.4082 | −398.4 | −3.5471 | 2.17 | 1028.0 | 8.55 | −0.0083 | ||
| Protoenstatite (pren) | −3084.57 | 0.67 | 137.00 | 6.476 | 0.3562 | −0.2990 | −596.9 | −3.1853 | 2.30 | 1059.0 | 8.65 | −0.0082 | ||
| Pseudowollastonite (pswo) | −1627.94 | 0.47 | 87.80 | 4.008 | 0.1578 | 0 | −967.3 | −1.0754 | 2.85 | 1100.0 | 4.08 | −0.0037 | ||
| Pyroxmangite (pxmn) | −1323.14 | 0.73 | 99.30 | 3.472 | 0.1384 | 0.4088 | −1936.0 | −0.5389 | 2.80 | 840.0 | 4.00 | −0.0048 | ||
| Rhodonite (rhod) | −1322.35 | 0.73 | 100.50 | 3.494 | 0.1384 | 0.4088 | −1936.0 | −0.5389 | 2.81 | 840.0 | 4.00 | −0.0048 | ||
| Walstromite (wal) | −1625.88 | 0.48 | 83.50 | 3.763 | 0.1593 | 0 | −967.3 | −1.0754 | 2.54 | 795.0 | 4.10 | −0.0052 | ||
| Wollastonite (wo) | −1633.75 | 0.47 | 82.50 | 3.993 | 0.1593 | 0 | −967.3 | −1.0754 | 2.54 | 795.0 | 4.10 | −0.0052 | ||
| Amphibole | Anthophyllite (anth) | −12066.85 | 2.48 | 537.00 | 26.540 | 1.2773 | 2.5825 | −9704.6 | −9.0747 | 2.52 | 700.0 | 4.11 | −0.0059 | |
| Anthophyllite (fanth) | −9624.53 | 8.80 | 725.00 | 27.870 | 1.3831 | 3.0669 | −4224.7 | −11.2576 | 2.74 | 700.0 | 4.11 | −0.0059 | ||
| Cummingtonite (cumm) | −12064.71 | 2.48 | 538.00 | 26.330 | 1.2773 | 2.5825 | −9704.6 | −9.0747 | 2.52 | 700.0 | 4.11 | −0.0059 | ||
| Ferroactinolite (fact) | −10503.82 | 2.88 | 710.00 | 28.420 | 1.2900 | 2.9992 | −8447.5 | −8.9470 | 2.88 | 760.0 | 4.10 | −0.0054 | ||
| Glaucophane (fgl) | −10880.25 | 5.15 | 624.00 | 26.590 | 1.7629 | −11.8992 | 9423.7 | −20.2071 | 1.83 | 890.0 | 4.09 | −0.0046 | ||
| Glaucophane (gl) | −11960.24 | 3.55 | 530.00 | 25.980 | 1.7175 | −12.1070 | 7075.0 | −19.2720 | 1.49 | 883.0 | 4.09 | −0.0046 | ||
| Grunerite (grun) | −9607.15 | 3.02 | 735.00 | 27.840 | 1.3831 | 3.0669 | −4224.7 | −11.2576 | 2.74 | 648.0 | 4.12 | −0.0064 | ||
| Pargasite (parg) | −12664.49 | 2.27 | 635.00 | 27.190 | 1.2802 | 2.2997 | −12359.5 | −8.0658 | 2.80 | 912.0 | 4.09 | −0.0045 | ||
| Riebeckite (rieb) | −10024.77 | 5.30 | 695.00 | 27.490 | 1.7873 | −12.4882 | 9627.1 | −20.2755 | 1.80 | 890.0 | 4.09 | −0.0046 | ||
| Tremolite (tr) | −12304.56 | 2.17 | 553.00 | 27.270 | 1.2602 | 0.3830 | −11455.0 | −8.2376 | 2.61 | 762.0 | 4.10 | −0.0054 | ||
| Tschermakite (ts) | −12555.30 | 1.77 | 533.00 | 26.800 | 1.2448 | 2.4348 | −11965.0 | −8.1121 | 2.66 | 760.0 | 4.10 | −0.0054 | ||
| Other chain silicates | Deerite (deer ) | −18341.50 | 6.45 | 1650.00 | 55.740 | 3.1644 | −2.7883 | −5039.1 | −26.7210 | 2.75 | 630.0 | 4.12 | −0.0065 | |
| Carpholite (fcar) | −4411.57 | 1.01 | 251.10 | 10.695 | 0.6866 | −1.2415 | 186.0 | −6.8840 | 2.21 | 525.0 | 4.14 | −0.0079 | ||
| Carpholite (mcar) | −4771.22 | 0.79 | 221.50 | 10.590 | 0.6830 | −1.4054 | 291.0 | −6.9764 | 2.43 | 525.0 | 4.14 | −0.0079 | ||
| Sapphirine (fspr) | −9659.86 | 5.87 | 485.00 | 19.923 | 1.1329 | −0.7348 | −10420.2 | −7.0366 | 1.96 | 2500.0 | 4.04 | −0.0017 | ||
| Sapphirine (spr4) | −11022.40 | 3.10 | 425.50 | 19.900 | 1.1331 | −0.7596 | −8816.6 | −8.1806 | 2.05 | 2500.0 | 4.04 | −0.0016 | ||
| Sapphirine (spr5) | −11135.69 | 3.83 | 419.50 | 19.750 | 1.1034 | 0.1015 | −10957.0 | −7.4092 | 2.06 | 2500.0 | 4.04 | −0.0016 | ||
| Mica | annite (ann) | −5144.23 | 3.19 | 418.00 | 15.432 | 0.8157 | −3.4861 | 19.8 | −7.4667 | 3.80 | 513.0 | 7.33 | −0.0143 | |
| Celadonite (cel) | −5834.87 | 2.83 | 290.00 | 13.957 | 0.7412 | −1.8748 | −2368.8 | −6.6169 | 3.07 | 700.0 | 4.11 | −0.0059 | ||
| Celadonite (fcel) | −5468.47 | 2.86 | 330.00 | 14.070 | 0.7563 | −1.9147 | −1586.1 | −6.9287 | 3.18 | 700.0 | 4.11 | −0.0059 | ||
| Eastonite (east) | −6330.48 | 3.04 | 318.00 | 14.738 | 0.7855 | −3.8031 | −2130.3 | −6.8937 | 3.80 | 530.0 | 7.33 | −0.0143 | ||
| Margarite (ma) | −6242.11 | 1.40 | 265.00 | 12.964 | 0.7444 | −1.6800 | −2074.4 | −6.7832 | 2.33 | 1000.0 | 4.08 | −0.0041 | ||
| Mn-biotite (mnbi) | −5477.59 | 4.85 | 433.00 | 15.264 | 0.8099 | −5.9213 | −1514.4 | −6.9987 | 3.80 | 530.0 | 7.33 | −0.0143 | ||
| Muscovite (mu) | −5976.56 | 2.90 | 292.00 | 14.083 | 0.7564 | −1.9840 | −2170.0 | −6.9792 | 3.07 | 490.0 | 4.15 | −0.0085 | ||
| Na-phlogopite (naph) | −6171.92 | 1.99 | 318.00 | 14.450 | 0.7735 | −4.0229 | −2597.9 | −6.5126 | 3.28 | 513.0 | 7.33 | −0.0143 | ||
| Paragonite (pa) | −5942.91 | 1.81 | 277.00 | 13.211 | 0.8030 | −3.1580 | 217.0 | −8.1510 | 3.70 | 515.0 | 6.51 | −0.0126 | ||
| Phlogopite (phl) | −6214.95 | 2.90 | 326.00 | 14.964 | 0.7703 | −3.6939 | −2328.9 | −6.5316 | 3.80 | 513.0 | 7.33 | −0.0143 | ||
| Chlorites | Al-free chlorite (afchl) | −8728.65 | 2.27 | 439.00 | 21.570 | 1.1550 | −0.0417 | −4024.4 | −9.9529 | 2.04 | 870.0 | 4.09 | −0.0047 | |
| Amesite (ames) | −9039.80 | 1.96 | 413.00 | 20.710 | 1.1860 | −0.2599 | −3627.2 | −10.6770 | 2.00 | 870.0 | 4.09 | −0.0047 | ||
| Clinochlore (clin) | −8909.23 | 1.55 | 437.00 | 21.140 | 1.1708 | −0.1508 | −3825.8 | −10.3150 | 2.04 | 870.0 | 4.09 | −0.0047 | ||
| Daphnite (daph) | −7116.71 | 3.20 | 584.00 | 21.620 | 1.1920 | −0.5940 | −4826.4 | −9.7683 | 2.27 | 870.0 | 4.09 | −0.0047 | ||
| Mn-chlorite (mnchl) | −7702.37 | 8.36 | 595.00 | 22.590 | 1.1365 | −0.5243 | −5548.1 | −8.9115 | 2.23 | 870.0 | 4.09 | −0.0047 | ||
| Sudoite (fsud) | −7900.11 | 2.08 | 456.00 | 20.400 | 1.4663 | −4.7365 | −1182.8 | −14.3880 | 2.08 | 870.0 | 4.09 | −0.0047 | ||
| Sudoite (sud) | −8626.91 | 1.65 | 395.00 | 20.300 | 1.4361 | −4.8749 | −2748.5 | −13.7640 | 1.99 | 870.0 | 4.09 | −0.0047 | ||
| Other sheet silicates | Antigorite (atg) | −71416.61 | 15.14 | 3600.00 | 175.480 | 9.6210 | −9.1183 | −35941.6 | −83.0342 | 2.60 | 496.0 | 6.31 | −0.0127 | |
| Chrysotile (chr) | −4360.96 | 0.98 | 221.30 | 10.746 | 0.6247 | −2.0770 | −1721.8 | −5.6194 | 2.20 | 628.0 | 4.00 | −0.0064 | ||
| Fe-talc (fta) | −4798.43 | 4.24 | 352.00 | 14.225 | 0.5797 | 3.9494 | −6459.3 | −3.0881 | 1.80 | 430.0 | 6.17 | −0.0144 | ||
| Greenalite (glt) | −3297.65 | 1.69 | 310.00 | 11.980 | 0.5764 | 0.2984 | −3757.0 | −4.1662 | 2.28 | 630.0 | 4.00 | −0.0063 | ||
| Kaolinite (kao) | −4122.10 | 0.78 | 203.70 | 9.934 | 0.4367 | −3.4295 | −4055.9 | −2.6991 | 2.51 | 645.0 | 4.12 | −0.0064 | ||
| Lizardite (liz) | −4369.14 | 1.08 | 212.00 | 10.645 | 0.6147 | −2.0770 | −1721.8 | −5.6194 | 2.20 | 710.0 | 3.20 | −0.0045 | ||
| Minnesotaite (minn) | −4819.29 | 1.49 | 355.00 | 14.851 | 0.5797 | 3.9494 | −6459.3 | −3.0881 | 1.80 | 430.0 | 6.17 | −0.0144 | ||
| Minnesotaite (minm) | −5866.01 | 10.26 | 263.90 | 14.291 | 0.6222 | 0 | −6385.5 | −3.9163 | 1.80 | 430.0 | 6.17 | −0.0144 | ||
| Prehnite (fpre) | −5766.75 | 1.35 | 320.00 | 14.800 | 0.7371 | −1.6810 | −1957.3 | −6.3581 | 1.58 | 1093.0 | 4.01 | −0.0037 | ||
| Prehnite (pre) | −6202.10 | 1.11 | 292.80 | 14.026 | 0.7249 | −1.3865 | −2059.0 | −6.3239 | 1.58 | 1093.0 | 4.01 | −0.0037 | ||
| Prl-talc (tap) | −5589.24 | 1.03 | 245.00 | 13.450 | 0.7845 | −4.2948 | 1251.0 | −8.4959 | 4.50 | 370.0 | 10.00 | −0.0271 | ||
| Pyrophyllite (prl) | −5640.68 | 1.01 | 239.00 | 12.804 | 0.7845 | −4.2948 | 1251.0 | −8.4959 | 4.50 | 370.0 | 10.00 | −0.0271 | ||
| Stilpnomelane (fstp) | −12550.45 | 9.09 | 930.20 | 37.239 | 1.9443 | −1.2289 | −4840.2 | −16.6350 | 3.68 | 513.0 | 7.33 | −0.0143 | ||
| Stilpnomelane (mstp) | −14288.03 | 25.51 | 847.40 | 36.577 | 1.8622 | −1.4018 | −8983.1 | −14.9230 | 3.71 | 513.0 | 7.33 | −0.0143 | ||
| Talc (ta) | −5897.17 | 1.16 | 259.00 | 13.665 | 0.6222 | 0 | −6385.5 | −3.9163 | 1.80 | 430.0 | 6.17 | −0.0144 | ||
| Tschermak-talc (tats) | −5992.20 | 0.98 | 259.00 | 13.510 | 0.5495 | 3.6324 | −8606.6 | −2.5153 | 1.80 | 430.0 | 6.17 | −0.0144 | ||
| Feldspar and feldspathoid | Albite (ab) | −3935.49 | 1.69 | 207.40 | 10.067 | 0.4520 | −1.3364 | −1275.9 | −3.9536 | 2.36 | 541.0 | 5.91 | −0.0109 | 2 |
| Albite-high (abh) | −3921.49 | 1.68 | 224.30 | 10.105 | 0.4520 | −1.3364 | −1275.9 | −3.9536 | 2.40 | 541.0 | 5.91 | −0.0109 | ||
| Analcite (anl) | −3307.25 | 1.68 | 232.00 | 9.740 | 0.6435 | −1.6067 | 9302.3 | −9.1796 | 2.76 | 400.0 | 4.18 | −0.0104 | ||
| Anorthite (an) | −4232.70 | 0.79 | 200.50 | 10.079 | 0.3705 | 1.0010 | −4339.1 | −1.9606 | 1.41 | 860.0 | 4.09 | −0.0048 | 2 | |
| Carnegieite-high (cgh) | −2077.99 | 1.76 | 135.00 | 5.670 | 0.2292 | 1.1876 | 0 | −1.9707 | 4.67 | 465.0 | 4.16 | −0.0089 | ||
| Carnegieite-low (cg) | −2091.70 | 1.76 | 118.70 | 5.603 | 0.1161 | 8.6021 | −1992.7 | 0 | 4.50 | 465.0 | 4.16 | −0.0089 | ||
| Kalsilite (kls) | −2122.89 | 2.91 | 136.00 | 6.052 | 0.2420 | −0.4482 | −895.8 | −1.9358 | 3.16 | 514.0 | 2.00 | −0.0039 | ||
| Leucite (lc) | −3029.23 | 2.82 | 198.50 | 8.826 | 0.3698 | −1.6332 | 684.7 | −3.6831 | 1.85 | 450.0 | 5.70 | −0.0127 | 2 | |
| Microcline (mic) | −3975.33 | 2.80 | 214.30 | 10.871 | 0.4488 | −1.0075 | −1007.3 | −3.9731 | 1.65 | 583.0 | 4.02 | −0.0069 | ||
| Nepheline (ne) | −2094.54 | 1.75 | 124.40 | 5.419 | 0.2727 | −1.2398 | 0 | −2.7631 | 4.63 | 465.0 | 4.16 | −0.0089 | 1 | |
| Sanidine (san) | −3966.68 | 2.80 | 214.30 | 10.871 | 0.4488 | −1.0075 | −1007.3 | −3.9731 | 1.65 | 583.0 | 4.02 | −0.0069 | 2 | |
| Silica minerals | Coesite (coe) | −907.02 | 0.27 | 39.60 | 2.064 | 0.1078 | −0.3279 | −190.3 | −1.0416 | 1.23 | 979.0 | 4.19 | −0.0043 | |
| Cristobalite (crst) | −904.24 | 0.27 | 50.86 | 2.745 | 0.0727 | 0.1304 | −4129.0 | 0 | 0 | 160.0 | 4.35 | −0.0272 | ||
| Quartz (q) | −910.70 | 0.27 | 41.43 | 2.269 | 0.0929 | −0.0642 | −714.9 | −0.7161 | 0 | 730.0 | 6.00 | −0.0082 | 1 | |
| Stishovite (stv) | −876.39 | 0.49 | 24.00 | 1.401 | 0.0681 | 0.6010 | −1978.2 | −0.0821 | 1.58 | 3090.0 | 4.60 | −0.0015 | ||
| Tridymite (trd) | −907.08 | 0.27 | 44.10 | 2.800 | 0.0749 | 0.3100 | −1174.0 | −0.2367 | 0 | 150.0 | 4.36 | −0.0291 | ||
| Other framework silicates | Heulandite (heu) | −10 545.09 | 1.80 | 783.00 | 31.700 | 1.5048 | −3.3224 | −2959.3 | −13.2972 | 1.57 | 274.0 | 4.00 | −0.0146 | |
| Hollandite (hol) | −37 91.94 | 5.27 | 166.20 | 7.128 | 0.4176 | −0.3617 | −4748.1 | −2.8199 | 2.80 | 1800.0 | 4.00 | −0.0022 | ||
| Laumontite (lmt) | −7262.64 | 1.12 | 465.00 | 20.370 | 1.0134 | −2.1413 | −2235.8 | −8.8067 | 1.37 | 860.0 | 4.09 | −0.0048 | ||
| Meionite (me) | −13 841.95 | 2.61 | 752.00 | 33.985 | 1.3590 | 3.6442 | −8594.7 | −9.5982 | 1.82 | 870.0 | 4.09 | −0.0047 | ||
| K-cymrite (kcm) | −4232.63 | 2.81 | 281.50 | 11.438 | 0.5365 | −1.0090 | −980.4 | −4.7350 | 3.21 | 425.0 | 2.00 | −0.0047 | ||
| Sodalite (sdl) | −13405.41 | 10.54 | 910.00 | 42.130 | 1.5327 | 4.7747 | −2972.8 | −12.4270 | 4.63 | 465.0 | 4.16 | −0.0089 | ||
| Stilbite (stlb) | −10 896.63 | 2.23 | 710.00 | 32.870 | 1.5884 | −3.2043 | −3071.6 | −13.9669 | 1.51 | 860.0 | 4.09 | −0.0048 | ||
| Wadeite (wa) | −4271.79 | 6.46 | 254.00 | 10.844 | 0.4991 | 0 | 0 | −4.3501 | 2.66 | 900.0 | 4.00 | −0.0044 | ||
| Wairakite (wrk) | −6662.40 | 1.11 | 380.00 | 19.040 | 0.8383 | −2.1460 | −2272.0 | −7.2923 | 1.49 | 860.0 | 4.09 | −0.0048 | ||
| Oxides | Baddelyite (bdy) | −1100.34 | 1.63 | 50.40 | 2.115 | 0.1035 | −0.4547 | −416.2 | −0.7136 | 2.00 | 953.0 | 3.88 | −0.0041 | |
| Bixbyite (bix) | −959.00 | 1.09 | 113.70 | 3.137 | 0.1451 | 2.3534 | 721.6 | −1.0084 | 2.91 | 2230.0 | 4.04 | −0.0018 | ||
| Corundum (cor) | −1675.33 | 0.75 | 50.90 | 2.558 | 0.1395 | 0.5890 | −2460.6 | −0.5892 | 1.80 | 2540.0 | 4.34 | −0.0017 | ||
| Cuprite (cup) | −170.60 | 0.11 | 92.40 | 2.344 | 0.1103 | 0 | 0 | −0.6748 | 3.33 | 1310.0 | 5.70 | −0.0043 | ||
| Eskolaite (esk) | −1137.35 | 4.31 | 83.00 | 2.909 | 0.1190 | 0.9496 | −1442.0 | −0.0034 | 1.59 | 2380.0 | 4.00 | −0.0017 | ||
| Geikielite (geik) | −1568.97 | 0.89 | 73.60 | 3.086 | 0.1510 | 0 | −1890.4 | −0.6522 | 2.15 | 1700.0 | 8.30 | −0.0049 | ||
| Hematite (hem) | −825.65 | 0.68 | 87.40 | 3.027 | 0.1639 | 0 | −2257.2 | −0.6576 | 2.79 | 2230.0 | 4.04 | −0.0018 | 1 | |
| Hercynite (herc) | −1953.09 | 0.85 | 113.90 | 4.075 | 0.2167 | 0.5868 | −2430.2 | −1.1783 | 2.06 | 1922.0 | 4.04 | −0.0021 | 2 | |
| Ilmenite (ilm) | −1230.43 | 0.84 | 109.50 | 3.169 | 0.1389 | 0.5081 | −1288.8 | −0.4637 | 2.40 | 1700.0 | 8.30 | −0.0049 | 1 | |
| Lime (lime) | −634.61 | 0.50 | 38.10 | 1.676 | 0.0524 | 0.3673 | −750.7 | −0.0510 | 3.41 | 1130.0 | 3.87 | −0.0034 | ||
| Manganosite (mang) | −385.55 | 0.41 | 59.70 | 1.322 | 0.0598 | 0.3600 | −31.4 | −0.2826 | 3.69 | 1645.0 | 4.46 | −0.0027 | ||
| Mg-corundum (mcor) | −1474.43 | 2.87 | 59.30 | 2.635 | 0.1478 | 0.2015 | −2395.0 | −0.8018 | 2.12 | 2110.0 | 4.55 | −0.0022 | ||
| Magnesioferrite (mft) | −1442.29 | 2.71 | 121.00 | 4.457 | 0.2705 | −0.7505 | −999.2 | −2.0224 | 3.63 | 1857.0 | 4.05 | −0.0022 | 1 | |
| Magnetite (mt) | −1114.51 | 0.95 | 146.90 | 4.452 | 0.2625 | −0.7205 | −1926.2 | −1.6557 | 3.71 | 1857.0 | 4.05 | −0.0022 | 1 | |
| Ni-oxide (NiO ) | −239.47 | 0.36 | 38.00 | 1.097 | 0.0477 | 0.7824 | −392.5 | 0 | 3.30 | 2000.0 | 3.94 | −0.0020 | 1 | |
| Periclase (per) | −601.55 | 0.27 | 26.50 | 1.125 | 0.0605 | 0.0362 | −535.8 | −0.2992 | 3.11 | 1616.0 | 3.95 | −0.0024 | ||
| Periclase (fper) | −271.97 | 2.05 | 60.60 | 1.206 | 0.0444 | 0.8280 | −1214.2 | 0.1852 | 7.43 | 1520.0 | 4.90 | −0.0032 | ||
| Picrochromite (picr) | −1762.60 | 3.28 | 118.30 | 4.356 | 0.1961 | 0.5398 | −3126.0 | −0.6169 | 1.80 | 1922.0 | 4.04 | −0.0021 | 2 | |
| Pyrophanite (pnt) | −1361.99 | 2.16 | 105.50 | 3.288 | 0.1435 | 0.3373 | −1940.7 | −0.4076 | 2.40 | 1700.0 | 8.30 | −0.0049 | ||
| Rutile (ru) | −944.37 | 0.78 | 50.50 | 1.882 | 0.0904 | 0.2900 | 0 | −0.6238 | 2.24 | 2220.0 | 4.24 | −0.0019 | ||
| Spinel (sp) | −2301.26 | 0.84 | 82.00 | 3.978 | 0.2229 | 0.6127 | −1686.0 | −1.5510 | 1.93 | 1922.0 | 4.04 | −0.0021 | 2 | |
| Tenorite (ten) | −156.10 | 2.18 | 42.60 | 1.222 | 0.0310 | 1.3740 | −1258.0 | 0.3693 | 3.57 | 2000.0 | 3.94 | −0.0020 | ||
| Ulvospinel (usp) | −1491.10 | 1.01 | 180.00 | 4.682 | −0.1026 | 14.2520 | −9144.5 | 5.2707 | 3.86 | 1857.0 | 4.05 | −0.0022 | ||
| Hydroxides | Brucite (br) | −923.65 | 0.30 | 63.20 | 2.463 | 0.1584 | −0.4076 | −1052.3 | −1.1713 | 6.20 | 415.0 | 6.45 | −0.0155 | |
| Diaspore (dsp) | −999.86 | 0.38 | 34.50 | 1.786 | 0.1451 | 0.8709 | 584.4 | −1.7411 | 3.57 | 2280.0 | 4.04 | −0.0018 | ||
| Goethite (gth) | −561.79 | 0.35 | 60.30 | 2.082 | 0.1393 | 0.0147 | −212.7 | −1.0778 | 4.35 | 2500.0 | 4.03 | −0.0016 | ||
| Carbonates | Ankerite (ank) | −1970.62 | 0.77 | 188.46 | 6.606 | 0.3410 | −0.1161 | 0 | −3.0548 | 3.46 | 914.0 | 3.88 | −0.0043 | 2 |
| Aragonite (arag) | −1207.82 | 0.46 | 89.80 | 3.415 | 0.1923 | −0.3052 | 1149.7 | −2.1183 | 6.14 | 614.0 | 5.87 | −0.0096 | 1 | |
| Calcite (cc) | −1207.88 | 0.46 | 92.50 | 3.689 | 0.1409 | 0.5029 | −950.7 | −0.8584 | 2.52 | 733.0 | 4.06 | −0.0055 | 1 | |
| Dolomite (dol) | −2325.76 | 0.58 | 156.10 | 6.429 | 0.3589 | −0.4905 | 0 | −3.4562 | 3.28 | 943.0 | 3.74 | −0.0040 | 2 | |
| Magnesite (mag) | −1110.93 | 0.32 | 65.50 | 2.803 | 0.1864 | −0.3772 | 0 | −1.8862 | 3.38 | 1028.0 | 5.41 | −0.0053 | ||
| Rhodochrosite (rhc) | −892.28 | 0.41 | 98.00 | 3.107 | 0.1695 | 0 | 0 | −1.5343 | 2.44 | 953.0 | 3.88 | −0.0041 | ||
| Siderite (sid) | −762.22 | 0.57 | 93.30 | 2.943 | 0.1684 | 0 | 0 | −1.4836 | 4.39 | 1200.0 | 4.07 | −0.0034 | ||
| Sulphides and halides | Anhydrite (any) | −1434.40 | 3.50 | 106.90 | 4.594 | 0.1287 | 4.8545 | −1223.0 | −0.5605 | 4.18 | 543.8 | 4.19 | −0.0077 | |
| Halite (hlt) | −411.30 | 0.22 | 72.10 | 2.702 | 0.0452 | 1.7970 | 0 | 0 | 11.47 | 238.0 | 5.00 | −0.0210 | ||
| Pyrite (pyr) | −171.64 | 1.28 | 52.90 | 2.394 | 0.0373 | 2.6715 | −1817.0 | 0.6493 | 3.10 | 1395.0 | 4.09 | −0.0029 | ||
| Pyrrhotite (trot) | −99.03 | 1.34 | 65.50 | 1.819 | 0.0502 | 1.1052 | −940.0 | 0 | 5.68 | 658.0 | 4.17 | −0.0063 | 1 | |
| Pyrrhotite (trov) | −96.02 | 1.17 | 57.50 | 1.738 | 0.0511 | 0.8307 | −669.7 | 0 | 5.94 | 658.0 | 4.17 | −0.0063 | 1 | |
| Troilite (lot) | −102.16 | 0.48 | 60.00 | 1.818 | 0.0502 | 1.1052 | −940.0 | 0 | 4.93 | 658.0 | 4.17 | −0.0063 | 1 | |
| Troilite (tro) | −97.76 | 0.48 | 70.80 | 1.819 | 0.0502 | 1.1052 | −940.0 | 0 | 5.73 | 658.0 | 4.17 | −0.0063 | 1 | |
| Sylvite (syv) | −436.50 | 0.22 | 82.60 | 3.752 | 0.0462 | 1.7970 | 0 | 0 | 11.09 | 170.0 | 5.00 | −0.0294 | ||
| Elements | Copper (Cu) | 0 | 0.00 | 33.14 | 0.711 | 0.0124 | 0.9220 | −379.9 | 0.2335 | 3.58 | 1625.0 | 4.24 | −0.0026 | |
| Diamond (diam) | 2.00 | 0.06 | 2.38 | 0.342 | 0.0243 | 0.6272 | −377.4 | −0.2734 | 0.49 | 4465.0 | 1.61 | −0.0004 | ||
| Graphite (gph) | 0.00 | 0.00 | 5.74 | 0.530 | 0.0510 | −0.4429 | 488.6 | −0.8055 | 1.67 | 312.0 | 3.90 | −0.0125 | ||
| Iron (iron) | 0.00 | 0.00 | 27.09 | 0.709 | 0.0462 | 0.5159 | 723.1 | −0.5562 | 3.56 | 1640.0 | 5.16 | −0.0031 | 1 | |
| Nickel (Ni) | 0.00 | 0.00 | 29.87 | 0.659 | 0.0498 | 0 | 585.9 | −0.5339 | 4.28 | 1905.0 | 4.25 | −0.0022 | 1 | |
| Sulphur (S) | 0.00 | 0.00 | 32.05 | 1.551 | 0.0566 | −0.4557 | 638.0 | −0.6818 | 6.40 | 145.0 | 7.00 | −0.0063 | ||
| Gas species | Methane (CH4) | −74.81 | 0.37 | 186.26 | 0 | 0.1501 | 0.2063 | 3427.7 | −2.6504 | 0 | 0 | 0 | 0 | |
| Carbon monoxide (CO) | −110.53 | 0.19 | 197.67 | 0 | 0.0457 | −0.0097 | 662.7 | −0.4147 | 0 | 0 | 0 | 0 | ||
| Carbon dioxide (CO2) | −393.51 | 0.08 | 213.70 | 0 | 0.0878 | −0.2644 | 706.4 | −0.9989 | 0 | 0 | 0 | 0 | ||
| Hydrogen (H2) | 0.00 | 0.00 | 130.70 | 0 | 0.0233 | 0.4627 | 0 | 0.0763 | 0 | 0 | 0 | 0 | ||
| Hydrogen sulphide (H2S) | −20.30 | 0.44 | 205.77 | 0 | 0.0474 | 1.0240 | 615.9 | −0.3978 | 0 | 0 | 0 | 0 | ||
| Oxygen (O2) | −0.00 | 0.00 | 205.20 | 0 | 0.0483 | −0.0691 | 499.2 | −0.4207 | 0 | 0 | 0 | 0 | ||
| Sulphur gas (S2) | 128.54 | 0.32 | 231.00 | 0 | 0.0371 | 0.2398 | −161.0 | −0.0650 | 0 | 0 | 0 | 0 | ||
| Water (H2O) | −241.81 | 0.02 | 188.80 | 0 | 0.0401 | 0.8656 | 487.5 | −0.2512 | 0 | 0 | 0 | 0 | ||
| Melt species | Albite liq (abL) | −3926.05 | 1.69 | 149.90 | 10.858 | 0.3580 | 0 | 0 | 0 | 3.37 | 176.0 | 14.35 | −0.0815 | 4 |
| Anorthite liq (anL) | −4277.91 | 0.84 | 29.00 | 10.014 | 0.4300 | 0 | 0 | 0 | 5.14 | 210.0 | 6.38 | −0.0304 | 4 | |
| Corundum liq (corL) | −1632.02 | 1.02 | 14.90 | 3.369 | 0.1576 | 0 | 0 | 0 | 7.03 | 150.0 | 6.00 | 0 | 4 | |
| Diopside liq (diL) | −3193.70 | 0.70 | 42.10 | 7.288 | 0.3340 | 0 | 0 | 0 | 8.51 | 249.0 | 8.04 | −0.0323 | 4 | |
| Enstatite liq (enL) | −3096.58 | 0.80 | −4.00 | 6.984 | 0.3536 | 0 | 0 | 0 | 6.81 | 218.0 | 7.20 | −0.0330 | 4 | |
| Fayalite liq (faL) | −1463.04 | 0.71 | 96.00 | 4.677 | 0.2437 | 0 | 0 | 0 | 10.71 | 290.0 | 10.42 | −0.0359 | 4 | |
| Forsterite liq (foL) | −2237.32 | 0.60 | −62.00 | 4.312 | 0.2694 | 0 | 0 | 0 | 9.20 | 362.0 | 10.06 | −0.0278 | 4 | |
| Water liq (h2oL) | −295.01 | 0.03 | 45.50 | 1.460 | 0.0800 | 0 | 0 | 0 | 46.33 | 46.2 | 1.50 | −0.0325 | 4 | |
| Halite liq (hltL) | −392.99 | 0.23 | 80.10 | 2.938 | 0.0720 | −0.3223 | 0 | 0 | 29.50 | 64.0 | 4.61 | −0.0720 | 4 | |
| K-feldspar liq (kspL) | −3980.06 | 2.80 | 132.20 | 11.431 | 0.3680 | 0 | 0 | 0 | 4.93 | 174.0 | 6.84 | −0.0393 | 4 | |
| Leucite liq (lcL) | −3068.37 | 2.82 | 102.00 | 8.590 | 0.2870 | 0 | 0 | 0 | 6.70 | 175.0 | 7.00 | −0.0394 | 4 | |
| Lime liq ( limL) | −692.37 | 0.52 | −47.50 | 1.303 | 0.0990 | 0 | 0 | 0 | 17.50 | 362.0 | 10.06 | −0.0278 | 4 | |
| Nepheline liq (neL) | −2116.71 | 1.76 | 52.90 | 5.200 | 0.2165 | 0 | 0 | 0 | 13.70 | 250.0 | 7.37 | −0.0295 | 4 | |
| Periclase liq (perL) | −654.14 | 0.36 | −64.30 | 0.839 | 0.0990 | 0 | 0 | 0 | 22.60 | 362.0 | 10.06 | −0.0278 | 4 | |
| Quartz liq (qL) | −921.03 | 0.27 | 16.30 | 2.730 | 0.0825 | 0 | 0 | 0 | 0 | 220.0 | 9.46 | −0.0430 | 4 | |
| Sillimanite liq (silL) | −2594.05 | 1.79 | 10.00 | 6.051 | 0.2530 | 0 | 0 | 0 | 4.08 | 220.0 | 6.36 | −0.0289 | 4 | |
| Sylvite liq (syvL) | −417.41 | 0.23 | 94.50 | 3.822 | 0.0669 | 0 | 0 | 0 | 30.10 | 56.0 | 4.65 | −0.0830 | 4 | |
| Wollastonite liq (woL) | −1642.20 | 0.51 | 22.50 | 3.965 | 0.1674 | 0 | 0 | 0 | 6.69 | 305.0 | 9.38 | −0.0308 | 4 | |
| Aqueous species | H+ | 0 | 0.00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 |
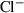 |
−167.08 | 0.11 | 56.73 | 1.779 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
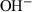 |
−230.02 | 0.11 | −10.71 | −0.418 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| Na+ | −240.30 | 0.11 | 58.40 | −0.111 | 0 | 19.1300 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| K+ | −252.17 | 0.11 | 101.04 | 0.906 | 0 | 7.2700 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| Ca++ | −543.30 | 1.09 | −56.50 | −1.806 | 0 | −6.9000 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| Mg++ | −465.96 | 1.09 | −138.10 | −2.155 | 0 | −4.6200 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| Fe++ | −90.42 | 3.28 | −107.11 | −2.220 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| Al+++ | −527.23 | 1.64 | −316.30 | −4.440 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
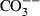 |
−675.23 | 0.11 | −50.00 | −0.502 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| AlOH3 | −1251.85 | 1.09 | 53.60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| AlOH4− | −1495.78 | 1.09 | 126.90 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| KOH | −473.62 | 1.31 | 109.62 | −0.800 | 0 | 9.4500 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| HCl | −162.13 | 0.87 | 56.73 | 1.779 | 0 | 9.0300 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| KCl | −400.03 | 1.42 | 184.81 | 4.409 | 0 | 5.4300 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| NaCl | −399.88 | 1.20 | 126.09 | 2.226 | 0 | 19.1300 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| CaCl2 | −877.06 | 1.31 | 46.00 | 3.260 | 0 | 13.6900 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| CaCl+ | −701.28 | 1.75 | 27.36 | 0.574 | 0 | −6.9000 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| MgCl2 | −796.08 | 2.29 | −22.43 | 2.920 | 0 | 23.9900 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| MgCl+ | −632.48 | 0.87 | −81.37 | 0.126 | 0 | −4.6200 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| FeCl2 | −375.34 | 3.28 | 109.88 | 2.700 | 0 | 45.0300 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| aqSi | −887.81 | 0.68 | 46.35 | 1.832 | 0 | 17.7500 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
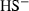 |
−16.04 | 5.46 | 68.00 | 2.065 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| HSO3− | −623.82 | 5.46 | 139.00 | 3.330 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| SO42− | −906.12 | 5.46 | 18.80 | 1.388 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
| HSO4− | −885.70 | 5.46 | 125.04 | 3.520 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 3 | |
-
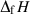 is the regressed enthalpy of formation from the elements;
is the regressed enthalpy of formation from the elements; 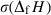 is 1SD on the enthalpy of formation;
is 1SD on the enthalpy of formation; 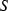 is the entropy;
is the entropy; 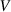 the volume (all properties at 1 bar and 298 K);
the volume (all properties at 1 bar and 298 K);  ,
, 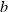 ,
,  and
and 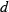 are the coefficients in the heat capacity polynomial
are the coefficients in the heat capacity polynomial 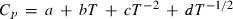 ;
;  and
and  are thermal expansion and bulk modulus;
are thermal expansion and bulk modulus; 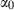 is the thermal expansion parameter;
is the thermal expansion parameter; 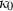 ,
, 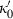 and
and 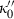 are the bulk modulus (at 298 K, 1 bar) and its first and second pressure derivatives;
are the bulk modulus (at 298 K, 1 bar) and its first and second pressure derivatives; 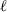 is a flag, 1 signifying a phase transition described via Landau theory and 2 signifying a phase transition described via Bragg-Williams theory, 3 signifies an aqueous species and 4 signifies a melt end-member.
is a flag, 1 signifying a phase transition described via Landau theory and 2 signifying a phase transition described via Bragg-Williams theory, 3 signifies an aqueous species and 4 signifies a melt end-member.
 |
 |
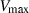 |
|
| lrn | 1710 | 10.03 | 0.0500 |
| sph | 485 | 0.40 | 0.0050 |
| q | 847 | 4.95 | 0.1188 |
| ne | 467 | 10.00 | 0.0800 |
| hem | 955 | 15.60 | 0 |
| NiO | 520 | 5.70 | 0 |
| ilm | 1900 | 12.00 | 0.0200 |
| mt | 848 | 35.00 | 0 |
| mft | 665 | 17.00 | 0 |
| cc | 1240 | 10.00 | 0.0400 |
| arag | 1240 | 9.00 | 0.0450 |
| trot | 598 | 12.00 | 0.0410 |
| tro | 598 | 12.00 | 0.0410 |
| lot | 420 | 10.00 | 0 |
| trov | 595 | 10.00 | 0.0160 |
| iron | 1042 | 8.30 | 0 |
| Ni | 631 | 3.00 | 0 |
-
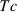 is the critical temperature at 1 bar,
is the critical temperature at 1 bar, 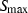 and
and 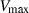 are the entropy and volume of disordering at
are the entropy and volume of disordering at 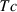 . See Holland & Powell (1998) for further details.
. See Holland & Powell (1998) for further details.
 |
 |
 |
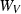 |
 |
Fac | |
|---|---|---|---|---|---|---|
| sill | 4.75 | 0.0100 | 4.75 | 0.0100 | 1 | 0.25 |
| geh | 7.51 | 0.0900 | 7.50 | 0.0900 | 1 | 0.80 |
| crd | 36.71 | 0.1000 | 36.70 | 0.1000 | 2 | 1.50 |
| hcrd | 36.71 | 0.1000 | 36.70 | 0.1000 | 2 | 1.50 |
| fcrd | 36.71 | 0.1000 | 36.70 | 0.1000 | 2 | 1.50 |
| mncrd | 36.71 | 0.1000 | 36.70 | 0.1000 | 2 | 1.50 |
| cats | 3.80 | 0.0100 | 3.80 | 0.0100 | 1 | 0.25 |
| ab | 14.00 | 0.0420 | 13.00 | 0.0420 | 3 | 0.90 |
| san | 8.65 | 0.0240 | 8.50 | 0.0240 | 3 | 0.80 |
| an | 42.01 | 0.1000 | 42.00 | 0.1000 | 1 | 2.00 |
| lc | 11.61 | 0.4000 | 11.60 | 0.4000 | 2 | 0.70 |
| sp | 8.00 | 0 | 1.20 | 0 | 2 | 0.50 |
| herc | 18.30 | 0 | 13.60 | 0 | 2 | 1.00 |
| picr | 8.00 | 0 | 1.20 | 0 | 2 | 0.50 |
| dol | 11.91 | 0.0160 | 11.90 | 0.0160 | 1 | 1.00 |
| ank | 11.91 | 0.0160 | 11.90 | 0.0160 | 1 | 1.00 |
-
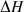 and
and 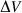 are the total enthalpy and volume of disordering,
are the total enthalpy and volume of disordering, 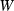 and
and 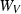 are the interaction energy terms used in
are the interaction energy terms used in 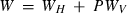 ,
,  is the number of Si disordering with each Al, and fac is a scaling factor on the energy of disordering. See Holland & Powell (1996a,b) for further details.
is the number of Si disordering with each Al, and fac is a scaling factor on the energy of disordering. See Holland & Powell (1996a,b) for further details.
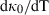 , the temperature dependence of the bulk modulus for melt end-members in the data set.
, the temperature dependence of the bulk modulus for melt end-members in the data set. 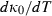 |
|
| SyvL | −0.02000 |
| hltL | −0.01500 |
| perL | −0.04100 |
| limL | −0.04100 |
| corL | −0.03500 |
| qL | −0.03500 |
| h2oL | −0.00001 |
| foL | −0.04400 |
| faL | −0.05500 |
| woL | −0.02000 |
| enL | −0.02400 |
| diL | −0.03730 |
| silL | −0.02900 |
| anL | −0.05500 |
| kspL | −0.00900 |
| abL | −0.02600 |
| neL | −0.00800 |
| lcL | 0 |
- See Holland & Powell (1998) for further details.
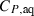 , the augmented
, the augmented 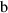 term in the heat capacity for aqueous species in the modified density model of Anderson et al., (1991),
term in the heat capacity for aqueous species in the modified density model of Anderson et al., (1991), 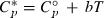 .
.  |
|
| Na+ | 0.0306 |
| K+ | 0.0072 |
| AlOH3 | 0.1015 |
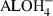 |
0.0965 |
| HCl | 0.0540 |
| CaCl2 | 0.0343 |
| CaCl+ | 0.0400 |
| MgCl2 | 0.0186 |
| MgCl+ | 0.1126 |
| FeCl2 | 0.0124 |
| aqSi | 0.0283 |
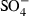 |
0.2680 |
| HSO4− | 0.0220 |
- See Holland & Powell (1998) for further details.
| ΔfH | σ | e * | hat | |
|---|---|---|---|---|
| fo | −2173.00 | 2.00 | −0.22 | 0.07 |
| fa | −1478.20 | 1.40 | −0.34 | 0.20 |
| teph | −1731.50 | 3.00 | 0.82 | 0.10 |
| lrn | −2306.70 | 3.00 | 0.11 | 0.08 |
| py | −6285.00 | 4.00 | −0.72 | 0.06 |
| alm | −5264.70 | 5.00 | −0.81 | 0.06 |
| gr | −6643.00 | 3.00 | −0.02 | 0.20 |
| andr | −5771.00 | 5.90 | −0.32 | 0.06 |
| and | −2589.90 | 2.00 | −0.59 | 0.10 |
| ky | −2593.80 | 2.00 | −0.39 | 0.10 |
| sill | −2586.10 | 2.00 | −0.13 | 0.10 |
| ak | −3865.40 | 3.00 | 0.08 | 0.08 |
| crd | −9161.50 | 5.90 | 0.34 | 0.06 |
| sph | −2602.90 | 3.00 | −0.41 | 0.09 |
| zrc | −2034.20 | 3.10 | 0.27 | 0.24 |
| en | −3091.20 | 3.00 | −0.32 | 0.04 |
| cen | −3091.10 | 3.00 | 0.01 | 0.04 |
| fs | −2390.40 | 6.00 | −0.28 | 0.02 |
| di | −3201.50 | 2.00 | 0.10 | 0.08 |
| jd | −3029.30 | 3.60 | −1.12 | 0.18 |
| cats | −3306.30 | 5.00 | 0.77 | 0.02 |
| rhod | −1321.60 | 2.00 | 0.38 | 0.11 |
| pxmn | −1322.30 | 2.00 | 0.42 | 0.11 |
| wo | −1634.80 | 1.40 | −0.75 | 0.09 |
| pswo | −1627.60 | 1.40 | 0.25 | 0.09 |
| prl | −5640.00 | 1.50 | 0.46 | 0.38 |
| ta | −5897.20 | 2.00 | −0.02 | 0.28 |
| kao | −4120.10 | 4.00 | 0.50 | 0.03 |
| chr | −4360.00 | 3.00 | 0.32 | 0.09 |
| ab | −3935.00 | 2.60 | 0.19 | 0.35 |
| abh | −3921.00 | 5.00 | 0.10 | 0.10 |
| mic | −3974.60 | 3.90 | 0.19 | 0.43 |
| san | −3965.60 | 4.10 | 0.26 | 0.39 |
| an | −4234.00 | 3.00 | −0.43 | 0.06 |
| q | −910.70 | 0.50 | −0.01 | 0.25 |
| trd | −907.00 | 4.00 | 0.02 | 0.00 |
| coe | −905.60 | 2.10 | 0.67 | 0.01 |
| ne | −2092.10 | 3.90 | 0.63 | 0.17 |
| cg | −2089.30 | 4.00 | 0.60 | 0.16 |
| anl | −3310.10 | 5.00 | −0.57 | 0.09 |
| lime | −635.10 | 0.90 | −0.54 | 0.26 |
| ru | −944.00 | 0.80 | 0.46 | 0.79 |
| per | −601.60 | 0.30 | −0.18 | 0.70 |
| fper | −260.00 | 5.00 | −0.03 | 0.42 |
| mang | −385.20 | 0.50 | 0.71 | 0.57 |
| cor | −1675.70 | 1.30 | −0.28 | 0.28 |
| hem | −826.20 | 1.30 | −0.43 | 0.23 |
| bix | −959.00 | 1.00 | 0 | 1.00 |
| NiO | −239.30 | 0.40 | 0.44 | 0.69 |
| pnt | −1360.10 | 4.00 | 0.47 | 0.24 |
| ilm | −1232.00 | 2.50 | −0.63 | 0.09 |
| bdy | −1100.60 | 1.70 | −0.15 | 0.77 |
| ten | −156.10 | 2.00 | 0 | 1.00 |
| cup | −170.60 | 0.10 | 0 | 1.00 |
| sp | −2299.10 | 2.00 | 1.08 | 0.15 |
| mt | −1115.73 | 2.10 | −0.58 | 0.17 |
| mft | −1441.50 | 3.00 | 0.26 | 0.68 |
| usp | −1493.80 | 3.00 | −0.90 | 0.09 |
| picr | −1762.60 | 3.00 | 0 | 1.00 |
| br | −924.50 | 2.00 | 0.58 | 0.02 |
| dsp | −1000.60 | 5.00 | −0.15 | 0.00 |
| gth | −562.60 | 2.10 | −0.39 | 0.02 |
| cc | −1207.40 | 1.30 | 0.37 | 0.11 |
| arag | −1207.40 | 1.40 | 0.30 | 0.09 |
| mag | −1113.30 | 4.00 | −0.59 | 0.01 |
| sid | −760.60 | 3.00 | 0.54 | 0.03 |
| rhc | −892.90 | 0.50 | −1.24 | 0.58 |
| dol | −2324.50 | 1.50 | 0.84 | 0.13 |
| syv | −436.50 | 0.20 | 0 | 1.00 |
| hlt | −411.30 | 0.20 | 0 | 1.00 |
| pyr | −171.50 | 1.70 | 0.08 | 0.48 |
| lot | −101.00 | 3.00 | 0.39 | 0.02 |
| trov | −97.50 | 5.00 | −0.30 | 0.05 |
| any | −1434.40 | 3.20 | 0 | 1.00 |
| diam | 1.90 | 0.10 | −1.01 | 0.26 |
| S2 | 128.60 | 0.30 | 0.19 | 0.98 |
| H2S | −20.60 | 0.70 | −0.42 | 0.33 |
| Reaction | T °C | H (cal) | σ | H (298) | e * | hat | ||
|---|---|---|---|---|---|---|---|---|
| mwd | mwd = fo | 702 | 30.0 | 3.0 | 32.3 | −0.6 | 0.02 | Akaogi et al. (1989) |
| mrw | mrw = fo | 702 | 39.1 | 2.6 | 43.6 | −0.5 | 0.04 | Akaogi et al. (1989) |
| mrw | mrw = mwd | 702 | 9.1 | 2.6 | 11.2 | 0.1 | 0.01 | Akaogi et al. (1989) |
| fwd | fwd = fa | 702 | 9.6 | 1.3 | 9.6 | −0.2 | 0.23 | Akaogi et al. (1989) |
| frw | frw = fa | 702 | 3.8 | 2.4 | 5.5 | −0.2 | 0.02 | Akaogi et al. (1989) |
| frw | frw = fwd | 702 | −5.8 | 2.7 | −4.1 | −0.1 | 0.07 | Akaogi et al. (1989) |
| mak | mak = mpv | 697 | −51.1 | 6.6 | −51.0 | −0.5 | 0.00 | Akaogi & Ito (1993) |
| mak | 2mak = en | 697 | 118.2 | 8.6 | 121.8 | 1.5 | 0.01 | Ashida et al. (1988) |
| mrw | mrw = mpv + per | 697 | −96.8 | 5.8 | −92.8 | −1.7 | 0.01 | Navrotsky (1995) |
| mag | mag = per + CO2 | 25 | −116.8 | 1.0 | −116.8 | −0.9 | 0.03 | Chai & Navrotsky (1993) |
| cc | cc = lime + CO2 | 25 | −178.3 | 1.2 | −178.3 | 1.2 | 0.04 | Chai & Navrotsky (1993) |
| dol | dol = per + lime + 2CO2 | 25 | −304.3 | 1.9 | −304.3 | −0.9 | 0.03 | Chai & Navrotsky (1993) |
| sill | sill = cor + q | 697 | −2.4 | 1.2 | −0.5 | −0.6 | 0.00 | Charlu et al. (1975) |
| and | and = cor + q | 697 | −5.0 | 1.2 | −3.6 | −0.7 | 0.00 | Anderson et al. (1977) |
| ky | ky = cor + q | 697 | −8.3 | 1.2 | −7.1 | −0.1 | 0.00 | Anderson & Kleppa (1969) |
| sp | sp = per + cor | 697 | −22.5 | 1.2 | −25.7 | −1.1 | 0.03 | Charlu et al. (1975) |
| py | py = 3per + cor + 3q | 697 | −74.1 | 5.5 | −69.8 | 0.1 | 0.01 | Charlu et al. (1975) |
| py | 2py = 3en + 2cor | 700 | 55.5 | 8.6 | 61.0 | 0.5 | 0.00 | Charlu et al. (1975) |
| fo | fo = 2per + q | 750 | −59.5 | 1.9 | −58.0 | 0.4 | 0.04 | Brousse et al. (1984) |
| en | en = 2per + 2q | 697 | −67.9 | 3.5 | −66.8 | −0.3 | 0.01 | Brousse et al. (1984) |
| mont | mont = lime + per + q | 750 | −104.8 | 1.7 | −103.4 | 0.6 | 0.03 | Brousse et al. (1984) |
| ak | ak = 2lime + per + 2q | 750 | −178.2 | 1.6 | −172.5 | 0.6 | 0.11 | Brousse et al. (1984) |
| crd | crd = 2per + 2cor + 5q | 697 | −68.9 | 3.0 | −58.6 | −0.8 | 0.02 | Charlu et al. (1975) |
| spr4 | spr4 = 4per + 4cor + 2q | 697 | −85.7 | 4.0 | −87.7 | 1.4 | 0.04 | Kleppa & Newton (1975) |
| di | di = lime + per + 2q | 697 | −146.4 | 1.7 | −143.6 | 0.3 | 0.04 | Charlu et al. (1975) |
| wo | wo = lime + q | 697 | −89.9 | 1.5 | −87.8 | 0.4 | 0.03 | Charlu et al. (1975) |
| pswo | pswo = lime + q | 697 | −83.3 | 1.3 | −80.3 | 1.8 | 0.04 | Charlu et al. (1975) |
| an | an = wo + cor + q | 727 | −13.5 | 1.5 | −10.7 | 1.5 | 0.03 | Zhu et al. (1993) |
| rhod | rhod = mang + q | 713 | −26.4 | 1.3 | −24.4 | 1.3 | 0.22 | Navrotsky & Coons (1976) |
| rhod | rhod = pxmn | 713 | 0.2 | 2.0 | 0.2 | −0.3 | 0.00 | Navrotsky & Coons (1976) |
| zrc | zrc = q + bdy | 25 | −24.0 | 3.0 | −24.0 | 0.0 | 0.01 | O'Neill 2006 |
| ky | ky = sill | 701 | −6.2 | 1.2 | −6.8 | 0.3 | 0.00 | Holm & Kleppa (1966) |
| and | and = sill | 701 | −2.8 | 1.0 | −3.3 | −0.4 | 0.01 | Holm & Kleppa (1966) |
| hcrd | hcrd = crd + H2O | 25 | −42.5 | 3.0 | −42.5 | 0.5 | 0.00 | Carey & Navrotsky (1992) |
| clin | 2clin = ames + afchl | 25 | −50.0 | 1.0 | −50.0 | 0 | 1.00 | This study |
| ep | 2ep = fep + cz | 25 | −25.0 | 10.0 | −25.0 | 0.0 | 0.00 | Holland & Powell (1998) |
| ab | ab = abh | 25 | −14.0 | 0.1 | −14.0 | −0.0 | 0.98 | Holland & Powell (1996) |
| mic | mic = san | 25 | −8.6 | 0.1 | −8.6 | −0.0 | 1.00 | Holland & Powell (1996) |
| cg | cg = cgh | 693 | −8.1 | 1.0 | −13.7 | 0.0 | 0.00 | Richet et al. (1990) |
| stv | stv = coe | 25 | 29.9 | 1.2 | 29.9 | −0.6 | 0.10 | Liu et al. (1996) |
| CO2 | CO2 = gph + O2 | 25 | −393.5 | 0.1 | −393.5 | 0.1 | 0.98 | Robie & Hemingway (1985) |
| H2O | 2H2O = 2H2+ O2 | 25 | −483.6 | 0.0 | −483.6 | −0.0 | 1.00 | Robie & Hemingway (1985) |
| H2S | H2S = 2H2+ S | 25 | −20.6 | 0.6 | −20.6 | −0.5 | 0.45 | Robie & Hemingway (1985) |
| CH4 | CH4 = gph + 2H2 | 25 | −74.8 | 0.3 | −74.8 | 0 | 1.00 | Robie & Hemingway (1985) |
| CO | 2CO = 2gph + O2 | 25 | −221.1 | 0.3 | −221.1 | 0 | 1.00 | Robie & Hemingway (1985) |
| aqSi | aqSi = q | 25 | 22.9 | 0.6 | 22.9 | 0 | 1.00 | Holland & Powell (1998) |
| corL | corL = cor | 2050 | 107.5 | 5.4 | 42.8 | −0.1 | 0.04 | Richet & Bottinga (1986) |
| diL | diL = di | 1397 | 137.7 | 7.0 | 8.1 | 0.0 | 0.00 | Lange et al. (1991) |
| faL | faL = fa | 1217 | 90.0 | 3.0 | 14.0 | −0.2 | 0.00 | Richet & Bottinga (1986) |
| foL | foL = fo | 1890 | 114.0 | 15.0 | −61.0 | 0.3 | 0.00 | Richet & Bottinga (1986) |
| anL | anL = an | 1557 | 134.0 | 3.0 | −38.2 | 2.3 | 0.01 | Richet & Bottinga (1986) |
| abL | abL = abh | 1120 | 64.5 | 3.0 | −6.9 | −0.8 | 0.00 | Richet & Bottinga (1986) |
| kspL | kspL = san | 1200 | 63.0 | 5.0 | −14.4 | −0.2 | 0.00 | Richet & Bottinga (1986) |
| qL | qL = crst | 1726 | 8.9 | 2.0 | −17.0 | −0.1 | 0.00 | Richet & Bottinga (1986) |
| enL | enL = en | 1561 | 155.6 | 12.0 | −9.8 | −0.3 | 0.00 | Richet & Bottinga (1986) |
| woL | woL = pswo | 1544 | 57.3 | 2.9 | −14.5 | −0.1 | 0.00 | Richet & Bottinga (1986) |
| neL | neL = ne | 1447 | 46.3 | 2.0 | −22.2 | −0.0 | 0.00 | Richet & Bottinga (1986) |
| lcL | lcL = lc | 1686 | 40.0 | 10.0 | −38.4 | 0.1 | 0.00 | Estimated, this study |
| cgh | cgh = neL | 1526 | −21.7 | 3.0 | 39.7 | 0.3 | 0.00 | Estimated, this study |
| perL | perL = per | 2825 | 77.0 | 10.0 | −53.7 | −0.1 | 0.00 | This study, Howald (1992) |
| limL | limL = lime | 2572 | 52.0 | 10.0 | −57.9 | −0.0 | 0.00 | This study, Howald (1992) |
| lot | lot = iron + S | 25 | −102.6 | 3.0 | −102.6 | −0.1 | 0.02 | Evans et al. (2010) |
| pyr | pyr = iron + 2S | 25 | −171.6 | 1.7 | −171.6 | −0.0 | 0.48 | Evans et al. (2010) |
Changes to Methodology
The principal differences in methodology from HP98 are outlined before the details of the new data set are presented and discussed.
Equation of state (EOS) for solids
The EOS for solid phases in HP98 involved a thermal expansion expression at 1 bar pressure, with an independent Murnaghan EOS to take the ambient pressure molar volumes to high pressures. To link the expansion and compression terms, a simple linear temperature dependence for the bulk modulus was used. This is now replaced with a more general EOS, and the expansion and compression terms are now linked.
Freund & Ingalls (1989) investigated nine separate EOS to determine which might be most suitable for high pressure work in solids. Their aim was to find a suitable EOS with only two or three adjustable parameters which best fit compression data to very high pressures. The modified Tait equation of Huang & Chow (1974) was one of the best of the equations investigated, in terms of fits to the compression data, and it is adopted here. We then augment this EOS for high temperature use by adding a thermal pressure term, as outlined below, thus integrating the expansion and compression contributions to Gibbs energy. Below, this modified Tait EOS, augmented with a thermal pressure term, is referred to as TEOS.
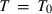 (where
(where 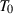 = 298.15K) is:
= 298.15K) is:
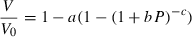 (1)
(1)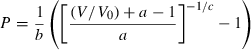 (2)
(2)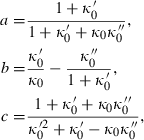 (3)
(3)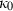 is the bulk modulus at ambient conditions,
is the bulk modulus at ambient conditions,
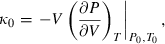
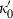 and
and 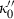 are the first and second derivatives of
are the first and second derivatives of 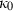 with pressure also at ambient conditions. Conversely,
with pressure also at ambient conditions. Conversely,
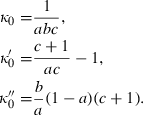 (4)
(4)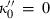 , TEOS reduces to the simpler two-parameter Murnaghan equation, with
, TEOS reduces to the simpler two-parameter Murnaghan equation, with
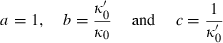
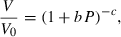
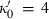 (or
(or 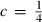 ).
).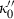 is known. Although Freund & Ingalls (1989) state that experiments do not allow this term to be determined to better than 100% error, their applications suggest that all the successful EOS do seem to point to a fairly uniform but small negative value of
is known. Although Freund & Ingalls (1989) state that experiments do not allow this term to be determined to better than 100% error, their applications suggest that all the successful EOS do seem to point to a fairly uniform but small negative value of 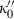 for the range of elements and compressible compounds investigated. Jackson & Niesler (1982) suggested that
for the range of elements and compressible compounds investigated. Jackson & Niesler (1982) suggested that 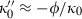 , where
, where 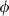 is a small number between 0 and 10, and this was confirmed for periclase by Jacobs & Oonk (2000). More importantly, a negative value for
is a small number between 0 and 10, and this was confirmed for periclase by Jacobs & Oonk (2000). More importantly, a negative value for 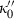 is shown to be a requirement in the analysis of Stacey (2005), and should therefore be implemented in such an EOS. Here, to maintain this requirement for a small negative
is shown to be a requirement in the analysis of Stacey (2005), and should therefore be implemented in such an EOS. Here, to maintain this requirement for a small negative 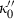 , we adopt the heuristic
, we adopt the heuristic 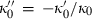 , with
, with 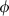 chosen to scale with
chosen to scale with 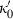 (see below). With this, the isothermal TEOS can be written in two-parameter form as:
(see below). With this, the isothermal TEOS can be written in two-parameter form as:
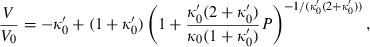
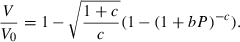 (5)
(5)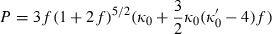
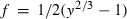 , and
, and 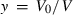 . Now, Murnaghan in terms of y is:
. Now, Murnaghan in terms of y is:
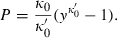 (6)
(6)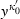 around 1 (i.e. no compression). For TEOS to the third power in
around 1 (i.e. no compression). For TEOS to the third power in 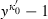 this gives
this gives
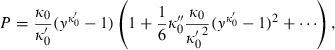 (7)
(7)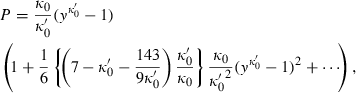 (8)
(8)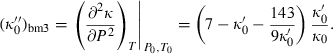 (9)
(9)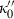 is specified by
is specified by  and
and 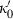 , in contrast to TEOS where
, in contrast to TEOS where 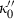 is a free parameter to be determined from data (or, e.g. via the heuristic above). Note that the term in brackets in equation (9) is close to
is a free parameter to be determined from data (or, e.g. via the heuristic above). Note that the term in brackets in equation (9) is close to 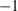 for
for 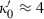 , in relation to the heuristic adopted above to approximate
, in relation to the heuristic adopted above to approximate 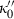 . Note also that fourth-order Birch–Murnaghan reduces to third order if the adjustable parameter
. Note also that fourth-order Birch–Murnaghan reduces to third order if the adjustable parameter 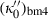 is substituted with the above expression for
is substituted with the above expression for 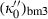 . Analogously fourth-order Birch–Murnaghan reduces to third-order Birch–Murnaghan, approximately, if the above heuristic,
. Analogously fourth-order Birch–Murnaghan reduces to third-order Birch–Murnaghan, approximately, if the above heuristic, 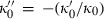 is adopted. Similar to third-order Birch–Murnaghan, in the so-called universal EOS of Vinet (e.g. Stacey, 2005),
is adopted. Similar to third-order Birch–Murnaghan, in the so-called universal EOS of Vinet (e.g. Stacey, 2005), 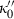 is specified by
is specified by 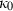 and
and 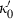
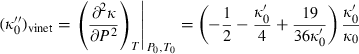 (10)
(10)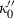 heuristic, equation (5), is derived only for ambient temperature. We may extend it to high temperature by adding a thermal pressure term
heuristic, equation (5), is derived only for ambient temperature. We may extend it to high temperature by adding a thermal pressure term 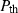 to equation (2), and using the relationship (Anderson, 1997):
to equation (2), and using the relationship (Anderson, 1997):
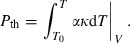 (11)
(11)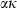 as a function of T, with
as a function of T, with 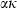 for some phases becoming constant to high-T, while others increase or decrease slightly. Rearranging the Grüneisen relation gives
for some phases becoming constant to high-T, while others increase or decrease slightly. Rearranging the Grüneisen relation gives 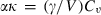 , and noting that
, and noting that 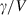 is nearly independent of temperature, the form of
is nearly independent of temperature, the form of 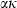 should have the shape of a heat capacity function, rising to an approximately constant value. That this is approximately so may be seen for the phases tabulated in Anderson & Isaak (1995) and illustrated here for their forsterite data in Fig. 1a. Here we adopt the simplest regularization that
should have the shape of a heat capacity function, rising to an approximately constant value. That this is approximately so may be seen for the phases tabulated in Anderson & Isaak (1995) and illustrated here for their forsterite data in Fig. 1a. Here we adopt the simplest regularization that 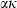 becomes constant to high-T, taking an Einstein function to represent how
becomes constant to high-T, taking an Einstein function to represent how 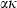 decreases to zero as temperature decreases to OK:
decreases to zero as temperature decreases to OK:
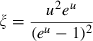
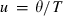 , and
, and  the Einstein temperature. For equation (11),
the Einstein temperature. For equation (11), 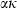 is written as
is written as 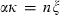 , where n is a normalization constant, equal to
, where n is a normalization constant, equal to 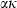 at infinite temperature, so
at infinite temperature, so 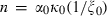 , and
, and 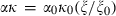 , with
, with 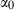 ,
, 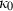 and
and 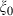 being the values of
being the values of  ,
,  and
and 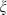 at ambient temperature. Then, using equation (11)
at ambient temperature. Then, using equation (11)
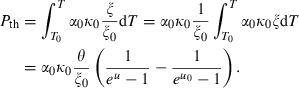
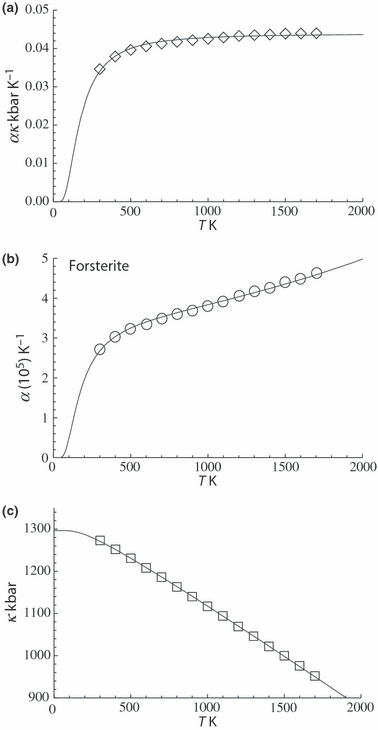
For forsterite, (a) 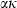 , (b)
, (b)  and (c)
and (c)  , are shown as a function of temperature, at 1 bar. The shape of the temperature dependence is a consequence of the involvement of the Einstein function in the thermal pressure term. The symbols are data from Anderson & Isaak (1995) and the curves are Tait equation of state fits to their data. The Anderson and Isaak data are used here because they present separate values for
, are shown as a function of temperature, at 1 bar. The shape of the temperature dependence is a consequence of the involvement of the Einstein function in the thermal pressure term. The symbols are data from Anderson & Isaak (1995) and the curves are Tait equation of state fits to their data. The Anderson and Isaak data are used here because they present separate values for  and
and  , but for the thermodynamic data set itself we have preferred to use the experimental molar volumes listed in Appendix 1.
, but for the thermodynamic data set itself we have preferred to use the experimental molar volumes listed in Appendix 1.
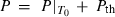 , this may be rearranged in volume explicit form as:
, this may be rearranged in volume explicit form as:
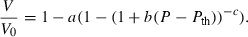 (12)
(12)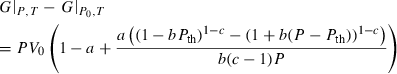 (13)
(13) , the thermal expansion
, the thermal expansion  is:
is:
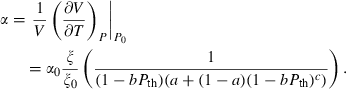
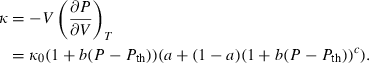
The form of TEOS for thermal expansion is shown in Fig. 1b, with the characteristic shape provided by the Einstein function, and in Fig. 1c the implicit negative temperature dependence of the bulk modulus. These curves are fits of TEOS to the experimental data for forsterite tabulated in Anderson & Isaak (1995). Use of the expressions above necessitates a value for the Einstein temperature  for each end-member. Only very rarely are accurate thermal expansion data made at temperatures below ambient, thus making direct determination of
for each end-member. Only very rarely are accurate thermal expansion data made at temperatures below ambient, thus making direct determination of  by data fitting effectively impossible. We have found that the value of
by data fitting effectively impossible. We have found that the value of  needs only to be known approximately, and affects mainly the low temperature thermal expansion and volume behaviour. An approximate value for
needs only to be known approximately, and affects mainly the low temperature thermal expansion and volume behaviour. An approximate value for  is derived for each end-member from the measured entropy (or via Holland, 1989). Thus for end-member i the value of
is derived for each end-member from the measured entropy (or via Holland, 1989). Thus for end-member i the value of 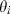 is given by the empirical relationship,
is given by the empirical relationship, 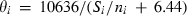 , where
, where 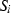 is the molar entropy (in J
is the molar entropy (in J 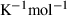 ) of i and
) of i and 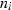 is the number of atoms in i.
is the number of atoms in i.
TEOS relates the volume at any P–T to the standard state volume with only three adjustable parameters (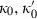 and
and 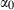 ). The data set includes a term for
). The data set includes a term for 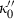 to anticipate for the rare occasion where a value other than
to anticipate for the rare occasion where a value other than 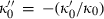 might be warranted. Fitting TEOS to volume data for phases where volumes have been measured to very high pressures and temperatures (grossular garnet, stishovite and periclase) and for phases where simultaneous high temperature and high pressure measurements have been made (magnesite, dolomite, aragonite, brucite, grossular, andradite, jadeite and muscovite) shows that it behaves very well (see Fig. 3), in fitting all the data, whether at ambient pressures and high temperatures, ambient temperature and high pressures or at combined high pressures and temperatures.
might be warranted. Fitting TEOS to volume data for phases where volumes have been measured to very high pressures and temperatures (grossular garnet, stishovite and periclase) and for phases where simultaneous high temperature and high pressure measurements have been made (magnesite, dolomite, aragonite, brucite, grossular, andradite, jadeite and muscovite) shows that it behaves very well (see Fig. 3), in fitting all the data, whether at ambient pressures and high temperatures, ambient temperature and high pressures or at combined high pressures and temperatures.
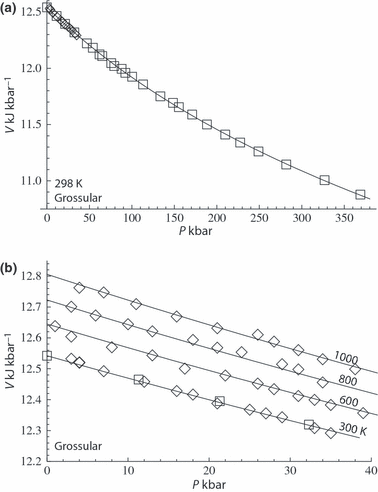
Experimental data of Pavese et al. (2001a,b) and the fitted curves from Tait equation of state. (a) The 298 K data to 360 kbar; (b) the high pressure–high temperature data to 1000 K and 40 kbar.
As an example, the data for stishovite to 2300 kbar are shown in Fig. 2a where the lower pressure data (up to 500 kbar) of Andrault et al. (2003) have been fitted with TEOS and, on extrapolation, appear to fit nicely the very high pressure data of Luo et al. (2002). The extrapolatory power of TEOS is seen to be excellent. Also shown in Fig. 2b is the volume thermal expansion data and the good form of the fit to the data. The way volume levels off at low temperature is a reflection of the way thermal expansion drops off to zero (Fig. 1) at low temperatures. Figure 3 illustrates the fit of the high pressure volume data for grossular from Pavese et al. (2001a,b), first as a function of pressure to over 350 kbar, and second as a function of both pressure and temperature to 1000 K and 40 kbar. TEOS appears to have a form that is well suited to represent such data.
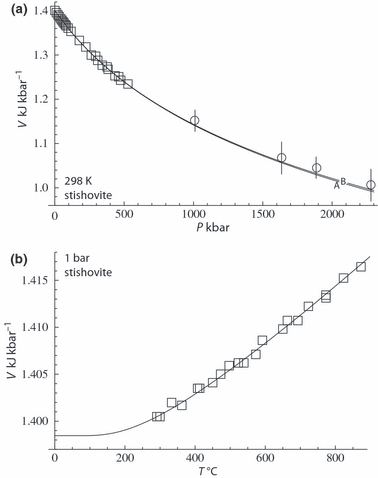
Stishovite volume data. (a) Precise data of Andrault et al. (2003) up to 500 kbar (squares) and the very high pressure data of Luo et al. (2002) to 2500 kbar (circles with error bars). Error bars for the lower pressure data are smaller than the symbols. Calculated curves: A – fit to low pressure data of Andrault et al., only; B – fit to all data with experimental uncertainties. (b) Volume expansion data of Ito et al. (1974) and the calculated fit.
Although using TEOS in place of Murnaghan makes little difference to the derived thermodynamic data, two related factors have led to significant improvement in the overall data fitting. First, not restricting the value of  to 4.0 has allowed better extrapolations to very high pressure, and second (and more significantly) the incorporation of the implicit thermal expansion and the consequent temperature dependence of bulk modulus
to 4.0 has allowed better extrapolations to very high pressure, and second (and more significantly) the incorporation of the implicit thermal expansion and the consequent temperature dependence of bulk modulus  through the thermal pressure has made the volume behaviour at high pressures and temperatures more reliable.
through the thermal pressure has made the volume behaviour at high pressures and temperatures more reliable.
Equation of state for fluid phases
Pure fluid species
The EOS for fluids used in HP98 was the CORK equation (Holland & Powell, 1991) which was derived for the purposes of extrapolation to high pressures. The equations of Pitzer & Sterner (1995) have now been substituted in place of CORK for both H2O and CO2 for the following two reasons: (i) the CORK expressions did not fit the volumes for H2O in the region of the critical point closely (fig. 2 of Holland & Powell, 1991), and (11) the CORK expressions involved a piecewise continuous transition in compressibility at 2 kbar which made for difficulties in root-finding algorithms for free energy. The differences between CORK and Pitzer & Sterner (1995) volumes and free energies are minor for H2O, and virtually indistinguishable for CO2. Change to the Pitzer & Sterner equations necessitated minor compensating adjustments in entropy for a number of hydrous phases. The CORK equation is, however, retained for calculating volumes and fugacities of CO, CH4, H2, S2 and H2S because of its ease in application of the corresponding-states principle. The constants for the CORK expressions for COH gases are taken from Holland & Powell (1991), table 2). For S2 and H2S the critical constants are taken from Reid et al. (1977) and used with equation (9) in Holland & Powell (1991).
Mixing in fluids
Mixtures of gases, such as H2O and CO2, as well as other species in the COHS system are now handled via a Van Laar model as described in Holland & Powell (2003), in which the volumes of the end-members control the asymmetry parameters directly, which allows a controlled extrapolation to very high pressures. Because the mixing properties are very similar to those generated by the modified Redlich–Kwong EOS, the latter were used to derive Van Laar parameters for all other COHS gas end-members. The COH  values are from Holland & Powell (2003), and the remaining ones from Evans et al. (2010). This change has led to an overall reduction in the misfit between mixed silicate-carbonate experiments and thermodynamic data.
values are from Holland & Powell (2003), and the remaining ones from Evans et al. (2010). This change has led to an overall reduction in the misfit between mixed silicate-carbonate experiments and thermodynamic data.
The earlier HP98 paper also involved aqueous solution thermodynamic properties, based on a modification of the Anderson density model (Anderson et al. (1991) which is retained here. A problem never addressed satisfactorily for aqueous fluids at geological conditions is that of the transition from the dilute region, where Debye–Huckel type (infinite dilution standard state) models are typically used, to the high ionic strength electrolytes such as saturated salt solutions where Raoult's Law type standard states are used. Progress towards resolving this has been made by Evans & Powell (2005), who devised a model which slides smoothly between the two types of behaviour, allowing a single activity–composition expression to be used for mixed aqueous electrolytes and dissolved COHS gas species. An example where such calculations have been used is given below and further examples may be found in Evans et al. (2010).
Use of univariant and divariant experimentally determined equilibria involving solid solutions
A new feature of this data set is the use of univariant equilibria in solving for enthalpies and mixing properties of solid solutions simultaneously. As an example, the univariant reaction sapphirine + quartz = orthopyroxene + sillimanite in the MAS system has been determined experimentally by Newton (1972), Hensen, (1972) and Chatterjee & Schreyer (1972). Along the length of this reaction, from 1050 °C to 1475 °C, the compositions of pyroxene and sapphirine change. By fitting simultaneously to a set of independent reactions between the end-members, the enthalpies of all end-members (spr4, spr5, en, mgts, sill, q) may be optimized together. Consideration of the variation of mixing properties, via the interaction energies ( and
and 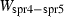 ) also allowed these values to be refined.
) also allowed these values to be refined.
As well as univariant reactions, many divariant equilibria were also fitted in the same manner, allowing easy refinement of mixing energies for a number of solid solutions involved across different reactions. This was particularly helpful in refining the properties of the chlorites in MASH (clin, ames, afchl) through the experiments of Baker & Holland (1996), Jenkins (1981) and Jenkins & Chernosky (1986). It has also been used in a number of Fe–Mg and other exchange equilibria between silicates and between silicates and carbonates.
Order–disorder and Landau models
Treatment of order–disorder in HP98 was done with a Landau tricritical model to account for the sharp lambda peaks in the heat capacity exhibited at the phase transition temperatures in such end-members. This was convenient in making a simple representation of the order–disorder characteristics in stoichiometric phases, but is not satisfactory when dealing with solid solutions involving disordering behaviour because the Landau expansion does not correctly incorporate the configurational entropy associated with cation ordering. We now represent many order disorder transitions with a macroscopic Bragg–Williams type of model, the SF or symmetric formalism of Holland & Powell (1996a,b)). End-members now characterized by the SF model include sillimanite, gehlenite, cordierite, albite, K-feldspar, anorthite, spinel, hercynite, dolomite, ankerite. Using the SF model allows solid solutions involving these end-members to be constructed with standard configurational entropies and thus activity–composition expressions, making them much easier to be used in multicomponent solid-solution phase equilibrium calculations.
Melt species
Following on from the initial modelling of simple granitic systems (Holland & Powell, 2001) and its extension into partial melting of pelitic compositions (White et al., 2001), the data for melt components has improved considerably over those initially presented in HP98. The principal differences lie in enforcing the heat of melting as a constraint, where known, in addition to fitting the experimental P−T curves and changes introduced through the relaxation of 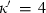 constraint. Many melt end-members now have their properties consistent with experiments which go to high pressures (e.g. qL to 60 kbar, faL to 70 kbar, foL to 153 kbar). In addition, several new melt end-members have been introduced since HP98 [perL (MgO), limL (CaO), corL (Al2O3), wolL (CaSiO3), neL (NaAlSiO4), lcL (KAlSi2O6), KCl and NaCl liquids].
constraint. Many melt end-members now have their properties consistent with experiments which go to high pressures (e.g. qL to 60 kbar, faL to 70 kbar, foL to 153 kbar). In addition, several new melt end-members have been introduced since HP98 [perL (MgO), limL (CaO), corL (Al2O3), wolL (CaSiO3), neL (NaAlSiO4), lcL (KAlSi2O6), KCl and NaCl liquids].
The new thermal expansion expressions used in TEOS are not suitable for melt end-members, as they are based on a vibrational model. The experimental data currently available do not warrant anything more elaborate than constant thermal expansion at the temperatures investigated (Lange, 1997), and so the constant thermal expansion and linear temperature dependence of bulk modulus as in HP98 is retained for melt end-members.
New End-Members in The Data set
The following is a brief outline of additions to the data set in a mineral group or system context; all the new end-members are indicated in Table 1. Changes in activity–composition relations that are implicit in data set generation for these and other end-members are included below in the next subsection.
For the first time, sulphides and sulphur-bearing minerals and fluid species have been incorporated into the data set. The details are published in Evans et al. (2010) and encompass the solid phases pyrite (FeS2), troilite (FeS), pyrrhotites (solid solution between hypothetical end-member trot, FeS and vacancy-bearing trov, 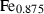 S), anhydrite (CaSO4), elemental sulphur S, gaseous S2 and H2S as well as aqueous species
S), anhydrite (CaSO4), elemental sulphur S, gaseous S2 and H2S as well as aqueous species 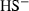 ,
, 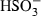 ,
, 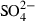 and HS
and HS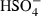 . Troilite is described as a low temperature form (lot) from 298 K up to 420 K and a high temperature form (tro) above 420 K. These solids are complicated, involving two lambda transitions in troilites (one at 420 K, one at 598K) and a lambda transition in trov at 595 K. Examples of phase diagram calculations, including pseudosections involving mixed silicates, carbonates and sulphides may be found in Evans et al. (2010).
. Troilite is described as a low temperature form (lot) from 298 K up to 420 K and a high temperature form (tro) above 420 K. These solids are complicated, involving two lambda transitions in troilites (one at 420 K, one at 598K) and a lambda transition in trov at 595 K. Examples of phase diagram calculations, including pseudosections involving mixed silicates, carbonates and sulphides may be found in Evans et al. (2010).
Several new pyroxene end-members are now included. Clinoenstatite (cen, Mg2Si2O6) and protoenstatite (pren) are new end-members whose enthalpy of formation and entropy are derived from experiments of Atlas (1952), Chen & Presnall (1975) and Boyd & England (1965). A calcium-eskola pyroxene end-member (caes, 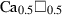 AlSi2O6) is introduced to account for vacancy substitutions seen in calcic pyroxene at high pressures, and is calibrated on the experimental results of Gasparik (1984). The activity model used assumes that some short-range ordering between Si–Al on tetrahedral and Mg–Al on octahedral sites can be accommodated by reducing the tetrahedral entropy of mixing to a quarter of the configurational contribution. This then gives the activities of caes and cats in a binary pyroxene as
AlSi2O6) is introduced to account for vacancy substitutions seen in calcic pyroxene at high pressures, and is calibrated on the experimental results of Gasparik (1984). The activity model used assumes that some short-range ordering between Si–Al on tetrahedral and Mg–Al on octahedral sites can be accommodated by reducing the tetrahedral entropy of mixing to a quarter of the configurational contribution. This then gives the activities of caes and cats in a binary pyroxene as 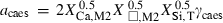 and
and 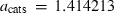
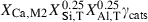 with activity coefficients from a regular solution with
with activity coefficients from a regular solution with  kJ.
kJ.
Chromium-bearing end-members are now included: the oxide eskolaite (esk, Cr2O3), the pyroxene kosmochlor (kos, NaCrSi2O6), the garnet knorringite (knor, Mg3Cr2Si3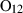 ) and the spinel picrochromite (picr, MgCr2O4). We have fitted the experiments on the exchange reaction 2jd + picr = 2kos + sp, assuming that jd–kos is ideal and that the sp–picr solid solution is non-ideal with a symmetrical interaction energy
) and the spinel picrochromite (picr, MgCr2O4). We have fitted the experiments on the exchange reaction 2jd + picr = 2kos + sp, assuming that jd–kos is ideal and that the sp–picr solid solution is non-ideal with a symmetrical interaction energy 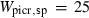 kJ (Carroll Webb & Wood, 1986). We have not added a large entropy increment to knorringite (as done by Klemme, 2004, and Klemme et al., 2000, who assumed that the low-T anomaly seen in the heat capacity of uvarovite applies to knorringite), and thus we have been able to fit the slope and positions of both the reactions 2knor = 3en + 2esk (Turkin et al., 1983) and knor + fo = picr + 2en (Klemme, 2004). The P–T slope of the experimental brackets of Irifune et al. (1982) for 2knor = 3en + 2esk are incompatible with the other studies and with the thermodynamic data.
kJ (Carroll Webb & Wood, 1986). We have not added a large entropy increment to knorringite (as done by Klemme, 2004, and Klemme et al., 2000, who assumed that the low-T anomaly seen in the heat capacity of uvarovite applies to knorringite), and thus we have been able to fit the slope and positions of both the reactions 2knor = 3en + 2esk (Turkin et al., 1983) and knor + fo = picr + 2en (Klemme, 2004). The P–T slope of the experimental brackets of Irifune et al. (1982) for 2knor = 3en + 2esk are incompatible with the other studies and with the thermodynamic data.
Carnegieite and high-carnegieite (cg, cgh, NaAlSiO4) are fitted to the experiments of Bowen & Greig (1923), Greig & Barth (1938) and Cohen & Klement (1967). These data depend on those for nepheline, and are in turn used to determine those for nepheline liquid and sodalite.
Stilpnomelane with end-members ferrostilpnomelane (fstp, 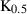 (Fe5Al)[Si8Al]
(Fe5Al)[Si8Al]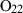
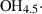 4H2O) and magnesiostilpnomelane (mstp,
4H2O) and magnesiostilpnomelane (mstp, 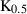 (Mg5Al)[Si8Al]
(Mg5Al)[Si8Al]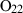
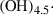 4H2O) is now included. The formula for stilpnomelane is not fully known, but the chosen formula units are based on Eggleton (1972) simplified and normalized to 8 Si pfu. The activities are given by assuming that octahedral Al resides on one site, with Fe and Mg mixing on five sites, so that
4H2O) is now included. The formula for stilpnomelane is not fully known, but the chosen formula units are based on Eggleton (1972) simplified and normalized to 8 Si pfu. The activities are given by assuming that octahedral Al resides on one site, with Fe and Mg mixing on five sites, so that 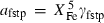 and
and 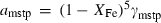 with activity coefficients from a regular solution with
with activity coefficients from a regular solution with 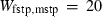 kJ. The data for the end-members are derived from the reaction 28fstp = 14ann + 5grun + 21alm + 79q + 156H2O and the partitioning of Fe and Mg between stilpnomelane and chlorite (Miyano & Klein, 1989).
kJ. The data for the end-members are derived from the reaction 28fstp = 14ann + 5grun + 21alm + 79q + 156H2O and the partitioning of Fe and Mg between stilpnomelane and chlorite (Miyano & Klein, 1989).
Minnesotaite [minn, Fe3Si4O10(OH)2] and its Mg equivalent [minm, Mg3Si4O10(OH)2] are derived from the experiments of Engi (1983) for the reaction 2minn = 3fa + 5q + 2H2O along with data for partitioning of Fe and Mg between carbonate and minnesotaite of Klein (1974). The activities are given by assuming that Fe and Mg mix on three sites, so that 
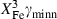 and
and 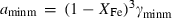 with activity coefficients from a regular solution with
with activity coefficients from a regular solution with 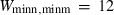 kJ.
kJ.
Greenalite [glt, Fe3Si2O5(OH)4] was derived using reactions glt + 2q = minn + H2O and 2glt + 5min = 3grun + 6H2O using the constraints discussed by Rasmussen et al. (1998).
 (OH)7], the FeAl end-member [fpm, Ca4FeAlAl4Si6
(OH)7], the FeAl end-member [fpm, Ca4FeAlAl4Si6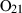 (OH)7] and the Fe
(OH)7] and the Fe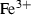 end-member julgoldite [jgd, Ca4Fe
end-member julgoldite [jgd, Ca4Fe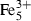 Si6
Si6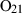 (OH)7] are included. As in HP98, the mpm end-member is derived from the experiments of Schiffman & Liou (1980), while data for the iron analogue are taken from the Fe–Mg partition between pumpellyite and chlorite of Evans (1990). The jgd end-member is derived from the
(OH)7] are included. As in HP98, the mpm end-member is derived from the experiments of Schiffman & Liou (1980), while data for the iron analogue are taken from the Fe–Mg partition between pumpellyite and chlorite of Evans (1990). The jgd end-member is derived from the 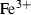 –Al partitioning data between epidote and pumpellyite given by Cho et al. (1986). Ordering of Mg and Fe onto a single M2a site is assumed for these pumpellyites and activities are given by
–Al partitioning data between epidote and pumpellyite given by Cho et al. (1986). Ordering of Mg and Fe onto a single M2a site is assumed for these pumpellyites and activities are given by
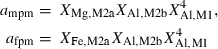
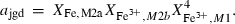
Talc now includes a pyrophyllitic end-member [tap, 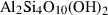 ] fitted to the experimental compositions reported by Newton (1972). All experiments involving aluminous talc (e.g. Chernosky, 1978; Massonne et al., 1981; Massonne, 1989; Massonne & Schreyer, 1989; Hoschek, 1995) have been fitted with a model involving both the tschermak substitution and the pyrophyllite-like substitution.
] fitted to the experimental compositions reported by Newton (1972). All experiments involving aluminous talc (e.g. Chernosky, 1978; Massonne et al., 1981; Massonne, 1989; Massonne & Schreyer, 1989; Hoschek, 1995) have been fitted with a model involving both the tschermak substitution and the pyrophyllite-like substitution.
Prehnite now includes a ferric end-member [fpre, Ca2AlFeSi3O10(OH)2]. Ferric iron is assumed to substitute for Al on one octahedral site only, and the activity relations simplify to 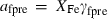 and
and 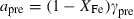 with activity coefficients from a regular solution with
with activity coefficients from a regular solution with  kJ. The data for fpre are derived from the
kJ. The data for fpre are derived from the  –Al partitioning data between epidote and prehnite given by Cho et al. (1986).
–Al partitioning data between epidote and prehnite given by Cho et al. (1986).
The halide minerals halite (hlt, NaCl) and sylvite (syv, KCl) and their molten equivalents (hltL and syvL) are included in the data set. The enthalpies of formation of halite and sylvite are taken from Robie & Hemingway (1995), and the molten end-members from fitting to the melting curves to 20 kbar pressure from Clark (1966). The experimental data of Aranovich & Newton (1997, 1998) involving concentrated brines (KCl and NaCl) in equilibrium with brucite and periclase may now be reproduced by direct calculation with the new data set.
Sapphirine has been a difficult phase to quantify thermodynamically, largely because available experiments have not been able to involve characterization of the composition of the sapphirine. A new model for sapphirine is adopted here, based on the revision of Kelsey et al. (2004), which involves the 2:2:1 end-members spr4 (Mg4Al8Si2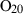 ) and fspr (Fe4Al8Si2
) and fspr (Fe4Al8Si2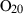 ) and the 3:5:1 end-member spr5 (Mg3Al10Si
) and the 3:5:1 end-member spr5 (Mg3Al10Si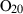 ). The activity relations, as discussed below, are found by optimization of the fit to the experimental data on sapphirine equilibria (Boyd & England, 1959; Hensen, 1972; Newton, 1972; Seifert, 1974; Doroshev & Malinovskiy, 1974; Malinovsky & Doroshev, 1975; Ackermand et al., 1975; Arima & Onuma, 1977; Perkins et al., 1981; Podlesskii, 1996; Fockenberg, 2008). In the fitting process, the compositions of sapphirine are predicted; they fall in the range
). The activity relations, as discussed below, are found by optimization of the fit to the experimental data on sapphirine equilibria (Boyd & England, 1959; Hensen, 1972; Newton, 1972; Seifert, 1974; Doroshev & Malinovskiy, 1974; Malinovsky & Doroshev, 1975; Ackermand et al., 1975; Arima & Onuma, 1977; Perkins et al., 1981; Podlesskii, 1996; Fockenberg, 2008). In the fitting process, the compositions of sapphirine are predicted; they fall in the range 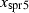 = 0.36–0.45 for most of the high pressure experiments, but do rise to
= 0.36–0.45 for most of the high pressure experiments, but do rise to 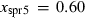 when coexisting with mullite. The fit to all these experiments is now quite good. Although a similar quality fit to the H2O-absent subset of the data in MAS was made by Podlesskii et al. (2008), their data set was only constrained within this subset of MAS rather than by all the other phases and equilibria used in this study.
when coexisting with mullite. The fit to all these experiments is now quite good. Although a similar quality fit to the H2O-absent subset of the data in MAS was made by Podlesskii et al. (2008), their data set was only constrained within this subset of MAS rather than by all the other phases and equilibria used in this study.
Mullite is a complex solid solution involving an end-member of sillimanite composition (Al2SiO5) into which the substitution Si +  O = Al +
O = Al +  occurs. This could in principle extend from Al2SiO5 (x = 0) to a Si-free end-member Al2Al
occurs. This could in principle extend from Al2SiO5 (x = 0) to a Si-free end-member Al2Al (x = 1), where x is the amount of the substitution above, but in practice rarely extends beyond x = 0.5 (Cameron, 1977). We have elected to use this intermediate composition (amul, Al2
(x = 1), where x is the amount of the substitution above, but in practice rarely extends beyond x = 0.5 (Cameron, 1977). We have elected to use this intermediate composition (amul, Al2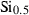
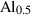
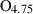 ) as the aluminous end-member in mullite in part because natural compositions rarely become more aluminous than this and in part because of the strong ordering of Al + Si and O +
) as the aluminous end-member in mullite in part because natural compositions rarely become more aluminous than this and in part because of the strong ordering of Al + Si and O +  . These two different ordering patterns (Al + Si and O +
. These two different ordering patterns (Al + Si and O +  ) lead to two different symmetries,
) lead to two different symmetries,  and
and 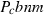 and an overall structure with an incommensurate modulation (Angel et al., 1991). Rather than attempt a detailed, and probably incorrect, activity model for this solid solution we take a pragmatic approach that assumes that the high degrees of Al,Si and
and an overall structure with an incommensurate modulation (Angel et al., 1991). Rather than attempt a detailed, and probably incorrect, activity model for this solid solution we take a pragmatic approach that assumes that the high degrees of Al,Si and  ,O ordering can be approximated by a simple two-site mixture of the end-members, such that
,O ordering can be approximated by a simple two-site mixture of the end-members, such that 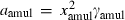 and
and 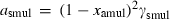 . Mullite enthalpies (for smul and amul) and the interaction energy (
. Mullite enthalpies (for smul and amul) and the interaction energy ( ) are derived from the experiments on the reactions muscovite + quartz = mullite + sanidine + H2O (Segnit & Kennedy, 1961), pyrophyllite = mullite + quartz + H2O (Carr & Fyfe, 1960), cordierite + corundum = sapphirine + mullite (Seifert, 1974) and the melting equilibria cristobalite + mullite + liquid and mullite + corundum + liquid (Klug et al., 1987). The calculated compositions of mullite are close to that of sillimanite at low temperatures and reproduce the aluminous compositions observed by Klug et al. (1987) at the melting temperatures. Calculations involving this mullite are included below.
) are derived from the experiments on the reactions muscovite + quartz = mullite + sanidine + H2O (Segnit & Kennedy, 1961), pyrophyllite = mullite + quartz + H2O (Carr & Fyfe, 1960), cordierite + corundum = sapphirine + mullite (Seifert, 1974) and the melting equilibria cristobalite + mullite + liquid and mullite + corundum + liquid (Klug et al., 1987). The calculated compositions of mullite are close to that of sillimanite at low temperatures and reproduce the aluminous compositions observed by Klug et al. (1987) at the melting temperatures. Calculations involving this mullite are included below.
Lizardite, one of the serpentine group minerals (with antigorite and chrysotile) is now included in the data set. Its properties are assumed to be like those of chrysotile, but with slightly smaller values for volume and entropy (Evans, 2004; Hilairet et al., 2006). We have accordingly also lowered the heat capacity and compressibility of lizardite. The enthalpy for lizardite, following the arguments of Evans (2004), is derived from accepting that lizardite transforms (metastably) to chrysotile between 413 and 431 °C at 2 kbar (Chernosky, 1975). The calculated stability of lizardite extends only up to 170 °C at 2 kbar where it breaks down to antigorite + brucite. More work needs to be done to determine unambiguously the stability of lizardite relative to chrysotile. The new measured compressibilities for lizardite and chrysotile (Hilairet et al., 2006) and for antigorite (Bose & Navrotsky, 1998) are used, allowing good fits to antigorite in very high pressure experiments (Wunder & Schreyer, 1997; Bose & Navrotsky, 1998; Pawley, 1998).
The new modified TEOS for solids allows reliable extrapolation of mineral volumes to very high pressures, and so we are starting to accumulate a set of thermodynamic data for phases at deep mantle pressures and temperatures. We present preliminary data on the end-members ferropericlase (fper, FeO), Mg-wadsleyite (mwd, Mg2SiO4), Fe-wadsleyite (fwd, Fe2SiO4), Mg-ringwoodite (mrw, Mg2SiO4), Fe-ringwoodite (frw, Fe2SiO4), Mg-perovskite (mpv, MgSiO3), Fe-perovskite (fpv, FeSiO3), Al-perovskite (apv, AlAlO3), Ca-perovskite (cpv, CaSiO3), Mg-akimotoite (mak, MgSiO3), Fe-akimotoite (fak, FeSiO3), majorite garnet (maj, Mg4Si4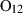 ), high-pressure clinoenstatite (hen, Mg2Si2O6), Ca-Si-titanite (cstn, CaSi2O5), walstromite (wal, CaSiO3), MgSi-corundum (mcor, MgSiO3), K-cymrite (kcm, KAlSi3O8.H2O), wadeite (wa, K2Si24O9) and hollandite (hol, KAlSi3O8). Experimental details for the equilibria used to extract the data may be found in Appendix 2. These data are tied into, and are consistent with the thermodynamic data for end-members at lower P–T (crustal) conditions.
), high-pressure clinoenstatite (hen, Mg2Si2O6), Ca-Si-titanite (cstn, CaSi2O5), walstromite (wal, CaSiO3), MgSi-corundum (mcor, MgSiO3), K-cymrite (kcm, KAlSi3O8.H2O), wadeite (wa, K2Si24O9) and hollandite (hol, KAlSi3O8). Experimental details for the equilibria used to extract the data may be found in Appendix 2. These data are tied into, and are consistent with the thermodynamic data for end-members at lower P–T (crustal) conditions.
Mixing model changes
Since HP98 we have changed slightly some solid solution models used in the data set generation. Only the ones which directly affect the fitted enthalpies are discussed here.
For MgAl orthopyroxene, the entropy of mixing is taken over octahedral and tetrahedral sites rather than the earlier octahedral site only model as in Wood & Banno (1973). This is done to facilitate multicomponent extensions to the model involving other substitutions. We take only a one-fourth of the full tetrahedral site entropy as an approximation for Al–Si and Mg–Al ordering, writing the activities of en and mgts as 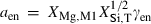 and
and 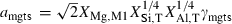 , with the activity coefficients taken from a macroscopic regular model (symmetric formalism; Powell & Holland, 1993a,b) with
, with the activity coefficients taken from a macroscopic regular model (symmetric formalism; Powell & Holland, 1993a,b) with 
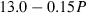 kJ derived from the measurements of Al solubility in aluminous pyroxenes coexisting with other phases in the data set, principally garnet and spinel.
kJ derived from the measurements of Al solubility in aluminous pyroxenes coexisting with other phases in the data set, principally garnet and spinel.
 kJ,
kJ,  kJ and
kJ and 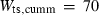 kJ derived from the experiments of Jenkins (1994), Hoschek (1995) and the results of Diener et al. (2007).
kJ derived from the experiments of Jenkins (1994), Hoschek (1995) and the results of Diener et al. (2007).Chlorite has been slightly simplified since HP98, keeping the basic model the same, but relaxing the degree of ordering required slightly. This has come about in part due to using the X-ray calibration of chlorite compositions from Jenkins & Chernosky (1986), Roots (1994) and Shirozu & Momoi (1972) rather than the data of Baker & Holland (1996) which yielded slightly lower volumes than the other studies. This has affected the adopted molar volumes of the clin, ames and afchl end-members. The molar volume of daph has been changed from the old value (213.4 J 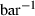 ) taken from Helgeson et al. (1978) and Holdaway & Lee (1977) to 216.2 J
) taken from Helgeson et al. (1978) and Holdaway & Lee (1977) to 216.2 J 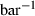 from Parra et al. (2005) as, even though their measurements are quite scattered, they are in better agreement with the measured data of James et al. (1976), Vidal et al. (2001) and with simple exchange models involving chlorite and biotite, olivine, orthopyroxene and chloritoid. In addition the entropy of clinochlore and daphnite have been taken from Bertoldi et al. (2007) with an extra 11.5 J
from Parra et al. (2005) as, even though their measurements are quite scattered, they are in better agreement with the measured data of James et al. (1976), Vidal et al. (2001) and with simple exchange models involving chlorite and biotite, olivine, orthopyroxene and chloritoid. In addition the entropy of clinochlore and daphnite have been taken from Bertoldi et al. (2007) with an extra 11.5 J 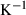 added for tetrahedral site configurational entropy. The entropies of afchl and ames were adjusted slightly in fitting to the phase equilibrium experimental results. The heat capacities were taken from Bertoldi et al. (2007), the thermal expansion from Nelson & Guggenheim (1993) and compressibility from Pawley et al. (2002). The mixing energies are very similar to those of the earlier data set
added for tetrahedral site configurational entropy. The entropies of afchl and ames were adjusted slightly in fitting to the phase equilibrium experimental results. The heat capacities were taken from Bertoldi et al. (2007), the thermal expansion from Nelson & Guggenheim (1993) and compressibility from Pawley et al. (2002). The mixing energies are very similar to those of the earlier data set 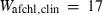 kJ,
kJ, 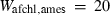 kJ and
kJ and 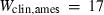 kJ with an enthalpy of
kJ with an enthalpy of 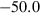 kJ for the internal equilibrium afchl + ames = 2 clin.
kJ for the internal equilibrium afchl + ames = 2 clin.
Epidote has also been slightly modified since HP98. The heat capacities of zoisite and clinozoisite have been refitted to high temperatures using a simple vibrational model. The values for both polymorphs are now very similar, with clinozoisite being very slightly lower than zoisite. The heat capacity of epidote is similarly extrapolated to high temperatures, fitting the experimental data of Kiseleva et al. (1974) and the entropy of epidote is taken from Kiseleva & Ogorodova (1987). The entropy of cz and fep end-members are adjusted slightly to fit phase equilibrium data for the reaction epidote = anorthite + garnet + hematite + quartz + H2O from Holdaway (1972) and Liou (1973). The activity model is the same as in HP98, but the mixing energies are changed (simplified) to 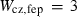 kJ,
kJ, 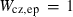 kJ and
kJ and 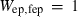 kJ. These small values are based on a value for
kJ. These small values are based on a value for 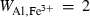 kJ for Al–
kJ for Al–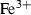 mixing in grossular-andradite garnet derived from fitting the experiments of Holdaway (1972) for coexisting garnet + anorthite + wollastonite + quartz. The enthalpy of the internal equilibrium fep + cz = 2ep is
mixing in grossular-andradite garnet derived from fitting the experiments of Holdaway (1972) for coexisting garnet + anorthite + wollastonite + quartz. The enthalpy of the internal equilibrium fep + cz = 2ep is 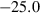 kJ to account for the degree of order in natural epidote (Dollase, 1973; Bird & Helgeson, 1980).
kJ to account for the degree of order in natural epidote (Dollase, 1973; Bird & Helgeson, 1980).
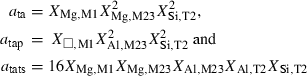
Sapphirine, following the treatment in Kelsey et al. (2004) involves two end-members spr4 and spr5 (see above) related by a tschermak substitution. The activities for the binary are given by 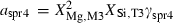 and
and 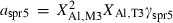 , with gammas found from a regular model with
, with gammas found from a regular model with 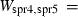
 kJ.
kJ.
Pyrrhotite is treated as a non-ideal solid solution of trov and trot (see above), with activities given by 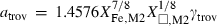 and
and 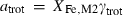 . The activity coefficients may be found from a regular model with
. The activity coefficients may be found from a regular model with 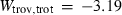 kJ. More details may be found in Evans et al. (2010).
kJ. More details may be found in Evans et al. (2010).
There are many additional changes to the data set, mainly relating to changes to thermodynamic parameters taken as assumed in data set generation (entropy, volume, heat capacity, etc.), and in the use of newer experimental data on phase stability that can be included in data set generation. Some changes are very minor and may be found by comparison with the tables in HP98, whereas others are more significant and are listed briefly in Appendix 3. One change that may be of greatest import to metamorphic petrologists is highlighted here, and concerns the aluminium silicate phases kyanite, andalusite and sillimanite. The choice of the Holdaway (1971) experiments, as opposed to those of Richardson et al. (1969) for the and = sill reaction is no longer arbitrarily imposed as a constraint. Instead, we prefer to return to the situation in our earlier data sets (Holland & Powell, 1985; 1998) in which no and = sill experimental brackets were used, and a triple point is allowed to emerge from the multitude of other equilibria involved in the data set. The calculated triple point from data in this study lies at 4.3 kbar, 534 °C, in between that of Holdaway (1971) and Richardson et al. (1969). The fact that the relaxation of the and = sill constraint yields a triple point almost identical to that advocated by Pattison et al. (2002) on the basis of field, petrographic and phase equilibria arguments, suggested to us that the combined reaction data used in the regression provide a reasonable justification of this decision.
Examples of Calculated Phase Equilibria
The following examples are of calculated phase equilibria highlighting new features of the internally consistent data set. All calculations were undertaken with thermocalc (Powell & Holland, 1988, 1998), and the activity–composition relations adopted are given in Table S2.
Sapphirine
Calculations in the literature on sapphirine phase equilibria using the Holland and Powell data set have used a special upgrade of the HP98 data set (tc-ds55s), for example, Kelsey et al. (2004), Baldwin et al. (2007) and Taylor-Jones & Powell (2010). The origin of the upgrade was that the fitting of the available experimental data in the fifth update of Holland & Powell (1998) in November 2003, tc-ds55 – the extant standard data set – was considered to be partially degraded by inclusion of the sapphirine experimental data. Now, as discussed above, a successful incorporation of the sapphirine end-members into the data set has been undertaken.
Sapphirine equilibria are important geologically as they have been used widely in higher temperature rocks in which sapphirine-bearing mineral assemblages occur to estimate P–T conditions of metamorphism. Phase equilibria in the simple systems MgO–Al2O3–SiO2 (MAS) and MgO–Al2O3–SiO2–H2O (MASH) are experimentally determined, so they in turn constrain the corresponding thermodynamic data of the mineral end-members Figure 4 shows the calculated phase equilibria in the systems MgO–Al2O3–SiO2, with the ultimate stability of sapphirine, and sapphirine + quartz indicated. The main invariant points (a–d) are at a slightly lower pressure (< 0.4 kbar) and higher temperature (< 30 °C) than those calculated with tc-ds55s. Note that mullite-bearing equilibria, at the highest temperature on Fig. 4, can now be calculated.
P–T projection for sapphirine equilibria in the MgO–Al2O3–SiO2 system, showing the maximum stability fields for sa (light shading) and sa + q (darker shading). Phases: g, garnet; sa, sapphirine; cor, corundum; sp, spinel; opx, orthopyroxene; ky, kyanite; and, andalusite; sill, sillimanite; cd, cordierite; mlt, mullite; q, quartz. a, b, c, d are invariant points from which FeO–MgO–Al2O3–SiO2 univariants emerge (see Fig. 5). For a–x relationships used, see Table S2.
Not specifically shown in Fig. 4 are the corresponding MASH equilibria as these can be easily envisaged in Fig. 4. Addition of H2O to MAS affects only equilibria involving cordierite, at least until melt is stabilized. Thus, on addition of H2O, the MAS invariant points become MASH univariant lines coincident with reactions not involving cordierite (or [cd], i.e. cd-out) MAS univariant lines. These extend up P–T from invariant points, a and b, in Fig. 4.
Extension of the phase equilibria from MAS into the FeO-bearing system, FMAS, is shown in Fig. 5. Out of each MAS univariant point comes a FMAS univariant line, depending on which phases involved more easily incorporate FeO. Focussing on point b, the [sp] FMAS univariant extends down temperature until garnet is stabilized, and the resulting FMAS invariant point is the lower temperature one of the familiar triangle of FMAS invariant points (as shown in the adjacent inset on Fig. 5). Extending into FMASH, the [cd] FMAS univariant reactions go up to higher P–T from this triangle of FMAS invariant points to become the FMASH univariants. As discussed in Kelsey et al. (2004) and Baldwin et al. (2007), the classic experimental results of Hensen (1972) are in (at least) FMASH, not FMAS, and so occur at rather higher P–T than those shown in Fig. 5, corresponding to the small amount of water in his experiments.
P–T projection for sapphirine equilibria in the FeO–MgO–Al2O3–SiO2 system (full curves) and the MgO–Al2O3–SiO2 subsystem (dashed curves). a, b, c, d are invariant points in MAS from which FMAS univariants emerge. Close to MAS invariant point b is the triangle of FMAS invariant points deduced by Hensen (1972)– although his experiments contained trace H2O and were at somewhat higher pressures (see text). For a–x relationships used, see Table S2.
Sulphur
As outlined above, the scope for calculating phase equilibria involving aqueous solutions, CHOS fluids and also sulphides and sulphate is now considerably increased (see above; also Evans & Powell, 2007; Evans et al., 2010). Calculated equilibria among magnetite, hematite, pyrite, pyrrhotite, anhydrite and siderite, in the presence of calcite, are shown in Fig. 6. These are simple end-members, apart from pyrrhotite, for which the non-stoichiometry is modelled as described in Evans et al. (2010), and outlined above. Focussing on phase equilibria at 5 kbar, Fig. 7 shows a back-projection of the phase relationships onto the pyrrhotite one-phase field for assemblages with calcite + graphite.
P–T projection for CaO–FeO–C–O–S with excess calcite (cc) to show calculated equilibria among the phases hem (hematite), mt (magnetite), gph (graphite), sid (siderite), po (pyrrhotite), pyr (pyrite), any (anhydrite). Compatibility tetrahedra are shown – see text for discussion.
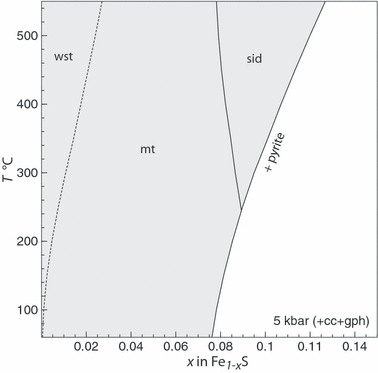
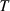 –
–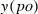 diagram at 5 kbar, with excess calcite and graphite, showing the calculated composition of pyrrhotite coexisting with wustite (wst), magnetite (mt), siderite (sid) and pyrite.
diagram at 5 kbar, with excess calcite and graphite, showing the calculated composition of pyrrhotite coexisting with wustite (wst), magnetite (mt), siderite (sid) and pyrite.
The fields on Fig. 6 are labelled with tetrahedral compatibility diagrams. Simpler triangular compatibility diagrams can be drawn for graphite-, and for pyrite-saturated, conditions. Whereas compatibilty diagrams of various sorts are commonly best adapted for representing mineral stabilities for geological processes (e.g. Powell et al., 2005), conventionally such relationships for the minerals involved here are represented on intensive variable diagrams, involving for example log activities. An equivalent diagram, calculated at 5 kbar and 500° C, in terms of chemical potentials, is shown in Fig. 8. The top surface of the 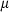 -
-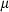 -
-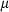 box is for graphite presence. Note that the
box is for graphite presence. Note that the 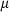 -
-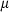 -
-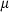 invariant points (a–d in Fig. 8) correspond to tie tetrahedra in the compatibility diagrams in Fig. 6. The calculations were performed on these divariant equilibria using the calcmu script in thermocalc, with
invariant points (a–d in Fig. 8) correspond to tie tetrahedra in the compatibility diagrams in Fig. 6. The calculations were performed on these divariant equilibria using the calcmu script in thermocalc, with 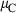 calculated from
calculated from 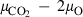 , and
, and 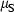 calculated from
calculated from 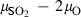 . Only the higher
. Only the higher  relationships are shown (for simplicity): from the compatibility diagram it can be seen that at lower
relationships are shown (for simplicity): from the compatibility diagram it can be seen that at lower  (moving away from the C apex), successive invariant points in the
(moving away from the C apex), successive invariant points in the  -
-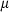 -
-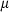 box, will involve pyr + mt + sid + any (at
box, will involve pyr + mt + sid + any (at  ), mt + hem + sid + any (at
), mt + hem + sid + any (at  ) and pyr + po + mt + any (at
) and pyr + po + mt + any (at 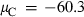 )
)
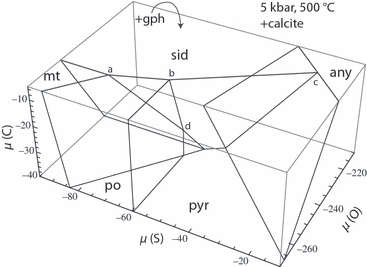
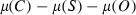 box at 5 kbar, 500 °C showing the fields for mt (magnetite), sid(siderite), any (anhydrite), pyr (pyrite) and po (pyrrhotite). The top surface is graphite-saturated. Invariant points a–d correspond with the compatibility tie-tetrahedra in Fig. 6.
box at 5 kbar, 500 °C showing the fields for mt (magnetite), sid(siderite), any (anhydrite), pyr (pyrite) and po (pyrrhotite). The top surface is graphite-saturated. Invariant points a–d correspond with the compatibility tie-tetrahedra in Fig. 6.
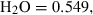
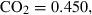
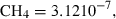
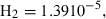
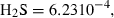

Phase equilibria at deep mantle pressures
A new departure in this data set is the inclusion of phases which become stable in the deeper parts of the Earth's mantle. The thermodynamic data now allow calculation of P–T grids in chosen chemical systems, and pseudosections for bulk compositions applicable to model mantle materials. This is an expanding field of endeavour, both experimentally and in modelling, and we present some examples of the types of phase diagram which may be calculated with this data set using thermocalc.
The first example is a P–T projection in the MgO–SiO2 system (Fig. 9) involving the phases olivine, wadsleyite (wad), ringwoodite (ring), high-pressure cpx (hcpx), akimotoite (aki), perovskite (pv), periclase (per) and stishovite (stv). The diagram pertains to pressures above the breakdown of orthopyroxene. The inferences that can be made from the MS system about mantle mineralogy are somewhat limited, and so we calculate a P–T diagram showing the MAS reactions emerging from the MS invariant points on introduction of alumina into the system (Fig. 10). Three stable invariant points ensue, labelled A, B and C in the figure, and these are the starting points for FMAS univariant reactions in the Fe-bearing system (arrow-ended curves in Fig. 10). These enable construction of the rather more petrologically interesting pseudosection for fixed bulk composition allowing portrayal of the different FMAS assemblages on the P–T diagram.
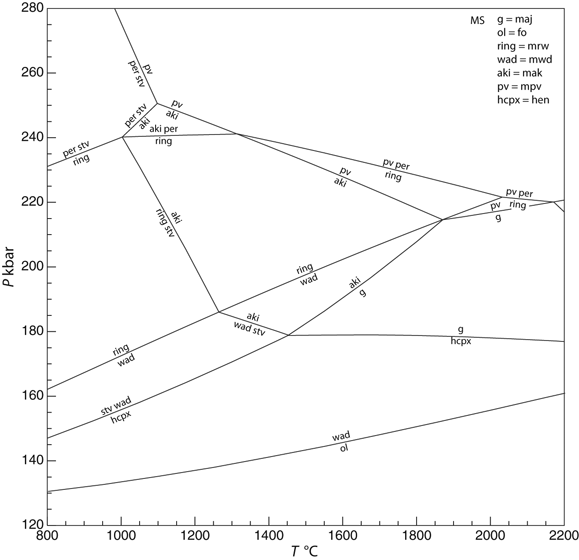
P–T projection for deep mantle phases in MgO–SiO2. Phases: pv, perovskite; aki, akimotoite (ilmenite); per, periclase; ring, ringwoodite; wad, wadsleyite; g, majorite garnet; stv, stishovite; hcpx, high-pressure clinoenstatite; ol, olivine. Legend provides the end-member names as used in thermocalc.
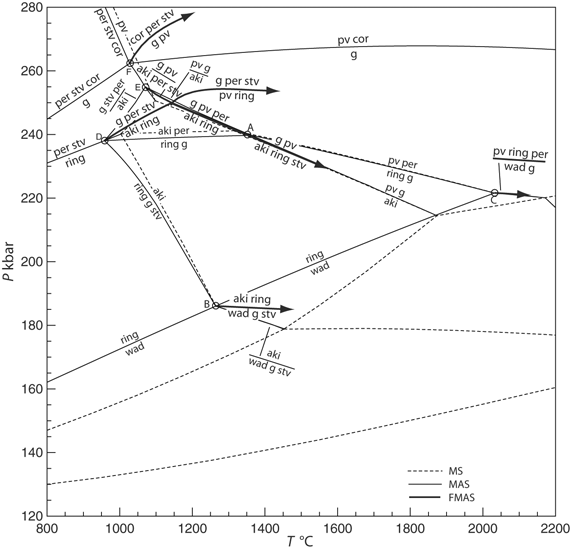
P–T projection for deep mantle phase in MgO–Al2O3–SiO2. Full thin curves are univariant equilibria in MAS and thin dashed curves are the MS equilibria. There are six MAS invariant points (A, B, C, D, E, F) with emergent FeO–MgO–Al2O3–SiO2 univariants shown by heavy lines and arrowed ends, as well as one full FMAS invariant point close to 250 kbar and 1200 °C. cor, corundum; other phase names as in Fig. 9. For a–x relationships used, see Table S2.
Figure 11 shows the pseudosection calculated for the Kilbourne Hole peridotite bulk composition (Takahash, 1986; Walter, 1998), simplified into the FMAS system. It is immediately clear that the nature of the 660 km transition ( 230 kbar) is likely to be more complex than that commonly interpreted from experimental data in smaller subsystems, changing through several assemblages involving incoming of perovskite and periclase. The range and variety of assemblages developed in P–T space shows how difficult it will be to perform and interpret experimental charges in chemically complex systems. Addition of calcium will further complicate the pattern of mineral assemblages, and such a calculation will be presented elsewhere. A word of caution is in order here, as there are a couple of major sources of uncertainty in the experiments used to derive these data. First, pressures and temperatures for the same experimental boundaries are often inconsistent among different investigators, and second, the pressure scale to be used in the experiments has not yet been satisfactorily resolved. Thus, the calculated equilibria may require adjustment in future as these experimental problems are resolved.
230 kbar) is likely to be more complex than that commonly interpreted from experimental data in smaller subsystems, changing through several assemblages involving incoming of perovskite and periclase. The range and variety of assemblages developed in P–T space shows how difficult it will be to perform and interpret experimental charges in chemically complex systems. Addition of calcium will further complicate the pattern of mineral assemblages, and such a calculation will be presented elsewhere. A word of caution is in order here, as there are a couple of major sources of uncertainty in the experiments used to derive these data. First, pressures and temperatures for the same experimental boundaries are often inconsistent among different investigators, and second, the pressure scale to be used in the experiments has not yet been satisfactorily resolved. Thus, the calculated equilibria may require adjustment in future as these experimental problems are resolved.
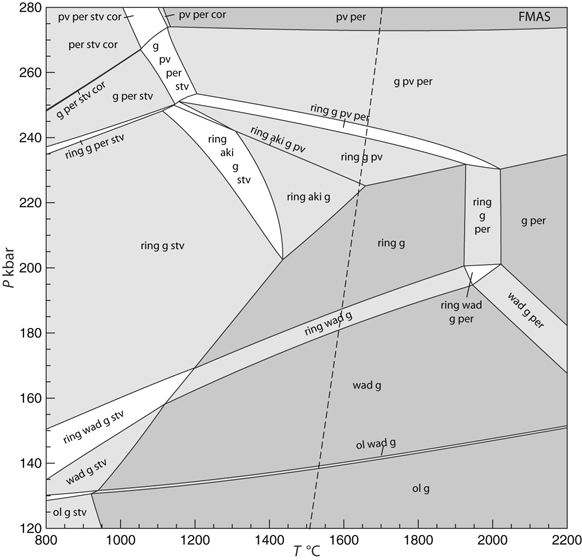
P–T pseudosection for FeO–MgO–Al2O3–SiO2 with a bulk composition corresponding to the Kilbourne Hole peridotite KLB-1 (Walter, 1998). The bulk composition sees short sections of some of the univariant curves in Fig. 10, but only below about 1400 °C and 240 kbar and so typical mantle geotherms are likely to pass to somewhat higher temperatures and may not intersect them. The dashed line represents one estimated geotherm smoothed from Stixrude & Lithgow-Bertelloni (2007). The lowest pressure part of this diagram is metastable with respect to inclusion of high-pressure cpx which was not considered for this diagram. cor, corundum; other phase names as in Fig. 9. For a–x relationships used, see Table S2.
Discussion
The internally consistent thermodynamic data set described here is a major improvement on previous ones because all the calorimetric and experimental data published in the 13 years since HP98 are now considered and incorporated if appropriate, and this increases the reliability of the data and expands the scope (via the incorporation of the new end-members that has become possible). The increase in reliability of the data set, in relation to the end-members already present in HP98, stems from the better implicit cross-checking between equilibria that involve the same end-members (the `internal consistency') as new data become available. In detail, if before there was an equilibrium with high `hat' (see HP98, table 7, or Table S1 here) – a measure of how constraining that equilibrium is – then addition of data involving that end-member will reduce the hat for the equilibria involved. Also additional data may simply suggest that equilibria taken to be correct in the past should now be considered untrustworthy and not used in data set generation. Methodological improvements also contribute to reliability. The expansion of scope is self-evident in the addition of a large number of new end-members, but also arises as a consequence of the methodological improvements that now allow calculations at high P−T, and in S-bearing systems, for example.
The ongoing development of the internally consistent thermodynamic data set is largely dependent on the calorimetric and phase equilibria experimental community, without whose best efforts our work will tend to founder. Although we think this data set is a substantial step forward in the quest for this aspect of quantification of petrological processes, much needs to be done. Obvious things are needed, for example the proper characterization of the phases in experimental charges and measurement of unit cell volumes to high pressures and temperatures, particularly those made at high temperatures at elevated pressures. As may be readily seen from Appendix 1, there remain many end-members for which no measured thermal expansion, compressibility or heat capacity values as yet exist. For some, for example, those fictive end-members which do not exist stably in nature or are not readily synthesized experimentally, such measurements will never be available but could in principle be calculated from molecular simulations. For many others in the table new measurements would be most welcome. Applications to well-characterized rocks from well-established geological settings will provide critical input to the evaluation of the data set, and we welcome feedback relating to this from people using the data set. Of course such applications are equally reliant on the activity–composition relations used for the phases involved, as well as a realistic appraisal of the likely geological processes involved in rock formation.
In generation of the data set, the enthalpies of formation of the end-members are solved for in the weighted least squares approach. As a part of this, the uncertainty on these enthalpies are calculated, as well as the correlations between them (e.g. Powell & Holland, 1993a,b). These uncertainties can be considered as reflecting `known unknowns' about the end-member properties. If in fact data used in the generation of the data set are incorrect, because the data were not sufficiently dense to identify this, then this amounts to `unknown unknowns' about the end-member properties (the results are incorrect, and we have no way of knowing about it). The former source of uncertainty can be accounted for in error propagation calculations, but the latter cannot be handled in this way and introduce a bias in the results if, later, such problems are recognized. It is for this reason that validation of the data set via more experimental studies, and/or appropriate applications is important.
In using the data set, the uncertainties inherent in the data set can be propagated through calculations using thermocalc, as is done routinely in average P–T calculations, but also can be done for P–T projection and pseudosection calculations (via the calcsdnle script). So, for example considering Fig. 5, the uncertainty on the positions of the invariant points that form the highlighted triangle at around 6 kbar and 1000 °C, from the data set uncertainties, at 2 level, in
level, in  kbar,°C
kbar,°C , are
, are  ,
, 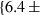
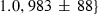 and
and 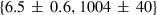 , with increasing temperature. If the uncertainties on the interaction parameters of the phases (Table S2) are also included, as they can be as outlined in Powell & Holland (2008), the uncertainties will be yet larger. These uncertainties are for the invariant points individually, and a way of looking at the correlations between the positions of the points as a consequence of the uncertainties is not yet implemented. It is conceivable that the uncertainties simply translate the triangle of points, rather than cause them to be involved in an inversion of topology. Work is in progress to address this aspect of uncertainties in calculated phase diagrams. Uncertainties, but with the same problem of not being able to ascertain correlations, can be done for pseudosection calculations. So, in Fig. 11, looking at the point on the divariant field, ring + g + pv + per, where the modes of pv and per are zero, the calculated uncertainty just with data set uncertainties is
, with increasing temperature. If the uncertainties on the interaction parameters of the phases (Table S2) are also included, as they can be as outlined in Powell & Holland (2008), the uncertainties will be yet larger. These uncertainties are for the invariant points individually, and a way of looking at the correlations between the positions of the points as a consequence of the uncertainties is not yet implemented. It is conceivable that the uncertainties simply translate the triangle of points, rather than cause them to be involved in an inversion of topology. Work is in progress to address this aspect of uncertainties in calculated phase diagrams. Uncertainties, but with the same problem of not being able to ascertain correlations, can be done for pseudosection calculations. So, in Fig. 11, looking at the point on the divariant field, ring + g + pv + per, where the modes of pv and per are zero, the calculated uncertainty just with data set uncertainties is 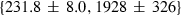 . In the case of propagated uncertainties for calculations at these conditions, the agreement of a pressure scale for experimental studies, as well as the reaching of a consensus on the position of end-member equilibria in P–T, should dramatically reduce the size of the uncertainties.
. In the case of propagated uncertainties for calculations at these conditions, the agreement of a pressure scale for experimental studies, as well as the reaching of a consensus on the position of end-member equilibria in P–T, should dramatically reduce the size of the uncertainties.
Acknowledgements
We thank K. Evans for her enthusiasm and direct involvement with generating the sulphur part of the data set story. R. White, J. Diener and E. Green are also thanked for suggestions and discussions on data set-related matters. We thank J. Ferry, J. Ganguly, M. Gottshalk and an anonymous reviewer for their helpful reviews, and J. Connolly for comments on TEOS. We thank M. Brown yet again for his editorial handling of our work. R. Powell thanks the support of ARC DP0451770 and DP0987731.
Appendices
Appendix 1: Sources for thermodynamic data
| Group | End-member | S | V | 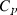 |
 |
 |
|---|---|---|---|---|---|---|
| Garnet and olivine | almandine (alm) | 3 | 4 | 0, 3 | 5 | 6 |
| andradite (andr) | 1 | 1 | 1 | 46 | 46 | |
| grossular (gr) | 42 | 1 | 43, 44 | 45, 46 | 46 | |
| knorringite (knor) | 0 | 47 | 0 | 0 | 0 | |
| majorite (maj) | 33 | 26 | 33 | 33 | 26 | |
| pyrope (py) | 0, 1 | 3 | 34 | 35 | 36, 37 | |
| spessartine (spss) | 38 | 39 | 38 | 40 | 41 | |
| clinohumite (chum) | 0 | 20 | 0 | 0 | 21 | |
| fayalite (fa) | 1 | 1 | 13 | 14, 15 | 16 | |
| forsterite (fo) | 1 | 1 | 1 | 10, 11 | 10, 12 | |
| larnite (larn) | 1 | 1 | 1 | 0 | 0 | |
| monticellite (mont) | 0, 1 | 1 | 1 | 18 | 19 | |
| tephroite (teph) | 1 | 1 | 1 | 17 | 0 | |
| Aluminosilicates | andalusite (and) | 1 | 1 | 52 | 53 | 54 |
| kyanite (ky) | 1 | 1 | 52 | 53 | 55 | |
| sillimanite (sill) | 1 | 1 | 52 | 53 | 54 | |
| mullite (amul) | 0 | 7 | 0 | 8 | 9 | |
| mullite (smul) | 0 | 7 | 0 | 8 | 9 | |
| chloritoid (mctd) | 61 | 59 | 61 | 62 | 63 | |
| chloritoid (fctd) | 61 | 64 | 61 | 62 | 63 | |
| chloritoid (mnctd) | 0 | 0 | 0 | 62 | 63 | |
| staurolite (mst) | 0 | 65 | 0 | 57 | 58 | |
| staurolite (fst) | 0 | 60 | 0 | 57 | 58 | |
| staurolite (mnst) | 0 | 0 | 0 | 57 | 58 | |
| topaz (tpz) | 0 | 66 | 0 | 40 | 0 | |
| Other orthosilicates | akermanite (ak) | 2 | 2 | 2 | 2 | 0 |
| gehlenite (geh) | 79 | 60 | 1 | 40 | 0 | |
| julgoldite (jgd) | 0 | 78 | 0 | 0 | 0 | |
| merwinite (merw) | 1 | 65 | 1 | 40 | 0 | |
| pumpellyite (mpm) | 0 | 77 | 0 | 0 | 0 | |
| pumpellyite (fpm) | 0 | 0 | 0 | 0 | 0 | |
| rankinite (rnk) | 1 | 1 | 1 | 40 | 0 | |
| sphene (sph) | 1 | 1 | 1, 88 | 89 | 90 | |
| spurrite (spu) | 1 | 1 | 0 | 0 | 0 | |
| tilleyite (ty) | 0 | 80 | 0 | 0 | 0 | |
| zircon (zrc) | 1 | 1 | 1 | 40 | 91 | |
| Sorosilicates | clinozoisite (cz) | 0 | 71 | 0 | 69 | 70 |
| epidote (ep) | 72 | 73 | 72 | 69 | 70, 74 | |
| epidote (fep) | 0 | 0 | 0 | 0 | 0 | |
| lawsonite (law) | 67 | 1 | 0, 67 | 69 | 76 | |
| piemontite (pmt) | 0 | 75 | 0 | 0 | 0 | |
| zoisite (zo) | 0, 67 | 68 | 0, 67 | 69 | 70 | |
| vesuvianite (vsv) | 0 | 49 | 0 | 50 | 51 | |
| Cyclosilicates | cordierite (fcrd) | 81 | 86 | 81 | 83 | 84, 85 |
| cordierite (hcrd) | 81 | 0 | 0 | 83 | 84, 85 | |
| cordierite (crd) | 81, 82 | 1 | 81 | 83 | 84, 85 | |
| cordierite (mncrd) | 0 | 0 | 0 | 83 | 84, 85 | |
| osumilite (osm1) | 18 | 18 | 18 | 0 | 0 | |
| osumilite (osm2) | 18 | 18 | 18 | 0 | 0 | |
| osumilite (fosm) | 18 | 18 | 18 | 0 | 0 | |
| High-pressure silicates | akimotoite (fak) | 0, 33 | 22 | 33 | 0, 33 | 33 |
| akimotoite (mak) | 0, 33 | 22 | 33 | 33 | 26 | |
| caSi-titanite (cstn) | 0 | 247 | 0 | 0 | 247 | |
| perovskite (apv) | 0, 27 | 22 | 0 | 0, 32 | 26 | |
| perovskite (cpv) | 0 | 246 | 0 | 0, 32 | 246 | |
| perovskite (fpv) | 0 | 249 | 0 | 0 | 249 | |
| perovskite (mpv) | 0, 27 | 22 | 32 | 32 | 26 | |
| phase A (phA) | 0 | 87 | 0 | 87 | 87 | |
| ringwoodite (mrw) | 0, 27 | 22 | 23 | 28 | 26 | |
| ringwoodite (frw) | 0 | 26 | 29, 30 | 31 | 30 | |
| wadsleyite (mwd) | 0 | 22 | 23 | 24 | 25 | |
| wadsleyite (fwd) | 0 | 22 | 0 | 0 | 26 | |
| Pyroxenes and pyroxenoid | acmite (acm) | 1 | 60 | 1 | 92 | 93 |
| Ca-tschermak's pyroxene (cats) | 94 | 94 | 94 | 94 | 0 | |
| Ca-Eskola pyroxene (caes) | 0 | 95 | 0 | 0 | 0 | |
| clinoenstatite (cen) | 0 | 96 | 97, 98 | 40 | 0 | |
| clinoenstatite (hen) | 0 | 102 | 0 | 0 | 107 | |
| diopside (di) | 1 | 99 | 1 | 100 | 101 | |
| enstatite (en) | 1 | 1 | 1 | 40 | 102 | |
| ferrosilite (fs) | 1 | 103 | 1 | 103 | 104 | |
| hedenbergite (hed) | 105 | 105 | 105 | 92 | 106 | |
| jadeite (jd) | 1 | 1 | 108 | 92, 109 | 109 | |
| kosmochlore (kos) | 0 | 110 | 0 | 92 | 111 | |
| Mg-tschermak’s pyroxene (mgts) | 0 | 112 | 0 | 0 | 0 | |
| protoenstatite (pren) | 0 | 60 | 0, 1 | 113 | 102 | |
| pseudowollastonite (pswo) | 1 | 1 | 0, 114 | 40 | 0 | |
| pyroxmangite (pxmn) | 1 | 1 | 1 | 115 | 115 | |
| rhodonite (rhod) | 1 | 1 | 1 | 115 | 115 | |
| walstromite (wal) | 248 | 248 | 0, 114 | 0,40 | 0, 116 | |
| wollastonite (wo) | 1 | 60 | 114 | 40 | 116 | |
| Amphiboles | actinolite (fact) | 0 | 120 | 0 | 0 | 0 |
| anthophyllite (anth) | 1 | 1 | 0 | 0 | 0 | |
| anthophyllite (fanth) | 0 | 0 | 0 | 0 | 0 | |
| cummingtonite (cumm) | 0 | 126 | 0 | 0 | 0 | |
| glaucophane (gl) | 123 | 124 | 123 | 124 | 119 | |
| glaucophane (fgl) | 0 | 0 | 0 | 0 | 0 | |
| grunerite (grun) | 0 | 127 | 0 | 0 | 128 | |
| pargasite (parg) | 0 | 122 | 0 | 103 | 119 | |
| riebeckite (rieb) | 0 | 125 | 0 | 0 | 0 | |
| tremolite (tr) | 0, 1 | 117 | 118 | 242 | 119 | |
| tschermakite (ts) | 0 | 121 | 0 | 0 | 0 | |
| Other chain silicates | deerite (deer) | 0 | 129 | 0 | 0 | 129 |
| carpholite (mcar) | 130 | 131 | 130 | 0 | 0 | |
| carpholite (fcar) | 130 | 132 | 130 | 0 | 0 | |
| sapphirine (spr4) | 0 | 133, 134 | 0 | 0 | 0 | |
| sapphirine (spr5) | 0 | 133, 134 | 0 | 0 | 0 | |
| sapphirine (fspr) | 0 | 0 | 0 | 0 | 0 | |
| Mica | annite (ann) | 0 | 60 | 0 | 0 | 0 |
| biotite (mnbi) | 0 | 0 | 0 | 0 | 0 | |
| celadonite (cel) | 0 | 135 | 0 | 137 | 138 | |
| celadonite (fcel) | 0 | 136 | 0 | 137 | 138 | |
| eastonite (east) | 0 | 139 | 0 | 0 | 0 | |
| margarite (ma) | 1 | 1 | 1 | 140 | 0 | |
| muscovite (mu) | 1 | 1 | 1 | 137 | 138 | |
| paragonite (pa) | 1 | 1 | 1, 141 | 137 | 138 | |
| phlogopite (phl) | 1 | 1 | 1 | 142 | 143 | |
| phlogopite (naph) | 0 | 144 | 0 | 0 | 0 | |
| Chlorite | chlorite (afchl) | 145 | 146, 147, 148 | 145 | 149 | 150 |
| chlorite (mnchl) | 0, 145 | 0 | 0 | 149 | 150 | |
| amesite (ames) | 0 | 146, 147, 148 | 145 | 149 | 150 | |
| clinochlore (clin) | 145 | 146, 147, 148 | 145 | 149 | 150 | |
| daphnite (daph) | 145 | 151 | 145 | 149 | 150 | |
| sudoite (sud) | 152 | 0 | 0 | 149 | 150 | |
| sudoite (fsud) | 0 | 0 | 0 | 149 | 150 | |
| Other sheet silicates | antigorite (atg) | 0 | 158 | 159 | 0 | 160 |
| chrysotile (chr) | 1 | 1 | 1 | 0 | 162 | |
| lizardite (liz) | 0 | 162 | 1 | 0 | 162 | |
| greenalite (glt) | 0 | 161 | 0 | 0 | 0 | |
| kaolinite (kao) | 1 | 1 | 1 | 0 | 0 | |
| minnesotaite (min) | 0 | 155 | 0 | 0 | 0 | |
| minnesotaite (minm) | 0 | 0 | 0 | 0 | 0 | |
| stilpnomelane (mstp) | 0 | 0, 155 | 0 | 0 | 0 | |
| stilpnomelane (fstp) | 0 | 155 | 0 | 0 | 0 | |
| prehnite (pre) | 67 | 67 | 67 | 0 | 156 | |
| prehnite (fpre) | 0 | 157 | 0 | 0 | 156 | |
| pyrophyllite (prl) | 1 | 22 | 153 | 0 | 150 | |
| talc (ta) | 22 | 1 | 1 | 154 | 150 | |
| talc (fta) | 0 | 0 | 0 | 154 | 150 | |
| talc (tap) | 0 | 0 | 153 | 0 | 150 | |
| talc (tats) | 0 | 0 | 0 | 154 | 150 | |
| Feldspar and feldspathoid | albite (ab) | 1 | 1 | 1 | 163 | 164 |
| albite (abh) | 0, 1 | 0, 1 | 1 | 163 | 164 | |
| analcite (anl) | 1 | 1 | 0 | 0 | 177 | |
| anorthite (an) | 1 | 1 | 167 | 168 | 169 | |
| carnegieite (cg) | 1 | 1 | 1 | 0 | 0 | |
| carnegieite (cgh) | 1 | 178 | 1 | 0 | 0 | |
| kalsilite (kls) | 1 | 179 | 1 | 179, 180 | 181 | |
| leucite (lc) | 1 | 182 | 0, 1 | 182 | 181 | |
| microcline (mic) | 1 | 1 | 1 | 165 | 166 | |
| nepheline (ne) | 1 | 1 | 1 | 40 | 177 | |
| sanidine (san) | 1 | 165 | 1 | 165 | 166 | |
| Silica minerals | coesite (coe) | 0, 174 | 1 | 174 | 0 | 0 |
| cristobalite (crst) | 0, 1 | 0, 1 | 1 | 0 | 0 | |
| quartz (q) | 1 | 1 | 1, 173 | 0 | 173 | |
| stishovite (stv) | 0, 1 | 1 | 33 | 175 | 176 | |
| tridymite (trd) | 0, 1 | 0, 1 | 0, 1 | 0 | 0 | |
| Other framework silicates | heulandite (heu) | 187 | 187 | 0 | 0 | 244 |
| hollandite (hol) | 171 | 172 | 172 | 172 | 172 | |
| laumontite (lmt) | 0 | 186 | 0 | 0 | 0 | |
| meionite (me) | 0, 183 | 183 | 0 | 184 | 185 | |
| K-cymrite (kcm) | 0 | 170 | 0 | 170 | 170 | |
| sodalite (sdl) | 245 | 245 | 245 | 0, 40 | 0, 177 | |
| stilbite (stb) | 0 | 188 | 0 | 0 | 0 | |
| wadeite (wa) | 171 | 170 | 170 | 172 | 171 | |
| wairakite (wrk) | 0 | 1 | 0 | 0 | 0 | |
| Oxides | baddeleyite (bdy) | 1 | 1 | 1 | 40 | 205 |
| bixbyite (bix) | 1 | 1 | 199 | 0 | 0 | |
| corundum (cor) | 1 | 1 | 199 | 200 | 201 | |
| corundum (mcor) | 0 | 0 | 0 | 0 | 0 | |
| cuprite (cup) | 1 | 1 | 1 | 0 | 206 | |
| eskolaite (esk) | 1 | 1 | 1 | 0 | 202 | |
| geikielite (geik) | 1 | 1 | 0, 1 | 0 | 0 | |
| hematite (hem) | 1 | 1 | 1 | 40 | 202 | |
| hercynite (herc) | 209 | 1 | 0 | 40 | 0 | |
| Ilmenite (ilm) | 1 | 1 | 1 | 204 | 204 | |
| lime (lime) | 1 | 1 | 1 | 189 | 190 | |
| magnesioferrite (mft) | 210 | 1 | 1 | 0 | 0 | |
| magnetite (mt) | 1 | 1 | 1 | 40 | 208 | |
| manganosite (mang) | 1 | 1 | 1 | 197 | 198 | |
| nickel oxide (NiO) | 1 | 1 | 1 | 0 | 203 | |
| periclase (per) | 1 | 1 | 193 | 194 | 195, 196 | |
| picrochromite (picr) | 211 | 1 | 1 | 0 | 0 | |
| pyrophanite (pnt) | 1 | 1 | 0, 1 | 0 | 0 | |
| rutile (ru) | 1 | 1 | 1 | 191 | 192 | |
| spinel (sp) | 0, 1 | 1 | 1 | 207 | 208 | |
| tenorite (ten) | 1 | 1 | 1 | 0 | 0 | |
| ulvospinel (usp) | 1 | 1 | 1 | 0 | 0 | |
| ferropericlase (fper) | 0, 1 | 26 | 1 | 40 | 26 | |
| Hydroxides | brucite (br) | 1 | 1 | 0, 1 | 212, 213 | 213, 214 |
| diaspore (dsp) | 1 | 22 | 0, 1 | 215 | 216 | |
| goethite (gth) | 1 | 1 | 0 | 0 | 0 | |
| Carbonates | ankerite (ank) | 0 | 227 | 0 | 0 | 226 |
| aragonite (arag) | 1 | 1 | 0, 1 | 40, 219 | 219 | |
| calcite (cc) | 1 | 1 | 0, 1 | 217 | 218 | |
| dolomite (dol) | 1 | 22 | 0, 1 | 224, 225 | 225, 226 | |
| magnesite (mag) | 1 | 1 | 0, 1 | 217, 220, 221 | 220, 221 | |
| rhodochrosite (rhc) | 1 | 1 | 1 | 222 | 223 | |
| siderite (sid) | 0, 1 | 22 | 0, 1 | 0 | 177 | |
| Halides and S-bearing | anhydrite (any) | 1 | 1 | 235 | 236 | 177 |
| halite (hlt) | 1 | 1 | 1 | 228 | 228 | |
| pyrite (pyr) | 1 | 1 | 229 | 40 | 230 | |
| pyrrhotite (trot) | 0 | 231 | 0, 233 | 231 | 232 | |
| pyrrhotite (trov) | 0 | 231 | 0, 233 | 231 | 232 | |
| troilite (tro) | 0 | 231 | 0, 233 | 231 | 232 | |
| troilite (lot) | 0 | 231 | 0, 233 | 234 | 232 | |
| sylvite (syv) | 1 | 1 | 1 | 228 | 228 | |
| Elements | copper (Cu) | 1 | 1 | 1 | 40 | 238 |
| diamond (diam) | 1 | 1 | 1 | 40 | 240 | |
| graphite (gph) | 1 | 1 | 1 | 40 | 239 | |
| iron (iron) | 1 | 1 | 0, 1 | 40 | 237 | |
| nickel (Ni) | 1 | 1 | 0, 1 | 40 | 177 | |
| sulphur (S) | 1 | 1 | 1 | 243 | 241 | |
| Gas species | methane (CH4) | 1 | – | 1 | – | – |
| carbon monoxide (CO) | 1 | – | 1 | – | – | |
| carbon dioxide (CO2) | 1 | – | 1 | – | – | |
| hydrogen (H2) | 1 | – | 1 | – | – | |
| hydrogen sulphide (H2S) | 1 | – | 1 | – | – | |
| sulphur gas (S2) | 1 | – | 1 | – | – | |
| water (H2O) | 1 | – | 1 | – | – | |
| oxygen (O2) | 1 | – | 1 | – | – |
-
Sources for entropy (S), molar volume (V), heat capacity (
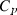 ), thermal expansion (
), thermal expansion ( ) and incompressibility (
) and incompressibility ( ) data.
) data.
- 0 Estimated or optimised in this study 1 Robie & Hemingway, 1995 2 Hemingway et al., 1986 3 Newton & Harlov (1993) 4 Geiger et al., 1987 5 Skinner, 1956 6 Takahashi & Liu, 1970 7 Cameron, 1977 8 Schneider & Eberhard, 1990 9 Balzar & Ledbetter, 1993 10 Hazen, 1976 11 Kajiyoshi, 1986 12 Downs et al., 1996 13 Robie et al., 1982 14 Smyth, 1975 15 Suzuki et al., 1981 16 Williams et al., 1990 17 Okajima et al., 1978 18 Lager & Meagher, 1978 19 Sharp et al., 1986 20 Yamamoto & Akimoto, 1977 21 Ross & Crichton, 2001 22 Smyth & McCormick, 1995 23 Ashida et al., 1987 24 Suzuki, 1980 25 Jacobs & de Jong, 2005 26 Stixrude & Lithgow-Bertelloni, 2005 27 Fei et al., 1990 28 Suzuki, 1979 29 Watanabe, 1982 30 Jacobs & Oonk, 2001 31 Mao et al., 1969 32 Gillet et al., 2000 33 Saxena, 1996 34 Tequi et al., 1991 35 Suzuki & Anderson, 1983 36 Hazen & Finger, 1989 37 Zhang et al., 1998 38 Dachs et al., 2009 39 Hsu, 1968 40 Skinner, 1966 41 Leger et al., 1990 42 Westrum et al., 1979 43 Bosenick et al., 1996 44 Thieblot et al., 1999 45 Isaak et al., 1992 46 Pavese et al., 2001a,b 47 Irifune et al., 1982 48 Holland et al., 1996 49 Hochella et al., 1982 50 Tribaudino & Prencipe, 1999 51 Tribaudino & Prencipe, 2001 52 Hemingway et al., 1991 53 Winter & Ghose, 1979 54 Burt et al., 2006 55 Comodi et al., 1997 56 Cameron, 1977 57 Gibbons et al., 1981 58 Grevel et al., 1998 59 Chopin & Schreyer, 1983 60 Robie et al., 1967 61 Koch-Müller et al., 2002 62 Ivaldi et al., 1988 63 Comodi et al., 1992 64 Rao & Johannes, 1979 65 Schreyer & Seifert, 1969 66 Wunder et al., 1993 67 Perkins et al., 1980 68 Chatterjee, 1976 69 Pawley et al., 1996 70 Comodi & Zanazzi, 1997 71 Jenkins et al., 1985 72 Kiseleva et al., 1974 73 Bird & Helgeson, 1980 74 Holland et al., 1996 75 Keskinen & Liou, 1979 76 Boffa-Ballaran & Angel, 2003 77 Schiffman & Liou, 1980 78 Artioli et al., 2003 79 Hemingway & Robie, 1984 80 Harker, 1959 81 Dachs & Geiger, 2008 82 Paukov et al., 2006 83 Mirwald et al., 1984 84 Mirwald, 1981 85 Schlenker et al., 1977 86 Mukhopadhyay & Holdaway, 1994 87 Pawley & Wood, 1995 88 Manon et al., 2008 89 Malcherek, 2001 90 Angel et al., 1999a,b 91 Hazen & Finger, 1979 92 Cameron et al., 1973 93 Kandelin & Weidner, 1988 94 Haselton et al., 1984 95 McCormick, 1986 96 Stephenson et al., 1966 97 White, 1919 98 Wagner, 1932 99 Krupka et al., 1985a 100 Finger & Ohashi, 1976 101 McCormick et al., 1989 102 Hugh-Jones & Angel, 1994 103 Sueno et al., 1976 104 Kandelin & Weidner, 1988 105 Haselton et al., 1987 106 Zhang & Hafner, 1992 107 Kung et al., 2005 108 Hemingway et al., 1998 109 Zhao et al., 1997 110 Carroll Webb & Wood, 1986 111 Origlieri et al., 2003 112 Gasparik & Newton, 1984 113 Jackson et al., 2003 114 Richet et al., 1991 115 Pinckney & Burnham, 1988 116 Vaidya et al., 1973 117 Hewitt, 1975 118 Krupka et al., 1985b 119 Comodi et al., 1991 120 Jenkins & Bozhilov, 2003 121 Jenkins, 1994 122 Lykins & Jenkins, 1992 123 Holland, 1988 124 Jenkins & Corona, 2006 125 Ernst, 1962 126 Evans & Ghiorso, 1995 127 Ghiorso & Evans, 2002 128 Zhang et al., 1992 129 Lattard & LeBreton, 1994 130 Bertoldi et al., 2006 131 Chopin & Schreyer, 1983 132 Viswanathan & Seidel, 1979 133 Seifert, 1974 134 Chatterjee & Schreyer, 1972 135 Schmidt et al., 2001 136 Coggon & Holland, 2002 137 Guggenheim et al., 1987 138 Comodi & Zanazzi, 1995 139 Circone et al., 1991 140 Symmes, 1986 141 Holland, 1979 142 Russell & Guggenheim, 1999 143 Pavese et al., 2003 144 Carman, 1974 145 Bertoldi et al., 2007 146 Baker & Holland, 1996 147 Jenkins & Chernosky, 1986 148 Roots, 1994 149 Nelson & Guggenheim, 1993 150 Pawley et al., 2002 151 Parra et al., 2005 152 Vidal et al., 1992 153 Krupka et al., 1979 154 Pawley et al., 1995 155 Miyano & Klein, 1989 156 Detrie et al., 2009 157 Rose & Bird, 1987 158 Mellini et al., 1987 159 King et al., 1967 160 Bose & Navrotsky, 1998 161 Rasmussen et al., 1998 162 Hilairet et al., 2006 163 Winter et al., 1979 164 Downs et al., 1994 165 Hovis et al., 1999 166 Allan & Angel, 1997 167 Richet & Fiquet, 1991 168 Grundy & Brown, 1974 169 Angel, 2004 170 Fasshauer et al., 1997 171 Yong et al., 2006 172 Akaogi et al., 2004 173 Dorogokupets, 1995 174 Hemingway et al., 1998 175 Ito et al., 1974 176 Andrault et al., 2003; Luo et al., 2002 177 Birch, 1966 178 Richet et al., 1990 179 Carpenter & Cellai, 1996 180 Hovis et al., 2003 181 Fasshauer et al., 1998 182 Palmer et al., 1989 183 Baker & Newton, 1994 184 Baker, 1995 185 Hazen & Sharp, 1988 186 Liou, 1971a 187 Cho et al., 1987 188 Liou, 1971b 189 Fiquet et al., 1999 190 Richet et al., 1988 191 Sugiyama & Takeuchi, 1991 192 Hazen & Finger, 1981 193 Richet & Fiquet, 1991 194 Dubrovinsky & Saxena, 1997 195 Fei, 1999 196 Hazen, 1976 197 Suzuki et al., 1979 198 Jeanloz & Rudy, 1987 199 Richet et al., 1992 200 Aldebert & Traverse, 1984 201 D'Amour et al., 1978 202 Finger & Hazen, 1980 203 Clendenen & Drickamer, 1966 204 Wechsler & Prewitt, 1984 205 Leger et al., 1993 206 Werner & Hochheimer, 1982 207 Fiquet et al., 1999 208 Finger et al., 1986 209 Klemme & Van Miltenburg, 2003 210 Klemme & Ahrens, 2005 211 Klemme et al., 2000 212 Fei & Mao, 1993 213 Fukui et al., 2003 214 Catti et al., 1995 215 Pawley et al., 1996 216 Xu et al., 1994 217 Markgraf & Reeder, 1985 218 Redfern & Angel, 1999 219 Martinez et al., 1996 220 Fiquet & Reynard, 1999 221 Zhang et al., 1997 222 Rao & Murthy, 1970 223 Martens et al., 1982 224 Reeder & Markgraf, 1986 225 Martinez et al., 1996 226 Ross & Reeder, 1992 227 Davidson et al., 1993 228 Walker et al., 2004 229 Chase, 1998 230 Adams & Williamson, 1923 231 Tenailleau et al., 2005 232 King & Prewitt, 1982 233 Gronvold & Stolen, 1991,1992 234 Taylor, 1970 235 Majzlan et al., 2002 236 Evans, 1979 237 Takahashi et al., 1968 238 Vaidya & Kennedy, 1971 239 Zhao & Spain, 1989 240 Alexandrov et al., 1987 241 Luo & Ruoff, 1993 242 Sueno et al., 1973 243 Wallis et al., 1986 244 Comodi et al., 2001 245 Sharp et al., 1989 246 Shim et al., 2000 247 Angel et al., 1999a,b 248 Chatterjee et al., 1984 249 Walter et al., 2004.
Appendix 2: Summary table of equilibria used for fitting the data set.
| 1) | 2knor = 3en + 2esk (Irifune et al., 1982) |
| 2) | 2knor = 3en + 2esk (Turkin et al., 1983) |
| 3) | knor + fo = picr + 2en (Klemme, 2004) |
| Equilibrium: crpx crsp (Carroll Webb & Wood, 1986), involving: | |
| 4) | 2kos + sp = 2jd + picr |
| 5) | lot = tro (fix at transition) |
| Equilibrium: po S2 (Rau, 1976), involving: | |
| 6) | 16trov = 14trot + S2 |
| 7) | 8trov + H2 = 7trot + H2S (Lin, 1976) |
| Equilibrium: po S2 (Toulmin & Barton, 1964), involving: | |
| 8) | 16trov = 14trot + S2 |
| Equilibrium: po pyr S2 (Toulmin & Barton, 1964), involving next two reactions: | |
| 9) | 14trot + S2 = 16trov |
| 10) | 2trot + S2 = 2pyr |
| Equilibrium: po pyr S2 (Schneeberg, 1973), involving next two reactions: | |
| 11) | 16trov = 14trot + S2 |
| 12) | 2pyr = 2trot + S2 |
| Equilibrium: iron tro fluid2 (Rosenqvist, 1954), involving: | |
| 13) | iron + H2S = tro + H2 |
| Equilibrium: iron tro fluid2 (Alcock & Richardson, 1951), involving: | |
| 14) | iron + H2S = tro + H2 |
| 15) | en = pren (Atlas, 1952; Chen & Presnall, 1975) |
| 16) | diam = gph (Kennedy & Kennedy, 1976) |
| 17) | q = trd (Ostrovsky, 1966) |
| 18) | trd = crst (Ostrovsky, 1966) |
| 19) | q = crst (Ostrovsky, 1966; Jackson, 1976) |
| 20) | coe = q (Bose & Ganguly, 1995) |
| 21) | coe = q (Bohlen & Boettcher, 1982; Gasparik, 1984) |
| 22) | stv = coe (Zhang et al., 1996) |
| 23) | arag = cc (Boettcher & Wyllie, 1968) |
| 24) | arag = cc (Crawford & Hoersch, 1972) |
| 25) | arag = cc (Johannes & Puhan, 1971) |
| 26) | arag = cc (Goldsmith & Newton, 1969) |
| 27) | arag = cc (Irving & Wyllie, 1975) |
| 28) | arag = cc (Suito et al., 2001) |
| 29) | arag + mag = dol (Morlidge et al., 2006) |
| 30) | arag + sid = ank (Morlidge et al., 2006) |
| 31) | cen = en (Boyd & England, 1965) |
| 32) | hen = en (Pacalo & Gasparik, 1990) |
| 33) | hen = cen (Angel et al., 1992) |
| 34) | mwd + stv = hen (Sawamoto, 1987; Kanzaki, 1987) |
| 35) | maj = 2hen (Ohtani, 1991) |
| 36) | 2mwd + 2stv = maj (Ohtani, 1991) |
| 37) | mwd = fo (Katsura & Ito, 1989; Fei & Bertka, 1999) |
| 38) | mrw = mwd (Katsura & Ito, 1989; Fei et al., 2004) |
| 39) | 2mak = mwd + stv (Sawamoto, 1987; Kanzaki, 1987) |
| 40) | 4mpv = maj (Katsura & Ito, 1989; Ohtani 1991) |
| 41) | mpv = mak (Katsura & Ito, 1989; Ohtani 1991) |
| 42) | mpv = mak (Ito & Takahashi, 1989) |
| 43) | frw = fa (Yagi et al., 1987; Akimoto et al., 1965, 1967) |
| 44) | fwd = fa (Fei & Bertka, 1999; Frost, 2003; Katsura & Ito, 1989; Akimoto, 1987) |
| Equilibrium: ol wd rg (Fei & Bertka, 1999; Frost, 2003; Katsura & Ito, 1989; Akimoto, 1987), involving next three reactions: | |
| 45) | fwd = fa |
| 46) | mwd = fo |
| 47) | mwd = mrw |
| 48) | mpv + per = mrw (Shim et al., 2001; Ito & Takahashi 1989; Fei et al., 2004) |
| 49) | per + cor = sp (Akaogi et al., 1989) |
| Equilibrium: pv aki (Ito & Yamada, 1982), involving next two reactions: | |
| 50) | fpv = fak |
| 51) | mpv = mak |
| Equilibrium: aki rg stv (Ito & Yamada, 1982), involving next two reactions: | |
| 52) | 2mak = mrw + stv |
| 53) | 2fak = frw + stv |
| Equilibrium: rg mwu stv (Ito & Yamada, 1982), involving next two reactions: | |
| 54) | mrw = 2per + stv |
| 55) | frw = 2fper + stv |
| Equilibrium: pv aki rg mwu (Ito & Yamada, 1982), involving next three reactions: | |
| 56) | fpv = fak |
| 57) | mpv = mak |
| 58) | 2mpv + frw = 2fpv + mrw |
| Equilibrium: pvk crn py (Hirose et al., 2001; Kubo & Akaogi, 2000), involving next three reactions: | |
| 59) | cor = apv |
| 60) | mcor = mpv |
| 61) | py = 3mpv + cor |
| 62) | wo = pswo (Osborn & Schairer, 1941; Huang & Wyllie, 1975) |
| 63) | wal = wo (Chatterjee et al., 1984; Essene, 1974) |
| 64) | lrn + cstn = 3wal (Gasparik et al., 1994) |
| 65) | 3cpv = lrn + cstn (Gasparik et al., 1994) |
| 66) | cc = lime + CO2 (Smyth & Adams, 1923) |
| 67) | cc = lime + CO2 (Baker, 1962) |
| 68) | cc + q = wo + CO2 (Zhu, Newton & Kleppa, 1993) |
| 69) | cc + q = wo + CO2 (Jacobs & Kerrick, 1981) |
| 70) | cc + q = wo + CO2 (Ziegenbein & Johannes, 1974) |
| 71) | cc + q = wo + CO2 (Greenwood, 1967a,b; Harker & Tuttle, 1956) |
| 72) | cc + q = wo + CO2 (Aranovich & Newton, 1999) |
| 73) | cc + q = wo + CO2 (Haselton et al., 1978) |
| 74) | 3cc + 2wo = ty + CO2 (Zharikov & Shmulovich, 1969) |
| 75) | ty = spu + CO2 (Zharikov & Shmulovich, 1969) |
| 76) | spu + 4wo = 3rnk + CO2 (Zharikov & Shmulovich, 1969) |
| 77) | spu + rnk = 4lrn + CO2 (Zharikov & Shmulovich, 1969) |
| 78) | ta + 2en = anth (Chernosky et al., 1985) |
| 79) | br = per + H2O (Barnes & Ernst, 1963) |
| 80) | br = per + H2O (Aranovich & Newton, 1996) |
| 81) | br = per + H2O (Schramke et al., 1982; Irving et al., 1977) |
| 82) | br = per + H2O (Irving et al., 1977) |
| 83) | br = per + H2O (Kanzaki, 1991) |
| 84) | 2ta = 3en + 2q + 2H2O (Chernosky, 1976a,b; Chernosky et al., 1985; Skippen, 1971) |
| 85) | 2ta = 3en + 2q + 2H2O (Chernosky et al., 1985) |
| 86) | 2ta = 3en + 2q + 2H2O (Jenkins et al., 1991) |
| 87) | 2ta = 3en + 2q + 2H2O (Aranovich & Newton, 1999) |
| 88) | 2ta = 3en + 2coe + 2H2O (Pawley & Wood, 1995) |
| 89) | 2fo + 2ta = 5en + 2H2O (Chernosky, 1976a,b; Chernosky et al., 1985) |
| 90) | 2fo + 2ta = 5en + 2H2O (Pawley, 1998) |
| 91) | 2anth = 7en + 2q + 2H2O (Chernosky & Autio, 1979) |
| 92) | 7ta = 3anth + 4q + 4H2O (Chernosky & Autio, 1979) |
| 93) | 2anth + 2fo = 9en + 2H2O (Chernosky et al., 1985) |
| 94) | 9ta + 4fo = 5anth + 4H2O (Chernosky et al., 1985) |
| 95) | br + chr = 2fo + 3H2O (Johannes, 1968; Kitahara et al., 1966) |
| 96) | 5chr = ta + 6fo + 9H2O (Chernosky, 1982; Kitahara et al., 1966) |
| 97) | liz = chr (Chernosky, 1975) |
| 98) | 17liz = atg + 3br (Evans, 2004) |
| 99) | atg = 4ta + 18fo + 27H2O (Evans et al., 1976) |
| 100) | atg = 4ta + 18fo + 27H2O (Wunder & Schreyer, 1997) |
| 101) | atg = 14fo + 10cen + 31H2O (Wunder & Schreyer, 1997) |
| 102) | atg = 14fo + 10cen + 31H2O (Wunder & Schreyer, 1997) |
| 103) | atg = 14fo + 10en + 31H2O (Bose & Navrotsky, 1998) |
| 104) | 2br + cen = 2fo + 2H2O (Wunder & Schreyer, 1997) |
| 105) | atg + 14ta = 45en + 45H2O (Pawley, 1996) |
| 106) | phA = 3br + 2fo (Pawley & Wood, 1995) |
| 107) | 6atg + 226fo = 62phA + 153en (Bose & Navrotsky, 1998) |
| 108) | anth = cumm (Ghiorso & Evans, 2002) |
| Equilibrium: cum enfs ol q H2O (Fonarev & Korolkov, 1980), involving next two reactions: | |
| 109) | 2cumm = 7en + 2q + 2H2O |
| 110) | 2grun = 7fs + 2q + 2H2O |
| 111) | chum = 4fo + per + H2O (Duffy & Greenwood, 1979) |
| 112) | chum = 4fo + per + H2O (Pawley, 2000) |
| 113) | chum = 4fo + br (Pawley, 2000) |
| 114) | 4fo + br = chum (Wunder, 1998) |
| 115) | 4fo + br = chum (Wunder, 1998) |
| 116) | mag = per + CO2 (Harker & Tuttle, 1955; Goldsmith & Heard, 1962) |
| 117) | mag = per + CO2 (Johannes & Metz, 1968; Philipp & Girsperger, 1990; Koziol & Newton, 1995) |
| 118) | mag = per + CO2 (Irving & Wyllie, 1975) |
| 119) | 2mag + 2q = en + 2CO2 (Johannes, 1969) |
| 120) | 2mag + 2q = en + 2CO2 (Koziol & Newton, 1995) |
| 121) | 2mag + 2coe = en + 2CO2 (Haselton et al., 1978) |
| 122) | 2mag + en = 2fo + 2CO2 (Haselton et al., 1978; Koziol & Newton, 1998) |
| 123) | ta + 5mag = 4fo + 5CO2 + H2O (Greenwood, 1967a,b) |
| 124) | 2wo + 2mont = di + merw (Yoder, 1968) |
| 125) | wo + mont = ak (Yoder, 1968) |
| 126) | di + merw = 2ak (Yoder, 1968) |
| 127) | di + 3mont = fo + 2ak (Walter, 1963; Yoder, 1968) |
| 128) | 2di + ta = tr (Jenkins et al., 1991) |
| 129) | di + 2mag = en + dol (Brey et al., 1983) |
| 130) | spu + 2mont = 2merw + cc (Walter, 1965) |
| 131) | 2tr = 3en + 4di + 2q + 2H2O (Yin & Greenwood, 1983) |
| 132) | 2tr = 3en + 4di + 2q + 2H2O (Boyd, 1959) |
| 133) | 2tr = 3en + 4di + 2q + 2H2O (Jenkins et al., 1991) |
| 134) | 2tr + 2fo = 5en + 4di + 2H2O (Jenkins, 1983) |
| 135) | dol = cc + per + CO2 (Goldsmith, 1980) |
| 136) | dol = cc + per + CO2 (Harker & Tuttle, 1955) |
| 137) | dol + 2q = di + 2CO2 (Slaughter et al., 1975; Eggert & Kerrick, 1981; Jacobs & Kerrick, 1981) |
| 138) | dol + 2q = di + 2CO2 (Eggler et al., 1976) |
| 139) | dol + 2coe = di + 2CO2 (Luth, 1995) |
| 140) | di + 3dol = 2fo + 4cc + 2CO2 (Kase & Metz, 1980) |
| 141) | 2dol + ta + 4q = tr + 4CO2 (Eggert & Kerrick, 1981) |
| 142) | di + cc = ak + CO2 (Walter, 1963) |
| 143) | ak + fo + cc = 3mont + CO2 (Walter, 1963) |
| 144) | fo + di + 2cc = 3mont + 2CO2 (Walter, 1963) |
| 145) | 5dol + 4ta = 6fo + 5di + 4H2O + 10CO2 (Skippen, 1971) |
| 146) | ta + 3cc + 2q = 3di + H2O + 3CO2 (Skippen, 1971) |
| 147) | 5dol + 8q + H2O = tr + 3cc + 7CO2 (Slaughter et al., 1975; Eggert & Kerrick, 1981) |
| 148) | 5ta + 6cc + 4q = 3tr + 6CO2 + 2H2O (Slaughter et al., 1977) |
| 149) | 3dol + 4q + H2O = ta + 3cc + 3CO2 (Eggert & Kerrick, 1981; Metz & Puhan, 1971; Gordon & Greenwood, 1970) |
| 150) | tr + 3cc + 2q = 5di + 3CO2 + H2O (Slaughter et al., 1975) |
| 151) | tr + 11dol = 8fo + 13cc + 9CO2 + H2O (Metz, 1976) |
| 152) | 3tr + 5cc = 11di + 2fo + 5CO2 + 3H2O (Chernosky & Berman, 1986a,b) |
| 153) | ky = and (Holdaway, 1971; Newton, 1966a; Richardson et al., 1969; Bohlen et al., 1991) |
| 154) | ky = sill (Newton, 1966b; Richardson et al., 1968; Holdaway, 1971; Bohlen et al., 1991) |
| 155) | and = sill (Pattison, personal communications) |
| 156) | and = sill (Holdaway, 1971; Bowman, 1975; Kerrick & Heninger, 1984) |
| 157) | and = sill (Richardson et al., 1969) |
| 158) | ky = cor + q (Harlov & Newton, 1993; Harlov & Milke, 2002) |
| 159) | cor + q = sill (Harlov et al., 2008) |
| 160) | cor + q = and (Harlov & Newton, 1993) |
| 161) | cor + stv = ky (Schmidt et al., 1997) |
| 162) | 2dsp = cor + H2O (Haas, 1972; Fockenberg et al., 1996) |
| 163) | 2dsp = cor + H2O (Vidal et al., 1994) |
| 164) | prl + 6dsp = 4and + 4H2O (Haas & Holdaway, 1973; Hemley et al., 1980) |
| 165) | 2dsp + 4q = prl (Theye et al., 1997) |
| 166) | 2dsp + 4coe = prl (Theye et al., 1997) |
| 167) | prl = cor + 4q + H2O (Chatterjee et al., 1984) |
| 168) | prl = and + 3q + H2O (Hemley et al., 1980; Kerrick, 1968) |
| 169) | prl = and + 3q + H2O (Haas & Holdaway, 1973) |
| 170) | kao + 2q = prl + H2O (McPhail, 1985; Hemley et al., 1980) |
| 171) | 2kao = 2dsp + prl + 2H2O (Hemley et al., 1980) |
| 172) | tpz = ky + H2O (Wunder et al., 1993) |
| 173) | gr + 2ky + q = 3an (Koziol & Newton, 1988; Goldsmith, 1980) |
| 174) | gr + 2ky + q = 3an (Gasparik, 1984; Hays, 1967) |
| 175) | gr + q = an + 2wo (Huckenholz et al., 1975; Newton, 1966c; Hays, 1967; Windom & Boettcher, 1976) |
| 176) | gr + cor = geh + an (Boettcher, 1970; Huckenholz et al., 1975) |
| 177) | 2gr = 3wo + geh + an (Huckenholz et al., 1975; Hays, 1967) |
| 178) | gr + 2cor = 3cats (Gasparik, 1984) |
| 179) | 2cats + 2caes = 3an (Gasparik, 1984) |
| 180) | gr + 3ky = 3an + cor (Gasparik, 1984) |
| 181) | gr + 3cats = 2an + 2geh (Hays, 1967) |
| 182) | 3cats = an + geh + cor (Hays, 1967) |
| 183) | gr + 3ky = 3an + cor (Gasparik, 1984) |
| 184) | 3an + cc = me (Baker & Newton, 1994) |
| 185) | 3an + cc = me (Goldsmith & Newton, 1977) |
| 186) | gr + cc + 2ky + q = me (Baker & Newton, 1994) |
| 187) | 4zo + q = 5an + gr + 2H2O (Boettcher, 1970; Newton, 1966; Chatterjee et al., 1984) |
| 188) | 4zo + q = 5an + gr + 2H2O (Newton, 1966) |
| 189) | 6zo = 6an + 2gr + cor + 3H2O (Boettcher, 1970; Newton, 1965; Chatterjee et al., 1984) |
| 190) | 2zo + ky + q = 4an + H2O (Goldsmith, 1981; Jenkins et al., 1983; Johannes, 1984) |
| 191) | 2zo + sill + q = 4an + H2O (Newton, 1966; Newton & Kennedy, 1963) |
| 192) | ma = an + cor + H2O (Chatterjee, 1974) |
| 193) | ma = an + cor + H2O (Storre & Nitsch, 1974) |
| 194) | ma + q = an + and + H2O (Storre & Nitsch, 1974) |
| 195) | ma + q = an + ky + H2O (Storre & Nitsch, 1974) |
| 196) | 4ma + 3q = 2zo + 5ky + 3H2O (Jenkins, 1984) |
| 197) | ma + q = an + and + H2O (Nitsch et al., 1981) |
| 198) | ma + q = an + ky + H2O (Nitsch et al., 1981) |
| 199) | 4ma = 2zo + 2ky + 3cor + 3H2O (Chatterjee et al., 1984) |
| 200) | law = an + 2H2O (Crawford & Fyfe, 1965) |
| 201) | 4law + 2q = 2zo + prl + 6H2O (Nitsch, 1972) |
| 202) | 12law = 6zo + 2ky + prl + 20H2O (Nitsch, 1972) |
| 203) | 5law = 2zo + ma + 2q + 8H2O (Nitsch, 1974) |
| 204) | 2law + dsp = zo + ky + 4H2O (Schmidt & Poli, 1994) |
| 205) | 4law = 2zo + ky + q + 7H2O (Schmidt & Poli, 1994; Chatterjee et al., 1984) |
| 206) | 4law = 2zo + ky + q + 7H2O (Newton & Kennedy, 1963) |
| 207) | 4law = 2zo + ky + q + 7H2O (Skrok et al., 1994) |
| 208) | pre = an + wo + H2O (Chatterjee et al., 1984) |
| 209) | 5pre = 2zo + 2gr + 3q + 4H2O (Connolly & Kerrick, 1985) |
| 210) | wrk = an + 2q + 2H2O (Liou, 1970) |
| 211) | lmt = an + 2q + 4H2O (Thompson, 1970) |
| 212) | lmt = wrk + 2H2O (Liou, 1971a,b,c) |
| 213) | law + 2q + 2H2O = lmt (Liou, 1971a,b,c) |
| 214) | law + 2q = wrk (Liou, 1971a,b,c) |
| 215) | lmt + 3q + 2H2O = heu (Cho et al., 1987) |
| 216) | stlb = lmt + 3q + 3H2O (Liou, 1971a,b,c) |
| 217) | 3cc + an + cor = 2geh + 3CO2 (Shmulovich, 1974) |
| 218) | 2cc + an = wo + geh + 2CO2 (Shmulovich, 1974) |
| 219) | wo + cc + an = gr + CO2 (Hoschek, 1974) |
| 220) | an + cor + 3cc = 2geh + 3CO2 (Hoschek, 1974) |
| 221) | 2an + 3cc = geh + gr + 3CO2 (Hoschek, 1974) |
| 222) | an + 2cc = geh + wo + 2CO2 (Hoschek, 1974) |
| 223) | 2zo + CO2 = 3an + cc + H2O (Allen & Fawcett, 1982) |
| 224) | cc + q + and = an + CO2 (Chernosky & Berman, 1991) |
| 225) | cc + q + and = an + CO2 (Jacobs & Kerrick, 1981) |
| 226) | cc + q + ky = an + CO2 (Jacobs & Kerrick, 1981) |
| 227) | per + cor = sp (Chamberlin et al., 1995) |
| Equilibrium: opx cor py (Gasparik & Newton, 1984), involving next two reactions: | |
| 228) | 3en + 2cor = 2py |
| 229) | en + mgts = py |
| Equilibrium: opx cor py (Fockenberg, 2008), involving next two reactions: | |
| 230) | 3en + 2cor = 2py |
| 231) | en + mgts = py |
| Equilibrium: py q opx sill (Perkins, 1983; Hensen & Essene, 1971), involving next two reactions: | |
| 232) | 2py + 2q = 3en + 2sill |
| 233) | en + mgts = py |
| Equilibrium: py opx q ky (Hensen, 1972), involving next two reactions: | |
| 234) | 2py + 2q = 3en + 2ky |
| 235) | en + mgts = py |
| Equilibrium: fo py sp opx (Danckwerth & Newton, 1978; Gasparik & Newton, 1984), involving next two reactions: | |
| 236) | fo + py = sp + 2en |
| 237) | en + mgts = py |
| 238) | en + sp = mgts + fo (Gasparik & Newton, 1984) |
| 239) | en + mgts = py (Perkins et al., 1981) |
| 240) | hcrd = crd + H2O (Mirwald et al., 1979) |
| 241) | hcrd = crd + H2O (Schreyer & Yoder, 1964) |
| 242) | hcrd = crd + H2O (Carey, 1995; Skippen & Gunter, 1996) |
| 243) | hcrd = crd + H2O (Mukhopadhyay & Holdaway, 1994) |
| Equilibrium: opx sp fo crd (Hertzberg, 1983), involving next two reactions: | |
| 244) | 5en + 2sp = 5fo + crd |
| 245) | en + sp = mgts + fo |
| Equilibrium: opx sp fo cd H2O (Seifert, 1974; Fawcett & Yoder, 1966), involving next three reactions: | |
| 246) | 5en + 2sp = 5fo + crd |
| 247) | en + sp = mgts + fo |
| 248) | hcrd = crd + H2O |
| Equilibrium: opx sill q crd (Newton, personal communication), involving next three reactions: | |
| 249) | en + 2sill + q = crd |
| 250) | 2mgts + 3q = crd |
| 251) | 3en + 6sill = 2mgts + 2crd |
| Equilibrium: opx sill cd cor H2O (Newton, 1972), involving next four reactions: | |
| 252) | 3en + 6sill = 2mgts + 2crd |
| 253) | en + 3sill = crd + cor |
| 254) | hcrd + cor = en + 3sill + H2O |
| 255) | hcrd = crd + H2O |
| Equilibrium: opx sa q crd (Newton, 1972; Perkins et al., 1981), involving next three reactions: | |
| 256) | 2crd = spr4 + 8q |
| 257) | 5crd = 2spr5 + 2en + 19q |
| 258) | crd = 2mgts + 3q |
| Equilibrium: sa q crd sill (Newton, 1972; Perkins et al., 1981), involving next two reactions: | |
| 259) | 2crd = spr4 + 8q |
| 260) | 3crd + 4sill = 2spr5 + 17q |
| Equilibrium: sa q opx sill (Newton, 1972; Hensen, 1972), involving next five reactions: | |
| 261) | spr4 + 6q = 2en + 4sill |
| 262) | 2spr5 + 14q = 3en + 10sill |
| 263) | en + spr5 = mgts + spr4 |
| 264) | spr4 + 2q = 4mgts |
| 265) | en + spr4 + 2sill = 6mgts |
| Equilibrium: py opx sa sill (Boyd & England, 1959; Arima & Onuma, 1977; Hensen, 1972), involving next three reactions: | |
| 266) | 6py = spr4 + 7en + 2sill |
| 267) | 7py = spr5 + 9en + 2sill |
| 268) | py = en + mgts |
| Equilibrium: py opx sa ky (Fockenberg, 2008), involving next four reactions: | |
| 269) | 6py = spr4 + 7en + 2ky |
| 270) | 7py = spr5 + 9en + 2ky |
| 271) | en + spr5 = mgts + spr4 |
| 272) | py = en + mgts |
| Equilibrium: py sp cor sa (Ackermand et al., 1975; Doroshev & Malinovskiy, 1974), involving next two reactions: | |
| 273) | 2py + 6sp + 4cor = 3spr4 |
| 274) | py + 6sp + 8cor = 3spr5 |
| Equilibrium: py cor sa sill (Malinovsky & Doroshev, 1975), involving next two reactions: | |
| 275) | 4py + 14cor = 3spr4 + 6sill |
| 276) | py + 6cor = spr5 + 2sill |
| Equilibrium: opx cor sa sill (Malinovsky & Doroshev, 1975), involving next two reactions: | |
| 277) | 2en + 6cor = spr4 + 2sill |
| 278) | 3en + 14cor = 2spr5 + 4sill |
| Equilibrium: sa opx cd sp H2O (Seifert, 1974), involving next four reactions: | |
| 279) | 2crd + 16sp = 5spr4 |
| 280) | 5spr5 + 5en = 3crd + 19sp |
| 281) | hcrd = crd + H2O |
| 282) | en + spr5 = mgts + spr4 |
| Equilibrium: cor opx sp sa (Podlesskii, 1996), involving next three reactions: | |
| 283) | en + 4sp + 6cor = 2spr5 |
| 284) | en + 2sp + 2cor = spr4 |
| 285) | en + 2cor = 2mgts |
| Equilibrium: chl cor cd sa H2O (Seifert, 1974), involving: | |
| 286) | 16clin + 64cor = 2crd + 19spr4 + 64H2O |
| Equilibrium: chl cd opx sa H2O (Seifert, 1974), involving next two reactions: | |
| 287) | 16clin + 6crd = 32en + 7spr4 + 64H2O |
| 288) | hcrd = crd + H2O |
| Equilibrium: chl cor sp sa H2O (Seifert, 1974; Ackermand et al., 1975), involving next two reactions: | |
| 289) | 2clin + 8cor + 2sp = 3spr4 + 8H2O |
| 290) | 2clin + 20cor + 8sp = 6spr5 + 8H2O |
| Equilibrium: chl opx fo py H2O (Pawley, 2003), involving: | |
| 291) | clin + en = 2fo + py + 4H2O |
| Equilibrium: chl opx fo sp H2O (Baker & Holland, 1996), involving next two reactions: | |
| 292) | clin = en + fo + sp + 4H2O |
| 293) | ames = en + 2sp + 4H2O |
| Equilibrium: chl opx fo H2O (Baker & Holland, 1996), involving next two reactions: | |
| 294) | clin = 2fo + mgts + 4H2O |
| 295) | 2clin = ames + 2fo + en + 4H2O |
| Equilibrium: chl cor sp H2O (Baker & Holland, 1996), involving: | |
| 296) | 3ames = 2clin + 2cor + 2sp + 4H2O |
| Equilibrium: chl cor py sp H2O (Ackermand et al., 1975), involving next two reactions: | |
| 297) | clin + 2cor = py + 2sp + 4H2O |
| 298) | 2py + 6sp + 12H2O = 3ames + 2cor |
| Equilibrium: chl opx fo sp H2O (Jenkins, 1981; Jenkins & Chernosky, 1986; Fawcett & Yoder, 1966), involving next two reactions: | |
| 299) | clin = en + fo + sp + 4H2O |
| 300) | ames = en + 2sp + 4H2O |
| Equilibrium: chl opx fo sp H2O (Jenkins, 1981; Jenkins & Chernosky, 1986; Fawcett & Yoder, 1966), involving next two reactions: | |
| 301) | clin = en + fo + sp + 4H2O |
| 302) | ames = en + 2sp + 4H2O |
| 303) | 2mcar = sud + q (Vidal et al., 1992) |
| Equilibrium: chl py fo sp H2O (Staudigel & Schreyer, 1977), involving: | |
| 304) | 2clin = py + 3fo + sp + 8H2O |
| Equilibrium: chl py fo sp H2O (Fockenberg, 1995), involving: | |
| 305) | 2clin = py + 3fo + sp + 8H2O |
| Equilibrium: chl q ky tlc H2O (Massonne et al., 1981), involving next two reactions: | |
| 306) | 3clin + 14q = 3ky + 5ta + 7H2O |
| 307) | 2clin + 4q = ames + 2ta + 2H2O |
| Equilibrium: chl opx fo cd H2O (Jenkins & Chernosky, 1986), involving: | |
| 308) | 2clin + 3en = 7fo + crd + 8H2O |
| Equilibrium: chl cd opx sp H2O (Jenkins & Chernosky, 1986), involving next two reactions: | |
| 309) | 5clin + crd = 10en + 7sp + 20H2O |
| 310) | hcrd = crd + H2O |
| Equilibrium: chl fo sp cd H2O (Chernosky, 1974; McPhail et al., 1990), involving: | |
| 311) | 5clin = 10fo + 3sp + crd + 20H2O |
| Equilibrium: chl q tlc cd H2O (Chernosky, 1978), involving: | |
| 312) | 6clin + 29q = 8ta + 3crd + 16H2O |
| Equilibrium: chl q tlc cd H2O (Massonne, 1989), involving: | |
| 313) | 6clin + 29q = 8ta + 3crd + 16H2O |
| Equilibrium: tlc sill q cd H2O (Newton, 1972), involving next four reactions: | |
| 314) | 2ta + 6sill + q = 3crd + 2H2O |
| 315) | hcrd = crd + H2O |
| 316) | 2ta + 6sill + q + H2O = 3hcrd |
| 317) | tap = sill + 3q + H2O |
| Equilibrium: tlc ky q cd H2O (Massonne & Schreyer, 1989), involving next two reactions: | |
| 318) | 2ta + 6ky + q = 3crd + 2H2O |
| 319) | hcrd = crd + H2O |
| Equilibrium: chl ky q cd H2O (Seifert & Schreyer, 1970), involving: | |
| 320) | 2clin + 8ky + 11q = 5crd + 8H2O |
| Equilibrium: chl and q cd H2O (Seifert & Schreyer, 1970), involving next two reactions: | |
| 321) | 2clin + 8and + 11q = 5crd + 8H2O |
| 322) | hcrd = crd + H2O |
| Equilibrium: chl and cd cor H2O (Seifert, 1973), involving: | |
| 323) | 2clin + 19and = 5crd + 11cor + 8H2O |
| Equilibrium: chl sill cd cor H2O (Seifert, 1973), involving: | |
| 324) | 2clin + 19sill = 5crd + 11cor + 8H2O |
| Equilibrium: chl ky cd cor H2O (Seifert, 1973), involving: | |
| 325) | 2clin + 19ky = 5crd + 11cor + 8H2O |
| Equilibrium: chl cor cd sp H2O (Seifert, 1974), involving: | |
| 326) | 5clin + 20cor = 3crd + 19sp + 20H2O |
| 326) | equil: chl cor cd sp H2O (Seifert, 1974) |
| 327) | clin + 2mag = 3fo + sp + 2CO2 + 4H2O (Chernosky & Berman, 1986a,b) |
| 328) | 3mctd = py + 2cor + 3H2O (Chopin & Schreyer, 1983) |
| Equilibrium: mctd tlc chl ky H2O (Koch-Müller & Wirth, 2001), involving: | |
| 329) | 7mctd + ta = 2clin + 5ky |
| 330) | 8mctd + 3cor + 7ky = 2mst + 4H2O (Schreyer, 1968) |
| Equilibrium: chl ky cor mst H2O (Massonne, 1995), involving: | |
| 331) | 8clin + 51ky + 31cor = 10mst + 12H2O |
| Equilibrium: chl ky cor mst H2O (Fockenberg, 1998), involving: | |
| 332) | 8clin + 51ky + 31cor = 10mst + 12H2O |
| Equilibrium: mst ky cor opx H2O (Fockenberg, 1998), involving: | |
| 333) | 2mst = 7ky + 11cor + 4en + 4H2O |
| Equilibrium: mst tlc ky cor H2O (Fockenberg, 1998), involving: | |
| 334) | 6mst = 8ta + 13ky + 41cor + 4H2O |
| 335) | 8mctd + 7ky + 6dsp = 2mst + 7H2O (Fockenberg, 1998) |
| 336) | 6mst = 8py + 21ky + 25cor + 12H2O (Fockenberg, 1998) |
| Equilibrium: tlc mst ky py H2O (Chopin & Sobolev, 1995), involving: | |
| 337) | 25ta + 12mst = 67ky + 41py + 49H2O |
| Equilibrium: tlc chl mst py H2O (Fockenberg, 2008), involving next three reactions: | |
| 338) | 67clin + 78ta + 16mst = 211py + 378H2O |
| 339) | 2ames + 2ta = clin + 3py + 6H2O |
| 340) | 67ames + 106ta + 8mst = 206py + 390H2O |
| Equilibrium: mcar q tlc ky H2O (Chopin & Schreyer, 1983), involving: | |
| 341) | 3mcar + q = ta + 3ky + 5H2O |
| Equilibrium: mcar chl ky tlc H2O (Chopin & Schreyer, 1983), involving: | |
| 342) | 14mcar = clin + 13ky + 3ta + 21H2O |
| Equilibrium: mcar chl ky q H2O (Chopin & Schreyer, 1983), involving: | |
| 343) | 5mcar = clin + 4ky + 3q + 6H2O |
| Equilibrium: tlc q ky H2O (Hoschek, 1995), involving next two reactions: | |
| 344) | 2ta + 3ky + H2O = 3tats + 2q |
| 345) | tap = ky + 3q + H2O |
| Equilibrium: zo tlc trts ky q H2O (Hoschek, 1995), involving next three reactions: | |
| 346) | 2ta + 3ky + H2O = 3tats + 2q |
| 347) | 5ts + 7q = 3tr + 7ky + 2zo + H2O |
| 348) | 12zo + 14ta = 3tr + 9ts + 14q + 8H2O |
| Equilibrium: phe tlc trts mbi zo q H2O (Hoschek, 1990), involving next two reactions: | |
| 349) | 9mu + 6tr = 9phl + 26q + ta + 6zo + 2H2O |
| 350) | 33phl + 21ta + 22zo = 26east + 7mu + 22tr + 10H2O |
| 351) | ts + 2di + 2q = tr + 2an (Jenkins, 1994) |
| 352) | ts + 2fo = tr + 2sp (Jenkins, 1994) |
| 353) | clin + 2dol = 3fo + 2cc + sp + 4H2O + 2CO2 (Chernosky & Berman, 1986a,b) |
| 354) | 3clin + 2cc = 2di + 5fo + 3sp + 2CO2 + 12H2O (Chernosky & Berman, 1986a,b) |
| Equilibrium: mpm cz gr chl q H2O (Schiffman & Liou, 1980), involving: | |
| 355) | 25mpm = 29cz + 14gr + 5clin + 6q + 53H2O |
| 356) | 2vsv + 6q = 11gr + 4di + wo + 9H2O (Hochella et al., 1982) |
| 357) | cg = cgh (Bowen & Greig, 1923; Cohen & Klement, 1967) |
| 358) | ne = cgh (Greig & Barth, 1938) |
| 359) | jd + q = abh (Holland, 1980) |
| 360) | jd + q = ab (Newton & Smith, 1967; Holland, 1980) |
| 361) | jd + ky = abh + cor (Essene et al., 1972) |
| 362) | 2jd = ne + abh (Gasparik, 1985; Robertson et al., 1957; Boettcher & Wyllie, 1968) |
| 363) | 6ne + 2hlt = sdl (Sharp et al., 1989) |
| 364) | sdl = 6cgh + 2hltL (Sharp et al., 1989) |
| 365) | pa = jd + ky + H2O (Holland, 1979) |
| 366) | pa = abh + cor + H2O (Chatterjee, 1970) |
| 367) | pa + q = abh + and + H2O (Chatterjee, 1972) |
| 368) | pa + q = abh + ky + H2O (Chatterjee, 1972) |
| 369) | jd + H2O = anl (Manghnani, 1970) |
| 370) | anl + q = abh + H2O (Thompson, 1971; Liou, 1971) |
| 371) | mu = san + cor + H2O (Chatterjee & Johannes, 1974) |
| 372) | mu + q = san + and + H2O (Chatterjee & Johannes, 1974) |
| 373) | mu + q = san + sill + H2O (Chatterjee & Johannes, 1974) |
| Equilibrium: mu q san mlt H2O (Segnit & Kennedy, 1961), involving next three reactions: | |
| 374) | mu + q = san + smul + H2O |
| 375) | 5mu + 2q = 5san + 4amul + 5H2O |
| 376) | 2smul + 3mu = 4amul + 3san + 3H2O |
| Equilibrium: prl q mlt H2O (Carr & Fyfe, 1960), involving next two reactions: | |
| 377) | prl = smul + 3q + H2O |
| 378) | 5prl = 4amul + 18q + 5H2O |
| Equilibrium: crd cor mlt sa (Seifert, 1974), involving next four reactions: | |
| 379) | 13smul + 2spr5 = 17cor + 3crd |
| 380) | 8smul + spr4 = 8cor + 2crd |
| 381) | 73smul + 6spr5 = 68amul + 9crd |
| 382) | 32amul + 6crd = 40smul + 3spr4 |
| Equilibrium: sp cor mlt sa (Seifert, 1974), involving next four reactions: | |
| 383) | 2smul + 3cor = 4amul |
| 384) | 26smul + 12spr5 = 40amul + 9spr4 |
| 385) | 2smul + 4spr5 = 10cor + 3spr4 |
| 386) | 4amul + 4spr5 = 13cor + 3spr4 |
| Equilibrium: mlt mqL (Klug et al., 1987), involving next two reactions: | |
| 387) | smul = silL |
| 388) | 4amul + 3qL = 5silL |
| Equilibrium: mlt crst mqL (Klug et al., 1987), involving next three reactions: | |
| 389) | crst = qL |
| 390) | smul = silL |
| 391) | 4amul + 3qL = 5silL |
| Equilibrium: mlt cor mqL (Klug et al., 1987), involving next three reactions: | |
| 392) | cor = corL |
| 393) | smul = silL |
| 394) | 4amul + 3qL = 5silL |
| 395) | kcm = san + H2O (Massonne 1999; Fasshauer et al., 1997; Thompson, 1994) |
| 396) | wa + ky + coe = 2san (Fasshauer et al., 1998; Yagi et al., 1994; Urakawa et al., 1994; Yong et al., 2008) |
| 397) | 2hol = wa + ky + coe (Yagi et al., 1994; Urakawa et al., 1994) |
| 398) | kls + san = 2lc (Scarfe et al., 1966; Lindsley, 1966; Fasshauer et al., 1998) |
| 399) | kls + 2coe = san (Fasshauer et al., 1998) |
| 400) | san + fo = lc + en (Luth, 1967) |
| 401) | 2phl + 3en = 2san + 6fo + 2H2O (Luth, 1967) |
| 402) | 2phl + san = 3lc + 3fo + 2H2O (Luth, 1967) |
| 403) | 2phl = kls + lc + 3fo + 2H2O (Luth, 1967) |
| Equilibrium: phe chl mbi ky q H2O (Bird & Fawcett, 1973), involving next two reactions: | |
| 404) | 5mu + 3clin = 5phl + 8ky + q + 12H2O |
| 405) | cel + east = mu + phl |
| Equilibrium: phe chl mbi ky q H2O (Massonne, unpublished), involving next two reactions: | |
| 406) | 5mu + 3clin = 5phl + 8ky + q + 12H2O |
| 407) | cel + east = mu + phl |
| Equilibrium: phe mbi q cd san H2O (Seifert, 1976), involving next two reactions: | |
| 408) | 6mu + 2phl + 15q = 3crd + 8san + 8H2O |
| 409) | cel + east = mu + phl |
| Equilibrium: phe chl q cd mbi H2O (Seifert, 1970), involving: | |
| 410) | mu + clin + 2q = crd + phl + 4H2O |
| Equilibrium: cd phe mbi sill q H2O (Seifert, 1970), involving next two reactions: | |
| 411) | 2phl + 8sill + 7q = 3crd + 2mu |
| 412) | cel + east = mu + phl |
| Equilibrium: tlc phe coe ky H2O (Massonne & Schreyer, 1989), involving next two reactions: | |
| 413) | 6cel + 6ky + 2H2O = 2ta + 6mu + 4coe |
| 414) | 2ta + 3ky + H2O = 3tats + 2coe |
| Equilibrium: tlc phe q ky H2O (Massonne & Schreyer, 1989), involving: | |
| 415) | 6cel + 6ky + 2H2O = 2ta + 6mu + 4q |
| Equilibrium: phe ky py coe H2O (Massonne & Szpurka, 1997), involving: | |
| 416) | 3cel + 4ky = py + 3mu + 4coe |
| Equilibrium: fphe ky alm coe H2O (Massonne & Szpurka, 1997), involving: | |
| 417) | 3fcel + 4ky = alm + 3mu + 4coe |
| Equilibrium: fphe ky alm q H2O (Massonne & Szpurka, 1997), involving: | |
| 418) | 3fcel + 4ky = alm + 3mu + 4q |
| Equilibrium: phe mbi san q H2O (Massonne & Schreyer, 1989), involving next four reactions: | |
| 419) | 3mu + 2phl = 3east + 2san + 3q + 2H2O |
| 420) | 3cel = phl + 2san + 3q + 2H2O |
| 421) | 3mu + 2phl = 3east + 2san + 3q + 2H2O |
| 422) | cel + east = phl + mu |
| Equilibrium: tlc phe mbi ky q H2O (Massonne & Schreyer, 1989), involving: | |
| 423) | ta + mu = phl + ky + 3q + H2O |
| Equilibrium: chl mbi q phe tlc H2O (Massonne & Schreyer, 1989), involving: | |
| 424) | 3clin + 3phl + 23q = 3mu + 8ta + 4H2O |
| 425) | 2phl + 6q = 3en + 2san + 2H2O (Aranovich & Newton, 1998) |
| 426) | 2phl + 6q = 3en + 2san + 2H2O (Berman et al., 1995) |
| 427) | 2phl + 6q = 3en + 2san + 2H2O (Bohlen et al., 1983a,b,c) |
| 428) | 2phl + 6q = 3en + 2san + 2H2O (Peterson & Newton, 1990) |
| 429) | 2phl + 6q = 3en + 2san + 2H2O (Wood, 1976) |
| 430) | 2jd + ta = gl ( Carman & Gilbert, 1983) |
| 431) | gl + 2q = ta + 2abh (Corona & Jenkins, 2007) |
| 432) | 2naph + 3en = 2abh + 6fo + 2H2O (Carman & Gilbert, 1983) |
| 433) | 5phl + 6cc + 24q = 3tr + 5san + 6CO2 + 2H2O (Hewitt, 1975) |
| 434) | 3dol + san + H2O = phl + 3cc + 3CO2 (Puhan & Johannes, 1974; Puhan, 1978) |
| 435) | mu + cc + 2q = san + an + CO2 + H2O (Hewitt, 1973) |
| 436) | 2zo + mu + 2q = 4an + san + 2H2O (Johannes, 1980) |
| 437) | 4law + ab = 2zo + pa + 2q + 6H2O (Heinrich & Althaus, 1980) |
| 438) | 4law + jd = 2zo + pa + q + 6H2O (Heinrich & Althaus, 1980) |
| 439) | 2parg = 3di + sp + an + 2fo + 2ne + 2H2O (Westrich & Holloway, 1981; Lykins & Jenkins, 1992) |
| 440) | 2tr + 2fo = 4di + 5en + 2H2O (Lykins & Jenkins, 1992) |
| 441) | 2ts = 2fo + 4an + en + 2H2O (Lykins & Jenkins, 1992) |
| 442) | 2parg + 5en = 2di + 8fo + 2an + 2abh + 2H2O (Lykins & Jenkins, 1992) |
| 443) | fs = fa + q (Bohlen et al., 1980) |
| 444) | 4mt + O2 = 6hem (Myers & Eugster, 1983) |
| 445) | 4mt + O2 = 6hem (Chou, 1978) |
| 446) | 3fa + O2 = 3q + 2mt (Chou, 1978) |
| 447) | 3fa + O2 = 3q + 2mt (Myers & Eugster, 1983) |
| 448) | 3fa + O2 = 3q + 2mt (Hewitt, 1978) |
| 449) | 3fa + O2 = 3q + 2mt (O'Neill, 1987a) |
| 450) | q + 2iron + O2 = fa (O'Neill, 1987b) |
| 451) | 3iron + 2O2 = mt (O'Neill, 1988) |
| 452) | 2gth = hem + H2O (Voigt & Will, 1981) |
| 453) | sid + hem = mt + CO2 (Koziol, 2004) |
| 454) | 2grun = 7fs + 2q + 2H2O (Lattard & Evans, 1992) |
| 455) | 2grun = 7fa + 9q + 2H2O (Lattard & Evans, 1992) |
| 456) | 2deer = 9fs + 6mt + 6q + 10H2O (Lattard & Le Breton, 1994) |
| 457) | deer + Ni = 6fs + 2mt + NiO + 5H2O (Lattard & Le Breton, 1994) |
| 458) | alm + 3hem = 3mt + ky + 2q (Harlov & Newton, 1992) |
| 459) | alm + 2sill = 3herc + 5q (Bohlen et al., 1986) |
| 460) | alm + 5cor = 3herc + 3sill (Shulters & Bohlen, 1989) |
| 461) | 2alm + 4sill + 5q = 3fcrd (Mukhopadhyay & Holdaway, 1994) |
| 462) | 6fst + 25q = 8alm + 46ky + 12H2O (Rao & Johannes, 1979) |
| 463) | 6fst + 25q = 8alm + 46ky + 12H2O (Ganguly, 1972) |
| 464) | 2fst + 15q = 4fcrd + 10sill + 4H2O (Richardson, 1968) |
| 465) | 23fctd + 7q = 2fst + 5alm + 19H2O (Rao & Johannes, 1979) |
| 466) | 8fctd + 10ky = 2fst + 3q + 4H2O (Rao & Johannes, 1979) |
| 467) | 3fctd = alm + 2cor + 3H2O (Ganguly, 1969; Vidal et al., 1994) |
| 468) | 3fctd = alm + 2cor + 3H2O (Ganguly, 1969) |
| 469) | 3fctd = 4dsp + alm + H2O (Vidal et al., 1994) |
| 470) | 6fst + 25q = 8alm + 46sill + 12H2O (Richardson, 1968) |
| 471) | 6fst + 25q = 8alm + 46sill + 12H2O (Dutrow & Holdaway, 1989) |
| 472) | 8fctd + 10sill = 2fst + 3q + 4H2O (Richardson, 1968) |
| 473) | 5fctd = fcrd + 3herc + 5H2O (Grieve & Fawcett, 1974) |
| 474) | 2fgl = 4abh + 3fa + q + 2H2O (Hoffmann, 1972) |
| 475) | rieb + 3hem = 2acm + 3mt + 4q + H2O (Ernst, 1962) |
| 476) | 2ann + 6sill + 9q = 3fcrd + 2san + 2H2O (Holdaway & Lee, 1977) |
| 477) | 2ann + 3q = 2san + 3fa + 2H2O (Rutherford, 1973) |
| 478) | 2ann + 3q = 2san + 3fa + 2H2O (Dachs & Benisek, 1995) |
| 479) | 2san + 2mt + 2H2O = 2ann + O2 (Dachs, 1994) |
| 480) | gr + 2alm = 3fa + 3an (Bohlen et al., 1983a,b,c) |
| 481) | gr + 2alm = 3fa + 3an (Perkins & Vielzeuf, 1992) |
| 482) | 2hed = 2wo + fa + q (Lindsley & Munoz, 1969) |
| 483) | 2fact = 3fa + 5q + 4hed + 2H2O (Jenkins & Bozhilov, 2003) |
| 484) | 2minn = 3fa + 5q + 2H2O (Engi, 1986) |
| 485) | glt + 2q = minn + H2O (Rasmussen et al., 1998) |
| 486) | 2glt + 5minn = 3grun + 6H2O (Rasmussen et al., 1998) |
| 487) | 3sid + minm = minn + 3mag (Klein, 1974) |
| 488) | 28fstp = 14ann + 5grun + 21alm + 79q + 156H2O (Miyano & Klein, 1989) |
| 489) | mstp + daph = fstp + clin (Miyano & Klein, 1989) |
| 490) | andr = 3pswo + hem (Huckenholz & Yoder, 1971) |
| 491) | 6andr + 3fa = 6mt + 18wo + 3q (Gustafson, 1974) |
| 492) | 6andr + 2Ni = 4mt + 18wo + 2NiO (Gustafson, 1974) |
| 493) | 6andr = 4mt + 18wo + O2 (Moecher & Chou, 1990) |
| 494) | 3andr + mt + 9q = 9hed + 2O2 (Burton et al., 1982) |
| 495) | 2andr + q + 3fa = 4hed + 2wo + 2mt (Liou, 1974) |
| 496) | 2andr + 4q + 2Ni = 4hed + 2wo + 2NiO (Liou, 1974) |
| 497) | 3andr + mt + 9q = 9hed + 2O2 (Moecher & Chou, 1990) |
| 498) | 2andr + 4q = 4hed + 2wo + O2 (Moecher & Chou, 1990) |
| 499) | 3cc + hem + 3q = andr + 3CO2 (Taylor & Liou, 1978) |
| 500) | cz = zo (Natural pairs, unpublished) |
| 501) | 2cz + ky + q = 4an + H2O (Jenkins et al., 1983) |
| Equilibrium: epi an grd hem q H2O (Holdaway, 1972; Liou, 1973), involving next five reactions: | |
| 502) | 2fep = andr + an + hem + q + H2O |
| 503) | 2ep = gr + an + hem + q + H2O |
| 504) | 6ep = 2andr + 6an + hem + 3H2O |
| 505) | 4cz + q = 5an + gr + 2H2O |
| 506) | 6cz + hem + 3q = andr + 9an + 3H2O |
| Equilibrium: grd q an wo (Holdaway, 1972), involving: | |
| 507) | gr + q = an + 2wo |
| Equilibrium: grd trd an wo (Holdaway, 1972), involving: | |
| 508) | gr + trd = an + 2wo |
| Equilibrium: epi grd (Perchuk & Aranovich, 1979), involving: | |
| 509) | 2cz + andr = 2ep + gr |
| 510) | 12pmt + 6cup = 8gr + 4spss + 12ten + 6H2O (Keskinen & Liou, 1979) |
| 511) | osm1 = crd + san + 2q (Olesch & Seifert, 1981) |
| 512) | 4phl + 3crd + 2san + 33q = 6osm2 + 4H2O (Olesch & Seifert, 1981) |
| 513) | en + san + 2sill + 3q = osm1 (Carrington & Harley, 1995) |
| 514) | py + osm2 = osm1 + 2en (Carrington & Harley, 1995) |
| 515) | osm1 + fs = fosm + en (Holland et al., 1996) |
| 516) | fosm + crd = osm1 + fcrd (Holland et al., 1996) |
| 517) | mag + ru = geik + CO2 (Haselton et al., 1978) |
| 518) | mag + ru = geik + CO2 (Ferry et al., 2002) |
| 519) | sph + ky = an + ru (Manning & Bohlen, 1991) |
| 520) | ru + cc + q = sph + CO2 (Hunt & Kerrick, 1977) |
| 521) | ru + cc + q = sph + CO2 (Jacobs & Kerrick, 1981) |
| 522) | 2ilm = 2iron + 2ru + O2 (O'Neill et al., 1988) |
| 523) | 2ilm = 2iron + 2ru + O2 (Anovitz et al., 1985) |
| 524) | 2usp = 2ilm + 2iron + O2 (O'Neill et al., 1988) |
| 525) | 2usp = 2ilm + 2iron + O2 (Anovitz et al., 1985) |
| 526) | alm + 3ru = 3ilm + sill + 2q (Bohlen et al., 1983a,b,c) |
| 527) | 2alm + gr + 6ru = 6ilm + 3an + 3q (Bohlen & Liotta, 1986) |
| 528) | zrc = bdy + crst (Butterman & Foster, 1967) |
| 529) | zrc + 2mag = bdy + fo + 2CO2 (Ferry et al., 2002) |
| 530) | 2NiO = 2Ni + O2 (O'Neill, 1987) |
| 531) | 2mag + fa = fo + 2sid (Dalton & Wood, 1993) |
| 532) | 2dol + fa = fo + 2ank (Dalton & Wood, 1993) |
| 533) | dol + sid = ank + mag (Anovitz & Essene, 1987) |
| 534) | dol + sid = ank + mag (Rosenberg, 1967) |
| 535) | dol + sid = ank + mag (Klein, 1978) |
| 536) | dol + sid = ank + mag (Klein, 1978) |
| 537) | py + ann = alm + phl (Ferry & Spear, 1978) |
| 538) | py + ann = alm + phl (Perchuk & Lavrent’eva, 1983) |
| 539) | 3fcrd + 2py = 3crd + 2alm (Perchuk & Lavrent’eva, 1983) |
| 540) | alm + 3cel = py + 3fcel (Green & Hellman, 1982) |
| 541) | alm + 3cel = py + 3fcel (Hynes & Forest, 1988) |
| 542) | alm + phl = py + ann (Hynes & Forest, 1988) |
| 543) | phl + mu = cel + east (Hodges & spear, 1988) |
| 544) | 2phl + mu + 2sill = 3east + 5q (Hodges & spear, 1988) |
| 545) | 2phl + mu + 2ky = 3east + 5q (Pigage & Greenwood, 1982) |
| 546) | 2mu + phl + py = 3east + 6q (Natural) |
| 547) | 2mu + phl + py = 3east + 6q (Hynes & Forest) |
| 548) | 5cel + daph = 5fcel + clin (Currie & Van Staal99) |
| 549) | ames + cel = mu + clin (Currie & Van Staal99) |
| 550) | 2hed + en = fs + 2di (Lindsley, 1983) |
| 551) | 2hed + fo = fa + 2di (Perkins & Vielzeuf, 1992) |
| 552) | fs + fo = en + fa (Matsui & Nishizawa, 1974) |
| 553) | fs + fo = en + fa (von Seckendorff & O'Neill, 1993) |
| 554) | 2py + 3fa = 2alm + 3fo (O'Neill & Wood, 1979) |
| 555) | 2py + 3fa = 2alm + 3fo (Hackler & Wood, 1989) |
| 556) | 2py + 3fs = 2alm + 3en (Lee & Ganguly, 1988) |
| 557) | 2py + 3fs = 2alm + 3en (Kawasaki & Matsui, 1983) |
| 558) | 2py + 3fs = 2alm + 3en (Harley, 1984) |
| 559) | alm + 3di = 3hed + py (Wood, 1976) |
| 560) | 2herc + fo = 2sp + fa (Jamieson & Roeder, 1984) |
| 561) | 2herc + fo = 2sp + fa (Engi, 1983) |
| 562) | fa + 2mft = 2mt + fo (Jamieson & Roeder, 1984) |
| 563) | 3en + 2ann = 2phl + 3fs (Fonarev & Konilov, 1986) |
| 564) | fact + 5di = tr + 5hed (Natural Kd) |
| 565) | 7en + 2fanth = 2anth + 7fs (Natural Kd) |
| 566) | 3tr + 5fgl = 5gl + 3fact (Natural Kd) |
| 567) | spr4 + 2fcrd = fspr + 2crd (Waters, 1986) |
| 568) | spr4 + 2fs = fspr + 2en (Natural Collected) |
| 569) | 2acm + pa + 2q = 3ab + hem + H2O (Holland & Ray, 1985) |
| 570) | jd + ep = acm + cz (Holland & Ray, 1985) |
| 571) | 5alm + 3clin = 5py + 3daph (Dickenson & Hewitt, 1986; Laird, 1989) |
| 572) | 5phl + 3daph = 5ann + 3clin (Laird, 1989) |
| 573) | clin + fact = tr + daph (Laird, 1982) |
| 574) | pre + ep = fpre + cz (Cho et al., 1986) |
| 575) | 5mpm + daph = 5fpm + clin (Evans, 1990) |
| 576) | fpm + 5ep = jgd + 5cz (Cho et al., 1986) |
| 577) | alm + 3mctd = py + 3fctd (Chinner & Dixon, 1974; Miller, 1986) |
| 578) | 3fctd + ta = 3mctd + fta (Chinner & Dixon, 1974; Chopin & Monie, 1984; Miller, 1986) |
| 579) | 5fctd + clin = 5mctd + daph (Vidal et al., 1999) |
| 580) | mcar + fctd = fcar + mctd (Natural, Seidel & Okrusch, 1977; Theye et al., 1992) |
| 581) | 5mcar + daph = 5fcar + clin (Natural, Theye et al., 1992) |
| 582) | 5sud + 2daph = 5fsud + 2clin (Theye et al., 1992) |
| 583) | pxmn = rhod (Maresch & Mottana, 1976) |
| 584) | rhc + q = pxmn + CO2 (Peters, 1971) |
| 585) | rhc = mang + CO2 (Huebner, 1969) |
| 586) | pxmn + rhc = teph + CO2 (Huebner & Eugster, 1968) |
| 587) | fo + 2mang = teph + 2per (Wood et al., 1994) |
| 588) | 2spss + 3fo = 2py + 3teph (Wood et al., 1994) |
| 589) | spss + 3ilm = alm + 3pnt (Pownceby et al., 1987) |
| 590) | phl + 3mnctd = mnbi + 3mctd (Mahar et al., 1997) |
| 591) | 4phl + 3mnst = 4mnbi + 3mst (Mahar et al., 1997) |
| 592) | 2phl + 3mncrd = 2mnbi + 3crd (Mahar et al., 1997) |
| 593) | 5phl + 3mnchl = 5mnbi + 3clin (Mahar et al., 1997) |
| 594) | phl + spss = mnbi + py (Mahar et al., 1997) |
| 595) | syv = syvL (Clark, 1966) |
| 596) | hlt = hltL (Clark, 1966) |
| 597) | di = diL (Clark, 1966) |
| 598) | san = kspL (Lindsley, 1966) |
| 599) | en = enL (Clark, 1966) |
| 600) | pswo = woL (Yoder, 1966) |
| 601) | cor = corL (Shen & Lazor, 1995 omitting UHP) |
| 602) | crst = qL (Jackson, 1976) |
| 603) | crst = qL (Jackson, 1976) |
| 604) | q = qL (Jackson, 1976) |
| 605) | q = qL (Hudon et al., 2002) |
| 606) | q = qL (Kanzaki, 1990) |
| 607) | coe = qL (Kanzaki, 1990) |
| 608) | coe = qL (Zhang et al., 1993) |
| 609) | an = anL (Clark, 1966; Goldsmith, 1980) |
| Equilibrium: an H2O anwL (Clark, 1966), involving next two reactions: | |
| 610) | H2oL = H2O |
| 611) | an = anL |
| 612) | lc = lcL (Lindsley 1967; (approx).) |
| 613) | per = perL (Bowen & Anderson, 1914) |
| 614) | lime = limL (Rankin & Wright, 1915) |
| 615) | fo = foL (Davis & England, 1964) |
| 616) | fo = foL (subset of Ohtani & Kumazawa, 1981) |
| 617) | fo = foL (low temperature exp's) |
| 618) | fa = faL (Clark, 1966) |
| 619) | sill = silL (Cameron, 1977; Holland & Carpenter, 1986) |
| 620) | cgh = neL (Bowen, 1912) |
| 621) | ne = neL (Smith, 2003) |
| 622) | abh = abL (Schairer & Bowen, 1956) |
| 623) | abh = abL (Boyd & England, 1963) |
| 624) | abh = abL (Nekvasil & Carroll, 1996) |
| Equilibrium: abh H2O abwL (Goldsmith & Jenkins, 1985), involving next two reactions: | |
| 625) | H2oL = H2O |
| 626) | abh = abL |
| 627) | abh = abL (Goldsmith & Jenkins, 1985) |
| 628) | h2oL = H2O (Goldsmith & Jenkins, 1985) |
| Equilibrium: san H2O kspwL (Lambert et al., 1969; Goldsmith & Peterson, 1990), involving next two reactions: | |
| 629) | h2oL = H2O |
| 630) | san = kspL |
| Equilibrium: trd H2O qwL (Kennedy et al., 1962), involving next two reactions: | |
| 631) | h2oL = H2O |
| 632) | trd = qL |
| Equilibrium: q H2O qwL (Kennedy et al., 1962), involving next two reactions: | |
| 633) | h2oL = H2O |
| 634) | q = qL |
| 635) | h2oL = H2O (Johannes & Holtz, 1996) |
| 636) | h2oL = H2O (Goranson, 1936) |
| 637) | h2oL = H2O (Behrens, 1995) |
| 638) | h2oL = H2O (Behrens, 1995) |
| Equilibrium: abh q abqL (Luth, 1969), involving next two reactions: | |
| 639) | abh = abL |
| 640) | q = qL |
| Equilibrium: abh trd abqL (Schairer & Bowen, 1956), involving next two reactions: | |
| 641) | abh = abL |
| 642) | trd = qL |
| Equilibrium: an anqL (Schairer & Bowen, 1947), involving: | |
| 643) | an = anL |
| Equilibrium: trd anqL (Schairer & Bowen, 1947), involving: | |
| 644) | trd = qL |
| Equilibrium: an trd anqL (Schairer & Bowen, 1947), involving next two reactions: | |
| 645) | an = anL |
| 646) | trd = qL |
| Equilibrium: ol olL (Bowen & Schairer, 1935), involving next two reactions: | |
| 647) | fo = foL |
| 648) | fa = faL |
- Univariant and divariant solid-solution equilibria start with the keyword `equilibrium' and are followed by one or more equilibrium relations involving end-members in solid solutions. Solid-solution names: crpx, Cr-cpx; crsp, Cr-spinel; po, pyrrhotite; tro, troilite; ol, Fe–Mg olivine; wd, Fe–Mg wadsleyite; rg, Fe–Mg ringwoodite; pv, Fe–Mg perovskite; aki, Fe–Mg akimotoite; mwu, Fe–Mg periclase; pvk, Mg–Al perovskite; crn, Mg–Al corundum; cum, Fe–Mg cummingtonite; opx, Mg–Al opx; cd, hydrous cordierite; sa, Mg–Al sapphirine; chl, Mg–Al chlorite; tlc, Mg–Al talc; trts, Al–tremolite; phe, Mg-phengite; mbi, Al-phlogopite; mlt, mullite; mqL, Al–Si liquid; epi, Fe–Al epidote; grd, grandite garnet; anwL, an-H2O liquid; abwL, ab-H2O liquid; kspwL, ksp-H2O liquid; qwL, q-H2O liquid; abqL, ab-q liquid; anqL, an-q liquid; olL, fo-fa liquid.
Appendix 3: Other data set changes
A list of some of the more important changes to thermodynamic data since HP98 follows. Further detailed information may be found on the website at: http://www.esc.cam.ac.uk/people/academic-staff/tim-holland.
- 1
New experiments by Aranovich & Newton (1998) on the reactions cc + q = wo + CO2 and 2ta = 3en + 2q + 2H2O, and by Koziol & Newton (1998) on 2mag + en = 2fo + 2CO2 at higher pressures and temperatures than before have led to improved thermodynamic data not only on these end-members but also on the mixing parameters for H2O–CO2 mixtures.
- 2
The data for clinohumite has been updated to incorporate the experimental results of Pawley (2000) on the reactions chum = 4fo + per + H2O and Pawley (2000) and Wunder (1998) on chum = 4fo + br. Compressibility data for chum are from Ross & Crichton (2001), thermal expansion is assumed as for forsterite.
- 3
Phlogopite data have been updated using the experiments of Aranovich & Newton (1998) on the reaction 2phl + 6q = 3en + 2san + 2H2O. There has been some controversy over the molar volume to use, as the synthetic phlogopites have a larger volume (
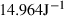 bar; Robie & Hemingway, 1995; Aranovich & Newton, 1998) than natural phlogopites (
bar; Robie & Hemingway, 1995; Aranovich & Newton, 1998) than natural phlogopites (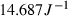 bar; Smyth & McCormick, 1995; Pavese et al., 2003). Until this is resolved we will use the synthetic volumes as they presumably reflect the synthetic material used in the experiments.
bar; Smyth & McCormick, 1995; Pavese et al., 2003). Until this is resolved we will use the synthetic volumes as they presumably reflect the synthetic material used in the experiments. - 4
The double carbonate reaction equilibrium reactions (arag + mag = dol and arag + sid = ank) are characterized by small free energy changes and are difficult to calculate with accuracy from thermodynamic data gained from a variety of mixed carbonate-silicate equilibria. The recent experimental study of Morlidge et al. (2006) means that these equilibria may now be fitted and refined, such that the small differences in free energy are made consistent with the experimental pressures. In addition, the experimental data for cc = arag is now known to much higher pressures and temperatures, and the experiments of Suito et al. (2002) may now also be fitted satisfactorily.
- 5
Data for chlorite have been updated using experiments of Pawley (2003) and Fockenberg (1995). The new heat capacity and entropy data for chlorite are from Bertoldi et al. (2007).
- 6
Compressibility data for pyrophyllite is taken from Pawley (2003). The thermal expansion has been increased somewhat higher than the measurements of Symmes (1986) to satisfy experiments.
- 7
The data for phengite and aluminous biotite are updated as discussed in Coggon & Holland (2002).
- 8
New experimental data on cor + q = ky from Harlov & Milke (2002) and Harlov et al. (2008) are now incorporated in the data fitting.
- 9
Heat capacity and entropy for carpholite are taken from Bertoldi et al. (2006).
- 10
New measurements are used for heat capacity and entropy for cordierite (Paukov et al., 2006; Dachs & Geiger, 2008).
- 11
Ferroactinolite enthalpy is fitted to the experiments of Jenkins & Bozhilov (2003).
- 12
Experimental data of Koziol (2004) on sid + hem = mt + CO2 are now used to derive enthalpy data for siderite.
- 13
Measurements of entropy of hercynite are taken from Klemme & Van Miltenburg (2003).
- 14
Chloritoid–chlorite Fe–Mg natural partitioning data are taken from Vidal et al. (1999) and used as low temperature constraints. Heat capacity and entropy for chloritoid and carpholite end-members have been modified using data of Koch-Müller et al. (2002) and Bertoldi et al. (2006).
- 15
Glaucophane data have been augmented by experiments of Corona & Jenkins (2007) for gl + q = ab + ta; new thermal expansion data for glaucophane are taken from Jenkins & Corona (2006).
- 16
Thermal expansion data for staurolite are now taken from Gibbons et al. (1981) and compressibility from Grevel et al. (1998).
- 17
Pargasite data are now fitted to the experiments of Westrich & Holloway (1981) and Lykins & Jenkins (1992) using a higher entropy than before. The derived enthalpy agrees well with measured values of Kahl et al. (2003). The amphibole mixing terms are from page 264 of Diener et al. (2007) except that, for good agreement with temperatures and amphibole compositions in the two experimental studies above,
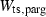 is now set at 2 kJ rather than
is now set at 2 kJ rather than 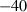 kJ.
kJ. - 18
Added high pressure experiments on antigorite and phase A from Wunder & Schreyer (1997) and Bose & Navrotsky (1998).
- 19
Added experiments of Aranovich & Newton (1999) on cc + q = wo + CO2, mag + en = fo + CO2 and ta = en + q + H2O, and phl + q = san + en + H2O. Also, those of Koziol & Newton (1998) for mag + en = fo + CO2.
- 20
Sphene thermodynamic data have been updated using heat capacities and entropy of Manon et al. (2008), thermal expansion from Malcherek (2001) and compressibility from Angel et al. (1999a,b).
- 21
Thermodynamic data for zircon and baddeleyite have been updated through the experimental data in Butterman & Foster (1967), Ferry et al. (2002) and are in excellent agreement with the Gibbs energies retrieved by Newton et al (2010).
- 22
Geikelite enthalpy has been improved via the additional experiments of Ferry et al. (2002) on mag + ru = geik + CO2.