Use of Stabilized Inverse Propensity Scores as Weights to Directly Estimate Relative Risk and Its Confidence Intervals
ABSTRACT
Objectives: Inverse probability of treatment weighting (IPTW) has been used in observational studies to reduce selection bias. For estimates of the main effects to be obtained, a pseudo data set is created by weighting each subject by IPTW and analyzed with conventional regression models. Currently, variance estimation requires additional work depending on type of outcomes. Our goal is to demonstrate a statistical approach to directly obtain appropriate estimates of variance of the main effects in regression models.
Methods: We carried out theoretical and simulation studies to show that the variance of the main effects estimated directly from regressions using IPTW is underestimated and that the type I error rate is higher because of the inflated sample size in the pseudo data. The robust variance estimator using IPTW often slightly overestimates the variance of the main effects. We propose to use the stabilized weights to directly estimate both the main effect and its variance from conventional regression models.
Results: We applied the approach to a study examining the effectiveness of serum potassium monitoring in reducing hyperkalemia-associated adverse events among 27,355 diabetic patients newly prescribed with a renin-angiotensin-aldosterone system inhibitor. The incidence rate ratio (with monitoring vs. without monitoring) and confidence intervals were 0.46 (0.34, 0.61) using the stabilized weights compared with 0.46 (0.38, 0.55) using typical IPTW.
Conclusions: Our theoretical, simulation results and real data example demonstrate that the use of the stabilized weights in the pseudo data preserves the sample size of the original data, produces appropriate estimation of the variance of main effect, and maintains an appropriate type I error rate.
Introduction
Observational studies have been used by medical researchers seeking to make inference on the effect of treatments on outcomes. Compared with those in randomized clinical trials, participants' characteristics in an observational study may not be balanced between treated and untreated groups. Consequently, the estimate of a treatment effect may be biased without appropriate adjustment when receipt of treatment is dependent on patients' characteristics (confounders) that also are associated with outcomes. Propensity scores were introduced by Rosenbaum and Rubin [1,2] and have been used by many researchers to obtain the treatments effects in observational studies [3–8]. A propensity score is the probability of receiving treatment given a set of known covariates and can be used to balance covariates between treated and untreated to obtain an unbiased estimate of treatment effects. Typically, propensity scores in an observational study can be obtained from ordinary logistic regressions if the treatment is binary.
The simplest use of propensity scores is that they can be included as covariates in outcome modeling. One can first fit a propensity score model that includes many potential covariates, and then the outcome model only has to include the propensity score and a few covariates that have no association with treatment [3,9]. But this approach can perform poorly if the sample linear discriminant based on covariates is not a monotone function of propensity score [1]. There are three additional strategies that use propensity scores to reduce selection bias: matching, stratification, and inverse probability of treatment weighting (IPTW). Matching subjects in treated groups with those in untreated groups with similar propensity scores can balance the known covariates and reduce selection bias. But it can also result in significant loss of observations of treated subjects, particularly if the untreated pool is small. Stratification places subjects into several mutually exclusive groups or strata. Based on their propensity scores, treatment effects are estimated from each stratum and averaged across strata to estimate the overall treatment effect [3,10]. The limitation of stratification is that one overall treatment effect may not be interpretable when the treatment effects of strata are very different in scale especially in direction. In addition, subjects in different strata may not separate into distinguishable groups that are meaningful to clinicians. The third propensity score approach is to use IPTW-weighted estimators to obtain treatment effects adjusting for known confounders [6,11,12]. This approach can incorporate time-dependent covariates and deal with censored data and produce one overall estimate of treatment effect.
For continuous outcome variables, there are three unbiased estimators for treatment effects [10,12] based on the IPTW, which have shown consistency but with different variance estimators. Nevertheless, these variance estimators are large-sample based and may produce large variance estimates and decrease efficiency of the estimators [10]. Estimators and variance estimates are less developed for discrete outcome variables. Accurate variance estimation of the treatment effect is critical to testing hypotheses. Underestimation of the variance produces inappropriately narrow confidence intervals and leads to falsely rejecting the null hypothesis. In addition to the large-sample-based variance estimators, others have suggested the use of the bootstrap method to obtain the variance of treatment effects [13,14], which can be used for medium or large samples and for different effect measures, for example, difference for continuous outcomes, incidence rate ratio for count data, and odds ratio for dichotomous outcomes. Nevertheless, the bootstrap method is not suitable for small data sets because there are few values to select from and it involves complex programming [15,16]. A robust variance estimator [13,17,18] has also been used to obtain standard error of the treatment effect. This approach adjusts for the lack of independence in replications of records for a subject in the pseudo data and is available in common statistical software packages such as the SAS PROC GENMOD (SAS Institute, Cary, NC). There are also a variety of weights developed based on sampling designs in survey studies to accurately compute estimates of population statistics and their standard errors from a small sample [19].
The aim of this study was to evaluate the use of stabilized weights (SWs) to obtain directly from conventional regression in observational studies both the treatment effects and their appropriate confidence intervals in the presence of confounders. In addition, we provide some comparisons of type I error rates using SWs to the robust variance estimator.
Statistical Methods
Let z be an indicator of binary treatment with 1 for treated and 0 for untreated, X be a row vector of confounders for the probability of treatment and outcome, π be the propensity score, and y be the outcome variable. Suppose that there are N subjects in a data set, with n1 subjects who received the treatment and n0 subjects who did not, N = n0 + n1. The probability of treatment without considering covariates is p = n1/N, and the probability of no treatment is 1 − p. The propensity score πi = prob (z = 1|Xi) is the probability of treatment given the observed covariates Xi. The propensity score can be estimated with a logistic regression model  , where β is a vector of parameters to be estimated from data. With the covariates X in the propensity score model using IPTWs as weights,
, where β is a vector of parameters to be estimated from data. With the covariates X in the propensity score model using IPTWs as weights, 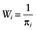 if zi = 1 and
if zi = 1 and 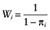 if zi = 0, where Wi denote the IPTW for subject i.
if zi = 0, where Wi denote the IPTW for subject i.
In the pseudo data using IPTWs, the number of observations is the sum of weights
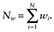
Nw is always greater than N, the sample size of the original data. To examine this further, assume that there is only one covariate, x1, which is dichotomous and associated with the probability of being treated with a coefficient βx1z. For subjects with x1 = 0, let m1 be the number of treated subjects and m0 be the number of untreated subjects, M = m1 + m0, and e0 is the probability of being treated when x1 = 0. For subjects with x1 = 1, let l1 be the number of treated subjects and l0 be the number of untreated subjects, and L = l1 + l0, and e1 is the probability of being treated when x1 = 1. The sample size of the pseudo data with IPTWs is
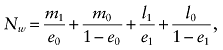 (1)
(1)where e0 and e1 are estimated from data, 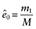 and
and 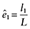 . Substituting
. Substituting 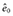 and
and 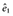 into Equation (1),
into Equation (1),
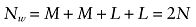 (2)
(2)Thus, the sample size doubles in the pseudo data. This is also true when there are other categorical variables that are associated with the probability of being treated. Consequently, regression estimates with IPTWs tend to reject the null hypothesis too frequently because of inflated sample sizes.
An improvement to the IPTW is the use of SWs. SWs have been proposed in modeling time-varying treatment status in reducing selection bias in observational studies [20,21]. The purpose of using SW in these studies is reducing the weights of either those treated subjects with low propensity scores or those untreated subjects with high propensity scores. For this article, we only considered constant treatment status, if zi = 1 then 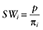 , and if zi = 0, then
, and if zi = 0, then 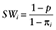 , where p is the probability of treatment without considering covariates. We will show that the use of SW reduces the type I error by preserving the sample sizes in pseudo data sets. Again, assuming that there is only one dichotomous predictor for the probability of being treated, x1, p can be estimated from data as
, where p is the probability of treatment without considering covariates. We will show that the use of SW reduces the type I error by preserving the sample sizes in pseudo data sets. Again, assuming that there is only one dichotomous predictor for the probability of being treated, x1, p can be estimated from data as  . Using the SWs,
. Using the SWs,
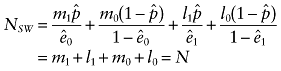 (3)
(3)Equation (3) demonstrates that using SWs in observational studies will result in a pseudo data with sample size that is the same as that of the original data. Thus, the variance estimate of treatment effect is appropriate directly from conventional regression with SWs. This is also true when other categorical variables that are associated with the probability of being treated exist. The impact of continuous variables on sample size in the pseudo data cannot be revealed in closed forms and will be evaluated by simulations in the next section.
Simulation Studies and Results
The simulations were designed to evaluate the use of SWs to estimate the effect of treatment and its variance in the presence of confounders and to obtain appropriate confidence intervals using conventional regressions analyzing data from observational studies. Specifically, we examined the sample sizes in the pseudo data sets and type I error rates when confounders in the propensity score and outcome models were dichotomous, categorical, and continuous.
Simulation Algorithm
Probability model for treatment, z. The treatment indicator variable, z, was simulated according to model (4)
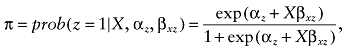 (4)
(4)where α is the intercept and is equal to 0.69 and X is a row vector of dichotomous, categorical, or continuous independent variables (confounders). We report the results with independent variables in model (4) being dichotomous, or dichotomous and continuous variables. Nevertheless, results were similar when categorical variables were included in model (4).
For simulations with only a dichotomous variable x1, distributions of the dichotomous variable x1 were either 50% = 0 and 50% = 1 or 66.6% = 0 and 33.3% = 1. For simulations with a dichotomous variable, x1, and a continuous variables, x2, when x1 = 0, the mean of x2 was either 1 or −1, and the variance was held constant at 1; when x1 = 1, the mean of x2 ranged from −4 to 4 by increments of 1, and the variance was held constant at 4. We also evaluated different values of the coefficients βx1z, βx2z, βx1y, and βx2y to reflect differing strengths of association with treatment and outcome. For dichotomous x1, we evaluated positive and negative values of 0.69, 1.39, and 1.79, which correspond to odds ratios of 2, 3, and 4 when positive. For the continuous variable x2, simulations used values of 0.3, 0.6, and 1.2 for βx2z and βx2y.
We then generated the dichotomous treatment variable zi based on the treatment probability model (4), i = 1 to 500.
Probability model for the outcome, y. The dichotomous outcome variable, y, was simulated, based on the following model:
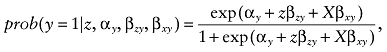 (5)
(5)where αy is the intercept and equals to 0.69, βzy is the coefficient for the association between treatment and outcome and is assigned zero to assess the type I error rates. X are confounders and βxy are the corresponding coefficients, and their values are the same as those of βxz in (4). The dichotomous outcome variable yi was generated based on the outcome probability model (5), i = 1 to 500.
Analysis of each simulated dataset. For each dataset we fit the propensity score models, obtained the IPTW and SWs, and then calculated the sample sizes in the pseudo data and fit outcome model. 5000 datasets were simulated and analyzed for each combination of parameters.
Evaluation Measures
Mean sample sizes and standard deviations from 5000 simulated data sets were estimated. Type I error rates were computed as the proportion of P-values less than 0.05 under a null hypothesis of no treatment effect (βzy = 0) based on Wald tests. In addition to IPTW and SW methods, type I error rates using robust variance estimator with IPTWs are also reported.
Simulation Results
Sample sizes and type I error rates when there is only a dichotomous confounder x1 and βzy = 0. We first evaluated the use of SWs when there is only a dichotomous confounder, x1 and there is no treatment effect, βzy = 0. Under a variety of conditions, the IPTW method clearly doubled the sample sizes in the pseudo data set and inflated the type I error rates (Table 1). SWs preserved the sample sizes and had type I error rates that were close to 5% (Table 1). The standard deviations of sample sizes in the pseudo data sets were small, indicating that the samples sizes of these 5000 pseudo data sets were all about 500, the original simulated sample size. The level of imbalance of the dichotomous confounding covariate between treated and untreated groups had no impact on the sample sizes of the pseudo data sets and type I error rates with the SW method. Compared with SWs, the robust variance estimator method consistently produced lower than 5% type I error rates because of slightly larger variance estimates. This is consistent with previous studies [17,18].
| x 1 = 1 (%) | βx1z/βx1y | Sample size (STD) | Type I error rate (%) | |||
|---|---|---|---|---|---|---|
| IPTW | SW | IPTW | SW | Robust variance estimator | ||
| 33.33 | 0.69 | 1000 (1.1) | 500 (0.3) | 21.2 | 4.6 | 4.2 |
| 1.39 | 1000 (3.4) | 500 (0.8) | 23.1 | 5.2 | 4.2 | |
| 1.79 | 1000 (5.5) | 500 (1.3) | 22.8 | 5.0 | 3.4 | |
| 50 | 0.69 | 1000 (0.9) | 500 (0.2) | 22.3 | 4.7 | 4.3 |
| 1.39 | 1000 (3.2) | 500 (0.6) | 25.7 | 5.2 | 4.1 | |
| 1.79 | 1000 (5.6) | 500 (1.0) | 26.2 | 4.6 | 3.6 | |
| 33.33 | −0.69 | 1000 (0.2) | 500 (0.1) | 17.7 | 4.6 | 4.2 |
| −1.39 | 1000 (0.3) | 500 (0.2) | 16.6 | 5.2 | 4.0 | |
| −1.79 | 1000 (0.7) | 500 (0.4) | 17.5 | 5.1 | 3.1 | |
| 50 | −0.69 | 1000 (0.2) | 500 (0.1) | 16.3 | 4.8 | 4.3 |
| −1.39 | 1000 (0.2) | 500 (0.1) | 16.1 | 5.2 | 3.8 | |
| −1.79 | 1000 (0.6) | 500 (0.2) | 17.7 | 5.4 | 3.3 | |
- IPTW, inverse probability of treatment weighting; STD, standard deviation; SW, stabilized weight.
Sample sizes and type I error rates when there are a dichotomous confounder x1 and a continuous confounder x2 and βzy = 0. Sample sizes with SWs remained similar to the original simulated sample size with small standard deviations in most of cases (Table 2). Larger differences emerged when the confounding effect of the continuous variable is strong (βx2z = βx2y = 1.2). In those simulations, standard deviations became relatively large, implying greater deviation of some pseudo data set sample sizes from the original, although the average sample size still remained about at 500. In addition, type I error rates became as high as 12%. Also, the level of imbalance of the continuous confounding covariate between treated and untreated groups has no impact on the sample sizes of the pseudo data sets and type I error rates with the SW method. Again, Table 2 showed that, on average, using IPTW doubled sample sizes in the pseudo data, with the type I error rates reaching as high as 44.0%. For most of the cases with continuous confounding covariate, the robust variance estimator method produced lower than 5% type I error rates because of slightly larger variance estimates.
| x 1 = 1 (%) | βx2z/βx2y | Means of x2 | Sample size (STD) | Type I error rate (%) | ||||
|---|---|---|---|---|---|---|---|---|
| x 1 = 0 | x 1 = 1 | IPTW | SW | IPTW | SW | Robust variance estimator | ||
| 50 | 0.3 | 1 | 1 | 999 (9.7) | 500 (2.0) | 25.9 | 5.1 | 4.6 |
| 0.6 | 1 | 1 | 999 (35.9) | 500 (6.7) | 28.4 | 6.3 | 4.0 | |
| 1.2 | 1 | 1 | 995 (196.7) | 499 (36.7) | 35.5 | 12.0 | 3.4 | |
| 0.6 | 1 | 2 | 999 (35.1) | 500 (5.1) | 32.1 | 5.1 | 4.0 | |
| 0.6 | 1 | 3 | 998 (38.4) | 500 (4.4) | 36.5 | 5.0 | 5.6 | |
| 0.6 | 1 | 4 | 999 (102.3) | 500 (4.6) | 41.5 | 6.0 | 5.8 | |
| 33.33 | 0.3 | 1 | 1 | 999 (8.8) | 500 (1.9) | 24.0 | 5.0 | 4.3 |
| 0.6 | 1 | 1 | 999 (31.1) | 500 (6.1) | 28.5 | 6.2 | 4.5 | |
| 1.2 | 1 | 1 | 996 (152.0) | 499 (29.0) | 32.8 | 9.0 | 3.0 | |
| 0.6 | 1 | 2 | 1000 (31.1) | 500 (4.4) | 32.9 | 5.0 | 4.4 | |
| 0.6 | 1 | 3 | 999 (35.7) | 500 (3.6) | 39.0 | 4.5 | 6.2 | |
| 0.6 | 1 | 4 | 1000 (49.3) | 500 (3.8) | 43.9 | 4.5 | 7.7 | |
| 0.6 | −1 | −1 | 999 (13.6) | 500 (5.9) | 17.2 | 5.6 | 3.3 | |
| 0.6 | −1 | −2 | 999 (12.9) | 500 (6.8) | 17.8 | 6.0 | 2.8 | |
| 0.6 | −1 | −3 | 999 (13.2) | 500 (8.0) | 20.4 | 6.8 | 2.2 | |
| 0.6 | −1 | −4 | 999 (16.5) | 500 (9.0) | 22.0 | 6.2 | 1.4 | |
- IPTW, inverse probability of treatment weighting; STD, standard deviation; SW, stabilized weight.
An Example
In a recent study examining the effectiveness of serum potassium monitoring in reducing hyperkalemia-associated adverse events during the first year of therapy, 27,355 diabetic patients newly prescribed with a renin-angiotensin-aldosteronesystem (RAAS) inhibitor between January 1, 2001 and December 31, 2006 were retrospectively identified. Table 3 shows that the patients with and without serum potassium monitoring in the original cohort were significantly different on many demographic and clinical characteristics. Nearly three-fourths of this cohort had serum potassium monitoring during their study follow-up period. This study is an example of when matching by propensity scores would not be optimal because the majority of those with serum potassium monitoring would be omitted because of a smaller number of those without serum potassium monitoring.
| Characteristic | Original cohort (n = 27,355) | Pseudo cohort (n = 27,407) | ||||
|---|---|---|---|---|---|---|
| Monitored | Not monitored | P-values | Monitored | Not monitored | P-values | |
| Mean age in years (STD) | 60.4 (13.0) | 55.5 (13.2) | <0.001 | 59.0 (13.1) | 59.3 (13.8) | 0.054 |
| Male sex (%) | 50.8 | 53.4 | <0.001 | 51.4 | 50.7 | 0.30 |
| Drug groups (%) | <0.001 | 0.98 | ||||
| ACEi | 91.9 | 93.1 | 92.5 | 92.3 | ||
| ARB | 5.70 | 5.5 | 5.4 | 5.6 | ||
| Spironolactone | 1.90 | 1.2 | 1.6 | 1.6 | ||
| Combinations | 0.50 | 0.2 | 0.5 | 0.5 | ||
| Kidney transplant during or before study entry (%) | 0.30 | <0.1 | <0.001 | 0.2 | 0.2 | 0.39 |
| Prior potassium monitoring (%) | 0.90 | 0.93 | 0.67 | 0.9 | 0.9 | 0.89 |
| Prior hyperkalemia diagnosis (%) | 0.57 | 0.38 | 0.05 | 0.5 | 0.5 | 0.79 |
| Hospitalization or emergency department visit(s) within 6 months before study entry (%) | 23.50 | 19.1 | <0.001 | 22.6 | 22.2 | 0.39 |
| Heart failure diagnosis (%) | 8.9 | 3.5 | <0.001 | 7.4 | 7.6 | 0.66 |
| Chronic kidney disease stage 3 or 4 (%) | 10.0 | 3.0 | <0.001 | 8.0 | 8.4 | 0.28 |
| Median chronic disease score (5th, 95th percentile) | 6 (3.11) | 6 (3.9) | <0.001 | 6 (3.10) | 6 (3.11) | 0.03 |
| Digoxin therapy (%) | 4.4 | 1.6 | <0.001 | 3.6 | 3.8 | 0.40 |
| Diuretic therapy (%) | 37.1 | 19.9 | <0.001 | 32.2 | 32.8 | 0.27 |
| Potassium supplement therapy (%) | 13.9 | 4.7 | <0.001 | 11.3 | 12.3 | 0.02 |
- ARB, angiotensin receptor blockers; STD, standard deviation.
We fit a logistic regression model to obtain the propensity scores and included the following variables: use of digoxin, use of diuretic, use of potassium supplements, study site, sex, drug groups of RAAS inhibitor, age, kidney transplant, a drug-dispensing-based chronic disease score based on a modification of the method of Clark et al. [22], potassium monitoring within 6 months before study entry, diagnosis of hyperkalemia within 6 months before study entry, inpatient hospitalization or emergency department visit within 6 months before study entry, the presence of heart failure, and the presence of chronic kidney disease. The SW-adjusted results of characteristics comparisons are presented in Table 3 as well. All covariates except age, chronic disease score, and the use of potassium supplements became comparable after SW adjustment between those whose potassium was monitored and those whose potassium was not monitored (see Table 3). Although age, chronic disease score, and the use of potassium supplements remained statistically different between groups, the magnitudes of difference were markedly reduced.
The sample size in the pseudo data using the SWs was 27,407 compared with 54,891 using IPTW. The sample size in the pseudo data using the SWs was only slightly larger than the original 27,355, and the impact on variance estimate of treatment effect was minimal. The incidence rate ratio and confidence intervals were 0.46 (0.34, 0.61) using SWs compared with 0.46 (0.38, 0.55) using typical IPTW. While adjusting for age, the use of potassium supplements, and chronic disease score using SWs, the incidence rate ratio was 0.49 (0.37, 0.66), which was very close to the results without the adjustment of these covariates in outcome model, indicating that the balance of age, the use of potassium supplements, and chronic disease score between the two groups with SWs was sufficient. Comparison of these two weights from this example showed that IPTWs have larger standard deviations and wider ranges than SWs (Table 4).
| Distribution characteristics | IPTW | SW |
|---|---|---|
| Mean | 2.01 | 1.00 |
| Median | 1.49 | 0.95 |
| Standard deviation | 1.59 | 0.40 |
| Minimum | 1.01 | 0.42 |
| Maximum | 42.59 | 12.39 |
- IPTW, inverse probability of treatment weighting; SW, stabilized weight.
Discussion
In this article, we demonstrate several advantages of SWs over IPTWs in analyzing data obtained from observational studies. First, using SWs can reduce the weights of either those treated subjects with low propensity scores or those untreated subjects with high propensity scores in the pseudo data sets. Our serum potassium monitoring example showed that IPTWs have larger standard deviation and wider range than SWs (Table 4). Thus, results using SWs are robust even with few observations with extreme IPTWs. Second, unlike variance estimators, no additional steps are needed when SWs are used because the SW approach provides appropriate variance estimates and confidence intervals of treatment effect from conventional regression models for fitting the outcome variables. Third, computer programming is simple for one to use SWs to obtain the effect of treatment effects and confidence intervals as compared with the bootstrap approach. One only needs to calculate the weights differently. Fourth, in our simulation studies and example, outcome variables are dichotomous. Unlike those developed estimators, the SW approach is applicable to outcome variables (e.g., dichotomous, continuous, and count data) that have a finite distribution. Our simulation results also show that SW is a reasonable alternative to the robust variance estimator and has the advantage of reducing influential weights.
The limitation of the SW approach is the uncertainty of the influence of continuous confounders when their association with the probability of being treated and outcome is very strong. As shown in simulation studies, the sample size in some of the pseudo data sets can be different from the original data set when the confounding effect is strong. Nevertheless, it is uncommon because our simulation results showed that the mean sample size approximated the original sample size. It is recommended that one always examine the difference between sample sizes in the original cohort and the pseudo cohort. When there is evidence that the sample size of the pseudo data is different from that of the original data set, one can use the robust variance estimator with IPTWs although this latter method can produce slightly larger standard errors.
Conclusion
Our theoretical, simulation results and the real data example demonstrate that the use of the SWs in the pseudo data preserves the sample size close to the original data. In addition, we conclude that use of SWs produces the appropriate estimation of the variance of the main effect and maintains an appropriate type I error rate. SWs may be a useful tool to balance confounders between groups in observational studies.
Acknowledgements
We thank Gwyn Saylor, BS, Xiuhai Yang, MS, and Junling Ren, MEd, for programming efforts, and Leslie A. Wright, MA, and Jill Mesa for project management.
Source of financial support: Diabetes and Drug-Associated Hyperkalemia: Effect of Laboratory Monitoring is supported by the National Institute of Diabetes and Digestive and Kidney Diseases (NIDDK) under the following grant number: R21DK075076.




