Estimation of Life Expectancy and the Expected Years of Life Lost in Patients with Major Cancers: Extrapolation of Survival Curves under High-Censored Rates
ABSTRACT
Objectives: There exists a lack of extrapolation methods for long-term survival analysis when censored rates are high (25–50%). This study aimed at estimating life expectancy (LE) after the diagnosis of cancer and the expected years of life lost (EYLL) using a newly developed semiparametric method.
Methods: Patients (n = 425,294) diagnosed with 17 different types of major cancer were enrolled. All of the patients were registered with the Taiwan Cancer Registry between 1990 and 2001; their survivals were followed through the end of 2004. The survival function for an age- and sex-matched reference population was generated using the Monte Carlo method from the life table of the general population. Lifetime survival of the cancer patients (up to 50 years) were obtained using linear extrapolation of a logit-transformed curve of the survival ratio between the cancer and reference populations. The estimates were compared with the results from the extrapolation of fitted Weibull models.
Results: The 15-year survival, LE, and EYLL for 17 different types of cancer were determined, of which the LE of breast, cervical, ovarian, and skin cancers exceeded 15 years; nasopharyneal, leukemia, bladder, kidney, and colorectal cancers exceeded 10 years. Validity tests indicated that the relative biases of the extrapolated estimates were usually <5% under high censoring rates.
Conclusions: The newly developed method is feasible and relatively accurate to project LE and EYLL, which could also be merged with data pertaining to quality of life, for a more detailed outcome assessment in the future.
Introduction
Cancer is an issue of major public health concern, not only because it can cause substantial suffering and shorten the natural lifespan of cancer patients, but also because of the significant impact it can have upon society as a whole [1]. The estimation of life expectancy (LE) from the date the diagnosis of cancer is made until death has been performed in many medical fields to generate measures of cancer survival relevant to clinicians, health economists, policymakers, and insurance companies [2]. In general, survival analysis provides an estimation of the survival rate during the observed study period, but there has been a lack of reliable method for lifetime extrapolation [3]. Parametric survival modeling, such as the Weibull distribution [4], Gompertz extrapolation technique [5,6], exponential distribution [7], and the log-normal distribution [8], are commonly used for lifetime extrapolation; however, the models may not be suitable for data with a high rate of right censoring, such as patients infected with human immunodeficiency virus [9].
We have developed a semiparametric method to incorporate LE information of the general population into the estimation process [9–14]. If the cancer-related excess hazard assumes constant after a period of time, cancer patients' LE can be projected from the available follow-up data with this semiparametric method [10]. In addition to estimating the LE after diagnosis, the method can also be used to compute the expected years of life lost (EYLL), which is a measure of the overall burden on individuals and on society as a whole [1], and a more accurate reflection of the social and economic impact of cancer than that provided by crude incidence rates or mortality data [15]. Moreover, a valid estimation of LE and EYLL in cancer patients is crucial for the outcome assessment of effectiveness for cancer management and resource allocation of health services [3,16,17].
Using the data from the National Cancer Registry and vital statistics, we sought to estimate the mean lifetime survival duration and EYLL for the major types of cancer in Taiwan. The estimates were compared with the results obtained from parametric survival modeling.
Methods
Cancer Cohorts
The Taiwan National Cancer Registry, with a total of 425,294 patients diagnosed with 17 major cancers between 1990 and 2001, was the primary data source for this study. The anatomic sites of the 17 major cancers included the oral cavity, nasopharynx, esophagus, stomach, colon and rectum, liver, gallbladder and extrahepatic bile ducts, pancreas, lung, leukemia, skin, breast, cervix, ovary, prostate, bladder, and kidney and other urinary organs.
Survival in the Cancer Populations
Each cancer patient was followed through the end of 2004, and the survival status of each patient was further verified by cross-checking with the national mortality certification database maintained by Taiwan's Ministry of the Interior [18]. We used the Kaplan–Meier method to estimate survival function based on the follow-up data from 1990 to 2004.
Extrapolation of Long-Term Survival for the Cancer Population after Follow-Up Limit
The detailed method, including the technical details and its proof, can be found in our previous articles [9,10]. The main idea of this approach is to borrow information from a reference population, of which the survival time is obtained from the available data of the national life table. Briefly, the extrapolation process comprised of three phases. First, we created a reference population of subjects whose age and sex matched with the cancer patients. The survival times of the reference population were generated from a general population with known survival times, using the Monte Carlo method. Second, we fitted a simple linear regression to the logit transform of the survival ratio between the cancer population and the reference population up to the end of the follow-up period. Finally, the estimated regression line and survival curve of the reference population was used to project a long-term survival curve beyond the follow-up limit. We presented the major procedures of the method below.
Survival in the Reference Population
The life tables for the general population were obtained from the national vital statistics, as published by the Department of Statistics, Ministry of the Interior, Executive Yuan, Taiwan. Because the individual survival time of the subjects in a hypothetical cohort cannot be directly derived from the life table of the general population, we used the Monte Carlo method to generate the simulated survival time of age- and sex-matched hypothetical subjects for each patient in the cancer cohorts. And the total collection of hypothetical subjects was used as the reference population. Then, the survival curve of the reference population is obtained by applying the Kaplan–Meier method to the simulated survival times [10].
Logit Survival Ratio Extrapolation
The semiparametric method was used to extrapolate the survival time beyond the follow-up limit of 15 years. The survival ratio between the survival functions of two populations is defined by the formula:

Because the cancer population has a worse survival than the reference population, the value of survival ratio, W(t), initially equals 1, then gradually decreases due to disease-associated excess mortality. Because the value of W(t) is limited to the range from 0 to 1, linear regression for the temporal trend is not applicable. We therefore used the logit transformation of W(t). Furthermore, if the cancer-associated excess hazard remains constant over time, the curve of the logit of W(t) will converge to a straight line.
We then fitted a simple linear regression for the logit of W(t) from the time point, which was usually after the unstable period (e.g., initial active diagnostic or therapeutic management) to the end of the follow-up. Finally, given the least squares estimates of the intercept and slope parameters, 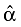 and
and 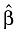 , we projected the long-term survival curve of the patient population beyond the follow-up limits as:
, we projected the long-term survival curve of the patient population beyond the follow-up limits as:
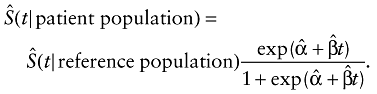
The standard error of survival estimates was obtained through a bootstrap method by implementing the extrapolation process with data simulated by repeatedly sampling techniques with replacement from a real data set 300 times [9,10,14]. To facilitate the computation, we developed a software program, MC-QAS, which was built in the R statistical package, which can be freely downloaded from http://www.stat.sinica.edu.tw/jshwang.
Estimation of EYLL
The average EYLL of a cancer cohort was defined in this study as the mean survival difference between the specific cancer cohort and an age- and sex-matched reference population. In other words, the average EYLL was the difference in the area between the mean survival curves of the cancer and reference populations. This parameter provides us with a measure of the burden of cancer on individual patients and yields an estimation of how much a patient's life is likely to be shortened by cancer [16]. The average EYLL was then multiplied by the total annual incidences of cancer for each cancer site in 1 year to obtain the subtotal of EYLL for the year; clearly, the subtotal of EYLL can be regarded as an indicator of the total burden of cancer on society as a whole [1].
Validation of the Monte Carlo Extrapolation and Comparison with the Parametric Method
Empirical cancer data from the National Cancer Registry provided us with an opportunity to validate actual performance. Thus, a selected subcohort of patients diagnosed between 1990 and 1996 with those cancers of interest to this study was created for each cancer site. It was assumed that the cohorts were only followed up until the end of 1996, or for a period of 7 years. We extrapolated the data through the end of 2004 using both the Monte Carlo method and the Weibull model for comparison. For every subcohort that was followed up until the end of 2004, the Kaplan–Meier method was calculated as the “gold standard” to determine the accuracy. The relative biases for each cancer site were also computed to compare the differences in values between the Kaplan–Meier estimates and the two extrapolation methods.
Results
LE and EYLL
The 15-year follow-up data were used to extrapolate the lifetime survival time to the 50th year after diagnosis for the estimation of the LE. The Kaplan–Meier estimate was applied to estimate the mean survival time in the 15-year follow-up. The LE and EYLL for the 17 major cancer sites are summarized in Table 1. The censoring rates for the survival analysis were between 8% and 67% by the end of the 15-year follow-up period. In terms of population sizes, liver cancer had the largest cohort, while gallbladder and extrahepatic bile duct cancers had the smallest cohort.
| Cancer site | Cohort size | Mean age at diagnosis (SD) | Censoring rate (%) | 15-year survival based on K–M estimate | Lifetime survival based on MC method (SE) | Average EYLL based on MC method (SE) | Subtotal of EYLL based on MC method |
|---|---|---|---|---|---|---|---|
| Pancreas | 7,931 | 65.6 (12.7) | 8.28 | 1.75 (0.05) | 2.81 (0.17) | 12.87 | 12,769 |
| Lung | 58,773 | 66.6 (11.7) | 9.97 | 2.20 (0.02) | 3.09 (0.07) | 11.79 | 79,584 |
| Liver | 68,585 | 60.4 (13.5) | 13.28 | 2.63 (0.02) | 3.45 (0.08) | 15.61 | 133,282 |
| Esophagus | 9,710 | 63.0 (12.1) | 11.28 | 2.42 (0.04) | 3.54 (0.20) | 13.25 | 16,279 |
| Gallbladder and extrahepatic bile duct | 5,097 | 66.5 (12.0) | 17.72 | 3.37 (0.07) | 4.98 (0.20) | 10.36 | 6,312 |
| Stomach | 35,477 | 64.9 (13.6) | 26.80 | 4.78 (0.03) | 7.51 (0.14) | 8.80 | 30,794 |
| Prostate | 14,288 | 73.1 (8.0) | 44.65 | 7.05 (0.06) | 8.17 (0.13) | 1.72 | 3,433 |
| Oral cavity | 26,681 | 53.8 (12.9) | 35.94 | 5.96 (0.04) | 9.58 (0.61) | 14.00 | 49,671 |
| Colon and rectum | 60,789 | 63.8 (13.7) | 41.94 | 7.00 (0.03) | 10.86 (0.11) | 6.36 | 45,905 |
| Kidney and other urinary organs | 11,671 | 62.7 (15.1) | 43.68 | 7.07 (0.07) | 10.97 (0.85) | 6.74 | 10,120 |
| Bladder | 15,092 | 66.7 (12.6) | 46.93 | 7.71 (0.05) | 10.99 (0.20) | 3.83 | 6,727 |
| Leukemia | 9,224 | 41.8 (25.5) | 28.49 | 4.97 (0.08) | 11.61 (0.94) | 19.34 | 18,602 |
| Nasopharynx | 15,231 | 49.6 (13.4) | 43.06 | 7.42 (0.05) | 12.59 (0.74) | 14.79 | 20,271 |
| Skin | 14,005 | 63.3 (16.9) | 62.18 | 9.71 (0.05) | 16.16 (0.22) | 1.59 | 2,873 |
| Ovary | 6,436 | 49.3 (17.0) | 52.59 | 8.46 (0.11) | 17.71 (0.80) | 11.91 | 8,775 |
| Cervix uteri | 29,636 | 54.7 (13.8) | 63.92 | 10.21 (0.03) | 19.77 (0.30) | 6.18 | 14,978 |
| Breast | 36,668 | 50.5 (12.5) | 66.94 | 10.41 (0.03) | 20.01 (0.80) | 9.35 | 43,633 |
- Extrapolation to lifetime survival and EYLL was based on the Monte Carlo (MC) method projected from 15 years to 50 years.
- SD, standard deviation; SE, standard error; EYLL, expected years of life lost.
We found that the cohorts with the longest LE were breast (20.01 years), cervical (19.77 years), and ovarian cancers (17.71 years), and the shortest LE were pancreatic (2.81 years), lung (3.09 years), and liver cancers (3.45 years). The estimated average EYLL of a cancer cohort is the difference between the areas of estimated survival curves for the reference population and the cancer cohort. As an example shown in Fig. 1, estimated EYLL for a gastric cancer patient was 8.8 years. The cohorts with the largest average estimated EYLL were leukemia (19.34 years) and cancers of the liver (15.61 years) and nasopharynx (14.79 years).
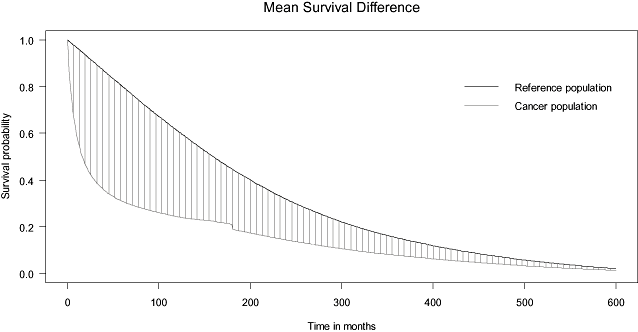
Mean survival difference between gastric cancer population and reference population after 50 years of extrapolation.
Following multiplication by the total annual incidences for the different types of cancer in 2001, the greatest health impacts on society, in terms of the subtotal of EYLL for the year, were cancers of the liver, lung, and oral cavity. Furthermore, the average expected life span could be obtained simultaneously after the consideration of the mean age at diagnosis and the mean LE after diagnosis. The patterns of the average expected life spans for the different types of cancer were different from those of LE using our method and are listed in Fig. 2. Leukemia (53.41 years), and cancers of the nasopharynx (62.19 years) and oral cavity (63.38 years), had the shortest average expected life span.
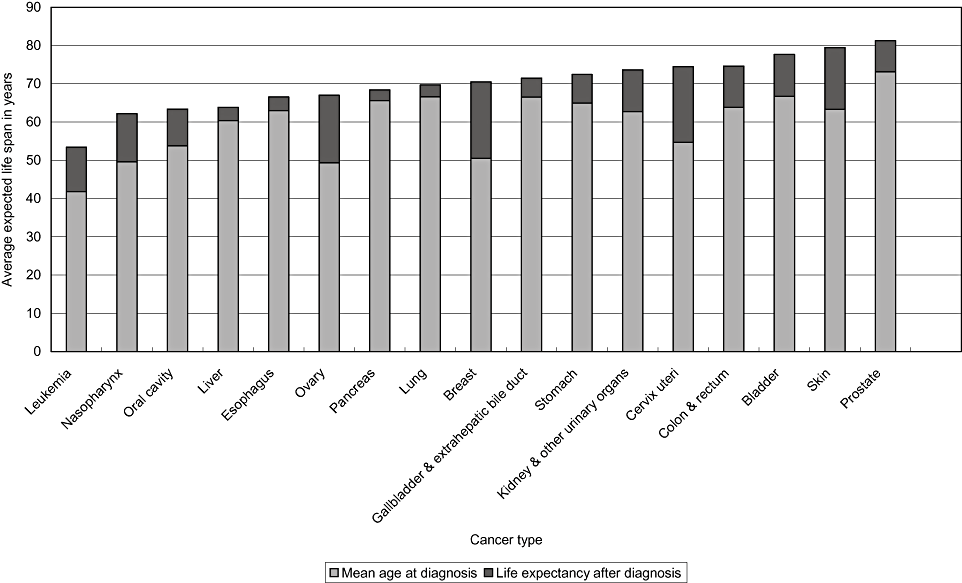
Average expected life span by cancer type. Estimates are shown as the sum of mean age at diagnosis and life expectancy after diagnosis.
Validity of Extrapolation
The cancer cohorts established during the 7 years between 1990 and 1996 were extrapolated to an additional 8 years and were then compared with actual survival estimated with the Kaplan–Meier method using the complete 15 years of follow-up, from 1990 to 2004. The calculations of the relative biases for the two methods are summarized in Table 2. The censoring rates at the end of the first 7-year follow-up period ranged between 21% and 81%. The absolute values of the relative biases for the Monte Carlo method ranged between 0.76% and 14.41% after 8 years of extrapolation; these values were generally much smaller than those obtained under the Weibull model, with the notable exceptions of skin and prostate cancers. Nevertheless, the standard errors for the Weibull model were generally smaller than those for the Monte Carlo method. There are some variations or differences between the Kaplan–Meier estimates in Tables 1 and 2 because they were calculated from two different periods of cohorts of cancer, namely, those diagnosed during 1990 to 2001 and 1990 to 1996, respectively.
| Cancer site | 15-year follow-up | Extrapolation based on the first 7-year follow-up | ||||||
|---|---|---|---|---|---|---|---|---|
| Kaplan–Meier estimate | Monte Carlo method | Weibull model | Censoring rate (%) | |||||
| Estimates | Estimates | SE | Relative bias (%) | Estimates | SE | Relative bias (%) | ||
| Colon and rectum | 7.12 | 7.06 | 0.14 | −0.76 | 6.40 | 0.06 | −10.07 | 62.73 |
| Leukemia | 4.99 | 5.05 | 0.17 | 1.19 | 4.10 | 0.11 | −17.83 | 43.41 |
| Skin | 9.74 | 9.85 | 0.28 | 1.21 | 9.71 | 0.14 | −0.26 | 80.53 |
| Bladder | 7.76 | 7.66 | 0.27 | −1.25 | 7.38 | 0.12 | −4.81 | 68.21 |
| Stomach | 4.82 | 4.93 | 0.08 | 2.19 | 3.78 | 0.05 | −21.61 | 42.85 |
| Cervix uteri | 10.10 | 9.82 | 0.16 | −2.82 | 9.01 | 0.09 | −10.84 | 77.69 |
| Breast | 10.03 | 9.73 | 0.18 | −2.99 | 8.93 | 0.10 | −10.98 | 80.52 |
| Esophagus | 2.59 | 2.68 | 0.1 | 3.58 | 1.73 | 0.05 | −33.02 | 27.91 |
| Ovary | 8.38 | 8.70 | 0.25 | 3.89 | 7.47 | 0.18 | −10.87 | 67.34 |
| Kidney and other urinary organs | 7.10 | 6.75 | 0.24 | −4.92 | 6.51 | 0.14 | −8.33 | 62.34 |
| Oral cavity | 5.68 | 5.38 | 0.17 | −5.38 | 4.43 | 0.07 | −21.94 | 54.28 |
| Prostate | 6.73 | 6.30 | 0.32 | −6.44 | 6.37 | 0.14 | −5.28 | 68.85 |
| Gallbladder and extrahepatic bile duct | 3.59 | 3.82 | 0.19 | 6.57 | 2.63 | 0.11 | −26.77 | 33.62 |
| Pancreas | 2.09 | 2.24 | 0.13 | 6.73 | 1.23 | 0.04 | −41.21 | 20.89 |
| Nasopharynx | 7.10 | 6.55 | 0.24 | −7.71 | 5.86 | 0.10 | −17.41 | 62.52 |
| Lung | 2.38 | 2.57 | 0.05 | 8.00 | 1.62 | 0.02 | −31.77 | 25.18 |
| Liver | 2.48 | 2.83 | 0.08 | 14.41 | 1.81 | 0.02 | −26.70 | 27.58 |
- The censoring rates were computed at the end of the first 7-year follow-up period.
- SE, standard error.
Discussion
The method adopted for this study incorporated data simultaneously from the mortality patterns of the general population based on vital statistics and actual experience of the cancer patients, which would be better than potential years of life lost, assuming an arbitrarily chosen potential limit of life such as 65 years [19]. Moreover, the method can estimate the lifetime survival for different types of cancer with a reasonable accuracy after about 7 years of follow-up, as shown in Table 2.
Some researchers assume that the survival of cancer patients at the end of follow-up is similar to that in the general population [2], such as children with acute lymphoblastic leukemia, who may enjoy an event-free survival for longer than 10 years [20]. In fact, the above assumption can be regarded as a special case in this method with the excess hazard presumed to be 0 after an initial period of treatment, and it was also applicable in other diseases, such as long-term survival after a head injury [21]. There are other methods dealing with censoring, which can be applied under different circumstances [22,23]. Nevertheless, the method proposed by us directly extrapolates the unfinished survival curves to lifetime and seems the most straightforward both in concept and in actual clinical practice for following up cancer cohorts, as our method only relies on the availability of vital statistics of the general population and an assumption of consistent premature mortality throughout lifetime.
In cost-effectiveness analyses, the Markov model is often applied to estimate LE, which uses a finite number of the hypothetical cohort to simulate effectiveness (e.g., survival) and cost, but requires external data and/or methods to facilitate the sensitivity analysis on some assumptions. Our method, which is based on the actual cohort data of follow-up, could be used to validate the results from the Markov model [9]. In fact, the result of the long-term survival (40 years) for breast cancer cohort in this study is similar with those based on a simulation from the Markov model, with and without treatment of trastuzumab [24], as shown in Fig. 3.

Long-term survival curve for patients with breast cancer (including all stages) in Taiwan using the Monte Carlo method, which was compared with published [24] survival curves of patients with early breast cancer simulated under the Markov model with and without treatment of trastuzumab.
The method may also be applied in clinical trials, in which at least two arms or cohorts of patients, say, treatment versus placebo, are followed for a period of time to observe their actual survival and quality of life. Thus, we would obtain two survival ratios, S(t|treatment)/S(t|reference) and S(t|placebo)/S(t|reference), at a different time t and they both could be extrapolated to lifetime with confidence intervals obtained through the bootstrap method for comparison [10]. Our method does not need to classify the study disease into a limited number of health states to obtain the transition probabilities. Instead, the quality of life data collected during clinical trials at each time t can provide the mean value that can be directly multiplied with the survival probability and summed up to obtain the quality-adjusted LE [12].
Based on our results, the methodology presented here could be more useful for cancer or some diseases in which survival is longer or prognoses are better, or there is a high censoring rate at the end of the follow-up, such as cancers of the breast, cervix, ovary, and nasopharynx. Furthermore, the incidence rates of the cancers of the oral cavity and breast have increased recently in Taiwan [25] and the ages at diagnosis are about 50 years of age, which is earlier than other common cancers, as shown in Fig. 2. From the results of this study, oral cancer had a large average EYLL (14.00 years) and subtotal of EYLL (49,671 years), and breast cancer also had a large subtotal of EYLL (43,633 years). Thus, we recommend that policymakers place the prevention of major causes of oral cancer, such as betel quid chewing, tobacco usage, and excess consumption of alcohol [26], at a higher priority. The screening program for breast cancer should be targeted to an earlier age group, such as the 40 to 49 years of age group, to possibly save more life years.
Although we have used the best national data currently available in Taiwan, the study still had some limitations that need to be addressed before wide adoption for outcome evaluation. The first limitation of the method was the uncertainty regarding the stability of excess hazard in the extrapolation period. Because the cancer-related excess hazard is unlikely to be exactly constant throughout the extrapolation period, a certain degree of prediction error is unavoidable [10]. In spite of the uncertainty, our semiparametric method avoids the large deviations in long-term projections seen with the parametric model, such as under the Weibull distribution, with the advantage of an input of information from the life table of the background general population. Even if the assumption of a constant excess hazard between the cancer and reference populations may not hold, the method used the median of slopes near the end of the follow-up, which was generally the least biased in the extrapolation [9,10,14]. Excluding those cancers with a low censoring rate, i.e., <25%, for which there is usually less need for a long period of extrapolation, the relative biases were usually <5.0%. The second limitation was that the extrapolation method required an assumption of premature mortality, which does not hold for skin cancer, and is therefore, slightly less accurate. Third, the lifetime extrapolation is based on current and prior experiences, such as life tables; however, it is clear that such a method could easily underestimate the actual survival of future cancer populations because it does not consider the active development and adoption of newer technologies for cancer diagnosis and management. Thus, our estimation of lifetime survival of cancer patients may be a conservative one, while the EYLL could easily be overestimated. Finally, because LE is also a function of comorbidity, disability, and cancer stage, in addition to age and cancer type [27], the current estimate provides only a rough estimation of the average loss of LE. It may be possible, in future studies, to stratify the cancer cohorts into subcohorts based on more available data on the stage of cancer, and/or other comorbidities, to improve the accuracy of the survival estimates. For example, because more than one-half of the patients with prostate cancer in Taiwan were detected at advanced ages and earlier stages based on the Cancer Registry Annual Report (1999–2004) [28], the frequent comorbidity and mixing of different stages in the same cohort may make the extrapolation of survival rates less accurate. Furthermore, if the data regarding quality of life at each duration to date for cancer could be collected, they could also be integrated with the survival curves to obtain the quality-adjusted LE [10,12,21,29], which could serve as the basis for outcome evaluation in cost–utility analysis.
Regarding the choice between semiparametric and parametric methods, one disadvantage of semiparametric methods is that they are less efficient than parametric methods. Therefore, the standard errors of the Weibull model were generally smaller than those of the Monte Carlo method, as shown in Table 2, indicating a trade-off between bias and efficiency for the two methods. In fact, the Monte Carlo method is generally less biased except for two cancers, skin and prostate, of which the assumption of premature mortality might be violated. Moreover, there is a general tendency of underestimation for the Weibull model, as the relative biases are all accompanied with a negative sign. In general, one would consider the efficiency of estimation only if the relative biases for different methods are very close or similar. Thus, we recommend the Monte Carlo method whenever the assumption of premature mortality seems to hold in extrapolation of survival curves for cancer.
In conclusion, by incorporating information from the life table of the general population, estimation using the logit survival ratio extrapolation method is a robust approach to calculating the lifetime survival of cancer patients, as based on national data. The estimation of average EYLL provides a quick overview of an individual's LE after diagnosis and potential loss of life due to a specific type of cancer, as well as being helpful in the outcome evaluation for cancer treatment and prevention. To communicate the cancer risk with a lay person, this would seem to be much more understandable than simply giving the 5-year survival rate or cumulative survival and could also be used directly to empower people to engage in proactive prevention. The subtotal of EYLL represents the greatest quantity that society could possibly save by the prevention of the cancer. In the future, the method could be integrated with quality of life data for the comparative assessment of the outcomes of cancer patients under different treatment protocols or different health-care plans for people to judge the competitiveness [11,12,30].
Supplementary material for this article can be found on http://www.ispor.org/publications/value/ViHsupplementary.asp.
Source of financial support: Two grants, one from the Bureau of Health Promotion at the Department of Health, Taiwan (DOH94-HP-1801) and another from the National Health Research Institute, Taiwan (NHRI-EX94–9204PP).




