Discrete-Event Simulation Applied to Analysis of Waiting Lists. Evaluation of a Prioritization System for Cataract Surgery
ABSTRACT
Objectives: To outline the methods used to build a discrete-event simulation model for use in decision-making in the context of waiting list management strategies for cataract surgery by comparing a waiting list prioritization system with the routinely used first-in, first-out (FIFO) discipline.
Methods: The setting was the Spanish health system. The model reproduced the process of cataract, from incidence of need of surgery (meeting indication criteria), through demand, inclusion on a waiting list, and surgery. “Nonexpressed Need” represented the population that, even with need, would not be included on a waiting list. Parameters were estimated from administrative data and research databases. The impact of introducing a prioritization system on the waiting list compared with the FIFO system was assessed. For all patients entering the waiting list, the main outcome variable was waiting time weighted by priority score. A sensitivity analysis with different scenarios of mean waiting time was used to compare the two alternatives.
Results: The prioritization system shortened waiting time (weighted by priority score) by 1.55 months (95% CI: 1.47 to 1.62) compared with the FIFO system. This difference was statistically significant for all scenarios (which were defined from a waiting time of 4 months to 24 months under the FIFO system). A tendency to greater time savings in scenarios with longer waiting times was observed.
Conclusions: Discrete-event simulation is useful in decision-making when assessing health services. Introducing a waiting list prioritization system produced greater benefit than allocating surgery by waiting time only. Use of the simulation model would allow the impact of proposed policies to reduce waiting lists or assign resources more efficiently to be tested.
Introduction
Computer simulation techniques have allowed the introduction of modeling methodologies that analyze complex systems through virtual experimentation to assess the impact of interventions in health services. Discrete-event simulation, or queuing theory, is a well-known technique in operations research, and has mainly been developed in the context of military research and manufacturing systems. In the medical setting, Markov models and decision trees have been used extensively despite their limitations in reproducing health-care problems accurately. Discrete-event simulation is gaining popularity because of its flexibility in representing real systems by taking into account patient characteristics and the scarcity of resources present in health services provision [1,2].
Study of needs and demand for health services is important because substantial unmet needs are observed. The gap between needs and services provision may be too great to be resolved, but models that assess the impact of changes on the amount of resources used or the impact of health policies on the management of need and demand are useful in decision-making [3].
Cataracts, or lens opacity, is an important health problem because it is the major cause of blindness worldwide [4]. Moreover, its treatment (surgical extraction of the lens and insertion of a calibrated intraocular lens) is one of the most frequent surgical procedures and its use has increased in the last few years [5]. In developed countries, the prevalence of cataract is high, especially among the elderly [6]; thus, the volume of need and demand for surgery is too great for current supply, and waiting lists arise. The result of delayed surgery in developed countries is visual disability associated with moderate to low levels of visual acuity; however, in less developed countries, delayed surgery may lead to blindness.
The Spanish health-care system provides universal coverage. Cataract patients are referred by their family physician to the primary health-care ophthalmologist and then to the hospital. In 2003, cataract surgeries in the private sector represented less than 10% of overall cataract surgeries because mutual or private health insurance companies do not cover the cost of the intraocular lens.
Recently, several governments have considered the need to prioritize patients on waiting lists for elective surgery, which would modify the principle of first-in, first-out (FIFO), i.e., prioritization according to waiting time [7–11]. Indeed, prioritization is based on the fact that the need for surgery differs in patients with appropriate surgical indication and introduces levels of need. In the specific context of elective surgery, several interventions may be tested. We focused on prioritization of cataract surgery waiting lists to illustrate the potential of discrete-event simulation to reproduce a health-care system and to allow hypothetical interventions to be assessed without intervening in the real system. Waiting lists reflect a situation in which scarcity causes competition for resources and entries to and exits from the waiting list follow a stochastic law. Treating waiting lists as a queue allows patients to be prioritized and the impact of the time waited related to the level of need for surgery to be quantified. In Spain, a project has recently been developed (before the study presented here) to work on prioritization criteria for cataract surgery [12–14] and knee and hip replacement [12,13,15]. By using the conjoint analysis technique [16], a prioritization system was obtained including clinical (visual impairment and recovery probability), functional (difficulty in performing activities of daily living and ability to work) and social (have someone to look after the patient and be a caregiver) criteria. The general population, patients and relatives, clinical specialists and related health professionals were involved in the development of the prioritization system. The prioritization system showed acceptable validity and reliability in establishing priority for surgery. Possible scores range between 0 and 100, higher scores representing greater need. The highest weighted criterion was visual impairment, followed by limitation in performing activities of daily living. The Department of Health requires that this prioritization system be applied. Nevertheless, a guaranteed waiting time of less than 6 months has been established in Catalonia and waiting times have decreased.
The simulation model was used to compare this prioritization system with the FIFO system, which represents the current management of waiting lists, ordered according to time waited. Several previous experiences have taken advantage of simulation to assess prioritization of demand [17–20] and assessment of needs in health services [21–23].
The objective of the present article was to outline the methodology used to build a discrete-event simulation model as an aid to decision-making in the context of a health system with limited resources. Specifically, the method was applied to assess needs and prioritization of waiting lists for cataract surgery. The methods section shows the steps used to construct and implement the model and the results section includes some illustrative results according to the objective of comparing waiting list strategies. The final section includes discussion of the methodology and of the results obtained.
Methods
Conceptual Model
The conceptual model referred to individuals from the general population, aged 50 years or older, at risk of need for cataract surgery, and focused on demand in the health system of Catalonia (Spain).
Cataract was defined as visual impairment due to lens opacity, and criteria for surgical indication as any lens opacity and visual acuity of 0.5 or less. The need for cataract surgery was defined as the prevalence of need for surgery according to the indication criteria. The event “Incidence” was defined as the occurrence of need for surgery (Fig. 1). Need for surgery was divided into “Nonexpressed Need” (explained below) and “Expressed Need” or, equivalently, “Waiting List.” Because senile cataracts are mostly bilateral and clinical guidelines recommend surgery on one eye at a time, “Nonexpressed Need” was divided into “Nonexpressed Need First Surgery” for persons with bilateral cataracts and “Nonexpressed Need Second Surgery” for persons who had already undergone surgery in one eye (aphakic). “Nonexpressed Need” represented the population that, even if they met the indication criteria, would not be included on a waiting list for several reasons (no perception of need, inaccessibility, preferences). This category was calculated by subtracting the number of patients on the waiting list from the number of prevalent cases. The event of expressing need (demand) was considered equivalent to the following process: an individual meeting indication criteria requests surgery in the public sector, he or she is indicated for surgery, assigned a priority score by an ophthalmologist and is included on a waiting list of the health system. Persons included on a waiting list were considered to have requested surgery. Moreover, because 24.7% of the inhabitants of Catalonia have double health-care coverage [24], the activity of the private sector for cataract surgery was taken into account (state “Private Sector”). Individuals may request surgery in the private sector after requesting surgery in the public sector and waiting for some time, or they may request surgery directly in the private sector, depending on their preferences. Figure 1 shows the flow chart for the conceptual model, which also includes the state of “Death.”
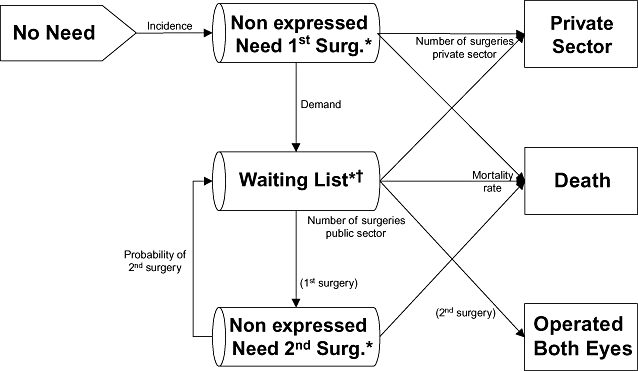
Conceptual model. *Prevalence of need is divided among these 3 states. †Patients on the waiting list have the priority score as an additional attribute.
The model included the following assumptions: 1) incident cases had bilateral cataracts (because cataract is an age-related disease); 2) patients did not improve (they remained the same or worsened) unless they underwent surgery; 3) there was no return from the private sector to the public sector waiting list [25,26]; 4) demand depended on supply capacity; 5) patients were operated on one eye at a time.
Importantly, the component “Waiting List,” which was implemented as a queue, included the waiting list management discipline (according to FIFO or to the prioritization system).
Parameter Estimation
Once the conceptual model has been described in detail, data must be analyzed to obtain distributions for times to events and for attributes to be randomly assigned to entities (in our case, the entities represent persons meeting the indication criteria for cataract surgery and most attributes depend on age and sex). The parameterization of the model also includes the initial state, that is, how many entities (prevalent cases of need) are included in each of the components of the model (“Waiting List” and “Nonexpressed Need” for first and second surgery) and the value of their attributes.
The model's parameters were estimated from several sources, including administrative and research databases (Table 1). Data from similar settings were used when data from the study's setting were unavailable. Because this was a continuous-time model, the parameters for transitions between states were estimated as distributions of time to an event. Moreover, the possible changes in parameters related to supply and demand through the 5-year time horizon were taken into account and models including time were used to update some parameters at the beginning of each month. Table 1 shows a list of the parameters with their sources of information and their estimations for the current scenario.
| Parameter | Source | Value |
|---|---|---|
| Related to initial state | ||
| Nonexpressed Need first surgery backlog | NLES & Census data | 318,752 |
| Nonexpressed Need second surgery backlog | NLES & Census data | 81,585 |
| Waiting list backlog | Waiting lists register | 19,586 |
| Proportion of patients waiting for second eye surgery | Pilot test | 0.209 |
| Static parameters | ||
| Incident cases per month | NLES & Census data | 5695.04 |
| Number of cases operated in the private sector per month | Hospital Discharge Minimum Data Set | 383.47 |
| Proportion of cases of the waiting list who switch to the private sector | Pilot test | 0.0613 |
| Top limit for waiting list contents (self-regulation) | Opportunistic | 0.15 |
| Increase in priority score (points) | Pilot test & Field work | 2.57 |
| Time between revisions of priority score (months) | Pilot test & Field work | 1 |
| Mortality hazard (Gompertz function) | Mortality register & Census data | |
| Male | 0.000018286 e0.102374095 age | |
| Female | 0.00000124309 e0.129010243 age | |
| Dynamic parameters | ||
| Number of surgeries per month | Hospital Discharge Minimum Data Set | s(t) = 2350 + 380 ln(60 + t)* |
| Probability of 2nd eye surgery | Hospital Discharge Minimum Data Set | p(t) = 0.2805 + 0.0645725 ln(27 + t)† |
| Number of bilateral cases entering the waiting list per month | Waiting lists register | d(t) = sec(t − 1) − 1266.5‡ |
- * From 3905.85 at t = 0 to 4169.25 at t = 60.
- † From 0.493 at t = 0 to 0.568 at t = 60.
- ‡ From 2632.96 at t = 0 to 2899.56 at t = 60.
- Census data and Mortality register data were obtained from the National Institute of Statistics (INE).
- Waiting lists register data and Hospital Discharge Minimum Data Set were obtained from the Catalan Department of Health.
- NLES: North London Eye Study data, obtained from the authors; Pilot test: Pilot test of the introduction of the prioritization system in the clinical practice.
To divide the initial distribution of prevalent cases of need for surgery among the states of “Nonexpressed Need” and “Waiting List,” prevalence estimates of cases of bilateral cataract and aphakia (surgery in one eye) with need for surgery were projected onto the Catalan population. All calculations were stratified by age and sex. The distributions of age conditioned on sex were obtained through the projected prevalent cases. As there are no primary data on the prevalence of cataracts in Catalonia or Spain, the database of the North London Eye Study, a population-based study of the prevalence of eye diseases in North London [27], was used and prevalence was calculated by age and sex. The number of inhabitants in Catalonia by age and sex was obtained from the 2001 census. In the absence of incidence data, prevalence was also used to estimate incidence through the Podgor and Leske method [28]. The prevalence of cataracts was smoothed by adjusting a logistic model by age and sex and incidence was obtained. The number of incident cases was calculated by projecting the estimated incidence by age and sex onto the population. The time between two consecutive incident cases was generated through an exponential distribution, as this is a plausible distribution for interarrival times that occur at a constant rate. The census population and the number of deceased by age and sex, obtained from the 2001 mortality register, were used to estimate the mortality hazard function (h(t)). The model that has been shown to be most appropriate for adjusting the mortality rate by age is a Gompertz [29] function. Thus, the mortality hazard function by age was modeled through: h(age) = α·e(βage). Different functions were adjusted for men and women. An approximate density function was calculated as the difference in probability of the cumulative distribution function, evaluated at 1-month intervals. The density function for lifetime represents the probability of a person aged x years of dying at age x + t given he or she has survived until age x + t − 1 [30].
To calculate surgery rates and the probability of second-eye surgery, the Hospital Discharge Minimum Data Set of the Catalan health service was used. The procedures of cataract extraction (according to the International Classification of Diseases, 9th Revision, Clinical Modification [ICD9-CM]) from 1999 through 2003 were included. The database structure allowed the public and private sectors to be differentiated and bilateral surgeries to be identified. The time between two successive surgeries was generated through an exponential distribution based on the monthly number of surgeries in the public sector. The model that best fitted the increase in the number of surgeries through time was a linear model using a logarithmic scale for time to predict future numbers of surgeries from December 2003 onwards. The model was specified as: y = β0 + β1ln(t). Patients with one or two surgeries within the period were identified. The probability of second-eye surgery was calculated as the proportion of second-eye surgeries divided by that of first-eye surgeries. This was calculated monthly and a logarithmic-increasing time-trend was also estimated. The time between two successive surgeries was generated through an exponential distribution based on the monthly number of surgeries in the public sector.
Because no tendency was observed between 1999 and 2003, the number of surgeries in the private sector was estimated through the monthly mean of the previous two available years. An exponential distribution was used for the time between successive surgeries. The probability of a patient in the state of “Waiting List” switching to the private sector was calculated by using the available data on reasons for leaving the waiting list. Dependence on the time spent waiting or priority was considered for the transition probability from “Waiting List” to “Private Sector”; however, neither the number of surgeries in the private sector, nor the proportion of individuals coming from the public waiting list was modified according to the waiting time of the public sector.
The number of monthly entries to the waiting list in 2003 and the number of patients waiting in June 2004 were obtained from the health system's Waiting Lists Register. The time between successive inclusions on the waiting list was modeled with an exponential distribution based on the average number of bilateral patients entered on the waiting list per month (aphakic patients entered the waiting list according to the probability of second-eye surgery). The number of inclusions on the waiting list increased through time by the same amount as the number of surgeries, that is, demand depended on supply but supply did not depend on demand. A delayed dependence on the increase in the number of surgeries was introduced. Moreover, to reproduce the natural mechanisms of waiting list regulation, a reduction factor was applied when the number of patients on the waiting list exceeded a specific proportion of the initial number. The reduction factor was expressed as a percentage and was calculated as the inverse of the square root of the current number of patients on the waiting list minus the maximum permitted plus one. This factor was applied to both the entries for first and second-eye surgeries and caused the waiting list to have a steady volume.
A pilot study to assess the introduction of the prioritization system in clinical practice [31] was used to calculate the distributions of priority score at entry to the waiting list and the proportions of patients with bilateral cataract and aphakia on the waiting list. The priority scores of patients entering the waiting list showed wide variability. The mean priority score was 34.7 points with a standard deviation of 23.2 points. Observed scores covered the whole range (from 0 to 100) both for patients with bilateral cataract and for those with aphakia. Different empiric distributions of the priority score were used for bilateral and aphakic patients because a statistically significant difference was found between means. Moreover, for patients entering the waiting list twice, a correlation of 0.55 was forced between priority scores by simulating the priority score for the second eye taking into account the value for the first eye. Because the prioritization system includes clinical and functional criteria that may worsen over time, the increase in priority score through time waited was evaluated. Priority score was assessed on entry to the waiting list and after a waiting time ranging between 3 and 9 months in patients included on the waiting list of a teaching hospital (Hospital de l'Esperança). The relationship between time waited and the increase in priority score could not be adjusted through a regression model, but was modeled as an increase of 18 points (the mean increase) divided by 7 (the mean time, in months, between assessments) each month.
Simulation Model
The conceptual model (Fig. 1) was implemented using the package SIMUL8 Release 10 standard edition (SIMUL8 Corporation, Boston, MA) [32]. The time units were months and the simulation horizon was 60 months (5 years). This horizon was considered sufficiently long to see how the system evolved without compromising the accuracy of the estimations that were unchanged throughout the time horizon. Lifetime horizon was not considered as appropriate because we were interested in analyzing need and utilization from the point of view of the health system, not in analyzing the evolution of individual patients. The initial state of the simulation imitated the current volume of patients in each state (that is, prevalent cases with the age and sex structure divided among the two states of “Nonexpressed Need” and “Waiting List”). These states were implemented as queues. SIMUL8 was linked to Excel to import and export data and to provide a more user–friendly interface.
Each patient had a set of attributes that included age, sex, priority for first- and second-eye surgery (when applicable), “type” of patient (bilateral or aphakic) and lifetime (conditioned by age and sex). The priority scores were generated when a patient entered the waiting list and took into account whether the patient had bilateral cataracts or aphakia. Under the prioritization system, the order of the patients on the waiting list according to priority score was updated each time that a new patient entered the waiting list and after updating the priority scores of the patients waiting the longest. Exits from the waiting list to surgery in the public or the private sector corresponded to patients at the front of the queue (with the highest priority score or the longest waiting time, according to the discipline). Moreover, the transition after surgery in the public sector depended on the “type” of patient.
Validation
The simulation model was verified during its implementation by checking the correctness of programming (debugging). Pilot runs were used to verify that simulated values corresponded to their respective input distributions.
Validation of the model should be checked, when possible, by quantitative statistical comparisons between the results of the model and real results obtained from observation of the system. Nevertheless, health-care systems may be too complex to allow reliable calculation of the result of interest and sometimes calculation may be even impossible. Additionally, even if we had obtained a sample of real-world data, it would have been autocorrelated, precluding the use of classical statistical techniques. In these cases, other types of validation, applying qualitative comparisons based on expert opinion, can be used to assess validity understood as the usefulness of the model to achieve the established objectives.
Due to the complexity of the system we modeled, the diversity of the sources, and the quality of the information used to estimate the parameters, the face validation [33] method was employed. This method consisted of presenting, in a systematic way, known results of the real system and the results of the model to a panel of 12 experts that included epidemiologists, statisticians, health economists, sociologists, ophthalmologists, and experts in simulation.
A sensitivity analysis was performed using a fractional factorial design of experiments, including all the input parameters and the uncertainty of their estimations.
Analysis of Results
Because waiting list management alternatives were compared and the impact of the time waited depended on the level of need, we considered that the waiting time weighted by priority score was the appropriate measure to use. This measure allowed waiting times to be compared between alternatives by taking into account how those times were assigned according to each patient's priority score. The mean weighted waiting time was calculated for all the patients (eyes) that entered the waiting list during the 5-year simulation horizon (those operated on in the public sector, those still waiting at the end of the simulation, those who switched to the private sector from the waiting list, and those who died while waiting); the weight was calculated as the priority score of each patient divided by the sum of the priority scores of all patients that entered the waiting list. Thus, the difference between the two alternatives can be interpreted as the time, weighted by need, saved or lost with one alternative versus the other (i.e., the prioritization system vs. the FIFO discipline). This comparison allows the benefit associated with the prioritization system to be quantified in terms of need-adjusted lifetime, giving greater importance to the time waited by patients with greater need, while lower weighted waiting times mean that patients with higher need waited for less time.
Our model was analyzed as a terminating simulation, i.e., one with a predetermined time horizon. To analyze the results, the fact that simulation is a sampling experiment obtained from a computer should be taken into account. If the executions start from the same initial conditions (representative of the real system), data from independent executions of the model can be analyzed simply. Confidence intervals may be constructed on a sample of means of independent runs and time plots of some variables are helpful to analyze the system's dynamic behavior [34].
Sample size (the number of replicates to be simulated) must be calculated to obtain sufficient precision for the result of interest. To do this, a first estimation of the variability of the result must be obtained from a trial with a small number of runs. Through the fixed-sample-size procedure [34], we calculated the number of replicates needed to obtain a prespecified precision of 0.1 months in estimating the difference in waiting time weighted by priority score between the FIFO and the prioritization system disciplines. First, we ran 10 replicates of the model and a standard deviation of 0.21 months was obtained. This value was used to calculate the sample size [34] with a 95% confidence level and resulted in 20 replications. These confidence intervals were based on Student's t distribution because, although the distribution function for some waiting times was clearly right-skewed, the assumption of normality could be accepted because the waiting time means of each run were calculated in sufficient numbers of patients [34].
A warm-up period should be considered in some simulation models to remove the initial transitory state from the analyses. No warm-up period was considered, but the time waited by patients in the initial waiting list backlog was not used in the calculation of the average waiting times. Outcomes of the evolution of the system through the 5-year simulation horizon included the mean priority score of all patients on the waiting list.
A two-way sensitivity analysis was performed by forcing different waiting time scenarios (by changing the number of patients on the initial waiting list backlog) crossed with waiting list discipline. The different mean waiting times for patients undergoing surgery under the FIFO discipline were used to identify scenarios for comparison. Sensitivity analyses were based not only on the waiting time weighted by priority score, but also on calculating thresholds of priority score according to eventual warranty times. These thresholds meant that all patients with higher priority scores underwent surgery in less than the warranty time.
Results
Validation
The panel of experts compared the results of the model under the FIFO discipline and the prioritization system and considered the model's results to be valid and credible. The mean waiting time of 4.5 months (95% confidence interval [CI] from 4.2 to 4.7) was considered similar to the value of 4.38 months obtained from the health authority (CatSalut, Barcelona, October 2004) for the mean waiting time for cataract surgery in Catalonia, June 2004. The results were also validated by changing the waiting list discipline from FIFO to the prioritization system to assess the impact of the prioritization system on the behavior of the system, and the resulting differences were in the expected direction. The panel of experts considered all results as valid and credible and the model as useful in achieving the established objectives.
Moreover, the results of the sensitivity analysis to assess the impact of the uncertainty of the parameter estimations showed that waiting time weighted by priority score was insensitive to the variations in all the parameters and their first-order interactions.
Main Results
Trials for each waiting list discipline included 20 independent runs. Each run processed around 7630 individuals, representing 1% of the simulated population. Regardless of the waiting list discipline, the number of patients in the “Nonexpressed Need” states and the overall number of patients with need for surgery (also including patients on the waiting list) increased across the 5-year time horizon (data not shown). “Nonexpressed Need for First-Eye Surgery” represented 75.9% of overall initial need, “Nonexpressed Need for Second-Eye Surgery” represented 19.4% and the “Waiting List” represented 4.7%. After 5 years, overall need increased by 85,530 patients (a 20% increase): “Nonexpressed Need for First- and Second-Eye Surgery” increased by 14% and 50%, respectively. The number of patients on the waiting list was stable throughout the 5-year period, as expected due to the regulation mechanism. Of the 152,780 patients who died during the 5-year period, 6020 (3.9%) did so while waiting for surgery. Of the 23,425 patients who underwent surgery in the private sector, 1340 (5.7%) switched from the public waiting list (data not shown).
For the comparison between the FIFO and the prioritization system, simulation of the current scenario of the waiting list for cataract surgery (data from 2003 and 2004) showed that the mean waiting time for patients undergoing surgery in the public sector was 4.5 months (95% CI from 4.2 to 4.7). When applying the prioritization system, the time was reduced to 3.8 months (95% CI from 3.6 to 4.0) (Table 2). Nevertheless, patients still waiting at the end of the simulation under the prioritization system had a mean waiting time of 5.8 months (95% CI from 5.4 to 6.1), which was 3.5 months longer than that for the FIFO system (95% CI from 3.2 to 3.8). Under the prioritization system, the waiting time of patients who died while waiting was 3.2 months longer (95% CI from 2.9 to 3.6) than that for the FIFO system (Table 2).
| Number of patients* | FIFO | Prioritization system | Paired differences† | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | % | Mean | 95% CI | Mean | 95% CI | Mean | 95% CI | |
| Operated patients | 2246.70 | 89.6 | 4.48 | [4.23 to 4.73] | 3.84 | [3.64 to 4.03] | 0.65 | [0.55 to 0.74] |
| Patients still waiting | 186.25 | 7.4 | 2.21 | [2.01 to 2.42] | 5.75 | [5.39 to 6.12] | −3.54 | [−3.84 to −3.24] |
| Patients who switched to the private sector | 13.40 | 0.5 | 4.71 | [4.49 to 4.93] | 4.19 | [3.64 to 4.73] | 0.52 | [−0.21 to 1.25] |
| Patients who died while waiting | 60.20 | 2.4 | 2.19 | [2.07 to 2.31] | 5.41 | [5.10 to 5.72] | −3.22 | [−3.55 to −2.90] |
- * Results shown for the FIFO discipline only, as they were similar between disciplines.
- † The mean shown is the mean of the 20 differences between mean waiting time under FIFO and mean waiting time under the prioritization system using the same chain of random numbers.
- Comparison between waiting list disciplines.
- FIFO, first-in, first-out.
Simulation always started with the same initial conditions. Nevertheless, although the mean priority score was stable for the FIFO discipline (around 34 points), it substantially decreased when the prioritization system was applied (Fig. 2). After 12 months, this score stabilized at around 10 points with little variability.
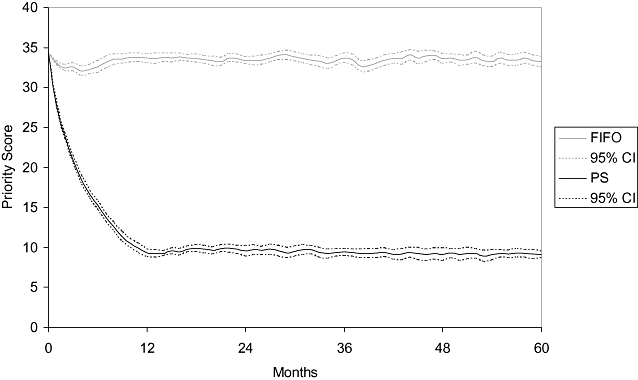
Evolution of the mean priority score of patients on the waiting list by waiting list discipline. FIFO, first-in, first-out; PS, prioritization system.
Sensitivity Analysis
For all scenarios of waiting time for surgical patients under the FIFO discipline, the waiting time weighted by priority score under the prioritization system was lower (Table 3). The time saved with the prioritization system was around 2 months. Moreover, the longer the unweighted waiting time, the greater the benefit (Table 3). Figure 3 shows the benefit of applying the prioritization system for scenarios shown in Table 3 and other scenarios. Figure 3 also shows that, the higher the unweighted waiting time, the higher the benefit of applying the prioritization system.
| Mean unweighted waiting time | Paired differences in waiting time | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Operated patients | Patients still waiting | Patients who switched to the private sector | Patients who died while waiting | Mean waiting time weighted by priority score | Waiting time weighted by priority score | ||||||
| FIFO | Prioritization system | FIFO | Prioritization system | FIFO | Prioritization system | FIFO | Prioritization system | FIFO | Prioritization system | Mean | 95% CI |
| 4.48 | 3.84 | 2.21 | 5.75 | 4.71 | 4.19 | 2.19 | 5.41 | 3.76 | 2.22 | 1.55 | [2.17 to 2.38] |
| 6.96 | 5.80 | 3.28 | 6.98 | 7.22 | 6.02 | 3.26 | 6.21 | 5.43 | 3.71 | 1.72 | [1.50 to 1.97] |
| 11.31 | 8.96 | 5.15 | 8.85 | 11.60 | 10.51 | 5.00 | 8.16 | 8.00 | 6.07 | 1.94 | [2.23 to 2.56] |
| 15.53 | 12.04 | 6.99 | 10.37 | 15.83 | 13.00 | 6.84 | 9.28 | 10.27 | 8.12 | 2.15 | [2.87 to 3.26] |
| 19.70 | 14.99 | 8.70 | 11.90 | 20.01 | 14.36 | 9.14 | 10.42 | 12.36 | 9.91 | 2.45 | [4.47 to 4.88] |
- FIFO, first-in, first-out.
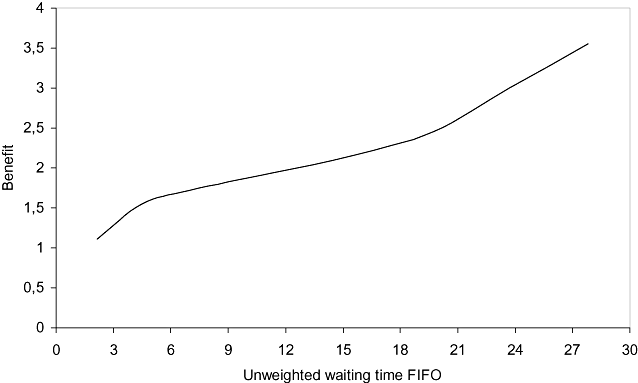
Benefit of introducing the prioritization system by unweighted waiting time of operated patients under the FIFO system. FIFO, first-in, first-out.
Figure 4 shows the minimum priority score needed to undergo surgery under an eventual warranty time. That is, for the current scenario, patients with a priority score (at entry to the waiting list) higher than 40.0 points underwent surgery in less than 3 months. Conversely, patients with less than 12.4 points underwent surgery after 12 months. For scenarios with higher waiting times, the profile was similar, but the threshold of priority indicating the highest waiting times increased. For example, for a warranty time of 6 months, the minimum priority score increased from 27.9 points for the current scenario (4.5 months of waiting time) to 72.5 points for the scenario with 19.7 months of waiting time (Fig. 4).
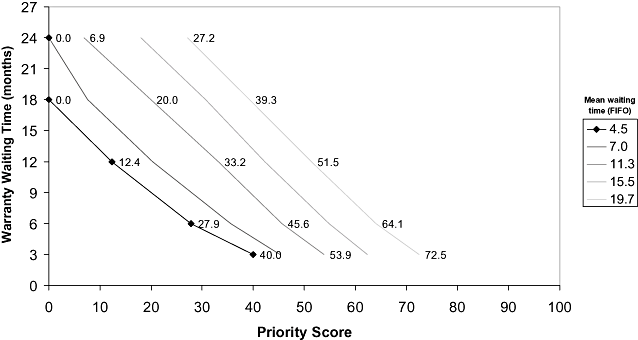
Minimum priority score (x-axis) to achieve an eventual warranty time (y-axis). Diamonds represent the results of the model in the scenario with current data. FIFO, first-in, first-out.
Figure 4 also shows which patients benefited from the prioritization system and which patients were penalized. For the current scenario, patients with priority scores higher than 27.9 points (56.8% of patients, according to the priority score distribution) had a waiting time of less than 6 months, although those with less than 12.4 points (23.6% of patients) waited for 12 months or longer. In all scenarios, patients with priority scores higher than 40 points (37.1%) had lower waiting times than the reference waiting time for the FIFO system.
Discussion
We used the example of cataract surgery waiting lists to illustrate that a discrete-event simulation model is useful in making decisions when assessing health services. The model described allows several factors that are commonly used separately by decision-makers to be integrated into a decision model.
When assessing the impact of interventions on health outcomes, the standard technique to represent the natural history of diseases is Markov models. Although Markov models ran as microsimulations can incorporate discrete events, our study shows the advantages of applying a full discrete-event simulation approach to analyze our specific problem in two key components of modeling. On the one hand, discrete-event simulation supplies model flexibility to represent epidemiological and care delivery events. On the other hand, the model output is more versatile.
When modeling health services, discrete-event simulation is a more flexible technique than Markov models. Although Markov models represent changes in patients' health status, discrete-event simulation has few restrictions and allows transparent representation of the underlying model, enabling all the characteristics of the real system (including facilities and resources) to be represented. Consequently, transitions may represent several kinds of action or changes. Moreover, although changes in the system are discrete, they occur on a continuous time scale, as each action is scheduled to happen at a time value drawn from a continuous random distribution. In discrete-event simulation, the patient is an explicit entity, characterized by attributes that can change through time or according to the patient's experience. Queues are a specific tool of discrete-event simulation. In our case, they allowed waiting list management to be modeled, which could not have been performed with Markov models.
The output of discrete-event simulation models is not only survival (or time spent) by state as in Markov models, but also the number of incident cases, population prevalence in the different states, and their evolution through the simulation horizon, among others. Moreover, the analyses can be stratified by groups because labels are attached to cases. This feature overcomes the Markovian assumption.
In our application to the analysis of needs and demand for health services, an important feature of discrete-event simulation models is that they enable the prevalence of states with different health needs to be calculated over time in the whole population, allowing cost-utility analyses that take survival of the prevalent population into account. In contrast, Markov models analyze patients in the initial cohort only [35]. The key point when assessing health services is the prevalence of diseases and the availability and consumption of resources through time. The capacity of resources to meet needs and demand is limited and queues may arise. Waiting lists are a particular type of queue: patients are not physically queuing for the service, but they are waiting to receive a specific health service.
The model shows that the prioritization system was more beneficial than allocating surgery by waiting time only. Given the same number of surgeries, the prioritization system distributes waiting time according to priority; thus, patients with greater need wait less time. The mean benefit was 1.54 months less waiting time, weighted by priority. Moreover, the benefit of the prioritization system was greater for scenarios with longer waiting times. Currently, in Catalonia, as in other countries such as the United Kingdom, Canada or Sweden, a waiting-time guarantee of 6 months has been established and waiting times have been reduced. This reduction was reflected in our model. Nevertheless, our results were useful to show the benefit of prioritization for longer waiting times and that waiting lists are an artifact because a substantial volume of unmet needs remain in the population in addition to waiting lists, even though cataract surgery is a highly cost-effective procedure. The guarantee time of 6 months was complied with in 56.8% of patients in our model (those with priority scores higher than 27).
Although the prioritization system was more beneficial at a population level, patients with lower priority scores had excessive waiting times. For example, patients with fewer than 12 points (23.6% of patients) would wait for 12 months or longer. Unless supply is increased, an excess waiting time of 1 year would exclude these patients from the system. Moreover, in our model, if the priority score had not been increased to take into account worsening of clinical criteria over time, these patients would never undergo surgery.
Importantly, the results of a discrete-event simulation model are only estimations that depend on the input values and, thus, on their quality. The principle of “garbage in-garbage out” applies. Moreover, the clarity and transparency of these models may lead their credibility to be overestimated, because models are always simplifications of reality.
The relationships among some parameters of the cataract model were difficult to assess, and several mathematical functions were defined to approximate their behavior within the system. These functions were used to simulate parameter relationships, such as the relationship between surgery and demand, and self-regulation of the waiting list. These relationships were not based on real data because the information needed to estimate them comes from sources with different levels of robustness and data must be compared over time. The results of estimating the parameters and the proposed relationships among them were also validated by a panel of experts and were considered as reasonable. Moreover, we checked through the multivariate sensitivity analysis that variations in these two parameters had little effect on the model's outputs.
Conclusions
Our study demonstrates that discrete-event simulation is a valid and robust tool to represent the flow of patients between need, waiting lists and surgery, considering that elective surgery is a scarce resource for which patients compete and that prioritization systems may be applied to assign surgeries according to need. Moreover, discrete-event simulation can be used as a tool for shared decision-making as patients can be presented with the expected waiting time according to their priority score and can decide whether they are willing to accept it.
Introducing a prioritization system for waiting lists was more beneficial than allocating surgery by waiting time only (FIFO) and the proportion of patients penalized with excessive waiting times was small and had low priority. In view of current data on waiting lists, testing the prioritization system through the simulation model allows definition of a (justifiable) level of need over which the public health system can appropriately meet demand. This alternative would make waiting list management transparent, would ensure that the waiting time of the most disabled patients is extremely reduced, and may be a less costly and more sustainable option than shock plans. Our results suggest that, under the prioritization system, patients with a priority score of 40.0 points or higher (37.13% of patients) would have a waiting time of 3 months or lower although those with a priority score of 27.9 points or lower (43.2% of patients) would wait 6 months or more.
The work performed for cataract surgery will be used in our future research to build models for other elective surgeries, such as arthroplasty and bariatric surgery, in which supply does not meet demand, and to perform cost-utility analyses of distinct interventions.
Source of financial support: This work was supported by grants from the Catalan Agency for Health Technology Assessment and Research (CAHTA) (089/07/2000) and the Fondo de Investigación Sanitaria (FIS) (PI020365, RedIRYSS [G03/202, PI052403] and RCESP [C03/09, PI052302]).
Supplementary material for this article can be found at: http://www.ispor.org/publications/value/ViHsupplementary.asp




