The Impact of Lifecycle Events on Women's Labour Force Transitions: A Panel Analysis*
The author would like to thank Thomas F. Crossley, Alice Nakamura, Yuri Ostrovsky, Michael Veall and anonymous referees for valuable comments, as well as Tina Hotton and James Chowan, at the Statistics Canada Research Data Centers (RDC) at the University of Toronto and McMaster University, for assistance with the data.
Abstract
This panel study explores the impact of different lifecycle events on women's labour force transitions. We explicitly investigate whether the factors that determine entry into the labour force differ from the factors that determine withdrawal from the labour force. The results demonstrate that labour force transitions – entry and withdrawal – occur more frequently among young women. The event of childbirth is strongly associated with labour force withdrawal, while marital separation and reductions in family earnings are strongly associated with labour force entry. Moreover, labour force transition probabilities are more sensitive to income-reducing events than to income-supplementing events.
I Introduction
In this paper, women's labour force transitions (LFTs) and their association with ‘trigger events’ over their lifecycle are examined. Included is an explicit investigation of both aspects of women's LFTs: labour force entry and withdrawal. We assess the factors which determine such transitions.
In Canada, during the 1970s and 1980s, the labour market participation of women grew steadily from < 50 per cent up to 70 per cent; throughout the 1990s it remained at around 75 per cent. This is lower than the relevant prime-age men's participation rates of over 90 per cent (Beaudry & Lemieux, 1999; Chaykowski & Powell, 1999). This leads us to question whether the women's labour market participation rate has reached a long-run steady-state level. If the labour force participation rate is constant at its long-run steady-state level in each period, it equals the labour force entry rate divided by the total LFT rate, which is the sum of the labour force entry and withdrawal rates.1 An explanation of female participation needs to relate their lifecycle behaviour to LFT.
Women's labour market participation is particularly interesting, because their lifecycle events are different to those of men. Obviously, giving birth is unique to women; there remains a likely perception of childcare and housework being women's work within the family. A US study (Akerlof & Kranton, 2000) shows that when men do all the market work, they contribute about 10 per cent to the housework, but as their share of outside work falls, their share of housework rises to no more than 37 per cent.2 An identity model of behaviour illustrates how the identity of ‘woman’ influences the decision to participate in the labour market (Akerlof & Kranton, 2000). Gender is not an identity solely of choice; it is an assigned identity associated with different ideal physical attributes and prescribed social behaviour. The identity model shows that if women's work at home enhances their identity, they will have weaker labour force attachment than do men.
Considering the more conventional neoclassical model of female labour supply, a married woman conditions her labour supply response on her husband's labour supply decision. Thus, a woman's labour force participation is more elastic, with respect to changes in wage and non-labour income and other fixed costs, than is that of the primary male earner. However, whether to treat women as secondary earners in families is an inconclusive argument.3 Therefore, in more recent years, a married woman's labour supply is more commonly based on unitary or non-unitary (non-cooperative or collective model) approaches to household behaviour. Departing from arguments concerning which models are more appropriate to explain married women's labour supply, it is observable that women's LFTs generally occur more frequently than do those of men. An example would be their transitions associated with childbearing and childcare. A woman who once withdrew from the labour force because of caring for children may re-enter after her children have grown up.
This study explicitly investigates some dynamics of women's labour market participation (labour force entry and withdrawal) and the association of those transitions with experiencing lifecycle events. The results provide a complementary summary of the degree to which transitions are associated with particular events. In addition, we investigate the symmetry assumption in our labour supply model by examining labour force entry and withdrawal separately.
Symmetry (or asymmetry) in labour supply behaviour is a relatively unexplored aspect of women's labour supply. Long and Jones (1980) questioned whether the hypothesised effects of wage, income and family size changes on labour force activity are reversible. The conventional labour supply theory assumes symmetric labour supply responses to changes in (relative) prices of choice variables. Therefore,Long and Jones (1980) attempted to find evidence of symmetry in married women's labour supply with a panel survey (National Longitudinal Survey of women 30–44) in 1967 and 1969, but their results suggest that the labour force participation relationship supported by cross-section data are not reversible. While Long and Jones focus on wage changes, our study gives a weight to women's experiencing lifecycle events. We attempt to find evidence of asymmetry in women's labour supply with respect to contrary events.
In the first part of this study we estimate the probability of entry and withdrawal from the labour force conditional on experiencing trigger events such as marriage, divorce, childbirth, and the financial consequences of changes in the employment status of other household members. In the process, we estimate (i) unconditional probabilities of entry and withdrawal from the labour force, (ii) unconditional probabilities of each trigger event, (iii) probabilities of LFTs conditional on lifecycle events, and (iv) probabilities of lifecycle events conditional on LFTs. Such statistics give us descriptive measures of the relative importance of various lifecycle events in LFTs. We can use them to construct a (descriptive) decomposition of the fraction of all transitions accounted for by each of the different lifecycle events. This methodology is adopted from Jenkins and Schluter (2003).4 We extend their analysis by estimating random effects panel probit models of LFTs with a set of control variables including trigger events, age, regional dummies, educational dummies and a correction term for sample selection bias. A two-step sample selection correction method is employed for a dynamic panel data model with a binary outcome, as suggested by Orme (1997).
The study results show that childbirth is strongly associated with labour force withdrawal, while marital separation and decreases in family earnings are strongly associated with labour force entry. In addition, LFT probabilities are more sensitive to income-reducing events than to income-supplementing events. Assessing the importance of various events as root causes of transitions may have important policy applications. Recognising the relevance of these dynamic dimensions has implications for policy making related to women's labour market participation.
The paper proceeds as follows. Section II summarises what we know about women's labour market participation in relation to lifecycle events, and it discusses a potential pitfall in the interpretation of findings from common empirical models. Section III describes the data, with explanations of the key definitions that are the basis of this exploratory analysis. Section IV examines trigger events and LFTs with three types of statistics. Section V presents the multivariate methods and reports the estimation results. Section VI contains concluding remarks.
II Empirical Literature on Women's Labour Market Participation and a Potential Pitfall in the Interpretation of Findings
Most of the literature gives attention to particular events of women's lifecycles such as childbirth and changes in marital status. First, it is not surprising that the effects of childbearing and childcare on women's labour market activities have received a lot of research attention. Nakamura and Nakamura (1992), Blundell et al. (1998) and Barrow (1999) report significant negative consequences of childcare on women's labour force participation. Yet Gunderson (1998) has shown that the magnitude of the negative effect of childcare on women's labour supply has declined over time. Carrasco (2001), Chun and Oh (2002) and Francesconi (2002) find strong negative effects from fertility for women's labour force participation. Dex et al. (1998) and Gutierrez-Domenech (2005) find that after giving birth, education is an important factor for the continuity of employment. Regardless of the countries studied, childbearing/caring has a negative impact on women's labour market attachment. In particular, empirical evidence shows that changing work patterns surrounding the birth of children (especially first births) provide crucial information on individual heterogeneity of the preference for work. Some studies demonstrate that women who return to work shortly after the birth of a first child are considerably more likely to be persistent workers throughout their lives (Mott & Shapiro, 1983; Shapiro & Mott, 1994). In this study we examine labour force withdrawals associated with childbirth and care, and labour force entries associated with becoming free from childcare responsibilities. This paper also contributes to the findings on exits by assessing the relative importance of childbearing/caring compared to other events.
The effect of marital status on women's labour supply is another strand of research. Johnson and Skinner (1986, 1988) are interested in the effect of divorce on women's labour supply. They find a positive association and Johnson and Skinner (1986) suggest that women who subsequently divorce increase their labour supply and labour force participation in the three years prior to separation. In their later study, Johnson and Skinner (1988) examine the correlation between increased labour supply among separated women and changes in observable characteristics (e.g. falls in family income and rises in the woman's after-tax wage rate). They address the problem that unobservable factors related to marital status are also important determinants of the change in women's labour force participation. In addition, Nakamura and Nakamura (1996) study the dynamics of women's labour supply using the US panel data from the 1969–1979 waves of the Michigan Panel Study of Income Dynamics (PSID) and they provide a descriptive analysis of the dynamics of labour supply. They find significant impacts from divorce and childbirth on women's labour supply, not only in the event year but also in the year prior to it. In this study, the impact of marriage and separation on women's LFTs is examined taking into account the financial consequences of these events.
As an empirical strategy, probit (or logit) models for a binary outcome are generally used to estimate women's labour market participation, conditional on characteristics such as marital status, children, education, and family income. However, using such models systematically imposes that labour force entry and withdrawal (which are responses to changes in wages, income, and fixed costs) are symmetric responses. Suppose Yt and Yt–1 are (time) independent, where Y is a binary outcome and a function of Xs, then the marginal effects of a change in X on the binary outcome of Y are symmetric.5 The systematic symmetry occurs not only with the probit model. It is imposed with other static state models, Yt = f(Xt), like the logit and linear probability models. Most studies simply focus on one side of labour force response (in most cases labour force participation or entry). However, they implicitly (or explicitly) regard the labour force response to changes in wages, income and fixed costs as symmetrical. This creates a potential pitfall in the interpretation of the existing empirical literature. For instance, the magnitude of the marginal effect of a decrease in family income on labour force entry is assumed equal to the magnitude of the marginal effect of an increase in family income on labour force withdrawal. In the panel perspective, this study explicitly investigates whether the factors which determine entry into the labour force differ from the factors which determine withdrawal. This approach also allows us to identify asymmetries in women's labour force entry and withdrawal responses to changes in lifecycle events.
III Data and Definitions
Data are used from survey reference years 1993–2000 of the Canadian Survey of Labour and Income Dynamics (SLID). The SLID is a longitudinal survey with a rotating panel structure. The first wave of the first panel was in 1993. The original sample of respondents was followed and interviewed at 1-year intervals for the next 6 years. The second 6-year panel began in 1996. Each wave comprises two separate interviews. One is a labour interview in January; the other is an income interview in May.6 For both interviews, the reference year is the previous calendar year. There are two reasons to use SLID here. First this panel study of female labour supply in Canada fills a gap in the literature. Second, from an international perspective the SLID data have some unique attractive features. SLID has more accurate income data compared with the self-reported (surveyed) income data of other panel studies. There are two potential sources of income data for SLID: respondents can either report income sources during the interview or grant permission to Statistics Canada to obtain their tax file data from Canada Revenue Agency for the purpose of the survey. In effect, well over half of SLID's income data comes directly from Canada Revenue Agency (63 per cent in 1994 and over 80 per cent in 2000). In addition, SLID provides clear information regarding marital status, and the child's relationship to the woman. The ‘marital status’ variable includes seven coding categories: married (legal marriage), common-law, separated, divorced, widowed, single (never married) and separated common-law. Own birth children can be separated from step, adopted and foster children. Accurate income and demographic information is critical in reducing measurement errors in estimates of LFT rates, especially when investigating asymmetric responses to changes in income and other demographic variables.
The sample panel for analysis includes 14 5987 women aged 19–65: 7025 from the first SLID panel (1993–1998), and 7573 from the second SLID panel (1996–2000). For the descriptive analysis in Section IV, the women are first grouped into four age categories (19–30, 31–40, 41–50, and 51–65) based on their ages in each year. This is because the incidence of lifecycle events associated with LFTs varies significantly with age. Second, the data are pooled from all 8 years. The events of interest are infrequent, particularly those associated with LFT in certain age groups, but pooling the data over all 8 years provides statistically reliable results. Later, for the multivariate analysis in Section V, the sample is treated as panel data to estimate the random effects probit model.
Definitions of LFTs and trigger events are based on the same two consecutive years. A woman's LFT is an entry if she is a participant in period t conditional on being a non-participant in the previous period t – 1. Conversely, a woman's LFT is a withdrawal if she is a non-participant in period t conditional on being a participant in the previous period t – 1. SLID has a variable for annual labour force status, but the coding of the variable makes it difficult to identify an individual's annual labour force status. LFTs are therefore defined on the basis of changes in monthly labour force status for September of each year.8
Consider demographic events associated with women's LFTs. Demographic trigger events related to labour force withdrawal are marriage, childbirth, and having preschool children. Demographic trigger events related to labour force entry are divorce (separation, or loss of spouse) and reduced responsibility for children, as a child enters school and leaves preschool. Applying the same rule, trigger events are defined on the basis of changes between two consecutive survey reference years. For example, a woman is counted as newly married, including common-law relationships, if her marital status changed from single to married between 2 years. Some ‘lifecycle event’ derived variables provided by Statistics Canada are utilised. For example, there is a family life event flag indicating whether a person became a (first) birth parent during the survey reference year. Also, childbirth is separated from other reasons for living with children in each reference year (e.g. step, adopted and foster). In addition, changes in the composition of a household because of marriage or separation may also have important financial consequences for women. A woman may have access to a higher income via income sharing with a working partner because of (re)marriage. Divorce, separation, or death may result in the loss of a spouse's income. We attempt to decompose the effect on LFTs of marriage and divorce into the impact of the trigger event itself and the impact of its financial consequences.
Another key class of trigger events is changes in the financial conditions of the family. Women's LFTs are precipitated by events such as changes in family members’ labour market attachment, or changes in family earnings. Women's labour supply, known as the added worker effect, may be an important aspect of the household consumption-smoothing response to a husband's job displacement (Seitchik, 1991; Stephens, 2002). Examples of income-supplementing events include an unemployed spouse or any other family member getting a job, and an already-employed spouse or any other member's increasing labour earnings (e.g. a change in job, promotion, or working longer hours) or other income. Examples of income-reducing events include job loss by an employed spouse or any other family member, and a decrease in the earnings of spouses or of other family members.9
It is quite difficult to define other family members’ labour market activity reliably in the data. Therefore, we define two different trigger events, relating to changes in earnings (and income) of other family members, as proxies indicating the occurrence of financial events in a woman's lifetime. First, we compute other family members’ earnings by subtracting the woman's earnings from the family's total earnings; then the event is counted if other family earnings increase or decrease by 20 per cent or more between two consecutive years. The threshold of 20 per cent is chosen to ensure that transitory earnings variations are not counted as events. These changes in family earnings, however, may also correspond to changes in the number of earners in the family. To separate out the effect of those changes, it might be desirable to have more disaggregated measures of the financial events affecting these households. Here, an event of ‘pure earnings change’ denotes differences in family earnings that occur without an increase or decrease in the number of earners, not including the woman, in the family.
IV Trigger Events and LFTs
Suppose that there is a set of mutually exclusive trigger events j = 1, ... , J, and that all labour force withdrawal (LFW) decisions occur because of one such event.
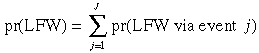
Then, among those women with a chance of withdrawal from the labour force between one year and the next, the proportion who withdraws is indicated by the sum of the proportions of women who withdraw in association with each of the different events.
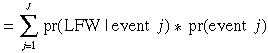
By the rules of joint probability, each term on the right-hand side can be rewritten as the product of the probability of withdrawal, conditional on event occurrence, and the probability of each event.
Similarly, the probability that women with a likelihood of entry will enter the labour force because of a set of mutually exclusive trigger events k = 1, ... , K can be related to the probabilities of each event and the probability of labour force entry (LFE), conditional on event occurrence:
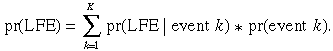
In this approach, we also consider the potential for a LFT associated with each event for the average woman. The relative importance of events is then summarised directly by considering the fraction of all transitions that are accounted for by each of the different events: pr(event j | LFE) for each event j, and pr(event k | LFE) for each event k. Using Bayes’ Rule, these statistics are related to each other by the following: for labour force withdrawal,
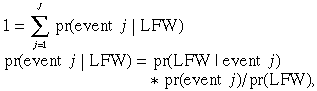
and for labour force entry,
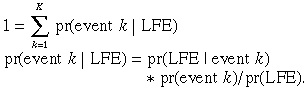
In the next subsection, LFT rates are examined using three types of statistics: first, the incidence of each trigger event: pr(event); second, the probability of LFTs conditional on experiencing such events: pr(LFT | event); and finally, the fraction of all transitions10 accounted for by each event: pr(event | LFT). The focus is on the short-term effects of these events on LFTs; both are measured over an interval of 1 year.
(i) LFTs and the Prevalence of Trigger Events by Age Group
Table 1 shows the annual rates of women's labour force entry and withdrawal broken down by age group. For all women, the average entry rate is 18.1 per cent and the average withdrawal rate is 6.6 per cent.11 Transition rates are substantially different across age groups, and this supports a separate examination of LFTs and trigger events in each group. Women aged between 19 and 30 have higher rates of both labour force entry and withdrawal than the rest of the sample. Their entry rate is 19.8 per cent higher than the average entry rate for women, and the withdrawal rate is 2.6 per cent higher than the average withdrawal rate for women.
| (Pooled data – September) | ||||||
|---|---|---|---|---|---|---|
| Age category | Participation rate | Standard Error | Entry rate | Standard Error | Withdrawal rate | Standard Error |
| All | 0.7372 | 0.0016 | 0.1810 | 0.0029 | 0.0660 | 0.0011 |
| 19–30 | 0.7700 | 0.0034 | 0.3793 | 0.0092 | 0.0921 | 0.0031 |
| 31–40 | 0.8135 | 0.0025 | 0.2696 | 0.0072 | 0.0508 | 0.0017 |
| 41–50 | 0.8121 | 0.0026 | 0.1878 | 0.0067 | 0.0425 | 0.0016 |
| 51–65 | 0.5121 | 0.0037 | 0.0504 | 0.0026 | 0.1096 | 0.0034 |
- Note: The statistics are based on pooled data. Total number of women at risk of labour force entry is 5840 and total number of women at risk of labour force withdrawal is 12 350.
Table 2 exhibits the incidence by age group of each trigger event in the analysis. We first consider being newly married, newly living with preschool children12 and giving birth as demographic events associated with labour force withdrawal. The incidence of these events falls with age. Regarding demographic events associated with labour force entry, women aged 19–30 have the greatest likelihood of becoming separated from their partner, while women aged 31–40 are most likely to become free from the care of preschool children. As discussed in Section III, changes in overall family earnings and income, and changes in family earnings and income without changes in the number of earners, are financial events associated with LFT. For the incidence of ‘pure’ increases or overall increases in family earnings and income, there are no notable differences across age groups except for a slight decrease in the oldest age group. The incidence of both ‘pure’ decreases and overall decreases in family members’ income and earnings is slightly higher in the youngest and oldest age groups relative to the middle groups. Over all age groups, family earnings increase without changes in the number of earners rather than from added earners. Roughly half of the incidence in falling family earnings is because of losing earners in the family.
| Age category | 19–30 | 31–40 | 41–50 | 51–65 | ||||
|---|---|---|---|---|---|---|---|---|
| Pr(event) | Standard error | Pr(event) | Standard error | Pr(event) | Standard error | Pr(event) | Standard error | |
| Withdrawal | ||||||||
| Newly married | 0.0602 | 0.0025 | 0.0168 | 0.0010 | 0.0093 | 0.0008 | 0.0061 | 0.0009 |
| Newly having pre-school children | 0.0536 | 0.0024 | 0.0189 | 0.0011 | 0.0015 | 0.0003 | – | – |
| Child birth | 0.0944 | 0.0031 | 0.0423 | 0.0016 | 0.0013 | 0.0003 | – | – |
| Family earnings increased | 0.2454 | 0.0046 | 0.2095 | 0.0032 | 0.2236 | 0.0034 | 0.1877 | 0.0043 |
| Family total income increased | 0.2246 | 0.0044 | 0.1908 | 0.0031 | 0.2170 | 0.0034 | 0.1868 | 0.0043 |
| Family pure earnings increased | 0.1623 | 0.0039 | 0.1538 | 0.0028 | 0.1365 | 0.0028 | 0.1263 | 0.0036 |
| Family pure total income increased | 0.1477 | 0.0038 | 0.1395 | 0.0027 | 0.1345 | 0.0028 | 0.1307 | 0.0037 |
| Entry | ||||||||
| Newly separated | 0.0203 | 0.0027 | 0.0140 | 0.0019 | 0.0074 | 0.0015 | 0.0030 | 0.0006 |
| Free from pre-school children | 0.0278 | 0.0031 | 0.0806 | 0.0044 | 0.0197 | 0.0024 | – | – |
| Family earnings decreased | 0.1841 | 0.0073 | 0.1204 | 0.0052 | 0.1507 | 0.0061 | 0.1720 | 0.0045 |
| Family total income decreased | 0.1777 | 0.0072 | 0.1167 | 0.0052 | 0.1345 | 0.0059 | 0.1497 | 0.0042 |
| Family pure earnings decreased | 0.0766 | 0.0050 | 0.0741 | 0.0042 | 0.0736 | 0.0045 | 0.0822 | 0.0033 |
| Family pure total income decreased | 0.0773 | 0.0050 | 0.0770 | 0.0043 | 0.0642 | 0.0042 | 0.0813 | 0.0033 |
- Notes: Labour force transitions and events each refer to changes between years t– 1 and t–: We cannot report the probabilities because of the small number of observations.
(ii) Trigger Events and their Association with the LFTs of Women
Table 3 reports the estimated probabilities of LFTs conditional on having experienced each trigger event.13 Regarding labour force withdrawal, the probabilities associated with childbirth or recently living with preschool children are relatively large for the age groups 19–30 and 31–40. Marriage is actually associated with a reduced probability of labour force withdrawal in the age group 19–30. The probability of withdrawal conditional on ‘newly married’ (6.9 per cent) is significantly smaller than the unconditional probability of withdrawal (9.2 per cent). The financial events of increases in pure family earnings do not raise or lower the probability of labour force withdrawal. Yet financial changes, either with or without an increase in the number of earners, have a more significant impact on the labour force withdrawal of women than the event of recent marriage for the age group 19–30. The probability of withdrawal associated with a pure total income increase (10.9 per cent) is greater than the probability of withdrawal associated with the experience of recent marriage (6.9 per cent).
| Age category | 19–30 | 31–40 | 41–50 | 51–65 | ||||
|---|---|---|---|---|---|---|---|---|
| Rate | Standard error | Rate | Standard error | Rate | Standard error | Rate | Standard error | |
| Withdrawal | ||||||||
| Pr(withdrawal) | 0.0921 | 0.0031 | 0.0508 | 0.0017 | 0.0425 | 0.0016 | 0.1096 | 0.0034 |
| Newly married | 0.0690* | 0.0109 | 0.0593 | 0.0144 | 0.0360 | 0.0158 | 0.2157* | 0.0576 |
| Newly having pre-school children | 0.1929* | 0.0181 | 0.1053* | 0.0176 | – | – | – | – |
| Child birth | 0.2226* | 0.0144 | 0.0969* | 0.0113 | – | – | – | – |
| Family earnings increased | 0.0998 | 0.0064 | 0.0578* | 0.0040 | 0.0420 | 0.0035 | 0.0895* | 0.0072 |
| Family total income increased | 0.1031 | 0.0068 | 0.0560 | 0.0042 | 0.0409 | 0.0035 | 0.1112 | 0.0080 |
| Family pure earnings increased | 0.1052 | 0.0081 | 0.0574 | 0.0047 | 0.0484 | 0.0047 | 0.0884* | 0.0088 |
| Family pure total income increased | 0.1087* | 0.0086 | 0.0566 | 0.0049 | 0.0486 | 0.0048 | 0.1139 | 0.0096 |
| Entry | ||||||||
| Pr(entry) | 0.3793 | 0.0092 | 0.2696 | 0.0072 | 0.1878 | 0.0067 | 0.0504 | 0.0026 |
| Newly separated | 0.3860 | 0.0645 | 0.4259* | 0.0673 | 0.2800 | 0.0898 | – | – |
| Free from pre-school children | 0.3974 | 0.0554 | 0.2774 | 0.0254 | 0.1791 | 0.0468 | – | – |
| Family earnings decreased | 0.4352* | 0.0218 | 0.3348* | 0.0219 | 0.2148 | 0.0182 | 0.0586 | 0.0067 |
| Family total income decreased | 0.4589* | 0.0223 | 0.3341* | 0.0223 | 0.2188 | 0.0193 | 0.0796* | 0.0083 |
| Family pure earnings decreased | 0.3442 | 0.0324 | 0.3474* | 0.0282 | 0.2280 | 0.0265 | 0.0570 | 0.0096 |
| Family pure total income decreased | 0.3502 | 0.0324 | 0.3311* | 0.0274 | 0.2156 | 0.0279 | 0.0785* | 0.0112 |
- Notes: Labour force transitions and events each refer to changes between years t – 1 and t–: We cannot report the probabilities because of the small number of observations. We test the statistical significance of the differences between unconditional transition probability and transition probability conditional on each trigger event (* statistically significant at the 5 per cent level).
Turning to labour force entry, among women within the age group 19–30 experiencing a new separation 38.6 per cent entered the labour force; among women in the age group 31–40 experiencing this event 42.6 per cent entered the labour force. Marital separation is significantly associated with an increased probability of labour force withdrawal in the age group 31–40. For other events, about one-third of women aged 19–40 experiencing the event of being free from the care of preschool children enter the labour force. Decreases in family earnings are associated with a high likelihood of entry into the labour force for all age groups. Particularly in the middle age group, the probabilities of entry conditional on having experienced a recent separation are larger than the probabilities of entry conditional on any other event. Moreover, the event of a new separation itself, not the financial consequences of the event, is relatively more important to a woman's decision to enter the labour force. For the age group 31–40, although both events of separation and family pure earnings (total income) decreases are significantly associated with an increased probability of labour force entry, the marginal effect of being newly separated on labour force entry is 15 per cent. On the other hand, the marginal effect of family pure earnings decreases on labour force entry is 8 per cent.14
As pointed out earlier, the factors that determine withdrawal from the labour force may differ from the factors that determine entry. Overall, the estimates reported in Table 3 show that the effect of changes in family earnings on women's labour force participation decisions is not symmetric. Their participation decisions are more sensitive to income-reducing events than to income-supplementing ones. For example, over 30 per cent of women within the age groups 19–30 and 31–40 who experience a decrease in family earnings enter the labour force, while less than 10 per cent of women experiencing an increase in family earnings withdraw from the labour force. It implies that we need to be careful in interpreting estimates from conventional methods on labour force participation (for example probit and logit). Asymmetry is more dramatic when comparing the probability of labour force withdrawal conditional on the event of becoming newly married, with the probability of labour force entry conditional on the event of becoming newly separated (7 per cent compared to 39 per cent among women aged 19–30; 6 per cent compared to 43 per cent among women aged 31–40). The event of a new separation has a much larger impact on the labour supply decision of women than the event of becoming newly married. Separation is actually associated with an increased probability of labour force entry in all age groups, while being newly married is significantly associated with a reduced probability of labour force withdrawal in the age group of 19–30.
Table 4 reports the incidences of events conditional on LFTs. It is interesting that a large fraction (more than 60 per cent) of all labour force entries is not associated with any of the events considered in this study: labour force entries may occur for a more diverse set of reasons than we considered. Across all age groups, the largest share of all entries is associated with a decrease in family earnings. In addition, consideration of the proportion of all labour force withdrawals accounted for by each event suggests that the main reasons for withdrawal from the labour force are less diverse than the reasons for labour force entry noted in Table 4. The events of childbirth and increases in family earnings associated with labour withdrawal represent relatively large fractions (22.8 and 26.6 per cent) of all labour force withdrawals in the youngest age group. On the other hand, for the other age groups, increases in other family earnings (for example job gains) account for a large share of all labour force withdrawals: about 23.8, 22.1 and 15.3 of labour withdrawals in the age groups 31–40, 41–50 and 51–65, respectively.
| Age category | 19–30 | 31–40 | 41–50 | 51–65 | ||||
|---|---|---|---|---|---|---|---|---|
| Rate | Standard error | Rate | Standard error | Rate | Standard error | Rate | Standard error | |
| Withdrawal | ||||||||
| Newly married | 0.0451 | 0.0072 | 0.0196 | 0.0048 | 0.0078 | 0.0035 | 0.0120 | 0.0036 |
| Newly having pre-school children | 0.1122 | 0.0110 | 0.0391 | 0.0068 | – | – | – | – |
| Child birth | 0.2280 | 0.0147 | 0.0807 | 0.0095 | – | – | – | – |
| Family earnings increased | 0.2659 | 0.0154 | 0.2384 | 0.0149 | 0.2214 | 0.0164 | 0.1533 | 0.0119 |
| Family total income increased | 0.2512 | 0.0151 | 0.2103 | 0.0142 | 0.2088 | 0.0161 | 0.1895 | 0.0130 |
| Family pure earnings increased | 0.1854 | 0.0136 | 0.1736 | 0.0132 | 0.1554 | 0.0144 | 0.1019 | 0.0100 |
| Family pure total income increased | 0.1744 | 0.0133 | 0.1553 | 0.0127 | 0.1538 | 0.0143 | 0.1358 | 0.0113 |
| Entry | ||||||||
| Newly separated | 0.0207 | 0.0044 | 0.0222 | 0.0046 | 0.0110 | 0.0041 | – | – |
| Free from pre-school children | 0.0291 | 0.0052 | 0.0829 | 0.0086 | 0.0188 | 0.0054 | – | – |
| Family earnings decreased | 0.2113 | 0.0125 | 0.1495 | 0.0111 | 0.1724 | 0.0150 | 0.2000 | 0.0212 |
| Family total income decreased | 0.2150 | 0.0126 | 0.1446 | 0.0109 | 0.1567 | 0.0144 | 0.2366 | 0.0226 |
| Family pure earnings decreased | 0.0695 | 0.0078 | 0.0955 | 0.0091 | 0.0893 | 0.0113 | 0.0930 | 0.0154 |
| Family pure total income decreased | 0.0714 | 0.0079 | 0.0945 | 0.0091 | 0.0737 | 0.0103 | 0.1268 | 0.0177 |
- Notes: Labour force transitions and events each refer to changes between years t– 1 and t–: We cannot report the probabilities because of the small number of observations.
V Multivariate Analysis of LFTs
The analysis is extended by estimating a random effects probit model of women's LFTs with a set of control variables including trigger events, age, regional dummies, educational dummies, and a correction term for sample selection bias.
Assuming the existence of a latent continuous dependent variable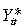 
which is defined as 
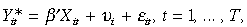where, Xit are explanatory variables, νiis the unobserved individual effects, ɛit ~ N(0, σ2), the non-observed latent variable 
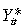and the observed binary outcome of Yit are related as follows: 
The main assumption of the random effects probit model is
(1) υi and Xi (Xit for all t) are independent and υi has a normal distribution,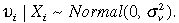 
Since the variance of the latent variable model is unity, the relative importance of the unobserved effect is measured as 
which is the proportion of the total variance contributed by the panel level variance component. These statistics lead to a simple test for the presence of the unobserved effects: the likelihood ratio test for the null hypothesis that ρ = 0. When ρ is zero, the panel level variance component is unimportant and the panel estimator is not different from the pooled estimator.
We turn to potential bias resulting from a problem with sample selection. In estimating the determinants of labour force withdrawal or entry, the group of women who have a possibility of withdrawing from the labour force, or who have a possibility of entering the labour force, is a non-randomly selected sample. On average, women in the risk set of labour force withdrawal have higher labour force participation rates; women in the risk set of labour force entry have lower labour force participation rates. This initial labour force state may be correlated with unobserved individual characteristics. To correct for such sample selection bias, we follow the method suggested by Orme (1997).15 First, an initial stage probit is estimated, which is a probit regression for labour force participation in the year the individuals are first observed.16 Then, a generalised residual (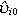
) is calculated from the initial stage probit and this is included as a regressor in the random effects transition probit. To summarise, the LFTit that equals one if individual i changes labour force status at time t: withdrawal or entry are modelled using a random effects probit:
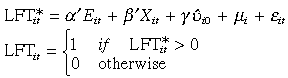(2)So that
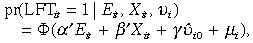
where 
is a latent dependent variable, Eit are trigger events,17 and Xit are demographic variables including age, age squared, regional dummies, level of education dummies, a current student dummy and a panel dummy. 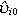is the generalised residual from the initial stage probit for labour force participation, µi ~ N(0, 1) is an (iid) individual random effect which is not correlated with an individual's initial observed labour force status,18 and ɛit is a (iid) error term having zero mean and known variance.
(i) Transition Probit Estimates
Initially 3831 women and 10 767 women are in the risk sets for labour force entry and withdrawal, respectively. To proceed appropriately with the sample selection correction method, multiple LFTs are not modelled for the same individual. Each woman is followed until she makes her first LFT (either entry or withdrawal). About 70 per cent of women provide more than 3 years of data: we observe 1735 entries (859 from the first panel and 876 from the second) and 2445 withdrawals (1234 from the first panel and 1211 from the second).
Tables 5 and 6 provide results from the random effects probits for labour force withdrawal and entry, respectively. The overall stories from the estimates are consistent with Table 3, which shows the probabilities of LFT conditional on trigger events. In Table 5, women giving birth and experiencing an increase in pure family earnings are significantly more likely to withdraw from the labour force. Childbirth has the greatest effect on the probability of labour force withdrawal. Table 6 reveals that women experiencing a separation or a decrease in pure family earnings are significantly more likely to enter the labour force. Separation has the largest effect on the probability of labour force entry. On the other hand, the events of being newly married (Table 5), and of ‘becoming free from the childcare of preschool children’ (Table 6), do not have significant effects on women's labour force withdrawal and labour force entry, respectively. Sample selection correction is important in both labour force withdrawal and entry estimates. The coefficient on the generalised residual from the initial stage probit is statistically significant in both transition probits. On the importance of allowing for the individual random effect, the likelihood ratio test for the null hypothesis that ρ = 0 is strongly rejected in the probit for labour force entry,19 but the likelihood ratio test for the null hypothesis that ρ = 0 could not be rejected for labour force withdrawal. In the case of withdrawal, it may be that the sample selection correction captures most of the unobserved individual heterogeneity.20 Finally, there is no finding of significant difference between the panels with respect to labour force entry; however, there is a positive and significant coefficient on the panel dummy in the labour force withdrawal probit.
| Variable | Coefficient | Standard error |
|---|---|---|
| Age | –0.1305*** | 0.0090 |
| Age squared | 0.0017*** | 0.0001 |
| Married | –0.0850 | 0.0750 |
| Childbirth | 0.6804*** | 0.0458 |
| Pure earnings increase | 0.05998** | 0.0285 |
| Region-Atlantic | 0.0824*** | 0.0299 |
| Region-QUE | 0.0249 | 0.0312 |
| Region-Prairies | –0.0552* | 0.0299 |
| Region-BC | 0.0058 | 0.0384 |
| Graduated high school | –0.1280*** | 0.0397 |
| Non-university postsecondary certificate | –0.2220*** | 0.0379 |
| University certificate or Bachelor's degree | –0.3163*** | 0.0500 |
| More than Bachelor | –0.4240*** | 0.0717 |
| Full-time student | 0.4907*** | 0.0325 |
| Panel 2 | 0.0612*** | 0.0205 |
| Generalized residual | 0.2410*** | 0.0836 |
| Constant | 0.6992*** | 0.2138 |
| N | 43371 | |
| σu | 0.0009 | |
| ρ | 8.32e-07 |
- Notes: The estimates of the random effects probit are not different from those of pooled probit since the likelihood ratio test for the null hypothesis that ρ = 0 could not be rejected. *** Significant at 1 per cent; ** significant at 5 per cent; * significant at 10 per cent.
| Variable | Coefficient | Standard error |
|---|---|---|
| Age | 0.1004*** | 0.0177 |
| Age squared | –0.0018*** | 0.0002 |
| Separation | 0.3603** | 0.1513 |
| Free from childcare | –0.0652 | 0.0877 |
| Pure earnings decrease | 0.1220* | 0.0653 |
| Region-Atlantic | –0.1256** | 0.0573 |
| Region-QUE | –0.1534*** | 0.0586 |
| Region-Prairies | 0.0869 | 0.0614 |
| Region-BC | 0.0781 | 0.0820 |
| Graduated high school | 0.2754*** | 0.0691 |
| Non-university postsecondary certificate | 0.6048*** | 0.0696 |
| University certificate or Bachelor's degree | 0.9585*** | 0.1071 |
| More than Bachelor | 1.2956*** | 0.1799 |
| Full-time student | 0.0634 | 0.0627 |
| Panel 2 | 0.0423 | 0.0395 |
| Generalized residual | 0.4592*** | 0.1102 |
| Constant | –1.8029*** | 0.2863 |
| N | 12 904 | |
| συ | 0.5817 | 0.0566 |
| ρ | 0.2528 | 0.0368 |
- Note: *** Significant at 1 per cent; ** significant at 5 per cent; * significant at 10 per cent.
VI Conclusions and Discussion
At the beginning of this paper we argued that a panel perspective on the LFTs of women would provide a better understanding of their labour market participation. If women's labour force participation rates remain constant over time, an explanation of this needs to relate their behaviour to LFT, because labour force participation results from labour force entry and withdrawal. Thus the primary determinants of those transitions could be different. This exploratory analysis specifically focuses on the association of women's LFTs with particular trigger events that occur in their lives.
Regarding methods, the probability of labour force entry and withdrawal is estimated as being conditional on trigger events such as marriage, separation, childbirth, free from childcare, and changes in the earnings of other household members. There is an explicit investigation of whether the factors that determine (re-)entry into the labour force differ from the factors which determine withdrawal. Subsequently, a random effects transition probit model is estimated to examine LFTs within a multivariate setting.
The results show that LFTs, not only entry but also withdrawal, occur more frequently among young women aged between 19 and 30. The event of childbirth is strongly associated with women's labour force withdrawal, while the events of separation and decreases in family earnings are strongly associated with women's labour force entry. Also, there are asymmetries in women's labour force entries and withdrawals with respect to contrary events. For example, these transitions are more sensitive to income-reducing events than to income-supplementing events. In Table 3, over 30 per cent of women within the age groups 19–30 and 31–40, who experience a decrease in family earnings, enter the labour force; <10 per cent of women experiencing an increase in family earnings withdraw from the labour force. Why do we see such asymmetric effects of changes in family earnings on women's labour force entry and withdrawal?
Work affects a person's utility in two ways. There is a direct effect derived from the activities and interactions associated with working itself. These direct effects can be positive, such as personal satisfaction from completing tasks, providing valued services, and social connections through work colleagues. They can be negative: frustration, anxiety, and stress associated with work. There is also the indirect (though often a primary) benefit from work: it provides income with which to purchase goods and services that increase a person's utility. In other words these are work incentives: self-achievement and financial well-being. Since the labour supply of a woman is conceivably more flexible than that of a primary earner in the family, we may observe how those two work incentives play their roles in women's labour supply decisions. Here, we observe an asymmetric response of women's labour force withdrawal and entry with respect to increases and decreases in family income. The magnitude from an increase in family income is smaller than the magnitude from a decrease in family income. Substantial increases in family income release a woman from her share of the family's financial burden; however, one is still motivated to work by an incentive of self-achievement because the value of her time for work is also high.21 Women's labour withdrawal, associated with family income increases, would be therefore less sensitive. Substantial decreases in the family's income threaten the financial well-being of a family. Women's labour force entry associated with income decreases would be more sensitive, even after taking into account the possibility of negative utility from working.
Also, the probability of entry conditional on becoming separated is larger than the probability of labour force withdrawal conditional on getting married. Indeed, recent marriage is actually associated with a reduced probability of labour force withdrawal, while separation is associated with an increased probability of labour force entry in the age group 19–30. These results may partially reflect asymmetric behaviour when women are faced with the financial consequences of separation. However, the emotional and sociological effects of separation are also important factors in determining women's labour force entry. The results show that the marginal effect of separation is larger than the marginal effect of pure income decreases on entry.
From the policy point of view, support for women's childbearing and caring is the most effective way to reduce women's labour force withdrawals. Baker et al. (2005) show that the availability of childcare has a positive effect on women's labour supply.22 Assisting women's roles in relation to children, especially infants and young preschool children is important to prevent women from leaving the labour market. The study shows that childbirth has the greatest effect on the probability of women's labour force withdrawal, and women are less likely to (re-)enter the labour force after their children have grown up.23 In addition, a childcare benefit has a negative income effect on women's work and makes the policy importance of women's willingness to continue working outside the home substantial.
As a last note, this study is an exploratory analysis of the LFTs of women. The observed asymmetric labour supply behaviour of women is of interest, but the shortcoming is that conventional labour supply models could not predict this asymmetric behaviour. Developing structural longitudinal labour supply models, in which asymmetric behaviour can be explained, would be good tasks for future research on women's labour supply patterns.
Footnotes
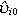(the correction term) and µi (the unobserved individual effects).
