Why Do the Rich Save More? A Theory and Australian Evidence*
We use confidentialised unit record data from the Household, Income and Labour Dynamics in Australia (HILDA) survey. The HILDA Project was initiated and is funded by the Commonwealth Department of Family and Community Services (FaCS) and is managed by the Melbourne Institute of Applied Economic and Social Research (MIAESR). The conclusions and views expressed in this paper are those of the authors and should not be attributed to either FaCS or MIAESR.
Abstract
We provide a theory to explain the existence of inequality in an economy where agents have identical preferences and have access to the same production technology. Agents consume a ‘health’ good which determines their subjective discount factor. Depending on initial distribution of capital the economy gets separated into different permanent-income groups. This leads to a testable hypothesis: ‘The rich save a larger proportion of their permanent-income’. We test this implication for savings behaviour in Australia. We find that even after controlling for lifecycle and health characteristics, higher permanent income is positively related with higher savings rates and better saving habits.
I Introduction
Household consumption and savings behaviour is an issue which remains at the heart of Macroeconomics. It is central to understanding the impact of tax and other government policies. It is also central to understanding the evolution of the wealth distribution. Researchers in this area have commonly used Friedman's (1957) permanent income hypothesis and Modigliani and Brumberg's (1954) lifecycle hypothesis as a theoretical framework to model consumption behaviour of households. These theories have spawned a large theoretical and empirical literature in macroeconomics. Hybrid theoretical models try to blend both permanent income and lifecycle motives to come up with a richer and more realistic theory of consumption. Empirical papers try to test whether the theoretical predictions of these models can be validated in the data.
In a recent paper, Dynan et al. (DSZ hereafter) (2004) show that with reasonable parametric specifications of the permanent income, the lifecycle and the hybrid models, it is impossible to reconcile with the savings behaviour in the USA. Using a variety of datasets, the panel study of income dynamics (PSID), the survey of consumer finances and the consumer expenditure survey, DSZ find, after controlling for lifecycle characteristics of the households, savings rates are increasing with permanent income.
In this paper, we propose a plausible theoretical channel which may explain savings heterogeneity in an economy. We study the role played by the rate of time preference of individuals, that is, the level of patience in determining their savings behaviour. The level of patience of an individual is an important aspect of her preferences. For example, if an agent is maximising welfare over two periods say t = 0 and t = 1, it is customary to represent her preference as
u(c0) + βu(c1),
where u(.) is the period utility function and c0, c1 are the level of consumption in periods 0 and 1. The parameter β ∈ (0, 1) is commonly referred to as the subjective discount factor or the level of patience. The level of patience is the weight given to future welfare in comparison to present welfare. A more patient individual (i.e. higher β) has a lower rate of time preference and therefore gives more importance to future welfare. Everything else remaining the same, she would save a larger proportion of her income. This enables her to accumulate more wealth over her lifetime in comparison to an impatient individual.
Differences in the rate of time preference across individuals can potentially explain persistence in inequality. Even if every individual has access to the same production technology, inequality could persist in an economy due to differences in the rate of time preference across individuals. The role of ‘rate of time preference’ in explaining inequality, however, has received relatively less attention in the theoretical literature.
In a standard permanent income model like Ben-Porath (1967), we allow the individual agents to choose their level of patience by consumption of a good which we interpret as the ‘health’ good. One possible interpretation of this could be that higher consumption of the ‘health’ good increases the probability of survival of an agent and makes her give more importance to future utility. The positive relationship between consumption and health has been well established in the development economics literature. Deaton (2003) reports a strong correlation between health status and income both across countries and within an economy. In USA, the probability of death at the age of 50 for both men and women is decreasing in family income. This suggests a particular channel through which income may affect the ‘rate of time preference’ of an individual. Smith (1999) also finds a strong relationship between economic and health status of households. While there have been empirical studies on the behaviour of savings rates across households, the theoretical work in this area is limited. For policy analysis, it is essential to have a theoretical model that explicitly models the behaviour of the ‘rate of time preference’. The theoretical model is necessary for an empirical purpose as well, because it helps identify the important causal relationship – do richer individuals save more or, more patient individuals save more and end up rich.
Our theoretical results show that even when agents in the economy are identical in terms of their preferences and have access to the same production technology there may be permanent income inequality in steady state. Also, richer agents save a larger proportion of their permanent income. Agents who consume more of the ‘health’ good are more patient and as such save more. This result is consistent with other empirical studies. In the PSID survey, Lawrance (1991) finds the ‘rate of time preference’ to be 3–5 percentage points higher for households with lower incomes than those with higher incomes. Controlling for race and education widens this difference even more.
We test the prediction of our model using the Household Income and Labour Dynamics in Australia (HILDA) dataset. As this dataset is fairly recent, we are forced to use an empirical strategy similar to DSZ. There have been empirical studies documenting the wealth distribution (Headey et al., 2005) and consumption inequality (Barrett et al., 2000) in Australia. However, to the best of our knowledge, this is the first study documenting the savings behaviour in Australia. We find strong evidence in favour of the theoretical implication of our model. After controlling for lifecycle characteristics of households, savings are increasing as households move up the permanent income quintiles. We also examine the impact of health status of households on their savings behaviour. For every proxy of the health status of a household, we find that the health status of the head of the household is positively and significantly associated with their savings behaviour.
The rest of the paper is organised as follows. The next section presents our model and we derive our basic results in Section III. In Section IV we explain our empirical strategy and provide details of our dataset in Section V. Our estimation results are in section VI and Section VII concludes.
II Model
(i) Production Technology
Consider an economy producing a single homogeneous commodity. Time is discrete and is indexed by t = 0, 1, 2, ... K. The economy consists of a continuum of infinitely lived agents who differ only in terms of their initial endowment of capital k0. Every agent is endowed with one unit labour time at each period however; they are able to accumulate capital by saving out of their income. The final good is produced using a standard neoclassical production technology
yt = F(kt, 1) ≡ f(kt),
where (kt, 1) denote the amount of capital and labour input employed by an agent in the production process in period t. The final good produced is denoted by yt.
(Assumption 1) The production function f(.) is increasing and concave in its argument and satisfies the Inada conditions.
(ii) Preferences
Our economy consists of agents who are born into dynastic households. The main difference of our paper from rest of the literature is the nature of preferences of the individual agents. Unlike the standard Ramsey (1928) and Ben-Porath (1967) model, the agents in our model use their income to consume a ‘utility’ good as well as a ‘health’ good. Let the period utility function be denoted by u(ct) where ct is the consumption of ‘utility’ good of an agent in period t. We assume that u(.) is increasing and concave in ct.
(Assumption 2) u(0) = 0, u′(.) > 0, u″(.) < 0.
The health good affects the agent's rate of time preference or the subjective discount factor and in a two period model the agent's preferences are given by
u(ct) + β(xt)u(ct+1),
(1)where xt denotes the consumption of the ‘health’ good by an agent in period t. The function β(xt) is assumed to be an increasing in the consumption of the ‘health’ good in period t.
(Assumption 3) 0 < 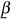 ≤ β(xt) ≤
≤ β(xt) ≤ 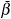 < 1, β′(.) > 0, β″(.) < 0.
< 1, β′(.) > 0, β″(.) < 0.
The concavity of the function β(.) ensures that the first order conditions for the maximum are also sufficient while we need the upper and lower bounds on the function to ensure that the agent's infinite horizon problem has a non-trivial solution.
(iii) The Agent's Problem
Now we state the infinite horizon problem facing an agent. An agent is identified by her initial endowment of capital. The agent maximises her lifetime welfare, that is
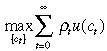 (2)
(2)subject to a period budget constraint
kt +1 = f(kt) + (1 − δ)kt − ct − xt,
(3)and the evolution of the discount factors given by
ρt +1 = β(xt)ρt.
(4)The initial conditions are ρ0 = 1 and k0. δ ∈ (0, 1) is the depreciation rate of capital. We should point out that although we refer to kt as capital it can be interpreted more generally. It can also be thought of as the innate ability or human capital of an agent without altering the motivation of our model. Equation (3) also assumes that the production good (yt) can be transformed one for one into consumption good (ct) and the health good (xt).1 The Lagrangian for the agent's problem is given by
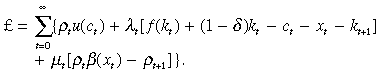
The first-order conditions for maximum are:
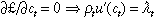 ((i))
((i))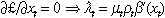 ((ii))
((ii))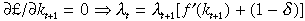 ((iii))
((iii))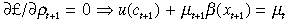 ((iv))
((iv))From Equations (i), (iii) and (4) we have
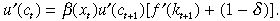 (5)
(5)Equation (5) is the standard intertemporal Euler equation except the discount factor is a function of the ‘health’ good. With forward substitution Equation (iv) can be written as
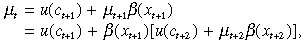
and with repeated substitution µt can be expressed as
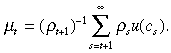 (6)
(6)µt represents the present discounted value of future welfare of an agent at time period t. Using Equation (i), Condition (ii) can be written as
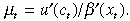 (7)
(7)From Equations (6) and (7), we get
 (8)
(8)Equation (8) summarises the trade-off facing an agent between the consumption of the ‘utility’ good and the ‘health’ good. At an optimum the loss in current welfare from sacrificing the ‘utility’ good must equal the gain in welfare by consuming the ‘health’ good in the form of the present discounted value of future welfare.
Definition 1:
The perfect foresight solution to an agent's problem are given by sequences
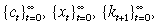 such that
Equations (3), (5) and (8)
hold with equality for a given k
0.
such that
Equations (3), (5) and (8)
hold with equality for a given k
0.
III Results
We first characterise the steady state solution to an agent's problem. At a steady state, ct = ct+1 = c, xt = xt+1 = x, and kt = kt+1 = k. Equations (5) and (8) are reduced to
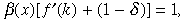 ((5′))
((5′))and
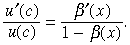 ((8′))
((8′))The left hand side of Equation (8′) is decreasing in c. However, the right hand side of the equation need not be monotonic in x. To derive a unique relationship between c and x we need to impose some additional restriction on the function β(.).
(Assumption 4)
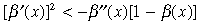
A commonly used functional form for β(.) is
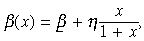
where 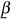 > 0,η > 0 and
> 0,η > 0 and 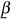 + η < 1. This functional form for β(.) is consistent with Assumptions 3 and 4. Assumption 4 implies that the steady state consumption of the ‘health’ good is a monotonically increasing function of the level of ‘utility’ good, that is, x = x(c) where x′(c) > 0. The positive relationship between economic and health status has been well-documented in the empirical literature.2 Our model provides a micro foundation behind this association. At steady state the budget constraint of the agent is
+ η < 1. This functional form for β(.) is consistent with Assumptions 3 and 4. Assumption 4 implies that the steady state consumption of the ‘health’ good is a monotonically increasing function of the level of ‘utility’ good, that is, x = x(c) where x′(c) > 0. The positive relationship between economic and health status has been well-documented in the empirical literature.2 Our model provides a micro foundation behind this association. At steady state the budget constraint of the agent is
c + x = f(k) − δk,
or,
c + x(c) = f(k) − δk.
((3′))Lemma 1 Let k max solve f′(k) = δ. At a steady state solution to an agent's problem, k ∈ (0, kmax).
Proof: The Inada condition on f(.) ensures that at a steady state an agent will always hold some amount of capital. However, an agent will never choose to hold more than kmax amount of capital in steady state. Let stock k1 > kmax be a steady state level of capital stock. Equation (3′) implies that it would be possible to maintain the same level of steady state level of ‘utility’ good consumption and ‘health’ good consumption with a lesser level of capital stock. Thus, it is possible to increase the welfare of an agent by reducing the level of capital stock and consuming it. Therefore, k1 cannot be an optimum. 
Lemma 1 and Equation (3′) imply that consumption of the ‘utility’ good can be expressed as a monotonically increasing function of capital, that is
c = g(k),
((3″))where g′(k) > 0 and k ∈ (0, kmax). Equation (3″) represents the relationship between c and k according to Equation (3′). Equation (5′) can be expressed as
β(x(c)) [f′(k) + (1 – δ)] = 1.
((5″))Equation (5″) implicitly defines an increasing monotonic relationship between c and k.3Equations (3″) and (5″) together characterise the steady state equilibrium of an agent.
Now we present some results regarding the existence and the number of steady state equilibria. It will be helpful to use Equation (3″) to substitute for c in Equation (5″) and write the steady state condition of an agent as an equation in one variable. Let us define
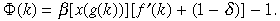
Notice when Φ(k) = 0 both Conditions (3″) and (5″) for the steady state equilibrium are satisfied.
Proposition 1 There exists at least one steady state solution to an agent's maximisation problem. The total number of steady state equilibria is odd.
Proof: The function β(.) is bounded below by 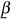 . Since f(.) satisfies the Inada conditions it follows that Φ(0) > 0. As β(.) ≤
. Since f(.) satisfies the Inada conditions it follows that Φ(0) > 0. As β(.) ≤ 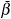 < 1 and f′(kmax) = δ, it means that Φ(kmax) < 0. Continuity of the function Φ(.) implies that there must exist at least one k ∈ (0, kmax) such that Φ(k) = 0. Without loss of generality, suppose there exist two steady state equilibria k1, k2 ∈ (0, kmax). Continuity of the function Φ(k) implies that there exists a
< 1 and f′(kmax) = δ, it means that Φ(kmax) < 0. Continuity of the function Φ(.) implies that there must exist at least one k ∈ (0, kmax) such that Φ(k) = 0. Without loss of generality, suppose there exist two steady state equilibria k1, k2 ∈ (0, kmax). Continuity of the function Φ(k) implies that there exists a 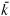 < kmax such that Φ(
< kmax such that Φ(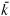 ) > 0. Since Φ(kmax) < 0 it follows that there must exist another steady state k3 ∈ (
) > 0. Since Φ(kmax) < 0 it follows that there must exist another steady state k3 ∈ (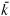 , kmax). Hence, the number of state equilibria is odd.
, kmax). Hence, the number of state equilibria is odd.
Figure 1 depicts a scenario where an agent's optimisation problem has three possible steady state solutions. kL denotes a low level equilibrium where the agent ends up with low level of capital and permanent income. kH on the other hand is a high level equilibrium where the agent accumulates larger amount of capital in steady state and ends up with a higher level of permanent income.
Steady States
The significance of the steady state kU will become clear soon. Although it is possible to have more than three steady state equilibria from a theoretical standpoint, all the interesting features of our model can be studied within such a scenario. Our next proposition characterises the global dynamics of the model. 
Proposition 2 Let k t be the endowment of capital of an agent at time period t. If the marginal product of capital exceeds the rate of time preference at k t , that is
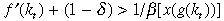
the agent will accumulate capital and vice versa.
Proof:
k
t
is the endowment of capital of an agent at time period t. If this was a steady state, then the equilibrium sequences solving an agent's maximisation problem would be given kt+1 = kt; ct = g(kt); and xt = x(g(kt)) for all t. We want to show that if f′(kt) + (1 − δ) > 1/β[x(g(kt))] then the sequences given above cannot be an optimum. Suppose we consider a one time deviation in the consumption of the ‘utility’ good, that is, let 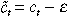 where ɛ is sufficiently small. If we keep xt constant the budget constraint Equation (3) implies that kt+1 = kt + ɛ. The loss in utility from foregoing consumption of ctin period t is given by u′(ct). The foregone consumption is accumulated as capital and allows higher level consumption in period t + 1. The present discounted value of the gain in utility is given by β(xt)[f′(kt) + (1 − δ)]u(ct). Since f′(kt) + (1 − δ) > 1/β(xt) it follows that the agent can increase welfare by consuming less and accumulating more capital. A similar argument can be applied to show that the capital stock is decreasing when f′(kt) + (1 − δ) < 1/[β(x(kt))].
where ɛ is sufficiently small. If we keep xt constant the budget constraint Equation (3) implies that kt+1 = kt + ɛ. The loss in utility from foregoing consumption of ctin period t is given by u′(ct). The foregone consumption is accumulated as capital and allows higher level consumption in period t + 1. The present discounted value of the gain in utility is given by β(xt)[f′(kt) + (1 − δ)]u(ct). Since f′(kt) + (1 − δ) > 1/β(xt) it follows that the agent can increase welfare by consuming less and accumulating more capital. A similar argument can be applied to show that the capital stock is decreasing when f′(kt) + (1 − δ) < 1/[β(x(kt))]. 
Proposition 2 helps in understanding which equilibrium will be reached by an agent in long run. It implies that an agent will accumulate capital when Φ(k) > 0 while she will reduce her capital stock when Φ(k) < 0. Hence, the steady state an agent attains in long run depends on her initial endowment of capital. Agents who have initial endowment of capital less than kU (i.e. k0 < kU) will converge to the low level steady state kL. Those agents with initial endowment above kU will converge to the high level equilibrium kH.
This result warrants some explanation. In the standard Ramsey model, every agent is assumed to have the same degree of patience, that is, the same subjective discount factor β. Hence, every agent accumulates capital until the marginal return from capital equals the rate of time preference, that is

In our model, the degree of patience of an agent is endogenously determined. The subjective discount factor of an agent depends on the level of consumption of the ‘health’ good. Hence, it is possible for an agent to have a very low endowment of capital (and a high marginal product of capital) and choose to reduce her capital stock due to a high rate of time preference.
In Figure 1, kU acts as the threshold level of capital needed to induce an agent to accumulate capital and reach the high capital steady state kH. Let Ψ0(k0) denote the initial distribution of capital in the economy. From Proposition 2, it follows that Ψ(kU) proportion of the agents in the population will converge to kL while (1 – Ψ(k0)) will converge to kH level of capital. With endogenous rate of time preference, it is possible to have inequality in permanent income even though agents are identical in terms of their preferences and have access to the same production technology.
We have provided a simple mechanism to explain the existence of inequality. Our basic model can be extended along a couple of dimensions without altering the results qualitatively. Firstly, we have assumed that the discount factor depends on the expenditure on the ‘health’ good in the immediately previous period. It is perhaps more realistic to believe that it should depend on cumulative health expenditures.4 Suppose the evolution of the discount factor is given by
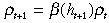 (9)
(9)where ht+1 is the accumulated health or say ‘health capital’ of an agent. The ‘health capital’ of an agent is
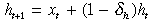 (10)
(10)where δh ∈ (0, 1) is the depreciation rate of ‘health capital’ and xt is the expenditure on the ‘health’ good in period t. Notice in the model presented in Section II we were implicitly assuming that δh = 1. However the results do not change qualitatively with this generalisation. The only difference is that in steady state the value of ‘health capital’ (h) is
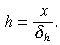
So far in our analysis we have not allowed for any kind of uncertainty. That is why we end up with a two point distribution in steady state. Suppose there is some uncertainty in the production process. For instance, let the production function take the following form
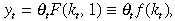
where θt is identically and independently distributed with a distribution function ξ(θt). The long run distribution of capital in such a case is shown in Figure 2.
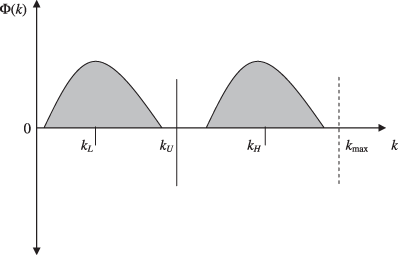
Distribution of Capital with Uncertainty
In the neighbourhood of the non-stochastic steady states there will exist rational expectations equilibrium. The shaded region in Figure 2 mirrors the density function of θt.
IV Empirical Strategy
The ideal way to test the empirical validity of our model would be to estimate the Euler equation generated by an agent's optimising behaviour given by equation
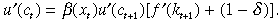 (5)
(5)This requires a large panel dataset with detailed breakdown of the household expenditures and wealth. Unfortunately, even the PSID dataset, a commonly used dataset in this literature has very limited data on household expenditures. It mainly consists of food and household rent. We face a similar paucity of data for Australia as well. However, there is another implication of our model which is possible to test by using cross-sectional techniques.
Proposition 3 Agents with higher permanent income have higher savings rates.
Proof: The steady state savings rate is given by s(k) = [f(k) − x − c]/f(k). Using Equation (3′), the savings rate can be written as: s(k) = δk/f(k). From the concavity of f(.), it follows that an agent with higher permanent income, that is, kH > kL, also has a higher savings rate, that is, s(kH) > s(kL). 
This prediction is consistent with the evidence provided by DSZ (2004). In this paper, we test whether such a relationship exists in Australia. Note that we are interested in the effect of a household's permanent income (not current income) on savings. The problem with permanent income is that it is inherently unobservable. To deal with this, we follow DSZ (2004) and use a two stage estimation procedure. In the first stage, we regress the log of current income on age dummies, control variables and instruments that are good predictors of permanent income. The fitted values from this regression are used as a proxy for permanent income. Then, we divide the distribution of fitted values up into quintiles and create dummy variables for each quintile. As argued in DSZ (2004), using these dummies allows for potential nonlinearities in the saving–income relationship.
Now let's turn to the measurement of saving. In this paper, we consider two variables. First is an active measure of savings, the savings rate. With this being the dependent variable, in the second stage, we run a regression where regressors include permanent income quintile dummies, age dummies, and other control variables. Here, as in DSZ (2004), we use median regression instead of ordinary least squares (OLS). The use of median regression is motivated by the presence of outliers in saving rates: a small number of households in the data have huge negative saving rates (i.e. consumption being far greater than after-tax income) as will be explained in the next section. This characteristic of the data makes median regression more suitable than OLS. Median regression is well known to be robust to outliers while they can severely distort OLS estimates.
The second measure of savings behaviour we consider is a qualitative variable representing a household's self-assessment of their savings habit. This variable takes discrete values between 1, 2 and 3: 1 if the household does not save; 2 if the household saves their left-over income; and 3 if the household follows a regular saving plan. Taking the ordered nature of this variable into account,5 we estimate an ordered probit model in the second stage. This estimation exercise allows us to examine whether higher permanent income is associated with better saving habits. In addition, it provides indirect evidence on the relationship between permanent income and saving rates under the assumption that better savings habits are likely to be associated with higher saving rates.
V Data Description
We use data from the HILDA. HILDA is the first large-scale panel dataset in Australia and covered the period from 2001 to 2003 at the time of this study. It initially provided information on 19 914 individuals and annually asks individuals a range of questions regarding income, work, health conditions, and socio-economic backgrounds. In what follows, we discuss how a measure of saving rate and a measure of saving habits are constructed and also discuss other variables used in this study.
(i) Saving Rate
The ‘true’ saving rate is not straightforward to measure for a variety of reasons. First, there are several saving measures that we may use, but there is no clear-cut answer for which measure we should use. For example, one measure is ‘active’ saving which is the difference between after-tax income and consumption. Another is the change in net wealth, which would include all aspects of saving. Each saving measure may yield a substantially different saving rate. Second, the saving rate depends on whether we calculate it at an individual or household level and for each level it must be measured in a different way. Finally, the saving rate also depends on whether or not we measure a gross or a net saving rate. If we calculate the net saving rate, then we must deduct consumption of fixed capital from gross (DSZ, 2004).
Due to data limitations we only have one saving measure available: the active saving measure. In particular, we define the saving rate to be the difference between household income (net of taxes) and consumption, all divided by after-tax household income. Note that current after-tax income, not permanent income, is used as the denominator, since data on permanent income is inherently unavailable. This may not be too much of a problem; DSZ (2004) test the sensitivity of a change in the denominator for their active saving measures and find that their results are quite robust. Consumption is defined as the sum of food consumption (i.e. grocery spending and spending on meals outside the home) and rental expenses. If households do not rent but instead own a mortgage, these loan repayments are used to proxy for rental expenses. We admit that the constructed saving rate is crude, but this limited measure is due to the lack of detailed information on consumption in HILDA.
When constructing the dataset, we restrict households to those containing ‘typical’ families –childless couples, couples with children, lone parents with children and single-person families, all of which do not have any other family or non-family members living with them. The head of the household is defined as the oldest male in households with couples and the lone parent in lone parent families. In case that the household consists of a single person, he/she gets head of the household status. Since we cannot determine the head of the household for all same-sex couples based on our definition of the household head, these families are excluded from the sample even if they have previously had children with former partners. Furthermore, we exclude any households with negative disposable income to ensure that negative saving rates occur only when consumption is greater than income. Finally, we do not use data for 2002 since no questions on food consumption were asked in that year. Having done this gives us the final sample of 5838 households for 2001 and 5420 households for 2003.
(ii) Saving Behaviour
We also use a qualitative variable representing a household's self assessment of their savings behaviour. Unlike the saving rate, all three waves of the survey contain information on saving habits. This results in a larger sample of 7025 households with heads aged sixteen and above and 15 855 household-year observations.
(iii) Health Variables
To control for health characteristics we consider several proxies. The first variable constructed to proxy for health is a dummy variable that takes one if the head of the household smoked at the time of the survey. There has been much research on the relationship between smoking and its contribution to poor health (see, for example, Smith & Johnson, 1997), which makes it relevant as an indicator of the health status. The second measure of health is a dummy variable that takes one if the head of the household reported that he was in poor health.6 The third measure of health is also a dummy variable that takes one if the respondent considered him/herself as having a long-term health condition, disability or other impairment.
(iv) Summary Statistics
Table 1 reports summary statistics with definitions of variables used in this study. Table 2 presents summary statistics of saving rates, income, smoking status, and health status across current income quintiles. All figures are expressed as percentages, except for income which is reported in 2001 dollars. We can glean some interesting information from this table. First, for the lowest quintile group, the average and median saving rates substantially differ. In 2001, for example, the mean is –118 per cent while the median is 41 per cent. This suggests the existence of outliers. In fact, as mentioned before, a small fraction of households have huge negative saving rates; the one percentile of saving rates is –429 per cent. This is a rationale for us to use median regression instead of OLS. Second, saving rates increase across the current income distribution. For example, in 2001, the median saving rate is 41 per cent for the lowest quintile group and reaches 77 per cent for the highest quintile group. Third, the median saving rate for each quintile is substantially high. This is entirely due to the lack of detailed information on consumption in HILDA as mentioned earlier. Finally, health status improves across current income quintiles, except when we use smoking status as a proxy for health status. The smoking rate peaks in the third quintile and then falls dramatically.
| Variable | Mean | Standard deviation | Definition |
|---|---|---|---|
| Save | 1.998 | 0.773 | 1 (do not save), 2 (save left-over) and 3 (follow saving plan) |
| Income | 44 290 | 36 056 | Real Disposable Income (2001$) |
| Tertiary education | 0.629 | 0.483 | 1 if having completed tertiary education |
| Secondary education | 0.084 | 0.278 | 1 if having completed secondary education |
| Ages 31–40 | 0.218 | 0.413 | 1 if respondent is between 31 and 40 |
| Ages 41–50 | 0.235 | 0.424 | 1 if respondent is between 41 and 50 |
| Ages 51–60 | 0.173 | 0.379 | 1 if respondent is between 51 and 60 |
| Ages 61 or above | 0.234 | 0.424 | 1 if respondent is 61 or above |
| Woman | 0.232 | 0.422 | 1 if respondent is woman |
| Smoke | 0.234 | 0.423 | 1 if respondent smokes |
| Poor health | 0.038 | 0.191 | 1 if respondent is in poor health condition |
| Long-term health | 0.265 | 0.441 | 1 if respondent has a long-term health condition or disability |
| Number of children | 1.912 | 1.525 | Number of children respondent has had that are still alive |
| Retired | 0.205 | 0.404 | 1 if respondent is retired |
| Year | Quintile 1 | Quintile 2 | Quintile 3 | Quintile 4 | Quintile 5 | |
|---|---|---|---|---|---|---|
| Average saving rate | 2001 | –118.02 | 52.32 | 60.5 | 67.4 | 74.85 |
| 2003 | –23.5 | 56.05 | 61.47 | 67.16 | 74.66 | |
| Median saving rate | 2001 | 40.81 | 56.66 | 62.17 | 68.86 | 76.62 |
| 2003 | 45.71 | 59.71 | 62.68 | 68.28 | 76.9 | |
| Median income (2001$) | 2001 | 10 820 | 22 320 | 35 121 | 51 401 | 78 968 |
| 2003 | 11 934 | 23 483 | 36 377 | 52 765 | 81 506 | |
| Smoke | 2001 | 26.05 | 28.25 | 29.45 | 25.45 | 17.81 |
| 2003 | 24.17 | 24.11 | 24.9 | 20.9 | 13.84 | |
| Poor health | 2001 | 8.91 | 6.08 | 3.25 | 1.46 | 1.71 |
| 2003 | 7.33 | 5.65 | 3.05 | 3.05 | 1.05 | |
| Long-term health | 2001 | 49.96 | 34.5 | 22.6 | 14.48 | 13.87 |
| 2003 | 48.81 | 38.56 | 26.43 | 19.85 | 16.98 |
- Note: All figures are percentages, except for income which is reported in 2001 dollars.
Table 3 presents the distribution of saving habits and health status across current income quintiles. All figures are expressed as percentages. The table suggests that the rich tend to have ‘better’ saving habits. The proportion of households that follow a regular saving plan rises monotonically across the income distribution. 23 per cent of households in the lowest quintile follow a regular saving plan and 41 per cent in the highest quintile. In contrast, the proportion of households that do not save falls as income increases; 41 per cent in the lowest quintile do not save, 31 per cent in the third, and only 17 per cent in the highest quintile.
| Quintile 1 | Quintile 2 | Quintile 3 | Quintile 4 | Quintile 5 | |
|---|---|---|---|---|---|
| Do not save (Save = 1) | 40.58 | 38.03 | 30.72 | 23.56 | 17.14 |
| Save left-over income (Save = 2) | 36.73 | 37.34 | 41.44 | 43.85 | 41.65 |
| Follow saving plan (Save = 3) | 22.69 | 24.63 | 27.85 | 32.59 | 41.21 |
| Smoke | 25.34 | 27.85 | 25.73 | 22.49 | 15.44 |
- Note: All figures are percentages.
Despite the clear-cut patterns observed in the data, one should not immediately conclude that the rich save more and have better saving habits. It is well known that saving rates are likely to be positively correlated with current income; those who have higher (lower) transitory income will save more (less) in anticipation of future reductions (increases) in their income (Friedman, 1957). Hence, we are required to examine permanent income, not current income, to draw a conclusion on the relationship between saving and income.
VI Estimation Results
For the first stage of estimation, we use as instruments a dummy for the head of the household having completed only secondary education and a dummy for him/her having completed tertiary education. Education is relatively stable across an individual's lifetime and is positively correlated with permanent income. It is commonly used as a proxy for permanent income (see, for example, Zellner, 1960; DSZ, 2004). As in past studies, we also find that both education dummies are positively and significantly associated with log of current income.7 Consumption has also been used as an instrument in this literature.8 However, as we have mentioned earlier the consumption measures in the HILDA survey are rather crude. As such, we have refrained from using it as an instrument.
(i) Estimation Results: Median Regression
Using permanent income quintile dummies created from the first stage of estimation, we run median regressions for 2001 and 2003. Standard errors of the parameters are computed by bootstrapping the entire two step procedures (the number of replications is 1000). This procedure deals with the generated regressor problem (Pagan, 1984); permanent income is estimated in the first stage and thus uncertainty in the estimate should be accounted for when we compute standard errors in the second stage.
Columns 1 and 3 of Table 4 contain the 2001 and 2003 results from the baseline model, where regressors are permanent income quintile dummies, age dummies, and the gender dummy. Similarly, columns 2 and 4 of Table 4 contain the 2001 and 2003 results from the model with additional explanatory variables: whether the respondent smoked, whether the respondent was in poor health, whether the respondent had a long-term health condition, how many children the respondent had, and whether the respondent was retired. The results provide strong evidence in favour of the theory. In the baseline model with 2001 data (Column 1), the coefficient on every quintile but the fifth is significantly greater than that on the previous quintile. This suggests that higher permanent income is associated with higher saving rates. When adding more control variables, the pattern becomes even stronger; the coefficients are always increasing across the permanent income quintiles (column 2). In both specifications, households in the highest quintile have a 12 per cent higher saving rate than those in the lowest quintile. A similar pattern is observed for 2003 (Columns 3 and 4), suggesting the robustness of the results across years.
| 2001 (N = 5838) | 2003 (N = 5420) | |||
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Quintile 1 | 0.488 (0.027) | 0.532 (0.023) | 0.503 (0.027) | 0.516 (0.024) |
| Quintile 2 | 0.525 (0.020)*** | 0.571 (0.015)** | 0.535 (0.014)** | 0.557 (0.015)** |
| Quintile 3 | 0.581 (0.013)*** | 0.597 (0.010)* | 0.571 (0.009)* | 0.598 (0.010)** |
| Quintile 4 | 0.614 (0.013)** | 0.634 (0.010)*** | 0.600 (0.019) | 0.622 (0.016)* |
| Quintile 5 | 0.620 (0.016) | 0.655 (0.012)* | 0.621 (0.020) | 0.630 (0.018) |
| Ages 31–40 | 0.002 (0.015) | 0.005 (0.011) | 0.004 (0.018) | 0.011 (0.015) |
| Ages 41–50 | 0.058 (0.013) | 0.067 (0.012) | 0.040 (0.020) | 0.062 (0.017) |
| Ages 51–60 | 0.138 (0.013) | 0.147 (0.011) | 0.128 (0.020) | 0.147 (0.017) |
| Ages 61 or above | 0.195 (0.015) | 0.187 (0.015) | 0.187 (0.014) | 0.218 (0.016) |
| Woman | –0.060 (0.015) | –0.070 (0.013) | –0.023 (0.024) | –0.014 (0.017) |
| Smoke | –0.026 (0.009) | –0.026 (0.010) | ||
| Poor health | –0.053 (0.025) | –0.009 (0.024) | ||
| Long-term health | –0.018 (0.010) | –0.027 (0.009) | ||
| Number of children | –0.010 (0.002) | –0.009 (0.003) | ||
| Retired | 0.004 (0.012) | 0.007 (0.019) | ||
| Pseudo R2 | 0.024 | 0.029 | 0.042 | 0.049 |
- Note: This table presents the estimation results of the median regression where the dependent variable is the saving rate. Quintiles 1, 2, 3, 4 and 5 represent dummy variables for permanent income quintiles. Bootstrap standard errors based on 1000 replications are in parentheses. ***, **, and * indicate that the coefficient on the permanent income quintile dummy is significantly greater than that for previous quintile at the 1, 5 and 10 per cent levels, respectively.
The coefficients on age dummies suggest that households save more as heads become older. For example, in the baseline model with 2003 data (Column 3), the saving rates for households with heads aged 41–50, 51–60, and aged 61 or above are higher than those with heads aged 30 or below by 4, 12.8 and 18.7 per cent, respectively. Similar findings are obtained when we include additional control variables (Column 4) and when we use 2001 data (Columns 1 and 2). It might be odd that households with heads aged 61 or above save more than those with heads < 60. This evidence runs contrary to the lifecycle theory of consumption. Lifecycle theory predicts that households should start dissaving as they age. We can conjecture a couple of explanations. First, our household data is a fairly recent one. The savings of the households with heads over the age of 61 could be higher due to generous tax benefits of superannuation contributions. Another possible explanation behind this behaviour could be the increase in average life expectancy in Australia.
The coefficients on the smoking dummy, the poor health dummy, and the long-term health condition dummy are all negative and significant at least at the ten percent level except that on the poor health dummy for 2003, suggesting that an improvement in the health status of household heads is associated with an increase in their saving rate. As these health-related variables are potentially endogenous, one should interpret the estimates as correlation rather than causation.
For comparison purposes, we also carried out OLS estimation of our model.9 Not surprisingly, the results substantially differ from those obtained by median regression. Most of the permanent income quintile dummies are found to be insignificant, which can be attributed to the presence of outliers in saving rates. However, when we control for health-related variables, the coefficient on the dummy variable for the fifth quintile were found to be positive and significant at the 5 per cent level in both 2001 and 2003 (0.73 and 0.43, respectively). Therefore, the OLS results also provide evidence for a positive association between permanent income and saving rates.
(ii) Estimation Results: Ordered Probit Model
As in the median regressions, we compute standard errors in ordered probit models by bootstrapping the entire two step procedures. In the data for the ordered probit estimation, we have four groups of individuals: (i) N1 individuals that participated in the survey just once (group 1), (ii) N2 individuals that participated in the survey twice in a row (group 2), (iii) N3 individuals that participated in the survey twice not in a row (group 3), and (iv) N4 individuals that participated in the survey three times in a row (group 4). To preserve the dependence structure of the panel, we sample Nj individuals with replacement from groups j, j = 1, ... ,4.
Column 1 of Table 5 reports parameter estimates in the baseline model (Specification 1). The coefficients on permanent income quintile dummies are found to be monotonically increasing across quintiles, suggesting that the propensity for better saving habits is higher when the household has higher permanent income. Columns 2–4 of Table 5 report marginal effects. As Column 2 shows, the probability of the household not saving at all decreases across permanent income quintiles. For example, from the first quintile to the second, the probability decreases by 0.07. Likewise, from the second quintile to the third, it decreases by 0.112 (= −0.182 − (−0.070)). Contrastingly, the probability of the household following a regular saving plan rises as the permanent income increases (Column 4). The probability increases by 0.047 when permanent incomes increase from the first quintile to the second, and by 0.102 (= 0.145 – 0.047) from the second to the third. The results thus suggest that households are more likely to follow a regular saving plan and are less likely to not save, as they have higher permanent income. There is no clear-cut pattern regarding the relationship between ages and saving habits. Households with heads aged 31–50 do not appear to have better saving habits (relative to households with heads being 30 or below, i.e. the reference group), while household heads aged 61 or above appear to have better saving habits.
| Variable | Specification 1 (log-likelihood = –17078.4) | Specification 2 (log-likelihood = –16771.3) | ||||||
|---|---|---|---|---|---|---|---|---|
| (1)Coefficient | (2) Pr(save = 1|x)/ Pr(save = 1|x)/ xk xk |
(3)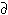 Pr(save = 2|x)/ Pr(save = 2|x)/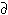 xk xk |
(4)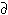 Pr(save = 3|x)/ Pr(save = 3|x)/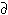 xk xk |
(5)Coefficient | (6) Pr(save = 1|x)/ Pr(save = 1|x)/ xk xk |
(7) Pr(save = 2|x)/ Pr(save = 2|x)/ xk xk |
(8) Pr(save = 3|x)/ Pr(save = 3|x)/ xk xk |
|
| Quintile 2 | 0.185 (0.064)*** | –0.070 (0.024) | 0.022 (0.009) | 0.047 (0.015) | 0.079 (0.056) | –0.029 (0.021) | 0.005 (0.004) | 0.024 (0.017) |
| Quintile 3 | 0.502 (0.092)*** | –0.182 (0.033) | 0.037 (0.010) | 0.145 (0.024) | 0.260 (0.078)*** | –0.091 (0.028) | 0.008 (0.005) | 0.083 (0.024) |
| Quintile 4 | 0.758 (0.108)*** | –0.261 (0.036) | 0.026 (0.009) | 0.235 (0.029) | 0.346 (0.093)** | –0.118 (0.032) | 0.006 (0.004) | 0.113 (0.029) |
| Quintile 5 | 0.829 (0.117) | –0.281 (0.038) | 0.019 (0.008) | 0.261 (0.033) | 0.402 (0.102) | –0.136 (0.034) | 0.003 (0.003) | 0.133 (0.032) |
| Ages 31–40 | –0.382 (0.067) | 0.137 (0.024) | –0.015 (0.005) | –0.122 (0.020) | –0.143 (0.048) | 0.049 (0.017) | –0.002 (0.001) | –0.047 (0.015) |
| Ages 41–50 | –0.410 (0.082) | 0.146 (0.030) | –0.015 (0.005) | –0.130 (0.025) | –0.063 (0.051) | 0.021 (0.017) | 0.000 (0.001) | –0.021 (0.017) |
| Ages 51–60 | –0.090 (0.062) | 0.031 (0.022) | –0.001 (0.001) | –0.030 (0.021) | 0.153 (0.052) | –0.050 (0.017) | –0.003 (0.002) | 0.052 (0.018) |
| Ages 61 or above | 0.340 (0.080) | –0.110 (0.025) | –0.010 (0.004) | 0.120 (0.029) | 0.361 (0.055) | –0.114 (0.016) | –0.011 (0.004) | 0.125 (0.020) |
| Woman | 0.217 (0.073) | –0.071 (0.023) | –0.004 (0.003) | 0.076 (0.026) | –0.011 (0.052) | 0.004 (0.018) | 0.000 (0.001) | –0.004 (0.017) |
| Smoke | –0.338 (0.031) | 0.119 (0.011) | –0.011 (0.002) | –0.108 (0.009) | ||||
| Poor health | –0.296 (0.058) | 0.105 (0.022) | –0.014 (0.005) | –0.092 (0.016) | ||||
| Long-term health | –0.150 (0.033) | 0.051 (0.011) | –0.002 (0.001) | –0.049 (0.011) | ||||
| Number of children | –0.079 (0.009) | 0.026 (0.003) | 0.000 (0.001) | –0.026 (0.003) | ||||
| Retired | 0.044 (0.051) | –0.015 (0.017) | 0.000 (0.001) | 0.015 (0.017) | ||||
| Constant | 0.111 (0.083) | 0.530 (0.079) | ||||||
| Threshold | 1.069 (0.014) | 1.095 (0.014) | ||||||
- Note: This table presents the estimation results of the ordered probit model where the dependent variable is Save (= 1 if the respondent does not save; 2 if the respondent saves left–over income; 3 if the respondent follows his/her saving plan). The number of observations is 15 855. Quintiles 2, 3, 4 and 5 represent dummy variables for permanent income quintiles. Bootstrap standard errors based on 1000 replications are in parentheses. *, **, and *** indicate that the coefficient on the permanent income quintile dummy is significantly greater than that for previous quintile at the 10, 5 and 1 per cent levels, respectively. Marginal effects, ∂Pr(Save = j|x)/∂xk (j = 1, 2, 3), are computed as average derivatives of the probability that Save = j. Year dummies are included, though not reported here.
Even after controlling for other factors (specification 2), we observe the same pattern in the baseline model. The coefficients on permanent income quintile dummies are found to be increasing (Column 5) across permanent income quintiles. As Column 8 shows, the probability of the household following a saving plan increases by 0.059 (= 0.083 0.024) and by 0.030 (= 0.113 0.083) as the permanent income moves from the second quintile to the third and from the third to the fourth, respectively. On the other hand, the probability of not saving at all decreases by 0.029 and by 0.062 (= −0.091 − (−0.029)) when the permanent income increases from the first quintile to the second and from the second to the third, respectively.
The results appear to suggest that households are less likely to save at all when heads have poor health. As column 6 indicates, being in poor health condition (having smoking habits) is associated with a 10.5 per cent (11.9 per cent) increase in the probability of not saving at all. The effect of having a long-term health condition or disability is not as strong, but still increases the probability of not saving at all by 5.1 per cent.
Whether the head of the household is retired or not does not appear to affect saving habits (Column 5). One may argue that households with retired heads have different saving habits than those with non-retired ones. To see whether this is indeed the case, we removed retired individuals from the sample and re-estimated the models. We again observed the same pattern: households with higher permanent income are more likely to follow a regular savings plan than those with lower permanent income.10 Overall, our results suggest that the rich have better saving habits.
VII Conclusion
In this paper we have provided a micro foundation behind increase in savings rates with permanent income. Our theoretical framework also can explain the existence of inequality in an economy even when agents are identical in terms of their preferences and have access to the same technology. We also test the implication of our model for Australia. We find that savings are increasing with permanent income. We also find a strong relationship between health and savings behaviour. The empirical results reported here should nonetheless be taken with caution due to the potential problems in data including inaccurate measurement of saving rates and the use of self-reported measure of saving habits. The reader may thus reserve ‘final’ judgement until perhaps better datasets in the future are able to confirm our results.
Recent empirical studies show an increase in income inequality in many developed countries such as U.S.A., U.K. and Australia. In that context, our findings have significant implications for Australia especially regarding macroeconomic and government policies such as support for healthcare. Our model can be extended in future to analyse the impact of various revenue neutral tax policies. A particular policy instrument worth investigating is the GST. A sales tax would increase the tax burden for poorer section of the society as they consume larger proportion of their income than those affluent whose saving ratio is higher. It may also lead to a higher level of inequality.




