Alfred Marshall's Mecca: Reconciling the Theories of Value and Development*
The origins of this paper rest in a kind invitation to address the Australian Conference of Economists, held at Curtin University, Western Australia, in September 2006. That lecture was necessarily discursive in form but underlying it was a sense of a formal evolutionary model that might resolve some of the difficulties Marshall faced in combining a theory of order with a theory of transformation. This is an attempt to realise that ambition. The recent flowering of a modern Marshall industry has made my task easier, and I particularly wish to acknowledge the stimulus I have received from Brian Loasby, Richard Arena, Michel Quere, Neil Hart, Marco Dardi and Tiziano Raffaelli, not all of whose writings are reflected in the references below. Curtin University provided me with a very congenial atmosphere for research and I take the opportunity to thank Harry Bloch and colleagues for their hospitality and engagement with itinerant visitors. Comments from Witold Kwasnicki, Harry Bloch, Peter Hall and two referees helped me revise an earlier draft and have resulted in improvements in substance, structure and style. Any remaining deficiences are mine alone.
Abstract
The purpose of this paper is to explore the evolutionary nature and content of Marshall's theory of value and the relation it bears to his theory of growth and development. In Marshall's work the two theories are inextricably linked, and the subsequent attempt to separate them has not only marginalised Marshall's rich analysis but also made it impossible to appreciate the role he gave to innovation, and its corollary the growth of knowledge and organisation, in the workings of a market economy. At its core is the relation between the growth of firms and the growth of markets, but this is not steady-state growth theory; rather, it is the different, mutually determined and ever changing growth rates of different groups of firms that is at the centre of attention. Quite how variation is linked to progress is the central topic of this essay, and the elucidation of its central role necessarily means that we must resurrect the representative firm. We conclude that Marshall was correct in stating that ‘the tendency to variation is a chief source of progress’ (Principles, V, 4, p. 355). We develop a set of evolutionary tools to show how and why this is so. But evolution is more than variation; it requires the organisation of firms and the market process to generate that correlation between differential knowledge and economic advance. Most importantly of all, the concept of a representative firm is re-established as an indispensable element in a Marshallian evolutionary analysis.
I Introduction
The purpose of this paper is to explore the evolutionary nature and content of Marshall's theory of value and the relation it bears to his theory of growth and development. In Marshall's work the two theories are inextricably linked, and the subsequent attempt to separate them has not only marginalised Marshall's rich analysis but also made it impossible to appreciate the role he gave to innovation, and its corollary, the growth of knowledge and organisation, in the workings of a market economy (Loasby, 1989; Dardi, 2006). To further this claim, we will outline a ‘Marshallian evolutionary model’ to help understand and take seriously Marshall's evolutionary credentials in general, and the concept of the representative firm in particular. At its core is the relation between the growth of firms and the growth of markets, but this is not steady-state growth theory; rather, it is the different, mutually determined and ever changing growth rates of firms that is at the centre of attention. Indeed, we might say that one of Marshall's definitive questions is ‘Why do firms (activities) develop and grow differently?’ The answer, I suggest, is closely connected to, indeed indistinguishable from, Marshall's managerial explanation of firm differentiation and innovation and his claim that variation is the chief source of progress. Quite how variation is linked to progress is the central topic of this essay, and the elucidation of its central role necessarily means that we must resurrect the representative firm.1
There can be no doubt that Marshall's attempt to combine value theory and development theory created more problems than it solved, particularly when viewed from the perspective of equilibrium economics (Loasby, 1978, 1990, 1991; Thomas, 1991; Hart, 2003a,b; Quere, 2003). I accept the force of the claim that Marshall's analysis is seriously incomplete but not because it fails to fit within a modern understanding of competitive general equilibrium. Consider instead Shackle's suggestion (1965, p. 36) that ‘Marshall's peculiar triumph is his creation of a unity out of the concepts of equilibrium and evolution’. This is nearer to the truth and it reflects Marshall's claim that ‘the problem of normal value belongs to economic dynamics’ (P, V, 5, p. 366, footnote 2), and explains why we should interpret the Principles as a work created to understand the restless nature of capitalism, not its stationary properties, for no such stationary properties are ever to be found. Yet Shackle surely cannot have expected to conjoin equilibrium and evolution in this way since systems in equilibrium do not and cannot evolve. Marshall's overarching idea that ceaseless economic development might flow from the mode of organisation of a market system must mean that any particular patterns of organisation are transient and, therefore, we must look for the enduring principles that sustain the logic of transformation. They are to be found in their broadest terms in the evolution of knowledge and the consequential adaptation of economic behaviour, and they depend on a concept of order and a dependence of order on organisation (Loasby, 2006). In Marshall, organisation is vested in firms and markets, the products of human activity and, thus, human knowing and how that knowledge is distributed. Marshall's system could never be in equilibrium if the idea of equilibrium is interpreted rigorously, and this is where he departs profoundly from the subsequent development of economic theory. Thus, pace Shackle, it is not evolution and equilibrium that are rendered consistent in Marshall but evolution and order. To place an economy in equilibrium is to place knowledge in equilibrium and, thus, to make stationary analysis, even of a regularly expanding economy, the only possible ground for theorising. To paraphrase Joan Robinson, if you are in it (equilibrium) you have always been in it and no one can ever be expected to conceive any idea that might lead to escape from it. With the benefit of hindsight, Marshall's mistake was to cover his quite profound views on endogenous, knowledge-based development in the cloak of equilibrium language, thus allowing his followers to interpret his economics from a quite different, non-developmental perspective.
In interpreting Marshall's evolutionary intent, it is vital to recognise that he portrayed two quite different forms of economic evolution in the Principles (Metcalfe, 2006). The first centres on the increasing returns story, the progressive refinement of the division of labour, and mode of organisation within and between firms and between industries. This is the organic development view of the co-evolution of knowledge, practice and organisation, where Marshall pays his respects to Adam Smith and the evolutionary biology of differentiation and integration of form2 (Hodgson, 1993; Limoges & Menard, 1994). This is by far the more complicated of the two forms of evolution deployed by Marshall and it has a quite different mode of operation and significance to the second form; the one based on a variation cum selection view of the world, operating in the main within industries and associated with the rising and falling of individual firms and the representative firm.3 In Marshall the two modes are intertwined, as they are in real life, but from an analytical point of view they are best kept separate. There is certainly a reconciliation problem in Marshall, a problem of combining an account of the forces generating market order and the forces transforming that order from within, but this problem is addressed through his famous periodisation scheme, different causal forces operate contemporaneously but with different velocities. Thus, the long and short periods are not descriptions of different kinds of equilibria but accounts of different temporal processes in which some events are permitted and other events excluded.4
To anticipate my argument, we build below on the variation cum selection scheme of evolutionary change and suppress entirely the increasing returns aspects that are synonymous with the differentiation and integration of activities. The key point is that directed evolution depends on an established order, defined as a structured pattern of economic relationships that is shaped by specific causal forces. If it is to evolve, an economy must possess structure and the necessary ordering forces are provided in Marshall by the market process, the reconciliation of demand and supply to establish long period normal value. Yet order promotes flux by stimulating the long period forces of investment in facilities, organisation, capability and knowledge to expand the capacity in an industry and adapt its firms to market opportunity. Flux is represented by Marshall's account of the rising and falling of individual firms but this is not a token gesture towards reality; rather, it is intrinsic to an explanation of the transformation of order. Flux is neither random nor without substantive effect, rather, it produces directional change and an evolution of the determinants of normal value. It is because firms have different growth and developmental histories that we need the representative firm and its two analytic roles: to be the attractor for long period value; and, to serve as the fulcrum around which the competitive process transforms the prevailing market order. It is the most immediate expression of Marshall's evolutionary turn of mind but it would never make sense in the context of a non-evolutionary account of order and transformation.
These themes are reflected in the contrasting roles of the marginal firm and the representative firm in Marshall's theory. Both analytical concepts only apply in a world in which firms behave differently in the same market context, and it is on this dichotomy that I build the ensuing argument. We need the marginal firm to distinguish different instantiations of long period order, and we need the representative firm not simply to deal with the messy fact of heterogeneous firms but rather to understand the dynamic consequences of their variation for the transformation of the prevailing order. Indeed, in Marshall, the heterogeneity of firms is more important than their rationality. His firms behave reasonably, making the best of their strategic opportunities but, even if they ever come close to optimising, their particular rational behaviours are different: they share one world but perceive different worlds and this provided the epistemic link between variation and progress. Of course, the representative firm remains controversial (Quere, 2003; Whitaker, 2003) long after Robbins condemned it as an afterthought: ‘like some pale visitant from the world of the unborn waiting in vain for the comforts of complete tangibility’ (1928, p. 387). We shall try to rescue it and give it substance so as to demonstrate the role of the concept in an evolutionary theory of order and transformation. In so doing, we will extend its properties beyond the single dimension of costs of production; separate it from any discussion of increasing returns, a conjunction that has only served to cloud understanding; and establish its relation to the marginal firm so as ‘to make compatible a theory of normal supply and demand with a theory of economic evolution’ (Quere, 2003, p. 188).
Let me anticipate a possible misunderstanding. I do not for one moment claim that I have reproduced Marshall's model. Rather, I offer a framework to explore and appraise the intention of Marshall's thought that is fully compatible with the evolutionary analysis of the Principles. Moreover, it is a framework that can readily accommodate increasing returns and the many aspects of that complementary modus operandi of evolution. It is Marshallian in so far as it deals with his problem of ‘economic order in the presence of disorder’ and the corollary that order leads to transformation of order (Taussig, 1924, p. 4). Marshall's economy is never at rest, but to understand why and how it changes we need a theory of market order as an integral part of a theory of evolution. Thus, order and evolution are not irreconcilable bedfellows but inseparable, long-term partners in unveiling the dynamics of knowledge-based capitalism. This is the frame of the Principles, and while its development certainly taxed Marshall's powers it is the necessary basis for taking seriously his evolutionary intent. A caveat though for the reader: I must necessarily leave aside many aspects of a Marshallian approach to industrial dynamics; entry, innovation and its link to increasing returns, and the recombination and fission of business activities are all important dimensions of Marshallian flux but I will not treat them here. They can be fitted naturally into the following framework but the immediate task is to identify the role and status of the representative firm in their absence. We will have more than enough to say on this topic in isolation without adding new dimensions to the problem.
II Marshall's Conundrum: Value and Variation
Marshall's conundrum can be stated as thus, ‘How, within the theory of value, can one reconcile the dynamic role of the representative firm with the static role of the marginal firm?’ It is not fanciful to claim that many of the subsequent difficulties that scholars faced in understanding the representative firm and its causal purpose begin with this problem. What we shall establish here is the complementary, interdependent nature of Marshall's two solutions to this conundrum. A demand curve and a particular expenses curve always co-define the long period market order and the normal price that coordinates the two sides of the market. But the particular expenses curve is transient; it is formed and continually reformed by the long period forces of investment in capital, knowledge and organisation, the determinants of firm capabilities. Moreover, the demand curve will generally be changing too and these two processes serve to redefine continuously the prevailing market order and with it the causes of long period transformation. It is in respect of this later point that the representative firm finds its role as the evolutionary fulcrum around which the market's order changes.
When firms in an industry have different costs of production, we may also ask, ‘Whose costs are measured by or reflected in long period normal market price?’ This is the dilemma that enfolds his value theory and Marshall offers two quite different answers. The first relies on the particular expenses curve, the array of firms in terms of declining efficiency and, thus, increasing unit costs of production (Viner, 1931; Whitaker, 1990). In a long period analysis, the normal price must be at least sufficient to make it profitable for the least efficient, marginal, active firm to cover costs (prime and supplementary) and stay in business, so that all the more efficient firms earn quasi-rents according to their differential abilities. Thus, in summarising the contents of Book V, Marshall tells us,
When different producers have different advantages for producing a thing, its price must be sufficient to cover the expenses of production of those producers who have no special and exceptional facilities; for if not they will withhold or diminish their production, and the scarcity of the amount supplied, relatively to the demand, will raise the price. When the market is in equilibrium, and the thing is being sold at a price which covers these expenses, there remains a surplus beyond their expenses for those who have the assistance of any exceptional advantages. (P, V, XV, p. 499).
All of this is a perfectly clear development of Ricardian rent theory applied to the circumstances of industrial firms. The particular advantages a firm enjoys may depend on access to free gifts of nature but in industry their source is far more likely to be found in interfirm differences in managerial performance and organisation, so giving rise to the notion of composite rents (Kondo, 2006). The second answer is of a quite different form couched in terms of the representative firm. Here Marshall tells us that the long period normal supply price of a commodity is equated to the normal expenses of production in the representative firm (P, V, III, pp. 342–343). The two answers are not obviously compatible and this has led scholars to ask, ‘What is this representative firm and what theoretical purpose does it serve?’ and ‘Why do we need two, apparently independent accounts of the determination of long period values?’
The representative firm is neither a firm at the beginning nor or end of its life cycle, it is managed with normal ability, it enjoys its fair share of internal and external economies, and it is, correspondingly, some kind of average firm. But, as Marshall tells us, there are many ways that the average can be construed (P, IV, XIII, p. 318) while providing no basis for its construction. Yet there is an important clue to its nature, a clue that hints at its dynamic purpose. When the total output of the industry is stationary, the output of the representative firm is also stationary; it maintains constant its market share. Consequently, when the total output of the industry is changing, the output of the representative firm(s) is also changing at the same rate, and so its relative size is always constant (P, V, III, p. 343 and V, V, p. 367). The crucial point is that its characteristics cause it to grow in step with the industry as a whole. Thus, the identification of the representative firm depends on this property and the kind of average that it defines must follow from the underlying theory of the growth of the firm and its industry. Consequently, the characteristics of a representative firm cannot be determined a priori, it is a product of, and changes with, the economic forces in a particular industry and market context.
Interpreted thus, the representative firm can serve two roles: to act as an attractor for long period values and to be a demarcation concept, a device to structure the industry from a dynamic viewpoint. Around the representative firm other firms are rising or falling and the industry is in a permanent state of flux, even though the normal price continually orders the market overall. Moreover, the patterns of rising and falling are related to the characteristics of each firm as reflected in its managerial capabilities and strategic purpose, characteristics that alter with the age of the firm. Thus, its purpose is dynamic, to uncover the adaptive significance of interfirm variations, and it has no function if we simply restrict the argument to the description of a given market order (Moss, 1984). Marshall was not misguided to write his economics in this way, he simply lacked the evolutionary tools to render manifest his powerful intuition.
Several consequences follow. First, the representative firm makes no sense as a short period concept; its proper role is in relation to those investment processes that result in the growth and decay of firms. Second, unless all the firms in an industry are uniform, in which case the notion is redundant, a price that equates to the average cost of the representative firm implies that those firms with above average costs are making losses and, thus, the position cannot be one of long period normality (Frisch, 1950). The marginal firm and the representative firm have to coexist. The point here is subtle. The operation of long period forces does not negate the logic of the particular expenses curve and the need for any marginal firm to break even by covering all its costs, prime and supplementary. In this context, infra-marginal firms are stationary or expanding, marginal firms are declining, even if they break even, and other firms are entering or leaving the trade with the consequence that the population of firms in view is ever changing. Even more fundamentally in Marshall, firms are innovating or experiencing changes in managerial ability, technology, organisational structure and purpose. Thus, the representative firm cannot be a fixed point in the analysis even if the aggregate output of the industry is constant. This is the consequence that has been missed; the representative firm evolves continually, its evolution is a mirror to the industry's evolution, and it only stops evolving in the never to be achieved stationary state when all long period forces are exhausted. Marshall grasped this but found no way to think through the deeper nature of the representative firm outside of stationary conditions where, unfortunately, it is redundant. Third, the idea of firms rising or falling is too imprecise, for this phenomenon may relate to relative or absolute changes in the size of the firm, and the two need to be distinguished since they imply very different firm behaviours. Fourth, the representative firm is typically treated in one-dimensional terms, it is representative in respect of its unit costs. This is far too restrictive if the evolution of the industry depends, as it does in Marshall, on other characteristics such as product design and quality, or on the ability to manage the investment processes that result in the growth or decline of the firm. Indeed, Marshall's own long period logic would seem to insist that firms differ not only in respect of their unit costs but also in respect of their rates of investment, so that two firms with the same profitability may expand at different rates. If the competitive process is driven by multiple characteristics, then any workable concept of the representative firm must reflect this, and be open to the possibility of a performance-related trade-off between those different characteristics. This, as we shall show, is exactly how the concept needs to be developed. Finally, Marshall's desire for continuity combined with his penchant to maintain contact with the world of ordinary business led him to write as if a particular, real firm could always be found and have a notice marked ‘representative’ posted at its entrance. But this is an irrelevance; the representative firm is an analytical construct, a statistical device, as Sraffa (1930), Robbins (1928) and Robertson (1956), among others, soon made clear.5 The question at stake is ‘What kind of analytical device?’
No doubt the ever cautious Marshall was aware that all was not watertight. No wonder a fierce critic like Samuelson found easy targets in Marshall's perverse regard for evolutionary principles and ‘prattle about the biological method’ (1967, p. 112); and here, of course, he was simply reflecting the fact that the development of post-Marshallian value theory had departed from the ground of Marshall's theory (Raffaelli, 2003). Yet, the marriage of Marshall's value theory to his growth and development theory can be consummated, and we can develop value theory in Marshall's evolutionary direction to better place variation and the implied growth of knowledge at the heart of the competitive process. In so doing, we can also give pride of place to the idea of a representative firm, but not before we have teased out the many complications surrounding this quintessentially evolutionary concept. Let us see how these claims can be validated.
III Evolutionary Growth as a Marshallian Process
The following framework is developed under two limiting assumptions that have opposing dynamic consequences. First, there are constant returns to scale at the level of the individual firm so that there are no limits to its size, only limits to its rate of growth set by the competition from rival firms and the rate of growth of the market. Implicitly, all inputs are in perfectly elastic supply at given factor prices that are common to all the firms in an industry. It turns out that most of the important aspects of industry evolution as an adaptive process can be explored in this particular case. Second, we develop the argument in the confines of a perfect market, an important case but not the only case in Marshall's theory, in which information is so diffused on both sides of the market as to require the output of each rival firm to be disposed of at a uniform price.6 This has the singular consequence that the notion of a market demand curve, as distinct from the individual demand curves of particular firms, is well defined. It is an important simplification and it has definite limits from the evolutionary viewpoint, although it serves to illustrate the principle that the organisation of the market process deeply influences the dynamics of competition.7 The more immediate losses are that it elides the difference between the idea of a customer base for a firm and the intensity with which individual customers buy the product, one of the important distinctions in Marshall's theory of demand. It is the individual customer who can express loyalty or inertia in choosing whether to switch custom to a different firm and, thus, give rise to the idea of the particular market for a firm, quite separately from the question of how much any individual customer might buy. This form of market ‘imperfection’ should be a characteristic element in evolutionary dynamics especially if product differentiation is allowed but we suppress it here. A perfect market also defines a fierce selection environment, one that facilitates the entry of new firms (by construction, customers have no loyalty to the firms they buy from), and is a harsh judge of firms on the margin of existence (there is no scope to set different prices to reflect different costs). Indeed, it is an environment that creates the maximum possible selection pressure on the population of firms defining the industry. While imperfect markets have the effect of slowing down the competitive process, increasing returns has the effect of speeding it up, so that in Marshall the former is deployed to tame the later.8 By focusing on constant returns and a perfect market we strike a middle ground that helps make transparent Marshall's evolutionary analysis and also keeps at bay the deeper complexities of the organic mode of evolution.
How are we to connect a theory of market order with the theory of economic evolution and to answer the question, ‘What patterns of market adaptation of costs to values might we expect to find in an industry characterised by rich interfirm variety?’ The costs and values in view cannot be equated with stationary values, for then the long-run forces of investment and entry, innovation and increasing returns would be exhausted and the industry would be effectively dead. Rather, our interpretation must focus on those hypothetical normal values that are shaped by the long period processes and where the long period normal price serves a twofold purpose: to coordinate demand with capacity, and to determine which firms are viable. The two roles provide the substrate of ordering principles around which the long period forces of investment can generate evolution. Our method is Marshallian; we break down the problem into components of successive simplicity. The foundation is provided by a fixed population of firms, each one differentiated by its efficiency and investment strategy. This leads directly to a variation cum selection treatment of Marshallian competition in which we establish the relation between the properties of the representative firm and long period normal price.
IV A Basic Marshallian Framework
We begin with the interplay between the firm and the market, and represent the industry demand curve by
D=N·η(p),
(1)where N is the total number of customers in this market, each of whom purchases identical quantities of the commodity according to the intensity of demand relationship η(p) with p being the long period, normal market price.
The firm, the unit for organising production and sales, is a member of a population of firms in the same trade producing the same commodity. The management and organisation of the firm underpin its behavioural characteristics which are two in number; namely, the efficiency with which production is carried out, and the investment strategy that it follows to expand or contract its capacity. Our firms differ in both dimensions reflecting, as they do in Marshall, idiosyncrasies of management style and purpose. Each firm (w) is described in terms of its given unit costs, hw, its capacity output level, xw, and its investment strategy as explained below. Since the concern is with long period normal conditions we assume throughout that capacity and output are one and the same, their deviations being the proper subject of a short period analysis.
(i) Market Order and the Particular Expenses Curve
By arranging the given set of firms in terms of ascending levels of unit cost we can draw the long period particular expenses curve represented by the array E–E in Figure 1(a).9 The differences between the ‘steps’ signify the degree of unit cost variation in the population and the lengths of the ‘steps’ signify the interfirm differences in installed capacity.10 The curve is a product of the industry's history, of the pattern of accumulation and of many of the creative forces that we have provisionally locked in the pound, ceteris paribus, particularly innovations in organisation and technique, entry and exit. Of course, its ‘position and shape’ are transient and one of the strongest of the consequences of competitive evolution is to narrow the gap between the least efficient active firm and the most efficient, or best practice, firm.
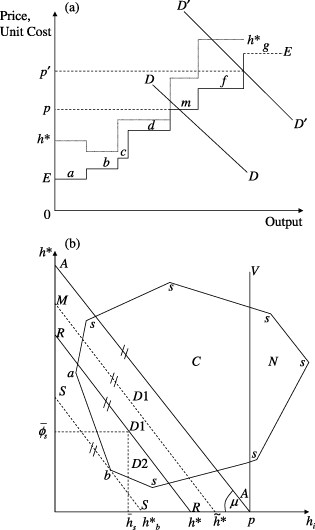
(a) The Augmented Particular Expenses Curve, and (b) the Selection Set
Since we are assuming a perfect market, a demand curve such as D–D may be imposed on the diagram and the resultant point of coordination defines the normal long period, market clearing price and identifies the ‘marginal firm’, should one exist. It is firm m with demand curve D–D, and this firm exactly breaks even taking account of prime and supplementary costs. However, with demand curve D′–D′ no firm is marginal although firm f is the closest to a state of marginality. Any firm with unit costs higher than the ruling normal price is deemed to be non-viable, to have ceased production and to have scrapped its capacity – hence, the dashed form of the curve beyond D′–D′. Thus, there are two possible configurations of a market order to contend with, and the differences between them play an important role in the analysis of industry evolution. Case I corresponds to curve D′–D′ in which long period market coordination is maintained through price adjustment. It is the flex price case. Case II corresponds to the demand curve D–D in which long period market coordination is maintained through quantity adjustment, that is to say, by changes in utilisation of the capacity of marginal firms selling at a price equal to their long period average costs. This is the fixed price case. The long period order captured in Figure 1(a) is the story Marshall tells in book V. The marginal firm, if it exists, just breaks even and all the other active firms earn surplus profits or composite, long period rents on their past investment in technique, organisation and knowledge. It is the surplus profits earned by the inframarginal firms that play the central role in the following account of Marshallian long period competition.
How does this relate to the representative firm? Not at all, if the purpose of the analysis is solely to characterise a given long period, normal market order. To give purpose to the representative firm we must investigate the transient nature of the particular expenses curve as it is reshaped by the investment strategies of the active firms, and how these strategies interact with the distribution of composite quasi-rents. This requires a theory of the growth of the firm, the purpose of which is to link value theory to the development of the industry.
We capture firm dynamics by a simple rule, a classical rule that links investment in new capacity to profitability but which allows for idiosyncratic variations in strategy. This rule is as follows. If the operating return is greater than a particular cut-off value, the firm expands at a rate determined by the finance it can raise. If the rate of return is less than the cut-off value, the firm does not invest, it is stationary although it may still be profitable. If the rate of return drops below zero, the no longer viable firm exits the industry.
To formalise this, let gi be the firm's growth rate of capacity and output, and let the accumulation rule be expressed as11
 (2)
(2)The ratio φi/µ defines for each firm its critical investment margin, equivalent to Marshall's ‘outer limit, or margin, of profitableness’ (P, V, 4, p. 356). The coefficient φi is interpreted as a strategic investment parameter, a measure of a firm's willingness to invest at a given rate of return and the coefficient µ, common to all firms, we call the investment coefficient. The smaller is φi, the more expansive is the investment strategy. We assume that each firm distributes profits to the owners and draws investment funds from the ‘capital market’ at a rate that depends on its profitability. Finance constrains growth, and the fact that µ is the same for all firms means that the capital market is not discriminating between firms with the same operating profit.12 We should notice immediately the asymmetrical nature of this investment strategy rule. The growing firm obeys (2) but the declining firm obeys a quite different set of rules in relation to the utilisation of existing capacity and the decision to scrap capacity that is underutilised. This is a crucial Marshallian distinction, the economics of decline are not the economics of expansion in reverse and this asymmetry plays an important role in the following analysis.13
In Figure 1(a) we can incorporate this new dimension of firm behaviour if we add the dotted, stepped line, labelled h*, lying above the particular expenses curve to show the normal price for each firm that corresponds to its critical investment margin. In the case of firm f and demand curve D′–D′ we see that this firm is profitable but that the prevailing long period price is below the critical value required to justify investment. Consequently, firm f is a profitable firm but it is also a stationary firm. It seems intuitively clear from Figure 1(a) that the relation between profitability and expansion in the aggregate depends on the joint distribution across the population of the two characteristics φ and hẇ, and so it will turn out to be. The significance of allowing the firms to differ in investment strategy, as well as in their unit costs, is that two firms with the same unit costs and profit margin may grow at very different rates in terms of capacity and market shares. While real world competition is certainly many dimensional, a framework with just two of many possible dimensions of interfirm variety is sufficient to provide the richness we need to explore and develop Marshall's linking of value to costs in the representative firm.
The final element we need relates to the dynamics of demand. The implication of (1) is that the rate of growth of demand for any firm depends on the growth of the overall number of customers, N, the change in the firm's share of this total number of customers, dw, and the change in the intensity of their demand, η(p), which depends in turn on the rate of change of the long period normal price. The first of these we can treat as an exogenous growth rate, the natural market growth rate, gN, under the supposition that new entrant or exiting customers are distributed across the existing firms in proportion to their current share of the total number of customers in the market. The last we treat by assuming that the elasticity of the intensity of demand, α, is the same for all customers.14 It is the second element, the shares of each firm in the total market that requires more elucidation. Here a perfect market provides a great simplification since customers are indifferent as to whom they buy from. Consequently, in long period normal conditions, the shares of each firm in total demand are determined by their shares of industry capacity, and it is the evolution of the capacity share that drives the corresponding share of market demand. In this way the evolution of the industry structure is tied to the prevailing long period market order, for how the shares in capacity evolve depends directly on the distribution of profit margins in relation to the distribution of investment strategies. Order results in the revision of order that is the implication contained in (1) and (2). What characteristics does the process of evolution have? The answer is that it has to have characteristics appropriate to a variation selection dynamic, or, as Marshall put it, a principle of substitution in which the processes of accumulation and market growth are mutually determining for the industry and for the differentiated firms.
The immediate consequence of combining the organisation of firm and market in this way is to highlight the possibility that a particular active firm can occupy one of several different, mutually exclusive categories according to its characteristics and the prevailing environment and, moreover, it can change the category it is located in. There are three possibilities:15
- •
Dynamic firms that are within their investment margin and are growing in absolute terms but may be further subdivided according to whether they are rising or falling in relative size. In addition to these two dynamic states we have:
- •
Stationary firms that are profitable but to a degree that is less than the amount required to induce them to invest, and hence they neither grow nor decline absolutely but do decline relatively to the rest of the (growing) market; and, finally,
- •
Marginal firms that have ceased to earn positive profits and are normally contracting absolutely and relatively, and heading for exit from the industry.
Of these three groups it is the dynamic group that drives the evolutionary process of Marshallian adaptation and it is this group that is the focus of the long period method.16 The stationary group may account for a large share of the total market but they do not impose development on the industry. For the marginal firms too, investment strategy is of no relevance; rather, their problem will be how to manage the relation between reductions in output and reductions in capacity.
To identify how the population of firms is distributed across the three groups, we introduce the device of a selection set and the operation of partitioning that set. The selection set is simply another way of representing the data from Figure 1(a) in relation to the particular expenses curve and the threshold prices that determine investment behaviour. Partitioning is the way that we introduce Marshall's flux into the depiction of evolution. In developing this evolutionary toolkit, we will uncover the significance of the representative firm, establish its relation to the marginal firm, and see how it is an essential element in the dynamic processes that Marshall sought to describe.
(ii) Finding the Representative Firm, Partitioning the Selection Set
The selection set is a primitive concept in this evolutionary framework. It is defined by the whole population of firms that are subjected to the same causal forces defined by relations (1) and (2). In principle, it may have any number of dimensions but in our terms it is defined by the two variational characteristics, φẇ and hẇ. We represent this in Figure 1(b) by the convex space defined by the set of points {s} and the linear boundaries that connect them.17 Any firm that has existed in this population since the foundation of the industry is represented by a point in this space, the boundary and interior of which may be sparsely or densely populated. In fact, only two firms are required to define a meaningful selection set. Over time, the nature of the set will change as new firms enter, possibly redefining the boundary, and as existing, active firms innovate by changing unit costs or investment strategy. For the moment let us hold all such changes in abeyance and explain the idea of an evolutionary partitioning while holding constant the number of firms.
Despite Marshall's emphasis on interfirm variety within an industry, it was tempting for post-Marshallians to take an essentialist position and argue, as Pigou (1928) did, that all this talk of differentiated firms and their ‘rising and falling’ was an inessential aspect of the working of the market process.18 Order could be understood without Marshall's resort to variation, its description could be rendered impervious to flux. Unfortunately, the central notion that variation leads to the transformation of order was lost in this approach and with it Marshall's evolutionary intentions. For adaptation and flux is latent in the variety contained in the selection set but how the three broad classes of firms mutually influence each other's differential growth, decline and survival requires some careful elucidation.
It is the prevailing long period normal price taken from Figure 1(a) that provides the first step in the partitioning, for it separates the viable from the non-viable firms. By erecting the locus AV at p on the unit cost axis we deem all the firms located to the right of this locus to be inactive. Cases I and II differ only in respect of the fact that, in the latter, some active, marginal firms are positioned on the AV locus. To the left of AV will lie the dynamic and stationary firms. It is the former that will drive the adaptive process, since it is only this group that invest and in so doing reshape the particular expenses curve and, depending on the co-movements of the demand curve, redefine the long period normal price. Any changes in this price will change the nature of the partitioning and transfer firms between the different possible categories. It is in this way that the evolutionary dynamics is premised on the prevailing market order; hence, Figure 1 is interconnected and our next task is to exploit this fact and further refine the partitioning and separate the dynamic from the stationary firms.
To do so we need the following measures of the population structure. Let si be the share of dynamic firm i in the total output of the dynamic group of firms, with sj and sk defined as the corresponding shares for a stationary firm and a marginal firm in their respective groups. Let e be the share of the non-dynamic firms in total output, and f be the share of marginal firms in the output of the non-dynamic firms.19 It follows that we can define the growth rates for each class as gs =∑ sigi; gc = ∑ sjgj; and gm = ∑ skgk. Since the growth rate of the stationary firms is by definition equal to zero, we can write the aggregate growth rate of the industry's output as20
g= (1 –e)gs+efgm.
(3)In normal conditions this must be equal to the rate of growth of total market demand which is given, from Equation 1, by,
gD=gN–αgp,
(4)where gp is the rate of growth of the long period normal price, gN is the rate of growth of the number of customers in this market, and α is the elasticity of market demand. Relations (3) and (4) capture the fundamental features of the evolution of the industry in which either the rate of change of the normal price or the rate of change of capacity in marginal firms maintains order over time. The distinction between the two cases of market order now becomes important.
(iii) Case I
To identify the boundary between stationary and dynamic firms, we need only equate the growth rate to zero in (2) to define the locus A–A in Figure 1(b), which cuts the horizontal axis at a value equal to the prevailing long period normal price, and has a slope of –µ. By construction, any firm located on or above this locus is stationary although it will be profitable. All the dynamic firms are located below this locus. Thus, a knowledge of the normal price provides the basic partitioning of the industry into non-viable firms in area N, marginal firms on the locus AV, stationary firms in the area C and on the locus AA, and dynamic firms in the areas D. Now that we have identified the subpopulation of dynamic firms, we can use the output shares si to define the average values of unit costs and the propensity to accumulate as  and
and 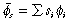 , respectively.
, respectively.
Because the stationary and marginal firms have no active role in the accumulation process, we can focus on the dynamic firms, and if we aggregate (2) across this group, using the weights, si, we find that their average growth rate is given by
 (5)
(5)By using (5) to eliminate p from (2), the growth rate of each dynamic firm, in normal conditions, can be expressed in terms of the deviations of φi and hi from their corresponding dynamic group population averages; thus
 (6)
(6)Equation 6 is fundamental to the evolutionary interpretation of Marshall's theory, since it captures the different contribution that each dynamic firm makes to the reshaping of the particular expenses curve and to changing the structure of the industry. It also embodies a distance from mean dynamic or replicator principle that is the signature of a variation cum selection-based evolutionary processes. The expansion of any one firm relative to the growth of capacity as a whole depends on how its characteristics compare to the population averages: a higher than average efficiency and a greater than average propensity to invest support growth at a rate greater than the group average.21 The relative rising and falling of firms also captures Marshall's principle of substitution in which the growth rate of each firm is mutually determined with the growth rates of its rivals. The growth rate diversity that ensues is the clue to Marshall's evolutionary dynamics.
By equating (6) to zero we can derive an alternative expression for the locus A–A in terms of the characteristics of the dynamic firms and their deviations from average behaviour in the dynamic group. Taking account of (3) we can write the stationary–dynamic boundary as
 (7)
(7)There is one further element in the partitioning to be uncovered, that which separates rising from falling firms, and this is where the representative firm makes its first appearance.
(iv) The Representative Firm
Where in the selection set can we locate the representative firm? To answer this question we have to deal with two problems. The first problem relates to the fact that the firms are differentiated in two dimensions, creating the possibility that representative behaviour serves only to define a trade-off between unit costs and investment strategies. The second problem is deeper, and connects to the very idea of Marshall's industries as populations of firms. By a population, we simply mean a set of entities constituting an ensemble. By an evolutionary population, we mean a set of entities whose changing relative importance in the set, however measured, is the caused outcome of specific selection and other causal processes operating equivalently on all the members of that population. Marshall's industries in this view are evolutionary populations unified by the action of common market forces. Hence, the problem: a representative firm is only representative relative to some evolutionary population, and if we change the population in terms of its constituent firms or the causal processes acting on them, then we change necessarily what we mean by representative.
Recall the definition above, a representative firm is some average firm that maintains constant its share in the output of the relevant population. From this we see immediately that two notions of representativeness come to the fore. One is Marshall's representative firm that grows as quickly as the total market, a definition that makes no distinction between the different categories of active firm, whether dynamic, stationary and marginal. Marshall's representative firm maintains constant its share in total market capacity and demand for the industry. The other is a dynamically representative firm, one that grows as quickly as the population of dynamic firms in the population. The dynamically representative firm maintains constant its share in the total output of the dynamic group. The two notions of what it is to be a representative firm are quite different and only equate to one another when the only active firms are in the dynamic category. One can see immediately, that, in general, the dynamically representative firm must expand more rapidly than Marshall's representative firm, which, of course, is growing at the same rate as the industry as a whole.
To locate the dynamically representative firm we proceed as follows. We have already identified the relevant population as the subset of firms located below the locus A–A in Figure 1(b). However, this ensemble of dynamic firms consists of two subgroups, occupying the regions labelled D1 and D2, according to whether the firms in question are rising or falling in terms of their relative outputs. To separate these two groups is to identify the dynamically representative firm. Because such a firm is growing at the average rate for the dynamic subpopulation, we set gi = gD/(1 – e) in (6), to define a locus labelled R–R in Figure 1(b). This locus passes through the point of population means for the dynamic subpopulation so that dynamically representative behaviour is described in terms of the capacity share weighted average characteristics of the firms in the dynamic group. This result is not arbitrary but flows from the underlying theory. The position of this locus is independent of the market growth rate and the structure of the active population, and it is given by
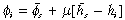 (8)
(8)It also has a slope of –µ, and it stands vertically below A–A by a distance that measures gs, the growth rate of the dynamic group. Like A–A, the locus R–R is a statistical construction, a demarcation, in this case, between two classes of dynamic firms. Any actual firm whose unit costs and strategic investment stance place it on this locus will be growing at the same rate as the dynamic group as a whole, and so may be labelled dynamically representative. Either side of the R–R locus we find Marshall's flux. Any firm in the region D1 between this locus and A–A is expanding absolutely but declining relatively to the output of the dynamic group as a whole. Any firm below R–R in the region D2 is expanding absolutely and relatively to the dynamic group.22 However, pace Marshall, ‘representativeness’ does not define a single firm but rather a whole possible family of them, in fact those hypothetical firms that lie on the locus R–R.23 Of course, no actual firm need lie on this locus at any one time, nor does our account require that there is such a firm. This locus simply defines the possibility that any firms that should happen to be on it will be growing absolutely but neither rising nor falling relatively in the dynamic group. This is the dynamic significance of the representative firm, a significance that is entirely lost in a static treatment of competition as a state rather than as a process.
If A–A identifies the stationary–dynamic boundary and locates the zero growth firms, we might now enquire which of the firms in the selection set will have the highest long period growth rate. Since growth rates increase as we move towards the origin from A–A, it follows immediately that it is firm b on the south-west boundary of the selection set that is the fastest growing, and is thus the dynamic firm on which the output of the industry is concentrating. Given the shape of the selection set, the location of this firm depends only on the investment coefficient, µ, that is to say on the assumed characteristics of the capital market and the investment requirements for expansion of the firms. It is immediately apparent that, in general, the fastest growing firm is not the least cost firm in the selection set, for this is firm a in Figure 1(b). As in any variation cum selection analysis, the competitive dynamic selects for the characteristics that maximise expansion (fitness), not the characteristics that only maximise efficiency. Indeed, only if all firms followed the same investment strategy would efficiency be maximised in this adaptive process.24
We have already indicated that our dynamically representative firm is not, in general, Marshall's representative firm. Where now do we locate Marshall's representative firm, that firm that maintains its share in the total market rather than any one submarket? Necessarily it too must be a dynamic firm, for it must be growing if the market is growing, although it is necessarily growing less rapidly than the dynamic representative firm we have just identified. To identify its properties we set gi = gD in (6) to define the locus labelled M–M in Figure 1(b). This locus is given by the equation
 (9)
(9)This locus lies in region D1 above the locus R–R and below the locus A–A, its position depending on the share of non-dynamic firms in the overall population of active firms, and on the overall growth rate of market demand. Any firm on this locus is maintaining a constant share in total industry capacity and thus market demand but has a falling share of the capacity within the dynamic group of firms. Where this locus cuts the unit cost axis is defined by the point h̃* in Figure 1(b).25 Around Marshall's representative firm there is flux too, not in terms of shares of output in the dynamic subpopulation, but in terms of changing shares of total industry output. It should now be clear why it is only in an industry consisting entirely of dynamic firms that the two concepts of the representative firm coincide. As soon as we allow for non-dynamic firms they diverge, and it is the notion of the dynamic representative firm that we must give primary attention to for it is the dynamic firms that are the carriers of long period adaptive forces. The dynamically representative firm therefore acts as the fulcrum around which the industry is evolving and around which all of the flux in the industry can be rendered intelligible.
The idea of a representative firm, in either form, is derived from the idea of a long period partitioning of the selection set. Partitioning provides a complete characterisation of the rising and falling of firms, their viability and non-viability. Indeed, Figure 1a and 1b are complementary ways of representing the relation between a market order and its self-transformation. Partitioning is also the way we give content to the idea of economic structure not only in terms of relative scale but also in terms of dynamic characteristics of different firms and groups of firms. This is Marshall's point, the industry is always coordinated but the firms are all different, in terms of growth or decline and whether they are dynamic, stationary or marginal. It is from this heterogeneity that the progress of the industry is derived. Before we turn to the question of the necessary restless nature of this partitioning it will be useful to introduce a simplifying analytical device.
(v) A Simplifying Device
The simplifying device is as follows. For any dynamic firm we identify a hypothetical shadow firm, its identical twin we shall call it, which always has the same growth rate when faced with the same long period normal price. Consequently, every statement made for the original firm can be rendered equivalently in terms of its twin. Each twin firm, however, is defined only in terms of a corresponding hypothetical unit cost level and can thus be located on the ordinate axis in Figure 1(b). To define each twin firm we set a zero value to the strategy parameter φi and compensate for the effects on its growth rate by assigning to it a hypothetical unit cost level denoted by  , where26
, where26
 ((10a))
((10a))It follows that we can define the dynamically representative twin in equivalent fashion as one with average, twin unit costs equal to
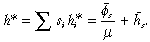 ((10b))
((10b))This particular value denotes the point at which R–R cuts the unit cost axis in Figure 1(b). Any dynamically representative firm, positioned on R–R, is dynamically equivalent to the twin firm defined by h*, while Marshall's representative firm, positioned on M–M, is dynamically equivalent to the twin firm defined by the hypothetical cost value, h̃*, where
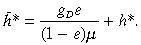 ((10c))
((10c))This simplifying device will help greatly in the following exposition and to illustrate this claim we use it to explore case II.
(vi) Case II
Very briefly, we must outline the case when some marginal firms are active and the demand curve is positioned as is curve D–D in Figure 1(a). This is the regime of quantity adjustment referred to above, in which the unit cost level in the active, marginal firms measures the long period normal price. It is not as straightforward a case as it might seem, and I will have to suppress many difficulties by sticking with the long period normal assumption that when output contracts absolutely, capacity contracts in step. On this assumption, marginal firms exit the industry when their output has contacted to zero, when their economic weight has disappeared. To state the method so boldly is simply to highlight its deficiencies, and to mask the importance of the processes associated with the demise of firms to the course of industry evolution. Accepting the magnitude of this unfinished business, we can still make some progress using the selection set and its partitioning.
All that changes in terms of Figure 1(b) is that we ‘lock’ the price at the unit cost level in the marginal firms to set p = hm, and since the locus A–V is now populated by these firms, their share in total output, f, is rendered positive. On the demand side there is a further consequence of the ‘locked’ price, namely, that gN = gD, and the rate at which the demand curve is being displaced, the natural growth rate of the market, is an important determinant of the fortunes of the marginal producers. What determines their aggregate growth rate? Since they are not investing, their problem is one of capacity utilisation and, since the price is ‘locked’, we can use (6b), (3) and (4) together with the twin cost values to determine their collective growth rate, which is given by
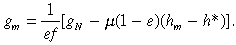 ((11a))
((11a))As illustrated in Figure 1(b), this growth rate is negative, that is to say, the long period normal price supports a growth rate of the dynamic firms consistent with the decline of marginal producers.27 Since gN = gD, it follows that the vertical distance between A–A and M–M now measures the natural market growth rate and any Marshallian representative firm located on M–M will be growing at the rate gN. Let the twin unit costs corresponding to this case be signified by h̃**. It follows that the value of h̃**, where M–M now cuts the unit cost axis in Figure 1(b), is equal to
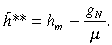 ((11b))
((11b))By setting gN = gD in (10c) we can also express this in terms of the twin costs of the dynamic representative firm rather than the costs of the marginal firm; thus28
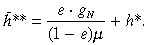 ((11c))
((11c))For completeness, we can also represent the growth rate of the marginal firms entirely in terms of the various, twin cost values using (11b) as
 ((11d))
((11d))How the market order evolves in the presence of marginal firms thus depends on the relation between their twin unit cost level, the natural growth rate of the market and the structure of the industry, as expressed in the output share of the non-dynamic firms. As this process evolves, we reach a point in time when all the marginal capacity has been eliminated and the order reverts to case I as described above. It will not be lost on the reader that a dynamically representative firm even plays a role in the fate of the marginal firms, a hint of its acting as a fundamental determinant of the industry's dynamics.
The point that we have attempted to establish so far is that Marshall's framework of industry analysis was designed to identify the evolutionary consequences of interfirm heterogeneity in behaviour. It is a rich framework, by no means limited to two dimensions of firm variation, and it is indeed a pity that Marshall is usually misinterpreted as conceiving of his firms in terms of cost differences alone. This is why we have added the second dimension of investment strategy to demonstrate Marshallian variation in relation to the long period forces of investment. There need be no limit to this process of generalisation; we can accommodate as many dimensions of interfirm variation as we wish, provided that they are relevant to the process of competition. Indeed, variations in product type and quality would be of prime importance in this regard.29 This is the great virtue of a Marshallian approach to economic evolution: the greater the variety. the more we are likely to explain about real world competitive processes. Variation is not the nuisance that the essentialists would have us believe, it is the route to understanding why the economic world changes in the way that it does. Marshall clearly sensed this fundamental fact and its relation to the ceaseless development of the system (Shackle, 1965, p. 42). But further elaboration of the framework is not our task here; rather, we must recognise that the market order and its partitioning is an evolving order. It is this elemental fact that raises so many potential difficulties in comprehending the nature of the representative firm, for it means that the representative firm is always changing its character. How is this evolution to be understood?
IV Flux and Revisions to Normal Value: The Dynamic Significance of the Representative Firm
We have already established how Marshall presented two accounts of the theory of normal values in the Principles. One, the marginal firm version, based on the interaction of a demand curve and a long period particular expenses curve, and the other, the representative firm version, based on the idea that the representative firm forms an attractor for normal value in the long period. Marshall's theory needs both but the two accounts play very different roles in his analysis. As Figure 1(b) illustrates, the normal, non-stationary state configuration of the market order is one in which p > h̃ > h* > hs. Marshallian long period normal value normally exceeds the unit costs of the representative firm, Marshallian or dynamic, but this does not render the concept redundant. What we shall establish now is that the dynamic representative firm plays two distinctive roles. It serves as one determinant of the attractor for normal value, and it serves as the fulcrum around which the long period transformative forces are ordered. The fundamental point to grasp is that an evolutionary process depends on a supporting concept of order and when the causal determinants of order change so the pattern of evolution will change too.
(i) Normal Value
How does normal value evolve? From Figure 1(a) it does so in a fashion that depends on the relative rates of change of the market demand curve and the particular expenses curve but how the later evolves depends on the changing nature of the partitioning in Figure 1(b). If we provisionally hold constant the structure of the industry, then we can obtain a partial grasp on the immediate evolution of long period normal value. Again the distinction between our two cases of market adjustment matters.
The fixed price case, II, with normal value locked by the cost structures of active, marginal firms is easily treated. As long as these firms are viable, the long period price is fixed by their costs and, consequently, no question of convergence to costs in the representative firm or any other firm for that matter can arise. This is the quantity adjustment case, and it continues to hold until we re-establish the conditions for case I. This later is more challenging, for now the process of investment in the dynamic subpopulation of firms redefines the particular expenses curve and changes the long period price, in a way that also depends on the rate at which the demand curve is changing. Thus, the rate of change of the long period normal price serves to maintain the market order by matching the rate of growth of total capacity with the rate of growth of demand. The combination of cases II and II in fact leads to a very clear outcome. Phases in which long period normal value is changing (case I) are punctuated by periods when it is stationary (case II). Consequently, the normal case, in which successive groups of marginal producers are eliminated, entails that the long period price follows a series of downward steps over time. Between the steps it varies at a rate determined by the relation between the growth of capacity and demand.30
How the long period, normal price evolves in case I is readily established. On equating (3) and (4), and noting that g = (1 – e)gs > gN, we derive the following logistic differential equation to capture its evolution.31
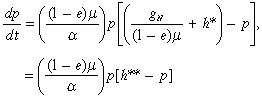 ((12a))
((12a))where h** is the twin cost value defined by
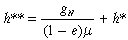 ((12b))
((12b))This twin cost value stands above unit costs in the dynamically representative firm by an amount that is greater the greater the natural growth rate of the market and the smaller is the share of the dynamic firms in the total output of the industry.32 This is the sense in which unit cost in the dynamically representative firm serves as the anchor for the system of price adjustment.
What can we say in the light of these results about Marshall's connection between long period value and the costs of the representative firm? Since p > h**, the normal price declines over time, and h** acts as its attractor; and, moreover, the system is globally stable for given values of gN and e.33 The rate of convergence to h** increases with the share of the dynamic firms in total capacity, it increases with the investment rate parameter, and it is smaller for larger values of the elasticity of demand. All this fits with the economic logic of long period evolution.
The wider significance of this formulation is that it is the dynamically representative firm, rather than Marshall's representative firm, which underpins the attractor for long period normal value. This attractor corresponds to a price, and a profit margin, that would enable a representative firm to grow at the same rate as the natural market growth rate, gN.34 This is the sense in which Marshall's theory correctly interpreted the evolutionary dynamic of the competitive process, yet there are important differences that we have uncovered between the different notions of a representative firm. Most importantly, the long period normal price converges on h** > h̃* > h* > h̄s and it is not attracted to costs in the twin representative firm except when the natural market growth rate is zero. Here again, Marshall's intuition was sound, when the market is stationary, the long period normal value is attracted to costs in the (dynamically) representative firm h*. However, it is the twin cost values not the actual costs that define the attractor, and the fact that twin and actual costs diverge is the direct consequence of allowing firms to have investment strategies, as they do in Marshall. Only if the strategic investment parameters, φi, are zero for each dynamic firm, will true unit cost in the dynamically representative firm be the attractor for long period normal value.
There is yet a further complication to Marshall's desire to equate long period normal value with unit cost for the representative firm. It is that the process defined by (12) of convergence of value to ‘representative costs’ is itself a partial process; one that is continually being revised by the long period forces that evolve the particular expenses curve. These forces are repartitioning the selection set continuously, so redefining the representative firm, and revising the structure of the industry and with it the relative importance of its dynamic firms. Consequently, the values of h** and e in (12) evolve too, and they only stop evolving when all the variety has been driven out of the population, and the industry has converged on the most dynamically efficient of the firms, firm b in Figure 1(b). It is in this process of convergence that the dynamic representative firm plays its second role as the fulcrum around which the industry is continually restructured and, moreover, it is a fulcrum that is continually changing under the influence of Marshallian flux.
(ii) Marshallian Flux
We have seen how partitioning generates a snapshot picture of the evolutionary structure of the industry and how different firms may fall into very different economic categories, yet an evolving system is one in which this partitioning is always changing. Repartitioning is the consequence of Marshallian flux, the restless dynamics of an industry in which firms differ in efficiency and investment strategy, and these fundamental evolutionary processes are of three distinct kinds: those due to market selection and the implied differential growth of firms; those due to the transfer of firms between the dynamic, stationary and marginal categories; and those due to the differential growth of the different groups of firms as a whole, and the consequent restructuring of the industry between the dynamic, stationary, marginal and non-viable groups. Each one is a different reflection of the principle of substitution, and not one of these processes could arise in an essentialist world of identical firms. Moreover, each one reflects the fundamental evolutionary principle that variation drives change, and to illustrate this principle we take each dimension of flux in turn.
The Dynamics of the Selection Process: Fisher's Principle
It is not unrealistic to claim that Marshall was very close to formulating an explicit theory of market evolution as a variation cum selection process; he certainly understood the significance of firm heterogeneity in relation to his principle of substitution, the closest he came to articulating the concept of dynamic selection in the Principles and in Industry and Trade (1919). Unfortunately, as many have argued, he lacked the means to spell this out in any detail.35 Yet within a decade of the publication of the last edition of the Principles, the biologist Fisher (1930) set out the necessary apparatus, an apparatus that became central to the subsequent development of evolutionary theory. Fisher's great contribution, judged with the benefit of hindsight, was to formulate evolutionary theory in terms of the distance from mean dynamics of the replicator principle. It is this crucial, conceptual innovation that immediately connects him to Marshall, the principle of substitution and the representative firm. At the centre of this scheme is a fundamental aspect of evolutionary dynamics; namely, that the evolution of the population depends on how the characteristics of its members are jointly distributed around the associated population means. From this it follows that the dynamic representative firm, far from being the fifth wheel of Marshall's analysis, is in fact the conceptual fulcrum around which an industry evolves. To establish this is straightforward. Beginning with our fundamental replicator relation (6a) we can rewrite this to express the evolution of the market shares of the dynamic firms as
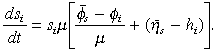 ((13a))
((13a))In terms of the twin equivalents this becomes
 ((13b))
((13b))This formulation makes the replicator dynamics of industry evolution particularly transparent, remembering that (13b) only holds for the dynamic firms satisfying p > 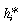 . Thus, we see immediately in (13b) how the dynamically representative firm is the fulcrum around which the dynamic group of firms evolves, rising or falling relatively according to how each individual firm stands in relation to the said representative firm when both are expressed in twin terms.
. Thus, we see immediately in (13b) how the dynamically representative firm is the fulcrum around which the dynamic group of firms evolves, rising or falling relatively according to how each individual firm stands in relation to the said representative firm when both are expressed in twin terms.
The fact that the dynamic firms are rising and falling relatively around the dynamically representative firm, naturally implies that the value of h* = ∑ si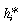 is changing too, even when the individual values of
is changing too, even when the individual values of 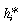 are constant. That is to say, the measure of this dynamically representative firm is not constant but evolves according to
are constant. That is to say, the measure of this dynamically representative firm is not constant but evolves according to
 (14)
(14)where Vs(h) is the variance of the hypothetical, twin cost values around h*.
This is an exact example of what biologists call Fisher's Fundamental Law of Selection, that the rate of evolution due to selection of some average population characteristic is proportional to the variation of that characteristic around the population average. In Marshallian terms, the dynamic representative firm evolves in a way that depends on the distribution of variety in firm's characteristics and on the economic significance of that variation for interfirm performance.36 What (14) captures is the centrality of the dynamically representative firm to an understanding of a Marshallian theory of competition: not perfect competition but open competition, competition that is only possible because the firms are different in their business traits and competitive characteristics.37
It also follows from (14) that the competitive process imparts a direction to the evolution of the industry. Indeed, competition serves to reduce h* over time, from which it follows that the locus R–R is always contracting towards the origin at a rate which is proportional to the variance of the twin cost values. The set of rising firms is being squeezed ever smaller by the competitive process as the industry concentrates on the dynamically fittest firm(s) in the selection set. Having established what happens in terms of the twin cost values, it is also of interest to enquire into the evolution of the true characteristic averages 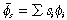 and
and 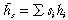 , for it is clear from the definition of h* that the following conservation condition must hold; namely,
, for it is clear from the definition of h* that the following conservation condition must hold; namely,
 (15)
(15)We know that this expression is negative, but this does not tell us how the component averages on the right-hand side evolve individually. To illustrate the problem, we can focus on the evolution of average unit costs in the dynamic group.38 By virtue of (6) we find that the evolution of average unit costs h̄s is represented by
 (16)
(16)where Cs(g, h) is the covariance between unit costs and growth rates across the population of dynamic firms. This is, once again, Fisher's principle at work, the rate and direction of evolution depends on the co-distribution of variation across all the characteristics in the relevant population; that is to say, it depends on correlation of characteristics, not just upon variation of characteristics. The covariance defined in (16) is what we might call a secondary moment, because it is defined in respect of variables, the firm growth rates, which are also determined by the causal forces acting on the population. If we use (6) to eliminate the growth rates, then we find that
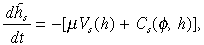 ((17a))
((17a))where and 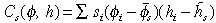 are primary moments of the subpopulation of dynamic firms.39 From relation (17a) it is not immediately apparent how the population average h̄s evolves. The variance term is reducing the average but this effect can, in principle, be offset by a sufficiently large negative value for the covariance term. Thus, while h* is invariably declining under the forces of selection, no such simple rule applies to h̄s. To make this finding even more precise, we can imagine the experiment of regressing the output share weighted values of siφi on the values of sihi, within the dynamic portion of the selection set (the region below A–A in Figure 1b) at a particular moment in time. The resulting coefficient for the slope of the regression line at that moment is
are primary moments of the subpopulation of dynamic firms.39 From relation (17a) it is not immediately apparent how the population average h̄s evolves. The variance term is reducing the average but this effect can, in principle, be offset by a sufficiently large negative value for the covariance term. Thus, while h* is invariably declining under the forces of selection, no such simple rule applies to h̄s. To make this finding even more precise, we can imagine the experiment of regressing the output share weighted values of siφi on the values of sihi, within the dynamic portion of the selection set (the region below A–A in Figure 1b) at a particular moment in time. The resulting coefficient for the slope of the regression line at that moment is
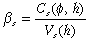
and so we can rewrite (17a) as
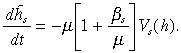 ((17b))
((17b))This is a much neater way to capture the force of Fisher's principle, and it follows that h̄s is decreasing if βs > –µ. Otherwise, it is increasing, and, on average, the industry would be growing less efficient at that moment.40 Thus, we see how statistical dependence and variation combine together in Marshall's evolutionary dynamics to redefine continually the dynamically representative firm and its component characteristics. Not by variation alone but by variation and correlation. That is why it is a dynamic concept and can play no useful role in a static theory of a competitive industry.
Transfer Effects
The rise and fall of individual firms, whether relatively or absolutely, is the central form of economic flux that we find in Marshall's theory of industrial change. The logic of our argument, however, uncovers flux of different kinds that we may dwell on briefly. The most interesting are consequent on any change in the long period normal price, for we have seen how that will repartition the selection set and potentially transfer active firms between the dynamic, stationary and marginal groups. Thus, for example, a lower market price relocates the A–A locus to the left, potentially transferring dynamic firms into the stationary group and stationary firms into the marginal or non-viable groups, and, thereby, changing the associated statistical distributions of firm characteristics. This repartitioning adds a further source of change to the population averages over and above those created by Fisher's principle and we can illustrate this briefly by focusing again on average unit costs.
Suppose the transfer is from the dynamic to the stationary group. Let the firms transferring into the stationary group have an aggregate output rate of Q at the moment of transfer. This rate of transfer, when expressed as a proportion of the output of the dynamic group, we define by the rate xs, and when expressed as a proportion of the output of the stationary group by the rate ϑc.41 Let h̄Q be the average unit cost level for the group of transferring firms, constructed by weighting the unit cost levels by their output shares within the transferring group. The total change in the respective average unit cost levels in the dynamic and stationary groups is then given by the augmented Fisher rule
 ((18a))
((18a))for the dynamic group, and
 ((18b))
((18b))for the stationary group.42 How h̄Q compares with the pretransfer averages in the two groups we cannot say because it depends on which firms make the transfer. There is certainly no presumption that they are the higher cost firms from the dynamic group, it all depends on the distribution within the selection set and the corresponding correlation of characteristics within the two groups before and after the transfer.43
Structural Change Effects
Having dealt with selection and transfer effects, it remains to record how the overall shares of the different groups change as a result of the different growth rates in their respective outputs. To illustrate, let us focus on the evolution of e, the share of non-dynamic firms in industry output. If we limit ourselves to case I, then it follows that44
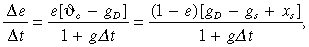
or in continuous time45
 (19)
(19)Similar expressions follow to capture the changes in the other measures of overall structure, as the reader may testify, but now it is appropriate to sum up.
The net outcome of the structural, transfer and selection effects is to repartition continually the selection set, to modify the process of convergence of p on h** and to evolve h** as indicated in (12). Thus, the establishment of order and the transformation of order are firmly intertwined. We can no more explain changes in the prevailing long period normal price without reference to the changing particular expenses curve than we can explain the changes in the particular expenses curve without reference to the changing normal price. This is the great virtue of Marshall's long period economics, transformation depends on order, the two notions are inseparable. It was the attempt to separate them in the hands of the post-Marshallians that effectively marginalised Marshall's economics and destroyed its links with evolutionary theory.
V Conclusion
The devices of the selection set and its partitioning provide an evolutionary toolkit to understand afresh Marshall's account of a market order and the representative firm: an account that is simultaneously combined with a great deal of internally generated market flux. Yet the reader may legitimately complain that we have not done justice to Marshall's thought. We have indeed set aside all the ‘living force and movement’ that is so central a feature of his work: innovation in technique, organisation and business strategy, entry of new firms, and external and internal economies are simply absent in this treatment but never in Marshall. It has long been recognised that the equilibrium status that Marshall gives to the industry is denied to the individual firms. In fact, in Marshall, neither firms nor the industry are in equilibrium; rather, they are each different forms of transient order coordinated by different principles of organisation. Firms are not only heterogeneous, they are continually changing and so is the industry. Nonetheless, innovation, entry and increasing returns have their meaning in terms of changes in the selection set, changes to which the market order adapts and in part induces. So this paper is merely the prologue to such an extended treatment. To understand their force we must first understand their evolutionary nature and this is what our framework provides, a basis for discussing the many ways in which economic self-organisation is combined with the transforming effects of novelties.
We have shown how Marshallian flux is essentially a process of adaptation to the variety contained in the industry population, and how the patterns of flux follow clear evolutionary principles. Marshall was correct ‘The tendency to variation is a chief source of progress’ (P, V, p. 355) and now we can see why. But evolution is more than variation; it requires the organisation of firms and the market process to generate that correlation between differential knowledge and economic advance. Most importantly of all, the concept of a representative firm is re-established as an indispensable element in a Marshallian evolutionary analysis. With due apology to the memory of Lionel Robbins we might conclude that this is some apparition!
Footnotes
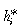 . We have met
. We have met 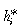 already in Figure 1(a).
already in Figure 1(a).