Terms-of-Trade Shocks and Exchange Rate Regimes in a Small Open Economy*
Abstract
We examine the impact of terms-of-trade shocks on key macroeconomic variables by numerically solving a dynamic stochastic general equilibrium model of a small open economy. The model considers nominal price rigidity under different exchange rate regimes. The numerical solutions obtained are consistent with the empirical regularities documented by Broda (2004), in which output responses to shocks are smoother in floats than in pegs; in moving from pegs to floats, the rise in nominal exchange rate volatility is coupled by the rise in real exchange rate volatility; and in both exchange rate regimes, net foreign assets is the most volatile variable.
I Introduction
The merit that is often attributed to flexible exchange rate regimes over fixed exchange rate regimes is their ability to insulate the economy more effectively against real shocks. This hypothesis was first proposed by Friedman (1953) in the early 1950s. Since then the choice of the exchange rate regime has been an area of great controversy and debate. In theory, the presence of price stickiness explains why the exchange rate regime may matter. When an economy is hit by real shocks, the economy that can change relative prices more quickly will have smaller and smoother adjustment in output. This is particularly true in an economy with price stickiness where the speed at which relative prices can adjust depends crucially on the exchange rate regime. Under flexible exchange rate regimes, relative prices can adjust instantly through changes in the nominal exchange rate; whereas under fixed exchange rate regimes, relative prices can adjust only at the speed that is permitted by price stickiness, which is usually much slower. Therefore, flexible exchange rate regimes allow smoother adjustment in output and quicker adjustment in relative prices than fixed exchange rate regimes.
The theoretical proposition by Friedman has subsequently prompted international economists to examine the effects of shocks on economic variables with different types of exchange rate regimes. Although some focused on building theoretical models (Poole, 1970 and Dornbusch, 1980), others focused on documenting empirical regularities (Baxter & Stockman, 1989; Taylor, 1993; Devereux, 2000; Bleaney & Fielding, 2002; Collard & Dellas, 2002; Broda, 2004).
From the theoretical perspective, many economists still believe that the relative merits of the exchange rate regimes crucially depend on the type and the nature of shocks hitting the economy.1 When the shocks are nominal in nature, fixed exchange rate regimes automatically prevent them from affecting real output. For instance, when money demand increases, under fixed exchange rate regimes, money supply increases as the monetary authority buys foreign currency to prevent the appreciation of the local currency. This leaves real output unchanged. In contrast, under flexible exchange rate regimes, money supply is left unchanged and the local currency is allowed to appreciate so real output falls and money demand returns to its initial level.
When the shocks are real in nature, flexible exchange rate regimes are more effective as they allow a smoother adjustment to real shocks. For instance, when terms of trade deteriorates in an economy where prices are sticky, under flexible exchange rate regimes the nominal exchange rate depreciates. The depreciation of the nominal exchange rate, in turn, increases the price of tradable goods that partially offsets the effect of the negative terms-of-trade shock. However, under fixed exchange rate regimes, money supply decreases as the monetary authority contracts money supply to prevent a nominal depreciation of the local currency. This response is inherently contractionary and induces an additional fall in real output. Therefore, fixed exchange rate regimes have to rely on the adjustment in domestic prices to pull the economy out of recession.
From the empirical perspective, the evidence is far from conclusive on the effects of shocks on real output, the real exchange rate and the nominal exchange rate. Baxter and Stockman (1989) show empirical insensitivity of output volatility to the type of exchange rate regime. They also find that a broad range of real macroeconomic variables are independent of the underlying exchange rate regimes. Devereux (2000) analyses the effects of supply, fiscal and money shocks using a model with nominal goods priced in the sellers’ currency and with prices that are sticky over one period. He finds that the exchange rate does not respond to either supply shocks or fiscal shocks, so macroeconomic volatility is the same across fixed and flexible systems. In contrast, Collard and Dellas (2002) suggest larger differences in volatility across regimes. They find that output volatility is significantly higher under fixed exchange rate regimes relative to flexible exchange rate regimes. Using data from 80 developing countries, Bleaney and Fielding (2002) also show that countries with fixed exchange rate regimes have a significantly greater output variance than a typical floating-rate country.
Although the theoretical literature emphasises that the relative merits of fixed and flexible exchange rate regimes depend on the nature of the shocks, the empirical literature does not clearly distinguish between nominal and real shocks. Hence, it would be meaningful for an empirical study to clearly identify real shocks from nominal shocks. This is particularly true if one can study the effects of terms-of-trade shocks on macroeconomic variables under alternative exchange rate systems. There are two reasons for choosing terms-of-trade shocks. First, terms-of-trade disturbances are regarded as a major source of output fluctuations in a small open economy (Mendoza, 1995 and Kose, 2002). Second, as most developing countries’ export earnings are dominated by a narrow range of primary commodities (Kose, 2002), and the prices of these primary commodities are subjected to large price fluctuations in the world market, terms-of-trade fluctuations in developing countries are observed to be more volatile.
Because of the prominent role played by exchange rate regimes in developing countries, Broda (2004) examines the effect of a single real shock given by terms-of-trade changes of a country under different exchange rate regimes. Using data from 75 developing countries from 1973 to 1996, he identifies the responses of real GDP, the real exchange rate and consumer prices to exogenous terms-of-trade changes across different regimes. His findings generally support Friedman's proposition. First, the short run real GDP response to terms-of-trade shocks is significantly smaller in countries with flexible exchange rate regimes than those with fixed exchange rate regimes. Second, the depreciation of the real exchange rate is immediate after a negative terms-of-trade shock under a flexible exchange rate whereas the depreciation is slower under a fixed exchange rate. Third, countries with flexible exchange rate regimes can absorb real shocks better than those with fixed exchange rate regimes.
Given the significance of terms-of-trade fluctuations on domestic macroeconomic variables, understanding the transmission and propagation of terms-of-trade fluctuations is crucial in the design and conduct of macroeconomic policies in both industrialised and developing countries. In this paper, we use an intertemporal equilibrium framework with nominal price rigidities and imperfect competitive markets to analyse the dynamics of some macroeconomic variables arising from terms-of-trade fluctuations under alternative exchange rate systems.2 We adapt the model of Lane and Milesi-Ferretti3 (2004) and construct an intertemporal framework with tradable and non-tradable sectors. The existence of traded and non-traded goods provides a richer framework for analysing the dynamics of important macroeconomic variables resulting from terms-of-trade shocks. Furthermore, by incorporating non-traded goods, the model is extended to involve both intertemporal and intratemporal substitution effects.
In our model, the non-traded sector is assumed to be a monopolistic competitive market4 where prices are sticky. The traded sector, on the other hand, is assumed to be a perfectly competitive market where prices are fully flexible and the law of one price holds. The asymmetric treatment of the two sectors allows us to show the link between the sectors when there is a terms-of-trade disturbance. We clearly show the propagation mechanism of terms-of-trade shocks on the dynamics of some macroeconomic variables.
We use numerical solution methods to demonstrate the impulse responses of macroeconomic aggregates induced by a negative terms-of-trade shock. We examine the link between terms-of-trade shock and some macroeconomic aggregates by numerically solving a dynamic stochastic general equilibrium model of a small open economy. The numerical solutions of the model are compared with the empirical regularities documented by Broda (2004). Our results are broadly consistent with the following empirical regularities. First, the responses of short-run output to shocks are significantly smoother in floats than in pegs; second, in moving from pegs to floats, the proportional rise in volatility of the nominal exchange rate is coupled by a rise in volatility of the real exchange rate; and third, in all types of exchange rate regimes, the most volatile variable is the holding of net foreign assets.
The paper is organised as follows: Section II lays out a dynamic general equilibrium model of a small economy that combines nominal price rigidity with a terms-of-trade shock; the model parameterisation is provided in Section III; the fluctuations of the output, the real exchange rate and the price level as a result of terms-of-trade shocks are analysed in Section IV; and the conclusions are in Section V.
II The Model
We derive an intertemporal model of a small open economy to analyse the way in which terms-of-trade shock affects some real variables in an economy with different exchange rate regimes. To address the intratemporal aspects of the problem, we make three main assumptions. First, the importable is consumed but not produced, and the exportable is produced but not consumed. In other words, the importable and the non-tradable are consumed domestically but the exportable and the non-tradable are produced domestically. Second, investment is held constant and the capital stock is an endowment that is not affected by the terms-of-trade shocks. Third, the economy is small in the sense that it cannot influence the terms of trade of the economy.5 We also assume that the output of the traded goods sector is an endowment of the tradable good yT, which is sold in the world markets at the export price of 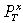 , where
, where 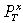 is measured in units of the imported consumption good and the imported consumption good is used as the numeraire. As consumption of the export goods is assumed to be zero,
is measured in units of the imported consumption good and the imported consumption good is used as the numeraire. As consumption of the export goods is assumed to be zero, 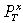 , by definition is the terms of trade and is exogenous to the country.
, by definition is the terms of trade and is exogenous to the country.
(i) The Households
Consider an economy populated by a continuum of yeoman-farmers along the unit interval [0, 1]. The representative agent aims to maximise the intertemporal utility function which is given by:
 (1)
(1)where β ∈ (0, 1), σ, h > 0. β is a preference parameter, which is known as the subjective discount or time-preference factor, σ is the intertemporal elasticity of substitution, and h is the marginal disutility of work. Et is the expectation operator. yNt(j) is the production of j-th variety of the non-traded goods. The subscripts N and t represent non-tradable goods and time, respectively. The second term in the objective function captures the disutility of work effort. The consumption index Ct, aggregates the consumption of traded goods (CTt) and non-traded goods (CNt):
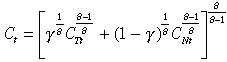 (2)
(2)where θ > 1 is the intratemporal elasticity of substitution between the traded and non-traded goods, and γ ∈ [0, 1] is the share of consumption of the traded good in total consumption. The consumption-based price index is given by:
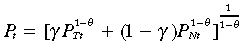 (3)
(3)where PTt is the price of the traded good expressed in units of domestic currency. PNt is the price of the non-traded good.
Agent j is the monopoly producer of variety j of the non-traded good. The optimal allocation of any given expenditure within each category of goods yields the demand function for any variety j:
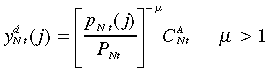 (4)
(4)for all j ∈ [0, 1], where µ is the price elasticity of demand faced by each monopolist and 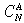 is the summation of the consumption of non-traded good j.
is the summation of the consumption of non-traded good j.
The j-th individual's consumption of non-traded goods can be written as:
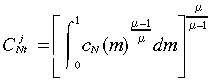 (5)
(5)where m ∈ [0, 1] denotes non-traded goods.
The price of non-traded goods is:
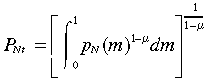 (6)
(6)Each domestic agent holds only one type of asset, namely an internationally traded bond, B. The agent produces a single non-traded good, yNt(j), in a monopolistic competitive way and he receives a constant endowment of yT units of traded good. The flow of budget constraint faced by agent j is given by:
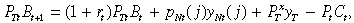 (7)
(7)where Bt is the number of real bonds that is denominated in tradables and rt is the return of the international bond. Maximisation of (1) subject to (4) and (7) generates the following relationships:
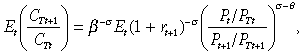 (8)
(8)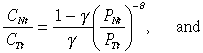 (9)
(9)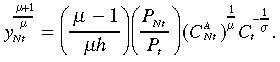 (10)
(10)Equation (8) is the Euler equation governing the dynamic evolution of consumption. Given the interest rate, if the aggregate price level relative to the price of traded goods is currently low relative to its future value, present consumption is encouraged over future consumption. However, it also encourages substitution from traded to non-traded goods. The former effect dominates if the intertemporal elasticity of substitution is greater than the intratemporal elasticity of substitution (σ > θ), and vice versa.
Equation (9) relates the consumption of non-traded and traded goods. When the relative price is unity, the relative consumption of non-traded good is larger the smaller the share of consumption of traded goods in total consumption (γ). Finally, Equation (10) shows the equilibrium supply of non-traded goods. The higher is the consumption index (C), the lower is the production level. Additionally, the larger is the relative price of the non-traded good to the aggregate price level, the larger is the production level.
(ii) Domestic Firms
The production sector is characterised by a household that acts as a monopoly in the production of a single non-traded good (and the household and the domestic firm are used interchangeably). The household j operates a constant return to scale linear technology, yNt = ALNt in which labour is the only factor of production and A is the total factor productivity shifter. Assume that the firm is a price taker in the labour market and a monopoly in the good market. In the labour market, the firm chooses optimal labour by taking the output level as given. Then, the cost minimisation condition for the choice of optimal labour implies that labour is paid according to its marginal productivity. Therefore, mct which is the firm's real marginal cost is defined as the real wage in terms of non-traded goods over the total factor productivity shifter. This real marginal cost is also defined as the nominal marginal cost over price of non-tradables (mct = MCt/PNt). In the good market, the firm maximises profits by choosing the price of the good j that it produces subject to the demand for this good. As in Calvo (1983), the firm sets price on a staggered basis where it is allowed to reset the output price according to a time-dependent rule where φ is the probability that the firm keeps its price fixed in a given period and 1 − φ is the probability that the firm changes its price. The probability draws are assumed to be independent and identically distributed (iid) over time. This implies that, when allowed to reset its price, domestic firm j will choose  to maximise:
to maximise:
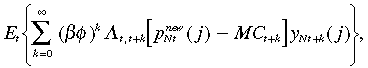 (11)
(11)subject to the demand schedule:
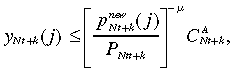 (12)
(12)where Λt,t+k is the time-varying portion of the firm's discount factor and MCt is the nominal marginal cost. The necessary first-order condition of this problem gives:
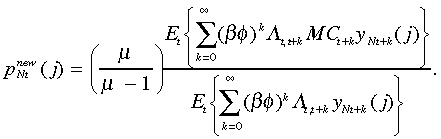 (13)
(13)This dynamic markup equation states that the current price is based on the firm's forecast of future demand and marginal cost. Note that if a firm was able to freely adjust its price each period, it will choose a constant mark-up over marginal cost, i.e. φ = 0 implies:
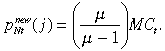 (14)
(14)Given the pricing rule, in a symmetric equilibrium where the law of large numbers holds, the non-tradable aggregate price index evolves according to:
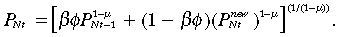 (15)
(15)(iii) International Capital Market
As in Soto (2003), we assume imperfect international capital markets where the interest rate depends on the stock of net foreign debt of the economy. In particular, the real interest rate is given by:
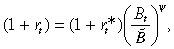 (16)
(16)where 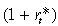 is the risk-free international interest rate and ψ ≥ 0 is a parameter that measures the premium the domestic economy must pay. As the real interest rate cannot be less than zero, we restrict Bt so that Bt 0. This expression implies that a country with a large stock of debt over a stock of minimum debt (B̃), starts paying a premium over the interest rate that prevails in the international capital market. However, for a stock of debt below this threshold, the country receives a discount.
is the risk-free international interest rate and ψ ≥ 0 is a parameter that measures the premium the domestic economy must pay. As the real interest rate cannot be less than zero, we restrict Bt so that Bt 0. This expression implies that a country with a large stock of debt over a stock of minimum debt (B̃), starts paying a premium over the interest rate that prevails in the international capital market. However, for a stock of debt below this threshold, the country receives a discount.
(iv) Prices and the Real Exchange Rate
The nominal exchange rate et is the price of one unit of foreign currency expressed in units of domestic currency. The real exchange rate is defined as:
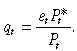 (17)
(17)The foreign price level is assumed to be given and the foreign price denominated in price of the tradable good is normalised to be one. When the law of one price holds for traded goods, it implies that qt = PTt/Pt.
(v) Monetary Policy and Exchange Rate Regimes
The formulation of monetary policy by the domestic authority follows a generalised rule in which deviations of inflation, non-traded output and the nominal exchange rate from their long-run targets have a feedback effect on short-run movements of the nominal interest rate. As in many others (Taylor, 1993; Rotemberg & Woodford, 1998; Clarida et al., 1999; and Monacelli, 2004), the following equation describes the target for the nominal interest rate:
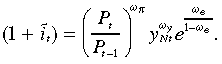 (18)
(18)where ?t is the target for the nominal interest rate, ωe, ωπ and ωy are weights assigned to the movements of the nominal exchange rate, inflation and non-tradable output, respectively. From Equation (18), the monetary authority reacts to the contemporaneous level of inflation, non-traded output and the nominal exchange rate. The determination of the actual short-run interest rate that accounts for the desire of the monetary authority to smooth changes in the interest rate is:
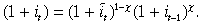 (19)
(19)(vi) Steady-State Equilibrium
We first consider the situation in which all prices are fully flexible. All variables are assumed to be constant at the steady state. Any variable with a bar on top denotes the variable at its steady state. We normalise the endowment of the traded good so that the relative price of non-traded goods in terms of traded goods is unity in the steady state, (P̃N0/P̃T0) = 1. In this symmetric equilibrium, ȳN0 = C̄N0 = (1 − γ)C̄0 and C̄N0 = (1 − γ)C̄T0/γ. The aggregate price level, the price of the traded good and consumption of traded goods are constant at the steady state. At the initial steady state, we also assume that the terms of trade is one, 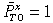 . Then, from Equation (8), the steady state value for the real domestic interest rate is:
. Then, from Equation (8), the steady state value for the real domestic interest rate is:
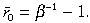 (20)
(20)Given the stock of minimum foreign debt B̃, at the steady state the following relationship is observed:
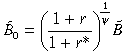 (21)
(21)If we assume r = r*, then B = B̃. From Equation (7), the consumption of traded goods in steady state satisfies:
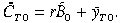 (22)
(22)The steady-state consumption and production of non-traded goods is given by
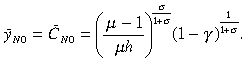 (23)
(23)The term (µ − 1)/µ is the inverse of the markup for the fully flexible prices case. From this expression, the output of non-traded goods will be larger, the more competitive is the non-traded goods sector (the larger is µ), the less taxing is the work effort (the smaller is h) and the larger is the weight placed on the consumption of non-traded goods in the utility function (the larger is (1 − µ)).
(vii) The Log-linearised Version of the FOC and Other Conditions
The model is solved by taking a log-linear approximation around the steady state. We let a variable with a hat denote the log-deviation of a variable from the steady state and a variable with a bar denote a variable at steady state. Then, the model can be described by a system of linear equations as discussed in the following subsections.
Aggregate Supply and Inflation
Let ◯Nt be the output gap in the non-traded sector, which is measured as the deviation between the stochastic component of current output and the potential output. The following equation shows the inflation of non-traded goods:
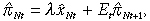 (24)
(24)where λ = (1 − φ)(1 − βφ)/φ and Et is the expectation operator. This equation suggests that inflation is positively related to the output gap.
Aggregate Demand
By taking a log-linear approximation of (8) and (17),
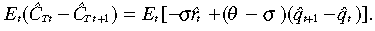 (25)
(25)This equation shows that the consumption of traded goods adjusts according to the evolution of the real interest rate and the real exchange rate. From the log-linear approximation of (3), (9) and (17), an expression that relates the output gap in the non-traded sector with the deviation of the real exchange rate from its steady state and the deviation of consumption of traded goods from its steady state is derived as:
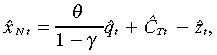 (26)
(26)where the last term denotes the potential output that is assumed to follow a stationary stochastic process.
Real Interest Rate and Current Account
The log-deviation of the real interest rate faced by domestic agents corresponds to
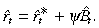 (27)
(27)Using Equation (7), the linear expression of the stock of foreign assets is
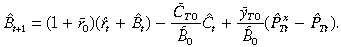 (28)
(28)Uncovered Interest Parity Condition with Nominal and Real Interest Rates
The uncovered interest parity defines a linear expression for the exchange rate expressed as:
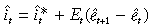 (29)
(29)where it and 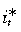 are the domestic and foreign nominal interest rates, respectively, and ît = log(1 + it/1 + ?). The relationship between the nominal and real interest rates is defined by:
are the domestic and foreign nominal interest rates, respectively, and ît = log(1 + it/1 + ?). The relationship between the nominal and real interest rates is defined by:
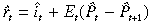 (30)
(30)Monetary Policy Rule
Equation (31) is obtained by taking a log-linear approximation of (18) and (19)
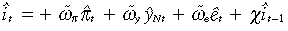 (31)
(31)where 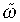 π ≡ (1 − χ)ωπ,
π ≡ (1 − χ)ωπ, 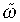 y ≡ (1 − χ)ωy, and
y ≡ (1 − χ)ωy, and 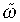 e ≡ (1 − χ)(ωe/1 − ωe). Following Monacelli (2004), this specification allows us to approximate the systematic behaviour of monetary policy under the floating and the fixed exchange rate regimes. In particular, ωe = 0 describes the behaviour of the monetary authority practicing the floating exchange rate regime; whereas ωe ∈ (0, 1] approximates the behaviour of the monetary authority practicing policies ranging from managed to the fixed exchange rate regimes.
e ≡ (1 − χ)(ωe/1 − ωe). Following Monacelli (2004), this specification allows us to approximate the systematic behaviour of monetary policy under the floating and the fixed exchange rate regimes. In particular, ωe = 0 describes the behaviour of the monetary authority practicing the floating exchange rate regime; whereas ωe ∈ (0, 1] approximates the behaviour of the monetary authority practicing policies ranging from managed to the fixed exchange rate regimes.
Exogenous Stochastic Process
The stochastic processes for the world (foreign) interest rate, terms-of-trade and potential output can be summarised as
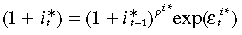 (32)
(32)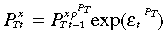 (33)
(33)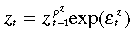 (34)
(34)with 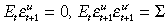 where u = i*,
where u = i*, 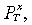 z where
z where  are iid.
are iid.
III Model Parameterisation
The model is solved numerically6 and the parameter choices for the model are summarised in Table 1. Following the business cycle literature, the discount rate β is set at 0.99 and the marginal disutility of work effort h is set at 3. The price elasticity between non-traded goods or the steady-state markup µ is set at 1.2. As it is now common in the literature using Calvo pricing, the probability of price non-adjustment φ is set at 0.75. In other words, this implies that the average frequency of price adjustment is four quarters. The elasticity of intertemporal substitution σ is set at 1/4, whereas the elasticity of intratemporal substitution θ is set at 1/6. This assumes that the intertemporal elasticity dominates the intratemporal elasticity of substitution. Following Soto (2003), these values are not based on any estimation but are arbitrary.7 The degree of economy openness is allowed to vary from completely closed to completely open. This implies that γ ∈ (0, 1).
| Parameter | Definition and description | Value |
|---|---|---|
| θ | Intratemporal elasticity of substitution | 1/4 |
| σ | Intertemporal elasticity of substitution | 1/6 |
| φ | Probability of price non-adjustment | 0.75 |
| γ | Degree of openness | 0.5 |
| λ | (1 − φ)(1 −βφ)/φ | 0.0858 |
| β | Discount rate | 0.99 |
| µ | Elasticity of substitution between non-tradables | 1.2 |
| h | Intertemporal elasticity of labour supply | 3 |
| ψ | Elasticity of net foreign asset to interest differentials | 0.015 |
| χ | Interest smoothing parameter | 0.5 |
| ρ i* | Autocorrelation of foreign nominal interest rate | 0.8 |
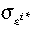 |
Standard deviation of foreign nominal interest rate | 1.379 |
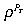 |
Autocorrelation of terms-of-trade | 0.414 |
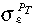 |
Standard deviation of terms-of-trade | 11.77 |
| ρz | Autocorrelation of potential output | 0.5 |
| σz | Standard deviation of potential output | 1 |
| ωe | Responsiveness of monetary policy to exchange rate | 0.25 and 0.99 |
| ωπ | Responsiveness of monetary policy to inflation | 1.5 |
| ωy | Responsiveness of monetary policy to output | 0 |
As to the monetary policy rule parameters, we follow the benchmark values in Monacelli (2004), where ωπ is set to 1.5, ωψ is set to 0 and ωɛ ∈ (0,1). To calibrate the sources of stochastic volatility, we assume that the US interest rate is the driving force describing the world (nominal and real) interest rate and the world price is constant. As a result, following Monacelli (2004), 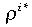 is 0.8 and
is 0.8 and 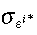 is 0.01379. Following Mendoza's (1995) study on developing countries, the mean serial correlation of the terms of trade
is 0.01379. Following Mendoza's (1995) study on developing countries, the mean serial correlation of the terms of trade 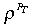 equals 0.414 and the standard deviation
equals 0.414 and the standard deviation 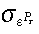 equals 0.1177. As the potential output is non-observable, the serial correlation of the potential output ρz and the standard deviation σz is arbitrarily fixed at 0.5 and 1, respectively. As the study concentrates on the effects of a terms-of-trade shock, the results from other shocks are not reported.
equals 0.1177. As the potential output is non-observable, the serial correlation of the potential output ρz and the standard deviation σz is arbitrarily fixed at 0.5 and 1, respectively. As the study concentrates on the effects of a terms-of-trade shock, the results from other shocks are not reported.
IV The Volatility of Output, the Real Exchange Rate and the Price Level
We conduct an experiment to investigate whether the baseline model illustrated above can replicate the quantitative evidence reported in Broda (2004). To characterise a fixed (flexible) exchange rate regime, we let ωɛ approach one (zero). The benchmark calibration described above permits us to choose ωɛ = 0.99 for a fixed exchange rate regime and ωɛ = 0.25 for a more flexible exchange rate regime. We then investigate whether the model described is able to generate similar volatility in output, real exchange rate and price levels as documented by Broda.
1a, 1b illustrates the effect of a negative shock to the terms of trade. Suppose there is a reduction in export demand that leads to deteriorating terms of trade. This results in a nominal depreciation of the domestic currency. As traded and non-traded goods are assumed to be close substitutes, the depreciation of the domestic currency induces a switch in consumption from the consumption of tradable to the consumption of non-tradables. This substitution effect causes an increase in the price of non-tradables. The degree of change in the price of non-tradables during the period of shock depends on two factors. First, with the same degree of nominal price rigidity, under a fixed exchange rate regime, as the nominal exchange rate is not allowed to respond much, the price of non-tradables jumps by more compared with the one under a flexible exchange rate regime. Second, under both exchange rate regimes, when the degree of nominal rigidity is low and prices are allowed to adjust freely, the jump in the price of non-tradables is therefore larger. Additionally, from the figures, overshooting in the nominal and real exchange rates is observed as the substitution effect takes place before the income effect. The size of the nominal depreciation during the period of shock is larger under a flexible than a fixed exchange rate regime. Over time, when income effect starts to dominate (as a result of lower purchasing power), the nominal exchange rate appreciates, so does the real exchange rate. The speed of adjustment of the real exchange rate is much faster under a flexible exchange rate regime.
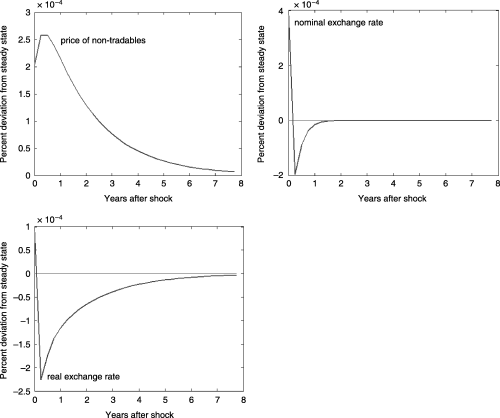
Effect of Negative Terms-of-trade Shock Under Fixed Exchange Rate Regime
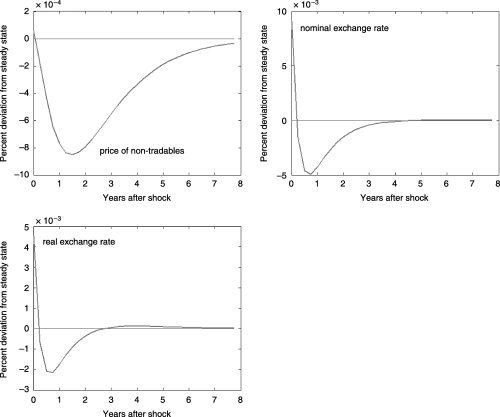
Effect of Negative Terms-of-trade Shock Under Flexible Exchange Rate Regime
(i) Sensitivity Analysis: Different Degree of Rigidities in the Nominal Exchange Rate
In this section, to investigate whether the model illustrated is able to replicate the empirical evidence reported by Broda (2004) and following the method of Monacelli (2004), the exercise consists of checking whether the model is able to generate similar volatility for a few key variables such as the price of non-tradables, nominal and real exchange rates, bonds, output and consumption. We define volatility as the standard deviations of these variables. Without shock in the terms of trade, all variables take on the values of their respective steady states. Table 2 and Figure 2 summarise the standard deviations of key macroeconomic variables with different degrees of rigidities in the nominal exchange rate when the model is driven by the terms-of-trade shock.
| Variable | Standard deviation HP-filtered | |||
|---|---|---|---|---|
| ωe = 0.25 | ωe = 0.50 | ωe = 0.75 | ωe = 0.99 | |
| Price of non-tradables, PN | 0.311 | 0.446 | 0.503 | 0.531 |
| Price, P | 1.020 | 0.804 | 0.701 | 0.647 |
| Nominal exchange rate, PT | 1.055 | 0.420 | 0.167 | 0.007 |
| Real exchange rate, q | 0.627 | 0.384 | 0.300 | 0.266 |
| Bonds, B | 11.474 | 12.638 | 13.275 | 13.619 |
| Non-tradable output, yN | 2.824 | 3.713 | 4.046 | 4.225 |
| Consumption, C | 0.642 | 0.778 | 0.820 | 0.602 |
- Notes: Standard deviations are obtained from Hodrick–Prescott filtered data. ωe shows the responsiveness of monetary policy to the exchange rate. The higher the value of ωe, the more responsive is the monetary policy to exchange rate implying the more rigid the exchange rate regime.
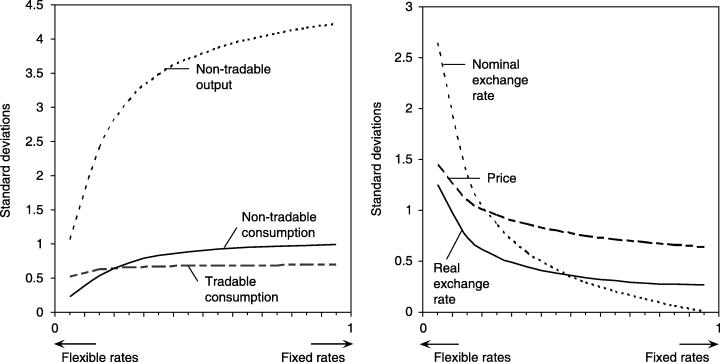
Variability of Some Macroeconomic Variables in Moving from Flexible to Fixed
Several interesting results emerge. First, under a flexible exchange rate regime, the real non-tradable output has a smaller fluctuation when countries are hit by a terms-of-trade shock, whereas the price level, the nominal and the real exchange rates have larger fluctuations. On the other hand, under a fixed exchange rate regime, the real non-tradable output tends to fluctuate more, whereas the price level, the nominal and the real exchange rates have smaller fluctuations. These observations are consistent with Broda (2004) and Mussa (1986). Second, in moving from fixed to a flexible exchange rate, the proportional rise in volatility of the nominal exchange rate is coupled by a rise in volatility of the real exchange rate. This observation implies that the nominal and real exchange rates are strongly correlated. Countries, moving from fixed to floating exchange rate regime, will experience a dramatic rise in the volatility of the real exchange rate. The correlation between the nominal and real exchange rates is consistent with Mussa's (1986) facts. Monacelli (2004) also shows that this result is robust to other types of shocks, such as productivity, preference, world interest rate and world demand shocks. Third, small open economies that peg their exchange rates achieve lower fluctuations in price than those whose exchange rates float. Fourth, the volatility of the holding of net foreign assets is always the largest in all types of exchange rate regimes, but this fluctuation tends to be smaller under a more flexible exchange rate regime.
Sensitivity Analysis: Different Degrees of Price Rigidities
We address the role of price rigidities under two exchange rate regimes: the flexible vs. the fixed exchange rate. We set the probability of price non-adjustment φ, at 0.25, 0.50 and 0.75. When φ = 0.25, φ = 0.50 and φ = 0.75, prices completely adjust after approximately 1.3 quarters, 2 quarters and 4 quarters, respectively. The simulation results are summarised in Table 3. Despite the type of regime adopted by a small open economy, the volatility of the non-tradable output increases when the probability of non-price adjustment increases from 0.25 (flexible prices) to 0.75 (rigid prices). This is particularly true under the fixed exchange rate regime. This result supports the conventional wisdom that real output, after experiencing a specific type of real shock, should have smoother responses if the price adjustments to shocks are quicker.
| Variables | Percent of standard deviation (HP-filtered) | |||||
|---|---|---|---|---|---|---|
| φ = 0.25 | φ = 0.50 | φ = 0.75 | ||||
| Fixed | Float | Fixed | Float | Fixed | Float | |
| Price of non-tradables, PN | 3.007 | 2.269 | 1.592 | 1.080 | 0.531 | 0.311 |
| Price, P | 0.638 | 1.131 | 0.639 | 1.071 | 0.647 | 1.020 |
| Nominal exchange rate, PT | 0.008 | 1.174 | 0.008 | 1.108 | 0.007 | 1.055 |
| Real exchange rate, q | 1.506 | 1.542 | 0.798 | 0.973 | 0.264 | 0.627 |
| Bonds, B | 13.679 | 11.466 | 13.649 | 11.469 | 13.619 | 11.474 |
| Non-tradable output, yN | 3.445 | 2.757 | 3.801 | 2.684 | 4.225 | 2.824 |
| Consumption, C | 0.908 | 0.684 | 0.866 | 0.659 | 0.840 | 0.642 |
- Note: φ shows the probability of non-price adjustment. When φ is 0.5, prices completely adjust after two quarters and when φ is 0.75, prices completely adjust after four quarters. In other words, the larger the value of φ, the higher the degree of rigidity in prices.
(ii) Sensitivity Analysis: Different Degrees of Openness
In this section, we test the sensitivity of the predictions of the model to alternative values of a critical parameter – degree of openness. The results are shown in Table 4. A few interesting results stand out. First, when the degree of openness reaches its highest possible value, the real exchange rate is almost twice more volatile under a flexible than it is under a fixed exchange rate. Second, both exchange rates – nominal and real – are always more volatile under flexible. Third, non-tradable output is always more volatile under fixed than floating exchange rates.
| Variables | Percent of standard deviation (HP-filtered) | |||||
|---|---|---|---|---|---|---|
| γ = 0.25 | γ = 0.50 | φ = 0.75 | ||||
| Fixed | Float | Fixed | Float | Fixed | Float | |
| Price of non-tradables, PN | 0.516 | 0.404 | 0.531 | 0.311 | 0.505 | 0.307 |
| Price, P | 0.302 | 1.246 | 0.647 | 1.020 | 0.472 | 1.114 |
| Nominal exchange rate, PT | 0.009 | 0.760 | 0.007 | 1.055 | 0.007 | 0.987 |
| Real exchange rate, q | 0.388 | 0.818 | 0.266 | 0.627 | 0.127 | 0.298 |
| Bonds, B | 6.892 | 8.271 | 13.619 | 11.474 | 8.096 | 6.416 |
| Non-tradable output, yN | 3.833 | 3.880 | 4.225 | 2.824 | 4.029 | 3.001 |
| Consumption, C | 0.718 | 0.865 | 0.840 | 0.642 | 0.781 | 0.684 |
- Note: γ measures the degree of openness where the larger the value of γ, the more open is an economy.
V Conclusions
We examine the link between terms-of-trade shocks and some macroeconomic variables by numerically solving a dynamic stochastic general equilibrium model of a small open economy. The model combines nominal price rigidity under different exchange rate regimes. The numerical solutions are compared with the observed empirical regularities. In the model, households consume tradable and non-tradable goods. The traded sector is viewed as a perfectly competitive market where prices are fully flexible and covered by the law of one price. The non-traded sector, on the other hand, is assumed to be a monopolistic competitive market where prices in this sector are sticky. The economy is small in the sense that it cannot influence the terms of trade of the economy.
Generally, the simulations show that the model duplicates many of the stylized facts documented by Broda (2004). First, under a more flexible exchange rate regime, the real non-traded output has smaller fluctuations but the price and real exchange rate have larger fluctuations when countries are hit by terms-of-trade shocks. This result is in favour of Friedman's prediction that short-run output responses to shocks are significantly smoother in floats than in pegs. Second, in moving from fixed to flexible, the proportional rise in volatility of the nominal exchange rate is coupled by a rise in volatility of the real exchange rate. This implies that countries, moving from fixed to floating exchange rate regime, will experience a dramatic rise in the volatility of the real exchange rate. Third, the volatility of the holding of net foreign assets is always the largest in all types of exchange rate regimes but this fluctuation tends to be smaller under a more flexible exchange rate regime.
Sensitivity analysis shows that despite the type of regime adopted by a small open economy, the volatility of non-tradable output increases when the probability of non-price adjustment increases. Additionally, despite the degree of openness, volatility of the non-tradable output is always higher under fixed than floating exchange rates.
The appealing results obtained from the model suggest other topics for further investigation. The artificial economy and the numerical methods employed here can be used to explore quantitatively the effects of other economic policies implemented in small open economies.




