Measuring the Effects of Exchange Rate Changes on Investment in Australian Manufacturing Industry*
Abstract
This paper examines the relationship between exchange rates and investment in Australian manufacturing between 1988 and 2001. The effects of exchange rates on investment are found to vary positively with the export share of sales and negatively with the share of imported inputs into production, with lower price-over-cost mark-ups increasing the response. For Australian manufacturing, a 10 per cent real appreciation of the Australian dollar leads to an average 8.0 per cent decrease in total investment through the export share channel, and an average 3.8 per cent increase through the imported input share channel, with most of the response occurring through investment in equipment, plant and machinery.
I Introduction
There have been substantial changes in the value of the Australian dollar (AUD) over the last decade, but we still have little detailed information about the implications of these movements for the Australian industry. There is now a considerable international literature on the factors that influence the initial stage of the adjustment process, the change in relative prices that follows an exchange rate change, usually referred to as exchange rate pass-through.1 However, few studies have extended this analysis to investigate the longer-term effects of exchange rates on investment and employment, and only for a limited number of countries (for example, Campa & Goldberg, 1995; Campa & Goldberg, 1999; Nucci & Pozzolo, 2001). This paper uses quarterly data from 1988 to 2001 to estimate the size and determinants of the effects of exchange rate changes on investment in the Australian manufacturing industry.
The optimal level of investment for a firm is an increasing function of the current and expected value of future profits. Exchange rate changes influence profits not only through changes in the prices of domestically produced goods sold in export markets but also through changes in the prices of imported goods used as inputs to production and in the prices of imports that compete with domestically produced goods. A firm with a larger share of sales in export markets, for example, would be expected to reduce investment in response to an appreciation of the domestic currency. Conversely, a firm that is highly dependent on the use of imported inputs into production would face a larger drop in variable costs and would consequently be expected to increase investment following an appreciation.
The exchange rate pass-through literature has also highlighted the importance of the competitive structure of industry in determining the size of the response to exchange rate changes (see, for example, Dornbusch, 1987). Firms in more competitive industries with lower price-over-cost mark-ups have less ability to absorb exchange rate changes in their mark-ups so that the change in prices for these firms following an exchange rate change will be larger. Lower levels of industry mark-ups would therefore be expected to interact with, and amplify, the effects of external exposure on investment.
The few empirical studies available have generally confirmed the conclusions of the theoretical models. In a cross-country survey, Campa and Goldberg (1999) estimated that a net increase of around 1–2 per cent in investment in total manufacturing in the USA would follow a 10 per cent appreciation of the USD, with a wide variation expected in industry response, ranging from an increase of 12 per cent to a decrease of 8.4 per cent. The authors showed that these results were due to the increasing importance of imported inputs into manufacturing in the USA. The Japanese industry generally showed a lower level of response, but with an overall increase in investment also expected following appreciation, and a similarly wide range of industry responses from an increase of 10 per cent to a decrease of 8.3 per cent.
Campa and Goldberg (1999) were unable to find any statistical significance in the exchange rate coefficients for the UK and Canada, which they found surprising given the size and extent of the external orientation of Canadian manufacturing. However, Nucci and Pozzolo (2001) reported that the results of their estimations of a panel data set of about 1000 Italian manufacturing firms strongly supported the implications of the theoretical model, with the overall effects of swings in the exchange rate on a firm's investment depending on which of the opposing export and imported input channels prevailed.
The rest of the paper is organised as follows. Section II outlines a theoretical framework that explicitly incorporates both changes in external exposure and industry mark-ups as determinants of exchange rate effects on profits and investment. The empirical model described in Section III is directly derived from this framework, and is estimated for total investment in the Australian manufacturing industry and for two investment subclasses, Equipment, Plant and Machinery, and Buildings and Structures.
The results presented in Section IV confirm the effects of external exposure and mark-ups expected from the theoretical model. They show that a 10 per cent real appreciation of the Australian dollar (AUD) leads to a net decrease of 4.2 per cent in total investment on average over the period, the combined effect of an 8.0 per cent decrease through the export share channel, and a 3.8 per cent increase through the imported input share channel. Almost all of the investment response occurs through changes in investment in equipment, plant and machinery. Section V draws some final conclusions.
II Theoretical Framework
The empirical framework is based on an optimising adjustment-cost model of investment developed by Campa and Goldberg (1999), in which a firm chooses investment for each period (It) to maximise the discounted sum of expected future profits less the overall cost of investment. The firm observes the exchange rate of each period (et) and chooses output for foreign and domestic markets and quantities of domestic and imported inputs in order to maximise per-period profit. Campa and Goldberg (1999) derive the following expression for the investment response to exchange rate changes:
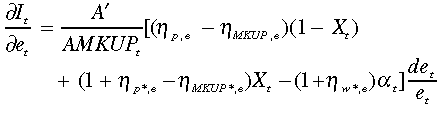 (1)
(1)where 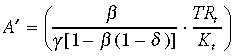
and ηp,e and 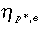 are exchange rate pass-through elasticities to domestic and foreign prices, respectively, ηMKUP,e and
are exchange rate pass-through elasticities to domestic and foreign prices, respectively, ηMKUP,e and 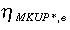 are exchange rate elasticities of mark-ups in domestic and foreign markets, respectively, TRt is total revenues, Xt is the share of TR from sales in foreign markets, αt is the share of imported inputs in total production costs,
are exchange rate elasticities of mark-ups in domestic and foreign markets, respectively, TRt is total revenues, Xt is the share of TR from sales in foreign markets, αt is the share of imported inputs in total production costs, 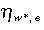 is the exchange rate elasticity of imported input costs, AMKUPt is the firm's average price-over-cost mark-up across all markets, β is the discount rate, Kt is capital stock at the start of period t, δ is the rate of capital depreciation and γ is a parameter of a standard quadratic cost of adjustment function.
is the exchange rate elasticity of imported input costs, AMKUPt is the firm's average price-over-cost mark-up across all markets, β is the discount rate, Kt is capital stock at the start of period t, δ is the rate of capital depreciation and γ is a parameter of a standard quadratic cost of adjustment function.
The three terms inside the square brackets in Equation (1) identify the three channels through which exchange rate changes can influence investment. Effects on the profitability of domestic sales (1 –Xt) and of export sales (Xt) will depend on the relative sizes of both markets, and on the exchange rate elasticities of price and mark-up that are determined by the structure of the market. For example, firms in more competitive markets will have smaller mark-ups and consequently will maintain constant domestic prices (lower ηMKUP,e and ηp,e) and pass-through exchange rate changes more fully to foreign prices (larger 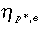 ).
).
Similarly on the imported input side, both more competitive markets for inputs (smaller mark-ups and larger 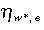 ) and a greater proportion of imported inputs in production costs (larger αt) will increase the countervailing effects of imported input costs on profitability and investment. In addition, smaller average mark-ups will amplify the effects on investment in competitive industries from all three channels, through (A′/AMKUP).
) and a greater proportion of imported inputs in production costs (larger αt) will increase the countervailing effects of imported input costs on profitability and investment. In addition, smaller average mark-ups will amplify the effects on investment in competitive industries from all three channels, through (A′/AMKUP).
III Empirical Estimation and Data
The empirical model to be estimated is derived from Equation (1) as:
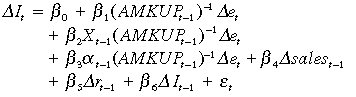 (2)
(2)where It is investment in private new capital expenditure at constant prices, and et is the real trade-weighted exchange rate in units of domestic currency per unit of foreign currency. From Equation (1), the coefficient β1 on the first exchange rate term is a function of 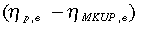 in the domestic market. The coefficient β2 on the exchange rate interacted with export share (Xt) is a function of the valuation and market effects on the export side
in the domestic market. The coefficient β2 on the exchange rate interacted with export share (Xt) is a function of the valuation and market effects on the export side 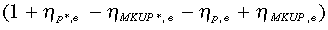 . Similarly, the coefficient β3 on the final exchange rate term interacted with imported input share (αt) is a function of the imported input elasticity
. Similarly, the coefficient β3 on the final exchange rate term interacted with imported input share (αt) is a function of the imported input elasticity 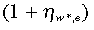 . All three exchange rate terms interact with the average mark-up (AMKUPt) as in Equation (1), incorporating the influence of competitive structure on exchange rate effects.
. All three exchange rate terms interact with the average mark-up (AMKUPt) as in Equation (1), incorporating the influence of competitive structure on exchange rate effects.
The discount rate included in the term in A′ in Equation (1) is represented by the real interest rate (rt). The estimation also includes a variable for the growth rate of real total sales in the industry (Δsalest) to control for other industry-specific factors that may have influenced the growth rate of investment over the period. The lagged values of the interaction terms (export and imported input shares and average mark-up) and the real interest rate are used to avoid possible correlation with the current exchange rate, and a lag on total sales is used to avoid a possible correlation with current investment.2 The final term, lagged investment (It–1), is included to represent the adjustment and implementation lags generally expected in investment projects (Driver & Dowrick, 1997; Nucci & Pozzolo, 2001). The symbol Δ indicates first differences in natural logarithms for all variables except for the real interest rate, which is differenced in level form.
The inclusion of the lagged dependent variable in Equation (2) raises the possibility of serial correlation and subsequent bias in the estimates. For this reason, instrumental variables estimation (2SLS) was employed, with additional lags of investment and sales included as instruments. The estimates were corrected for any remaining serial correlation using the Newey–West technique (Newey & West, 1987).
Equation (2) was estimated for total investment in the Australian manufacturing industry (ANZSIC Division C) and for the two investment subclasses, Equipment, Plant and Machinery, and Buildings and Structures, using quarterly data for the period 1988:Q1 to 2001:Q4. Details of data sources are available in the Appendix. Export share (Xt) is calculated as the ratio of the value of exports to the value of total sales of goods and services. Imported input share (αt) is constructed from sectoral input–output data combined with import value shares for each input sector to give the total value of imported inputs used in the manufacturing industry. The share of imported inputs in production is then derived as the ratio of the value of imported inputs to the total cost of production, including both materials and labour inputs.3
Marginal costs for the direct calculation of price-over-cost mark-ups are not observable. Domowitz et al. (1986) suggest a method for computing a measure of profit margin per unit price:
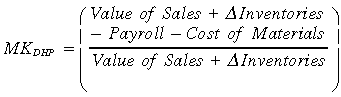 (3)
(3)This formula is used to derive a measure for the average mark-up (AMKUP) as ‘average price-over-average cost’ to represent market power in the industry:
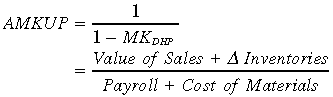 (4)
(4)This method is not intended to give a definitive measure of industry mark-ups, but it does allow the consistent comparison of changes in profit margins over time as exchange rates change.
IV Results
The results of the estimation of Equation (2) for total investment and the two investment subclasses are given in Table 1. For total investment, the exchange rate variables interacted with export shares and imported input shares are both significant and of the expected sign, indicating that an appreciation (a decrease in et) leads to a decrease in total investment through the export price channel and an increase through the imported input prices channel. The results for the interacted terms in the regression for equipment, plant and machinery are very similar but with slightly smaller coefficients. Investment in equipment, plant and machinery constituted around 85 per cent of total investment on average over the period, consistent with the results obtained.
| Variables | Dependent variable: investment | ||
|---|---|---|---|
| Total | Equipment, plant and machinery | Buildings and structures | |
| Constant | 0.010 | 0.052 | 0.376 |
| (0.058) | (0.045) | (0.498) | |
| (AMKUPt–1)−1Δet | −0.748 | −1.010 | 5.767 |
| (0.932) | (0.658) | (7.736) | |
| X t–1(AMKUPt–1)−1Δet | 4.014* | 3.633* | −1.400 |
| (1.962) | (1.257) | (25.351) | |
| α t–1(AMKUPt–1)−1Δet | −3.109** | −2.508* | −5.525 |
| (1.914) | (1.332) | (19.138) | |
| Δsalest–1 | 0.002 | 0.002* | −0.006 |
| (0.001) | (0.001) | (0.010) | |
| Δrt–1 | 0.208* | 0.225* | −0.149 |
| (0.102) | (0.080) | (0.856) | |
| ΔIt–1 | −0.840* | −0.806* | −0.491* |
| (0.089) | (0.089) | (0.103) | |
| R̄ 2 | 0.76 | 0.77 | 0.22 |
- Note: * and ** indicate significance at 5 and 10 per cent levels, respectively.
- Standard errors are reported in brackets below parameter estimates.
- Each equation is estimated using 2SLS and corrected for fourth-order serial correlation. Jacques–Bera tests for skewness and kurtosis indicate that all residuals are normal, and Hansen's J-statistic tests indicate that instrumental variables are exogenous.
The regression for investment in buildings and structures has a markedly poorer fit (R̄2 = 0.22) and only the lagged dependent variable is significant. Driver and Dowrick (1997) also found less explanatory power in the equations for buildings and structures in their estimations of the effects of investment intentions on investment in Australian manufacturing industry. Investment in buildings and structures is likely to involve much larger costs, suggesting longer lead times in planning and implementation that may induce ‘lumpiness’ in investment spending. The wedge thus created between the benefits and costs embodied in an optimal investment policy may lead to parameter and model instability by weakening the link between investment spending and shifts in economic determinants, such as exchange rates (Chirinko, 1993). The negative and significant coefficients on the one-period lag of investment in all three estimations, also found by Driver and Dowrick (1997), support the idea that investment spending generally has some degree of ‘lumpiness’, as higher levels of investment spending last period will be followed by lower levels of spending this period whatever the external economic conditions.
The coefficient on the real interest rate for the first two regressions is significant, but small and of the wrong sign. To check that this did not indicate the need to allow for a longer time delay on the interest rate effect, all three equations were re-estimated with lags of up to five quarters on the real interest rate variable. Insignificant lags were eliminated using the general-to-specific methodology, but only the first lag remained significant in all three regressions. Interestingly, Campa and Goldberg (1995) found similar small but positive and significant coefficients in their estimations of the effects of exchange rate changes on investment in the manufacturing industry in the USA. Campa and Goldberg (1995) offered no explanation for their findings, but the relative size of the coefficients for both Australia and the USA support the general conclusion of neoclassical models of investment that effects on output or sales, as generated here by exchange rate changes, have the dominant effect on investment with user cost having a minor role (Chirinko, 1993).4
The implications for the Australian industry of the investment effects of exchange rate changes can be shown by combining the estimated coefficients on the interacted exchange rate terms in Table 1 with industry-specific data on export share, imported input share and mark-ups. Table 2 gives the responses expected for total manufacturing industry and the 2-digit ANZSIC manufacturing subdivisions following a 10 per cent real appreciation of the AUD. Ideally, the exchange rate coefficients would also be allowed to vary between subdivisions, but the figures calculated here do show the variation that can be expected in effects between industries as a result of differences in mark-up and the degree of external exposure.5
| Industry (ANZSIC code) | Total investment | Investment in equipment, plant and machinery | ||
|---|---|---|---|---|
| Export channel | Imported input channel | Export channel | Imported input channel | |
| Div. C: total manufacturing | −8.0 per cent | 3.8 per cent | −7.3 per cent | 3.1 per cent |
| Subdivisions: | ||||
| 21 Food, beverages and tobacco manufacturing | −8.9 per cent | 1.5 per cent | −8.1 per cent | 1.2 per cent |
| 22 Textile, clothing, footwear and leather manufacturing | −8.3 per cent | 4.4 per cent | −7.5 per cent | 3.6 per cent |
| 23 Wood and paper product manufacturing | −2.7 per cent | 2.7 per cent | −2.5 per cent | 2.2 per cent |
| 24 Printing, publication and recording media | −1.0 per cent | 2.2 per cent | −0.9 per cent | 1.8 per cent |
| 25 Petroleum, coal and chemical manufacturing | −5.1 per cent | 5.0 per cent | −4.6 per cent | 4.0 per cent |
| 26 Non-metallic mineral product manufacturing | −1.0 per cent | 1.5 per cent | −0.9 per cent | 1.2 per cent |
| 27 Metal product manufacturing | −16.7 per cent | 3.3 per cent | −15.1 per cent | 2.6 per cent |
| 28 Machinery and equipment manufacturing | −8.9 per cent | 7.0 per cent | −8.0 per cent | 5.6 per cent |
| 29 Other manufacturing | −4.8 per cent | 3.6 per cent | −4.3 per cent | 2.9 per cent |
- Note: The estimates are calculated using period averages of export share, imported input shares and mark-ups for each industry, combined with the relevant coefficients from Table 1.
A 10 per cent real appreciation leads to an overall net decrease of around 4.2 per cent in investment for Australian manufacturing as a whole, but effects vary from a 1.2 per cent net increase in investment for printing, publishing and recording media to a 15 per cent decrease for metal products. These results contrast with those reported by Campa and Goldberg (1999) in their cross-country survey. They estimated a net increase in investment in total manufacturing in both the USA and Japan following a 10 per cent appreciation of the domestic currency, with a wider variation in industry response than that found here.
However, the four Australian industries showing the largest effects in Table 2 (21, 22, 27 and 28) are those with the largest export shares, averaging over 20 per cent export share over the period, and in the case of metal products, over 40 per cent. They are also among the largest subdivisions overall, together averaging more than 60 per cent of the total sales of the manufacturing industries. These results highlight the continued importance of the export channel for exchange rate effects for Australia. They also emphasise the importance of country- and industry-specific influences in determining the direction and size of the response to exchange rate changes.
The remaining industries, more than half the industry subdivisions (23, 24, 25, 26 and 29), experience net changes of around 1 per cent or less, indicating that even quite substantial reductions in investment through the export price channel can be counterbalanced by gains through the prices of imported inputs, as for example in petroleum, coal and chemical products.
V Conclusion
This paper provides quantitative measures of the size and direction of the effects of exchange rate changes on investment in the Australian manufacturing industry between 1988 and 2001. The empirical results confirm the conclusions of the theoretical model that the magnitude of the effects varies with the external exposure of industry, positively with export share of sales and negatively with the share of imported inputs into production.
For individual manufacturing subdivisions, the expected response to a 10 per cent appreciation of the AUD varies from a 1.2 per cent net increase in total investment to a 15 per cent net decrease. For the manufacturing division as a whole, the decrease of around 4.2 per cent is a result of an 8 per cent decrease in investment through the export price channel and a 3.8 per cent increase through the imported input price channel. Almost all of the investment response occurs through investment in equipment, plant and machinery.
For Australia, the estimates suggest that export share remains the most important channel for exchange rate effects overall, although there are significant differences between industries. The results found here demonstrate the need for further research to address the determinants of differences in exchange rate effects both between industries and between countries.
Footnotes
REFERENCES
Appendix: Data
Investment (It): Data on total investment, and investment in equipment, plant and machinery, and buildings and structures, at current prices are taken from ABS, Private New Capital Expenditure and Expected Expenditure, Australia, Cat. no. 5625.0. They are deflated by the chain price indices for total private gross fixed capital formation from ABS, Australian National Accounts: National Income, Expenditure and Product, Cat no. 5206.0.
Exchange rate (et): Data on the real trade-weighted index are taken from Real Exchange Rate Indices – Quarterly on the RBA website (http://www.rba.gov.au/Statistics/).
Interest rate (rt): The real interest rate is calculated as the quarterly average of the interest rate on 2-year Treasury bonds from RBA, Interest Rates and Yields: Money Market and Commonwealth Government Securities, Occasional Paper no. 10 (updated), minus the expected change in manufacturing selling prices from ABS, Australian Business Expectations, Cat. no. 5250.0.
Export share (Xt) and Sales (salest): The value of exports is taken from ABS, International Trade in Goods and Services, Australia, CAT. no. 5368.0. Data on sales of goods and services are taken from ABS, Business Indicators, Australia, CAT. no. 5676.0.
Imported Input Shares (α i ): Data on the input–output structure of production are taken from the ABS, Australian National Accounts: Input–Output Tables, Cat. no. 5209.0 for 1996/97. Import shares for each input industry are calculated as the ratio of the value of imports from ABS, International Trade in Goods and Services, Australia, Cat. no. 5368.0, to the value of sales of goods and services for each industry from ABS, Summary of Industry Performance, Australia, Cat. no. 8140.0.55.002. Labour costs are taken from ABS, Wage and Salary Earners, Australia, Cat. no. 6248.0, and deflated by the price index for materials used in manufacturing from ABS, Producer Price Index, Cat. no. 6427.0.
Average Mark-up (AMKUPt): Data on company gross operating profits, sales and inventories are taken from ABS, Business Indicators, Australia, Cat. no. 5676.0.




