In vivo neurochemical profiling of rat brain by 1H-[13C] NMR spectroscopy: cerebral energetics and glutamatergic/GABAergic neurotransmission
Abstract
J. Neurochem. (2010) 112, 24–33.
The quantification of excitatory and inhibitory neurotransmission and the associated energy metabolism is crucial for a proper understanding of brain function. Although the detection of glutamatergic neurotransmission in vivo by 13C NMR spectroscopy is now relatively routine, the detection of GABAergic neurotransmission in vivo has remained elusive because of the low GABA concentration and spectral overlap. Using 1H-[13C] NMR spectroscopy at high magnetic field in combination with robust spectral modeling and the use of different substrates, [U-13C6]-glucose and [2-13C]-acetate, it is shown that GABAergic, as well as glutamatergic neurotransmitter fluxes can be detected non-invasively in rat brain in vivo.
Abbreviations used:
-
- AFP
-
- adiabatic full passage
-
- Ace
-
- acetate
-
- FID
-
- free induction decay
-
- Gln
-
- glutamine
-
- Glu
-
- glutamate
-
- KG
-
- α-ketoglutarate
-
- Lac
-
- lactate
-
- MCS
-
- Monte Carlo simulations
-
- NAA
-
- N-acetyl aspartate
-
- RF
-
- radio frequency
-
- SNR
-
- signal-to-noise ratio
-
- TCA
-
- tricarboxylic acid
-
- TE
-
- echo time
-
- TR
-
- repetition time
Neurochemistry is concerned with the study of molecular and cellular processes of the nervous system and their relationship to function. Energy metabolism and neurotransmission are two crucial processes affecting almost all aspects of cerebral function. Proper characterization not only involves determination of absolute metabolite concentrations, but also requires knowledge of the dynamic metabolic turnover of the metabolites involved. 1H NMR spectroscopy is currently the only technique that allows the non-invasive detection and quantification of a wide range of neurochemicals (Pfeuffer et al. 1999a). Direct 13C (Behar et al. 1986; Beckmann et al. 1991; Gruetter et al. 1994) or indirect 1H-observed, 13C-edited (1H-[13C]) NMR spectroscopy (Rothman et al. 1985, 1992) enables the dynamic detection of 13C labeled product formation, like [4-13C]-glutamate, [4-13C]-glutamine, and [2-13C]-GABA, which are derived from intravenously infused 13C enriched substrates, such as [1-13C]-glucose. 1H-[13C] NMR spectroscopy provides spectral information similar to the more traditional direct 13C NMR spectroscopy approach, but with the higher sensitivity of proton detection.
Previously, 13C and 1H-[13C] NMR spectroscopy have been used to study energy metabolism in the human (Rothman et al. 1992; Gruetter et al. 1994, 2001; Mason et al. 1995; Shen et al. 1999) and animal (Rothman et al. 1985; Fitzpatrick et al. 1990; Mason et al. 1992; Sibson et al. 1998, 2001; de Graaf et al. 2003) brain during hibernating (Henry et al. 2007), resting (Rothman et al. 1985, 1992; Fitzpatrick et al. 1990; Mason et al. 1992, 1995; Gruetter et al. 1994, 2001; Sibson et al. 1998, 2001; Shen et al. 1999; de Graaf et al. 2003; Deelchand et al. 2009a,b) and stimulated (Chen et al. 2001; Chhina et al. 2001; Patel et al. 2004) conditions. Glutamatergic neurotransmission has been assessed as a glutamate–glutamine neurotransmitter cycle between neurons and astroglia (Sibson et al. 1997). In addition, some of the smaller metabolic pathways like anaplerosis (Sibson et al. 2001; Mason et al. 2007) and astroglial energy metabolism (Bluml et al. 2002; Lebon et al. 2002) have been studied with alternate substrates, such as [2-13C]-acetate (Ace) and [2-13C]-glucose. The results of 13C MR spectroscopy have been validated through the use of fluorodeoxyglucose (18F-FDG PET) in the monkey brain (Boumezbeur et al. 2005). One of the most important findings from these studies was the linear correlation between increments of cerebral energy metabolism and total neurotransmitter cycling (Sibson et al. 1998). This relation was subsequently refined by separating the contributions of excitatory glutamatergic and inhibitory GABAergic neurotransmission. However, because of the low concentration of GABA and the strong spectral overlap with other metabolites and macromolecules, studies were necessarily performed ex vivo (Patel et al. 2005). Fortunately, with the availability of higher magnetic fields and the subsequent increase in spectral resolution and signal-to-noise ratio (SNR), the detection of lower-concentration metabolites, like GABA, became feasible. Several studies have qualitatively observed the formation of [3-13C]-GABA following [1-13C]-glucose or [1,6-13C2]-glucose infusion (Pfeuffer et al. 1999b; de Graaf et al. 2003; Deelchand et al. 2009b). However, because of limited SNR and/or spectral resolution, to date no studies have appeared that quantitatively assess the metabolic fluxes associated with GABA turnover in the normal rat brain in vivo. Yang et al. (2007) were able to measure cerebral GABA turnover in vivo, but only after administration of a GABA-transaminase inhibitor to elevate GABA levels (Manor et al. 1996; de Graaf et al. 2006a).
The aim of this study is to assess the extent to which 1H-[13C] NMR spectroscopy can provide reliable and quantifiable neurochemical information about brain metabolite concentrations and turnover under physiological conditions in rat brain in vivo at 9.4 T. In particular, the ability to quantitatively determine metabolic fluxes of GABA, as well as glutamate, in vivo will be established. The detection of both excitatory and inhibitory neurotransmission and cerebral energetics should provide a valuable, non-invasive tool in the understanding of brain function.
Methods
Animal preparation
Animal experiments were conducted in accordance with federal guidelines on the care and use of laboratory animals under approved protocols by the Yale Animal Care and Use Committee.
Following an overnight fast (12–16 h), ten Wistar rats (165.6 ± 12.0 g, mean ± SD) were anesthetized with 2–3% halothane in a mixture of N2O and O2 (70/27–28%), tracheotomized and ventilated. A femoral artery was cannulated for monitoring of mean arterial blood pressure and blood sampling to determine arterial blood gasses (pCO2 and pO2) and pH. Small adjustments in tidal volume and ventilation frequency kept these physiological variables within normal limits (pCO2 = 33–45 mmHg; pO2 ≥ 120 mmHg; pH = 7.30–7.58; mean arterial blood pressure = 90–110 mmHg). Body core temperature was measured with a rectal thermometer and maintained at 37 ± 1°C by means of a heated water pad. A femoral vein was cannulated for infusion of [U-13C6]-glucose (Glc, n = 5) or [2-13C]-Ace (n = 5; Cambridge Isotope Laboratories Inc, Andover, MA, USA). Briefly, animals received an initial 250 μL intravenous bolus of 0.75 M [U-13C6]-glucose (per 200 g body weight) followed by an intravenous infusion of 0.75 M [U-13C6]-glucose. The infusion rate was decreased manually every 30 s according to a decreasing exponential function during the first 8 min and was constant at 13.7 μL/min for the remainder of the experiment. For acetate, animals received an initial 200 μL intravenous bolus of 2.0 M [2-13C]-Ace over 15 s. The infusion rate was decreased to 50–25 μL/min at 15 s and 240 s, respectively, and remained constant at 12.5 μL/min for the remainder of the experiment (t > 480 s). Following surgery, halothane was reduced to 0.5–1% to maintain a stable blood pressure. Animal heads were shaven to allow for better coil positioning and animals were placed in the probe, restrained in a head holder and were further immobilized with d-tubocurarine (0.5 mg/kg/40 min, i.p.). After the magnetic resonance experiments, the rats were killed while still anaesthetized.
Magnetic resonance spectroscopy
Experiments were performed on a 9.4 T Magnex magnet and Bruker console (Bruker, Billerica, MA, USA) equipped with a 9-cm-diameter gradient coil insert (Resonance Research Inc, Billerica, MA, USA, 490 mT/m in 175 μs). A 14-mm-diameter surface coil was used for 1H radio frequency (RF) pulse excitation and signal reception (400.5 MHz). RF pulse transmission on 13C (100.2 MHz) was achieved with two orthogonal 21 mm diameter surface coils driven in quadrature (Adriany and Gruetter 1997). Multi-slice echo planar images [field of view 2.56 × 2.56 cm, matrix 128 × 128, ten slices of 1 mm thickness, repetition time (TR)/echo time (TE) = 2500/10 ms] were acquired and used to position the spectroscopic volume of interest (6 × 5 × 6 mm) over the hippocampal area as close to the surface coil as possible, but remaining at least 0.5 mm away from the edges of the brain to improve magnetic field homogeneity. The rostral-caudal center of the voxel was positioned in the slice that showed the most dorsal portion of the medial hippocampus.
The magnetic field homogeneity over the volume of interest was optimized with the non-iterative, Fast Automatic Shimming Technique by Mapping Along Projections, FASTMAP, for all first- and second-order shim coils (Gruetter 1993). This resulted in signal line widths of 14–16 Hz for water and 9–11 Hz for metabolites in the localized volume of 180 μL. Localized 1H NMR spectra were obtained with the NMR pulse sequence described previously (de Graaf et al. 2003). In short, 3D localization was achieved by a combination of outer volume suppression, image-selected in vivo spectroscopy, and slice-selective excitation. Water suppression was performed with Selective Water suppression with Adiabatic Modulated Pulses, SWAMP (de Graaf and Nicolay 1998), an adiabatic analog of the CHEmical Shift Selective, CHESS (Haase et al. 1985), technique. Discrimination between 1H-[13C] and 1H-[12C] NMR signals was achieved by executing a 4.0 ms adiabatic full passage (AFP) pulse [sin40 modulation, 10 kHz bandwidth (Tannus and Garwood 1996)] on the 13C channel on alternating acquisitions, after which the free induction decays (FIDs) obtained with and without the 13C inversion were stored in separate memory blocks. 1H-[13C] NMR signals were obtained by subtraction of the 13C-inverted FIDs from the non-inverted FIDs. Broadband adiabatic 13C decoupling was applied during the total acquisition time of 204.8 ms. The decoupling sequence was executed with a 1.6 ms AFP pulse [HS4 modulation, 6.25 kHz bandwidth (Tannus and Garwood 1996)] incorporated in a 20-step supercycle (Fujiwara and Nagayama 1988) to provide adiabatic, frequency-selective decoupling (de Graaf 2005). With the decoupling frequency centered on the [4-13C]-glutamate resonance at 34.2 ppm, the decoupling sequence provides frequency-selective decoupling between c. 3 and 65 ppm, while leaving the [1-13C]-glucose resonances at 92.7 and 96.6 ppm unperturbed. Since the αH1-glucose resonance is resolved in 1H NMR spectra at 9.4 T, frequency-selective decoupling allows for direct quantification of the 13C fractional enrichment of cerebral glucose from total, unedited 1H NMR spectra (de Graaf 2005).
The total GABA concentration was obtained through homonuclear spectral editing with a double spin-echo sequence using 20 ms Gaussian refocusing pulses selective for the GABA-H3 protons at 1.89 ppm (Mescher et al. 1998). An echo time of 68 ms (= 1/2J) was chosen to optimize the detection efficiency of the GABA-H4 protons at 3.01 ppm. RF pulse calibration was performed on the water resonance. Editing efficiency on individual animals was calculated from the residual water signal in the presence of spectral editing pulses. The experiments were performed with a TR of 4.0 s and 64 repetitions with interleaved editing. The GABA-edited spectrum was obtained by subtracting the non-edited from the edited spectra.
Data acquisition and processing
All FIDs were acquired with a 32-s time resolution (eight image-selected in vivo spectroscopy increments with TR = 4.0 s) to minimize the effects of small frequency shifts between acquisitions and to evaluate motion artifacts. Following a complete experiment of approximately 32 min of continuous signal acquisition, FIDs were zero-filled to 8 K data points, apodized (1.0 Hz Gaussian line broadening), Fourier transformed, and phase corrected (only zero-order phase). The spectra were frequency corrected to account for drift in the main magnetic field, but no amplitude or phase corrections were performed on individual spectra. Next, spectra acquired over 16 min were added to increase the SNR and used for subsequent quantification of metabolite concentrations and fractional enrichments by an in-house frequency-domain fitting program written in Matlab 7.0.4 (The Mathworks, Natick, MA, USA). Similar to LCmodel (Provencher 1993), the algorithm models the in vivo NMR spectrum as a superposition of a basis set of in vitro NMR spectra of pure metabolite solutions. 1H NMR spectra were collected in vitro under controlled pH and temperature conditions from Ace, alanine (Ala), aspartate (Asp), creatine (Cr), GABA, Glc, [U-13C6]-Glc, glutamate (Glu), glutamine (Gln), GSH, glycerophosphorylcholine, lactate (Lac), myo-inositol, N-acetyl aspartate (NAA), NAA-glutamate, phosphocreatine (PCr), phosphocholine, phosphoethanolamine, taurine and valine. A macromolecular baseline was measured separately on a number of animals by ‘nulling’ the metabolite resonances with a double inversion recovery element preceding the 1H-[13C] NMR sequence with 1.0 ms hyperbolic secant modulated AFP pulses (bandwidth 10 kHz), inversion recovery time = 1950 and 550 ms and TR = 6000 ms (de Graaf et al. 2006b). Following spectral fitting, the absolute metabolite concentrations were calculated with respect to total creatine (tCr = PCr + Cr) under the assumption of a 10 mM tCr concentration. No correction for differential T2 relaxation was performed. A separate version of the fitting program with additional constraints and a reduced basis set (Ace, Ala, Asp, GABA, Glc, Gln, Glu, Lac, NAA) was used for quantification of the edited 1H-[13C] NMR spectra. Specifically, while the resonance amplitudes of the different isotopically-labeled peaks within one molecule (e.g. [2-13C], [3-13C] and [4-13C]-glutamate) were unconstrained, the line width, phase, and frequency were forced to be identical. The reliability of the spectral fit was evaluated by Monte Carlo simulations (MCS) using 50 iterations. The traditional Cramer-Rao lower bounds were not used, as they are not valid in the presence of an unknown macromolecular baseline. Although the Cramer-Rao lower bounds can be modified to include so-called ‘nuisance’ parameters related to the baseline (Ratiney et al. 2005), we found the use of MCS a more straightforward alternative. The MCS results are expressed as the % (SD MCS/mean MCS) to indicate the percentage of uncertainty in the concentration that is determined from the spectral fitting.
Metabolic modeling
To obtain the rates of the glutamatergic and GABAergic tricarboxylic acid (TCA) cycles (VTCA,Glu and VTCA,GABA) and the rates of glutamatergic and GABAergic neurotransmission (Vcycle,GluGln and Vcycle,GABAGln), the study was designed with two different substrates, [U-13C6]-Glc and [2-13C]-Ace. The dynamic [U-13C6]-Glc study provides information on VTCA,Glu, VTCA,GABA and Vcycle,total = Vcycle,GluGln + Vcycle,GABAGln. The individual glutamatergic and GABAergic neurotransmitter cycling rates cannot be separated during a [U-13C6]-Glc study since both neurotransmission cycles label the same [4-13C]-Gln position in the astroglial compartment (Patel et al. 2005). As detailed below, the steady-state [2-13C]-Ace study is used to obtain the ratio between the neurotransmitter cycle rate and the TCA cycle rate for each neuronal compartment. This ratio is used as a constraint during the metabolic modeling of the dynamic [U-13C6]-Glc study to obtain all four independent rates, VTCA,Glu, VTCA,GABA, Vcycle,GluGln, and Vcycle,GABAGln.
Time-courses for [3-13C]-Glu, [4-13C]-Glu, [3-13C]-Gln, [4-13C]-Gln, [2-13C]-GABA, and [4-13C]-GABA were reconstructed over 16 min intervals during infusion of [U-13C6]-Glc. During the [2-13C]-Ace infusion only the endpoint fractional enrichments were calculated. The glucose time courses were analyzed using a three-compartment metabolic model, comprising glutamatergic neuronal, GABAergic neuronal, and astroglial compartments, similar to the model described by Patel et al. (2005). Briefly, blood glucose enters the brain via Michaelis-Menten-based transport across the blood–brain barrier. However, since [1-12C]-αΗ1-glucose and [1-13C]-αΗ1-glucose levels could be detected and quantified directly in the brain compartment, no assumptions were required regarding glucose transport across the blood–brain barrier. Brain glucose is converted to pyruvate, which enters either the neuronal or astroglial TCA cycles. The 13C label of [U-13C6]-glucose will arrive at the TCA cycle intermediate [4-13C]-α-ketoglutarate (KG), which is in rapid exchange with [4-13C]-Glu at a rate Vx. Since [3-13C]-Glu and [3-13C]-Gln were both measured and included in the model, no assumptions about Vx were required. After labeling of [4-13C]-Glu, the [4-13C]-Gln position is ultimately labeled by the action of a glutamatergic neurotransmitter cycle between the glutamatergic neuronal and astroglial compartments. After one additional turn of the TCA cycle also [3-13C]-Glu and [3-13C]-Gln will label. In the GABAergic neuronal compartment, [4-13C]-Glu is quickly converted to [2-13C]-GABA, which ultimately labels [4-13C]-Gln through a neurotransmitter cycle between the GABAergic neuron and the astroglial compartment. In a subsequent turn of the TCA cycle, both [3-13C]-GABA and [4-13C]-GABA are labeled. Infusion of [2-13C]-Ace will first label the small astroglial [4-13C]-Glu pool, after which the label will appear in the larger astroglial [4-13C]-Gln pool. Gln is subsequently shuttled from the astroglia to the neurons where it will label the [4-13C]-Glu pools of both the GABAergic and glutamatergic compartments. Further details on the metabolic model can be found in (Patel et al. 2005).
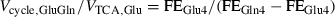 (1)
(1)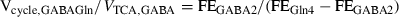 (2)
(2)The model was further constrained by assuming the pyruvate carboxylase flow (Vpc) to be 20% of the rate of total glutamine synthesis (Sibson et al. 2001). Dilutional fluxes were iterated for the three separate compartments. The cerebral metabolic rates were determined from the best fits of the model to the time-courses of 13C labeling with a Levenberg-Marquardt algorithm hybridized with simulated annealing (Alcolea et al. 1999). Cerebral metabolic rates of glucose oxidation [CMRGlc(ox)] were calculated as ½VTCA. The GABA pool was assigned to the GABAergic neuronal compartment, whereas Glu was divided between glutamatergic neurons (88%), astroglia (10%), and GABAergic neurons (2%) (Storm-Mathisen et al. 1983; Chaudhry et al. 1995). Gln was assumed to be synthesized in the astroglial compartment and degraded in the neuronal compartment.
With the described prior knowledge and restrictions, the metabolic model was used to determine the glutamatergic neuronal TCA cycle rate (VTCA,Glu), the GABAergic TCA cycle rate (VTCA,GABA) and astroglial TCA cycle rate (VTCA,A), the rate between α-KG and Glu (Vx), the glutamatergic neurotransmitter cycle rate (Vcycle,GluGln), the GABA shunt (VGABA), the GABAergic neurotransmitter cycle rate (Vcycle,GABAGln), and the dilutional rates (Vdil,Glu, Vdil,Gln, and Vdil,GABA).
Results
Figure 1 shows a typical 1H NMR spectrum from rat brain in vivo at 9.4 T acquired between 120 and 150 min following the start of intravenous [U-13C6]-glucose infusion. Figure 1(c) shows, besides the experimentally measured spectrum (top trace), the total spectral fit, the spectral contributions of glutamate, glutamine, GABA, and Lac to the total fit, the macromolecular baseline and the difference between the measured and fitted spectra (bottom trace). The absolute metabolite concentrations are listed in Table 1. Since the adiabatic decoupling sequence provides frequency-selective decoupling (from c. 3 ppm to 65 ppm on the 13C channel) all 1H-[13C] NMR resonances upfield from water are perfectly decoupled. Since the 13C resonances from [1-13C]-glucose fall outside the decoupling range, the 1H resonances of [1-13C]-αH1-glucose are not decoupled (Fig. 1a). The 13C inversion pulse inverts the 1H-[13C] resonances relative to the 1H-[12C] resonances on subsequent scans. However, since the 13C inversion pulse is also frequency-selective, the [1-13C]-αH1-glucose resonances do not invert and are thus identical in the absence (upper trace) or presence (lower trace) of the 13C editing pulse. Besides the excellent spectral fit, the most noticeable feature of Fig. 1(c) is the origin of the signal at 2.2–2.3 ppm as indicated by the dotted line. Even though this signal is commonly referred to as GABA-H2, it is clear from Fig. 1(c) that the majority of this signal must be assigned to macromolecules with only a minor, shifted contribution from GABA-H2. When the macromolecular baseline is properly accounted for, it has been shown that GABA can be accurately quantified from short TE 1H NMR spectra (Pfeuffer et al. 1999a). However, in this study, the obtained GABA concentration showed a clear deviation (0.50 ± 0.07 mM) from known GABA levels when calculated directly from the short TE 1H NMR spectrum. As a result, GABA detection was achieved with more conventional homonuclear spectral editing. Figure 2 shows two 1H NMR spectra with and without selective refocusing of GABA-H3. The difference between the two NMR spectra reveals the outer two resonances of the GABA-H4 triplet at 3.01 ppm. The finite bandwidth of the selective refocusing pulses leads to partial co-editing of N-acetyl aspartate at 2.01 ppm and glutamate/glutamine at 3.75 ppm. However, these resonances are well-separated from GABA-H4 and do not affect the GABA quantification. As a result of the increased chemical shift dispersion at 9.4 T, co-editing of macromolecules was minimal. The GABA concentration obtained through homonuclear spectral editing was 1.17 ± 0.31 mM.
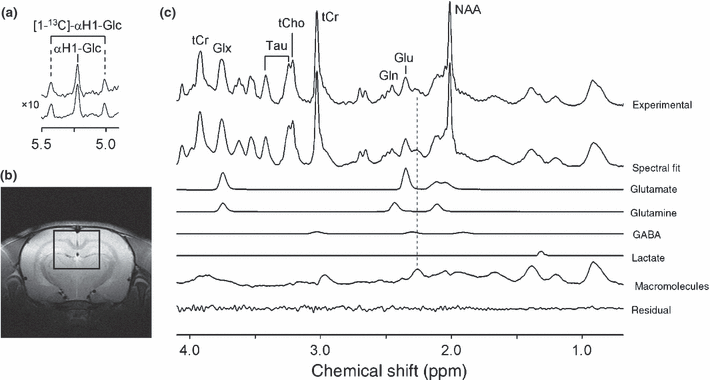
Localized 1H-[13C] NMR spectroscopy of rat brain in vivo at 9.4 T acquired between 120 and 150 min following the start of intravenous [U-13C6]-glucose infusion. (a) The [1-12C]-αH1-glucose signal appears at 5.22 ppm, whereas the [1-13C]-αH1-glucose signal appears, because of selective decoupling, as a doublet signal with a one-bound 1H-13C scalar coupling of 169 Hz. Because of selective spectral editing, the proton glucose resonances are identical in the absence (upper trace) and presence (lower trace) of the 13C inversion pulse. (b) Location of the 180 μL (= 6 × 5 × 6 mm) voxel. (c) Experimental 1H NMR spectrum averaged over 32 min in the absence of a 13C inversion pulse (top trace), together with the total spectral fit, the spectral contributions of glutamate, glutamine, GABA, lactate, and macromolecules to the total spectral fit and the difference between the experimental and fitted 1H NMR spectra (lower trace). Glx, sum of Gln and Glu; tCho, total choline representing the sum of glycerophosphorylcholine and phosphocholine; tCr, total creatine respresenting the sum of Cr and PCr.
| Mean (mM) | SD (mM) | MCS (%) | |
|---|---|---|---|
| Alanine | 0.27 | 0.09 | 58.30 |
| Aspartate | 2.48 | 1.00 | 11.89 |
| Choline (total) | 1.71 | 0.09 | 9.90 |
| Glycerophosphorylcholine | 0.99 | 0.08 | 11.59 |
| Phosphocholine | 0.72 | 0.06 | 24.88 |
| GABAb | 1.17 | 0.31 | 16.68 |
| Glutamate | 10.11 | 0.93 | 4.67 |
| Glutamine | 4.56 | 0.53 | 7.30 |
| GSH | 1.98 | 1.28 | 9.77 |
| Myo-inositol | 3.84 | 0.48 | 3.15 |
| N-acetyl aspartate | 8.95 | 0.44 | 1.26 |
| NAAG | 2.90 | 0.69 | 13.58 |
| Lactate | 0.82 | 0.15 | 30.08 |
| Phosphoethanolamine | 1.58 | 0.11 | 10.48 |
| Taurine | 3.54 | 0.11 | 4.06 |
| Valine | 0.39 | 0.07 | 20.81 |
- aAll concentrations are referenced to 10 mM total creatine (n = 10). bObtained from J-difference edited ‘H NMR spectra. NAAG, NAA-glutamate.
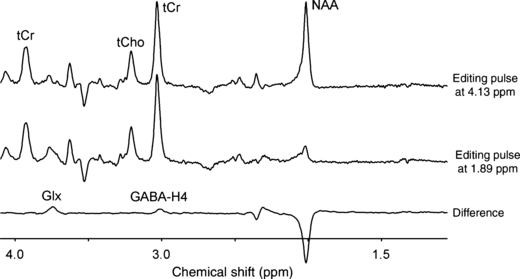
Spectral editing of GABA in rat brain in vivo at 9.4 T. 1H NMR spectra are acquired in which the 20 ms Gaussian editing pulses selectively refocus the GABA-H3 resonance at 1.89 ppm (middle trace) or at a control position (4.13 ppm, upper trace) mirrored relative to the total creatine resonance at 3.01 ppm. The difference spectrum displays the edited GABA-H4 resonance at 3.01 ppm together with co-edited signals from glutamate/glutamine-H2, GABA-H2, and N-acetyl aspartate.
Figure 3 shows the edited 1H-[13C] NMR spectrum obtained from rat brain 120 min following the onset of the [U-13C6]-glucose infusion. The most prominent resonances originated from glutamate, glutamine, and GABA. Note that all spectra were acquired in the presence of selective 13C decoupling, thus eliminating splitting because of heteronuclear scalar coupling. The decoupling and editing pulses did not affect the [1-13C]-α-glucose resonances at 92.7 ppm, such that (i) heteronuclear scalar coupling is still visible on the αH1-glucose resonance at 5.22 ppm; and (ii) [1-13C]-αΗ1-glucose does not appear in the 1H-[13C] difference spectrum (see also Fig. 1a). Figure 3 also shows the best fit of the measured 1H-[13C] NMR spectrum as well as the spectral contributions of glutamate, glutamine, GABA and Lac. Note that [2-13C]-GABA appears as a clear upfield shoulder of the [4-13C]-glutamate resonance. Repeating the spectral fit without the inclusion of [2-13C]-GABA (data not shown) resulted in a significant residual, indicating that GABA is an essential part of the 1H-[13C] NMR spectrum.
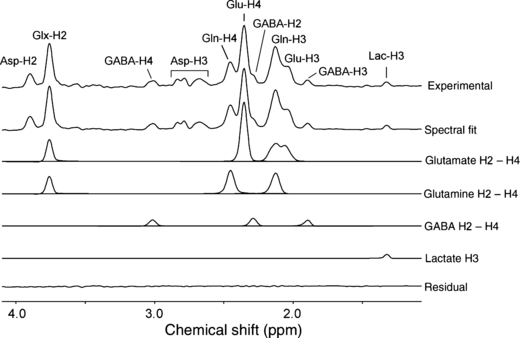
Localized 1H-[13C] NMR spectroscopy of rat brain in vivo at 9.4 T acquired between 120 and 150 min following the start of intravenous [U-13C6]-glucose infusion. The 13C-edited 1H NMR spectrum is shown (top trace), together with the total spectral fit, as well as the spectral contribution of the glutamate, glutamine, GABA, and lactate resonances to the total fit. The lower trace shows the difference between the experimental and fitted 13C-edited 1H NMR spectra.
Typical turnover curves from a single animal for [4-13C] and [3-13C]-glutamate (Fig. 4a), [4-13C] and [3-13C]-glutamine (Fig. 4b), and [2-13C] and [4-13C]-GABA (Fig. 4c) together with the best fit of the metabolic model as described in the Methods section. Experimental data was averaged over 16 min to increase the SNR.
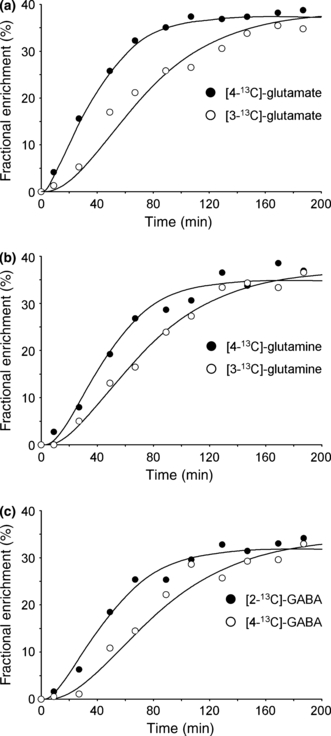
Metabolic turnover curves for (a) [3-13C] and [4-13C]-glutamate, (b) [3-13C] and [4-13C]-glutamine, and (c) [2-13C] and [4-13C]-GABA during the infusion of [U-13C6]-glucose. The dots represent the experimentally measured fractional enrichment, whereas the solid curves represent the best fit to the metabolic model.
Figure 5 shows the endpoint 1H-[13C] spectrum acquired 120 min following the start of [2-13C]-Ace infusion. Besides the large [2-13C]-Ace resonance at 1.91 ppm, an increased [4-13C]-glutamine resonance relative to the [4-13C]-glutamate is characteristic, as has been shown previously by direct 13C NMR detection (Bluml et al. 2002; Lebon et al. 2002). The [3-13C]-GABA resonance was overwhelmed by the much larger [2-13C]-Ace resonance and could not be quantified. The signal upfield from the [4-13C]-Glu resonance can only be explained by the presence of [2-13C]-GABA (dotted line). Omission of GABA leads to a strong degradation of the spectral fit. The MCS uncertainties for GABA-H2 in the glucose and acetate studies were 18.3% and 21.2%, respectively.
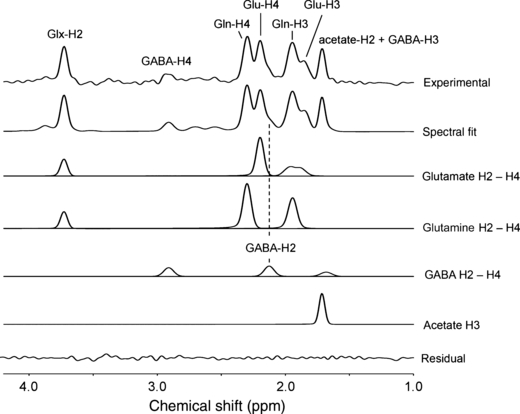
Localized 1H-[13C] NMR spectroscopy of rat brain in vivo at 9.4 T following intravenous [2-13C]-Ace infusion. The 13C-edited 1H NMR spectrum is shown (top trace), together with the total spectral fit, the spectral contributions of the H2, H3, and H4 label positions of glutamate, glutamine and GABA, the spectral contribution of acetate and the difference between the experimental and fitted 13C-edited 1H NMR spectra (lower trace). The experimental data (top trace) is averaged between 120 and 150 min following the onset of [2-13C]-Ace infusion.
From the steady-state [2-13C]-Ace experiment, the ratio between Vcycle and VTCA was determined for the glutamatergic (Vcycle,GluGln/VTCA,Glu = 0.58 ± 0.076) and GABAergic neurons (Vcycle,GABAGln/VTCA,GABA = 0.54 ± 0.063). The endpoint fractional enrichments for Glu-H4, Gln-H4 and GABA-H2 are 11.06 ± 1.50%, 27.11 ± 3.68%, and 9.51 ± 1.49%, respectively. These values were used to constrain the metabolic model during the fitting of the data obtained with [U-13C6]-glucose. The resulting TCA cycle rates were given by VTCA,Glu = 0.472 ± 0.040 μmol/min/g, VTCA,GABA = 0.062 ± 0.009 μmol/min/g, and VTCA,A = 0.144 ± 0.025 μmol/min/g. Using the [2-13C]-Ace data as constraint, the excitatory and inhibitory neurotransmitter cycle rates were given by Vcycle,GluGln = 0.274 ± 0.023 μmol/min/g and Vcycle,GABAGln = 0.033 ± 0.005 μmol/min/g, representing 89.2% and 10.8% of the total neurotransmitter cycling fluxes, respectively. The GABA shunt, VGABA, was determined as 0.025 ± 0.006 μmol/min/g, whereas the exchange rate between α-KG and Glu, Vx, was 5.5 ± 2.4 μmol/min/g. The dilutional rates were all < 0.065 μmol/min/g.
Discussion
Here, we have shown that the metabolic turnover of the excitatory and inhibitory neurotransmitters, glutamate and GABA, can be detected simultaneously by 1H-[13C]-NMR spectroscopy in rat brain in vivo. The infusion of [U-13C6]-glucose gives information about glutamatergic and GABAergic energy metabolism, as well as total neurotransmission. When used in combination with steady-state fractional enrichments following a [2-13C]-Ace infusion, the total neurotransmitter cycle rate can be separated into the glutamatergic and GABAergic contributions.
In this study, we were able to detect the fractional enrichment and concentration of cerebral glucose directly through a combination of selective heteronuclear editing and decoupling and very selective water suppression. The primary benefit of direct cerebral glucose detection is that no assumptions are necessary regarding blood-to-brain glucose transport kinetics. Furthermore, in vivo detection allows for a much higher temporal resolution than would be possible with arterial blood sampling.
Although the results demonstrate the feasibility of detecting cerebral GABA turnover by 1H-[13C] NMR spectroscopy, the technique is demanding and optimal experimental conditions must be obtained for successful completion of the study. Foremost, the magnetic field homogeneity must be sufficient to allow the differentiation of glutamate-H4 and GABA-H2. At 9.4 T, this condition required that the line width of water be no more than 16 Hz. Such a line width could only be achieved through the use of all first- and second-order spherical harmonics shims in combination with stabile and optimal animal physiology. To account for temporal magnetic field drifts, it was crucial to store each FID separately and perform a post-acquisition frequency correction prior to any further processing.
Besides optimal magnetic field homogeneity, the spectral SNR was also important for reliable GABA detection. Given a GABA concentration of 1.17 ± 0.31 mmol/L (Table 1) and an endpoint fractional enrichment of c. 35% during [U-13C6]-glucose infusion, the spectral sensitivity must be sufficient to detect 0.4 mM GABA in 16 min. The volume size of 180 μL at 9.4 T in this study was sufficient to detect GABA turnover reliably. In future studies, the volume size can potentially be decreased, especially when the magnetic field homogeneity over the smaller volume improves.
The spectral fitting algorithm yielded the total GABA concentration from the total, non-edited 1H NMR spectrum, as was previously reported (Pfeuffer et al. 1999a). However, the non-edited GABA concentration (0.50 ± 0.07 mM) displayed a clear deviation from known GABA concentrations (0.83–2.30 mM; Pfeuffer et al. 1999a) in rat brain in vivo. The total GABA concentration (1.17 ± 0.31 mM) obtained by homonuclear spectral editing was in good agreement with literature values. The accuracy of the GABA concentration obtained by spectral editing was lower than that obtained by short TE NMR spectroscopy, likely because of a lower spectral SNR. However, the GABA extracted from short TE 1H NMR spectra was biased toward a lower concentration. This can be attributed to significant spectral overlap of GABA at all spectral positions and a strong correlation between GABA and the macromolecular baseline (Ratiney et al. 2005). In contrast, the edited GABA 1H NMR spectrum has no macromolecular baseline and minimal spectral overlap, such that the accuracy is directly related to the spectral SNR. Given the importance of the absolute GABA concentration, the reliability of homonuclear spectral editing was preferred over the precision of short TE MR spectra.
The value of Vcycle,GABAGln = 0.033 ± 0.005 μmol/min/g is lower than a previous estimate by Patel et al. (2005) of 0.135 ± 0.015 μmol/min/g measured for the rat cortex under similar physiological conditions (halothane anesthesia). In contrast, Yang et al. (2007), using a selective inhibitor of GABA transaminase (gabaculine) to elevate the GABA pool and enhance 13C label trapping from [1-13C]-glucose, determined a value Vcycle,GABAGln = 0.030 ± 0.007 μmol/min/g for the brain of α-chloralose anaesthetized rats. This value is consistent with previous estimates of GABA synthesis and Vcycle,GABAGln after acute GABA-transaminase inhibition under similar physiological conditions (Mason et al. 2001), but is less than values determined in the absence of such inhibitors. The higher GABA turnover rate in our previous study (Patel et al. 2005) is likely to result from a higher fraction of pure cortical tissue, whereas the large 180 μL volume of this study contains large amounts (> 60%) of white matter and subcortex, including corpus callosum, hippocampus, and thalamus (Fig. 1b). The similarity in the present value of VTCA,n (= VTCA,Glu + VTCA,GABA = 0.53μmol/g/min) to the subcortex (0.44 μmol/g/min), but not to the cortex (0.73 μmol/g/min) from a previous study (de Graaf et al. 2004) supports this contention.
Yang et al. (2007) were not able to detect [2-13C]-GABA labeling during [2-13C]-Ace infusion under normal conditions (i.e., without vigabatrin). However, given the low GABA-H2 fractional enrichment and concentration and the 3.5 times smaller volume, the absence of [2-13C]-GABA detection by Yang et al. (2007) may simply be explained by an inadequate spectral SNR. Patel et al. (2005) studied GABAergic neurotransmission in the rat cortex ex vivo and found significant GABA turnover from [2-13C]-Ace (Vcycle,GABAGln/VTCA,GABA = 0.45), consistent with other studies reporting ex vivo measurements of GABA labeling from [1,2-13C2]-Ace in extracts of rat (Preece and Cerdan 1996) and mouse (Hassel et al. 1998) brain.
Conclusions
This work has shown that detection of glutamatergic and GABAergic neurotransmission and the associated energy metabolism in rat brain in vivo is possible at 9.4 T under optimal experimental conditions. This capacity opens the possibility of studying excitatory and inhibitory neurotransmission during a wide range of conditions, including functional activation and neurological disorders, like epilepsy.
Acknowledgements
This research was supported by NIH grants R01 DK027121 (K. L. B.), K02 AA13420 (G. F. M.) and P30 NS052519 and grants (NEF 04-15 and NEF 08-10) from the National Epilepsy Fund of The Netherlands (P. v. E. and K. P. J. B.). The authors thank Bei Wang for expert animal preparation, Peter Brown for construction and maintenance of the 1H-[13C] RF coil, and Terence Nixon and Scott McIntyre for system maintenance.




