Country Size, Technology and Manufacturing Location
Abstract
Country size, technology and trade costs jointly affect the location of manufacturing activity. In this paper, the combined effects of country size and technology differences on manufacturing location are examined in a simple new economic geography model. The specification yields a closed-form, analytic relationship between measures of relative productivity, country size and trade costs. The patterns of agglomeration are consistent with recent empirical evidence. Market and supplier access favor manufacturing agglomeration in large countries for high to intermediate trade costs. High productivity countries, however small, are favored for low trade costs. The model's tractability facilitates welfare analysis.
1. Introduction
The new economic geography (NEG) has contributed to our understanding of firm location choices by explicitly modeling trade costs in general equilibrium. While NEG models have recently begun to explicitly account for country size and technology differences, the agglomeration effects of either size or technology are usually considered in isolation. Yet size and technology jointly interact as trade costs change. The outcome of this process is not immediately evident. Where firms locate, what they produce, and the employment patterns and wages that result are interdependent. In this paper, both size and technology differences are incorporated into a simple NEG model. The structure is highly stylized, but approximates empirical trade and firm location patterns well.
The role of distance and geography on trade flows remains unsettled. A recent review by Disdier and Head (2008), summarizing estimates from over 100 papers, found that on average a 10% increase in distance results in a 9% reduction in bilateral trade volumes. A survey by Harrigan (2003) reviewed the empirical role of distance in fitting standard and new trade theory to the data. Despite the empirical support, Harrigan noted that theoretically grounded motivations for the role of distance remain difficult to disentangle from comparative advantage and factor abundance.
Recent empirical investigations reveal specific relationships between technology, country size, and trade costs. Eaton and Kortum (2002) carefully estimated a general equilibrium model of trade and geography for Origanisation for Economic Cooperation and Development (OECD) countries. They found that as geographic barriers fall the share of manufacturing employment rises in larger, less productive countries. Further declines in geographic barriers reverse the pattern, favoring technological efficiency and manufacturing specialization in small countries. Aiginger and Pfaffermayr (2004) found a similar pattern for industry concentration in the European Union following the implementation of the Single Market. Several results in Amiti and Javorcik (2008) indicated that interactions between market size, production costs, and distance are important. They estimate a NEG model for the entry of foreign firms into Chinese provinces. In their model, firms require supplier access to sector-specific intermediate inputs and market access to customers. Measures of market and supplier access both within and outside provinces have a positive and significant effect on firm entry. Differences in variable costs also have a quantifiable impact on the location of firms. Redding and Venables (2004) used an NEG structural model for cross-country analysis and found evidence that market and supplier access effects decline with distance.
A central modeling challenge is to merge these elements together while maintaining some tractability. This paper extends the simple NEG model of Ottaviano (2002) to examine the relationship between country size, productivity, and trade costs. Agglomeration is driven by input–output linkages between firms. The spatial allocation of manufacturing adjusts endogenously to maximize profits. The main qualitative contribution is the realistic emergence and structure of core-periphery style agglomeration. Market and supplier access effects dominate for high to intermediate trade costs. This favors agglomeration in large countries. Further trade cost reductions can reverse this pattern when the large country is less technologically efficient than a smaller neighbor. Even for relatively small countries, Ricardian efficiency in variable production costs dominates when trade costs are low. One consequence is that early industrializers in a nearly free trade world will gain a strong advantage. Once a manufacturing core has formed, the peripheral regions must do more than play technological catch-up and copycat to overcome the agglomeration rents. The results are broadly applicable to the entire class of NEG models with input–output linkages (cf. Ottaviano and Robert-Nicoud, 2005). This paper derives a closed-form, analytical relationship for the interaction of technology with size and trade costs that can be used to determine the equilibria and critical points of the model. The main results hold even when factor price equalization is relaxed.
A recent set of theoretical extensions are closely related to this paper. A variety of NEG specifications show that industrial production can agglomerate against Ricardian comparative advantage. Venables (1999) embedded an NEG framework into a rather complex multi-sector Ricardian model with a continuum of goods. He found differentiated goods industries can agglomerate against comparative advantage. Ricci (1999) analyzes comparative advantage in a model with labor migration and employed a non-full specialization condition to impose factor price equalization. He identified the trade-off between size and comparative advantage as trade costs fall. Forslid and Wooton (2003) used heterogeneous fixed costs of developing new varieties that increase with the number of firms in each country. Each country has a fixed cost comparative advantage over a range of product varieties, and agglomeration occurs through labor migration. The fixed cost structure becomes a type of congestion externality that dominates market access advantages as trade costs fall. As a result, falling trade costs lead initially to manufacturing agglomeration and then to a dispersed production equilibrium. Forslid and Wooton conjectured in a footnote that qualitative results should be similar for variable cost differences, but this paper shows this is not the case.
Country size has been analyzed in two-factor Hecksher–Ohlin models and in terms of relative labor endowments. Amiti (2005) and Epifani (2005) considered aspects of well-specified two factor models within a NEG framework. They showed that agglomeration patterns can defy the predictions of factor abundance and lead to non-monotonic Stolper–Samuelson effects. New trade theory has also addressed country size in two factor models (Amiti, 1998) and one factor labor models (Laussel and Paul, 2007) while holding technology symmetric. This approach necessarily requires small countries to pay lower wages to attract manufacturing and ignores productivity differentials. Yet improving productivity is an especially relevant channel for regions that are unlikely to overcome pure size disadvantages through population growth or rapid capital investment. Size differences are evaluated using comparative statics by testing small deviations from symmetry (e.g. Forslid and Ottaviano, 2003). This partial equilibrium approach can miss more complex outcomes for large size and technology differences.
The rest of this paper is organized as follows. In section 2, size and technological asymmetry is incorporated into an NEG framework. Section 3 analyzes the features of long-run equilibria under price equalization. In section 4, factor price equalization is relaxed and it is shown that the qualitative results are the same. Section 5 explores welfare implications and Section 6 concludes.
2. The Model
Endowments
There are two regions denoted Home and Foreign. Two goods are produced in a homogenous agriculture (A) sector and differentiated manufacturing (M) sector. Labor is the only primary factor of production. Labor is mobile within each country and between the agriculture and manufacturing sectors. Using sL to denote labor shares, the size of the labor endowment in Home is sLLw, the size of Foreign is (1 − sL)Lw and λ = (1 − sL)/sL is the ratio of endowments. Foreign variables and parameters carry an asterisk and world aggregates are denoted by superscript w.
Geography enters via iceberg transportation costs in the manufacturing sector. Locally consumed goods have zero transport costs. A fraction of a shipped good melts away in transit. For one unit of a good to arrive at its destination τ ∈ [1, ∞) units of the good must be shipped.
Preferences
 (1)
(1) (2)
(2)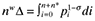 and
and 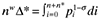 . The final destination price paid on imported and domestic goods is pi and nw = n + n* measures the aggregate mass of firms.
. The final destination price paid on imported and domestic goods is pi and nw = n + n* measures the aggregate mass of firms.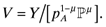 (3)
(3)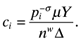 (4)
(4)The Dixit–Stiglitz CES sub-utility imparts a “love of variety” to preferences. Utility is increasing in the number of goods available. So (4) implies that total consumption of good i is a function of its own price and total expenditure weighted by the price index of all other M-sector goods.
Production and Market Structure
Agricultural sector
The A-sector employs only labor and is characterized by perfect competition, constant returns to scale technology and zero transport costs.1 Variable costs are such that it requires one unit of labor to produce one unit of the agricultural good in both countries. Marginal cost pricing will equate prices and wages,  . The A-sector good is chosen as the numeraire with the price set to unity.
. The A-sector good is chosen as the numeraire with the price set to unity.
Manufacturing sector
The M-sector is characterized by monopolistic competition and increasing returns. Firms produce using labor and an intermediate input that is a composite of all M-sector goods. The intermediate input creates cost-linkages between manufacturing firms that are an agglomeration mechanism.
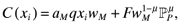 (5)
(5) is the producer price index for the M-sector composite. Marginal costs are incurred in terms of labor where aM is the Home unit labor requirement and q is a scaling parameter that is constant across countries. Firms also pay a fixed cost F, that is Cobb–Douglas with expenditure shares of (1 − µ) for labor and µ for an intermediate composite good of all M-sector varieties. The producer price index,
is the producer price index for the M-sector composite. Marginal costs are incurred in terms of labor where aM is the Home unit labor requirement and q is a scaling parameter that is constant across countries. Firms also pay a fixed cost F, that is Cobb–Douglas with expenditure shares of (1 − µ) for labor and µ for an intermediate composite good of all M-sector varieties. The producer price index,  , is identical to the consumer price index because the expenditure shares are equal, thus
, is identical to the consumer price index because the expenditure shares are equal, thus  .
. (6)
(6)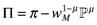 (7)
(7)Each firm maximizes monopoly profits in its own differentiated variety. The first order conditions for profit maximization imply a markup rule of pi(1 − 1/σ) = aMqwM. Following the markup rule, operating profits of each firm become πi = pixi/σ. The numerator is the value of total sales for each variety where  . A higher elasticity of substitution (higher σ), lowers profits.
. A higher elasticity of substitution (higher σ), lowers profits.
Labor markets
 (8)
(8)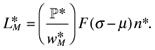 (9)
(9)Relative Productivity
Labor productivity, the inverse of aM, is country specific. One interpretation of this specification is to define the firm as mobile with implicit, identical managerial or firm specific technology across countries. Remaining productivity differences measured by aM and 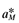 are outside the firm's control. A second interpretation sidesteps a global definition of the firm. Manufacturing firms are defined by the cost function (5) alone and not internationally mobile. Firms enter in response to profit opportunities and exit in response to losses within each country. Changes in industrial structure are accomplished by allocating labor between agriculture and manufacturing.
are outside the firm's control. A second interpretation sidesteps a global definition of the firm. Manufacturing firms are defined by the cost function (5) alone and not internationally mobile. Firms enter in response to profit opportunities and exit in response to losses within each country. Changes in industrial structure are accomplished by allocating labor between agriculture and manufacturing.
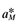 ) are the sole parameters of interest. Using notation in Baldwin et al. (2003), relative productivity is indexed by χ
) are the sole parameters of interest. Using notation in Baldwin et al. (2003), relative productivity is indexed by χ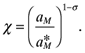 (10)
(10) and q = (1 − 1/σ) are chosen to set foreign prices equal to wages. Then Home unit labor requirement in terms of χ are
and q = (1 − 1/σ) are chosen to set foreign prices equal to wages. Then Home unit labor requirement in terms of χ are  . Productivity differences correspond to deviations of χ from unity.2
. Productivity differences correspond to deviations of χ from unity.2 (11)
(11) . Thus Home's competitiveness depends multiplicatively on transport costs, relative productivity and relative wages. Substituting these price expressions into the price indices reduces the Δ and Δ* terms in equation (2) to the following compact formulas:
. Thus Home's competitiveness depends multiplicatively on transport costs, relative productivity and relative wages. Substituting these price expressions into the price indices reduces the Δ and Δ* terms in equation (2) to the following compact formulas:
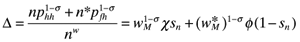 (12)
(12) (13)
(13)Short-run Equilibrium and Market Clearing
The geographical allocation of industry is taken as given and there is no firm entry and exit in the short run. Consumers maximize utility, firms maximize profits and markets clear.
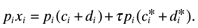 (14)
(14) (15)
(15) (16)
(16)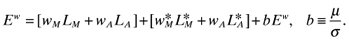
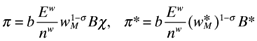 (17)
(17)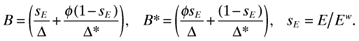
 (18)
(18) (19)
(19) (20)
(20) is Home's share of the wage bill. The size of each market in expenditure terms is directly related to its shares of manufacturing (sn) and labor (sL).
is Home's share of the wage bill. The size of each market in expenditure terms is directly related to its shares of manufacturing (sn) and labor (sL).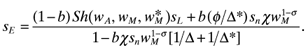 (21)
(21)3. Long-run Equilibrium Analysis
Non-full Specialization and Wages
To fix ideas, the model is simplified by imposing a non-full specialization condition. This assumption is relexed in section 4. If the A-sector good is produced in both locations, factor price equalization prevails and manufacturing wages are 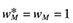 . Labor market clearing can be ignored and the profit equations (7) are two equations in two unknowns (sn, nw). This requires a non-full specialization (NFS) condition of (1 − µ) > max{sL, (1 − sL)}Lw. The A-sector must be a large enough share of total consumption that no single country can be fully specialized in the M-sector. As a result, the Agricultural good is always produced in both countries.
. Labor market clearing can be ignored and the profit equations (7) are two equations in two unknowns (sn, nw). This requires a non-full specialization (NFS) condition of (1 − µ) > max{sL, (1 − sL)}Lw. The A-sector must be a large enough share of total consumption that no single country can be fully specialized in the M-sector. As a result, the Agricultural good is always produced in both countries.
Firm Entry and Exit
In the long run, profits in each country are driven to zero by the entry and exit of firms. Atomistic and myopic firms will enter the M-sector in either location when profits in (7) are positive and exit when profits are negative.
The NFS condition admits three feasible and stable equilibria: (1) full agglomeration at Home when n* = 0, Π = 0 and profits to entry in Foreign are negative, (2) full agglomeration in Foreign when n = 0, Π* = 0 and Home profits are negative and (3) an interior case when Π = Π* = 0 and firms are active in both locations. Assessing the stability conditions of these three equilibria is the subject of the rest of this section.
An Illustrative Example
Total profits are two nonlinear equations in two unknowns (sn and nw). Completely solving the model for all stable and unstable equilibria requires numerical simulation. Fortunately, most of the critical points in the model can be found without extensive numerical methods. Before proceeding to derive more analytical results, it will be useful to present a fully solved and informative case. Consider a stylized dichotomy of global integration where a relatively large country opens to trade with a small country that has a productivity advantage in manufacturing. How will the location of manufacturing respond as these two countries move from autarky to free trade?
A large labor force is a larger market for goods. When trade costs are high, profits of the representative firm will be higher by producing for a large local market and exporting abroad. This market access effect is clear from expenditure equations (15), (16), and (21). A production–cost effect is the second agglomeration force. A larger share of firms in one country will lower its producer price index, raise profits and encourage firm entry. Relative productivity differences enter through this channel, but the price lowering impact is on locally consumed and exported goods. This productivity advantage raises profits and supports a larger number of firms in equilibrium. Trade costs will moderate the relative strength of these forces when Home has high manufacturing productivity and Foreign is large.
In Figure 1, Home has a modestly higher productivity. The relative productivity index is χ = 1.1 and Foreign is twice as large, λ = 2. Panel (a) plots the the share of world manufacturing in Home against trade costs. All stable equilibria are shown as solid lines. Panel (b) shows the contemporaneous share of employment in manufacturing in Home and Foreign. There are three phases of integration as trade costs fall: (1) dispersion, (2) full agglomeration in the large Foreign market followed by (3) full agglomeration in the more efficient Home market.
Evolution of Manufacturing Location and Employment Shares when Foreign is Large (λ = 2) and Home has a Manufacturing Relative Productivity Index of χ = 1.1. (a) Home Share of World Manufacturing (Parameters µ = 0.3; σ = 4, λ = 2, χ = 1.1); (b) Employment Share of Manufacturing
Beginning from autarky, high trade barriers naturally favor the larger market of Foreign. A market crowding effect keeps a small share of manufacturing firms in Home. As trade costs fall, Foreign's initial advantage is self-reinforcing. Higher consumer demand in Foreign results in a higher share of firms. This creates higher local demand for intermediate goods, lowers the Foreign price index and raises profits. More firms in Foreign enter manufacturing leading consequently to a shift in manufacturing employment. This process continues until manufacturing fully agglomerates in Foreign and profits are driven to zero. The level of trade costs where agglomeration in Foreign becomes sustainable is denoted by  . No manufactured goods are produced in Home even though it has higher manufacturing productivity.
. No manufactured goods are produced in Home even though it has higher manufacturing productivity.
This would be the end of the story with size asymmetry alone, but this economy continues to respond to falling trade costs. Agglomeration in Home eventually becomes stable (profitable) as trade costs fall. In this case though, the sustain point for Home,  , comes after the sustain point for Foreign. As a result, when history has favored Foreign and the rents to agglomeration are high, firms will have no incentive to establish manufacturing operations in Home.
, comes after the sustain point for Foreign. As a result, when history has favored Foreign and the rents to agglomeration are high, firms will have no incentive to establish manufacturing operations in Home.
At an even lower level of trade costs, the rents to agglomeration in Foreign vanish. Despite the larger local market in Foreign, transport costs are low enough that it is cost effective to manufacture goods in Home and export to Foreign. This occurs for levels of trade costs above  . The agglomeration is catastrophically3 reversed and a Ricardian pattern emerges. Panel (b) reflects this change in labor market shares. Nearly all of Home's labor endowment is engaged in manufacturing for very low trade costs.
. The agglomeration is catastrophically3 reversed and a Ricardian pattern emerges. Panel (b) reflects this change in labor market shares. Nearly all of Home's labor endowment is engaged in manufacturing for very low trade costs.
While this bifurcation diagram is rich with features, they are not always robust to variation in size and technology. Figure 2 repeats the analysis of Figure 1 when Home has even higher relative productivity of χ = 1.3. Now lowering trade costs from autarky benefit Foreign initially, but not enough that Foreign captures all manufacturing industry. Home achieves full agglomeration quickly as trade costs fall with a commensurate increase in manufacturing employment.
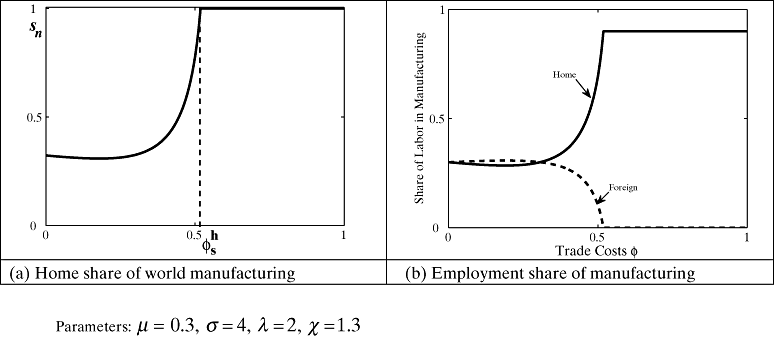
Evolution of Manufacturing Location and Employment Shares when when Foreign is Large (λ = 2) and and Home has a larger Manufacturing Relative Productivity Index of χ = 1.3. (a) Home Share of World Manufacturing (Parameters: µ = 0.3; σ = 4, λ = 2, χ = 1.3); (b) Employment Share of Manufacturing
In the following sections a more analytical approach is used to answer a number of questions. For what relative productivity can the initial size effect be overcome as in Figure 2? Can the sustain points defined above be ordered? How do the equilibria respond to variation in relative productivity? Will free trade always favor the country with the highest manufacturing productivity, regardless of size?
The Mass of Firms with Full Agglomeration
Productivity differences in variable costs will effect the equilibrium number of firms for agglomeration outcomes, but labor endowments will not. A more productive labor force, will support a larger number of firms and varieties. Deriving this result is straightforward.
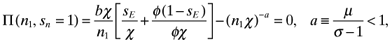 (22)
(22) (23)
(23)Free Trade Produces a Ricardian Allocation of Industry
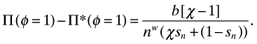 (24)
(24)Proposition 1. Under free trade (φ = 1) with asymmetric technology (χ ≠ 1) full agglomeration in the country with higher productivity is the only stable, long-run equilibrium when the non-full specialization condition is satisfied.
For a small open economy, high manufacturing productivity can only be exploited by moving to free or nearly free trade. Faced with competition from a larger trading partner, the suggested response from Proposition 1 is to lower trade costs as far as possible. Falling trade costs diminish the effects of market and supplier access and intensify competition that favors greater efficiency. Near zero trade costs change the location incentives and firms will prefer to produce in the more efficient location and export to the large market.
This confirmation of Ricardian trade patterns rectifies a fundamental indeterminacy of standard NEG models. In symmetric technology models with free trade, the equilibrium division of manufacturing is indeterminate even when countries differ in size. This can be seen by setting χ = 1 in (24). Profits are equalized in both locations and the share of manufacturing firms is indeterminate.
Agglomeration and Intermediate Trade Costs
 (25)
(25)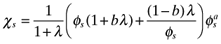 (26)
(26)Figure 3 plots the locus of sustain points defined in (26) for two cases of size asymmetry. Agglomeration in Home is stable for all ordered pairs (φ, χ) above the 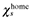 locus. Above this line, the profits of an atomistic firm entering to Foreign are negative. Agglomeration in Foreign is stable below the
locus. Above this line, the profits of an atomistic firm entering to Foreign are negative. Agglomeration in Foreign is stable below the 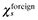 locus.
locus.

Agglomeration Sustaining Loci and Size Asymmetry (λ). (a) λ = 2 (Parameters: µ = 0.3; σ = 4, λ = 2); (b) λ = 3/2 (Parameters: µ = 0.3; σ = 4, λ = 3/2)
The value and ranking of the critical thresholds of φ required to sustain agglomeration are determined by relative productivity. These sustain points occur where the horizontal line for χ = 1.1 cuts the two loci. The location, ranking and number of sustain points depends on relative productivity. In panel (a), the parameters are set to match the scenario in the example of the Firm Entry and Exit subsection. The overlap of the stability ranges for φ is easy to observe and the sustain points can be ordered as  .
.
Agglomeration Rents
Many advanced, industrialized countries are relying on high productivity to prevent the erosion of manufacturing employment. In the case where Foreign is relatively large, Figure 3(a) indicates that nearly complete trade liberalization is required for Home to exploit its productivity advantage. Alternatively, the productivity advantage could be high enough that no level of trade costs supports agglomeration in Foreign. Panel (b) depicts such a scenario when the size advantage of Foreign is reduced to λ = 3/2 and relative productivity remains at χ = 1.1. Now there is a single sustain point and Home is the only stable agglomeration outcome.
 (27)
(27) . The minimum relative productivity that sustains agglomeration in Home is:
. The minimum relative productivity that sustains agglomeration in Home is:
 (28)
(28) can be derived for Foreign. The value of
can be derived for Foreign. The value of  is increasing in λ. Even slight size asymmetry requires that χ > 1 must hold to sustain agglomeration when Home is small. Conversely, large countries can sustain agglomeration for somewhat severe levels of disadvantage.
is increasing in λ. Even slight size asymmetry requires that χ > 1 must hold to sustain agglomeration when Home is small. Conversely, large countries can sustain agglomeration for somewhat severe levels of disadvantage.The rents to agglomeration in Home decrease when χ falls. As defined,  is the level of χ below which the rents to agglomeration are completely overwhelmed by the gains from superior technology in Foreign. This result is summarized in the following proposition:
is the level of χ below which the rents to agglomeration are completely overwhelmed by the gains from superior technology in Foreign. This result is summarized in the following proposition:
Proposition 2. The rents to agglomeration (25) in Home (Foreign) vanish when χ is less (greater) than

 for any level of trade costs.
for any level of trade costs.
Relation to Symmetric NEG Models
Fully symmetric NEG models are included as a special case of this model when χ = λ = 1. Asymmetry resolves some of the fundamental indeterminacy in standard NEG models. When trade costs fall, the pattern of agglomeration is predicted by relative size and technology rather than chance events. The model does display a mild form of hysteresis when trade costs are increased. The qualitative pattern of manufacturing location is reversed, but at different threshold levels of trade costs.
This simple specification shares the same “genome” with a large class of vertical linkage models examined in Ottaviano and Robert-Nicoud (2005). The qualitative behavior examined above should be the same in less tractable models. The results apply directly to regional NEG models such as Forslid and Ottaviano (2003) where cross-country, skilled labor migration, rather than vertical linkages are the agglomeration mechanism.4
4. Generalizing the Model
Relaxing the NFS Condition
The NFS condition can be relaxed for the sake of realism at the expense of simplicity. Wages and the allocation of labor within each country are potentially endogenous without factor price equalization. The NFS condition is a restriction on the share of manufactured goods in consumer and firm expenditure. If µ is larger than Home's share of world labor but smaller than Foreign's share, full manufacturing specialization in Home is possible.
Consistent with Ricardian predictions, full specialization only occurs in the country with a higher productivity in manufacturing. For example, say Home is small and more productive. The entire manufacturing sector is too large to fit entirely in Home, but low trade costs combined with higher productivity can make entry profitable. For low enough trade costs specialization in Home will be inevitable. Home manufacturing wages will necessarily exceed those in agriculture to attract labor. Foreign will still maintain some manufacturing and all agricultural employment at equalized wages of unity.
Qualitative Results
Figure 4 replicates Figures 1 except that µ = 0.5. A higher share of intermediate goods in fixed costs strengthens the production–cost linkages. As before, Foreign's initial size advantage in terms of market and supplier access is amplified as trade costs fall from autarky levels. Manufacturing shares will shift from Home to Foreign. This also effects the share of manufacturing employment in each country.
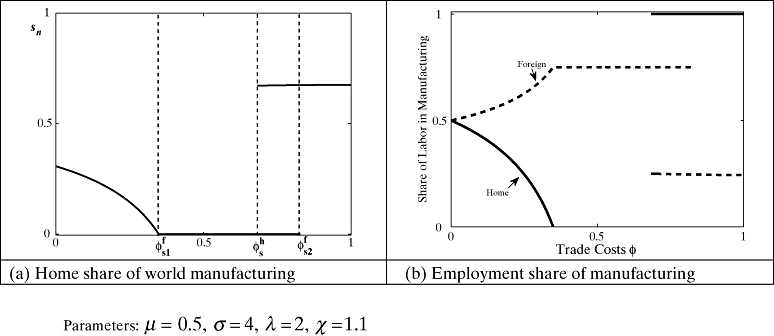
Evolution of Manufacturing Location and Employment Shares with full Specialization in Home: λ = 2, χ = 1.1. (a) Home Share of World Manufacturing (Parameters: µ = 0.5; σ = 4, λ = 2, χ = 1.1); (b) Employment Share of Manufacturing
Similar to before, at some level of lower trade costs full specialization, rather than full agglomeration, in Home becomes possible but not inevitable. As trade costs fall further, full agglomeration in Foreign is no longer sustainable and Foreign loses part of it's manufacturing core to Home. Labor shares follow suit, but now Foreign retains some manufacturing employment. Home devotes its entire labor endowment to manufacturing and imports all of it agricultural good from Foreign. Given these small adjustments to the nature of equilibria, the patterns and intuition of section three are qualitatively preserved.
Analytical Results
Some of the tractability of section 3 can be salvaged. The agglomeration sustaining locus for Home is lost because wages, the labor allocation and number of firms in Home are changing with trade costs. The situation with respect to the Foreign version of equation (26) is different. The condition in (26) assumes wages are unity in both countries. When manufacturing agglomerates in Foreign, these assumptions continue to hold. For the levels of trade costs (φ) and technology (χ) where it is exactly satisfied, a firm can enter the Home market at the prevailing wage and turn a profit in the short run. In the long run, more firms enter, compete for labor and bid up the wage rate until Home is fully specialized in manufacturing.
5. Welfare Implications

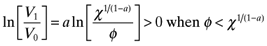 (29)
(29) (30)
(30)The country with higher productivity will always prefer own country agglomeration. In the case of Home, φ < χ1(1−a) for all levels of trade costs when χ > 1. A less productive Foreign country might be better off with Home agglomeration. This is true only for the right combination of low trade costs and high productivity (high χ) in Home. There is a range for χ in the interval φ1−a < χ < φa−1 where full agglomeration causes a welfare loss to the periphery. High trade costs can overwhelm the benefit of low prices from more efficient production. This establishes the following result:
Proposition 3. Full agglomeration in Home is welfare improving for all if and only if φ > χ1/(a−1). Otherwise, Labor in in the periphery will experience a welfare loss.
Unlike symmetric models, agglomeration is not always welfare improving for a representative agent in the host country. The well-being of the periphery depends positively on the productivity level abroad and negatively on trade costs. There are ranges of trade costs where an improvement in Home technology would not necessarily benefit Foreign. Consider the example from Figure 1 where χ = 1.1. Agglomeration of all manufacturing shifts from Foreign to Home for φ > 0.77 but it is not welfare improving in Foreign until φ > 0.9. A similar calibrated result is obtained by Eaton and Kortum (2002). Welfare is increasing when a trading partner's technology improves for nearby countries, but less so for countries that are far away.
6. Conclusion
The main results shed light on several issues of regional and global integration. Neither country size or relative productivity necessarily determine the location of manufacturing firms. Throughout a range of trade costs, size and productivity differences, a rich set of outcomes emerges. The dynamics of agglomeration are regulated by trade costs in three phases: (1) dispersion at high trade costs (2) large customer and supplier markets favored at intermediate trade costs, and (3) high productivity regions favored for low trade costs. This application of the model is consistent with empirical findings and the geography of trade integration (Eaton and Kortum, 2002; Amiti and Javorcik, 2008).The model generally avoids the stark outcomes and indeterminate dynamics of NEG models that have been noted by Neary (2001). Moving from autarky to free trade leaves room for both country size and Ricardian predictions. For levels of trade costs in between, the rich features of NEG models are preserved.
For small countries attempting to attract manufacturing industries, mere trade liberalization might not be enough. Governments can compete for industry by lowering transport costs and improving infrastructure as in Long and Wong (2009), but in this model only a combination of trade liberalization and improved productivity will induce firms to move. Most advanced, industrialized economies have secured an early-industrializer advantage. Atomistic firms might stay put even when it would be more profitable if all firms relocated to the more productive country.
References
Notes
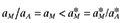 , then χ > 1.
, then χ > 1.




