The Red–Green Channel Dilemma: Customs Declaration and Optimal Inspection Policy
Abstract
Despite the evolvement of an extensive literature on the economics of smuggling, the evasion of customs duties under the common red–green channel system has failed to attract any theoretical attention. The present paper develops a simple three-passenger-type model to examine the passenger's decision of whether to pass through the green or red channel, as well as to derive the optimal inspection policy for a revenue-maximizing customs authority. The analysis reveals that if net revenue collection when inducing truthful declaration is positive, it is never optimal for the customs authority to provide incentives for passing through the green channel, although it may be optimal to provide incentives for cheating at the red channel. However, if the penalty for evasion is large enough to wipe out passengers' income, providing incentives for passing through the green channel may be the optimal policy.
1. Introduction
The revised International Convention for the Simplification and Harmonization of Customs Procedures, adopted by the World Customs Organization in June 1999, recommends the Red–Green Channel (RGC) system as a means of handling customs declarations of dutiable commodities by incoming passengers. Under the RGC system, currently used at a large number of airports around the world, passengers arriving at entry checkpoints must pass through either a red or a green channel. If they are carrying dutiable commodities they should pass through the red channel at which they must fully declare their dutiable items and pay the duties due. Otherwise, if they have nothing to declare, they may pass through the green channel. Customs officials may select passengers going through either channel for baggage inspection. A passenger found with undeclared dutiable commodities may be liable to prosecution or penalty in addition to paying the regular duties. Nevertheless, passengers carrying dutiable commodities may attempt to evade customs duties by passing through the green channel or by declaring just a fraction of their dutiable items at the red channel.
Surprisingly, despite the evolvement of an extensive economic literature on smuggling—e.g. Bhagwati and Hansen (1973), Martin and Panagariya (1984), Sheikh (1989), Fausti (1999)—and tax evasion—see surveys by Cowell (1990), Andreoni et al. (1998), Slemrod and Yitzhaki (2002)—the evasion of customs duties under the widespread RGC system has failed to attract any theoretical attention. The present paper develops a simple three-passenger-type model, with a discrete (three-valued) distribution of dutiable commodities, to address the issue of duty evasion from the passenger and customs authority perspectives.1 First, the paper analyzes the passenger's decision of whether to pass through the green or red channel, and, if passing through the latter, of whether to declare his or her dutiable commodities in full or in partial. Second, the paper derives the optimal inspection policy for a revenue-maximizing customs authority (henceforth, CA) that announces its inspection policy to incoming passengers, while taking into account their expected reactions to its policy.
The analysis yields distinct policy recommendations, depending on whether the penalty for failing to declare a dutiable commodity is small relative to the passenger's income or large enough to wipe out the entire income, and on whether the CA's net revenue collection when inducing truthful declaration is positive or negative. When the penalty is small relative to income, it is never optimal to provide incentives for passing through the green channel if net revenue collection when inducing truthful declaration is positive. However, depending on the parameter values of the model, it may be optimal to provide incentives for cheating at the red channel. Specifically, it may be optimal to avoid inspection altogether at the red channel, allowing passengers to safely declare just a fraction of their dutiable commodities, while ensuring that the probability of inspection at the green channel is sufficiently high to deter any passenger who is carrying dutiable commodities from choosing that channel. In contrast, if net revenue collection when inducing truthful declaration is negative, it will either be optimal to avoid inspection at all in both channels, or to avoid inspection in the red channel only while deterring passengers from passing through the green channel. However, when the penalty for duty evasion is large enough to wipe out the passengers' income, providing incentives for passing through the green channel by setting the probability of inspection there a bit below the level that would deter passengers from choosing that channel, may be the optimal policy even if net revenue collection when inducing truthful declaration is positive.
2. The Setting
Suppose that there is only one point of entry into the country and only one dutiable commodity. Suppose also that an incoming passenger cannot carry more than two units of the dutiable commodity.2 Consequently, incoming passengers can be divided into three types: those carrying two units of the dutiable commodity (type 2), those carrying just one unit (type 1), and those not carrying the dutiable commodity at all (type 0).3 Passengers of type 0 will naturally choose the green channel. Passengers of type 1 may choose between the red channel (truthful declaration) and the green channel (evasion). Passengers of type 2 may choose between the red channel—where they either declare two units of the dutiable commodity (truthful declaration) or one unit only (fraudulent declaration/partial evasion)—and the green channel (full evasion). The CA cannot distinguish between the three types of passengers. However, suppose that it knows that in any given day a fraction α of all incoming passengers are of type 0, a fraction β are of type 1, and a fraction γ are of type 2.
Suppose further that the duty rate per unit of the dutiable commodity is t percent of its estimated value,4 which is normalized to unity. Declaring a unit of the dutiable commodity at the red channel thus involves the payment of t dollars. Attempting to evade this payment by passing through the green channel or declaring fraudulently at the red channel might trigger inspection that is bound to uncover the undeclared unit. Consequently, a penalty, in proportion f > 0 to the evaded duty, will be added to the payment. While the penalty rate is determined by the law and is identical in both channels, the probabilities of inspection, pG in the green channel and pR in the red channel, are chosen by the CA and announced to passengers at the incoming-passenger hall. Passengers will then choose their preferred channel, which the CA takes into account when announcing its inspection policy. The CA, by assumption, is able to commit to its announced policy,5 accordingly adjusting the number of inspections at each channel to the number of passengers who are about to pass through that channel.
3. Passenger Choice
Being informed of the probabilities of inspection in the green and red channels, type 1 and 2 passengers must make a choice. Suppose first that the penalty for failing to declare the dutiable commodities (ft and 2ft, for one and two units, respectively) is small relative to passengers' income. Suppose further that all passengers are risk-neutral, therefore choosing the channel with the lowest expected payment. Which channel will they choose?
Type 1 Passenger
A type 1 passenger may choose between the red channel, truthfully declaring one unit of the dutiable commodity, and the green channel, where he or she is evading the duty due on this unit. Payment if passing through the red channel is t. Expected payment if passing through the green channel is t(1 + f)pG. Hence, the passenger will choose the green channel if pG < 1/(1 + f) and the red channel otherwise.
Type 2 Passenger
A type 2 passenger may choose between the red channel—where he or she is either truthfully declaring two units of the dutiable commodity or fraudulently declaring one unit only—and the green channel, where he or she is evading the duty due on two units. Payment if passing through the red channel and truthfully declaring two units is 2t. Expected payment if passing through the red channel and fraudulently declaring one unit is t + t(1 + f)pR. Expected payment if passing through the green channel is 2t(1 + f)pG.
Consider first the passenger's choice between the green channel and truthful declaration at the red channel. If pG < 1/(1 + f), he or she will choose the green channel. Otherwise, the red channel will be chosen. Consider next the passenger's choice between fraudulent and truthful declaration at the red channel. If pR < 1/(1 + f), he or she will choose to declare fraudulently. Otherwise, truthful declaration will be chosen. Consider finally the passenger's choice between the green channel and fraudulent declaration at the red channel. If pG < 1/[2(1 + f)] + pR/2, he or she will choose the green channel. Otherwise, fraudulent declaration will be chosen.
1, 2 summarize these results graphically, dividing passengers' choices at various combinations of pG and pR into four probability regions. Type 1 passengers will choose the red channel in regions A and D, but the green channel in regions B and C. Type 2 passengers will choose the red channel with truthful declaration in region A, the green channel in region B, and the red channel with fraudulent declaration in regions C and D. A quick glance at 1, 2 reveals that in order to induce truthful declaration by all passengers, pG and pR must be raised (at least) to 1/(1 + f). If pG is lowered slightly, type 1 passengers will switch to the green channel. Type 2 passengers will follow suit providing that pR remains at its high level. However, if pR is lowered too, type 2 passengers may still opt to pass through the red channel, fraudulently declaring one unit only (region C). Only if pG falls sufficiently, below 1/[2(1 + f)] + pR/2, will type 2 passengers find it worth their while to pass through the green channel.
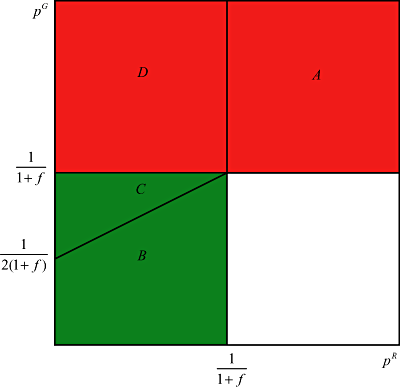
Optimal Choices for a Type 1 Passenger
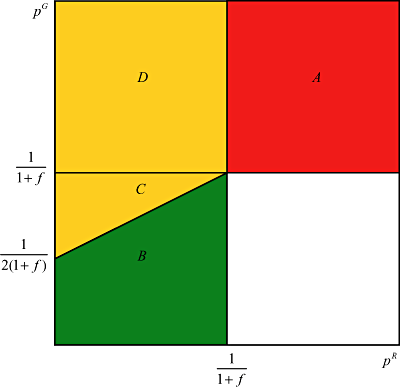
Optimal Choices for a Type 2 Passenger
4. Optimal Inspection Policy
Having studied passengers' declaration choices for given probabilities of inspection in the green and red channels, the CA must determine its preferred inspection policy. This involves the choice of the probabilities pG and pR in a way that satisfies some predetermined target, while taking into account passengers' responses to this choice. Suppose that in any given day S passengers are expected to arrive in the country. The CA announces its inspection policy to all incoming passengers, who choose their declaration strategies accordingly (as illustrated in 1, 2). The CA will then figure out the number of passengers who are about to pass through either channel, inspecting a fraction pG of those passing through the green channel and a fraction pR of those passing through the red channel and declare one unit only. Inspection is, of course, costly. Suppose that the CA faces a fixed cost per inspection, denoted by c > 0, and that t(1 + f) > c. That is, the increment to revenue associated with uncovering an undeclared unit of the dutiable commodity exceeds the inspection cost.
Suppose now that the CA chooses the probabilities of inspection in the alternative channels so as to maximize its expected revenue net of inspection costs.6 To solve this problem, the CA may first identify the probabilities of inspection that maximize its expected net revenue within each region of 1, 2. Comparing its potential achievements in the alternative regions, the CA will then choose the probabilities of inspection for which the expected net revenue is the highest.
Region A
In this region, type 1 and type 2 passengers opt to pass through the red channel, declaring their dutiable commodities truthfully. The CA will collect tβS from type 1 passengers and 2tγS from type 2 passengers, inspecting a fraction 1/(1 + f) of αS passengers who pass through the green channel and of βS passengers who declare one unit at the red channel.7 Net revenue collection in this region, R(A), is thus
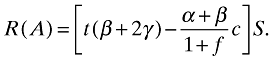(1)Notice that inspection is not yielding any revenue directly, since the CA will inspect passengers who either do not carry any dutiable commodity (type 0) or declare their dutiable commodity truthfully (type 1). The sole purpose of inspection in the two channels is deterrence.
The sign of (1) is indeterminate, depending on the parameter values of the model. Suppose first that it is positive, hence inducing truthful declaration is economically desirable.8 The interesting question, however, is whether the CA can do better in any other region. Consider the following proposition:
Proposition 1. If (i) the penalty for duty evasion is small relative to passengers' income and (ii) net revenue collection when inducing truthful declaration is positive, then (a) it is never optimal to provide incentives for passing through the green channel; (b) it may be optimal to provide incentives for cheating at the red channel.
Proof. To prove part (a) of Proposition 1, consider the CA's expected net revenue collection in region B, where type 1 and type 2 passengers opt to pass through the green channel, as well as in region C, where passengers of type 1 opt to pass through this channel.
Region B
In this region, type 1 and type 2 passengers opt to pass through the green channel, failing to declare their dutiable commodities. With probability pG the CA will collect t(1 + f)βS from type 1 passengers and 2t(1 + f)γS from type 2 passengers, inspecting a fraction pG of the entire passenger population, S, who will pass through the green channel (and a fraction pR = 0 of zero passengers passing through the red channel). Expected net revenue collection in this region, R(B), will thus be
(2)It immediately follows that if R(A) ≤ cγS/(1 + f), the CA's best policy is to set pG = 0, in which case R(B) = 0. Otherwise, if R(A) > cγS/(1 + f), the CA's best policy is to set pG as high as possible. However, since pG must be lower than 1/[2(1 + f)], substituting this value for pG in (2) reveals that
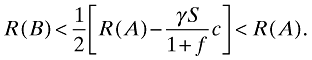((2′))Hence, an inspection policy that provides incentives for all passengers to pass through the green channel is strictly dominated by a policy that induces truthful declaration at the red channel. The reason for this is that while the CA's revenue from uncovering an undeclared unit of the dutiable commodity is augmented by 1 + f, as compared to the revenue from a declared unit, the probability of uncovering an undeclared unit is less than 1/(1 + f). Hence, the expected revenue from uncovering an undeclared unit is lower than the certain revenue from a declared unit (i.e. lower than t). In addition, uncovering an undeclared unit involves additional costs, since it requires the inspection of type 2 passengers who are exempted from inspection when declaring truthfully.
Region C
In this region, type 1 passengers opt to pass through the green channel, failing to declare their dutiable commodity, whereas type 2 passengers opt to pass through the red channel, fraudulently declaring one unit only. With probability pG the CA will collect t(1 + f)βS from type 1 passengers and with probability pR it will collect t(1 + f)γS from type 2 passengers, who also pay tγS voluntarily. The CA will inspect a fraction pG of (α + β)S passengers who pass through the green channel and a fraction pR of γS passengers who declare one unit at the red channel. Expected net revenue collection in this region, R(C), will thus be
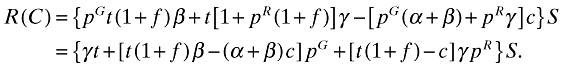(3)By assumption, t(1 + f) > c. Hence, the CA's best policy is to set pR as high as possible. Given that t(1 + f) > c[(α + β)/β], the CA's best policy is to set pG as high as possible too. Substituting pR = pG = 1/(1 + f) in (3) reveals that
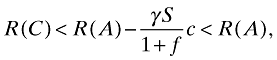((3′))since pR and pG must be lower than 1/(1 + f) in this region. However, if t(1 + f) ≤ c[(α + β)/β], the CA's best policy is to set pG at its lowest possible level. Substituting pG = 1/[2(1 + f)] + pR/2 into (3) and rearranging yields
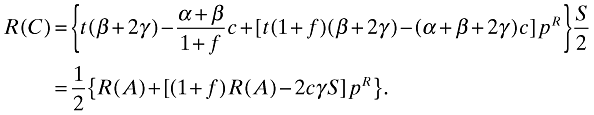((3″))Given that R(A) ≤ 2cγS/(1 + f), the CA's best policy is to set pR = 0, in which case R(C) = R(A)/2. Otherwise, if R(A) > 2cγS/(1 + f), the CA's best policy is to set pR as high as possible. Substituting pR = 1/(1 + f) in (3″) yields (3′) again.9 Hence, an inspection policy that still provides incentives for type 1 passengers to pass through the green channel and for type 2 passengers to fraudulently declare one unit only is also strictly dominated by a policy that induces truthful declaration.□
Proof (continued). To prove part (b) of Proposition 1, consider now the CA's expected net revenue collection in region D where type 2 passengers opt to pass through the red channel without declaring their dutiable commodities in full.
Region D
In this region, type 1 and type 2 passengers opt to pass through the red channel. However, while type 1 passengers truthfully declare their dutiable commodity, type 2 passengers fraudulently declare one unit only. The CA collects tβS from type 1 passengers and, with probability pR, will collect t(1 + f)γS from type 2 passengers, who also pay tγS voluntarily. The CA will inspect a fraction 1/(1 + f) of αS passengers who pass through the green channel and a fraction pR of (β + γ)S passengers who declare one unit at the red channel. Expected net revenue collection in this region, R(D), will thus be
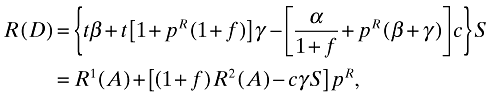(4)where
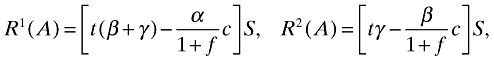
and R1(A) + R2(A) = R(A). Suppose first that R2(A) > 0. Then if R2(A) ≤ cγS/(1 + f), the CA's best policy is to set pR = 0. Consequently, R(D) = R1(A) < R(A). Otherwise, if R2(A) > cγS/(1 + f), the CA's best policy is to set pR as high as possible. Still, substituting pR = 1/(1 + f) in (4) implies that
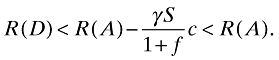((4′))If, alternatively, R2(A) ≤ 0, the CA's best policy is to set pR = 0. Consequently, R(D) = R1(A) ≥ R(A).10 Hence, if R2(A) = 0, R(D) = R(A). However, if R2(A) < 0, R(D) > R(A)! It thus follows that an inspection policy that induces truthful declaration might be strictly dominated by a policy that deters passengers from passing through the green channel but avoids inspection altogether at the red channel. To understand this result, notice that R1(A) and R2(A) reflect the net revenue from inducing truthful declaration of the first unit (by both type 1 and type 2 passengers) and the second unit, respectively. In particular, while the additional benefit from inducing truthful declaration of the second unit is tγS, the additional cost of doing so is cβS/(1 + f), as it requires the inspection of passengers who declare one unit with probability 1/(1 + f). When the additional cost exceeds the additional benefit, as is the case if R2(A) < 0, the CA will be better off ignoring evasion through the red channel while strictly deterring evasion through the green channel.□
Finally, suppose that the sign of (1) is negative, implying that inducing truthful declaration is not desirable. Consider the following proposition:
Proposition 2. If (i) the penalty for duty evasion is small relative to passengers' income and (ii) net revenue collection when inducing truthful declaration is negative, then it is either optimal to avoid inspection altogether, or to avoid inspection in the red channel only while deterring passengers from passing through the green channel.
Proof. The proof of Proposition 2 is straightforward. Equation (2) reveals that if R(A) < 0, the best policy in region B is to set pG = 0. Hence, R(B) = 0. Also, substituting R(A) < 0 in equations (3′) and (3″) implies that R(C) < 0. Examining region D, suppose first that R1(A) < 0. Then, if R2(A) ≤ 0, equation (4) implies that R(D) < 0, while if R2(A) > 0, equation (4′) implies so. It thus follows that avoiding inspection altogether strictly dominates any active inspection policy that can be taken in any region. However, if R1(A) ≥ 0, R2(A) must be negative and equation (4) implies that R(D) = R1(A) ≥ 0. Hence, deterring passengers from passing through the green channel while avoiding inspection in the red channel may dominate an overall noninspection policy.□
5. An Income-Exhausting Penalty
So far we have assumed that the penalty for failing to declare the dutiable commodities is small relative to the passenger's income. We now examine the case where the penalty is large enough to exhaust the passenger's income. Suppose, for simplicity, that all passengers have the same residual income (left after buying the dutiable commodities abroad), I. Being risk-neutral, passengers will choose the channel with the highest expected net income.
Type 1 Passenger
A type 1 passenger may choose between the red channel, truthfully declaring one unit of the dutiable commodity, and the green channel, where he or she is evading the duty due on this unit. Net income if passing through the red channel is I − t. Expected net income if passing through the green channel is (1 − pG)I, since with probability pG, inspection will result in zero net income. Hence, the passenger will choose the green channel if pG < t/I and the red channel otherwise.
Type 2 Passenger
A type 2 passenger may choose between the red channel—where he or she is either truthfully declaring two units of the dutiable commodity or fraudulently declaring one unit only—and the green channel, where he or she is evading the duty due on two units. Net income if passing through the red channel and truthfully declaring two units is I − 2t. Expected net income if passing through the red channel and fraudulently declaring one unit is (1 − pR)(I − t). Expected net income if passing through the green channel is (1 − pG)I.
Consider first the passenger's choice between the green channel and truthful declaration at the red channel. If pG < 2t/I, he or she will choose the green channel. Otherwise, the red channel will be chosen. Consider next the passenger's choice between fraudulent and truthful declaration at the red channel. If pR < t/(I − t), he or she will choose to declare fraudulently. Otherwise, truthful declaration will be chosen. Consider finally the passenger's choice between the green channel and fraudulent declaration at the red channel. If pG < [t + pR(I − t)]/I, he or she will choose the green channel. Otherwise, fraudulent declaration will be chosen.
Notice that the critical values of pG and pR that determine whether or not evasion is practiced are inversely related to income. Hence, the poorer the passenger, the more reckless he or she is likely to be (i.e. willing to take his or her chances at higher probabilities of inspection). Having said this, we may proceed by normalizing I to 1, consequently restricting the analysis in this case to t < 1. Passengers of type 1 will now prefer the green channel to truthful declaration at the red channel if pG < t, whereas passengers of type 2 will exhibit this preference as long as pG < 2t. Passengers of type 2 will prefer fraudulent to truthful declaration at the red channel if pR < t/(1 − t) and the green channel to fraudulent declaration at the red channel if pG < t + pR(1 − t).
Turning now to examine the CA's best inspection policy, suppose that c < 1. That is, the cost of inspecting a passenger is lower than the revenue associated with uncovering evasion, which is the passenger's income, I (= 1).
Proposition 3. If the penalty for duty evasion is large enough to exhaust the passenger's income, providing incentives for passing through the green channel may be the optimal policy even if net revenue collection when inducing truthful declaration is positive.
Proof. To prove Proposition 3, compare the CA's net revenue collection when inducing truthful declaration at the red channel, R(red), with its expected net revenue collection when allowing passengers to pass through the green channel, R(green). In the first case, the CA will collect tβS from type 1 passengers and 2tγS from type 2 passengers, inspecting a fraction 2t of αS passengers who pass through the green channel and a fraction t/(1 − t) of βS passengers who declare one unit at the red channel. Net revenue collection will thus be
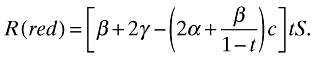(5)In the second case, with probability pG the CA will collect βS from type 1 passengers and γS from type 2 passengers (recall that I = 1), inspecting a fraction pG of the entire passenger population, S, who will pass through the green channel. Expected net revenue collection will thus be
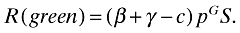(6)Suppose that c < β + γ (< 1), hence R(green) > 0. If R(red) < 0, the CA is clearly better off inducing passengers to pass through the green channel. To maximize its expected net revenue, the CA will set pG slightly below t, collecting an amount that approaches (β + γ − c)tS. However, if R(red) > 0, substituting (5) in (6), with pG = t, we have
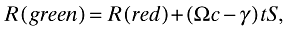(7)where Ω ≡ 2α − 1 + β/(1 − t). Hence, R(green) > R(red) if Ωc > γ. A prerequisite for this is Ω > 0, which requires that t < 1 + β/(2α − 1) if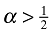 
(a requirement satisfied by the assumption of t < 1), or that t > 1 + β/(2α − 1) if 
.
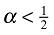While providing incentives for passing through the green channel may dominate a truthful declaration policy, the latter may still dominate a policy that induces cheating at the red channel. To see that, notice that when declaring truthfully, type 2 passengers pay 2tγS, whereas by cheating at the red channel, their expected payment is γ(t + pR)S, which approaches [(2 − t)/(1 − t)]tγS when pR is set just slightly below t/(1 − t). Allowing cheating at the red channel would thus increase expected revenue by [t/(1 − t)]tγS. However, it would also increase costs by [t/(1 − t)]cγS, since the population inspected at the red channel will include type 2 passengers as well. Hence, truthful declaration is preferable if the increased costs of allowing fraudulent declaration outweigh the increased revenue. This will be the case if t < c. It thus follows that even when net revenue collection when inducing truthful declaration is positive, a policy that provides incentives for passing through the green channel may strictly dominate both a truthful declaration policy and one that induces cheating at the red channel.□
6. Concluding Remarks
The present paper has addressed the red-and-green channel dilemma facing an incoming passenger who is carrying commodities that are subject to customs duties, as well as the optimal inspection policy of a revenue-maximizing customs authority. Choice of the red or green channel is deemed to be the equivalent to making a formal declaration to customs, and may be viewed as a miniature reflection of the general tax-evasion problem: choosing the red channel is analogous to filing a tax return and either underreporting or truthfully reporting one's true income, whereas choosing the green channel is analogous to nonfiling a return at all (becoming a “ghost,” in the tax administration's jargon). As is the case with the present dilemma, the probability of detecting an underreporter is not the same as the probability of detecting a ghost. The former usually depends on the information contained in the tax return (e.g. reported income, profession, etc.), whereas the latter depends on signals of earning capacity (e.g. conspicuous consumption) or on tips collected from tax informants. With a few exceptions—e.g. Cowell and Gordon (1997), Yaniv (2003)—the tax-evasion literature has entirely focused on the tax agency's problem of selecting the probability of auditing a filer. In particular, there is no discussion in the literature of the joint determination of the probabilities of auditing filers and nonfilers. The present paper may be viewed as a first step in this direction, suggesting an hypothesis for future investigation: if net revenue collection when inducing honesty is positive, it is never optimal to provide incentives for nonfiling, yet it may be optimal to provide incentives for some underreporting.
There are several ways by which the present model can be extended to capture some more realistic features of the passenger's dilemma, albeit at the cost of greater mathematical complexity. First, some incoming passengers with dutiable commodities can be assumed to be habitual compliers who declare their luggage truthfully regardless of the pecuniary incentives for evasion. Second, the distribution of incoming passengers by type can be made endogenous, dependent upon the probabilities of inspection in the green and red channels and the penalty expected in case of detection. This is particularly interesting if the penalty is large enough to wipe out the passenger's income, because if detected the outcome will be the same (zero net income) irrespective of the number of units carried. Third, rather than being well-informed of the customs authority's inspection policy, incoming passengers can be assumed to face some uncertainty regarding the probabilities of inspection in the alternative channels. In reality, customs authorities do not announce their inspection policies to incoming passengers. An interesting question is whether keeping passengers in the dark really helps increase compliance or perhaps such a policy has effects opposite than intended.
