Measuring the Impact of Ethanol Plants on Local Grain Prices
Abstract
A considerable number of farmer-owned ethanol plants have been built in the past few years, with many more planned. In part, farmers' investment in ethanol plants is an attempt to increase grain prices in their local market. We examined this issue by estimating the impact on local grain prices of twelve ethanol plants that opened from 2001 to 2002. We find that these new ethanol plants increased local grain prices, but the impact was not uniform around the plant. Markets downstream from a new plant, where prices tend to be higher, experienced a smaller price impact from the ethanol plant. On average across plants, corn prices increased by 12.5 cents per bushel at the plant site, and some positive price response was felt 68 miles away from the plant.
There are few areas of agriculture that have witnessed such consistent and robust growth as the U.S. ethanol industry. Since 1980, U.S. ethanol production has increased 13% per year and in 2003, production was up an astonishing 32% (Renewable Fuels Association 2004).
Ethanol, which is mostly produced from corn, is used as a gasoline additive. The ethanol industry began in the 1970s as escalating oil prices led to concerns about national energy security. At the time, fuel ethanol was considered an attractive gasoline extender that could reduce U.S. dependence on foreign oil. Even today, energy security concerns have many policymakers favoring expanded ethanol use (Lugar and Woolsey).
By the 1980s and 1990s, environmental policies began to shape the course of the ethanol industry. The Clean Air Act Amendments of 1990 required that gasoline be reformulated with one of two oxygenates—ethanol or methyl tertiary butyl ether (MTBE). Although MTBE has historically been the oxygenate of choice, this will likely change as MTBE has been found to contaminate ground and surface water. As of 2003, eighteen states had policies to limit or ban the use of MTBE in the near future.
Along with environmental policies, other federal policies have stimulated ethanol production and use. Since 1978, ethanol has been exempt from the Federal Excise Tax on gasoline and various states have enacted ethanol tax credits to promote its use (Rask). Likewise, a series of federal, state, and local policies have been enacted to encourage investments in ethanol plants. The U.S. Senate introduced the Fuels Security Act of 2003 that would require ethanol use to double in the next decade.
With such favorable policies, it is not surprising that ethanol production and the number of ethanol plants have increased significantly. Recently, U.S. farmers have shown considerable interest in ownership of ethanol plants. In 2003, ten of the thirteen new ethanol plants under construction were farmer-owned cooperatives, and numerous additional plants are in the planning phase (Renewable Fuels Association 2003).
Two reasons potentially motivate farmers' interest in ethanol plant ownership. First, the outlook for increasing ethanol demand combined with a history of declining real grain prices means ownership of an ethanol plant could generate profits. Second, many believe that the existence of a plant will boost local grain prices, thereby providing indirect returns to farm ownership of the plant even if the plant earns zero profit (Hayworth).
While numerous case and feasibility studies exist that provide an assessment of the expected profit potential (e.g., Sparks Companies and Kansas State University; Herbst et al.; Fruin and Halbach; Outlaw et al.), no research has considered the impact of ethanol plants on local corn prices. This is especially problematic since the ethanol industry appears to be highly competitive with no significant entry barriers. Thus, above-normal profits are not likely to be sustainable.1 As such, the indirect returns of owning the plant through higher corn prices may be a vital component to the financial payoff to farmers who own a plant.
We developed a model of spatial equilibrium that illustrates the impact on regional prices from introducing an ethanol plant. This model serves as a useful framework for empirically estimating the impact of the twelve corn-based ethanol plants that opened between 2001 and 2003.
A Model for Opening an Ethanol Plant
The U.S. grain distribution system comprises farms, storage elevators, and transportation networks involved in moving grain from production areas to domestic and overseas markets. Because transportation costs are one of the largest components of grain marketing costs, the system plays an important role in grain commodity price on several levels. First, costly transportation leads to declining prices as one moves away from demand centers. Second, shocks to demand, supply, or transportation costs can induce shifts in trade patterns and lead to differential impacts on farm-level and terminal market prices (McNew 1996; Fackler and Goodwin). This latter scenario is consistent with the opening of a new ethanol plant. The introduction of a new demand source for grain can induce shifts in trade patterns as well as adjust the spatial characteristics of prices around the plant.
A graphical representation of a spatial model is presented in this section (see the Appendix for a mathematical treatment of the problem). The model is patterned after the agents-on-links spatial equilibrium model, which assumes that production occurs along a line segment (i.e., the links). The links contain demand centers at various points (see e.g., Faminow and Benson; Dahlgren and Blank for applied examples in agriculture).2
Assume initially that there is one demand center, which we also refer to as a terminal market, located at the end of a line segment measured in distance d ε [0, 1]. Grain production is assumed to occur uniformly along this line segment with total production assumed to be exogenous and fixed for the purposes of this analysis. Grain is shipped to the terminal market located at d = 1 and producers receive a net price at their location adjusted for transportation costs, which is assumed to be proportional to the distance shipped.
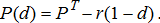 (1)
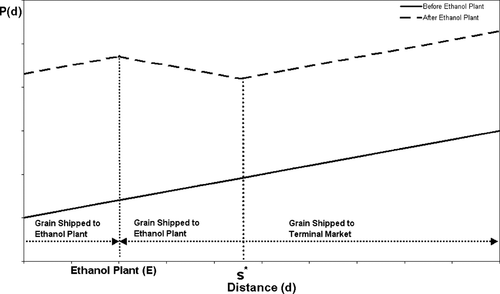
(1)Suppose that an ethanol plant opens at some exogenously determined point E ε [0, 1). This plant brings a new grain demand source to the market and can potentially alter shipping patterns. In this model, it can be shown that a boundary between the ethanol plant and the terminal market exists, which delineates the two demand markets. This point, s*, signifies the spatial boundary of grain shipments to the ethanol plant and the terminal market. Producers located along the line segment dE ∈ [0, s*] will ship grain to the ethanol plant while producers along dT ∈ (s*, 1] will ship to the terminal.
Impact on spatial price surface from an ethanol plant
As a result of the new ethanol plant, grain prices increase along the entire line segment, but the price impact varies spatially across three distinct regions. First, producers who continue to ship to the terminal market (i.e., dT ∈ (s*, 1]), still receive a positive price impact as a result of the ethanol plant. This is because demand for grain from the ethanol plant reduces the amount of grain shipped to the terminal market. Thus, prices increase even in areas that do not ship to the plant as a result of lower grain supplies reaching the terminal.
Prices for producers that ship to the plant increase even more because of lower transportation costs. Before the ethanol plant, producers around the plant had to ship grain to the far away terminal market. With a nearby plant, their shipping costs are lowered, which translates into higher regional prices for these producers. However, not all producers shipping to the plant save equally on shipping costs so the price impacts around the plant vary.
For example, those producers “upstream” from the plant (i.e., in a low-priced region relative to the plant) will see the largest impact because they enjoy the greatest transportation cost savings. This region is depicted in figure 1 by the area to the left of the plant site, E. All upstream producers have the same price impact from the plant because each producer reduces shipping costs by the amount r(1 − E), which is the cost of shipping from the ethanol plant to the terminal market. A producer located upstream from the plant at point d0 < E, for example, would incur a shipping cost of r(1 − d0) to the terminal market. After the plant opens, however, shipping costs are r(E − d0), so the transportation cost savings is r(1 − E), which is the same for all producers (i.e., does not depend on d0).
For producers who ship to the plant but are on the downstream side, the transportation costs savings diminish as the distance from the plant increases. This is because producers in this region must ship grain back to the plant and therefore they do not receive the full transportation cost savings of upstream producers. The further away from the plant, the higher the cost of back hauling, and the lower the price impact from the new plant.
In what follows, we develop a spatial econometric model that estimates the regional impact on grain prices from opening ethanol plants. Our econometric work is motivated by this simple spatial model, which suggests that the impacts will vary depending on whether the locations are upstream or downstream from a new plant, as well as what the distance from the plant is.
Data and Methodology
Daily local corn price data were obtained from the Cash Grain Bids Data Service for March 2000 through March 2003. This unique dataset contains over 2,000 U.S. corn markets. Because our interest is on the local impact of an ethanol plant opening, we converted daily cash prices to basis values using nearby CBOT corn futures prices for the same time period. The basis, defined as the local cash price less the futures price, is more likely to be influenced by local supply and demand conditions, transportation costs, and storage costs relative to the cash price, which is influenced by not only these local forces but also by national and global shocks. Daily basis values for each market were averaged by month, yielding 37 monthly observations per market from March 2000 to March 2003.
Over this same time period, thirteen corn-based ethanol plants began operations (table 1). Not surprisingly, the plants are mostly in the Midwest ranging geographically from Missouri in the southwestern section of the Cornbelt to Michigan in the Upper Midwest. Data on each plant including the start-up date and the plant capacity were obtained through the Renewable Fuels Association press releases.
| Plant Location | Start-Up Date | Plant Capacity (Million Gallons per Year) | Number of Markets in 150-m Square Area |
|---|---|---|---|
| Craig, MO | February 2001 | 20 | 28 |
| Wentworth, SD | September 2001 | 45 | 37 |
| Sioux Center, IA | December 2001 | 14 | 61 |
| Rosholt, SD | January 2002 | 18 | 33 |
| Galva, IA | March 2002 | 18 | 96 |
| Big Stone City, SD | July 2002 | 45 | 35 |
| Stanley, WI | July 2002 | 15 | 8 |
| Coon Rapids, IA | August 2002 | 45 | 109 |
| Lena, IL | August 2002 | 40 | 38 |
| Watertown, SD | September 2002 | 45 | 35 |
| Caro, MI | November 2002 | 45 | 2 |
| Lakota, IA | November 2002 | 45 | 83 |
| Monroe, WI | November 2002 | 40 | 34 |
Although the cash grain price dataset contains over 2,000 U.S. markets, we considered only those markets in the analysis that reported corn prices over the sample period and were within a 150-mile square area centered on a new ethanol plant. This process allowed us to consider a definite market impact area for each plant. Since several plants opened nearly simultaneously (e.g., two plants per month opened in July 2002 and August 2002; three plants in November 2002), it was necessary to define the market area for each plant so that the price impact could be identified. In essence, we assumed that the price impact of each plant is contained in the 150-mile square region centered on the plant.3Table 1 provides a summary of the number of markets contained in each plant region. Because of the lack of markets within the Caro, MI plant region, it was excluded from the analysis, leaving 316 cash markets and 12 ethanol plants.
To quantify the impact of an ethanol plant opening, it would be empirically appealing to compare prices before and after a plant opens. Any differences in prices could then be attributed to the plant opening. However, in practice, other economic factors also influence prices over time, thus making a direct comparison of before and after prices problematic. Our approach is to model prices using a spatial econometric model that accounts for economic forces that influence local prices. We attribute remaining variation in prices to the opening of an ethanol plant.
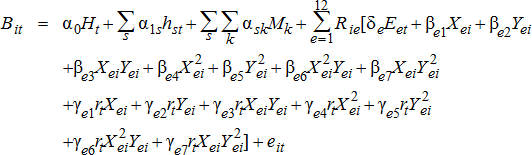 (2)
(2)Within each region, we estimated a basis surface utilizing the distance from each plant, where Xie is the east-west distance in miles that market i is from plant e and Yie is the north-south distance that market i is from plant e. A negative (positive) value for the (Xie, Yie) coordinate indicates that market i is northwest (southeast) of plant e. We estimated a second-order quadratic expansion using the (Xie, Yie) coordinates to capture the spatial variation inherent in basis. In addition, it seems likely that the basis surface will change depending on the cost of transportation. We used the U.S. average retail diesel price, rt, as a proxy for grain trucking costs. Thus, the diesel price rt interacting with the distance measures (Xie, Yie) allows for the price surface to adjust depending on transportation rates. Finally, the term Eet is a dummy variable signifying that ethanol plant e is open in period t. As such, the coefficient on this term (γe) represents the average price change in region Re after the ethanol plant has opened.
While equation (2) provides an estimate of the average impact in a plant region, it provides little evidence about the variation of the plant's impact over space. Indeed, the theoretical reasons outlined above suggest that such impacts will vary depending on whether a market is upstream or downstream from a plant. In particular, downstream markets are likely to see less impact than upstream markets.
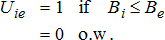
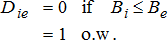
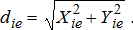
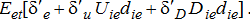 (3)
(3)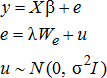
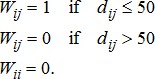 (4)
(4)Results
The model of spatial basis variation given by equation (2) was estimated using maximum likelihood methods subject to our choice of the spatial weight matrix specified in equation (4). For space reasons, we do not present the estimated coefficients on the state-level seasonal dummies, although they were significant and exhibited typical seasonality patterns prominent in grain prices. Table 2 presents all other estimated parameters. The spatial autocorrelation parameter λ was statistically significant as expected, indicating the importance of accounting for spatial autocorrelation in the errors.
| Prod. Coeff. | MO-Cr. | SD-We. | SD-Ro. | IA-Si. | IA-Ga. | SD-Bi. | WI-St. | IA-Co. | IL-Le. | SD-Wa. | IA-La. | WI-Mo. | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| U.S. | −0.005** | X | 0.67 | 1.07 | −4.25** | 1.09* | −1.98** | 1.12 | −2.54** | 2.59** | −0.36 | −0.43 | −2.67** | 2.76** |
| IL | 0.041** | Y | 5.52** | −1.12 | −4.19** | 0.28 | 1.45* | 0.75 | 1.45 | 0.98* | 0.18 | 0.27 | 0.01 | 1.37* |
| IA | −0.002* | X2 | 5.07** | 3.54* | −3.91 | −4.97** | 2.90** | −1.40 | 1.76** | 8.97** | −19.5** | −0.81 | 5.27** | 17.0** |
| KS | −0.136** | Y2 | 6.08** | −4.96** | −15.9** | −1.22 | −4.32** | −4.51** | 1.05 | −2.57** | 1.56 | −10.4 | 0.51 | −5.46** |
| MN | −0.007** | XY | 21.8** | −11.3** | 4.20 | −7.67** | 0.70 | 4.60 | −2.83** | −1.38 | −32.4** | −5.96 | 1.95 | −6.78 |
| MO | −0.001 | X2Y | 13.6** | 0.99 | 37.1** | −3.98 | −12.5** | 3.35 | −7.60** | −0.94 | 27.0** | 0.61 | 7.73** | 10.2 |
| NE | −0.051** | XY2 | 17.1** | 11.1** | −17.4 | −10.8* | 9.93** | −6.76 | −7.81* | 10.97** | 64.7** | 9.49 | −2.56 | 10.5* |
| ND | 0.136** | Xr | −0.12 | −0.44 | 0.70* | −0.27* | −0.20 | −0.08 | −0.14** | −0.28** | 0.04 | 0.05 | 0.06 | −0.60** |
| SD | −0.052** | Yr | 0.27 | 0.25 | −0.64* | −0.04 | −0.03 | 0.53* | 0.22 | −0.23 | −0.42** | −0.64 | −0.42** | 0.35* |
| WI | −0.118** | X2r | −1.50** | 0.35 | −1.41 | −0.12 | −0.56** | −0.58 | −0.58* | −1.54** | −0.48 | −1.68 | −2.19** | −0.02 |
| Y2r | −0.28 | 0.27 | −0.74 | 0.14 | −0.24 | −0.75* | 1.19 | −0.23 | −1.73** | −0.42 | −0.63** | −0.33 | ||
| Xyr | −0.39 | −0.71* | 1.99 | −0.14 | 0.54** | −0.18 | 2.18 | 0.15 | −0.58 | −0.27 | 0.02 | 2.27* | ||
| X2Yr | −0.61 | 1.05 | −1.92 | 1.54 | −0.38 | −2.52* | −8.91 | −0.02 | 2.69 | 3.55 | −1.77** | −5.70** | ||
| XY2r | 0.19 | 0.42 | 3.65 | −1.74 | −0.11 | −1.93 | −6.52 | −0.96* | −0.83 | 0.01 | 2.77** | −2.56* | ||
| Plant | 7.26* | 6.49** | 11.89** | 4.16** | 4.51** | 3.81** | 6.83** | 4.76** | 9.52** | 6.48** | 3.63** | 1.53** | ||
| open (Et) |
- Note: R2 = 0.8687, the spatial error coefficient λ = 0.467 and has a p-value of 0.001.
- * Significant at the 5% level.
- ** Significant at the 1% level.
As expected, production at the national and state levels tends to influence basis levels with higher production leading to a lower basis. The U.S. corn production negatively impacts basis at a local level. For example, a 500-million bushel increase in U.S. corn production, a magnitude that is consistent with year-to-year variation in the last five years, would cause basis levels to decline by 2.5 cents per bushel. Also, decreases in state-level production caused basis levels to increase in eight of the nine states. The exception was Illinois, which showed a positive response from state-level production. The measures of distance from the plant, as given by the (X, Y) coordinates and the transportation cost, r, showed significant impacts on basis within each plant region. However, not all coefficients were significant and the significance of coefficients was not uniform across plant regions. This suggests that basis variation over space is not uniform. That is, basis levels may increase/decrease more in the north-south directions, relative to east-west directions.
All twelve plant regions showed higher prices after the plant opened. The parameter estimate for the variable Eet measures the average change in basis within the 150-mile square region of each plant. All of the estimated parameters for Eet are highly significant and positive, although considerable variation exists across regions. At the low end, the Monroe, WI region experienced a 1.5-cent improvement in the basis while the Rosholt, SD region had a nearly 12-cent increase in the basis. On average, these twelve plant regions had a 5.9-cent increase in the basis.
Given that the opening of ethanol plants appears to have raised corn basis levels within a region, an empirically interesting issue is to identify the nature of the price impact depending on distance and location relative to the plant. Equation (3) augments the plant dummy variable Eet to include a measure of distance from the plant and whether a market is upstream or downstream. The hypothesis from the theoretical model is that upstream markets should have identical impacts while downstream markets should experience a declining price impact as distance from the plant increases.
Table 3 presents the results of equation (3) for the plant impact, and downstream/upstream impacts. All other coefficients were similar to those presented in table 2 and are not reported. The intercept column in table 3 signifies the price impact at the plant site (in cents per bushel), while the upstream/downstream slope terms measure the change in price depending on the miles away from the plant.
| Plant | Intercept | Slope-Downstream | Slope-Upstream | Price Impact from Plant (Miles) |
|---|---|---|---|---|
| Craig, MO | 6.09 (0.036) | 0.1466 (0.126) | −0.1515 (0.287) | * |
| Wentworth, SD | 12.33 (0.001) | −0.2089 (0.001) | 0.0504 (0.301) | 59.0 |
| Rosholt, SD | 13.45 (0.001) | 0.1024 (0.148) | 0.1964 (0.101) | * |
| Sioux Center, IA | 11.01 (0.001) | −0.1086 (0.001) | −0.0074 (0.714) | 101.4 |
| Galva, IA | 5.59 (0.001) | 0.0283 (0.316) | −0.0607 (0.016) | 92.1 |
| Big Stone City, SD | 9.75 (0.002) | −0.2348 (0.001) | −0.010 (0.909) | 41.5 |
| Stanley, WI | 10.95 (0.001) | −0.1405 (0.082) | 0.0015 (0.877) | 77.9 |
| Coon Rapids, IA | 10.88 (0.001) | −0.2422 (0.001) | −0.0214 (0.455) | 44.9 |
| Lena, IL | 19.33 (0.001) | −0.2278 (0.029) | −0.0244 (0.792) | 84.9 |
| Watertown, SD | 14.34 (0.001) | −0.1750 (0.042) | 0.1333 (0.203) | 81.9 |
| Lakota, IA | 4.63 (0.001) | 0.0031 (0.926) | 0.0740 (0.109) | * |
| Monroe, WI | 6.70 (0.007) | −0.2124 (0.017) | 0.0293 (0.245) | 31.6 |
- Note: R2 = 0.884, the spatial error coefficient λ = 0.439 and has a p-value of 0.001.
- * Impact distance is not defined when slope coefficients are positive or insignificant.
The estimated price impact at the plant site is given by the intercept coefficient. For the twelve ethanol plants, the estimated price impact at the plant site was positive and statistically significant. Unlike the price impact measure reported in table 2, which measures the average over the 150-mile plant region, the intercept estimate in table 3 provides a direct measure of the impact at the plant site. In general, impacts at the plant site are greater than those for the 150-mile region impacts, suggesting that the price increase is spatially concentrated around the plant. Price impacts at the plant sites ranged from 4.6 cents in Lakota, IA, to a high of 19.3 cents in Lena, IL. On average across the twelve plants, the price was 12.5 cents higher at the plant site.
In addition to significant impacts at plant sites, the slope coefficient estimates in table 3 indicate the presence of asymmetric downstream and upstream impacts around the plant. From our theoretical model, the null hypothesis of the plant impact is that δ′U = 0 and δ′D < 0. That is, upstream markets should experience the same impact from a new plant as the plant site itself, while downstream markets should experience a decaying effect based on the distance from the plant. Of the twelve plants considered, eight conformed to the downstream/upstream hypothesis with statistical significance indicating that the price impact decayed for markets that were downstream from the plant. The price impacts were constant for markets upstream from the plant.
Of the four markets that did not conform to the hypothesis, three (Craig, MO; Rosholt, SD; and Lakota, IA) were not statistically different from zero for either the downstream or upstream slopes. Thus, price impacts appeared uniform across all local markets. The final market, Galva, IA, showed a negative and significant upstream coefficient but an insignificant downstream coefficient suggesting the grain for this plant comes from upstream locations. Since our computation of upstream/downstream markets does not account for transportation networks, such as roads and rail lines, our proxy for transportation costs may be problematic for Galva, IA. Even so, it is encouraging that the majority of the plants showed the expected price impacts with constant upstream impacts and a decaying downstream impact.
With a decaying downstream impact, it is informative to estimate how far away from the plant the price impact will reach. This is provided by the term δ′e/δ′D, which measures how far downstream the price impact spreads (last column of table 3). For the Galva, IA plant, we present the price impact using the upstream slope coefficient, which is negative and significant. For the three plants that did not have a significant negative slope coefficient, no estimate of the price impact distance is given.
The estimated distance from the plant ranged from 31.6 miles for the Monroe, WI plant to 101.4 in Sioux Center, IA. On average across the nine plants for which a distance calculation could be made, the price impact reached 68 miles from the plant.
Price Impact Variation among Plants
Given that ethanol plants appear to increase corn prices, an interesting issue is how the impact varies among plants. Based on our parameter estimates, the price impact at the plant sites varied from 4.6 cents to 19.3 cents per bushel, suggesting considerable variation across plants. One would expect that available corn in the area relative to a plant's needs would influence the price impact. Plants that have relatively greater corn needs or areas where corn supplies are relatively low would likely have a greater price impact than smaller plants or regions with more corn production.
To investigate this empirically, we constructed a distance measure of available corn supplies relative to a plant's needs. Because ethanol is produced in fixed proportions (one bushel of corn yields 2.7 gallons of ethanol), we computed the annual corn needs of each plant based on plant capacities (see table 1). We used county production data from USDA's National Agricultural Statistics Service to measure an area's available corn supply. Because each county has a different land base, we standardized production by the county land area (in square miles) resulting in a measure of corn density per square mile. Assuming that corn production is uniformly distributed across the county, we computed the distance needed to acquire the necessary needs for each plant.
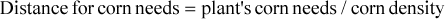 (5)
(5)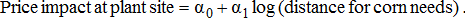 (6)
(6)The regression results show statistically insignificant impacts based on distance (table 4). In addition, the poor R2 suggests that the variation in the price impact is not explained well by the distance for corn needs variable.
| Variable | Parameter Estimate |
|---|---|
| Intercept | −0.333 (0.964) |
| Log (distance for corn needs) | 1.64 (0.183) |
- Note: R2 = 0.209.
Available corn supplies relative to a plant's needs is only one factor influencing the price impact from an ethanol plant. Unfortunately, a limited number of plant observations prevent us from testing these factors formally, so we simply mention them as possibilities.
First, although the majority of the plants considered in this analysis are farmer owned, plants have different grain procurement policies that may influence the price impact. Of the twelve plants in the analysis, two (Galva, IA, and Lakota, IA) have policies requiring grain to be delivered by its farm owners and disallows purchases from non-owners. These two plants showed the lowest price impact in the study. With farmers required to deliver grain to the plant, this may limit the price impact since the plant does not have to attract grain by offering higher prices. Consequently, farmers might consider forming cooperatives in conjunction with LLCs (limited liability corporations) if their goal is to increase prices.
Second, distance to terminal markets could also explain some of the variation in the price impacts across plants. From our theoretical model, a new ethanol plant reduces transportation costs for those producers that ship to the plant versus terminal markets. Thus, those ethanol plants farther away from terminal markets may be expected to have a larger price impact. For example, a comparison of the price impact of South Dakota versus Iowa plants shows a larger impact in South Dakota. On average, the four South Dakota plants had a 12.5-cent impact at the plant site versus 8 cents for the four Iowa plants. Grain moving from these regions largely flows to the Mississippi River for export through the Gulf. Thus, South Dakota markets incur higher transportation cost to the traditional export markets, but benefit more from transportation savings offered by a local plant.
Finally, this research did not address whether the price impacts persist over time. The presence of sizable price impacts in the plant regions would suggest local producers may respond by increasing production. However, we are unable to identify a potential supply response since most of the plants opened within the 2002 crop year and, thus, producers would not be expected to increase supplies until fall 2003. Intuitively, it seems likely that the price impact of a plant would diminish as local producers increase corn supplies over time. As such, estimates here are likely short-run impacts and not indicative of the long-term price impact from an ethanol plant.
Lessons for Future Development
Although ethanol plants appear to impact local grain prices, there are some important caveats to consider for those wishing to develop local plants. First, as was theoretically and empirically demonstrated, price impacts will differ around the plant with upstream markets experiencing the same impact as markets near the plant. As such, when setting a new plant, it is important to consider the availability of corn in the upstream markets (as opposed to downstream markets) since this is where the majority of the grain should be sourced. Likewise, producers considering investing in a new plant should know whether they are in an upstream market with potentially big impacts, or in a downstream market with smaller impacts. Distance to the plant will also limit the benefit.
Second, the plant size relative to the available local corn supplies weakly influenced prices. Other factors, such as grain procurement policies and distance to terminal markets may also influence this impact, although we are unable to quantify these impacts.
Finally, positive price impacts on corn prices may actually be a detriment to the profitability of an ethanol plant. Corn costs account for around 50% of the operating costs of an ethanol plant. Thus, higher corn prices will reduce the profitability of an ethanol plant. In addition, plants that require farm owners to deliver corn may experience a smaller price impact from the plant. As such, there seems to be a trade-off between farm ownership of a plant and the impact on grain prices. Whether farmers would be better off owning an ethanol plant and receiving lower corn prices or not owning the plant and having higher corn prices is an empirical question that should be carefully explored in a development strategy for new ethanol plants.
Acknowledgments
The authors wish to appreciate the helpful comments of Gary Brester and Dave Buschena.
Endnotes
Appendix A
Spatial Grain Pricing and the Opening of an Ethanol Plant
In this section, we develop a theoretical model of a grain production, transportation, and consumption system. Although several alternative model structures exist for spatial market analysis, we utilize the agents-on-links model that Faminow and Benson and Dahlgren and Blank employed in their studies of agricultural commodity markets.7
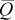 . Grain is shipped to the terminal market located at d = 1 with the demand for grain at the terminal given by:
. Grain is shipped to the terminal market located at d = 1 with the demand for grain at the terminal given by:
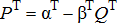 (A1)
(A1)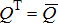 ), the price at any location d is:
), the price at any location d is:
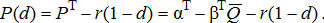 (A2)
(A2)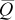 ) will lead to identical price impacts at all points along the line segment. In addition, prices continuously increase as one moves closer to the terminal market (d approaches 1) with the transportation rate r dictating the slope of the price surface.
) will lead to identical price impacts at all points along the line segment. In addition, prices continuously increase as one moves closer to the terminal market (d approaches 1) with the transportation rate r dictating the slope of the price surface.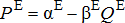 (A3)
(A3)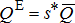 (A4)
(A4)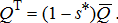 (A5)
(A5)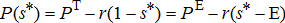 (A6)
(A6)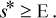
 (A7)
(A7)The optimal boundary solution given by equation (A7) can now be used to solve for equilibrium prices at the ethanol plant site, PE, and the terminal market, PT. These prices reflect the allocation of the total market supply, 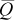 , between the ethanol plant (which receives the proportion s*) and the terminal market (which receives the proportion 1 − s*).
, between the ethanol plant (which receives the proportion s*) and the terminal market (which receives the proportion 1 − s*).
 (A8)
(A8) (A8′)
(A8′)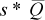 is the lost quantity at the terminal market as a result of the ethanol plant, and the price impact of this lost quantity is determined by the slope of the terminal market demand curve. All producers receive this price enhancement (Δ PT) resulting from the ethanol plant opening even though not all producers ship to the plant.
is the lost quantity at the terminal market as a result of the ethanol plant, and the price impact of this lost quantity is determined by the slope of the terminal market demand curve. All producers receive this price enhancement (Δ PT) resulting from the ethanol plant opening even though not all producers ship to the plant.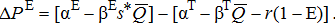 (A9)
(A9)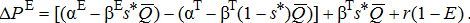 (A9′)
(A9′)The price impact at the site of the ethanol plant (equation (A9′)) consists of three components. First, the term in brackets is the price spread between the ethanol plant and the terminal market, which could be negative if the terminal market price is above the ethanol market price. Second, the term 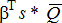 is the effect on the terminal market price from the opening of the plant, which impacts all producers regardless of whether they ship to the ethanol plant or the terminal market. Finally, the term r(1 − E) is the transportation savings to those producers located at the plant site E who formerly shipped to the terminal market, a distance of (1 − E). With the new ethanol plant these producers now ship directly to the plant site E at no cost.8 Indeed, all producers located to the left of the plant site E (referred to as “upstream” producers) enjoy the same price impacts as those located at the plant. This is because all producers in this region enjoy the same transportation cost savings by shipping to the ethanol plant compared to the terminal market. On the other hand, downstream producers do not enjoy the full transportation cost savings of r(1 − E) because they must haul their grain back to the ethanol plant, at a cost of r(d0 − E) for some location d0 where E ≤ d0 ≤ s*.
is the effect on the terminal market price from the opening of the plant, which impacts all producers regardless of whether they ship to the ethanol plant or the terminal market. Finally, the term r(1 − E) is the transportation savings to those producers located at the plant site E who formerly shipped to the terminal market, a distance of (1 − E). With the new ethanol plant these producers now ship directly to the plant site E at no cost.8 Indeed, all producers located to the left of the plant site E (referred to as “upstream” producers) enjoy the same price impacts as those located at the plant. This is because all producers in this region enjoy the same transportation cost savings by shipping to the ethanol plant compared to the terminal market. On the other hand, downstream producers do not enjoy the full transportation cost savings of r(1 − E) because they must haul their grain back to the ethanol plant, at a cost of r(d0 − E) for some location d0 where E ≤ d0 ≤ s*.




