Socially responsible investment fund performance: the impact of screening intensity
We thank the Social Investment Forum for providing mutual fund screening data and Eugene Fama and Kenneth French for allowing free and open access to their data sets. We also thank an anonymous referee and the editor for comments on an earlier version of this paper.
Abstract
Perhaps the most common criticism of socially responsible investment funds is that imposing non-financial screens restricts investment opportunities, reduces diversification efficiencies and thereby adversely impacts performance. In this study we investigate this proposition and test whether the number of screens employed has a linear or curvilinear relation with return. Moreover, we analyse the link between screening intensity and risk. Screening intensity has no effect on unadjusted (raw) returns or idiosyncratic risk. However, we find a significant reduction in α of 70 basis points per screen using the Carhart performance model. Increased screening results in lower systematic risk – in line with managers choosing lower β stocks to minimize overall risk.
1. Introduction
Socially responsible investment (SRI) funds offer an opportunity to many investors who seek a financial gain from a portfolio that is consistent with their social conscience. In the development of an SRI fund, the fund manager must screen the assets selected to ensure that they meet certain ethical, environmental, social and/or governance criteria. There is immense variation between the funds in terms of the implementation and intensity of the screening criteria. SRI investors are a heterogeneous group and differences between funds reflect differences in investors’ values, norms and ideologies as well as market and stakeholder forces (Sandberg et al., 2009). In this paper we assess the impact of screening intensity on the risk and return of SRI funds.
Social Investment Forum (2005) identifies 11 screening criteria that are widely used in practice: alcohol, tobacco, gambling, defence/weapons, animal testing, product/services, environment, human rights, labour relations, equal employment and community investment. Mutual funds may impose negative or positive screens or a combination of these SRI screens. Negative (positive) screening excludes (includes) assets based on a set of non-financial criteria. The Social Investment Forum provides screening data on many SRI funds including the type and number of screens employed by each fund. Of particular interest is that alcohol, tobacco, gambling and defence/weapons screens are employed by the majority of SRI funds – and each of these are negative (i.e. exclusionary) screens. Indeed, more than 80 per cent of SRI funds use negative SRI screening practices as part of their portfolio formation process (Social Investment Forum, 2005).
Portfolio theory would imply that SRI funds, by limiting the firms that can be included in a portfolio, cannot effectively diversify and, hence, should underperform the market and other well-diversified funds. By definition, SRI funds could be required to reject any number of lucrative investments due to their screening practices. Consequently, the popular view is that there should be a significantly negative linear relation between screening intensity and the returns of SRI funds. Screening intensity could also lead to higher levels of risk as SRI managers are unable to form a sufficiently diversified portfolio (Langbein and Posner, 1980; Knoll, 2002).
In addition, Fabozzi et al. (2008) show that sin portfolios outperform the market on a total return and risk-adjusted basis. They argue that there is a cost in applying social standards which is not incurred by sin stocks. Further, sin companies are more difficult and perhaps costly to establish, which suggests that surviving companies may earn high monopolistic returns.
On the other hand, it has been argued that the screening process may not always have this adverse effect on return and risk. Barnett and Salomon (2006) (henceforth BS) and Renneboog et al. (2008) (henceforth RTZ) argue that screening may either enhance or erode the performance of SRI funds, depending on the intensity or type of screen employed. Specifically, any loss in diversification from selecting SRI firms could be offset by benefits received from investing in firms that have strong corporate social performance (CSP). These firms are said to be more effectively managed and consequently offer superior performance. The hypotheses, derived from stakeholder theory, suggest that maximizing stakeholder interests may result in higher firm productivity and value (Freeman, 1984; Wicks et al., 1999).
Graves and Waddock (2000) show that companies that invest in stakeholder relations have above-average return on equity, return on assets and return on sales. Others suggest firms focusing on stakeholder interests will reduce firm-specific risk as they reduce exposure to demand from various interest groups (Cornell and Shapiro, 1987). The proponents of stakeholder theory also expect the demand for shares in responsible firms to be higher than demand for less responsible firms – and higher demand will result in an increase in price (Filbeck et al., 2009).
From a fund manager’s perspective an abnormal return (α) is the additional return above that justified by the systematic risk(s) involved. A simple process of screening the portfolio on SRI criteria is unlikely to result in a positive abnormal return. Indeed SRI funds are conceptually similar to focused funds where managers concentrate their holdings in a small number of stocks and seek to identify undervalued stocks using their superior knowledge of that sector. Interestingly, Sapp and Yan (2008) do not find evidence of out-performance by focused funds.
We investigate whether the number of screens an SRI fund imposes on its portfolio impacts the portfolio’s return. In an important extension to previous literature, we also examine whether screening intensity impacts the fund’s risk. Although the relation between screening intensity and return has been examined by BS and RTZ, we provide several methodological improvements on these studies, including allowing β to vary over time, using a more refined homogeneous group of funds and performing a comprehensive analysis of a large number of performance measures. In an extension to BS and RTZ, we also analyse the impact of screening intensity on total, systematic and idiosyncratic risk.
We find that screening intensity has no effect on raw (unadjusted) performance. However, if we use a model based on Carhart (1997), performance is reduced by 70 basis points for each additional screen imposed by the fund. In contrast to previous research, we do not find evidence of specific screens systematically impacting the performance of SRI funds. Our risk analysis shows an overall reduction in total risk as screening intensity increases. However, there is no relationship between idiosyncratic risk and screening intensity. Even with a large number of screens, SRI funds are able to diversify adequately and do not take on increased unsystematic risk.
Further analysis shows that screening intensity in fact has a negative relation with systematic risk. However, if we allow for the possibility that the relation between risk and screening intensity could be curvilinear (u-shaped), we find that funds’ systematic risk initially decreases, but then increases as we move from funds which impose an average number of screens to those that impose a large number of screens. We conjecture that SRI managers are aware of the criticism that their funds are more risky than conventional funds, so attempt to reduce the overall risk of the fund by choosing bigger, lower β stocks. However, as the fund imposes more and more screens, managers are less able to find large, low β stocks that fall within their SRI mandate and, thus, are effectively forced to hold smaller, higher β stocks.
The remainder of this paper proceeds as follows. Prior research on screening intensity is reviewed in Section 2 and the empirical design (including the data) is presented in Section 3. Results are presented in Section 4 and robustness tests are found in Section 5. Section 6 concludes the paper.
2. Prior research on screening intensity
To date, there are only two studies which have considered the impact of screening intensity on the performance of SRI funds: BS and RTZ. BS analyse the relation between screening intensity and performance for a sample of US SRI funds. They do not find evidence of a linear relation between screening intensity and the return of SRI funds. However, they do find evidence of a significant curvilinear relationship between screening intensity and performance – screening intensity first erodes and then enhances SRI fund performance.
Barnett and Salomon (2006) propose that their results reconcile stakeholder theory and portfolio theory. They argue that funds with low levels of screening intensity have an investment opportunity set similar to conventional funds. These funds’ portfolios are sufficiently diversified and performance is effectively maximized within the traditional mean–variance framework. By contrast, funds with stringent screening processes select from an investment pool of companies that have high socially responsible standards. These companies are expected to have higher performance due to their positive stakeholder relationships. However, the performance of funds which apply middle-level screening intensities are expected to suffer because these funds do not hold a mean-variant efficient portfolio but also do not screen stringently enough to hold only firms with the best CSP. Therefore, performance is expected to decrease initially as the screening process intensifies because the benefits of diversification are lost, but then increase as the benefits of positive stakeholder relationships begin to take effect. BS only consider the impact of screening intensity on performance and do not consider whether screening intensity also has an effect on the risk of SRI funds.
Renneboog et al. (2008) also examine the relation between SRI screens and performance. The authors find some weak evidence (coefficients are significant at the 10 per cent level) that social screens may adversely affect returns but find no relation between performance and the intensity of sin, ethical or environmental screens. They do not examine or control for the significant curvilinear relation found by BS. RTZ also investigate the effect screening intensity has on the manner in which SRI funds load onto each of Carhart’s (1997) four factors, but like BS the authors do not directly test whether screening intensity affects a fund’s total or diversifiable risk.
We also note a number of methodological limitations with both the BS and RTZ studies. First, both studies’ measure of risk-adjusted performance assumes that each fund’s β is constant over the entire life of the mutual fund. For RTZ and BS this would assume a constant β for the oldest funds of as long as 13 and 29 years, respectively. Kon and Jen (1978) were amongst the first to demonstrate that the assumption of a static β is unsatisfactory because mutual funds’ systematic risks vary over time due to the active buying and selling decisions of their managers. Portfolio βs (i.e. systematic risk) can change substantially merely by altering a fund’s exposure to particular industries or stocks. Managers can also vary their funds’βs simply by increasing or decreasing their exposure to non-equity products such as cash, bonds or property. In our data set we find that some of the mutual funds’ cash holdings can vary by as much as 30 per cent of total holdings.
Significant changes in β can also occur during structural changes in the market, such a bull or bear market. There is a large body of literature demonstrating that significant time variation exists in β estimates and the use of static βs often results in biased and unreliable α coefficients (Admati and Ross, 1985; Ferson and Schadt, 1996; Otten and Bams, 2004). We find evidence of significant variation in β estimates over time in our data set. For example, the standard deviation of our estimated β coefficients across different periods is on average 21.4 per cent. To overcome the problem associated with time-varying βs, we calculate risk-adjusted performance every 3 years. This 3 year horizon is also better aligned with the minimum investment horizon typically required for equity funds.
3. Empirical design
3.1. Research method
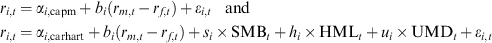()The Jensen and Carhart αs are calculated for each fund using the last 36 months of non-overlapping returns and, for comparability and consistency, are reported as annualized risk-adjusted returns.
Previous research interprets a finding of positive α as indicating that the manager has been able to identify undervalued stocks and is therefore skilled. Alternatively, a positive α could indicate a misspecification of the pricing model – funds may be loading on risk factors not captured by the CAPM. Fama and French (1993) and Carhart (1997) develop extended models which include proxies for various risk factors in the underlying stock market. One possibility is that idiosyncratic risk matters and is in fact priced by financial markets (Malkiel and Xu, 1997; Campbell et al., 2001). If idiosyncratic risk matters, this will have significant implications for our study. Both Fletcher (2007) and Lee and Faff (2009) find that standard asset pricing models have difficulty correctly pricing idiosyncratic risk.
If an SRI fund’s investable universe is restricted by the fund’s mandate, SRI portfolios might not be able to obtain full diversification and will bear significant levels of idiosyncratic risk (Sauer, 1997). Sauer (1997) proposes performance models that allow for total risk which might be more appropriate measures for SRI funds vis-à-vis the pricing models commonly employed in the SRI literature. By contrast, stakeholder theory suggests that a highly screened SRI portfolio will have low idiosyncratic risk because the firms comprising this portfolio are low-risk firms. Boutin-Dufresne and Savaria (2004) find that socially responsible portfolios have lower total risk because the unethical component of total risk is eliminated. Further they find that the residual volatility of a socially responsible portfolio is less than that of a conventional portfolio (see also Lee and Faff, 2009). However, Bello (2005) compares SRI funds with conventional funds and finds that the residual variance does not differ between the two groups.
()
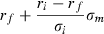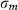and 
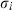are the standard deviation of the market and the fund.In addition, we allow for the possibility that an SRI fund may be forced to forgo diversification efficiency in the search for stocks which are both ‘winners’ and meet the portfolio’s SRI restrictions. Like Fletcher (1995), we employ the methodology developed by Fama (1972).
The basis of Fama’s technique is to attribute a fund’s absolute performance to two factors: risk taking (i.e. portfolio risk) and security selection skill (i.e. selectivity). The model assumes the ex ante market line is derived from an equilibrium relationship between expected risk and return. Therefore, we include a number of ‘selectivity’ and ‘diversification’ terms. As fund managers attempt to select outperforming stocks, they must by definition exclude a proportion of the investable universe of stocks from their portfolios. This exclusion could mean that managers move away from holding a fully diversified portfolio. The diversification term indicates the annualized return required for not being fully diversified. This is a particularly useful measure for those SRI funds that are constrained from obtaining full diversification by their restrictive screening processes. The diversification terms are calculated as follows. First, a fund’s expected return, given its total risk, is calculated. Next, the fund’s expected return given its systematic risk is calculated for the CAPM and Carhart (1997) models. The difference between the two figures is then taken to give the required return due to a lack of diversification, which we label CAPM diversification and Carhart diversification, respectively. Positive diversification values indicate the additional return required of a fund due to inadequate diversification. For consistency, the diversification (i.e. risk-related) results are reported alongside the other measures of risk as outlined below.
Selectivity is calculated by taking the actual return on the fund minus its expected return given its systematic risk and exposures to other risk factors. We calculate selectivity using the CAPM and Carhart models. Selectivity is essentially α plus the residual term. Both BS and RTZ use this measure to calculate performance and we include selectivity measures for comparability of our study with theirs. However, these models assume that only systematic risk is rewarded by financial markets. If we recognize that total risk may be priced, then a net selectivity measure is also required. Net selectivity is calculated by subtracting the diversification term from the selectivity term. Net selectivity is a measure of risk-adjusted performance given a fund’s total risk.
We also measure fund risk in a variety of other ways. First, total risk is measured as the standard deviation of the fund’s returns over the previous 3 years. Second, we follow Lee and Faff (2009) and use the residual variance from the CAPM and Carhart model equations as our measures of idiosyncratic risk. Each measure of performance and risk is regressed on a measure of screening intensity and a series of control variables. Consistent with BS, screening intensity is proxied by number of screens.
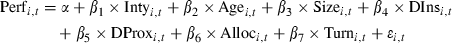()In cases where the performance measure is α, the equation is estimated in two steps. First, the α of each fund is calculated over each non-overlapping 3 year period for each fund. The αs from these regressions are then annualized and used as the dependent variable in equation (3). We note that, consistent with the vast majority of studies on fund performance, a large number of these αs are insignificant, and there is variation in the precision of α estimates (i.e. the standard errors of the αs vary).2 We therefore estimate equation (3) using weighted least squares, where the weights are the reciprocals of the standard errors of the αs. This allows us to take the precision of the α estimate into account: those αs with lower standard errors are given more weight than αs with higher standard errors (see Chan and Faff, 2003). This procedure is an improvement over BS and RTZ who do not adjust their analysis for this heterogeneity in the precision of their α estimates. For all other performance measures, OLS is used to estimate equation (3). We also include period dummies for each 3 year period and correct for heteroskedasticity using White’s adjusted standard errors.
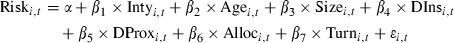()For comparison with BS and RTZ, we also run a number of other tests. First, to determine whether the relation between performance and screening is curvilinear, we include the square of the intensity variable.3 Second, we measure whether specific screens have an impact on a fund’s risk and return. Finally, we investigate the effect of screening intensity on a fund’s systematic risk and each of the Fama and French (1993) and Carhart (1997) factor loadings.
3.2. Data
Social Investment Forum (2005) reports that 201 mutual funds in the USA could be classified as SRI funds and screening data are available for 104 of these funds. To ensure that our sample of SRI funds is homogenous we further filter the funds to include only US equity funds, as determined by the Social Investment Forum. Our final sample is 61 funds. Monthly fund data and index data are sourced from the Morningstar Direct Database.4 Data for the SMB, HML and UMD factors are obtained from the Kenneth French Data Library. Our study examines the 18 year period from 1989 to 2006.5
4. Results
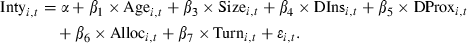()| Panel A | ||||||||
|---|---|---|---|---|---|---|---|---|
| Number of screens | Age (months) | Size | Turnover | Allocation to non-equity assets | ||||
| Average | SD | Average | SD | Average | SD | Average | SD | |
| 1 | 58.71 | 21.25 | 89 705 652 | 205 482 600 | 0.71 | 0.28 | 0.02 | 0.02 |
| 2a | 50.00 | 0.00 | 117 347 153 | 0 | 1.06 | 0.00 | 0.02 | 0.00 |
| 5 | 48.25 | 18.64 | 38 231 595 | 38 061 453 | 0.41 | 0.67 | 0.08 | 0.07 |
| 6 | 70.33 | 22.37 | 36 661 692 | 39 702 720 | 1.19 | 0.35 | 0.08 | 0.05 |
| 7 | 86.00 | 46.48 | 14 244 232 | 11 649 620 | 0.30 | 0.25 | 0.03 | 0.01 |
| 8 | 76.40 | 33.11 | 101 917 657 | 128 847 351 | 0.92 | 0.58 | 0.03 | 0.03 |
| 9 | 96.71 | 38.05 | 284 940 949 | 365 502 875 | 0.50 | 0.34 | 0.08 | 0.09 |
| 10 | 87.10 | 46.63 | 94 502 357 | 138 587 252 | 0.60 | 0.35 | 0.04 | 0.06 |
| 11 | 165.00 | 77.77 | 32 956 222 | 20 366 191 | 0.36 | 0.17 | 0.07 | 0.08 |
| All funds | 85.56 | 46.33 | 119 132 558 | 207 066 060 | 0.64 | 0.43 | 0.05 | 0.06 |
| Panel B | |
|---|---|
| Variable | Coefficient |
| Constant | 11.17** (4.69) |
| Age | 0.030** (6.49) |
| Size | −0.292** (−2.73) |
| DIns | 0.720** (2.05) |
| DProx | 5.118** (10.20) |
| Alloc | −0.13 (−0.06) |
| Turn | −0.401 (−1.17) |
| R 2 | 0.560 |
-
Panel A provides the descriptive statistics for age, size, turnover and allocation to non-equity assets for the sample of SRI equity mutual funds over the full 1989–2006 period. Panel B shows the results from estimating equation (5):
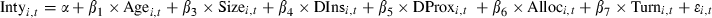where Intyi,t is the number of screens the fund uses; Agei,t is the age of the fund at the beginning of period t; Sizei,t is the natural log of the average year total net assets for the fund i; DInsi,t is 1 if fund i is an institutional fund in period t and 0 otherwise; DProxi,t is 1 if the fund has a policy to participate in proxy voting or 0 otherwise; Alloci,t is the average proportion of the assets in fund i allocated to assets other than equity across each 3 year period; Turni,t is the turnover of fund i in period t. Significant at **5 and *10 per cent levels.
- aNote, there is only one fund in this category.
4.1. Socially responsible investment and screening intensity – performance results
Table 2 presents the results from estimating equation (3). The screening intensity variable (INTY) is statistically insignificant when the total return, Sharpe ratio, information ratio, M2 or net selectivity variables are the chosen measure of performance. Similar results are found when using the CAPM. However, when the Carhart model is examined we find a statistically significant negative relation between screening intensity and risk-adjusted performance – where each additional screen is associated with a 70 basis points per annum erosion of a fund’s performance. This is of some concern for those SRI funds with 10 or more screens as this suggests that on average approximately 7 per cent of their annual return is sacrificed due to screening intensity alone. Results for the Carhart selectivity variable are similar to the Carhart α results, although the coefficient on INTY is not as large (associated with a 40 basis point erosion). Our results are in line with RTZ who also find evidence of a significant negative relation between Carhart selectivity and intensity.6
| Variable | Totalreturn | Sharperatio | Inforatio | M 2 | CAPM α | Carhart α | CAPMselect | Carhartselect | Netselect |
|---|---|---|---|---|---|---|---|---|---|
| Constant | 0.076(0.98) | 0.065(0.13) | −0.939(−0.95) | 0.094(1.45) | −0.040(−0.40) | 0.091(1.12) | −0.014(−0.19) | 0.093(1.42) | −0.005(−0.07) |
| Inty | −0.001(−0.37) | 0.002(0.14) | 0.009(0.25) | 0.000(0.08) | 0.001(0.19) | −0.007**(−2.57) | 0.001(0.28) | −0.004*(−1.93) | 0.001(0.32) |
| Age | 0.000(−0.45) | −0.001(−0.77) | −0.001(−0.24) | 0.000(−0.93) | 0.000(−1.36) | 0.000(1.18) | 0.000(−0.38) | 0.000(1.16) | 0.000(−0.74) |
| Size | 0.004(0.90) | 0.013(0.50) | 0.061(1.18) | 0.002(0.55) | 0.006(1.00) | 0.003(0.61) | 0.002(0.40) | 0.000(−0.02) | 0.001(0.20) |
| DIns | −0.004(−0.23) | −0.030(−0.26) | −0.048(−0.21) | −0.004(−0.26) | −0.002(−0.08) | 0.007(0.36) | −0.003(−0.16) | 0.010(0.68) | −0.003(−0.15) |
| DProx | 0.007(0.35) | 0.055(0.40) | 0.263(1.00) | 0.002(0.10) | −0.049**(−2.07) | 0.010(0.57) | −0.004(−0.22) | 0.018(1.03) | −0.002(−0.10) |
| Alloc | 0.207**(2.17) | 1.930**(3.08) | 2.093*(1.73) | 0.255**(3.20) | 0.276**(2.61) | 0.137*(1.83) | 0.280**(2.96) | 0.139*(1.73) | 0.297**(3.03) |
| Turn | −0.024*(−1.90) | −0.291**(−3.49) | −0.264*(−1.64) | −0.030**(−2.84) | −0.007(−0.45) | −0.023*(−1.91) | −0.033**(−2.64) | −0.033**(−3.12) | −0.042**(−3.20) |
| R 2 | 0.581 | 0.560 | 0.133 | 0.638 | 0.20 | 0.42 | 0.147 | 0.260 | 0.256 |
-
Results from equation (3) are shown:
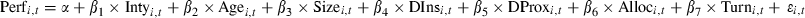where Perfi,t is the 3 year (t) annualized performance measure for fund i; Intyi,t is the screening intensity for fund i measured as the number of screens the fund uses; Agei,t is the age of the fund at the beginning of period t; Sizei,t is the natural log of the average year total net assets for the fund i; DInsi,t is 1 if fund i is an institutional fund in period t and 0 otherwise; DProxi,t is 1 if the fund has a policy to participate in proxy voting or 0 otherwise; Alloci,t is the average proportion of the assets in fund i allocated to assets other than equity across each 3 year period; Turni,t is the turnover of fund i in period t; Dummy variables are included for each 3 year period (results on these variables are not reported). Regressions are based on 145 observations. White’s adjusted t-statistics are reported in parentheses. Significant at **5 and *10 per cent levels.
Consistent with prior literature, the allocation to non-equity asset classes and turnover both impact significantly on performance. The negative turnover coefficient indicates that those SRI managers with higher levels of turnover are subject to greater costs and lower performance. The positive non-equity coefficient suggests that many of these SRI equity managers would be better placed to manage cash rather than equities (see Blake et al., 1993; Wermers, 2000). Finally, we observe that age, size, type of fund (institutional or not) and proxy voting status do not have a statistical association with any measure of performance.
4.2. Socially responsible investment and screening intensity – risk results
The results from estimating equation (4), where risk is modelled as a function of screening intensity, are shown in Table 3. There appears to be no significant relation between a fund’s idiosyncratic risk and screening intensity. This result confirms and enhances Bello (2005) who finds little difference in the idiosyncratic risk of SRI and conventional funds. The coefficient on INTY for Carhart diversification is significantly negative – which again confirms that higher screening intensity does not result in increased idiosyncratic risk: managers are not required to provide additional return to compensate for a loss in diversification.
| Variable | SD | CAPM residual | Carhart residual | CAPM divers | Carhart divers |
|---|---|---|---|---|---|
| Constant | 0.204** (5.65) | 0.019* (1.68) | 0.018** (2.33) | −0.009 (−0.47) | 0.098* (1.66) |
| Inty | −0.002* (−1.76) | 0.000 (0.80) | 0.000 (1.00) | 0.000 (−0.21) | −0.005** (−2.56) |
| Age | 0.000 (0.85) | 0.000 (1.25) | 0.000** (2.98) | 0.000 (1.53) | 0.000** (2.28) |
| Size | 0.003 (1.52) | 0.000 (0.41) | 0.000 (−0.84) | 0.001 (0.79) | −0.001 (−0.29) |
| DIns | 0.004 (0.49) | −0.001 (−0.32) | −0.001 (−0.45) | 0.000 (−0.02) | 0.013 (0.96) |
| DProx | 0.005 (0.48) | −0.003 (−1.13) | −0.003 (−1.27) | −0.002 (−0.46) | 0.020 (1.27) |
| Alloc | −0.037 (−0.83) | 0.039** (2.85) | 0.033** (3.47) | −0.017 (−0.72) | −0.158** (−2.17) |
| Turn | 0.041** (6.94) | 0.014** (7.78) | 0.009** (7.50) | 0.008** (2.66) | 0.008 (0.85) |
| R 2 | 0.773 | 0.513 | 0.588 | 0.488 | 0.427 |
-
Results from equation (4) are shown:
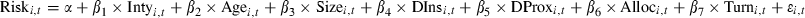where Riski,t is the 3 year annualized risk of fund i measured as standard deviation or the residual variance from the CAPM of Carhart model equations. Intyi,t, Agei,t, Sizei,t, DInsi,t, DProxi,t, Alloci,t and Turni,t are as outlined in Table 2. Dummy variables are included for each 3 year period (results on these variables are not reported). Regressions are based on 145 observations. White’s adjusted t-statistics are reported in parentheses. Significant at **5 and *10 per cent levels.
Interestingly, the coefficient on INTY is significant (at the 10 per cent level) when standard deviation is used as the dependent variable. The coefficient is negative, suggesting that an increase in screening intensity lowers the total risk of the fund. This finding is in line with Boutin-Dufresne and Savaria (2004), RTZ and Lee and Faff (2009) who find that SRI funds exhibit lower total risk than conventional funds.
Our results suggest that total risk is reduced by imposing SRI screens. However, as there is no evidence of significant differences in idiosyncratic risk, the reduction in total risk must be due to lower levels of systematic risk.7 We examine this issue further when we investigate the effect of screening intensity on systematic risk.
5. Additional analysis
5.1. Curvilinear relation between screening intensity, return and risk
We test the proposition put forward by BS that the relation between screening intensity and performance is curvilinear by including a squared intensity variable in the empirical models. This curvilinear relation was not examined by RTZ. Unlike BS, we find that the square of screening intensity is not significant in any of our tests. We do not find evidence of a curvilinear relation between screening intensity and return. For brevity we do not report the results.8
We extend BS’s analysis by also examining whether the relation between risk and screening intensity is curvilinear. The results are presented in Table 4. Notably, there is little evidence of a curvilinear relation with any of the measures of idiosyncratic risk. However, the INTY2 coefficient is significant and positive when risk is measured by standard deviation. The INTY variable retains its significantly negative role, indicating that SRI funds reduce the total risk of their fund as screening intensity increases. However, the positive INTY2 coefficient indicates that funds could experience an increase in their risk as the number of screens increases. We plot this relation in Figure 1. Standard deviation decreases until funds impose six screens and then increases as the number of screens increase. As more screens are imposed, fund managers can find it difficult to identify and trade stocks which have both low βs and meet their screening criteria. Highly screened funds might therefore have to invest in high β (and smaller) stocks. We return to this point below.
| Variable | Standard deviation | CAPM residual | Carhart residual | CAPM divers | Carhart divers |
|---|---|---|---|---|---|
| Constant | 0.216** (5.99) | 0.021* (1.88) | 0.019** (2.47) | −0.006 (−0.31) | 0.111* (1.85) |
| Inty | −0.013** (−2.47) | −0.002 (−1.09) | −0.001 (−0.75) | −0.003 (−0.97) | −0.016* (−1.85) |
| Inty2 | 0.001** (2.10) | 0.000 (1.32) | 0.000 (1.02) | 0.000 (0.94) | 0.001 (1.27) |
| Age | 0.000 (0.84) | 0.000 (1.24) | 0.000** (2.97) | 0.000 (1.52) | 0.000** (2.28) |
| Size | 0.003 (1.50) | 0.000 (0.38) | 0.000 (−0.86) | 0.001 (0.77) | −0.001 (−0.31) |
| DIns | 0.005 (0.67) | −0.001 (−0.21) | −0.001 (−0.36) | 0.000 (0.06) | 0.014 (1.06) |
| DProxy | 0.016 (1.49) | −0.001 (−0.31) | −0.001 (−0.58) | 0.000 (0.08) | 0.032* (1.74) |
| Alloc | −0.032 (−0.73) | 0.040** (2.92) | 0.033** (3.53) | −0.016 (−0.66) | −0.153** (−2.10) |
| Turn | 0.043** (7.24) | 0.015** (7.91) | 0.010** (7.57) | 0.009** (2.76) | 0.010 (1.01) |
| R 2 | 0.778 | 0.516 | 0.589 | 0.488 | 0.429 |
-
Results from equation (4) are shown, including the INTY2 variable.
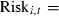
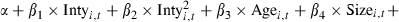
where Riski,t is the 3 year annualized risk of fund i measured as standard deviation or the residual variance from the CAPM or Carhart model equations. Intyi,t, Agei,t, Sizei,t, DInsi,t, DProxi,t, Alloci,t and Turni,t are as outlined in Table 2. Dummy variables are included for each 3 year period (results on these variables are not reported). Regressions are based on 145 observations. White’s adjusted t-statistics are reported in parentheses. Significant at **5 and *10 per cent levels.
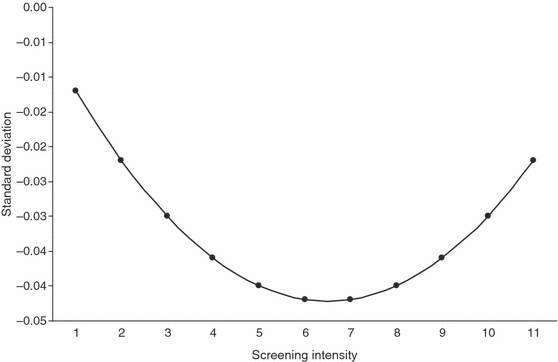
Non-monotonic effect of screening on risk (standard deviation).
5.2. An analysis of screen type on the performance and risk of a fund
We also examine whether the return and risk that an SRI investor can expect is dependent on the type of screen the fund employs. For example, BS find that equal employment screens negatively impact on performance, whilst community relations contribute to performance. Similar results for community relations are found by RTZ. Contrary to both BS and RTZ, we find little evidence that different types of screens systematically benefit or detract from performance.9 Rather, our analysis above would suggest that, if anything, it is the number of screens that appears to have the biggest impact on performance – albeit this is limited to when we use market models of performance.
Table 5 presents the results on the relation between a fund’s level of risk and the type of screen. There is little evidence of specific screens having an impact on the measures of idiosyncratic risk. When total risk is examined, we find that screens for gambling and community investment significantly increase total risk; while screens for tobacco, weapons and human rights significantly reduce total risk. As there is no relation between these screens and idiosyncratic risk, this implies that the lower total risk is derived from an exposure to lower β risk.10 This result is surprising given that tobacco- and weapons-based stocks typically have lower βs (Hong and Kacperczyk, 2008). A possible explanation is that many SRI funds exclude other stocks that are associated with these sectors. For example, KLD Research and Analytics, a well-known US SRI participant, excludes firms that derive 15 per cent or more of their total revenues from alcohol, tobacco, adult entertainment and/or firearms. The cut-off is as low as 2 per cent for firms deriving revenue from the sale of weapons or weapon systems. Additionally, firms are excluded if they operate or have any ownership interest in nuclear power plants. Finally, many firms are excluded if they own 20 per cent or more of another company involved in these areas (KLD Research and Analytics, 2007). Consequently, a large number of firms could be excluded despite not being primarily involved with these industries. This is perhaps the biggest issue with the exclusionary SRI screening practices that define much of the US SRI marketplace.
| Variable | Std Dev | CAPM residual | Carhart residual | CAPM divers | Carhart divers |
|---|---|---|---|---|---|
| Constant | 0.301** (6.68) | 0.029** (2.05) | 0.017* (1.91) | −0.010 (−0.39) | 0.149* (1.84) |
| Alc | 0.007 (0.37) | 0.000 (−0.03) | −0.001 (−0.22) | −0.006 (−0.60) | −0.043 (−1.31) |
| Animal | −0.029 (−1.37) | 0.004 (0.63) | 0.009** (2.02) | 0.001 (0.09) | −0.060 (−1.59) |
| Equal_emp | 0.004 (0.11) | 0.007 (0.55) | −0.003 (−0.34) | −0.013 (−0.62) | 0.018 (0.26) |
| Tob | −0.068** (−2.77) | −0.013* (−1.69) | −0.006 (−1.30) | −0.008 (−0.54) | −0.033 (−0.76) |
| Gamb | 0.017** (1.99) | 0.000 (0.18) | −0.002 (−1.38) | −0.002 (−0.36) | 0.010 (0.64) |
| Weap | −0.023** (−2.65) | −0.001 (0.53) | 0.001 (0.42) | 0.010* (1.95) | 0.020 (1.29) |
| Proserv | 0.019 (0.57) | 0.010 (0.97) | 0.012* (1.80) | 0.016 (0.83) | 0.028 (0.45) |
| Envir | 0.006 (0.14) | 0.001 (0.04) | −0.004 (−0.44) | 0.011 (0.48) | 0.037 (0.51) |
| Huma | −0.045** (−2.04) | −0.014* (−1.93) | −0.007 (−1.57) | −0.008 (−0.64) | −0.027 (−0.69) |
| Lab_rel | −0.004 (−0.21) | −0.002 (−0.27) | 0.001 (0.31) | −0.003 (−0.22) | −0.037 (−0.97) |
| Com_inv | 0.024** (2.95) | 0.005* (1.79) | 0.003* (1.88) | −0.004 (−0.76) | −0.018 (−1.24) |
| DProxy | −0.016 (−0.88) | −0.005 (−0.88) | 0.000 (0.00) | −0.004 (−0.37) | −0.017 (−0.51) |
| Age | 0.000 (1.57) | 0.000 (1.02) | 0.000** (2.57) | 0.000* (1.78) | 0.000** (3.07) |
| Size | 0.000 (0.22) | 0.000 (0.26) | 0.000 (−0.34) | 0.001 (1.11) | −0.002 (−0.61) |
| DIns | −0.002 (−0.27) | 0.000 (−0.12) | 0.001 (0.43) | 0.004 (0.96) | 0.020 (1.41) |
| Alloc | −0.009 (−0.20) | 0.038** (2.59) | 0.028** (2.97) | −0.047* (−1.75) | −0.237** (−2.81) |
| Turn | 0.048** (8.20) | 0.017** (9.19) | 0.012** (9.76) | 0.010** (3.01) | 0.010 (0.92) |
| R 2 | 0.811 | 0.578 | 0.694 | 0.511 | 0.426 |
-
Results from extending equation (4) to include different types of screens:
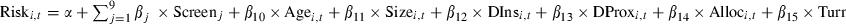where Riski,t is the 3 year annualized risk of fund i measured as standard deviation or the residual variance from the CAPM or Carhart models, Screen = Alc = alcohol, Animal = animal testing, Equal emp = equal employment, Tob = tobacco, Gamb = gambling, Weap = weapons, Proserv = products and services, Envir = environment, Huma = human rights, Lab_rel = labour relations, Com_inv = community investment. Agei,t, Sizei,t, DInsi,t, DProxi,t, Alloci,t and Turni,t are as outlined in Table 2. Dummy variables are included for each 3 year period (results on these variables are not reported). Regressions are based on 145 observations. White’s adjusted t-statistics are reported in parentheses. Significant at **5 and *10 per cent levels.
5.3. An analysis of risk loadings
Similar in spirit to RTZ, we examine the relation between screening intensity and systematic risk, the Fama and French and Carhart factor loadings. That is, we use each fund’s loading on the market risk premium, SMB, HML and UMD factors as the dependent variable and regress this against screening intensity and our control variables. Results are presented in Table 6. We find evidence that all of the risk loadings for SRI funds are significantly associated with screening intensity. Funds with more screens tend to invest more in larger stocks; more heavily in value stocks and more in past winner stocks.
| Variable | β | SMB | HML | UMD |
|---|---|---|---|---|
| Constant | 1.117** (5.17) | 0.404 (0.82) | −0.477 (−1.30) | −0.895** (−3.59) |
| Inty | −0.012* (−1.85) | −0.028* (−1.75) | 0.058** (4.59) | 0.030** (3.55) |
| Age | 0.000 (0.66) | 0.001 (0.85) | −0.001 (−1.22) | −0.003** (−5.09) |
| Size | 0.008 (0.72) | 0.041 (1.55) | 0.007 (0.33) | 0.032** (2.33) |
| DIns | 0.050 (1.03) | −0.067 (−0.57) | −0.207** (−2.21) | 0.127** (1.99) |
| DProxy | 0.027 (0.56) | 0.079 (0.70) | −0.471** (−5.78) | −0.307** (−5.54) |
| Alloc | −1.057** (−4.85) | −0.404 (−0.70) | 0.315 (0.77) | 0.371 (1.26) |
| Turn | 0.039 (1.26) | 0.352** (4.50) | −0.180** (−2.95) | 0.147** (3.46) |
| R 2 | 0.217 | 0.161 | 0.559 | 0.476 |
-
Results from a modification of equation (4) are shown:
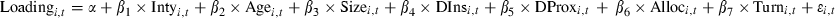where Loadingi,t is the fund’s factor loading on the four factors in the Carhart model equations. Intyi,t, Agei,t, Sizei,t, DInsi,t, DProxi,t, Alloci,t and Turni,t as outlined in Table 2. Dummy variables are included for each 3 year period (results on these variables are not reported). White’s adjusted t-statistics are reported in parentheses. Significant at **5 and *10 per cent levels.
Perhaps the most interesting finding is the significantly negative relation between screening intensity and β, the fund’s level of systematic risk. This result suggests that an increase in the number of SRI screens is associated with SRI funds tending to hold a greater proportion of stocks with lower βs, and is consistent with our previous finding of a significant negative relation between screening intensity and total risk, but not idiosyncratic risk. One plausible explanation is that SRI fund managers are aware of the widely held criticisms that imposing SRI screens will increase the fund’s risk. In an attempt to mitigate an increase in overall risk, managers deliberately choose lower β stocks.
We also investigate whether the relation between screening intensity and the factors is curvilinear. We find some evidence of a curvilinear relationship in the case of β and SMB.11 This is an interesting finding and corresponds with our total risk results that also demonstrate a curvilinear relation. This could mean that funds with few screens are similar to conventional funds and hold smaller, higher β stocks in their portfolios. As the number of screens increases, managers choose bigger, lower β stocks, possibly in an effort to reduce the overall risk of the fund. As the majority of screens are exclusionary, as funds impose more and more screens, there are less large stocks with lower βs in which the funds can invest. Intensely screened funds are therefore forced to invest in smaller, higher β stocks.
6. Summary and conclusions
We revisit the question of whether there is any benefit or cost associated with investing in SRI funds and in particular whether the number of screens applied by such funds impacts return and risk. The common view is that as imposing SRI screens will restrict the investable universe, less efficient portfolios will result and consequently SRI funds will have lower returns and higher (idiosyncratic) risk than their non-SRI counterparts.
We take a slightly different approach to much of the existing literature and consider whether the intensity of screening has an impact on a fund’s performance. While there have been two studies to date which have analysed the relation between screening intensity and performance, we recognize that there are two aspects to performance measurement: return and risk. In an important extension to previous research, we therefore consider the relation between screening intensity and both return and risk. We also provide a number of methodological enhancements in this study and use a wide range of risk and return measures to test this relation.
We find that, overall, the level of screening does not affect a fund’s raw (unadjusted) return. However, we do find evidence of a decrease in performance of 70 basis points per screen when using the Carhart model. In terms of risk, we find that screening intensity does not have an impact on unsystematic risk. However, an increase in screening intensity does appear to reduce the fund’s total risk (as proxied by standard deviation). Further investigation reveals that this is driven by a negative relation between systematic risk and the number of screens. We conjecture that SRI managers are aware of the criticism that imposing screens will increase the risk of a fund, and therefore deliberately choose lower β stocks in an attempt to decrease their overall risk. However, as screening intensity increases, less low β stocks are available in the investable universe and funds are effectively forced to hold smaller, lower β stocks. That is, we find a curvilinear relation between screening intensity and systematic risk. We also find some evidence that the type of screen has an impact on overall risk.
In conclusion, we recommend that investors in SRI funds seriously consider funds that do not screen too intensively. While increased screening intensity does not adversely affect risk, highly screened funds do suffer in terms of risk-adjusted performance. We note that investors in SRI products are not likely to be homogenous: for example, some investors will be more concerned about screening on environmental factors, while others may want to screen out the traditional ‘sin’ industries such as tobacco and alcohol. As such, investors should select SRI funds which screen for only those issues which they deem sufficiently important.
