Accounting & Finance
Volume 50, Issue 1 pp. 143-169
Full Access

Size and momentum in European equity markets: empirical findings from varying beta Capital Asset Pricing Model

George Karathanasis, 

George Karathanasis

Departments of Business Administration

Search for more papers by this author
Konstantinos Kassimatis, 

Konstantinos Kassimatis

Departments of Business Administration

Search for more papers by this author
Spyros Spyrou, 

Spyros Spyrou

Accounting and Finance, Athens University of Economics and Business, GR10434 Athens, Greece

Search for more papers by this author
First published: 23 February 2010
https://doi.org/10.1111/j.1467-629X.2009.00314.x
Citations: 5

Abstract

We use securities listed on 13 European equity markets to form size and momentum portfolios. We find limited evidence of a size premium but significant momentum returns in eight sample markets. We find that these premia may not constitute an anomaly because they are consistent with a varying-beta Capital Asset Pricing Model. We also show that systematic risk is related to the business cycle. Furthermore, the results suggest that although size and especially momentum returns are significant, it would be difficult to exploit them in the short to medium run, because they are positive and sizeable in very few years in our sample.

1. Introduction

Many empirical studies find that small capitalization stocks have higher average returns than big capitalization stocks (Banz, 1981; Reinganum, 1981) and that this premium is linked to a January seasonal (Keim, 1983; Ritter and Chopra, 1989). More recent studies document a size premium in international markets as well (Clare et al., 1997; Bagella et al., 2000, for the UK market; Heston et al., 1995, for 12 European markets, among others). Size is not the only firm characteristic that appears related to average returns since other firm characteristics, such as book-to-market value, leverage, earnings-price, etc., also seem to play a role (Basu, 1983; Rosenberg et al., 1985; Bhandari, 1988); however, Fama and French (1992) show that the combination of size and book-to-market equity seems to absorb the role of the other firm characteristics. Furthermore, Jegadeesh and Titman (1993, 2001) show that, in the USA, a portfolio of stocks with the highest recent performance (Winners) outperforms a portfolio of stocks with the lowest recent performance (Losers) by about 1 per cent per month for the 12 months following portfolio formation. The results of Rouwenhorst (1998) and Liew and Vassalou (2000) also indicate that the momentum effect is present in major international markets as well. These findings contradict the Efficient Market Hypothesis and the Capital Asset Pricing Model (CAPM) and are often termed ‘market anomalies’, although Fama and French (1996) argue that the momentum effect is the only effect not explained by the three-factor asset pricing model (for US data).

A number of recent studies cast doubt on the existence of a small-firm premium as a solid stock market anomaly. For example, Jegadeesh and Titman (2001) point out that the average Fama and French size factor in the USA for the period between 1965 and 1981 is 0.53 per cent per month with a t-statistic of 2.34, while for the 1982–1998 period it is –0.18 per cent with a t-statistic of –1.01. Dimson and Marsh (1999) argue that after the UK size premium was documented and disseminated, a historical small-cap premium of 6 per cent was followed by a small-cap discount of around 6 per cent. Knez and Ready (1997) find that, when outliers are accounted for, the US size premium becomes negative, whereas Brown et al. (1983) find that the size premium disappears in certain subperiods. Wang (2000) examines Compustat and CRSP data and argues that the size effect is largely a spurious statistical inference resulting from survival bias, not an asset pricing anomaly. The momentum effect appears much stronger, although Bekaert et al. (1997) find contradicting evidence for emerging equity markets and Liew and Vassalou (2000) report statistically insignificant momentum returns for Japan and Italy (and when annual portfolio rebalancing is employed, for Australia and Canada as well). Note also that for both effects the evidence suggests cyclicality related to the economic conditions. For instance, Chordia and Shivakumar (2002) show that abnormal momentum profits for the US market can be explained by a set of lagged macroeconomic variables and argue that time-variation in expected returns may be a possible explanation, while Kim and Burnie (2002) find that the small-firm effect is strong during the expansion phase of the economic cycle but not during the contraction phase (see Bhardwaj and Brooks, 1993).

Overall, the evidence in the literature indicate that the small-firm premium has largely disappeared during recent years, while the momentum effect might not be significant in all markets. Furthermore, there is evidence that both effects are related to the economic cycle and, therefore, their significance may be time-varying. In addition, these results have been obtained for mainly developed international equity markets and smaller equity markets are often neglected in the literature. Motivated by this, the present paper aims to address four issues related to the size and momentum effects for a sample of 13 European markets of varying size, importance, trading systems, liquidity and market microstructure. First, the profitability of size and momentum portfolios is examined. We find that Small Minus Big (SMB) average mean monthly portfolio returns range from –0.03 per cent for Germany to 1 per cent for Greece and are statistically significant (i.e. statistically different from zero) for only 2 out of 13 markets, whereas average monthly Winner Minus Loser (WML) returns range between 0.37 per cent in Spain and 1.37 per cent in Greece and are statistically significant for 8 markets.

Second, we examine the frequency and consistency of the profitability of size and momentum portfolios over time. Many previous studies often draw conclusions based on long-term averages or various subsamples and often neglect the issue of the relative frequency of ‘anomalous’ returns. This is an important issue since, as the results of the paper show, the effects have a very low frequency of occurrence over time. We show that the positive returns of arbitrage size and momentum portfolios in Europe seem to be due to very few sample years where returns are large and significant. For example, for France the WML portfolio has, on average, statistically significant abnormal returns for the whole sample period. A year-by-year analysis indicates that WML abnormal returns are statistically significant in only 4 out of 19 sample years; for Germany WML abnormal returns are statistically significant in 3 out of 19 years, for Greece in 1 out of 19 years, etc.

Third, this paper utilizes a time-series procedure to examine whether these effects are consistent with the CAPM in both a static and a time-varying framework. For instance, the initial studies on size and momentum portfolios rejected the CAPM on the grounds that the betas generated by the static version of the model could not explain the portfolios returns. However, there is a growing literature on time-varying risk premia (e.g. Campbell and Vuolteenaho, 2004; Fama and French, 2006; Ang and Chen, 2007; Adrian and Franzoni, 2008) and some of these studies cast doubt on the early findings; for example, Ang and Chen (2007) find that if we account for time variation in market risk, the CAPM cannot be rejected. In the present study, the zero-intercept hypothesis (e.g. Fama and French, 1996) is tested with both an ordinary least-squares (OLS) and a rolling least-squares (RLS) estimation methodology. The RLS estimation allows the estimation of coefficients over successive rolling periods of a fixed length and captures more adequately time-variation in slope coefficients and intercepts. The findings of the paper indicate that size and momentum arbitrage portfolio returns are consistent with the static CAPM in about half of the sample markets; however, when the methodology accounts for time-variation in systematic risk, arbitrage portfolio returns appear consistent with the CAPM for all sample markets.

Fourth, we investigate whether the time-varying systematic risk of small-firm, large-firm, SMB, winner, loser, and WML portfolios is related to the business cycle. We use time-series regressions of the beta coefficient history for each portfolio and each market on a set of variables that capture the economic cycle, and find evidence consistent with the hypothesis that systematic risk is related to the economy and, therefore, it may exhibit significant time-variation. Overall, the findings of the paper confirm previous results on a limited small-firm premium and a sizeable momentum premium, which, as we show, are due to very few sample years of large and significant returns.

2. Data and methodology

The data are obtained from DataStream and consist of end-of-month prices in local currencies on securities listed in 13 European markets: Austria, Denmark, France, Germany, Greece, Ireland, Italy, the Netherlands, Norway, Spain, Sweden, Switzerland, and the UK. A major issue with DataStream data is errors; for instance, Ince and Porter (2006), who examine DataStream data for US equities and four European markets, identify a series of problems and argue that naïve use of DataStream data can have a significant impact on economic inference. To improve the quality of our dataset and rectify possible problems, we use four filters proposed by Ince and Porter: (i) all equities not listed on the exchanges of the reference country are deleted; (ii) non-common equities are deleted (e.g. ADRs, warrants); (iii) zero returns resulting from the delisting of a stock are deleted; and (iv) extremely high returns which are reversed in the next month are deleted (these returns are very few and are due to incorrect data entries; however, they may have a significant impact on results if not addressed). The sample period ends in December 2006 for all markets and starts in January 1988 for all markets except Greece, where the sample period starts in January 1989 due to data availability. Table 1 presents the average number of stocks available for each market by sample year. It should be noted that the list of securities during the first years of the sample might not be complete. In other words, some survivorship bias might exist, but only for the first years of the sample period.

Table 1.
Number of securities available for the portfolios each year for each country
Year/Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
1987 70 60 124 184 57 285 219 122 61 292 296 1675
1988 77 158 174 256 98 68 310 223 118 76 314 335 1753
1989 82 227 383 476 120 77 330 219 120 109 424 358 1735
1990 96 234 517 518 140 83 348 215 137 127 487 398 1698
1991 109 248 604 551 187 84 358 209 138 133 446 390 1622
1992 122 289 620 574 203 76 364 206 135 138 361 374 1535
1993 139 291 642 584 208 70 351 201 137 144 248 349 1510
1994 141 286 709 603 230 67 335 196 153 144 269 336 1579
1995 145 282 766 624 269 67 327 199 155 145 279 331 1630
1996 140 283 844 647 285 65 317 197 169 147 288 317 1733
1997 137 277 993 667 293 65 314 206 191 156 320 308 1823
1998 136 279 1005 718 296 63 305 230 223 164 371 307 1812
1999 133 268 974 837 306 61 317 242 224 166 408 311 1698
2000 138 259 1020 1008 342 60 335 234 208 161 430 316 1672
2001 145 242 1047 1085 365 58 345 214 206 162 436 320 1731
2002 141 220 1028 1081 369 53 341 195 195 156 411 319 1745
2003 137 207 974 1047 369 46 321 183 179 145 390 302 1696
2004 131 196 928 1035 369 43 298 173 172 138 381 285 1738
2005 118 186 922 1030 350 41 299 162 186 134 393 275 1959
2006 114 186 945 1091 327 39 310 156 200 136 427 271 2121
Average 123 234 761 731 256 62 325 204 168 137 369 325 1723

We consider an annual momentum strategy based on the most widely used ranking and holding period (e.g. Griffin et al., 2003). Specifically, the ranking period during which winners and losers are determined is 6 months, excluding the most recent month in order to eliminate problems associated with microstructure issues that have been suggested as a possible explanation of the momentum effect (see Asness, 1995). The holding period is also 6 months. All portfolios are equally weighted and each month we assume that we hold equal proportions of six portfolios, formed during the past 6 months. The winner and loser portfolios consist of the top and bottom 20 per cent of stock returns, respectively. To measure the size effect, we follow the Fama and French (1993) methodology. Each year, we split the sample into two groups based on the median size of the sample at year-end, and we rebalance the two portfolios annually. The first ranking is done using the 1987 December–end market capitalization; hence, our sample of size-sorted portfolio returns starts in 1988. All portfolios are equally weighted.

3. The size premium in European markets

Table 2 reports mean monthly returns for the 13 sample markets by year, for the Small stock portfolio. Statistical significance at the 5 per cent level is denoted with an asterisk. The table also reports the average mean monthly return for each market and the average market value of the small companies in each country for the whole sample period. The average value of small companies ranges from €18.05 m in Denmark to €63.96 m in Spain. The rather high value of the average small company in Spain is probably due to the low number of available securities for this country, especially during the beginning of the sample period. However, the difference between the average small company in Spain and other countries is not high enough to distort our results. For the other sample countries, average values are rather close.

Table 2.
Mean monthly percentage returns for small stock portfolio by year
Year/Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
1988 2.11* 4.21* 6.38* 2.51* 1.67 2.12 3.59* 3.73* 3.51* 3.21* 2.30* 1.32
1989 5.99* 2.66* 2.96* 3.39* 5.55 3.95* 3.21* 4.06* 3.32* 0.96 1.55 0.27 0.55
1990 1.98 1.70 –1.69 0.38 6.36 –2.83* –0.82 –0.88 1.23 –2.15 –2.93* –1.13 –3.37*
1991 –1.13 0.43 0.72 0.01 1.52 0.19 –0.57 0.30 –2.08 0.43 –2.37 –0.44 0.76
1992 –2.28 –0.88 –0.45 –0.48 –0.24 –0.16 –1.48 –1.58 –2.76 –2.71 –0.22 –1.14 0.10
1993 2.74 1.30* 3.11* 2.44* 6.86* 4.72* 1.54 2.33* 10.67* 3.44* 10.37* 4.79* 4.97*
1994 0.38 2.62 0.70 –0.01 0.66 0.21 1.43 2.21 1.05 3.91* 1.15 –0.14 0.67
1995 –1.42 1.25* –0.64 –0.52 1.55 1.06 –0.50 1.05 2.20* 0.46 0.80 0.18 0.85
1996 0.31 2.94* 1.98* 0.03 –0.21 3.36* 0.61 2.17* 3.93* 3.37* 4.18* 2.77 1.38*
1997 0.35 3.12 1.72* 1.99 1.93 3.55* 4.66* 2.13 1.75 5.35* 2.16 3.33* 0.67
1998 0.72 –1.33* 2.59 1.84 6.58* –0.44 4.99 1.13 –2.54 6.03 –0.48 2.69 –0.49
1999 0.17 0.64 2.09* 1.71 28.24* 4.33* 2.17* 1.64 3.87* –0.16 4.85* 2.77* 6.00*
2000 0.06 1.35 3.69* 0.24 –8.73 2.10 3.57* –0.19 0.47 –0.21 0.64 1.55 0.75
2001 0.29 –0.30 1.14 –2.39 0.40 –1.20 –1.69 –0.69 –1.09 1.67 –0.22 –1.15 –0.82
2002 1.03 0.19 0.17 –3.27 –3.47 –0.26 –1.22 –2.17 –3.26 0.08 –1.49 –1.88 –1.68
2003 4.91* 2.50* 3.61* 4.45* 3.78 5.25* 1.57 3.70 8.27* 2.47* 4.70* 2.58* 4.21*
2004 5.91* 2.49* 3.79* 1.15 –3.00 1.48 0.68 2.25* 3.45 2.29* 3.46 1.49 1.10
2005 3.41 4.66* 4.17* 3.60* 1.73 2.02 2.28 2.03* 3.69* 3.67* 3.80* 2.25* 0.27
2006 1.60 3.31* 3.74* 1.49 3.27* 1.91 1.41 2.06* 1.91* 3.81* 1.48 2.06* 0.82
Average 1.43* 1.73* 2.09* 0.98* 2.93 1.63* 1.26* 1.32* 1.99* 1.91* 1.82* 1.22* 0.95
Average market value 21.90 18.05 28.77 26.94 19.04 35.02 57.41 45.34 29.52 63.96 20.08 57.79 18.27
  • This table presents mean monthly returns (times 100) for the small MV stock portfolio, by year, for 13 European markets. The row labelled ‘Average’ reports the average mean monthly return for the whole sample period. The bottom row reports the average market value of the small stock portfolio during our sample period. To make the figures comparable, all market values are reported in millions of euros. For the non-euro countries, we converted the average market values using the end of 2005 exchange rate. *denotes significance at the 5 per cent level.

The results in Table 2 suggest that average monthly returns for the Small stock portfolio are positive for all markets and range from 0.95 per cent for the UK to 2.93 per cent for Greece. In addition, mean monthly returns are statistically significant for all markets except for Greece and the UK at the 5 per cent level. The year-by-year analysis indicates that for many markets this might be the result of a few years where small firm returns are large and statistically significant. For instance, for Austria, out of the 19 sample years, there are only 4 years with positive and statistically significant (at the 5 per cent) small stock portfolio returns (1988, 1989, 2003 and 2004). Table 3 reports results for the Big stock portfolio for the 13 sample markets. Average monthly returns for the whole sample period are statistically significant for all markets (except Greece) and positive, ranging from 0.87 per cent (UK) to 1.94 per cent (Greece). Again, the year-by-year analysis indicates that this might be the result of few years where large firm returns are large and statistically significant. For instance, for the Big stock portfolio in the UK, out of the 19 sample years there are only 4 years with statistically significant returns at the 5 per cent.

Table 3.
Mean monthly returns for big stock portfolio by year
Year/Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
1988 2.05* 4.21* 3.51 2.46 2.59 1.92 3.27* 1.82 1.79 3.37* 1.95* 1.18
1989 5.89* 2.81* 2.56* 3.59* 5.29 2.06 2.20 1.85* 3.44 1.36 2.33* 1.01 1.14
1990 0.82 –0.77 –2.23 0.54 7.51 –3.33* –1.46 –0.52 –1.07 –2.06 –3.10 –1.87 –2.14
1991 –0.64 0.63 0.93 –0.11 –0.35 0.49 –0.09 0.05 –1.58 0.96 –1.10 0.01 1.24
1992 –1.55 –2.24* 0.03 –1.19 –0.73 –0.82 –0.95 –0.45 –1.87 –1.25 –1.15 –0.24 1.05
1993 2.44 2.84* 3.31* 2.72* 4.26* 4.08* 2.53 3.37* 5.97* 3.84* 5.42* 4.18* 2.80*
1994 –0.40 0.71 –0.41 0.32 –0.60 0.34 0.62 0.35 0.42 –0.38 1.15 –0.21 –0.14
1995 –1.27 0.19 –0.40 –0.16 0.43 1.70* –0.98 0.80 1.30 0.64 0.86 0.75 1.26
1996 0.41 2.42* 2.22* 0.44 –1.10 2.06* 0.58 2.76* 2.42* 2.60* 3.13* 1.03 1.20
1997 1.35 1.42 1.78 1.75 3.76 3.67* 3.71* 2.15 2.46* 3.21* 1.98* 2.90* 0.77
1998 1.25 –1.18 1.73 2.51 6.93 0.73 4.00 0.67 –2.41 3.07 –0.20 1.48 –0.31
1999 0.63 1.13 2.59* 1.36 14.97* 1.31 1.75 1.60 4.02* –0.61 3.43* 2.18* 3.28*
2000 0.17 1.48* 1.24 –0.40 –7.40* 1.62 1.94 0.02 0.95 0.59 –0.53 1.49 0.45
2001 –0.95 –0.84 –0.73 –1.99 –1.17 0.43 –1.71 –0.99 –1.20 0.71 –0.34 –2.37 –0.86
2002 0.08 –0.37 –0.88 –2.86 –3.69 –1.67 –1.18 –2.34 –2.94 –0.45 –2.21 –2.06 –2.25
2003 2.21* 3.32* 2.36 3.89* 2.96 3.45* 1.81 2.74 4.29* 2.60* 3.30* 2.65 3.24*
2004 2.63* 3.00* 1.97* 1.72 –1.39 2.12* 1.57* 1.62* 3.03 2.17* 1.98 1.28 1.51
2005 2.39* 4.09* 2.26* 3.28* 2.27 2.59* 1.78 2.50* 4.21* 2.45* 3.43* 2.02* 1.53*
2006 1.43 2.44* 1.75* 1.33 2.90* 2.52* 2.07* 2.04* 2.17* 2.82* 2.34 2.39* 1.59
Average 1.00* 1.33* 1.24* 1.01* 1.94 1.36* 1.06* 1.13* 1.34* 1.27* 1.27* 0.98* 0.87*
Average market value 819.28 618.39 1812.34 1651.62 322.46 1159.77 2098.91 4069.96 634.87 2004.94 999.77 2651.86 1675.98
  • This table presents mean monthly returns (times 100) for big MV stock portfolio, by year, for 13 European markets. The row labelled ‘Average’ reports the average mean monthly return for the whole sample period. The bottom row reports the average market value of the big stock portfolio during our sample period. To make the figures comparable, all market values are reported in millions of euros. For the non-euro countries, we converted the average market values using the end of 2005 exchange rate. *denotes significance at the 5 per cent level.

The returns for the SMB portfolio are presented in Table 4 and indicate that: (i) SMB average mean monthly returns range from –0.03 per cent for Germany to 1 per cent for Greece; (ii) for only 2 out of 13 markets (France and Spain) are SMB returns statistically significant at the 5 per cent level; and (iii) SMB returns are statistically significant for few years throughout the sample period: for example, for Spain SMB returns are statistically significant in 3 out of 19 years. These results are consistent with the results of previous studies for the US and UK markets (e.g. Dimson and Marsh, 1999; Wang, 2000; Jegadeesh and Titman, 2001) and with the results of Liew and Vassalou (2000) who, with a sample period that ends in 1995, also report statistically insignificant SMB returns for a number of European markets. Overall, the results indicate that although small-firm portfolios in Europe have slightly higher returns on average than large-firm portfolios, this difference is not statistically significant and is confined to very few years per market. In other words, an investor aiming to exploit the small firm premium should be ready to accept sizeable losses for a considerable amount of time.

Table 4.
Mean monthly returns for SMB zero-investment portfolio by year
Year/Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
1988 0.06 0.00 2.87* 0.05 –0.93 0.20 0.33 1.90 1.73* –0.16 0.35 0.14
1989 0.11 –0.15 0.40 –0.20 0.26 1.89 1.01 2.20* –0.12 –0.39 –0.78 –0.73 –0.58
1990 1.16 2.47 0.55 –0.17 –1.16 0.50 0.64* –0.36 2.30* –0.09 0.17 0.74 –1.23
1991 –0.48 –0.20 –0.22 0.13 1.87 –0.30 –0.48 0.25 –0.51 –0.53 –1.27 –0.45 –0.49
1992 –0.73 1.36 –0.48 0.71 0.49 0.66 –0.52 –1.13* –0.89 –1.45 0.93 –0.90* –0.94
1993 0.30 –1.54* –0.20 –0.29 2.60** 0.63 –1.00 –1.03 4.70 –0.40 4.96* 0.61 2.17*
1994 0.78 1.91* 1.10 –0.33 1.26 –0.13 0.82 1.86* 0.63 4.29* –0.01 0.08 0.81
1995 –0.15 1.06* –0.24 –0.36* 1.11 –0.64 0.48 0.25 0.90 –0.18 –0.06 –0.58 –0.42
1996 –0.09 0.53 –0.24 –0.40 0.89 1.30 0.04 –0.59 1.51* 0.77 1.05 1.75 0.18
1997 –0.99 1.70 –0.06 0.25 –1.83 –0.12 0.95 –0.02 –0.71 2.14 0.17 0.44 –0.10
1998 –0.53 –0.16 0.87 –0.67 –0.36 –1.18 0.99 0.46 –0.12 2.96 –0.29 1.22 –0.18
1999 –0.46 –0.49 –0.50 0.35 13.28* 3.02* 0.42 0.04 –0.14 0.44 1.41 0.59 2.73*
2000 –0.11 –0.13 2.45* 0.63 –1.33 0.48 1.63 –0.22 –0.47 –0.80 1.17 0.06 0.30
2001 1.23 0.55 1.87* –0.40 1.58 –1.63 0.02 0.30 0.11 0.96 0.12 1.22 0.04
2002 0.95 0.56 1.05 –0.42 0.22 1.41 –0.03 0.17 –0.32 0.53 0.71 0.18 0.57
2003 2.70* –0.82 1.25 0.56 0.81 1.80 –0.24 0.96 3.98 –0.12 1.40 –0.07 0.98
2004 3.28 –0.50 1.82* –0.58 –1.61* –0.64 –0.89* 0.63 0.42 0.11 1.47 0.22 –0.41
2005 1.02 0.57 1.90* 0.32 –0.53 –0.56 0.50 –0.47 –0.52 1.23* 0.37 0.23 –1.26*
2006 0.17 0.86 1.99* 0.16 0.38 –0.61 –0.67** 0.02 –0.26 0.99 –0.86 –0.33 –0.77
Average 0.43 0.40 0.85* –0.03 1.00 0.26 0.20 0.19 0.65 0.64* 0.55 0.24 0.08
  • This table presents mean monthly returns (times 100) for Small Minus Big (SMB) portfolio, by year, for 13 European markets. The last row reports the average mean monthly return for the whole sample period. *denotes significance at the 5 per cent level.

4. The size premium and the zero-intercept hypothesis

The results so far seem to suggest that although small-firm returns are positive in all markets they may not be consistently higher than big-firm returns and the ‘size anomaly’ might not be exploitable in practice by a zero-investment strategy at all times. As Brennan and Xia (2001) among others argue, an asset pricing anomaly is a statistically significant difference between the realized average returns of securities associated with certain characteristics of the securities and the returns predicted by a particular asset pricing model. Consider, for example, the Sharpe–Linter CAPM, which posits that expected excess returns must be linearly related to market betas:

image()

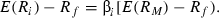In equation (1), Ri is the return on asset i, Rf is the risk-free rate and RM is the return on the market portfolio (M ). Fama and French (1996) argue that for the CAPM to be violated, the hypothesis of a zero intercept must be statistically rejected in a regression of excess returns on the excess returns of the market. For instance, Fama and French (1998) run similar regressions for global value and growth portfolios and find statistically significant intercepts, which indicate that the international CAPM cannot explain the returns on the global style portfolios. To investigate this issue further, we estimate equation (1) for the three portfolios (Small, Big, SMB) and for all countries as follows:

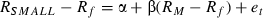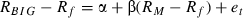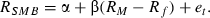image()
image()
image()

In equations (2), (3) and (4) RBIG is the return on the portfolio of big capitalization firms, RSMALL is the return on the portfolio of small capitalization firms, and RSMB is the return on the arbitrage portfolio. As a proxy for the risk-free rate, the 1 month Treasury bill rate is used where available. For Austria, Denmark, Ireland, the Netherlands and Norway, for which a Treasury bill rate is not available to us, we use the 1 month Interbank rate instead. As a proxy for the market portfolio the DataStream Total Market Index is used for Greece, Italy, Norway, Switzerland and the UK, while for the other markets we use a total return index of a representative market index. The OLS alpha coefficient estimates and their corresponding t-statistics for all markets are reported in Panel A of Table 5. The zero-intercept hypothesis is rejected for the small-firm portfolio for Denmark, France, Ireland, and Spain at the 5 per cent level. For the large-firm portfolio, the hypothesis is accepted for all markets at the 5 per cent level. For the SMB portfolio, the zero-intercept hypothesis is rejected for Austria, Denmark, France, Norway, Spain and Switzerland at the 5 per cent level.

Table 5.
The market value portfolios and the zero-intercept hypothesis
Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
Panel A: Ordinary least-squares estimation
A1: RSMALL–Rf = α + β(RM – Rf) + et
 α 0.0055 0.0053* 0.0118* 0.0028 0.0113 0.0069* 0.0036 0.0047 0.0077 0.0081* 0.0057 0.0041 0.008
 t(α) 1.95 2.00 4.86 1.34 1.52 2.18 1.29 1.30 1.68 2.72 1.32 1.05 0.15
A2: RBIG–Rf = α + β(RM – Rf) + et
 α –0.0004 0.0003 0.0031 0.0032 –0.0004 0.0014 0.0010 0.0014 –0.0013 0.0015 –0.0008 –0.0009 –0.0013
 t(α) –0.26 0.16 1.86 0.89 –0.06 0.84 0.73 0.99 –0.48 1.07 –0.45 –0.59 –0.70
A3: RSMB = α + β(RM – Rf) + et
 α 0.0059* 0.0049* 0.0086* –0.0004 0.0117 0.0055 0.0027 0.0033 0.0090* 0.0066* 0.0066 0.0050* 0.0021
 t(α) 2.07 2.63 2.99 –0.40 1.54 1.91 1.36 1.86 3.09 2.70 1.74 3.07 1.32
Panel B: Rolling least-squares estimation
B1: RSMALL–Rf = α + β(RM – Rf) + et
 α 0.0039 0.0072 0.0128 0.0048 0.0148 0.0055 0.0039 0.0065 0.0071 0.0082 0.0065 0.0053 0.0011
 t(α) 0.37 0.77 1.31 0.57 0.66 0.40 0.42 0.62 0.48 0.68 0.36 0.54 0.10
B2: RBIG–Rf = α + β(RM – Rf) + et
 α 0.0008 0.0021 0.0044 0.0049 0.0005 0.0012 0.0009 0.0016 –0.0002 0.0018 0.0005 0.0013 –0.0005
 t(α) 0.15 0.29 0.61 0.62 0.04 0.17 0.15 0.01 –0.03 0.37 0.07 0.21 –0.07
B3: RSMB = α + β(RM – Rf) + et
 α 0.0031 0.0052 0.0084 –0.0001 0.0143 0.0042 0.0030 0.0049 0.0073 0.0064 0.0060 0.0040 0.0016
 t(α) 0.32 0.67 1.34 –0.03 0.96 0.33 0.48 0.64 0.63 0.61 0.41 0.58 0.27
  • This table presents OLS regressions (Panel A) and RLS regressions (Panel B) for 13 European markets. The sample period starts in January 1988 for all markets except Greece, where the sample period starts in January 1989 due to data availability and ends in December 2006 for all markets. The RLS estimation results in a time-series of coefficients and the table reports the mean coefficient and the t-statistic (the ratio of the mean coefficient to the mean standard error). *denotes significance at the 5 per cent level. The t-tests have been computed using the Newey–West autocorrelation consistent standard errors.

The estimation of equation (1) with OLS assumes a constant slope coefficient (i.e. systematic risk) throughout the estimation period. This assumption is unlikely to hold in practice for long periods of time. Therefore, we also use an RLS methodology with a window length of 12 and 24 months to estimate (2), (3) and (4) instead of just OLS as in many previous studies. This allows the estimation of coefficients over successive rolling periods of a fixed length and captures more adequately time-variation in slope coefficients and intercepts. The RLS procedure generates a coefficient history for both the slope and the intercept and in Panel B of Table 5 we present the average intercept and a t-test for the null that the average coefficient is equal to zero, for all markets and portfolios. We find that the intercept is statistically insignificant for all portfolios and all markets. In other words, when the assumption of constant systematic risk over the estimation period is addressed, the zero-intercept hypothesis is accepted for all sample markets. Although this implies that the intercept is not significant, it could be the case that the estimates produced are not stationary. However, this is not the case. We test for stationarity of the estimated rolling intercepts using the Augmented Dickey–Fuller test (available upon request) and find that the null hypothesis of a unit root is rejected for most markets at the 5 per cent level and for all markets at the 10 per cent level. Overall, the results of this section indicate that the small-firm premium in Europe is largely non-existent and might be explained by the static CAPM (in most markets) or a time-varying CAPM (in all markets).

5. The January effect

Previous studies link the ‘size-effect’ with a January seasonal in stock returns (Keim, 1983; Ritter and Chopra, 1989; among others). To investigate this issue further, we re-estimate average mean returns (as in Tables 2–4) for (i) January only, and (ii) February through December, for all portfolios and all markets. We present the results in Table 6: Panel A for the small-firm portfolio, Panel B for the big-firm portfolio and Panel C for the SMB portfolio. For example, the average mean January return for the small-firm portfolio in France (Panel A) is 6.23 per cent with a t-statistic of 4.31 and the February–December return is 1.72 per cent with a t-statistic of 5.72. Note that although small firm returns are statistically significant for both January and the February–December period, they are much higher in January: during January they range between 2.72 per cent in Switzerland to 10.73 per cent in Sweden, whereas for the February–December period they range between 0.63 in the UK to 2.77 in Greece. Although January returns seem economically larger compared to the rest of the year average, a pairwise t-test for the null hypothesis that the mean January return is equal to the mean February–December return indicates that equality cannot be rejected for any of the sample markets (results available upon request). Therefore, despite the apparent economic significance of the January returns, statistically they are indistinguishable from the returns of the rest of the year.

Table 6.
Mean monthly returns by month for size portfolios
Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
Panel A: Small portfolio
 January 3.10 5.55* 6.23* 3.43* 4.71 7.21* 3.58* 4.52* 8.53* 6.88* 10.73* 2.72* 4.54*
 t-test 1.56 4.25 4.31 3.44 1.57 4.59 2.17 3.83 6.15 3.67 3.71 2.43 3.13
 February–December 1.28* 1.38* 1.72* 0.75 2.77* 1.12* 1.05* 1.03* 1.40* 1.45* 1.01* 1.08* 0.63*
 t-test 3.87 6.28 5.72 2.48 3.05 3.23 2.61 3.23 3.08 3.50 2.05 3.69 1.98
Panel B: Big portfolio
 January 3.16* 4.86* 3.04* 2.89* 3.28 4.63* 3.47* 3.00* 5.23* 3.93* 4.64* 2.49* 3.36*
 t-test 2.38 5.15 2.73 2.77 1.33 4.71 2.24 3.56 3.68 3.93 4.44 2.72 3.36
 February–December 0.80* 1.01* 1.08* 0.84* 1.81* 1.07* 0.84 0.96* 0.98* 1.02* 0.96* 0.84* 0.64
 t-test 2.56 3.84 3.43 2.93 2.42 3.02 1.94 3.10 2.28 2.95 2.16 2.69 1.95
Panel C: SMB portfolio
 January –0.06 0.68 3.19* 0.55 1.43 2.58* 0.11 1.52* 3.30* 2.96* 6.09* 0.23 1.17
 t-test –0.04 0.97 3.40 0.98 1.00 2.22 0.17 2.18 4.00 2.42 2.32 0.50 1.21
 February–December 0.48 0.37 0.64* –0.09 0.96* 0.05 0.21 0.07 0.41 0.43 0.05 0.24 –0.02
 t-test 1.94 1.80 3.48 –0.79 2.13 0.16 1.18 0.37 1.28 1.72 0.18 1.27 –0.11
  • This table presents mean January and February–December monthly returns for the small, big, and SMB stock portfolio, for 13 European markets. The sample period starts in January 1988 for all markets except Greece, where the sample period starts in January 1989 due to data availability and ends in December 2006 for all markets. *denotes significance at the 5 per cent level.

Similar results are reported for the big-firm portfolio January returns (Panel B). With the exception of January returns in Greece and February–December returns for France, all other periods and markets experience statistically significant returns. As with small firms, there is an economically significant January seasonal: during January large-firm returns range between 2.49 per cent in Switzerland to 5.23 per cent in Norway while for the February–December period they range between 0.64 in the UK to 1.81 per cent in Greece. This implies that the January effect in Europe is not confined to small firms. More evidence on this is provided in Panel C, for the SMB returns. If the January was confined to small stocks only, we should find sizeable January returns for most of the SMB portfolios. However, this is not the case as SMB January returns are statistically significant for only 6 out of 13 markets. The findings suggest that returns are higher in January (a finding extensively documented in the literature) but this effect is not confined to small stocks.

6. Momentum returns in European markets

Tables 7–9, report year-by-year average monthly returns for the Winner, Loser and WML portfolios, respectively, for all sample markets. Returns for the Winner portfolio (Table 7) are all positive and statistically significant and range from 1.32 per cent in Germany to 3.16 per cent in Greece. Note also that average monthly Winner portfolio returns are quite high (above 1.3 per cent) for all markets. For the Loser portfolio (Table 8) average returns are also positive but they are statistically significant in only 4 markets and much lower than Winner portfolio returns. As a result, average WML returns (Table 9) range between 0.37 per cent in Spain and 1.37 per cent in Greece, and are statistically significant for 8 markets at the 5 per cent level. These results are broadly consistent with the results of Liew and Vassalou (2000), who find positive and statistically significant momentum returns for France, Germany, the Netherlands, Switzerland and the UK.

Table 7.
Mean monthly returns for winner portfolio by year
Year/Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
1988 2.36* 4.11* 3.86 2.88* 2.61 1.72 3.49* 5.63* 2.77 2.59* 2.43* 1.30
1989 7.80* 2.98* 3.54* 3.60* 8.12 2.34* 2.85* 4.27* 3.92* 1.42 2.43* 1.47 1.22
1990 0.81 –0.25 –1.41 0.74 8.41 –2.45* –0.63 –0.77 –0.04 –1.71 –2.80 –1.66 –1.62
1991 0.59 0.82 0.91 –0.16 0.98 0.59 –0.72 0.64 –1.73 –0.86 –0.75 –0.42 1.90
1992 –1.25 –0.87 0.53 –0.56 1.11 –0.23 –0.96 –0.78 –2.60 –0.67 –0.85 –0.03 1.42
1993 2.14 2.24 3.55* 2.50* 7.95* 3.12* 2.18 3.05* 8.00* 3.37* 8.91* 4.69* 4.50*
1994 –0.16 2.24 0.51 0.02 –0.56 0.33 0.43 2.44 0.93 2.06 1.40 –0.34 0.79
1995 –0.80 1.24 0.06 0.62 1.01 2.42* –0.26 2.31* 3.74* 0.82 1.36 1.44* 1.93*
1996 0.55 4.10* 2.57* 1.30* 0.01 2.08 1.55 3.69* 3.11* 3.80* 4.00* 2.35* 2.01*
1997 1.43 2.31 2.61* 2.20 4.26 4.52* 3.71* 2.97 4.04* 4.61* 1.85 3.74* 1.16
1998 1.04 –0.68 2.18 3.18* 7.48* 0.62 4.71 1.98 –2.09 5.69 0.75 2.80 0.48
1999 0.04 0.59 3.83* 1.59 25.41* 2.58 4.89* 2.55 4.25* 0.23 5.11* 4.11* 6.62*
2000 –0.80 1.93 3.00 –1.62 –7.93 1.27 4.08 –1.55 1.14 0.34 –2.84 2.46 –0.36
2001 –0.50 –0.59 1.08 –1.07 –0.52 1.14 –0.98 –0.36 –0.10 1.24 0.63 –1.63 –0.36
2002 –0.51 –0.07 –0.14 –2.69 –3.35 –0.23 –0.87 –1.69 –1.97 0.54 –1.15 –1.38 –0.99
2003 7.13* 4.09* 3.89* 4.81* 1.67 4.59* 1.27 1.85 7.02* 2.49* 4.78* 3.10* 4.18*
2004 8.64* 2.92* 4.04* 2.40 –1.81 2.41 1.74 2.82* 4.54 2.25* 3.10 1.46 1.75
2005 4.48* 5.59* 5.05* 3.91* 2.22 4.66* 2.98* 3.74* 6.18* 4.22* 5.00* 2.92* 1.24
2006 2.03 2.55 3.87 1.55 2.62 1.35 2.40 2.36 1.51 3.58 0.98 1.83 1.46
Average 1.84* 1.84* 2.26* 1.32* 3.16* 1.78* 1.57* 1.72* 2.41* 1.87* 1.83* 1.54* 1.51*
  • This table presents mean monthly returns (times 100) for the Winner stock portfolio, by year, for 13 European markets. The last row reports the average mean monthly returns for the whole sample period. *denotes significance at the 5 per cent level.
Table 8.
Mean monthly returns for loser stock portfolio by year
Year/Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
1988 2.59* 4.18* 5.77 3.07* –0.02 2.25 2.96* 3.79 3.10 3.63* 2.50* 0.95
1989 4.17* 1.22* 1.83* 3.30* 6.35* 3.58 2.40 3.80* 2.35 0.49 1.44 0.36 –0.03
1990 0.94 2.61 –2.45 0.48 5.11* –4.16* –2.02 –1.53 –0.39 –3.44 –3.19 –1.32 –4.87*
1991 –1.29 1.14* 1.13 0.00 –1.55 –0.46 –0.04 –1.54 –3.14 2.25 –3.65 –0.29 –0.09
1992 –2.99 –3.31* –1.14 –1.58 –1.20 –0.66 –1.71 –2.70* –1.89 –4.09 0.16 –1.97 0.18
1993 2.68 3.44* 3.76* 2.83* 5.04* 6.36 1.53 3.37 13.07* 3.98* 10.36* 5.06* 4.40*
1994 –0.24 2.03 0.64 0.19 0.06 0.68 1.48 1.74 1.05 1.45 0.80 0.32 0.04
1995 –3.13* 0.44 –1.18* –1.12 1.23 0.21 –1.01 –0.14 1.16 1.22 0.26 0.03 0.26
1996 0.18 2.51* 2.35* –0.61 –1.24 3.77* 0.07 1.27* 3.82* 4.83 4.77* 3.37 0.63
1997 0.74 3.58 1.87 2.34 1.54 2.31 4.16* 1.80 0.89 4.16* 1.43 4.11* –0.13
1998 0.48 –2.46* 2.73 1.56 5.84 –1.14 4.61 0.53 –4.01 6.33 –1.88 2.94 –1.45
1999 0.79 1.64 1.95 0.44 19.45* 4.62* 0.83 2.02 6.09* –0.66 6.41* 2.15* 5.33*
2000 –0.34 1.46 2.94 –1.33 –7.93* 1.34 1.64 –1.47 –0.09 –0.40 1.37 –0.17 0.21
2001 –1.25 –2.59 –0.91 –4.21 0.09 –2.84 –3.19 –2.70 –3.66 0.81 –1.76 –3.83 –3.24
2002 0.51 –1.12 –0.27 –5.25 –4.02 –1.31 –2.31 –4.23 –7.18* –1.01 –2.26 –3.44 –3.84
2003 3.75* 2.02 4.18* 6.39* 4.87 5.93* 1.60 7.50 10.43* 3.25* 4.42* 3.72 5.05*
2004 3.96 1.63 3.47* 0.94 –4.26 0.83 –0.39 1.01 3.31 2.33* 2.77 0.89 0.80
2005 3.23 4.54* 3.68* 4.61* 1.73 0.89 1.04 0.79 2.76* 2.37* 3.75* 1.81* –0.67
2006 1.74 1.99 3.48 0.88 1.34 0.02 –0.16 1.32 0.90 1.55 0.84 0.85 –0.98
Average 0.85 1.30* 1.74* 0.68 1.79 1.07 0.58 0.71 1.55 1.50* 1.58* 0.90 0.16
  • This table presents mean monthly returns for the Loser stock portfolio, by year, for 13 European markets. The last row reports the average mean monthly returns for the whole sample period. *denotes significance at the 5 per cent level.
Table 9.
Mean monthly returns for WML portfolio by year
Year/Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
1988 –0.23 –0.07 –1.91 –0.19 2.63 –0.53 0.53 1.84 –0.33 –1.03* –0.07 0.35
1989 3.62* 1.76 1.71 0.30 1.76 –1.24 0.46 0.47 1.56 0.94 0.99 1.11* 1.25*
1990 –0.13 –2.87 1.04* 0.26 3.30 1.71 1.39* 0.75 0.36 1.73 0.38 –0.33 3.25*
1991 1.89 –0.32 –0.22 –0.17 2.53 1.04 –0.68 2.17 1.41 –3.11 2.90 –0.13 1.99
1992 1.74 2.44* 1.67* 1.02* 2.31 0.44 0.75 1.92* –0.71 3.42* –1.01 1.94* 1.24
1993 –0.54 –1.20 –0.21 –0.33 2.91 –3.25 0.65 –0.32 –5.07 –0.61 –1.44 –0.37 0.10
1994 0.08 0.21 –0.13 –0.17 –0.61 –0.35 –1.05 0.70 –0.12 0.61 0.60 –0.66 0.75
1995 2.33* 0.79 1.24* 1.74* –0.22 2.21 0.75 2.46* 2.58 –0.41 1.10 1.41* 1.67*
1996 0.37 1.59 0.22 1.90* 1.25 –1.69 1.49 2.42* –0.71 –1.03 –0.77 –1.03 1.38*
1997 0.68 –1.27 0.74 –0.14 2.73* 2.21 –0.46 1.17 3.15 0.45 0.42 –0.37 1.29*
1998 0.56 1.78* –0.54 1.62 1.64 1.77 0.10 1.44 1.92 –0.64 2.63* –0.14 1.93*
1999 –0.75 –1.06 1.88* 1.15 5.96 –2.03 4.06* 0.54 –1.84 0.90 –1.30 1.97 1.29
2000 –0.46 0.47 0.06 –0.29 0.00 –0.07 2.44 –0.08 1.23 0.74 –4.21* 2.64 –0.57
2001 0.76 2.00 1.99 3.14 –0.61 3.98* 2.21 2.34 3.56 0.43 2.38 2.20 2.89
2002 –1.02 1.05 0.13 2.56 0.67 1.08 1.44 2.54* 5.21* 1.55 1.11 2.06 2.85*
2003 3.38 2.06 –0.29 –1.58 –3.20 –1.35 –0.33 –5.64 –3.42 –0.76 0.36 –0.62 –0.87
2004 4.68 1.29 0.56 1.46 2.45 1.58 2.13* 1.82 1.23 –0.08 0.33 0.57 0.95
2005 1.25 1.05 1.37 –0.70 0.49 3.76* 1.95* 2.95* 3.41* 1.85 1.25 1.12* 1.92*
2006 0.29 0.56 0.39 0.68 1.28 1.33 2.56* 1.04 0.61 2.03 0.13 0.98 2.44*
Average 0.99* 0.54 0.51* 0.65* 1.37* 0.71 0.98* 1.01* 0.86 0.37 0.26 0.64* 1.35*
  • This table presents mean monthly returns for the Winner Minus Loser (WML) stock portfolio, by year, for 13 European markets. The last row reports the average mean monthly returns for the whole sample period. *denotes significance at the 5 per cent level.

An interesting pattern that emerges from the results is that for all portfolios, returns are statistically significant for very few years throughout the sample period. Take the Winner portfolio for instance: on average, returns are statistically significant for all markets; however, mean monthly returns are significant for few of the sample years: Winner portfolio returns are statistically significant for 5 out of 19 years in the UK, for 8 out of 19 years in France, for 7 out of 19 years in Germany, etc. When we look at the WML portfolio, the pattern is even more striking. With the exception of the UK where WML returns are statistically significant for 9 out 19 years, all other markets have 5 or fewer years of significant momentum return: in France WML returns are significant in 4 out of 19 years, in Germany in 3 out of 19 years, in Greece in 1 out of 19 years, etc. Similarly to the results with the size premium, the findings suggest that the momentum profits documented in earlier studies are driven by very few years of significant momentum returns.

We also test for a January seasonal in Winner, Loser and WML returns and re-estimate average monthly returns, for (i) January and (ii) February to December The results are reported in Panels A, B and C of Table 10 for the Winner, Loser and WML portfolio, respectively. It becomes apparent from the results in Table 10 that during the month of January, both Winner and Loser portfolio average monthly returns are much higher than the rest of the year for all markets in the sample: for the Winner portfolio mean January returns range between 3.90 per cent in Germany to 9.47 per cent in Norway while for the rest of the year they range between 1.08 per cent in Germany to 2.95 per cent in Greece; for the Loser portfolio mean January returns range between 1.46 per cent in Austria to 12 per cent in Sweden, while for the rest of the year they range between –0.22 per cent in the UK to 1.56 per cent in Greece. WML returns in January are statistically significant and positive for only 2 markets while from February to December, average momentum returns are positive and significant for 7 markets. In other words, both Winner and Loser portfolio returns are economically significant in January compared to the rest of the year and, therefore, January returns for the WML portfolio appear lower. However, note that a pairwise t-test indicates that equality between January and February–December mean returns cannot be statistically rejected for any of the sample markets (results available upon request).

Table 10.
Mean monthly returns by month for momentum portfolios
Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
Panel A: Winner portfolio
 January 6.73* 5.58* 5.92* 3.90* 5.54* 7.25* 4.55* 5.38* 9.47* 6.09* 7.86* 4.42* 5.35*
 t-test 2.46 4.18 3.85 3.25 2.03 5.50 3.12 4.15 5.30 4.61 4.04 3.56 4.34
 February–December 1.38* 1.49* 1.92* 1.08* 2.95* 1.27* 1.29* 1.38* 1.76* 1.47* 1.27* 1.27* 1.15*
 t-test 3.27 5.70 5.52 3.40 3.17 3.38 3.00 3.99 3.52 3.75 2.45 3.67 3.19
Panel B: Loser portfolio
 January 1.46 7.51* 7.60* 4.01* 4.38 6.59* 2.81 4.30* 9.39* 7.45* 12.00* 1.99 4.25*
 t-test 0.75 5.44 4.22 2.49 1.40 3.53 1.46 2.79 5.47 3.26 3.72 1.48 2.60
 February–December 0.79* 0.72* 1.20* 0.37 1.56 0.56 0.38 0.38 0.83 0.95 0.61 0.80 –0.22
 t-test 2.10 2.06 2.73 0.78 1.89 1.17 0.74 0.74 1.23 1.70 0.88 1.77 –0.52
Panel C: WML portfolio
 January 5.27* –1.93 –1.69 –0.11 1.16 0.66 1.74 1.08 0.08 –1.36 –4.14 2.43* 1.10
 t-test 4.21 –1.80 –1.35 –0.07 0.66 0.36 1.68 0.97 0.06 –0.91 –1.69 2.06 1.36
 February–December 0.59 0.77* 0.72* 0.72* 1.39* 0.72 0.91* 1.00* 0.93 0.53 0.67 0.47 1.37*
 t-test 1.63 2.54 2.27 2.36 2.46 1.62 3.07 2.52 1.92 1.28 1.52 1.49 6.00
  • This table presents mean January and February–December monthly returns for the Winner, Loser, and WML stock portfolio, for 13 European markets. The sample period starts in January 1988 for all markets except Greece, where the sample period starts in January 1989 due to data availability and ends in December 2006 for all markets. *denotes significance at the 5 per cent level.

7. Momentum returns and the zero-intercept hypothesis

In this section the zero-intercept hypothesis is examined by regressing Winner, Loser and WML portfolio returns on the excess returns of a market portfolio for each country, with both the OLS and the RLS method, as in equations (2), (3) and (4). The results are reported in Table 11 (Panel A for the OLS regressions and Panel B for the RLS regressions) and indicate that: (i) the static CAPM (OLS method) fails to explain Winner portfolio returns in 7 out of 13 markets at the 5 per cent level; (ii) the static CAPM explains Loser portfolio returns for all markets except France; (iii) the static CAPM fails to explain WML portfolio returns in 7 out of 13 markets (the zero-intercept hypothesis is rejected at the 5 per cent level for Austria, France, Germany, Greece, Italy, the Netherlands and the UK); and (iv) the time-varying version of the CAPM (RLS method) explains adequately Winner, Loser and WML portfolio returns in all markets (the zero-intercept hypothesis cannot be rejected for any market). An augmented Dickey–Fuller test (not reported here but available upon request) suggests that the intercept is stationary for all markets at the 10 per cent level and for most at the 5 per cent level.

Table 11.
The momentum portfolios and the zero-intercept hypothesis
Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
Panel A: Ordinary least-squares estimation
A1: RWINNER–Rf = α + β(RM – Rf) + et
 α 0.0075* 0.0057* 0.0141* 0.0066 0.0111 0.0082* 0.0069* 0.0079* 0.0099* 0.0083 0.0064 0.0055 0.0058
 t(α) 2.03 2.23 3.96 1.79 0.97 2.53 2.04 2.65 3.08 3.47 1.81 1.55 1.65
A2: RLOSER–Rf = α + β(RM – Rf) + et
 α –0.0003 0.0004 0.0076* –0.0009 –0.0004 0.0001 –0.0033 –0.0034 0.0010 0.0035 0.0016 –0.0014 –0.0083
 t(α) –0.09 0.12 2.05 –0.17 –0.05 0.02 –1.26 –0.64 0.13 0.84 0.28 –0.33 –1.53
A3: RWML = α + β(RM – Rf) + et
 α 0.0078* 0.0053 0.0064* 0.0075* 0.0115* 0.0081 0.0102* 0.0113* 0.0089 0.0047 0.0048 0.0070 0.0142*
 t(α) 2.35 1.77 3.33 2.48 2.19 1.84 3.61 2.57 1.91 1.19 1.09 1.81 5.53
Panel B: Rolling least-squares estimation
B1: RWINNER–RF = α + β(RM – Rf) + et
 α 0.0025 0.0065 0.0137 0.0080 0.0134 0.0068 0.0057 0.0081 0.0081 0.0063 0.0041 0.0070 0.0063
 t(α) 0.22 0.77 1.33 0.91 0.68 0.52 0.71 0.80 0.56 0.69 0.27 0.76 0.59
B2: RLOSER–Rf = α + β(RM – Rf) + et
 α –0.0006 0.0039 0.0118 0.0030 0.0016 0.0007 –0.0011 0.0004 0.0053 0.0077 0.0060 0.0021 –0.0063
 t(α) –0.05 0.29 0.81 0.23 0.08 0.04 –0.10 0.03 0.25 0.48 0.27 0.15 –0.49
B3: RWML = α + β(RM – Rf) + et
 α 0.0031 0.0026 0.0020 0.0050 0.0117 0.0061 0.0068 0.0077 0.0028 –0.0015 –0.0020 0.0050 0.0126
 t(α) 0.22 0.21 0.17 0.46 0.61 0.33 0.66 0.54 0.14 –0.10 –0.11 0.41 1.59
  • This table presents OLS regressions (Panel A) and RLS regressions (Panel B) for 13 European markets. The sample period starts in January 1988 for all markets except Greece, where it starts in January 1989 due to data availability and ends in December 2006 for all markets. *denotes significance at the 5 per cent level. The RLS estimation results in a time-series of coefficients. This table reports the mean coefficient and the t-statistic (the ratio of the mean coefficient to the mean standard error). t-tests have been computed using the Newey–West autocorrelation consistent standard errors.

8. Time-varying betas and the business cycle

The results thus far indicate that while the static CAPM performs poorly in explaining size and momentum returns, the varying-beta CAPM performs satisfactorily. This relationship is well documented in the literature. To address the time-variation in betas, researchers usually model betas as a function of lagged macroeconomic variables. For example, Jagannathan and Wang (1996) use a conditional version of the CAPM that includes human capital and allows for time-variation in portfolio betas. Chordia and Shivakumar (2002) use a set of lagged macroeconomic variables to explain momentum returns, while Basu and Stremme (2007) also use lagged macroeconomic variables to explain momentum, book-to-market and industry portfolio returns. Lettau and Ludvigson (2001) find evidence in favour of a conditional consumption CAPM, while Goetzmann et al. (2009) find that lagged expected real GDP does a better job at explaining the cross-section of stock returns than other variables, often used in this type of study. Ang and Chen (2007) model time variation in betas as slowly mean reverting first order autoregressions in a latent variable model. They find that their model captures most of the cross-sectional variation in the stock returns of their sample.

Although these (and several other papers not mentioned here) have used different methodologies to capture time variation in betas, they have one thing in common. They all find that the varying beta CAPM can adequately explain the cross section of stock returns. For example, Basu and Stremme (2007) find that while the static CAPM can explain only 12 per cent of the momentum premium in US stock returns, the varying-beta CAPM can explain up to 75 per cent of the momentum premium. Jagannathan and Wang (1996) find that adding a human capital factor to a varying-beta CAPM can explain 55 per cent of the cross-section variation in average stock returns and firm size does not have any additional explanatory power. The bottom line of these studies (and our findings) is that while the static CAPM cannot explain stock returns, the varying-beta CAPM probably can.

To explore this issue further and link our results with the results of previous papers, we examine if time variation in betas of European stock portfolios is related to the business cycle. Unlike most previous studies, we do not make any assumptions about the beta-generating process; many previous studies impose their own certain structure on conditional betas which is why the results in the literature exhibit significant divergence. While making assumptions about the beta-generating process is necessary in order to derive a conditional CAPM, it increases the risk of model misspecification. For example, Harvey (2001) shows that the estimates of betas obtained from instrumental variables are very sensitive to the choice of instruments used and Ghysels (1998) shows that varying-beta models often under-perform even their static counterparts. Examining which conditional model does the best job is beyond the scope of the present paper. We are interested in whether time variation in betas is related to economic activity or not. To this end, we regress the rolling beta estimates on a set of macroeconomic variables that prior studies have shown to be related to the business cycle. Specifically, we use three variables; the 3 month Treasury bill rate, which Fama (1981) and Fama and Schwert (1977) show is negatively related to stock market returns and is related to future economic activity; the dividend yield on the market, which several studies show is related to the business cycle (e.g. Fama and French, 1988 and Campbell and Shiller, 1988); and the term spread, defined as the difference between the 10 year government bond yield and the 3 month Treasury bill rate, which is closely related to the business cycle (Fama and French, 1988). Therefore, we estimate for each country the following equation:
image()
where RBt is the rolling SMB and WML beta estimates, DYt is the dividend yield, YDt is the 3 month Treasury bill rate and TERMt is the term spread calculated as the difference between the 10 year government bond yield and the 3 month Treasury bill rate.

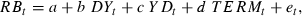The results are reported in Table 12. It is obvious that for most countries there is a relationship between systematic risk and the real economy. For most countries, at least one of the macroeconomic variables is significant at the 5 per cent level. For example, for the WML portfolio beta the Dividend Yield coefficient is statistically significant for Austria, Denmark, France, Germany, Greece, Italy, the Netherlands and the UK, while the Yield coefficient is statistically significant for Austria, Germany, Italy, Norway and Sweden. This seems to indicate that systematic risk varies (to some extent) with the business cycle and therefore this time-variation might be responsible for the failure of the static CAPM to explain realized returns.

Table 12.
Size and momentum returns and the real economy RBt = a + b DYt + c YDt + d TERMt + et
Market Austria Denmark France Germany Greece Ireland Italy Netherlands Norway Spain Sweden Switzerland UK
Panel A: The dependent variable is the SMB rolling beta for each respective country
 a 0.93* 0.00 –0.05 0.28* –0.59 –0.25 –0.32* –0.18 0.35 0.37* 0.27 –0.42* –0.11
(2.43) (0.07) (0.47) (2.83) (–1.84) (–1.64) (–3.22) (–1.61) (1.11) (2.18) (1.39) (–3.06) (–1.60)
 b –44.97* –2.11* 0.96 –1.66 6.74 1.75 2.50 –4.04 –14.57* –3.24 –11.83 7.49 –5.33
(–3.71) (–3.20) (0.26) (–0.56) (1.43) (0.21) (1.03) (–1.49) (–2.20) (–0.44) (–1.74) (0.96) (–1.37)
 c –4.35 –3.82* –3.42* –4.56* 9.32 –0.95 0.64 2.04 –4.93* –2.42 –0.54 0.84 0.39
(–1.47) (–3.82) (–2.46) (–6.06) (1.87) (–0.32) (0.80) (1.02) (–1.70) (–1.25) (–0.40) (0.48) (0.20)
 d –5.47 –1.97 –7.12* –3.82* 18.57* –0.46 2.60 –0.73 –2.38 –24.61* –3.57 1.47 –1.73
(–1.29) (–1.10) (–2.57) (–2.14) (2.25) (–0.15) (0.73) (–0.23) (–0.61) (–5.49) (–1.13) (0.46) (–0.61)
 Adjusted R2 0.234 0.246 0.128 0.326 0.255 0.008 0.029 0.050 0.142 0.417 0.062 0.002 0.058
Panel B: The dependent variable is the WML rolling beta for each respective country
 a 1.77* 0.30 0.73* 0.14 0.69 0.47* 0.49* –0.01 0.58 –0.12 –0.30 0.37 0.40*
(5.08) (1.78) (2.87) (0.52) (1.43) (2.37) (3.82) (–0.06) (1.18) (–0.46) (–1.21) (0.96) (2.12)
 b –48.45* –5.03* –33.11* –37.64* –48.20* –7.17 –16.75* –13.50* 1.15 0.68 –13.22 –37.66 –18.07*
(–4.38) (–3.91) (–2.94) (–4.33) (–4.93) (–0.57) (–3.33) (–2.14) (0.09) (0.05) (–1.74) (–1.82) (–2.29)
 c –11.84* –2.45 3.45 8.23* 4.68 –6.42 –3.46* 6.879 –10.71* –2.18 5.13* 3.22 2.22
(–3.43) (–1.06) (1.45) (3.19) (0.61) (–1.65) (–3.61) (1.97) (–2.16) (–0.42) (2.68) (0.64) (0.65)
 d –14.54* –3.76 5.11 8.33 12.19 –3.23 –2.43 7.95 1.96 16.23 14.32* 0.59 –0.55
(–2.14) (–0.83) (1.48) (1.50) (1.02) (–0.71) (–0.69) (1.38) (0.31) (1.36) (2.81) (0.06) (–0.11)
 Adjusted R2 0.329 0.052 0.240 0.247 0.471 0.170 0.206 0.073 0.291 0.105 0.222 0.039 0.122
  • This table presents OLS regressions of rolling SMB and WML betas (RB) on each country's dividend yield (DY), 3 month T-bill rate (YD) and term spread (TERM), calculated as the difference between the 10 year government bond yield and the 3 month T-bill rate, for Austria, Denmark, France, Germany, Greece, Ireland, Italy, Netherlands, Norway, Spain, Sweden, Switzerland, and the UK. *denotes significance at the 5 per cent level. The t-tests have been computed using the Newey–West autocorrelation consistent standard errors.

9. Conclusion

We study the small-firm and momentum premium for a large sample of European equity markets of varying size, market development and market microstructure. We find that SMB average mean monthly returns range from –0.03 per cent for Germany to 1 per cent for Greece and are statistically significant for only 2 out of 13 markets, while average monthly WML returns range between 0.37 per cent in Spain and 1.37 per cent in Greece and are statistically significant for 8 markets. An interesting finding indicating significant time-variation is that a year-by-year analysis shows that both SMB and WML returns are due to very few sample years where returns are large and significant. Furthermore, SMB returns are consistent with the static CAPM in 7 out of 13 markets and WML returns are consistent with the static CAPM in 6 out of 13 markets. When the methodology accounts for time-variation in systematic risk both SMB and WML returns appear consistent with the CAPM for all sample markets. We also show that systematic risk may be related to the business cycle.

Overall, our findings confirm previous results of a limited small-firm premium but a sizeable momentum premium. Taking advantage of these ‘anomalies’ though is a different matter, as the premia during our sample period are attributed to few years only and, in addition, portfolio returns are consistent with a time-varying beta. Therefore, the static structure imposed on the CAPM might have been the reason behind the rejection of the model by earlier studies and the inconsistency between equity returns and estimated systematic risk.

Footnotes

  • 1 The momentum effect has been examined by several researchers for other time horizons as well and has been found economically significant. For example, among others, Jegadeesh and Titman (1993) and Rouwenhorst (1998) examine 3 to 12 month horizons; Rouwenhorst (1999) examines 6 month horizons. Griffith et al. (2003) examine a 6 month holding period after portfolio formation, which is the methodology we use in the present study, too.
  • 2 For example, a request for all French equities retrieves 4892 equities. For some of these equities, DataStream reports prices from listings on different exchanges; for example, for the company Alti, DataStream reports prices from the Paris and the Frankfurt stock exchanges.
  • 3 DataStream often maintains equities in its database and reports a price for them long after they have been delisted. The reported price is always the last closing price before the delisting, resulting in zero returns after that.
  • 4 We examine such cases if the return for one month exceeds 200 per cent (with a subsequent large negative return in the following month). Where possible the prices for these cases have been cross-referenced with other databases.
  • 5 This problem is inherent to all studies which use the DataStream stock market database.
  • 6 Average monthly returns are insignificant for Greece at the 5 per cent level even though it has the highest average small stock portfolio monthly return in our sample. This is because these returns exhibit the highest variance among the respective sample countries.
  • 7 By statistically significant we mean a return that is statistically different from zero. The statistical significance of the returns is evaluated with the t-statistic: t = (mean AR)/(σ/√N), where mean AR is the mean return, σ is the standard deviation, and N is population.
  • 8 For example, the average monthly SMB return for Austria is 0.43 per cent. However, a long position on small firms and a short position on large firms in 1995 was generating losses until 2001.
  • 9 Specifically, we use the ATX index for Austria, the Copenhagen KFX for Denmark, the CAC 40 for France, the DAX 30 for Germany, the ISEQ for Ireland, the AEX for the Netherlands, the Madrid Genaral for Spain and the Affarsvarlden for Sweden. Note that there could be an issue in using portfolios based on large capitalization stocks as a benchmark for work involving small stocks. However, this issue may arise for only a few of the indices used. For instance, for many markets we use the DataStream Total Market Index as a proxy for the market portfolio (i.e. a general index). As regards to the rest of the markets: (i) the Affarsvarlden is a also a general index of Swedish stocks; (ii) the ISEQ for Ireland is also a general index (capitalization-weighted) of all Official list equities in the Irish Stock Exchange (ISEQ Overall Index); (iii) the ATX index is the main index of Austria and contains all stocks listed on the prime market segment; (iv) the Madrid Stock Exchange General Index (IGBM) is also a general capitalization-weighted index for the Madrid Stock Exchange and represents the construction, financial services, communications, consumer, capital/intermediate goods, energy, and market services sectors; (v) the Copenhagen KFX includes growth companies in the medical, telecommunications, biotechnology, and information technology sectors. Therefore, only for three indices there could be an issue using them as a benchmark for work involving small stocks: the CAC 40 for France, the DAX 30 for Germany, and the AEX for the Netherlands (25 most actively traded stocks). However, note that the CAC40 and the DAX30 are main indices and are often used in empirical studies to proxy the market portfolio in France and Germany (see, among others, Jansen and Nahuis, 2003; Lasfer et al., 2003; Pagano and Schwartz, 2003).
  • 10 Numerous studies report that market risk is time varying (e.g. Campbell and Vuolteenaho, 2004; Ang and Chen, 2007; Adrian and Franzoni, 2008). Ang and Chen (2007) find that if we account for time variation in market risk, the CAPM cannot be rejected.
  • 11 Fama and French (2006) compare estimation windows for the CAPM and find that a 1 year estimation period is the best alternative in terms of explanatory power. The results remain the same irrespective of the window length. We only report the results with the 12 month window. The 24 month window results are available upon request.
  • 12 Chordia and Shivakumar (2002) report positive momentum profits in the USA only during non-January months. While our results are not as extreme, it seems that European stocks behave broadly similarly to US stocks.
  • 13 Most studies in the field also include the default spread, defined as the difference between the average yield on BAA rated bonds and AAA rated bonds. The only relevant data available to us are the yields on a portfolio of BAA and AAA bonds respectively, compiled by Lehman Brothers for the whole of Europe. These series begin in 1998 and including them in the regressions would force us to leave half of our sample period out of the tests. Therefore, initially, we run the regressions with the three variables discussed above and subsequently re-estimated the regressions including the default spread as well for the 1998–2006 period. The later results are not presented here (available upon request) but indicate that in several occasions the default spread was statistically significant and improved considerably the adjusted R2 of the regressions.
  • 14 Considering that due to lack of data, our results do not include transactions costs, the significance of the portfolio returns is overstated. In other words, size and momentum profits may occur even less frequently across European markets.

      • The full text of this article hosted at iucr.org is unavailable due to technical difficulties.