A resource ratio theory of cooperation
Abstract
Ecology Letters (2010) 13: 349–359
Resource ratio theory predicts that two species may coexist in the presence of two limiting nutrients provided that each species is limited by the resource it is least able to deplete. We modify this classical competition model to allow interspecific cooperation through trading. We show that resource trade expands the realm of stable coexistence, and that optimal trading partners competitively invade and exclude any other trading or non-trading strategy. We show that natural selection favours evolution towards establishment of a trading relationship so long as partners can establish long-term associations even though cooperation may result in a decrease in abundance of one species. This theory substantively expands traditional applications of resource competition models and suggests additional empirical experimentation.
Introduction
Understanding conditions under which natural selection may favour cooperation over competition remains an evolutionary and ecological challenge. Mutually beneficial interactions in natural systems are ubiquitous (Boucher et al. 1982; Bronstein 1994b; Richardson et al. 2000; Stachowicz 2001). Theory addressing the issue of mutualism has expanded significantly in recent years to include a broad range of game theory (e.g. Doebeli & Hauert 2005) as well as other modelling platforms (e.g. Noe & Hammerstein 1994; Schwartz & Hoeksema 1998; de Mazancourt et al. 2001; Hoeksema & Schwartz 2003). Developing a broad and synthetic theoretical context for understanding the evolution, dynamics and stability of mutually beneficial interactions remains an important area of study (Doebeli & Hauert 2005).
The majority of this ecological literature has focused on the interaction between mutualism and parasitism (Bronstein 1994b; Bronstein et al. 2003), and how mutualism may evolve from parasitic precursors (Roughgarden 1975; de Mazancourt et al. 2005). Nevertheless, ecologists recognize the many forms of mutualisms (Connor 1995). In this paper, we address whether it is possible for mutualism to evolve from a competitive interaction, an issue currently lacking in ecological theory. To do so, cooperating individuals would need to outperform competitive conspecifics at a stable equilibrium and at all stages along an evolutionary pathway allowing cooperation to evolve.
An emerging class of models has focused on biological markets as a framework that establishes conditions under which mutually beneficial interactions may arise (e.g. Noe & Hammerstein 1994; Schwartz & Hoeksema 1998). Market models based on comparative advantage (e.g. Schwartz & Hoeksema 1998) allow resource acquisition and requirement functions to vary to understand conditions under which resource exchange benefits both trading partners. These market models suggest an economic advantage of cooperation and trade over competition. A limitation of market models, however, has been a lack of context with which to understand population dynamics to assess whether natural selection would favour the evolution of trading behaviours.
In this study, we use resource ratio theory (Tilman 1982, 1988) as a framework for modelling population dynamics of a biological market for trading limiting resources. Thus, we investigate situations where both partners require the same resources, such as several nutrients required by competing plants, or nutrients and carbohydrates in plant–mycorrhizal interactions or lichens. In particular, we use resource ratio theory to ask questions of biological markets for growth limiting resources. We use resource ratio theory because it is an important unifying body of theory with which to understand resource consumption, competition for resources (Tilman 1982) and niche partitioning for resources (Chase & Leibold 2003). In a recent review, Miller et al. (2005) show that overall, experimental tests supported predictions of this theory 75% of the time, making it one of the most successful theories in ecology. Coexistence may occur through trade-offs in resource use and different resource requirements between organisms. Resource requirements depend on organisms attributes such as growth rate (Hessen & Lyche 1991; Elser et al. 2000; Klausmeier et al. 2004), characteristic biochemical pathways or growth form (Sterner & Elser 2002). Miller et al. (2005) list five studies that found experimental evidence for coexistence through resource ratio mechanism. An important attribute of this theory, however, is that resource uptake is limited to use by the individual acquiring the resource (Tilman 1982). However, it is well known that organisms are able to take up resources beyond their requirement levels. A common example is luxury consumption, where organisms, particularly phytoplankton, take up more resources than they need and store them (Droop 1974; Elrifi & Turpin 1985; Chapin et al. 1990; Sterner & Schwalbach 2001; Klausmeier et al. 2008). This phenomenon has also been observed in a wide array of vascular plants (Lawrence 2001; Tripler et al. 2002; Boivin et al. 2004). Given that organisms can take up nutrients in excess of their needs, would they be able to exchange excess resources for net gain? Nutrient exchange does occur in all examples of trading mutualisms such as between plants and their mycorrhizae (Govindarajulu et al. 2005), or between legumes and their rizhobia (Kiers et al. 2003). Less understood, and clearly indirectly, plants may also exchange nutrients through a common mycorrhizal network (Simard et al. 1997).
Therefore, we vary the two species, two limiting resources model to allow trade and explore if and when natural selection favours such behaviour. We constrain individuals and their resource acquisition so that they do not completely specialize in acquisition of one resource or the other, although species differ in nutrient acquisition capabilities. Individuals within each species then carry a heritable attribute that defines their willingness to provide resources to their trading partners. This willingness to provide resources is independent of the partner’s willingness to reciprocate.
We do not model the specific mechanisms through which resources are exchanged; we assume that resource exchange occurs on a one-to-one basis. This is notable because of the attention that has been given to cheating within mutualisms. Policing of fair resource exchange and cutting off cheaters can increase costs to the point of counterbalancing potential benefits gained. Recognizing the existence of mechanisms that can thwart resource exchange mutualisms, we model mechanisms that facilitate such an interaction given the observation that these exist in nature.
We begin by using a global model of competition where trading pairs compete for nutrients. In this model, we demonstrate the conditions under which trading strategies outperform and exclude other strategies. With this set of simulations, we show that trading increases the potential area of resource supply that results in coexistence between two species. We then explore the consequences of trading on total population biomass. Empirical studies have shown that mutualistic relationships bear close resemblance to parasitic relationships (Bronstein 1994a) implying that resource exchange may, or may not, result in a mutualism. In second set of simulations, we present an evolutionary, individual-based model to check that trading would evolve from a non-trading ancestral population if partner pairing were possible. In this case, the simulation begins with populations of individuals in ancestral non-trading populations where trading and partnering traits are subject to heritable variation. Finally, we discuss an empirical application that may be used to test our model within a plant–mycorrhizae relationship.
Model and analysis
R* model platform
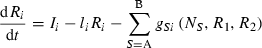 (1)
(1)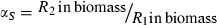
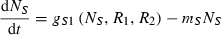 (2)
(2)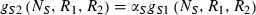 (3)
(3)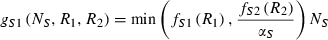 (4)
(4)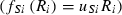 and Monod type
and Monod type 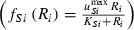 uptake functions (Appendix S1), as well as a generic function fSi that can be any monotonically increasing function. Note that the uptake kinetics for a nutrient is more efficient when it is limiting (uptake is then at the maximum value) than when it is non-limiting (where uptake is limited by the other, limiting nutrient), consistent with empirical observations (Turpin 1988). Also note that we do not deal with plastic or potentially evolving allocation towards the uptake of resource 1 vs. 2. We assume that the allocation to the uptake machineries for both resources are fixed, and that maximum uptake of both resources is feasible – it is realized when the two resources are co-limiting.
uptake functions (Appendix S1), as well as a generic function fSi that can be any monotonically increasing function. Note that the uptake kinetics for a nutrient is more efficient when it is limiting (uptake is then at the maximum value) than when it is non-limiting (where uptake is limited by the other, limiting nutrient), consistent with empirical observations (Turpin 1988). Also note that we do not deal with plastic or potentially evolving allocation towards the uptake of resource 1 vs. 2. We assume that the allocation to the uptake machineries for both resources are fixed, and that maximum uptake of both resources is feasible – it is realized when the two resources are co-limiting.The two species differ in their ability to deplete a resource when limiting ( for species S, resource i) and resource ratio requirements (αS). Resource depletion (
for species S, resource i) and resource ratio requirements (αS). Resource depletion (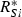 , see Appendix S1) is the minimum level of the resource pool that allows the plant to maintain a positive growth rate and defines a zero net growth isocline (ZNGI; Fig. 1a). From this basic modelling structure, Tilman (1982) demonstrated that we can assess resource depletion exerted by each species assuming some initial resource supply point, to understand how various patterns in
, see Appendix S1) is the minimum level of the resource pool that allows the plant to maintain a positive growth rate and defines a zero net growth isocline (ZNGI; Fig. 1a). From this basic modelling structure, Tilman (1982) demonstrated that we can assess resource depletion exerted by each species assuming some initial resource supply point, to understand how various patterns in  affect competitive outcomes and species coexistence (Fig. 1a). In particular, stable coexistence is predicted when each species requires more of the resource that is most limiting to that species (Fig. 1b; Appendix S1; Tilman 1982). Extreme resource supply regions, of either resource, result in competitive exclusion by one species or the other (Fig. 1b). In this manuscript we investigate the effect and evolution of trade in situations that can potentially lead to coexistence as in Fig. 1b. In Appendix S1, we generalize our conclusions to situations with potential founder control (Appendix S1).
affect competitive outcomes and species coexistence (Fig. 1a). In particular, stable coexistence is predicted when each species requires more of the resource that is most limiting to that species (Fig. 1b; Appendix S1; Tilman 1982). Extreme resource supply regions, of either resource, result in competitive exclusion by one species or the other (Fig. 1b). In this manuscript we investigate the effect and evolution of trade in situations that can potentially lead to coexistence as in Fig. 1b. In Appendix S1, we generalize our conclusions to situations with potential founder control (Appendix S1).

Competition for two essential and non-substitutable resources as viewed by Tilman’s resource competition model (panels a, b), and adding optimal resource trading (panel c). The x-axis represents the amount of resource 1, the y-axis represents the amount of resource 2. (a) A species is characterized by (1) its ZNGI, that delimitates the regions of resource levels that lead to positive population growth (shaded area) and (2) its impact vector with slope αSl1/l2, where αS is the resource ratio requirement for population growth and l1/l2 is the ratio of nutrients leaching rates. A given resource supply corresponds to an equilibrium supply point without consumer (black dot). When present, a species depletes resource levels according to its impact vector until resource levels reach the ZNGI, down to equilibrium point A*. Resource level space can be partitioned into two sets of equilibrium resource level at supply where each resource becomes the limiting factor, as indicated by the dashed line. (b) Adding a second species when conditions for potential coexistence are fulfilled, the resource level plane is now partitioned into sets of equilibrium resource level at supply where none of the species can grow (white), only one can grow (species A in blue, species B in red), or there is coexistence (purple). Conditions for coexistence are that each species is better able to deplete one of the resources than the other species, and that they require more of the resource they are not good at depleting. Coexisting competitors deplete resources down to the coexistence equilibrium point C*. Panel (c) mirrors (b) but allows for trading. Sets of equilibrium resource levels at supply points where there is one optimal trading strategy are shown in orange shading. The orange line between the ZNGI of the two species is potential resource depletion by optimal trading pairs.
Allowing trading in the model
For any resource supply point within the region of potential coexistence, uptake of one resource is constrained because the other resource becomes limiting (Fig. 1a). This excess of potentially accessible resource is left unused in the traditional resource ratio model because it cannot be utilized owing to a rate-limiting constraint imposed by the other resource. When two species coexist, each species has potential access to the very resource that limits the other species (Fig. 1b). This creates the opportunity for each species to over-consume non-limiting resources and exchange these resource for the other, rate limiting, resource by relaxing the assumption that species do not acquire resources unless they can immediately apply them to growth.
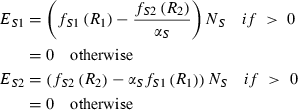
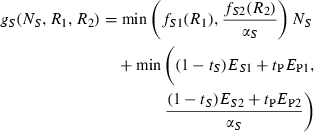
Note that we assume no cost for uptake of excess resource nor transfer to or from partner, thus giving no incentive for cheating.
Trading strategy optimization
Imagine that competing individuals of the two species have the option to function as a single unit exchanging resources. We can calculate the properties of a two species unit that maximizes ecosystem resource utilization and resource depletion (Appendix S1). In this optimally trading pair, individuals take up both resources at their physiological maximum rate and those resources are used to produce biomass of both species. As demonstrated for example in Tilman (1982), in a pure resource competition framework, such as the one presented here, the competitive strategy that wins in competition is the one that can deplete resources below a level of positive growth for its competitors. As we show in Appendix S1, an optimally trading unit as defined above does indeed do that. The region of resource depletion points where optimally trading units can drive resource depletion below that of species acting on their own is graphically depicted by the orange shaded region in Fig. 1c. Every combination of resource supply within this shaded region carries the potential of optimal resource depletion by a trading unit. In this case, an optimal pair is capable of depleting resources down to the orange line, below the level achieved by two species competitive coexistence (equilibrium point C* in Fig. 1b). Thus, we can delimit the environmental conditions where optimal trading is potentially the best competitive strategy, and the result is an increased potential for coexistence between species (Fig. 1c) relative to traditional resource competition (Fig. 1b). Competitive simulation runs (Appendix S1) show that optimal trading units are the only trading pairs that cannot be invaded by any other trading pair or non-trading individual: they are evolutionary stable strategies in the sense of Maynard Smith (1982).
The conditions that support potential trading are fairly general. First, the two resources must be non-substitutable and essential, i.e. growth is a minimum function and the ZNGI are L shaped. Second, one species must be relatively better at depleting one of the resources, i.e. 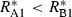 and
and 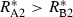 . Economists refer to this condition as comparative advantage (Schwartz & Hoeksema 1998). This model, however, makes simplifying assumptions that may be unrealistic. We assume that the cost of excess resource acquisition and resource transfer between species is negligible. As discussed later, this means that there is no benefit to cheating. These assumptions are likely to be violated in many natural systems. Increasing the cost of maintaining resource exchange would decrease the capacity for trading pairs to outperform competing individuals.
. Economists refer to this condition as comparative advantage (Schwartz & Hoeksema 1998). This model, however, makes simplifying assumptions that may be unrealistic. We assume that the cost of excess resource acquisition and resource transfer between species is negligible. As discussed later, this means that there is no benefit to cheating. These assumptions are likely to be violated in many natural systems. Increasing the cost of maintaining resource exchange would decrease the capacity for trading pairs to outperform competing individuals.
Effect of trade on population sizes
An interesting outcome of this simple model, however, is that while cooperation maximizes system-wide resource depletion and biomass production, it does not necessarily increase biomass production for both of the trading partners. To assess the population consequences of trading, we compare optimal trading outcomes with those of both single species resource consumption and two species competition. These situations encompass the three possible combinations of presence/absence of trading and presence/absence of competition (Table 1).
| Trading | |||
|---|---|---|---|
| + | - | ||
| Competition | + | Optimal Trade | Pure Competition |
| - | NA | Monoculture | |
There are three possible outcomes of in terms of species biomass relative to trading or not trading. Biomass achieved per species in competition (COMP) is always lower than species biomass in monoculture (MONO). However, trading (TRAD) can result in the maximum biomass (TRAD > MONO > COMP), intermediate biomass (MONO > TRAD > COMP) or the least biomass (MONO > COMP > TRAD) for each species (Fig. 2). Resource supply is critical in determining the outcome biomass for each species. Trade maximizes potential biomass for each species when there is a low supply of the resource for which a species is a superior competitor (Fig. 2). Thus, both species increase potential biomass when resource supplies are low for both resources. Biomass outcomes are intermediate between their performance in isolation and their performance competing with the other species when resource supplies are high and not lacking in the resource for which the focal species is a good competitor (Fig. 2). Finally, biomass with trade is lower than in competition when resource supply is high and close to the region where competitive exclusion would result in the elimination of the other species in a competitive relationship. Although the exact parameter space configuration is system specific, this array of outcomes suggests that trading interactions span a competition – antagonism – mutualism continuum when assessing interactions with their effect on biomass or population size.
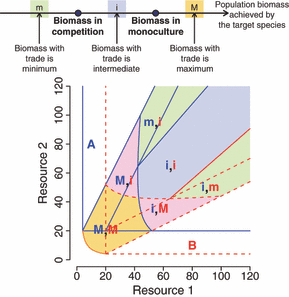
Population size consequences of trading in the case where there is potential coexistence (as in Fig. 1C). The two axes represent equilibrium resource levels in the absence of organisms. Biomass in competition is always lower than biomass when grown in monoculture; however, biomass in the optimal trading pair might be maximal (M), intermediate (i) or minimum (m). At low resource abundance, population size is maximal with trading for both species (yellow region); a removal experiment measuring population size response rather than fitness response would suggest a mutualistic interaction at low resource abundance. Population size with trading becomes intermediate for one of the species at intermediate resource abundance (pink region), a removal experiment measuring population size response would suggest a parasitic interaction at intermediate resource abundance. When both resources are high, biomass in the optimal trading relationship is either intermediate or minimum for both species (blue and green regions), a removal experiment measuring population size response would suggest a competitive interaction. At high levels of one of the resource, optimal trading yields lower biomass for one of the species than in competition (green regions): this is close to the area where in competition, the target species would exclude the other and have all the resources for itself. In an optimal trading situation, the target species releases some of its resources to its partner, losing some biomass in the process.
Natural selection and the evolution of trade
We alter the framework to an individual-based model to assess whether trade is able to evolve from a competitive precursor. Each individual in this model has a strategy that is described by two traits: (a) the fraction of resources that it gives to its trading partner tS and (b) its propensity to associate with a partner pS. Free individuals may form pairs at random from the pool of available individuals at a rate increasing with their propensity to associate with partner [rate of association is (pA + pB)/2 per unit time]. A pair can break down as a consequence of either individual defecting from the partnership, at rate 1 − (pA + pB)/2 per unit time, or as a consequence of the death of one of the individuals. Resources are lost from individuals continuously through a metabolic rate. Death of individuals occurs for two reasons. First, if nutrient supply does not meet demand, an individual loses biomass and does not survive below a threshold size. In addition, background mortality is captured by a constant low rate of individuals randomly selected to die and be removed from the population at each time step. Population size is constant and similar for both populations, enabling 1 : 1 pairing between individuals and matching with theoretical predictions for optimal trading. Replacement of dead individuals come from asexual reproduction. Probability of reproduction is proportional to biomass. Offspring inherit their parents strategies for both trading and partnership fidelity, with some probability of mutation. In other respects (i.e. resource use) this model is analogous to the previous deterministic model.
In the absence of trade this model behaves exactly as we expect. The system quickly moves to an equilibrium abundance for each species (Fig. 3a), and nutrients are depleted to the two species equilibrium (Fig. 3b). When trade and continued association in partnerships are allowed to evolve (Fig. 3c–f), then the dynamics go to a new, and different, equilibrium abundance of the two species (Fig. 3c). This new equilibrium depletes resources to a lower equilibrium point (Fig. 3d). This lower depletion is achieved by the evolution of trade (Fig. 3e) and long-term relationship with partner (Fig. 3f). Under these conditions, the natural selection drives evolution towards forming long associations and the optimal trading strategy predicted by our theoretical calculations. This combination of traits is more efficient at depleting nutrients and can outcompete any other strategy. This result is robust to whether nutrient levels are set such that both species benefit or whether nutrient levels are close to the competitive exclusion barrier, where trading results in a seemingly parasitic relationship between species. However, it does require that the system starts with coexisting competitors, and that mortality be sufficiently low so that long-term partner association between individuals is possible.
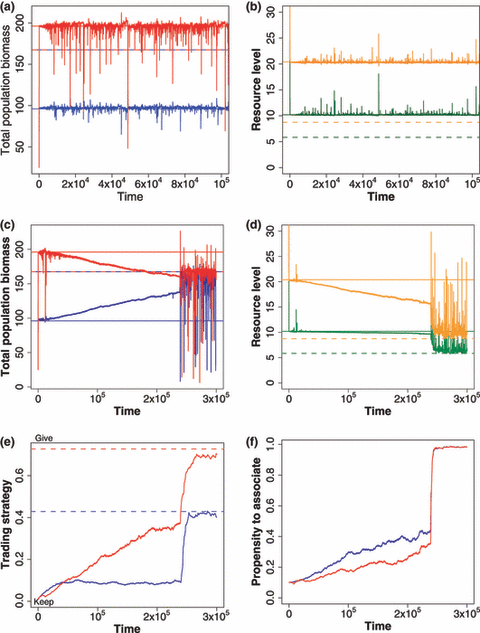
Results of the evolutionary model as described in the text. In all panels, species A is featured in blue, species B in red, resource 1 in green, resource 2 in orange; solid lines represent equilibrium levels without trading, dashed lines represent equilibrium levels at optimal trading (Appendix S1). (a, b) Results when evolution is not allowed, so the partners remain non-trading competitors. (a) population dynamics through time; abundance is total population biomass in kg of resource 1 in biomass ha−1. (b) Resource levels through time quickly go down to the coexistence resource depletion levels (solid lines). (c–f) Results with evolution from non-trading ancestors. (c) Population dynamics through time as in A, but with evolution of trading, showing that species abundance goes towards their abundance under optimal trading (dashed lines). Note that species B is less well with the evolution of trading than without. (d) Resource levels through time, showing that resource depletion goes below the depletion levels by non-trading competitors (solid lines), towards resource depletion by optimal trading pairs (dashed lines), thus excluding such non-trading strategies. (e) Evolution of trading strategies through time, going towards the optimal trading strategy. (f) Evolution of partner fidelity through time, showing strong selection for partner fidelity. Parameters used for all figures are given in Appendix S1.
This natural selection example illustrates the paradox highlighted in the previous section. At each time step individuals that join in trading partnerships enjoy a selection advantage over those that do not trade or do not remain in trading relationships, yet the end result may be that one species ends up with a lower net biomass than is found under a non-trading condition (Fig. 3c). Total nutrient uptake in the system is increased as a consequence of trade, but the advantage may accrue to just one of the two species. Individuals of the ‘losing’ species, however, must evolve towards trade or else they are eliminated from the environment by their trading conspecifics that have higher relative fitness. Those results were reasonably robust to adding a moderate cost to trading. We ran simulations where trading strategies had a lower nutrient uptake, and the reduction was proportional to the level of trading. Trading took much longer time to evolve and evolved to lower levels, and the biomass of both species were lower than without a cost (results not shown).
Discussion
Resource trade and coexistence
The model presented here predicts that conditions allowing coexistence with competition could actually favour natural selection towards establishing a cooperative trading relationship. Many biological attributes may prevent resource exchange, but the model suggests two important observations. First, it should be possible for cooperation to evolve from a competitive precursor. This observation is complementary to Roughgarden (1975), who predicted mutualisms evolving from parasitic precursors. Second, this model shows that natural selection can favour the evolution of trading relationships despite a ‘parasitic’ effect of that relationship on biomass or population size.
A number of biological attributes may preclude competitors from exchanging nutrients. Nevertheless, the observation that cooperation broadens the domain of coexistence (Fig. 1c) is an important observation in terms of considering the maintenance of diversity. The only conditions for there to exist a trading strategy that outperforms a competitive strategy are low mortality to enable long-term partnerships between individuals of the two species, and that each organism is less efficient than the other organism at depleting one of the two resources. This closely corresponds to conditions highlighted by comparative advantage biological market models where the poorer competitor only need to experience a differential cost in acquiring the two resources (Schwartz & Hoeksema 1998; Hoeksema & Schwartz 2003). Trading thus widens an existing coexistence region, and may create a coexistence region in the founder-control situation (Appendix S1). However, coevolution towards an optimal trading pair requires long-term contact between individuals of the two species, therefore coexistence. Outside regions of coexistence, an optimal trading pair will displace non-trading individuals, but it needs to have evolved from a different environment, or for other reasons.
Evolution of trading
We showed that trading should evolve when there is coexistence. This comes about because when an individual feeds its partner, its partner increases in abundance, and if its partner also happens to trade, that in turn helps the target individual. This positive feedback brings the species to an efficient level of trading.
What about cheaters? Cheaters are individuals that take the resources from their partners without providing goods or services in return (Bronstein 2001; Yu 2001). Because we assume a strict resource competition, and no cost to trading, there is an alignment of interest of the two partners to deplete the resources optimally: optimal trading is the only way they can become together a super-competitor unit that survives at such low resource levels and exclude all other competing strategies. To demonstrate this alignment of interest, we evolved the trading traits the other way around: individual strategies determined how much they received from their partner rather than how much they gave to their partner. They evolved to the same optimal trading level, and evolution towards trading occurred faster (results not shown). In our model, partner fidelity (Sachs et al. 2004) evolved to enable stable partnerships and the evolution of trading. Cooperation was not costly to individuals, and it was beneficial to the individual. Theory does not predict the evolution of cheating in such case. Cheaters might evolve if the alignment of interest was broken, for example if not all individuals could enter a trading relationship, or if parasites were allowed to evolve in the system. There is no gain for cheating if there are no costs to cooperate, it is just not an option for competitors if it prevents them from surviving at low resource levels.
The mutualism – antagonism – competition continuum
One of the most intriguing result we obtained was that trade could evolve even though it would decrease the total population biomass of one of the partner species. It is well known that fitness and population sizes are often unrelated, so that populations might even evolve to extinction (Webb 2003). In our model, fitness is determined by the ability to grow and survive and reproduce at low resource availability. Trading enables an optimal ‘trading unit’ to optimize resource use and deplete resources to lower levels than any other strategies can tolerate (Fig. 3). At high and unbalanced resource levels (Fig. 2), the optimal balance shifts resources away from the competitively superior species, as resource use is optimized when some of the resources previously consumed by the target species are shifted to its partner species.
It is important to realize that depending on the criterion used to define mutualism, we arrive at qualitatively very different conclusions. An effect-based definition, separating pairwise interactions along the classical (+, 0, −) gradient in interaction effects can classify interactions depending on their net effect on population sizes, population growth rates or individual fitness (Abrams 1987). One possible criterion is based on population size response to partner removal: whether population size achieved by either species in optimal trading is larger or smaller than population size achieved in the absence of the partner (Abrams 1987). With this definition in mind, we would define resource exchange relationships as spanning a continuum from mutualism (+,+) at low resource supplies, through antagonism (+, −) at intermediate resource supplies and to competition (−, −) at high resource supplies.
However, we suggest that mutualism and parasitism should be defined not by population-level effects but by fitness effects, as seems to be the consensus in mutualism studies (Abrams 1987). In a resource competition setting, individual fitness is based on its ability to grow and survive at low resource density. It is clear that optimal trading enables survival and growth at lower levels of resources, and therefore provides a positive effect on individual fitness is all the region of resource supply points where an optimal trading pair is the best competitive strategy. A fitness-based definition would thus find that the interaction is mutualistic wherever it occurs, even though it presents a context dependent outcome on population size. As we argue below, an appropriate test to contrast the effect of trading on fitness vs. total biomass would be to perform new competition experiments.
Finally, there is yet another definition of mutualism, based on the evolutionary dynamics of an interaction (i.e. mutualistic evolution as defined in de Mazancourt et al. 2005). If both partners actively invest to put an interaction in place through the process of natural selection, then we would call resource exchange a mutualism no matter what the resource supply and biomass outcome. Our evolutionary simulation results were robust to trading strategies bearing a moderate cost, although evolution of trading took much longer (results not shown). Therefore the interaction would be a mutualism according to that criterion too, even if population biomass decreased.
Our model demonstrates that, across a large spectrum of resource supply, there is selection to pair up and establish trading relationships. The key factor that explains this apparent paradox is the fact that population size, or the biomass achieved by any individual, is not a measure of fitness. Fitness is determined by the ability of an individual to survive at low resource abundance, thus depleting the resources until all competitors are driven to extinction. An optimal trading pair is a super-competitor at all resource supply levels. In that sense, there is a strong benefit of the interaction for both species engaging in the interaction at all resources supplies in the area where an optimal trading pair is the best competitive strategy, whatever the population consequences (Fig. 2).
Generally, the model we present here supports the empirical observations of fungal – plant interactions moving along the continuum from mutualism to saprophytes (e.g. Koide et al. 2008) and parasitism (e.g. Egger 2006). In addition, this model framework may explain the evolution of mycorrhizae from saprophytic precursors (e.g. Hibbett et al. 2000). Assume species A is a mycorrhizal fungus, species B is a plant; resource 1 is phosphorus, and resource 2 is light (Fig. 4a). The fungus cannot have positive growth on its own, as it cannot use light to photosynthesize. Fungus A can however assist the plant to deplete light and convert it into the carbon source the fungus requires. We therefore focus on the region of resource space that is below the mycorrhizae’s ZNGI (Fig. 4a). We find that the model makes predictions that match existing experimental results (Johnson 1993; Hibbett et al. 2000; Rice & Currah 2002; Egger 2006; Koide et al. 2008). We can follow the effect of the trading partnership on the biomass of both partners along gradients of phosphorus at high and low light levels (Fig. 4). When phosphorus supply is too low, the plant cannot grow either with or without the mycorrhizae (Fig. 4d,e). As phosphorus supply increases, the plant cannot grow independently but can grow in association with the mycorrhizae. At higher levels of phosphorus supplies, the plant grows better with the mycorrhizae than without. Further increasing the level of phosphorus supply, the plant grows better without the mycorrhizae (Fig. 4d). Finally, at yet higher levels of phosphorus supply, the plant competitively excludes the mycorrhizae (Fig. 4d,e). Johnson (1993) showed that mycorrhizae from higher P soils appear less mutualistic. Our theory predicts that even though mycorrhizae might appear less mutualistic or even parasitic at some phosphorus levels, it might still be in plant’s best interest to enter the association and thus become a super-competitor. We thus question whether the interaction is really parasitic when the plant appears to grow less well in the presence of a mycorrhizae, and suggest that there could be an increased fitness for the plant due to the interaction. This could be tested with a direct competition experiment between a plant associating with its mycorrhizae and an otherwise identical plant genetically modified to inhibit mycorrhizal association.
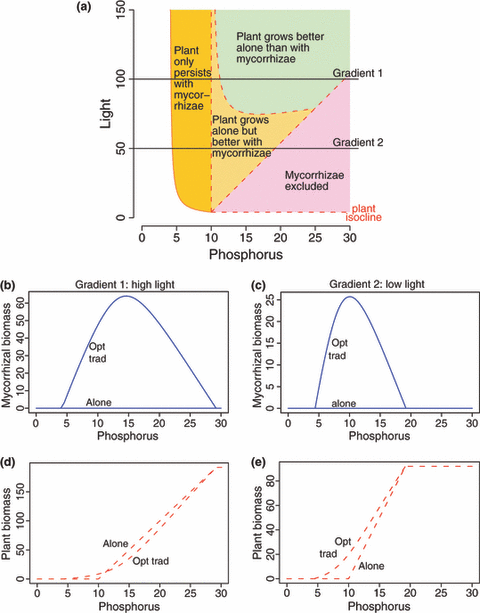
Metaphor for plant–mycorrhizal system. (a) Zero net growth isocline and trading region in the equilibrium resource plane. The two resources are phosphorus and light; the fungus cannot use light and therefore cannot survive on its own in any of the parameter space. However, the fungus can use the carbohydrates produced by the plant through light absorption. (b–e) Fungus and plant biomass in trading and on their own along the two phosphorus gradients outlined in panel (a). The fungus cannot grow on its own and shows a positive biomass response to trading. The plant may show a higher or lower biomass in trading than alone depending on the conditions.
Resource exchange models and mutualism theory
Mutualism theory is proceeding along multiple lines (Hoeksema & Bruna 2000). One body of work relies principally on game theory to address the issue of cheating within a cooperative relationship (Doebeli & Knowlton 1998; Doebeli & Hauert 2005). Progress in this field has focused on conditions that would result in stable cooperation in the face of selection for self-interested defection from a cooperative relationship (Doebeli & Hauert 2005). Market theory has developed as an alternative approach to understanding mutualism (Noe & Hammerstein 1994; Schwartz & Hoeksema 1998; Hoeksema & Schwartz 2003; Akcay & Roughgarden 2007).
Our model contributes to this expanding literature by placing biological markets within the context of intratrophic resource competition and population dynamics. We show that trading should evolve under strict global resource competition, whenever conditions are sufficient to support stable coexistence, and long-term partnership is possible. This is an important observation because virtually all other models of mutualistic behaviour emerge from parasitic precursors (e.g. Boucher 1985; de Mazancourt et al. 2005), or simply do not address the evolution of the relationship (Hoeksema & Schwartz 2003; Doebeli & Hauert 2005).
Ecological theory associated with mutualism is expanding and diversifying as we better understand the breadth and variety of interspecific relationships that may be defined as mutualism. We have used a simple, and realistic, variation from a classic resource exchange model to expand ecological theory in two realms. First, we use this platform to broaden our understanding of the possible outcomes of resource competition and how we might understand resource competition to influence the maintenance of species diversity. Second, we use this model to expand our understanding of mutualisms and show how a mutualism may evolve from a competition precursor. Finally, by examining predicted biomass outcomes derived from different regions of resource supply, we show that selection may paradoxically favour partnering and engaging in resource exchange despite the fact that the resulting biomass production or population size may decrease from that in a strictly competitive environment.
Our models provide an important first step to understand the evolution of resource trade from a competitive precursor. Further development should probably address the question of resources made available to a range of individuals rather than just one partner. It could potentially be adapted to study the evolution of microbial social interactions (West et al. 2006) or nutrient exchange between plants through mycorrhizal networks (Simard et al. 1997). It could include policing mechanisms or evolution of specialization once in a trading relationship. Nevertheless, our model represents a broad new landscape in which to consider positive interspecific interactions.
Acknowledgements
James Grover, Frederick Adler and three anonymous referees provided helpful comments on the manuscript. We thank Michel Loreau and Doug Yu for helpful discussions on this topic. Henri de Parseval helped with finding analytical solutions of this model and generate Fig. 2. Oliver Dutczak helped with the plant–mycorrhizae literature. The NERC Centre for Population Biology at Silwood Park provided funds to initiate this collaborative effort. Claire de Mazancourt acknowledges a Discovery grant from the Natural Sciences and Engineering Council of Canada.




