Functional and effective connectivity in an fMRI study of an auditory-related task
Abstract
This study investigates the sets of brain areas that are functionally connected during an auditory goal-directed task. We used a paradigm including a resting state condition and an active condition, which consisted in active listening to the footsteps of walking humans. The regional brain activity was measured using fMRI and the adjusted values of activity in brain regions involved in the task were analysed using both principal component analysis and structural equation modelling. A first set of connected areas includes regions located in Heschl's gyrus, planum temporale, posterior superior temporal sulcus (in the so-called ‘social cognition’ area), and parietal lobe. This network could be responsible for the perceptual integration of the auditory signal. A second set encompassing frontal regions is related to attentional control. Dorsolateral- and medial-prefrontal cortex have mutual negative influences which are similar to those described during a visual goal-directed task [T. Chaminade & P. Fonlupt (2003) Eur. J. Neurosci., 18, 675–679.]. Moreover, the dorsolateral prefrontal cortex (DLPFC) exerts a positive influence on the auditory areas during the task, as well as a strong negative influence on the visual areas. These results show that: (i) the negative influence between the medial and lateral parts of the frontal cortex during a goal-directed task is not dependent on the input modality (visual or auditory), and (ii) the DLPFC activates the pathway of the relevant sensory modality and inhibits the nonrelevant sensory modality pathway.
Introduction
Functional neuroimaging has enabled a functional segregation of the brain areas that are active when performing a task to be established. More recently, ‘functional integration’ studies have described how functionally specialized areas, i.e. areas whose activity is modified during the realization of a task, interact within a large-scale neural network (Lee et al., 2003). These studies have used multivariate techniques that provide an analytical tool to understand integrated systems. These techniques are based on the analysis of the covariance matrix computed from the activity of several brain areas. Principal component analysis (PCA) allows neuroimaging data to be decomposed into a set of modes (Worsley et al., 1997) reflecting the functional connectivity. The functional system underlying a cognitive task can then be identified by comparing the temporal expression of a few of these modes with the occurrence of behavioural events. PCA does not require the definition of an a priori model but does not provide insight about causal influence. One method to study these causal influences is structural equation modelling (SEQM), generally termed effective connectivity. SEQM is a linear technique combining an anatomical (constraining) model and interregional covariances of activity (Büchel & Friston, 2000). When applied to datasets obtained during visual-related tasks, these different approaches have led to a widely accepted functional model involving an occipito-parieto-frontal network. For example, the connectivity between primary visual cortex, V5, and parietal cortex has been showed during a task manipulating the attention level (Rees et al., 1997). The connectivity within the dorsal (parietal) and ventral (temporal) pathway during visual object- or movement-related tasks (McIntosh et al., 1994) has been established. Some studies of connectivity have also demonstrated the control exerted by the dorsolateral prefrontal cortex (DLPFC) on the visual pathway (Büchel & Friston, 1997; Fletcher et al., 1999; Bullmore et al., 2000; Chaminade & Fonlupt, 2003), which is in agreement with the increase of DLPFC activity induced by attention (Rees et al., 1997; Kanwisher & Wojciulik, 2000; Rees & Lavie, 2001). Compared to the visual system, the structure and function of the central auditory system in human is relatively poorly understood. Some studies have shown that integration areas (including dorsolateral prefrontal areas) implicated during auditory attention are overlapping with the visual attention network (Bushara et al., 1999; Corbetta & Schulman, 2002). An enhanced activity in the auditory areas (Heschl's gyrus and planum temporale) has also been reported when directing attention towards the auditory modality (Woldorff et al., 1993; Downar et al., 2000; Lipschutz et al., 2002). However, only a limited number of studies have focused on the connectivity during auditory-related tasks. The available reports have only modelled connections within the auditory areas (Gonçalves et al., 2001; Langers et al., 2005) or areas involved in auditory-language pathways (Horwitz & Braun, 2004; Parker et al., 2005). An extended network including the frontal areas has not yet been considered in the context of auditory-directed attention.
In the present study, our aim was to establish the connectivity between areas involved in an auditory task. To determine the connectivity between the areas composing the network involved in an auditory task, we performed a novel analysis of the dataset used in a previous publication reporting the neural correlates of listening to human footsteps (Bidet-Caulet et al., 2005). The paradigm used in this study allowed the attention directed towards a sound object to be manipulated.
Materials and methods
Experimental procedure
Ten subjects with normal hearing (three females, aged 20–29 years) gave written informed consent and the study was approved by French National Ethical Regulation (no. RBM 03–18).
Auditory stimulus (6-s duration) consisted of the footsteps of two persons, one walking on the left side of the subject, and the other one walking on the right side. One of the two walkers started moving across the auditory scene from one side to the opposite side, while the other one kept on walking straight in his/her initial side. The beginning of the crossing (left-to-right or right-to-left, equiprobably) randomly occurred 1, 2, 3, or 4 s after stimulus onset and was completed 2 s later. Subjects were required to indicate the motion direction of the crossing walker by clicking on the right or left button of a response box with the right hand, and then to wait passively until the end of the stimulus. With this procedure, the subject has to direct his attention towards the auditory scene during different time spans within the full 6-s auditory stimulus, depending on the time of footstep crossing. At the end of the 6-s stimulus, four scans of 1.5 s were acquired and followed by a delay of 4.5 s before the beginning of the next stimulus. Resting state trials were identical except that the stimulus was replaced by a silent period of 6 s. According to the nature of the trial, auditory or rest trial, a green or grey square was presented during the whole trial. In summary, each trial lasted 10.5 s; 4.5 s silence + 6 s stimulus or silence + 4.5 s of scan acquisition. Two runs composed of 24 auditory footstep stimuli and 12 resting states (no sound, no task) were acquired for each subject. Among the 24 footstep trials, the crossing started 1, 2, 3, 4 s after sound onset, in 6, 6, 3, 9 trials, respectively.
We used an fMRI protocol that produces a magnetization steady state at the initiation of image acquisition, as described in Seifritz et al. (2002). fMRI was acquired with a sparse sampling protocol in a 3T whole-body scanner MEDSPEC 30/80 AVANCE (Brücker, Ettlingen, Germany) equipped with a circular polarized head coil. An EPI sequence was used with TE, 0 ms; TR, 1580 ms; acquisition bandwidth 123 kHz, 64 × 64 matrix, 192 × 192 mm field-of-view. The resulting in-plane resolution was 3 × 3 mm. Twenty-six adjacent axial slices (3-mm thickness, 0.5-mm interslice gap) were acquired parallel to the bicommissural plane.
fMRI analysis
The first level of data processing has been extensively described in a previous report (Bidet-Caulet et al., 2005). Briefly, the data were preprocessed (intrasubject realignment, normalization in MNI space, and smoothing) with SPM2 software (Wellcome Department of Cognitive Neurology, London, UK) implemented in Matlab® and the functional data were analysed using a general linear model (Friston et al., 1995; Wicker & Fonlupt, 2003). Analysis was performed on the average of the four scans (acquired after each stimulus presentation) to avoid making assumptions about the shape of the haemodynamic response. We used a mixed-effect model allowing for inference about the population by taking into account intersubject variance (called ‘random-effect analysis’ in SPM software). The selection of volumes of interest (VOIs) was performed at the group level using the value of the contrast ‘footstep minus rest’ in cortical areas. The map corresponding to the contrast ‘footstep minus rest’ is given in Supplementay material, Fig. S1 (A). Defining a VOI by drawing a geometrical shape (sphere or cube) centred around the voxel exhibiting the highest t-value of the cluster can lead to nonhomogeneous activity within the VOI. To avoid it, we have defined each VOI by choosing the activated voxels adjoining the voxel exhibiting the highest t-value. In practice, we have first selected the clusters surviving a t > 2.26 threshold. For each cluster a further thresholding allowed the definition of VOIs embedding no more than 120 voxels. Each of the VOIs included in the model was represented by a single time series calculated as the mean of the adjusted values of all voxels in the VOI. Each time series included 36 values per subject; 12 values for ‘resting state’ and 24 values for ‘footstep condition’.
Principal component analysis (PCA)
PCA was performed using the matrix formed by the whole time series (360 values) of all the VOIs with a procedure implemented in Matlab®. The matrix is partitioned into a set of orthogonal components that are mutually uncorrelated. The components are ordered according to the amount of variance they explain. The mean values for the five conditions (rest and 1, 2, 3, 4 s delays before walk crossing) were calculated on the first two components, as well as the loading of each of the VOIs on these components.
SEQM: anatomical model
The areas considered in the model were chosen according to two criteria. The first one was that their activities along the time series had to exhibit some variation during the task. More precisely, the value of the contrast ‘footstep minus rest’ had to be significantly different from zero with either positive or negative variation. The second criterion concerns the cognitive relevance of the brain areas; the clusters inserted in the model were located in cortical regions known to be specifically linked to auditory and/or attentional processes. The regions included: (i) the sensory-specific areas (Heschl gyrus/Planum temporale for the auditory modality and V1/V2 for the visual modality); (ii) the parietal and STS areas because these areas are involved in the task for motion processing (Bushara et al., 1999) and human feature perception (Puce & Perrett, 2003), respectively, and (iii) the dorsolateral and medial frontal areas as they are involved in attentional processes (Bushara et al., 1999; Lewis et al., 2000; Chaminade & Fonlupt, 2003) and the inferior part of the frontal lobe, which has been reported to be involved in auditory attention (Hall et al., 2000; Binder et al., 2004).
SEQM: path coefficient determination
All path models were estimated using a maximum likelihood method implemented in Amos 4.01 software (SmallWaters Corp., Chicago, USA).
The maximum likelihood method approach finds the path coefficients that minimize the discrepancy between the observed interregional correlation matrix and the matrix predicted by the model. Two approaches are then possible. The path coefficients can be deduced from the correlation matrix calculated with the time series obtained by the concatenation of the time series of all subjects. This approach assumes that the pattern of connectivity estimated over all subjects is a good approximation of the underlying connectivity in each subject. Thus, the inferences about the group of subjects are drawn under the assumption that the variations in connectivity from subject to subject are random and well-behaved (Mechelli et al., 2002). However, this approach may be problematic when intersubject variability is pronounced. An alternative way is to deduce path coefficients separately from the correlation matrix calculated with the time series of each subject (Rowe et al., 2005) and to submit the individual path coefficient to a second-level analysis (Chaminade & Fonlupt, 2003; Honey et al., 2003).
When we have used the time series concatenated across subjects, we have tested the null hypothesis that the calculated correlation matrix is equal to the observed correlation matrix by computing the discrepancy value (which is asymptotically distributed as a chi square). More precisely, a high χ2 value leads to the rejection of this null hypothesis with a low risk, P, which allows us to affirm that the proposed model does not fit the experimental data. In contrast, a low χ2, associated with a high P-value when rejecting null hypothesis, does not allow the refutation of the model. However, in order to accept the model, one also needs to consider some indicators of the goodness of fit (for a complete discussion see Bullmore et al., 2000), such as Akaike's information criterion (AIC) and parsimonious fit index (PFI). The difference between two models or two conditions was calculated using the stacked model. In the stacked model (McIntosh et al., 1994), the two networks to be compared are combined in a single program run. Statistical inferences about condition differences are based on the comparison of a free model, in which all connections are allowed to vary between the two groups, with a restricted model, in which a given connection is forced to be equal for both groups. The significance of the difference between the two models is expressed by the difference in the χ2 goodness of fit. The resulting χ2 statistic has n degrees of freedom, where n is the difference in the degrees of freedom between the free and restricted models.
When the time series of the individual subjects have been used, the statistical inferences were performed at the second-level analysis. We fitted the connectivity model separately to the interregional covariance matrix constructed for each subject. After optimal model fit for each subject, the path coefficients were treated as dependent variables in one sample t-tests. This second-level analysis allowed us to investigate the consistency of each interregional coupling by testing the null hypothesis that each path coefficient was zero. Two sample t-tests were used to investigate the modification of the path coefficients between two models or two conditions by testing the null hypothesis that path coefficients were identical in the two conditions.
Results
The clusters considered for the connectivity analysis are described in Table 1 and the topography is reported in the Supplementary material (Fig. S1, B). It can be seen that the frontal regions (DLF-R, MeF-1), the parietal regions (Par-L, Par-R, Pcu), and the visual areas (Vis-L, Vis-R) involved, are located close to the areas that we have been considered previously in the study of functional (Mazoyer et al., 2002) or effective (Chaminade & Fonlupt, 2003) connectivity during a visual task.
| Side and region | Abbreviation | MNI coordinates | t-value | Cluster size (in voxels, each 8 mm3) | ||
|---|---|---|---|---|---|---|
| x | y | z | ||||
| Activity greater during listening to human step than during resting state | ||||||
| L Heschl's gyrus | Hec-L | −44 | −18 | −13 | 8.86 | 72 |
| R Heschl's gyrus | Hec-R | 46 | −8 | −15 | 8.77 | 70 |
| L Planum temporale | Pla-L | −51 | −29 | 6 | 3.17 | 91 |
| R Planum temporale | Pla-R | 62 | −32 | 10 | 2.70 | 37 |
| L Superior temporal sulcus | STS-L | −52 | −41 | 4 | 6.71 | 36 |
| R Superior temporal sulcus | STS-R | 53 | −46 | 9 | 6.70 | 119 |
| L Supramarginal gyrus/Inferior parietal lobule | Par-L | −45 | −60 | 42 | 7.70 | 56 |
| R Supramarginal gyrus/Inferior parietal lobule | Par-R | 55 | −51 | 33 | 7.99 | 95 |
| R Inferior frontal gyrus/Precentral gyrus | DLF-R | 52 | 17 | 25 | 5.92 | 26 |
| R Inferior frontal gyrus (orbital)/Insula | IF-R | 48 | 24 | −8 | 4.16 | 24 |
| Supplementary motor area | SMA | 3 | 6 | 58 | 8.06 | 82 |
| Activity lower during listening to human step than during resting state | ||||||
| R Inferior occipital gyrus/Lingual gyrus | Vis-R | 27 | −90 | −16 | −5.23 | 79 |
| L Inferior occipital gyrus/Lingual gyrus | Vis-L | −18 | −92 | −20 | −5.33 | 48 |
| R Superior frontal gyrus (medial) | MeF-2 | 7 | 57 | 18 | −6.61 | 50 |
| L Superior frontal gyrus (medial) | MeF-1 | −15 | 52 | 34 | −8.34 | 36 |
| Precuneus | Pcu | −3 | −61 | 14 | −5.90 | 85 |
- x, y and z correspond to the stereotaxic coordinates (mm) in the MNI reference brain provided with SPM2. For each cluster, the t-value corresponds to the significance of the difference between activity during the auditory task and the resting state. This value was computed from the mean activity of the cluster. Cluster size represents the number of contiguous voxels showing significant activation (2 × 2 × 2 mm3 voxels). The locations of the clusters on the MNI template are provided in the Supplementary material, Fig. S1 (B), according to the name given to each cluster.
PCA results
Figure 1 shows the result of the PCA of the data. In order to associate a ‘cognitive’ meaning to the first two components of the PCA, we have calculated the mean of the values of the scans corresponding to the five types of trials on these two components (Fig. 1A). For the first component, the mean value for the ‘resting state’ is greater than the means corresponding to the four ‘footstep detection’ conditions. For the second component, the ‘resting state’ and ‘footstep detection’ conditions with 1-s and 2-s delays before walk crossing were separated from the ‘footstep detection’ conditions with 3-s and 4-s delays before crossing. This second component thus separates the conditions where the subject's attention has been directed to the auditory stimulus during a long or a short duration within the total time of stimulus presentation.
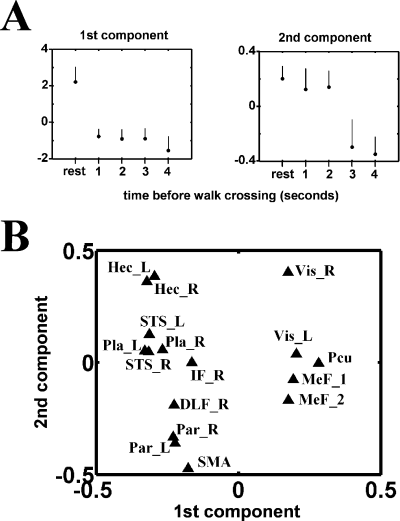
Principal component analysis of the cluster activities described in Table 1. Adjusted values of the haemodynamic response were calculated by removing the contribution of noninterest factors from the original values and the correlation matrix was analysed by principal component analysis. The upper panel (A) represents the means of the values of the scans corresponding to the five types of trials on the first two components retrieved from the PCA, which explain, respectively, 26 and 14% of the total variance. The lower panel (B) shows the loading of each VOI on these two components.
After this attribution of a cognitive meaning to the first two components resulting from PCA, we plotted the loading of the VOIs on these first two components (Fig. 2B) to allocate a functional role to these regions and determine the functional linkage between VOIs. The functional linkage between two VOIs is revealed by the close location of their representative points on the eigenimages (Fig. 2B). Two sets of regions can be distinguished along the first axis; values for visual areas (Vis-R, Vis-L), medial frontal areas (MeF-1, MeF-2) and precuneus (Pcu) are located in the proximity of the high values of the first component, while the other areas are located in the low value range of the first component. Sensory areas (Hec-R, Hec-L, Vis-R, Vis-L) are located in the upper range of the second component while frontal (DLF-R) and parietal areas (Par-R, Par-L) are located in the lower range of the second component.
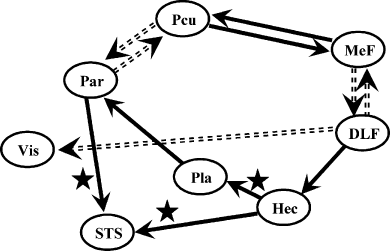
Inter-regional connections as determined by the structural equation model. Only path coefficients significantly different from zero (P < 0.05) are represented. The plain and dashed arrows represent the interregional connections exhibiting positive and negative influences, respectively. Path coefficients that are also significantly different from zero using the correlation matrix calculated from the task-independent time series are labelled with a star shape.
SEQM results
Effective connectivity was determined using SEQM as described previously (McIntosh et al., 1994). SEQM requires a model including the regions and connections between those regions to be proposed a priori. The strengths of the connections (represented by the path coefficients) are then determined by minimizing the difference between the covariance matrix derived from these path coefficients and the empirical covariance matrix derived from experimental data. The efficiency of such a method is dependent on both the careful selection of the brain areas considered in the analysis and the constraints set on the path coefficients between the areas. We have introduced in our model only cortical areas of the right hemisphere and the medial wall (excluding left-hemispheric areas), in order to be coherent with the model studied during a visual task (Chaminade & Fonlupt, 2003) and to avoid modelling the interhemispheric relations. They are indeed poorly understood for the considered areas and artificially increase the goodness of fit for the model. We have introduced the following paths. (i) Reciprocally between DLF-R/MeF-1, MeF-1/Pcu, and Pcu/Par-R because these areas have been showed to be interconnected during a visual task (Chaminade & Fonlupt, 2003) and we hypothesized that these relations are not specific of the sensory modality. These connections are chosen reciprocal because there is no a priori argument to decide of the direction of these connections. (ii) From DLF-R to visual (Vis-R) and auditory (Hec-R) areas because the influence of dorsolateral prefrontal cortex on visual areas has been largely demonstrated (Rees & Lavie, 2001) and our aim was to test the hypothesis of a similar influence over the auditory areas. (iii) From Hec-R to Pla-R and from Pla-R to Par-R because these connections represent the auditory ascending pathway from primary areas to secondary areas and then areas involved in movement analysis. (iv) From Hec-R to STS-R and from Par-R to STS-R because STS is responsible for human motion detection (Puce & Perrett., 2003) and is likely to receive information from both auditory areas (Hec-R) and areas specifically involved in movement detection (Par-R).
We performed a group analysis by applying SEQM to the correlation matrix derived from the adjusted values of the entire time series (concatenation of the time series of the ten subjects). All the path coefficient values are significantly different from zero (P < 0.05). The χ2-values and the corresponding P-values are reported in Table 2. To test if the connections are specific of the auditory task, we compared (with a nested model analysis) the path coefficients retrieved from this analysis to the path coefficients obtained with the same model but using the correlation matrix computed from the time series formed by the variations that are not linked to the task (i.e. residual variation from the fMRI data analysis). All the paths coefficients were found to be different between the two models, except that no significant differences were observed for the three path coefficients: Hec-R to STS-R, Hec-R to Pla-R and Par-R to STS-R.
| Group analysis | Individual analysis | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Path coefficientsdeterminedusing theconcatenatedtime series | Difference betweenpath coefficientsobtained usingtask-related variationand residual variation | Pathcoefficientsdeterminedfor each of the10 subjects | Difference between path coefficients obtained using task-related variation and residual variation | |||||||
| Value | P-value | χ2-value | P-value | Value* | t-value | P-value | Difference* | t-value† | P-value | |
| DLF-R → Vis-R | −0.56 | 0.004 | 4.466 | 0.035 | −0.28 ± 0.06 | −4.36 | 0.001 | −0.16 ± 0.07 | −2.40 | 0.020 |
| DLF-R → Hec-R | 0.60 | 0.001 | 7.376 | 0.007 | 0.27 ± 0.09 | 3.13 | 0.006 | 0.24 ± 0.06 | 4.04 | 0.002 |
| DLF-R ⇆ MeF-1 | −0.31 | 0.002 | 7.310 | 0.007 | −0.06 ± 0.02 | −2.30 | 0.024 | −0.05 ± 0.01 | −4.28 | 0.001 |
| MeF-1 ⇆ Pcu | 0.25 | 0.010 | 3.877 | 0.049 | 0.09 ± 0.05 | 2.05 | 0.036 | 0.05 ± 0.01 | 3.70 | 0.003 |
| Pcu ⇆ Par-R | −0.24 | 0.016 | 4.591 | 0.032 | −0.09 ± 0.05 | −1.85 | 0.049 | −0.08 ± 0.02 | −3.39 | 0.004 |
| Par-R → STS-R | 0.33 | 0.015 | 0.002 | 0.960 | 0.39 ± 0.08 | 4.88 | 0.000 | 0.02 ± 0.03 | 0.72 | 0.245 |
| Pla-R → Par-R | 0.38 | 0.043 | 6.400 | 0.011 | 0.02 ± 0.07 | 0.21 | 0.420 | 0.16 ± 0.04 | 3.88 | 0.002 |
| Hec-R → Pla-R | 0.51 | 0.011 | 2.392 | 0.122 | 0.33 ± 0.14 | 2.30 | 0.024 | 0.15 ± 0.05 | 2.87 | 0.009 |
| Hec-R → STS-R | 0.58 | 0.000 | 1.777 | 0.183 | 0.45 ± 0.08 | 5.28 | 0.000 | 0.10 ± 0.06 | 1.53 | 0.080 |
- *Data presented as means ± SD. Path coefficients represent the response of a target area to a unitary change in activity of the source area. Group analysis: the time series concatenated across the ten subjects was used for correlation matrix computation. The P-value (χ 2 = 21.1; d.f. = 19) corresponding to the model rejection was 0.332 (that is the model could not be rejected) and the Akaike Information Criterion was 55 (72 for saturated model and 105 for independence model), which argues for the appropriateness of the model. The P-values listed in the table are given by Amos software and represents the significance of the difference of the path coefficients from zero. A nested model analysis was used to compare the path coefficients obtained with the task-related variation and the residual variation. For each connection, Amos software provided the χ2 value (d.f. = 1) and the P-value testing the path coefficient difference between the two models. Individual analysis: a correlation matrix was computed from the adjusted time series for each subject and the path coefficients were determined using Amos software. For each connection, the mean of the ten values obtained was compared to zero by t-test. The path coefficients were also determined from the correlation matrix computed from the residual time series for each subject. The table gives the mean of the differences between the path coefficients obtained using the two correlation matrices. †The significance of these differences was assessed using paired t-tests.
Such a group analysis can be criticized because the observed path coefficients do not take into account the intersubject variability. Therefore, we performed individual analysis; the correlation matrix computed from the time series of each subject was analysed. Then, for each path coefficient, the mean of the ten values (one per subject) was compared to zero using a t-test. Only one path coefficient, from Pla-R to Par-R was not found different from zero (P > 0.05, see Table 2). The comparison between the path coefficients obtained with the task-related and the task-unrelated correlation matrix led to results very similar to the same comparison in the group analysis. The only difference was that the path coefficients for the Hec-R to Pla-R connection were now different between the two models.
Discussion
The aim of the current study was to uncover the connectivity between areas involved in an auditory task. We have analysed the interaction between areas during an auditory task using both PCA and SEQM to assess functional and effective connectivity, respectively. In the SEQM analysis we have introduced a priori hypothesis about the effective connectivity between areas engaged in a visual-related task, in order to test the adequation of this pattern of connections to describe activity during an auditory task. To date, there are only few reports about the connectivity during an auditory-directed task and our work allows us to infer a broader model of connectivity than those described so far.
The first two components found in the PCA allow the considered brain areas to be separated according to task-related factors. Along the first component, high values were observed during the resting state and low values during performance of the auditory task. Therefore, the high score of MeF, Pcu and visual areas on this component can be interpreted as reflecting both a high activity of these regions during resting state (that implicates a lower activity during the auditory task), as well as the correlations between the activities of these areas. Such a pattern of high and correlated activity in MeF and Pcu has already been established in the resting state (Gusnard & Raichle, 2001; Chaminade & Fonlupt, 2003). The additional correlation of the activity of the visual areas with the activity of the areas active during the resting state showed that directing attention towards the auditory modality has a negative effect on the visual areas. The second component retrieved in the PCA separated short and long durations of active monitoring of the auditory stimulus. For this component, we observed that the areas were organized according to their position along the integration pathway of the auditory input from primary areas to frontal areas. The frontal areas included DLPFC and SMA, which are implicated in attentional (Rees & Lavie, 2001) and motor (Rushworth et al., 2004) control, respectively.
To characterize further the relations between the different areas, we have tested a causal model using SEQM. The observation of the path coefficients retrieved from this analysis allows the distinction of at least two subsystems. A sensory integration pathway involves Hec-R, Pla-R and STS-R. The positive path value from Hec-R to Pla-R was in accordance with a previous report (Gonçalves et al., 2001), but in contrast with this previous report, we obtained a good reproducibility across subjects. The second positive coefficient from Hec-R to STS-R represents a higher level of integration of the auditory input because STS plays a key role in the representation of human features (Puce & Perrett, 2003) and could be a convergence point for the visual and auditory modalities (Grèzes et al., 2001; Bidet-Caulet et al., 2005). Moreover, the values of the path coefficients determined from the activity not related to the task (i.e. the residual time series obtained after subtraction of the task-related time series from the raw data) are not significantly different. This suggests that these relations within the auditory integration pathway are largely automatic and constitute a structural feature that is not dependent on the task.
Another set of areas, including Pcu, MeF-1, and DLF-R, can be identified as part of a control system exerting a modulatory effect on sensory pathways according to task demands. This hypothetical regulatory role is suggested by the significantly greater values of path coefficients calculated from the task-related variation than those calculated from the task-independent variations. The relations between anterior (MeF-1) and posterior (Pcu) medial areas are similar to those previously observed during a visual-related task (Chaminade & Fonlupt, 2003). The positive relation observed between MeF-1 and Pcu can be related to the covariation of their activities observed during the comparison of the resting state to various perceptual tasks (Wicker et al., 2003) or the comparison of self-referential tasks to goal-directed task (Gusnard et al., 2001). Moreover, the MeF-1 and Pcu clusters are close to the areas that have been found connected during active tasks (Johansen-Berg et al., 2004). The negative relation between the lateral (DLF-R) and medial (MeF-1) parts of the frontal cortex can be explained by the shift of attention between internal (self) and external (environment) goals (Gusnard et al., 2001) and extend the results previously found for the visual modality (Chaminade & Fonlupt, 2003). The observed negative relation between Par-R and Pcu is consistent with the negative relation observed during a visual task (Chaminade & Fonlupt, 2003), although no clear interpretation can be proposed for this relation. Finally, the two path coefficients relative to the effect of DLF-R on visual and auditory areas have significant negative and positive values, respectively. This area of the lateral part of the frontal cortex is connected to sensory areas and has been repeatedly demonstrated as exerting a positive influence on visual areas (Rees & Lavie, 2001) when attention is directed towards this modality (Ress et al., 2000; Ress & Heeger, 2003). Here, a similar positive influence over auditory areas is shown when attention is directed towards the auditory modality. Moreover, to date, only positive effects of the lateral part of frontal cortex on visual pathways have been reported and the negative effect shown here permits us to propose an extended role for this part of frontal cortex. Increased activity in DLPFC during a goal-directed task induces activation of the areas processing the relevant sensory modality and inhibition of the areas processing the nonrelevant sensory modality.
Conclusion
Our results support a model of connectivity within a temporo-parieto-frontal network engaged in an auditory goal-directed task similar to the connectivity models within occipito-parieto-frontal networks described in tasks directing attention towards the visual modality. In particular the mutual inhibitory connections between the medial and lateral prefrontal cortex, well described when directing attention towards the visual scene, are also found here when directing attention towards the auditory scene. Further, the DLPFC has been repetitively reported to exert a positive influence over the visual areas during visual tasks. Here we show a positive influence on the auditory areas during an auditory task accompanied by a negative influence on the visual areas. The DLPFC thus appears to operate a balance between the activity of the task-relevant and task-irrelevant sensory pathways.
Acknowledgements
We thank J.L. Anton, B. Nazarian, and M. Roth from the fMRI Centre, Marseille, France for their helpful assistance.
Abbreviations
-
- DLPFC
-
- dorsolateral prefrontal cortex
-
- PCA
-
- principal component analysis
-
- SEQM
-
- structural equation modelling
-
- VOI
-
- volume of interest




