Optimizing interpolation of shoot density data from a Posidonia oceanica seagrass bed
Abstract
A case study on the optimization of Posidonia oceanica density interpolation, using a data set from a large meadow at Porto Conte Bay (NW Sardinia, Italy), is presented. Ordinary point kriging, cokriging and a weighted average based on inverse square distance were used to interpolate density data measured in 36 sampling stations. The results obtained from different methods were then compared by means of a leave-one-out cross-validation procedure. The scale at which interpolation was carried out was defined on the basis of the Hausdorff dimension of the variogram. Optimizing spatial scale and data points search strategy allowed obtaining more accurate density estimates independently of the interpolation method.
Problem
Posidonia oceanica (L.) Delile is the most abundant seagrass in the Mediterranean Sea (Lipkin et al. 2003; Procaccini et al. 2003). This phanerogam forms large and widespread beds, covering about 40,000 km2 (Pergent 1993), and is one of the most productive Mediterranean ecosystems (Ott 1980; Buia & Mazzella 1991; Mazzella et al. 1992). Because of its important role in the marine environment, several direct and indirect methods have been developed to evaluate the ecological status of the meadows (Giraud 1977; Ott & Maurer 1977; Fresi & Saggiomo 1981; Meinesz et al. 1981; Boudouresque et al. 1983; Belsher et al. 1988; Buia et al. 1992; Pasqualini et al. 1998; Marcos-Diego et al. 2000). Among direct methods, measuring density (number of shoots m−2) is probably the most straightforward. Shoot density depends on structure and functionality of a meadow as well as on its ability to adapt to substrate variability. Moreover, shoot density plays an important role when estimates of quantitative properties of P. oceanica beds are to be calculated (e.g. for primary production studies; Wittmann 1984; Romero 1989; Buia et al. 1992; Cebrian & Duarte 2001; Dumay et al. 2002). The assessment of shoot density is usually carried out by counting the number of shoots within square frames, and then averaging several counts (Giraud 1977; Pergent-Martini & Pergent 1996). If the positioning of the frames is not biased and if enough counts are available, reasonably accurate estimates can be obtained of the mean shoot density within the sampling area. However, small scale spatial analyses showed very complex patterns (Panayotidis et al. 1981; Balestri et al. 2003; Gobert et al. 2003; Zupo et al. 2006), which were observed even within apparently dense and homogeneous stands in P. oceanica beds (i.e. 56 regularly spaced counts in 40 × 40 cm squares ranged from 238 to 1438 shoots m−2 within a 16 × 16 m area, according to Valiante L. M., Casola E., Procaccini G. & Sordino P., unpublished data).
To use density data to reconstruct large scale patterns or to integrate over space other ecological properties of P. oceanica beds that are related to density, punctual density estimates have to be interpolated. Several techniques are available, but geostatistical methods (e.g. kriging) have been shown to be the most effective ones (Field et al. 1987; Scardi et al. 1989; Pergent 1990; Zupo et al. 2006). The application of these methods to P. oceanica density interpolation, however, is not as straightforward as in other applications. This is because of both the complex spatial structure of the P. oceanica beds and the above mentioned small scale variability.
This paper focuses on the optimization of some features in the interpolation of P. oceanica density data, such as selection of appropriate methods and spatial scales, using a data set from a central-western Mediterranean bed. Results obtained on the basis of different interpolation approaches will be presented and discussed. These results, however, are only based on a subset of all the possible combinations of methods, scales and other options and therefore our conclusions are to be considered as a starting point for further research rather than as those of a fully exhaustive geostatistical study. In fact, such a study would have been too complex to be presented in a single paper.
Material and Methods
Study area
Porto Conte Bay (Sardinia, Italy, 40°35′ N–8°12′ E) is a large inlet, approximately 6 km long and 3.5 km wide, where a large Posidonia oceanica bed stretches from 4 to 30 m depth. In this Posidonia bed several morphological features can be found (Chessa et al. 1988), with the interposition of two other phanerogams (i.e.Cymodocea nodosa and Nanozostera noltii) and of the green alga Caulerpa prolifera. The overall sea floor area covered by the P. oceanica bed is about 6 km2.
Sampling methods
The interpolation procedures presented in this paper were based on a data set collected in June 1986. At first 30 sampling stations were randomly set in the innermost part of the bay, within the area in which nautical charts reported the presence of phanerogams (i.e.‘weeds’). Posidonia oceanica was actually found in 26 out of 30 sampling stations (black and white triangles in Fig. 1), while six out of these 26 stations were located outside the limits of the main bed (white triangles in Fig. 1). The exact upper limit of the main bed was outlined by means of aerial photography after sampling (dashed line in Fig. 1). After a preliminary analysis of the density data, 10 supplementary sampling stations (crosses in Fig. 1) were added where the variance of the density estimates was the highest. Therefore, a data set including 36 sampling stations was available for spatial analysis and interpolation.
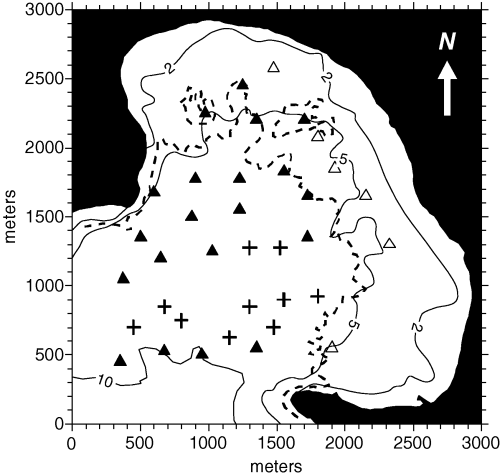
Sampling stations and depth in Porto Conte Bay (Sardinia, Italy). The dashed line shows the upper limit of the main Posidonia oceanica bed. At first 26 sampling stations were randomly set: 20 of them were located within the main bed (black triangles), whereas six were outside its limits (white triangles). After a preliminary spatial analysis 10 more sampling stations were added where the interpolation error was the largest (crosses).
Station positioning, and all the maps (including the one shown in Fig. 1), were based on an UTM grid (zone 32T). In order to simplify graphical outputs and computation of distances, all coordinates in our study are expressed as distances in meters from the origin of our maps (lower left corner). These coordinates were obtained by subtracting the UTM coordinates of the origin from all the other points. The zone 32T coordinates of the origin of our maps were 431083 E–4493744 N, corresponding to WGS84 geodetic coordinates 40°35′29.85′′ N–8°11′08.02′′ E.
Shoot density was measured by SCUBA divers, who counted the shoots within five square frames (40 × 40 cm) randomly located in the P. oceanica bed within a 25-m diameter circle centered on the station point. Afterwards, the mean value of the five counts was converted to density expressed as shoots m−2. The percentage of sea floor that was actually covered by P. oceanica within the circular sampling area was independently assessed by two divers. Then the average cover percentage was assumed as the best estimate of sea floor cover, which is also needed for computing relative density (i.e. density × sea floor cover, also defined as ‘global density’ by Romero 1985). Cartesian coordinates of the sampling stations as well as their depth, sea floor cover and absolute density data are shown in Table 1.
| x (m) | y (m) | Depth (m) | Cover (%) | Absolute density (shoots m−2) |
|---|---|---|---|---|
| 350 | 450 | 10.5 | 65 | 281 |
| 675 | 525 | 11.0 | 85 | 350 |
| 950 | 500 | 10.0 | 35 | 119 |
| 1350 | 550 | 8.5 | 60 | 256 |
| 1900 | 550 | 5.0 | 28 | 456 |
| 375 | 1050 | 8.5 | 55 | 231 |
| 650 | 1200 | 7.5 | 100 | 394 |
| 1025 | 1250 | 8.0 | 100 | 400 |
| 1725 | 1350 | 6.0 | 100 | 381 |
| 2325 | 1300 | 4.0 | 10 | 69 |
| 500 | 1350 | 8.0 | 100 | 488 |
| 875 | 1500 | 8.5 | 70 | 450 |
| 1225 | 1550 | 8.0 | 90 | 475 |
| 1725 | 1650 | 6.0 | 100 | 388 |
| 2150 | 1650 | 5.0 | 28 | 138 |
| 600 | 1675 | 7.0 | 73 | 413 |
| 900 | 1775 | 7.0 | 75 | 481 |
| 1225 | 1775 | 6.0 | 100 | 506 |
| 1550 | 1825 | 6.0 | 90 | 331 |
| 1925 | 1850 | 6.0 | 42 | 175 |
| 975 | 2250 | 5.0 | 45 | 525 |
| 1350 | 2250 | 5.0 | 50 | 344 |
| 1700 | 2200 | 5.5 | 55 | 188 |
| 1800 | 2075 | 4.5 | 38 | 175 |
| 1250 | 2525 | 3.0 | 50 | 644 |
| 1475 | 2575 | 3.5 | 45 | 531 |
| 450 | 700 | 10.5 | 80 | 394 |
| 800 | 750 | 10.0 | 45 | 313 |
| 675 | 850 | 11.0 | 45 | 375 |
| 1300 | 850 | 9.5 | 50 | 400 |
| 1550 | 900 | 7.5 | 60 | 475 |
| 1800 | 925 | 7.0 | 70 | 369 |
| 1525 | 1275 | 7.0 | 90 | 388 |
| 1300 | 1275 | 9.0 | 80 | 394 |
| 1150 | 625 | 9.0 | 40 | 294 |
| 1475 | 700 | 9.0 | 70 | 394 |
The purpose of these two ways of evaluating density is obviously not the same, as well as their interpretation. Absolute density is more closely related to the health of the bed and to its short-term dynamics, whereas relative (or global) density is more useful in ecosystem scale studies and reflects the outcome of long-term colonization dynamics (Romero 1985).
Data analysis
Our analyses focused on density (i.e. on the shoot density within the area covered by P. oceanica) rather than on relative (or global) density. The interpolation of density data was based on three techniques. The simplest one was a weighted average based on inverse square distances from known points. Ordinary point kriging (Journel & Huijbregts 1978; Cressie 1991) was also used, as well as cokriging (Isaaks & Srivastava 1989; Cressie 1991). Inverse square distance and kriging interpolation were carried out using software developed by the Authors, whereas a software package by Bogaert et al. (1995) was used for cokriging.
Independently of the method, interpolation was carried out on grids whose mesh size was equal to the diameter of the circular sampling areas (25 m). Detrending was not needed for kriging and cokriging interpolation, as no significant trends were detected in the data set. In all kriging and cokriging interpolations, variograms were modeled using a combination of nugget and spherical terms, optimized by means of a least squares procedure. Accuracy of interpolation methods was assessed on the basis of the mean square error obtained from a leave-one-out cross-validation procedure (Yates & Warrick 1987). To optimize interpolation results, the spatial scale beyond which spatial ‘noise’ was larger than spatial ‘signal’ was estimated after the Hausdorff dimension (D) of the omnidirectional variogram. The Hausdorff dimension is related to the way an object occupies space and to the concept of fractal dimension. Details about its application to variograms as well as estimates obtained in different geological and ecological applications can be found in Burrough (1981). As the topological dimension of a variogram (as well as that of a line) is one, its Hausdorff dimension ranges from one to two depending on the way the variogram occupies its (bidimensional) space, i.e. on how much crumpled it is. The Hausdorff dimension can be estimated on the basis of the slope b of the log–log variogram, given that D = (4 − b)/2. If variograms were perfect fractal entities, then the estimated dimension D would be invariant with respect to the maximum distance between data pairs considered in the variogram, but in real world situations spatial scale does affect D. As D = 1 implies an absolutely smooth spatial structure and D = 2 an infinitely complex one, the midpoint of this range (i.e. the distance at which D becomes larger than 1.5) is of particular interest, and it might indicate the largest significant spatial scale at which the available information can contribute in a meaningful way to the interpolation. Therefore, optimized interpolations were performed using a search radius equal to one-half of the distance at which D = 1.5. Further optimization was then achieved by dividing the resulting search circle into four 90° sectors and interpolating only points that had neighboring data points in more than a single sector.
Results
General remarks
An underwater survey carried out in the innermost part of Porto Conte Bay showed that the Posidonia oceanica bed was apparently dense below 5 m, while in shallower sites it became more sparse, being substituted by Caulerpa prolifera or Cymodocea nodosa (the latter occasionally mixed with patches of Nanozostera noltii). Intermatte channels were often present at depths between 5 and 10 m, particularly in the westernmost part of the bay. The matte height ranged from 70 to 130 cm. In the western part of the bay (at depths from 8 to 10 m) there were evident signs of mechanical disturbance on the bed (e.g. scars due to trawling gear, boat anchoring), and rhizomes were easy detachable by hand.
Basic interpolation
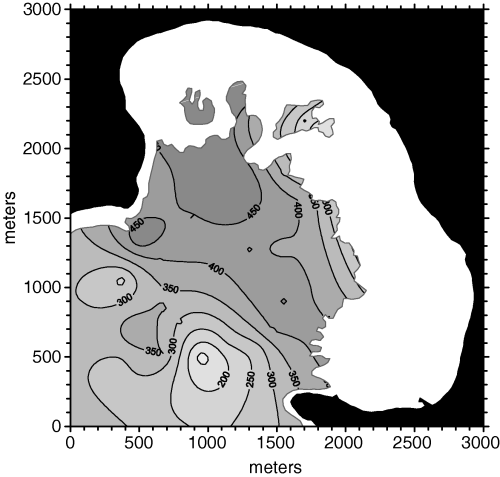
The first attempt at interpolating density data was carried out using a weighted average based on the inverse square distance of all known points from the point to be interpolated. This is a very popular and straightforward technique that partly takes into account the spatial structure of P. oceanica bed density, although in a simplified way that does not require variogram modeling. The leave-one-out cross-validation MSE (mean square error) was 10,090 and the resulting map of the P. oceanica bed density is shown in Fig. 2. The overall density structure is clear, but several circular features in the isopleths are present and they can be regarded as artifacts because of high local heterogeneity in density data.
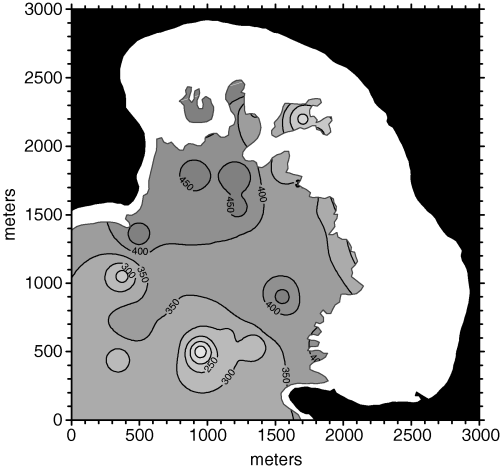
Posidonia oceanica bed density map obtained from unoptimized weighted average based on inverse square distance.
Taking into account spatial properties of the variable to be interpolated by means of variogram analysis allows using geostatistical tools, like kriging and cokriging. These methods require user interaction for variogram modeling, but, in theory, they should be more effective than simpler methods.
As no anisotropy was detected in density data, an omnidirectional variogram was used. The empirical variogram and the modeled one are shown in Fig. 3. The modeled variogram was spherical (range = 1334 m; scale = 14,910) with a nugget effect [γ(0) = 975.5]. Posidonia oceanica density data were then kriged using this variogram, and a significant improvement in the interpolation accuracy was achieved (MSE = 7197). The kriged density map is shown in Fig. 4.
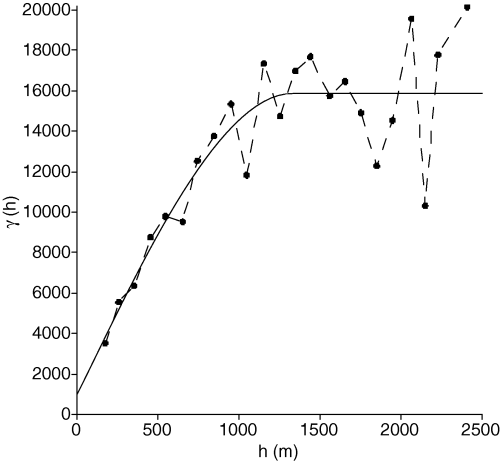
Empirical (dashed line) and modeled (solid line) omnidirectional variograms. Spatial variance γ is shown as a function of distance h. A spherical model (range = 1334 m, scale = 14910) with nugget effect (975.5) was selected.
Posidonia oceanica bed density map obtained from unoptimized ordinary point kriging.
To improve the interpolation accuracy, covariables (i.e. variables that tend to covariate with P. oceanica density) were then taken into account. The relationship between depth and density is generally well known, although not significant in Porto Conte Bay. However, density was significantly correlated to the percentage of sea floor covered by P. oceanica in Porto Conte Bay (r = 0.458**). Therefore, both depth and sea floor cover were associated to density and normalized variograms and covariograms were computed (Fig. 5).
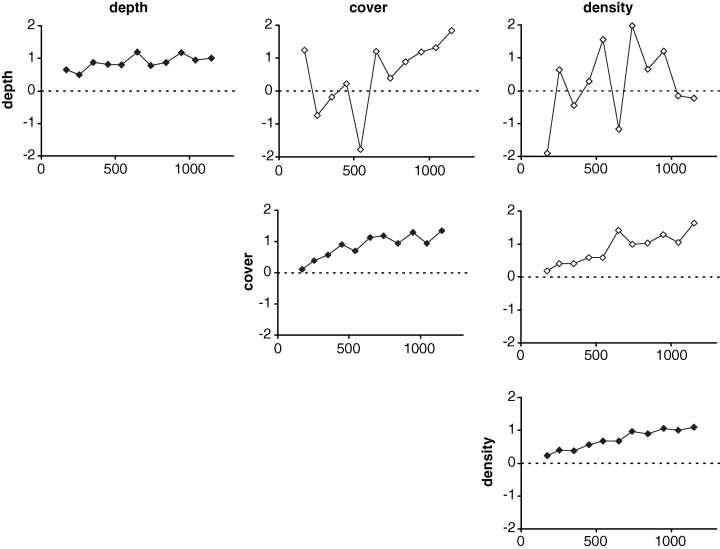
Empirical standardized variograms and covariograms for depth, substrate cover and density of the Posidonia oceanica bed.
Depth, although relevant in most sites, did not play a significant role as a covariable in the Porto Conte P. oceanica bed, and its almost random covariograms were a clear evidence for this lack of correlation. On the contrary, sea floor cover covariated with density, and the corresponding covariogram showed this tendency. These (co)variograms were then used for density cokriging, using spherical models (not shown in Fig. 5) with the same range as the one that was used for ordinary point kriging (see Fig. 3). However, the cross-validation results did not show improvement over ordinary point kriging, as the MSE was slightly larger than in the latter case. The density map obtained from cokriging is shown in Fig. 6, and it is evident that it very closely resembles the kriged one.
Posidonia oceanica bed density map obtained from unoptimized cokriging.
Optimizing interpolation technique
The results of density interpolation obtained by means of (co)kriging were certainly adequate for most purposes, but our aim was to reduce as much as possible the cross-validation error. To increase the interpolation accuracy, the amount of spatial ‘noise’ affecting the interpolation had to be minimized. Variograms usually convey useful information about this kind of disturbance, but a suitable method was needed for separating the really meaningful part of the variograms from the rest. In particular, when a variogram is plotted on log–log scale (Fig. 7) its Hausdorff dimension, which ranges from 1 to 2, depends on its slope and can be assumed as a measure of variogram complexity. However, as real variograms are not fractal objects, their slope is not constant and the estimate of their Hausdorff dimension, which is related to the slope b of the log–log variogram [D = (4 − b)/2], varies depending on the spatial scale. In other words, the slope estimated after the first two points in the log–log variogram is not the same as the one estimated after the first three points, and the latter is not the same as the one estimated after the first four points, and so on. Therefore, the estimate of the Hausdorff dimension is a function – usually monotonically growing – of the maximum distance between data points.
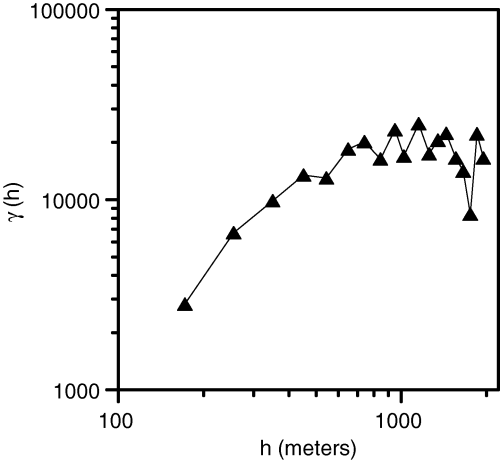
Log–log omnidirectional variogram of density data. The slope (b) of this variogram is related to its Hausdorff dimension [D = (4 − b)/2], which can be regarded as a measure of spatial complexity of the density structure.
In the case of Porto Conte P. oceanica density, the variogram slope decreased with maximum distance between data points and therefore the estimate of its Hausdorff dimension increased with this distance (Fig. 8). The distance at which the estimate of the Hausdorff dimension became D = 1.5, which in our data set was approximately equal to 1050 m, could be regarded as the maximum spatial scale at which P. oceanica density patterns were smooth and ordered enough to be useful for geostatistical analyses. Therefore, taking into account only data points that were no farther than 1050 m from each other was a sensible choice for optimizing P. oceanica density interpolation independently of the adopted method.
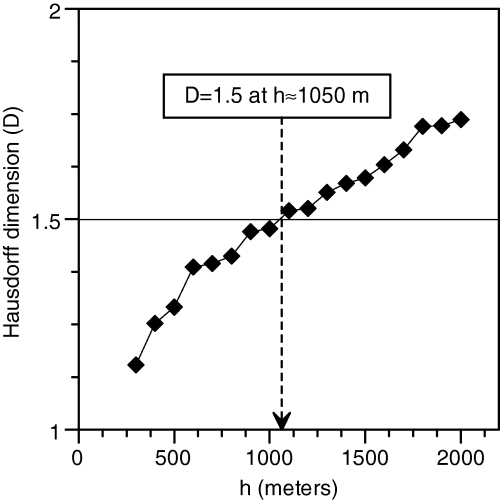
Hausdorff dimension of the density variogram versus maximum distance between data points. If the variogram were a perfect fractal object, its log–log slope would be scale-invariant and its Hausdorff dimension would be constant. In real world conditions, however, the estimate of the Hausdorff dimension depends on spatial scale. D = 1.5 was reached at 1050 m and this can be assumed as the spatial scale at which spatial ‘noise’ became larger than spatial ‘signal’.
The cokriging interpolation was then performed again, limiting the data point search radius to 525 m. The cross-validation results were better than those of the unconstrained cokriging interpolation, as the MSE was 15% lower (MSE = 6330). The density map in Fig. 9 is obviously similar to the one obtained without limitations in the search radius, although some finer features appeared.
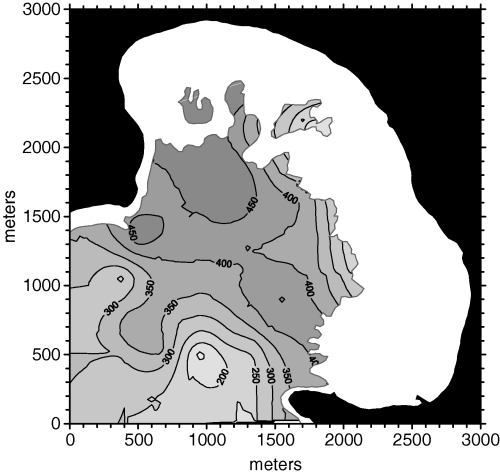
Posidonia oceanica bed density map obtained from cokriging with a 525 m maximum search radius.
Optimizing search strategy
A further improvement in interpolation accuracy was obtained by constraining the search for data points not only within a given radius, but also by dividing the search circle into four sectors and excluding from the interpolated grid those points that did not have at least two neighbors within the search radius (525 m), but in different sectors. As the variogram was omnidirectional, the role of search sectors was limited, because it only involved an optimized geometry of data points used for interpolation.
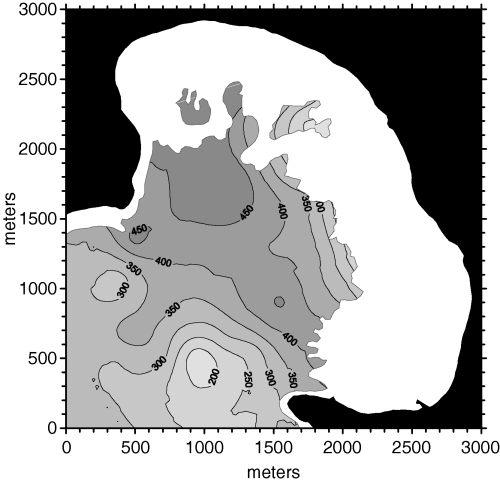
Applying these constraints to ordinary point kriging led to a gain in accuracy that was certainly limited, but not negligible (MSE = 6123). The density map obtained from this approach is shown in Fig. 10. The hashed area in the lower left part of the map was not kriged because of the lack of data points within 525 m in more than one search sectors out of four.
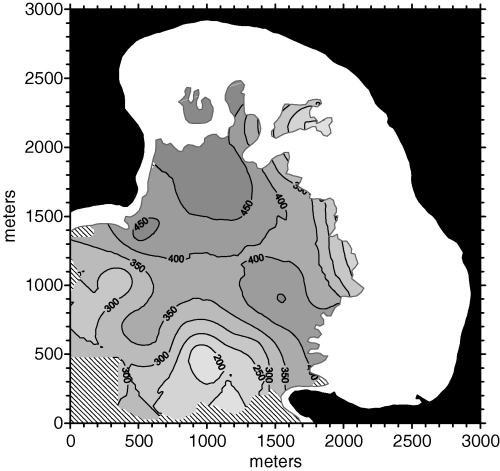
Posidonia oceanica bed density map obtained from ordinary point kriging with a 525 m maximum search radius and directional data point search strategy (four sectors).
Is (co)kriging the best interpolation method?
The selection of suitable interpolation methods and appropriate constraints in searching for neighboring data points led to a consistent improvement in cross-validation MSE. However, in order to better understand the relative weight of these components, we also applied the search constraints that were set for the last kriging interpolation to an inverse square distance interpolation. Surprisingly, the cross-validation results showed that this method, although much simpler, was slightly more accurate than kriging (MSE = 6006). The hashed areas in the resulting density map are those where not enough neighboring data points were available for interpolation (Fig. 11). The overall density structure depicted by this method was obviously similar to the kriged one, although it seemed more influenced by single data points. For instance, there are two low density ‘cores’ in the lower left part of the map that are deeper than in the kriged map. The reason for this difference was that local variance was considered in kriging thanks to the nugget effect in variograms, while it had no effect in inverse distance interpolation.
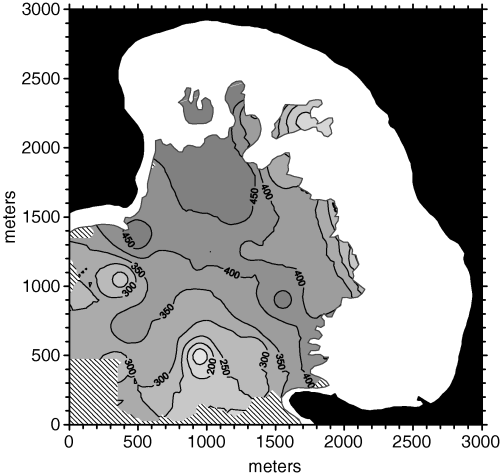
Posidonia oceanica bed density map obtained from weighted average based on inverse square distance with a 525 m maximum search radius and directional data point search strategy (four sectors).
Discussion
Independently of the interpolation method, Posidonia density was higher in the middle of Porto Conte Bay and tended to decrease in outer areas, thus ranging from about 400 shoots m−2 [Type III bed according to Giraud (1977)] to about 200 shoots m−2 [Type IV bed according to Giraud (1977)]. This range corresponds to abnormal density (AD) in most shallow stands (depth < 6 m) and to normal to lower subnormal density (ND to LSD) in the central part of the Bay, according to the classification proposed by Pergent et al. (1995) and Pergent-Martini & Pergent (1996). The main source of disturbance was probably illegal bottom trawling (Chessa & Fresi 1994; Cossu et al. 2001) and extensive SCUBA diving inspections supported this hypothesis.
From a methodological point of view, it was surprising to find out that a rather simple interpolation method, like a weighted average based on inverse square distance, was slightly better than more complex – and theoretically more effective – geostatistical methods in interpolating P. oceanica density data (Table 2). Assuming that cross-validation was the only reliable way to compare interpolation methods in a data-limited situation, differences in MSE between inverse square distance, kriging and cokriging became very small (<5%) once a suitable data point search strategy was defined. Therefore, selection of the interpolation method seemed less important than definition of an optimal spatial scale for interpolation.
| Interpolation method | MSE |
|---|---|
| Inverse square distance, r = ∞ | 10,090 |
| Kriging, r = ∞ | 7197 |
| Cokriging, r = ∞ | 7333 |
| Cokriging, r = 525 m | 6330 |
| Kriging, r = 525 m, 4 sectors | 6123 |
| Inv. square dist., r = 525 m, 4 sectors | 6006 |
Geostatistical techniques, which are supposed to be more effective than other methods, rely upon theoretical assumptions that were probably not met by P. oceanica density data and this could be the reason why they did not outperform a simpler approach. The large local variability of density measurements obviously played a major role, but other features like, for instance, discontinuities and patchiness in P. oceanica bed structure, were not less important.
Moreover, density of seagrass beds is an ill-defined concept, as it changes according to the way field measurements are carried out and to the way density data are processed. In both cases this mainly depends on spatial scale, which is probably the most critical choice in the optimization of a procedure for density interpolation.
Defining an appropriate spatial scale affects all the phases of a geostatistical study, from data collection to data analysis and from interpolation to graphical output or spatial integration. Different approaches can be selected for optimizing each phase, but variogram analysis is certainly fundamental for optimizing interpolation options. Of course, even variogram analysis is not independent of spatial scale and therefore a (theoretically) scale-invariant approach to variogram analysis should be selected.
Computing the Hausdorff dimensions of a variogram at increasing spatial scales is a very simple way to assess the spatial ‘signal’ to spatial ‘noise’ ratio in a set of density data. Thus, its breakeven point (corresponding to D = 1.5) might suggest which is the largest radius within which the spatial ‘signal’ can be exploited by geostatistics or by simpler methods. This claim is obviously based on theoretical issues only, as P. oceanica density estimates are inherently scale-dependent and no information about the ‘real’ density structure of a P. oceanica bed will be ever available. Therefore, the selection of an interpolation method in P. oceanica density studies is probably a subordinate issue within a more complex problem (involving spatial scale, sampling design, software availability, etc.).
In particular, the latter problem cannot be overlooked, as cokriging, that in theory should be at least as effective as ordinary kriging, and therefore a good choice in most cases, is not available in user-friendly commercial software packages. The package by Bogaert et al. (1995) used in this study, on the other hand, was developed 10 years ago and it is too slow for complex tasks. For instance, the first cokriged map in this paper (Fig. 9), which was based on a 105 × 113 grid like all other maps, was computed in about 28 h by a 2.6 GHz PC. Other geostatistical packages include cokriging, but they are very expensive and require specific training. Finally, covariables that effectively support density interpolation are not easy to find. Depth is the most obvious choice, and substrate cover (which in some cases can also be obtained from Side-Scan Sonar surveys) is a second option, but others are neither obvious nor always available.
At the opposite end of the spectrum of interpolation methods, weighted average based on inverse square distance performed very well, providing the smallest MSE in our cross-validation tests. However, it estimated more accurately density values that were not too far from average, while it was slightly less accurate than geostatistical methods with very small and very large values. The same problem was also observed with (co)kriging, although to a lesser extent. It obviously depends on the lack of adequate information about the complex patterns in the P. oceanica bed, whose structure can be only roughly approximated (and therefore smoothed) by interpolation methods.
In this framework, ordinary point kriging is probably the best compromise between simplicity and efficiency. It is not as straightforward as a weighted average, but it is available in user-friendly software packages and, if properly applied, provides additional information that can be very useful in sampling optimization. In fact, like cokriging, it allows computing an estimate of the variance or standard deviation associated to each interpolated value. Knowing how large is the expected interpolation error may be very useful for planning additional sampling, thus improving the accuracy of density estimates where the interpolation error is large. This way, for instance, ten additional sampling stations were added to our data set after a preliminary analysis.
However, variogram modeling plays a critical role in assessing the interpolation error, which is reliable only in case the experimental variogram effectively describes the spatial properties of the variable to be interpolated, and the modeled variogram nicely fits experimental data. Even in this case, search strategy (radius and other constraints) should be carefully optimized.
In conclusion, our results suggested that the selection of the interpolation method in P. oceanica density studies was not as critical as the selection of an appropriate spatial scale. Constraining search radius and directional criteria allowed defining an optimal neighborhood within which the spatial properties of density data could be best exploited, thus providing reliable density estimates even when a very simple interpolation method was used (i.e. weighted average based on the inverse square distance). Even in this case, one must always bear in mind that P. oceanica density is an ill-defined concept, because of its scale dependency. Moreover, the density we measure – at a given spatial scale – in a P. oceanica bed is the outcome of long-term interactions between P. oceanica growth dynamics and adaptation to the substrate. In older beds the former certainly plays a major role, whereas the latter is probably more relevant in younger beds or in cases where the underlying geomorphological features are very complex.
In both cases, however, correct interpolation of P. oceanica density data is much more difficult than interpolation of variables whose spatial properties are generated by simpler processes (e.g. diffusion). Therefore, we can rely upon density interpolation for integrating in space relevant properties of a P. oceanica bed (e.g. primary production), but we cannot expect to discover hidden patterns or other fine details [e.g. micro-scale density variation (Gobert et al. 2003)], unless an appropriate study is carefully planned and carried out at the appropriate scale. Moreover, an inherent limitation in the results of interpolation is a tendency toward underestimation of high values and overestimation of low values, which is proportional to the local variance of density data (i.e. on the nugget effect in variograms). On the other hand, if local variance is ignored or underestimated, interpolation is likely to produce artifacts (e.g. nestlike structures).
Given the complexity of the processes that generate density patterns in P. oceanica beds, mathematical modeling might be a successful alternate approach or a complement to interpolation. Viable modeling strategies include rhizome growth models and empirical density models. The latter are probably easier to develop, as they can exploit the information conveyed by a number of environmental variables that are possibly (although not certainly) related to density (e.g. bottom slope, exposure to light or to waves, substrate type, etc.). In this framework, artificial neural networks might play a role, as they are the most effective tool in empirical modeling and a very promising addition to the marine ecologist's toolbox (Scardi 2003).
Summary
Shoot density is an important structural descriptor when estimating the quantitative properties of Posidonia oceanica beds. This study focuses on the optimization of the interpolation of P. oceanica density data collected in a central-western Mediterranean bed (Porto Conte Bay, NW Sardinia, Italy). At first 26 sampling stations were randomly set in the innermost part of the bay, while 10 more stations were added after a preliminary analysis of the density data, thus totaling 36 sampling stations. Density was measured by counting shoots within five square frames (40 × 40 cm) randomly located in the P. oceanica bed within a 25-m diameter circle centered at the station point. Interpolation of density data was carried out by ordinary point kriging, cokriging and a weighted average based on inverse square distance. In all cases, data were gridded using a mesh size that was of the same size as the diameter of the sampling stands, i.e. 25 m. The results of different interpolation procedures were compared by means of a leave-one-out cross-validation. Geostatistical techniques (i.e. kriging and co-kriging) provided better results when applied without optimization, while differences between methods were negligible when interpolation spatial scale and data points search strategy were optimized. The Hausdorff dimension (D) of the omnidirectional variogram was analysed to define the largest scale at which spatial ‘signal’ was still larger than spatial ‘noise’. Assuming that such a scale corresponded to D = 1.5, the resulting radius (525 m) was then used for optimized interpolation. Finally, data points within this radius were searched directionally, i.e. by dividing the search circle into four sectors and interpolating only points that had neighbors in at least two different sectors. As the accuracy of spatially optimized interpolation was almost independent of the technique, other issues were taken into account to select the most effective approach. Ordinary point kriging is probably the best compromise between ease of use, accuracy and information content of the results. In fact, it is widely available even in user-friendly software packages and it also provides estimates for the interpolation error. The conclusions of our study should be regarded as an ecologist's perspective rather than as thorough and rigorous geostatistical study, as we optimized the interpolation procedure taking into account only a limited subset of all the possible combinations of methods and parameters. Therefore, further work is needed to confirm and possibly to generalize our results.
Acknowledgements
This paper is a tribute to the memory of Lucia Mazzella, head of the Marine Benthos Laboratory of the Stazione Zoologica of Naples, a leading scientist as well as a close personal friend. Her loss was deeply felt not only by all the people who collaborate with her, but also by a large number of world scientists. Research was funded by Fondazione Banco di Sardegna.




