Dispersal and genetic structure in the American marten, Martes americana
Abstract
Natal dispersal in a vagile carnivore, the American marten (Martes americana), was studied by comparing radio-tracking data and microsatellite genetic structure in two populations occupying contrasting habitats. The genetic differentiation determined among groups of individuals using FST indices appeared to be weak in both landscapes, and showed no increase with geographical distance. Genetic structure investigated using pairwise genetic distances between individuals conversely showed a pattern of isolation by distance (IBD), but only in the population occurring in a homogeneous high-quality habitat, therefore showing the advantage of individual-based analyses in detecting within-population processes and local landscape effects. The telemetry study of juveniles revealed a leptokurtic distribution of dispersal distances in both populations, and estimates of the mean squared parent–offspring axial distance (σ2) inferred both from the genetic pattern of IBD and from the radio-tracking survey showed that most juveniles make little contribution to gene flow.
Introduction
Dispersal has long been recognized as a key process affecting the evolution of populations, both in terms of demographic and adaptative trajectories. A large body of research has accordingly been dedicated to the elaboration of this process. The collection of information on dispersal remains challenging, however, for a wide array of species, limiting our understanding of dispersal mechanisms. In this context, the development of ‘indirect’ approaches based on the study of gene flow and genetic structure has proved increasingly useful. For example, under simplifying assumptions of equal population sizes (N) and constant rates of migration (m) independent of the spatial distribution of populations, the island model allows quantifying the effective dispersal rate between populations (Nm) directly from observed levels of genetic structure as FST = 1/(4Nm + 1) (Wright 1931; Dobzhanski & Wright 1941). This approximation may, however, be strongly affected by departures from infinite island settings (Whitlock & McCauley 1999). A different approach of dispersal rates based on the contrast in co-ancestry among age classes in highly structured populations has recently proved less sensitive to such departures (Vitalis 2002; Fontanillas et al. 2004), therefore providing a valuable indirect approach to estimate dispersal rates, for instance in metapopulations. Dispersal rates between populations may also be estimated through assignment procedures based on genotype likelihoods. While not relying on simplifying assumptions made by demographic models, the success of this approach is highly dependent on the magnitude of sampling and on the level of differentiation among populations (Paetkau et al. 2004).
In cases where the rate of exchange of individuals depends on the geographic distance separating populations, the genetic structure of populations may be represented by the model of isolation by distance (IBD, Wright 1943). This model states that spatially limited gene flow may cause a nonrandom distribution of genetic variation among populations, characterized by an increase of genetic differentiation with increasing geographic distances among groups of individuals (‘groups’ will be hereafter referred to as ‘samples’, using the statistical meaning of this word). The process of IBD may also be characterized at the individual level within continuous populations, where spatially limited dispersal results in a decrease of the correlation of genetic variation among individuals with increasing geographic distances (e.g. Rousset 1997; Rousset 2000). Both approaches, either considering sample-based or individual-based analyses of IBD, allow inferring some information on dispersal. Under IBD, the relationship between pairwise genetic and geographic distances among individuals or samples may be used to infer the mean squared parent–offspring axial distance σ2, a useful demographic parameter that can also be calculated from the observed distribution of dispersal distance (e.g. Chepko-Sade & Shields 1987; Waser & Elliott 1991; Rousset 1997; Sumner et al. 2001).
A case in point is the American marten (Martes americana), a mid-sized carnivore that is generally associated with conifer-dominated forests in North America. Dispersal behaviour remains poorly documented in this species. Previous studies have shown that genetic structure in this species follows a pattern of IBD at the continental scale (Kyle et al. 2000; Kyle & Strobeck 2003). However, Kyle et al. showed that the increase in genetic differentiation with geographic distance appears surprisingly low when compared to the genetic structure for other larger mustelid carnivore species, with presumably greater dispersal potential such as wolverines (Gulo gulo) or fishers (Martes pennanti). Some marten populations separated by large distances (up to several hundred kilometers) appeared in fact genetically undifferentiated (Kyle & Strobeck 2003). Such a weak genetic structure may possibly result from extensive gene flow at a large spatial scale, suggesting great dispersal capacity in M. americana. Furthermore, the failure to detect stronger structure in the southern range of M. americana distribution, where significant forest harvesting has occurred, suggested that habitat fragmentation due to forest harvesting may not necessarily impede marten movement (Kyle & Strobeck 2003). Daily movements of radio-collared martens of up to 22 km (Davis 1983), and several instances of dispersal movements up to 163 km (Thompson & Colgan 1987; Slough 1989; Fecske & Jenks 2002) have in fact been reported for this species. These observations support the hypothesis that marten dispersal reduces the strength of IBD at large spatial scales. On the other hand, marten populations reintroduced into areas from which they had previously been extirpated showed slow rates of range expansion, of the order of 8–16 km per decade (de Vos 1951; Gardner & Gustafson 2004), suggesting much lower dispersal rates. Furthermore, simulations of marten movement using a spatially explicit individual-based model of dispersal suggest that landscape features could significantly affect dispersal patterns in M. americana (Gardner & Gustafson 2004).
Since direct observations of juvenile dispersal through telemetry studies are scarce, dispersal features remain largely unknown in this secretive species. In particular, it is not known whether the distances cited above are representative of usual dispersal behaviour or if they represent rare events of long-distance dispersal. Here we analysed local spatial patterns of genetic structure in two marten populations sampled in two landscapes differing in habitat quality, with the following objectives: (i) to contrast sample-based and individual-based approaches in examining the fine-scale genetic structure of M. americana; (ii) to infer a synthetic descriptor of dispersal, the mean squared parent-offspring axial distance σ2, from IBD, compared with direct observations of natal dispersal obtained from radio-tracking of juveniles; and (iii) to investigate the sensitivity of individual vs. sample-based analyses in detecting alterations of the dispersal process in fragmented habitat.
Methods
Species and study area
The American marten, Martes americana, is a mid-sized carnivore that is widespread in forested areas throughout Canada. Reproduction in this solitary and territorial species occurs from late June to early September. Implantation is delayed until mid-winter and litters of 2–5 young are born mid-March to late April. In late summer, early fall (i.e. August–September), the young may leave the natal area in search of a new location for territorial establishment for survival and reproduction. Although martens may mate in their first year, they do not reach sexual maturity until their second year (Strickland & Douglas 1987). It has been suggested that breeding dispersal may also occur among M. americana populations, but it was not observed in our study.
This study was conducted in a black spruce/jack pine-dominated boreal forest in northwestern Ontario (Fig. 1), where the ecological requirements of martens (provision of high-quality undisturbed habitat) must be met before any timber harvesting plan is approved according to forest management guidelines (Watt et al. 1996). The study site was characterized by two distinct landscapes differing in harvesting history (hereafter referred to as ‘logged’ and ‘unlogged’ landscapes). The unlogged landscape (c. 1900 km2) was dominated by uncut old-growth forest (i.e. ≥ 80 years old), whereas the logged landscape (c. 900 km2) was composed by a mixture of stands of different ages and types, regenerating after clear-cutting (Fig. 2). The former is considered optimal marten habitat whereas the latter is suboptimal (e.g. Thompson 1994; Thompson & Harestad 1994).
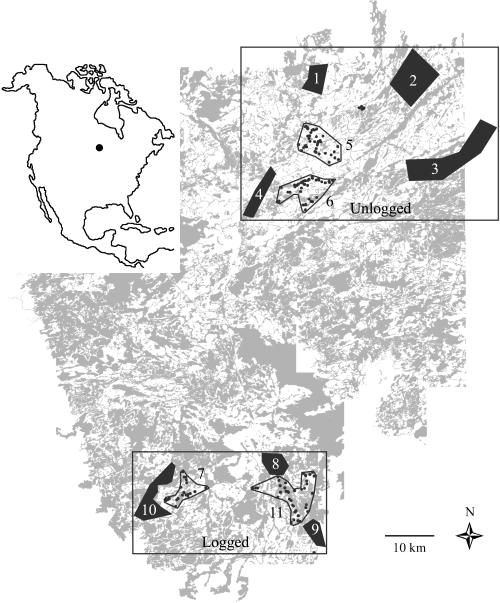
The study area located near Ear Falls, Ontario (50°38′N, 93°13′W), was divided into two landscapes. White areas represent old-growth forest of fire-origin. Regenerating harvested forest (< 40 years old) and water areas are represented in grey. Hair was taken from live-trapped individuals (black dots) from four locations (represented by open polygons): samples 5 (n = 59), 6 (n = 51), 7 (n = 25) and 11 (n = 47). Muscle tissue was collected from marten carcasses from seven commercial trap lines (represented by solid polygons): samples 1 (n = 36), 2 (n = 30), 3 (n = 41), 4 (n = 56), 8 (n = 30), 9 (n = 16) and 10 (n = 28). Edge-to-edge distance between samples within each landscape ranged from 0.2 to 30.2 km. Samples 5 and 6, containing only live-trapped martens characterized by individual geographic coordinates, were used for analyses of isolation by distance between individuals in the logged landscape. Similarly, samples 7 and 11 were used for analyses of fine-scale genetic structure in the unlogged landscape. Black dots not included in any sample represent other live-trapped individuals (n = 10) that were also used in individual-based analyses in logged vs. unlogged landscapes.
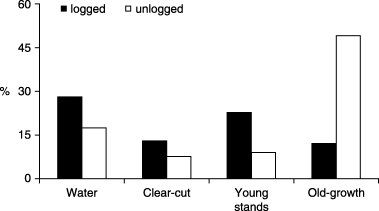
Proportions of forest stands, clear-cuts and water areas in the landscapes under study, based on Forest Resource Inventory data. ‘Old-growth’ stands refer to unlogged and > 60 years old, ‘regenerating’ stands were logged 10–60 years ago, and ‘clear-cuts’ were recently logged (< 10 years). Respectively 24% and 17% of uninformed land cover should be added to these values for the logged and the unlogged landscapes.
Sampling
Martens were captured in Tomahawk live-traps in both landscapes (Fig. 1) in fall and winter 2001, 2002 and 2003. Live-trapped individuals were anaesthetized using a mixture of ketamine and xylazine (Strickland & Douglas 1987). Penicillin was also administered to every individual, and an ear tattoo and electronic pit tag were applied for identification. The first premolar was extracted for cementum annuli ageing (Strickland & Douglas 1987; Poole et al. 1994). A total of 166 juveniles were fitted with radio-collars (MI-2, Holohil Systems). Hair were also plucked from live-trapped individuals and stored dry in plastic Eppendorf tubes at room temperature for DNA extraction. Martens were then kept in trap until fully recovered (1–2 h) and released.
Additional tissue samples were collected in 2001 and/or 2002 on carcasses of martens harvested from four commercial trap lines in the unlogged landscape and three trap lines in the logged landscape (Fig. 1). Tissue samples were stored in absolute ethanol prior to DNA extraction.
Genetic analyses
A Chelex-100 method (Walsh et al. 1991) was used to extract DNA from hair and tissue. Approximately 10 mg of muscle was added to 200 µL of a 10% Chelex solution containing 15 µL of proteinase K. After full digestion of tissues (≥ 1 h at 56 °C), the solution was heated to 100 °C for 10 min and centrifuged before storing at −20 °C. The same protocol was used to extract DNA from hair (using 20 hair roots at least) except that 400 µL of a 5% Chelex solution was used and no proteinase K was added, following Gagneux et al. (1997).
Genetic analyses were conducted using nine microsatellite loci: Ma1, Ma2, Ma5, Ma8, Ma9, Ma11, Ma14, Ma19 and Gg7 (Davis & Strobeck 1998). One microlitre of DNA extract (5 µL for hair-based extractions) was used as template in each polymerase chain reaction (PCR). Amplification reactions were performed in a total volume of 25 µL with ready-to-go PCR beads (Amersham Biosciences) following the supplier's protocol. DNA fragments were visualized using an ABI PRISM™ 310 DNA sequencer, and analysed with GenScan™ Analysis.
Given that the genetic analyses were based on samples collected in 2001, 2002 or 2003, we first tested for temporal genetic structure. To this end, G-tests implemented in the software fstat (Goudet 1995; Goudet 2001) were used to test for differentiation between groups of individuals sampled in different years in the same geographic area. fstat was also used to test for linkage disequilibrium and departure from Hardy–Weinberg equilibrium in each sample. All tests involved in the genetic analyses mentioned here were based on 10 000 permutations.
Genetic structure
The spatial genetic structure of M. americana was investigated using two methods, one using measures of differentiation among samples, and the other among individuals. FST coefficients (following Weir & Cockerham 1984) were calculated between pairs of samples and the differentiation among samples was tested using a G-test (Goudet et al. 1996). A Mantel test for correlation between genetic distances FST/(1 –FST) and logarithm of geographic distances (as measured edge-to-edge between the polygons delineating the samples in Fig. 1) was performed in fstat following Rousset (1997) to test for IBD (Wright 1943).
Live-trapped martens were used to investigate the spatial genetic structure at the individual level. Genetic distance a (Rousset 2000) was computed between pairs of live-trapped individuals (nunlogged = 118, nlogged = 73, Fig. 1) using the program genepop 3.4 (Raymond & Rousset 1995), and geographic distances among individuals were calculated using UTM coordinates of the original location of capture. IBD between individuals was then investigated within each landscape using a Mantel test for correlation between pairwise genetic distances (a) and logarithm of geographic distances (r) as described in Rousset (2000).
Indirect estimate of dispersal
Assuming IBD in a two-dimensional space, the average squared axial parent–offspring distance (σ2) may be estimated using the slope of the regression of pairwise genetic distances (a) on the logarithm of physical distances (r) among individuals following Rousset (2000). The inverse of the slope (b) of this regression is an estimate of the product 4Dπσ2, where D is the effective density in the population (see equation 5 in Rousset 2000). The average squared axial parent–offspring distance σ2 may then be estimated as:
σ2= 1/(b · 4Dπ)
((eqn 1))Since a pattern of IBD among individuals was detected in the unlogged landscape (see Results), genepop version 3.4 was used to infer b and compute a 95% confidence interval for this estimate using an ABC bootstrapping procedure.
To allow for an estimation of σ2 following equation 1, the effective density in the unlogged landscape was also determined. Using the geographic information system arcmap 8.1, we calculated the total surface area within the average radius of male and female home ranges (radiusmale = 1.39 km, n = 9 males and radiusfemale = 1.01 km, n = 15 females) from live-trap locations. Assuming our live-trapping efforts caught all resident martens, this buffer represents the area live-trapped effectively. Effective density was calculated as the number of adults captured divided by the total trapped area for each year and each sex, separately. These values were averaged to calculate an overall density.
Direct estimate of dispersal distances
Radio-collared juveniles were located between fall 2001 and summer 2004 using telemetry antennas mounted on vehicles. Ground telemetry fixes were plotted using locate ii (version 1.82). Additional information on missing individuals and long-distance dispersers came from aircraft telemetry and reports on the location of radio-collared martens found in conibear traps by fur-trappers.
Dispersal distance was calculated as the straight-line distance between birthplace or location of original capture and settlement (i.e. Euclidian dispersal distance). Using the original location capture could potentially underestimate dispersal distances, particularly for juveniles live-trapped late during the dispersal period. However, we detected no effect of time of capture on dispersal distance (data not shown). Juveniles were considered settled when located within the same 6 km2 and 3.2 km2 area for males and females, respectively (size of adult home range estimated as average 100% minimum convex polygon, N = 9 males and N = 15 females), for ≥ 5 locations (i.e. a month or more).
Comparison of direct vs. indirect estimates of dispersal
The term σ2 is the expected value of squared axial distances between parents and offspring. Assuming homogeneous dispersal in two dimensions, this is equivalent to (e.g. Rousset 2001; see also appendix 1 in Sumner et al. 2001):
σ2= 1/2 · E(r2)
((eqn 2))with r the Euclidean dispersal distance between parents and offspring. Following this equation, σ2 may be estimated from dispersal distances (r) obtained for radio-tracked individuals, and then be compared with the indirect estimate based on the IBD pattern.
Results
Genetic diversity
A total of 428 martens (range 16–59 individuals per sample, see Fig. 1 for details) were genotyped at seven microsatellite loci (not including Ma1 and Ma14, discarded because of linkage disequilibrium). Sample 5 appeared to have experienced significant differentiation between years 2002 and 2003 (FST = 0.05, P = 0.014). However, because samples at this site did not differ between 2001 and 2003 (P = 0.183), and no other differentiation between years was detected at the other sampling sites (P > 0.05), samples from different years were pooled by geographic location in subsequent analyses. Two loci (Ma2 and Ma8) deviated from Hardy–Weinberg equilibrium in sample 4 (P < 0.05, not significant if Bonferroni corrections were applied). As these deviations occurred only in a single sample, and given that every other locus conformed to Hardy–Weinberg equilibrium, all loci were retained for analyses.
Genetic structure
Previous hierarchical analysis of genetic differentiation revealed weak but significant divergence between samples from the logged vs. unlogged landscape (Broquet 2004). In the present study, we focused on levels of genetic divergence within each landscape. In the unlogged landscape, pairwise FST coefficients ranged from −0.0055 to 0.0079 (Table 1), with only one pair presenting significant genetic differentiation (samples 3–4, G-test P < 0.05). Similarly in the logged landscape pairwise FST coefficients ranged from −0.0059 to 0.0069 (Table 1), with also only one pair of samples being significantly differentiated (samples 7–11, G-test P < 0.05). Mantel tests revealed that differentiation among samples within each landscape was not correlated with distance (punlogged = 0.35; plogged = 0.75). The distributions of average pairwise FST/(1 –FST) with increasing distance classes for the two landscapes are presented in Fig. 3a and b.
| Unlogged landscape | ||||||
|---|---|---|---|---|---|---|
| Sample | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 0.0033 | −0.0006 | −0.0051 | −0.0055 | −0.0036 | |
| 2 | 13.5 | 0.0037 | 0.0079 | 0.0004 | −0.0032 | |
| 3 | 22.5 | 12.8 | 0.0062 | −0.0009 | −0.002 | |
| 4 | 17.9 | 30.2 | 27.5 | −0.0013 | 0.0012 | |
| 5 | 6.9 | 18.1 | 14.5 | 7.3 | −0.0018 | |
| 6 | 17.6 | 22.8 | 15.6 | 2.3 | 3.9 | |
| Logged landscape | |||||
|---|---|---|---|---|---|
| Sample | 7 | 8 | 9 | 10 | 11 |
| 7 | −0.0057 | −0.0041 | −0.0002 | 0.006 | |
| 8 | 12.3 | −0.0059 | 0.0004 | 0.0007 | |
| 9 | 21.1 | 11.1 | −0.001 | 0.0006 | |
| 10 | 1.2 | 18.1 | 27.4 | 0.0069 | |
| 11 | 8.9 | 0.2 | 0.9 | 16.6 | |
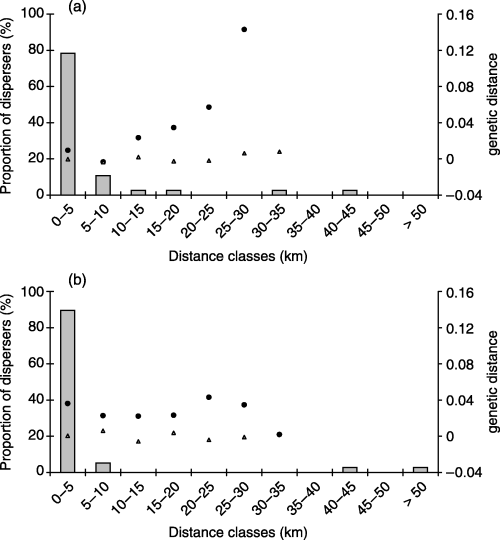
Distribution of dispersal distances and pairwise genetic differentiation in unlogged (3a) vs. logged landscapes (3b). Histograms represent the frequency distribution of distance between capture site and site of settlement for radio-tracked juvenile martens (nunlogged = 37; nlogged = 38). Open triangles represent the pairwise genetic distance FST/(1 – FST) between samples (samples 1–6 in the unlogged; 7–11 in the logged), computed for each distance classes (one triangle corresponds to the genetic distance between two samples or averaged over 2–4 pairs of samples depending on geographic distance class). Black dots represent the distribution of the mean pairwise genetic distance a (Rousset 2000) among individuals (nunlogged = 118; nlogged = 73). Average genetic distances were preferred to raw data points (respectively 6903 and 2628 data points) in the purpose of illustrating spatial patterns. As shown in Fig. 4, pairwise genetic distances among individuals within each distance class are very variable, and significance of spatial patterns was tested only through Mantel tests (significant pattern of isolation by distance among individuals in the unlogged landscape, Fig. 3a).
At the individual level, a significant pattern of IBD between individuals was observed in the unlogged landscape (Mantel test P = 0.01), but not in the logged landscape (Mantel test P = 0.42). Average pairwise genetic distances (a) vs. geographic distance classes are shown in Fig. 3a and b.
Indirect estimate of dispersal
The slope (b) of the regression of genetic (a) vs. logarithm of geographic distances (r) in the unlogged landscape was estimated to 0.012 (Fig. 4). The 95% confidence interval of the regression slope was [0.0036–0.0317]. This translates into a product 4Dπσ2 equal to 83 individuals [95% confidence interval 32–278 individuals]. The estimated average density of adults over 3 years was 0.46 ind./km2 (Table 2). Using b = 0.012 and D = 0.46 ind./km2 in equation 1 gives σ2 = 14.4 km2[i.e. σ = 3.8 km (95% confidence interval 5.48–10 km)].
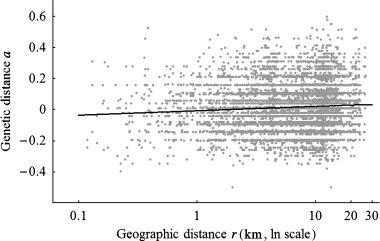
Regression of interindividual genetic distances a (Rousset 2000) on the natural logarithm of geographical distance r among individuals in the unlogged landscape. Regression line shown for r≥ 0: ar = −0.0088 + 0.012 ln(r). Note the ln scaling of the x-axis.
| Year | Sex | Radius (km) | Trapped area (km2) | No. of individuals | Density (individual/km2) |
|---|---|---|---|---|---|
| 2001 | M | 1.39 | 173.1 | 34 | 0.20 |
| F | 1.01 | 126.12 | 19 | 0.15 | |
| Total | 53 | 0.35 | |||
| 2002 | M | 1.39 | 193.06 | 65 | 0.34 |
| F | 1.01 | 143.44 | 44 | 0.31 | |
| Total | 109 | 0.64 | |||
| 2003 | M | 1.39 | 110.72 | 22 | 0.20 |
| F | 1.01 | 81.15 | 15 | 0.18 | |
| Total | 37 | 0.38 | |||
| Average | 199 | 0.46 | |||
Direct estimate of dispersal distances
Out of a total of 305 live-trapped martens captured during 7386.5 corrected trap-nights (i.e. corrected for closed traps = 0.5 trap-nights and nonfunctional traps = 0 trap-nights) 38 and 37 radio-collared juveniles originally trapped in the logged and the unlogged landscapes, respectively, were radio-tracked until settlement. The earliest capture was 29 July, and the latest was 29 of November. Settlement occurred between 29 July (no dispersal) and 4 April. The distributions of dispersal distances are shown in Fig. 3a and b for the unlogged and the logged landscapes, respectively. The mean dispersal distance recorded between capture and site of settlement was 5.14 km (median = 1.72 km) in the unlogged and 5.11 km (median = 1.77 km) in the logged landscape. Both distributions were highly leptokurtic [g2unlogged = 11.67, P < 0.001 and g2logged = 24.03, P < 0.001, tested using t0.001[8] following Sokal & Rohlf (1995), p. 174]. The distribution of dispersal distances did not differ significantly between the unlogged and the logged landscape (Kolmogorov–Smirnov test for goodness of fit P = 0.48).
Comparison of direct vs. indirect estimates of σ 2
Empirical σ value estimated from dispersal distances (i.e. following equation 2) was 7.25 km in the unlogged landscape. This value is approximately twice the value of σ based on the pattern of genetic structure which was ~3.8 km (from equation 1).
Discussion
Local genetic structure: individuals vs. samples
The local genetic structure in Martes americana was investigated at two levels. We first considered the genetic differentiation among arbitrarily defined samples using pairwise FST coefficients, then we investigated the spatial distribution of individual genotypes within two groups using pairwise interindividual genetic distances a. Classically, the scale relevant to the hypotheses tested in a study should dictate the choice of one of these two levels, either considering discrete finite subpopulations or a large continuously distributed population (e.g. see Epperson 2003, p. 7 for discussion), although the distinction between the two may not be obvious in the wild. Using the two approaches here allowed us to highlight the difference of sensitivity of individual- vs. sample-based methods: no genetic structure could be revealed using FST coefficients among samples within the unlogged landscape, whereas a pattern of IBD was detected among individuals at the same spatial scale (Fig. 3a). This observation confirms the logical prediction that sample-based F-statistics may not always be advantageously used to measure spatial structure within populations, since combining individuals in subpopulations is often arbitrary and necessarily causes loss of information (e.g. Epperson 2003, p. 284; see also Castric & Bernatchez 2004). While a low level of genetic structure among samples is not surprising in such a highly mobile species, and is in full agreement with previous results (Kyle & Strobeck 2003), the pattern of IBD among individuals suggested that the decrease of genetic correlation due to limited dispersal can be identified at the spatial scale of this study.
Given that very little gene flow is needed to equilibrate the genetic variance among samples (e.g. Hartl & Clark 1997, p. 194), it is also possible that rare long-distance dispersers have a prominent effect on the genetic divergence recorded by FST coefficients among samples. Hence, it is possible that leptokurtic dispersal results in local genetic structure among individuals which remains undetected at larger scale by FST coefficients, because a few successful long-distance dispersers (fat tail) create enough gene flow to significantly reduce the differentiation among samples. Modelling studies are needed to help delineate the influence of dispersal kurtosis on dispersal inference from measures of genetic structure.
Dispersal in Martes americana
As expected, radio-tracking showed that juvenile martens were able to cover long distances during dispersal. Out of a sample of 75 individuals, the martens which traveled the longest distance established its home range 82 km away from the place where it was captured. However, the distribution of dispersal distances was highly leptokurtic in both landscapes, most individuals settling in home ranges at surprisingly short distances from the place where they were captured (Fig. 3). We were not able to trap every juvenile in the territory of its mother, which may result in an underestimation of the dispersal distance recorded for martens already dispersing when radio-collared. However, dispersal distances were not correlated with dates of capture (data not shown), which suggests that our data were not strongly affected by potentially unrecorded dispersal. Moreover, the dispersal distance recorded for six individuals trapped in the territory of their mother ranged from 0.2 to 2.9 km, which is consistent with the values recorded for other individuals. This may be explained by the fact that many juveniles were observed to come back fairly close to their natal territory after travelling much longer distances during dispersal (C. A. Johnson, unpublished). If such loops are common, then the distances sampled in this study are equally likely to be under- or overestimated. Hence, in the absence of reliable models of movement for dispersing martens, any attempt at correcting the dispersal distance for those individuals potentially already dispersing when radio-collared is unlikely to increase the reliability of our results. A comparison with indirect estimates based on analyses of genetic structure seems to constitute a better alternative, at least in this study.
The average squared axial parent–offspring distance σ2 calculated following the genetic approach of Rousset (2000) was estimated to 14.4 km2. This estimation of σ2 from the pattern of IBD relies on a number of assumptions: genetic structure is stationary and results solely from isotropic limited gene dispersal, the sampling scale is adequate, and the effective density is homogeneous and constant (Rousset 2000; Vekemans & Hardy 2004). Our sampling scale (individuals trapped within an area of 5.5σ × 6.5σ, Fig. 1) was somewhat more restricted than the ideal sampled area of 10σ × 10σ (Rousset 2000), and the distribution of martens may be aggregated in the study area. Also, not all martens in the study area were caught, nor did densities remain constant over time. However, the effect of these factors on our estimate of σ2 is likely to be limited, as the estimation of product 4Dπσ2 from the pattern of IBD in continuous populations is robust to departures from the ideal sampling scheme (Leblois et al. 2003) and to spatial and temporal heterogeneity in population density (Leblois et al. 2004). Finally, the estimation of σ from product 4Dπσ2 directly depends on the effective density D. There is some uncertainty associated with our estimate of D = 0.46 ind./km2, as we assumed that every individual located within a somewhat arbitrary (although biologically meaningful) distance from trap would be captured, and as we approximated the effective density as the density of adults in the study area. So far, we have no means of improving the precision of effective density estimates, since critical data (e.g. variance in reproductive success) are lacking.
More importantly, despite the fact that the reliability of both the direct and the indirect approaches to dispersal pattern in the American marten show some limitations, the two approaches lead to comparably small estimates for σ (indirect estimate of 3.8 vs. direct estimate of 7.25 km). The twofold difference between our genetic and empirical estimates is similar to that of other studies (e.g. Rousset 1997; Sumner et al. 2001), and may be partly due to undetected causes. While we do not intend the distributions of dispersal distances and the σ estimates presented here for the American marten to be perfectly accurate, we believe that they may be used as a basis for subsequent studies in need of such data. Combining genetic and demographic methods to estimate dispersal has proved increasingly useful, especially in the context of IBD in continuous populations (Waser & Elliott 1991; Epperson et al. 1999; Rousset 2000; Sumner et al. 2001; Vekemans & Hardy 2004). In this study, this complementary approach allowed to gain some insight into dispersal in the American marten despite the limits inherent to each method that may not be easily overcome otherwise (processing more juveniles before they leave their natal territory or sampling every marten in a 10σ by 10σ sampling area are both problematic).
Local genetic structure in logged vs. unlogged landscapes
No difference in genetic structure as measured by FST coefficients among samples was detected between these two landscapes (absence of differentiation between pairs of samples within each landscape). However, individual-based statistics revealed different patterns of fine-scale structure. No pattern of IBD was detected in the fragmented landscape (Fig. 3a, b), suggesting that marten dispersal is altered in suboptimal habitat (Broquet et al. 2006). This observation illustrates that major issues such as the influence of the environment on gene flow (Wiens 2001) may advantageously be investigated through individual-based analyses.
Acknowledgements
We thank A. Butet and N. Perrin for helpful discussions, and F. Rousset, O. Hardy and three anonymous reviewers for their advice and critical comments on an earlier draft of this paper. We are grateful to the trappers of the region of Ear Falls, Ontario (Canada), who provided us with marten carcasses. R. Routledge, P. Wiebe, M. Herzog and M. Andruskiw largely contributed to the fieldwork. Thanks are also due to Y. Colin for genetic data formatting. Financial support for this work was provided by the Forest Ecosystem Science Cooperative Inc., the Natural Sciences and Engineering Research Council/CFS Research Partnership Program, the Sustainable Forest Management Network, the Ontario Ministry of Natural Resources, CFS-NRCan, a Fonds pour la formation de Chercheurs et l’Aide à la Recherche (FCAR) scholarship (to C. A. Johnson), and an allocation ministérielle de recherche (to T. Broquet).
References
Thomas Broquet's research is directed at the ecology of specialist species confronted to habitat fragmentation, with particular interest in the inference of dispersal and landscape connectivity from genetic data. This work was part of his PhD on marten ecology, co-supervised by Françoise Burel, a landscape ecologist interested in the role and measure of connectivity, and John M Fryxell, whose research interests center on the interplay between behaviour and population dynamics, with emphasis on terrestrial vertebrate species in tropical and temperate systems. Ian Thompson has conducted research on ecological interactions of mammals and birds in the boreal zone for the past 20 years, with application to the sustainable harvesting of forests. Cheryl A. Johnson is interested in the consequence of behaviour on individual and Malthusian fitness, particularly with respect to habitat selection. Eric Petit investigates sex and environmental influences on mammalian dispersal patterns using population genetic tools.




