Domestication and the distribution of genetic variation in wild and cultivated populations of the Mesoamerican fruit tree Spondias purpurea L. (Anacardiaceae)
Abstract
Domestication occurs as humans select and cultivate wild plants in agricultural habitats. The amount and structure of variation in contemporary cultivated populations has been shaped, in part, by how genetic material was transferred from one cultivated generation to the next. In some cultivated tree species, domestication involved a shift from sexually reproducing wild populations to vegetatively propagated cultivated populations; however, little is known about how domestication has impacted variation in these species. We employed AFLP data to explore the amount, structure, and distribution of variation in clonally propagated domesticated populations and sexually reproducing wild populations of the Neotropical fruit tree, Spondias purpurea (Anacardiaceae). Cultivated populations from three different agricultural habitats were included: living fences, backyards, and orchards. AFLP data were analysed using measures of genetic diversity (% polymorphic loci, Shannon's diversity index, Nei's gene diversity, panmictic heterozygosity), population structure (FST analogues), and principal components analyses. Levels of genetic variation in cultivated S. purpurea populations are significantly less than variation found in wild populations, although the amount of diversity varies in different agricultural habitats. Cultivated populations have a greater proportion of their genetic variability distributed among populations than wild populations. The genetic structure of backyard populations resembles that of wild populations, but living fence and orchard populations have 1/3 more variability distributed among populations, most likely a reflection of relative levels of vegetative reproduction. Finally, these results suggest that S. purpurea was domesticated in two distinct regions within Mesoamerica.
Introduction
Domestication is an ongoing evolutionary process that occurs over time as humans select and cultivate wild plants (Hancock 2004). Genetic drift and genetic bottlenecks associated with the domestication process both restrict and alter genetic variation in cultivated populations (e.g. Fisher 1930; Clegg et al. 1984; Gepts & Clegg 1989; Eyre-Walker et al. 1998; Saunders et al. 2001; Anthony et al. 2002), although subsequent gene flow from wild ancestors into cultivated populations may increase variation in some crop species (e.g. Anderson 1952). Recently, mounting concerns about low levels of genetic variation in economically important plant populations have refocused attention on crop species and their ancestors. It has been suggested that over the last hundred years, as much as 80% of variation of cultivated populations and their wild relatives has been lost in some species (Tanksley & McCouch 1997; Tuxill 1999). Native forests harbouring the ancestors of cultivated plants have gone extinct, and more centralized agricultural practices have promoted the adoption of a few high-yielding, uniform cultivars over broad areas at the expense of genetically variable indigenous varieties (Altieri & Merrick 1988; Nabhan 1992; Tanksley & McCouch 1997; Lanaud 1999; Tuxill 1999; Brush 2000).
The amount and structure of variation in cultivated populations is shaped, in part, by the way genetic material is passed from one cultivated generation to the next. In sexually reproducing crop species, seeds from a limited number of wild plants were used to found the cultivated populations (Ladizinsky 1985; Zamir 2001; Abbo et al. 2003). The resulting founder effect, coupled with ongoing selection of seeds from the initial pool of cultivated genotypes, produced a genetic bottleneck in the cultivated populations (Zohary 2004). In contrast, during the course of the domestication of many tree species, humans selectively cultivated individual plants from cuttings (vegetative propagation), a process that led to a shift from sexually reproducing wild populations to cultivated populations that were propagated exclusively vegetatively (Zohary & Spiegel-Roy 1975; Ladizinsky 1998; Zohary 2004). In these species, cultivated individuals were propagated vegetatively and any new individuals were simply clonal reproductions of the most attractive wild individuals (Zohary & Spiegel-Roy 1975; Zohary 2002, 2004).
Many of the world's oldest and most well-known fruit trees are propagated vegetatively, including olives, figs, breadfruit, and dates (Zohary & Spiegel-Roy 1975; Sonnante et al. 2002; Lumaret et al. 2004; Zerega et al. 2004, respectively). The domestication process in vegetatively propagated cultivated trees likely involved few recombination and sexual cycles, resulting in cultivated populations that may not have diverged significantly from their wild progenitor's gene pool (e.g. Zohary 2002). Analyses of clonally reproduced olive trees in the Mediterranean have shown that cultivated populations represent a sample of the genetic variation present in contemporary wild olive populations in the region (Lumaret & Ouazzani 2001). Aside from this study, little is known about how the domestication process has impacted the extent and distribution of genetic variation in populations of vegetatively propagated fruit trees.
Mesoamerica (Mexico and Central America) is one of the global centres of plant domestication (Harlan 1971, 1975; MacNeish 1992; Vavilov 1992; Hernández Xolocotzi 1993; Casas & Barbera 2002). A number of cultivated fruit trees were domesticated from plants growing in the forests of Mesoamerica including anona (Annona cherimola), avocado (Persea americana), cas (Psidium friedrichsthalianum), jocote (Spondias purpurea), nance (Byrsonima crassifolia), mamey (Mammea americana), matasanos (Casimiroa edulis), and sapote (Manilkara zapota); many of these species are propagated from stocks (Morton 1987; MacNeish 1992; Vavilov 1992; FAO 1993; Tedlock 1996; Super & Vargas 2000; Casas et al. 2001). Today, some Mesoamerican fruit trees are cultivated in modern agricultural environments (e.g. orchards), although most are found in more traditional agricultural habitats, such as backyard gardens (e.g. González-Soberanis & Casas 2004). Because traditional agricultural habitats can include domesticated plants as well as propagules derived directly from wild individuals, it has been suggested that these populations may represent one portion of a continuum of genetic differentiation ranging from wild to domesticated variants (Harris 1989; Tanksley & McCouch 1997; González-Soberanis & Casas 2004). Consequently, the native crop species of Mesoamerica provide a unique opportunity to document the impact of domestication on levels of genetic variation in cultivated populations growing in a range of agricultural habitats.
In this study we compare levels of genetic variation in cultivated and wild populations of a vegetatively propagated Neotropical fruit tree, S. purpurea (n.v. Jocote, Ciruela Mexicana). S. purpurea presents an ideal system to survey genetic diversity in a range of populations because (i) there are clear morphological differences between cultivated and wild S. purpurea populations; (ii) cultivated S. purpurea populations occur in a variety of agricultural habitats including low-input cultivation (e.g. backyard/home gardens, living fences) and more formal agricultural habitats (orchards); and (iii) known wild populations provide a basis for comparison. The goals of this study were (i) to quantify the amount of genetic variation in wild S. purpurea populations and S. purpurea populations cultivated in three different types of agricultural habitats; (ii) to compare the structure of genetic variation in wild S. purpurea populations and S. purpurea populations cultivated in three different types of agricultural habitats; and (iii) to investigate the geographic structure of genetic variation in cultivated and wild S. purpurea populations.
Materials and methods
Study system
Spondias purpurea is cultivated for its plumlike fruits which are eaten fresh, sold in local markets, and made into jams and beverages (Mandujano et al. 1994; Avitia García 1997; Baraona Cockrell 2000; Mitchell 2000; Pimienta-Barrios & Ramirez-Hernandez 2003). Jocote trees are propagated exclusively vegetatively; it has been reported that the seeds of cultivated populations are not viable (Juliano 1932; Cuevas 1994). Cultivated mature fruits vary widely in colour, size, texture, and taste (Cuevas 1994; A.J.M., personal observation). At the time of the European colonization, jocotes were grown widely from Mexico to the northern regions of South America (Cuevas 1994). Today, the majority of trees are planted in backyard gardens, living fences, and small multicrop farms, although some formal cultivation exists in orchards (Cuevas 1994). The wild progenitors of cultivated jocote populations occur in the fragmented tropical dry forests of Mexico and Central America (Mandujano et al. 1994; Mooney et al. 1995; Miller & Schaal 2005); it has been estimated that as little as 2% of the original forest remains (Janzen 1988). The wild S. purpurea populations are polygamo-dioecious, and reproduce from seed to form age-structured populations. Fruits of wild jocotes are usually bright red. They are smaller and more acidic than cultivated fruits, with considerably less flesh surrounding the seed (A.J.M., personal observation).
Sampling
Field studies were conducted in the summers of 2000–2002 in Costa Rica, El Salvador, Guatemala, Honduras, Mexico, Nicaragua, and Panama (Fig. 1). A total of 216 individuals of S. purpurea representing 34 distinct populations were sampled from wild populations and three types of cultivated habitats: backyards, living fences, and orchards (Appendix 1). Leaves for DNA extraction were preserved in silica gel. Herbarium specimens (collected for each population) were deposited at the Missouri Botanical Garden and in herbaria in the country of origin (CR, USJ, ITIC, UVAL, EAP, TEFH, GUADA, CICY, YUC, MEXU, ENAG, SCZ, STRI, PMA). The precise geographic location of each sampled population was determined using a Garmin GPS unit.
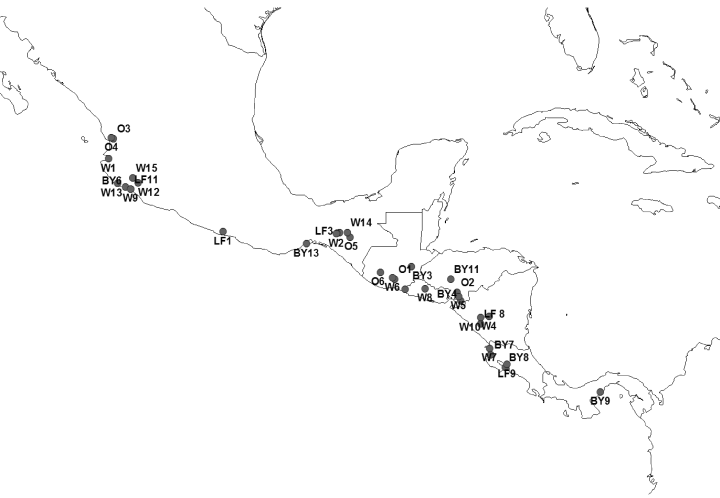
Geographic distribution of populations included in Spondias purpurea AFLP analysis. Numbers correspond to samples listed in Appendix 1 (W, wild; LF, living fence; BY, backyard; O, orchard).
DNA extraction
Extraction of DNA was attempted first using kits (Viogene DNA Extraction, QIAGEN DNEasy, Epicentre Plant DNA Extraction) and variations on the cetyltrimethyl ammonium bromide (CTAB) method with both 1.5-mL and 30-mL volumes (Doyle & Doyle 1987), none of which yielded sufficient amounts of DNA (e.g. < 9 ng/µL). Consequently, we developed a mini-extraction procedure that yielded 20–50 ng/µL DNA. First, in a mortar and pestle, dried leaves were frozen with liquid nitrogen. Finely powdered glass was added to aid in grinding the leaves to a fine powder. Next, the crushed leaves (∼200 mg) were washed with a 2× HEPES buffer (Sambrook et al. 1989) to remove some of the secondary compounds. Then, DNA was extracted from washed leaf material using a modified (5×) CTAB extraction. Finally, extracted DNA was purified using the GeneCleanII kit (Qbiogene, Inc.).
Amplified fragment length polymorphism methods and data set construction
The amplified fragment length polymorphism (AFLP) method uses restriction enzymes to fragment genomic DNA, and then, through two selective rounds of polymerase chain reaction (PCR), amplifies a subset of the fragments (Vos et al. 1995; Jones et al. 1997; Hartl & Seefelder 1998; Mueller & Wolfernbarger 1999; Newton et al. 1999). AFLPs have been used successfully to examine genetic variation in several cultivated plants (e.g. Heun et al. 1997; Saunders et al. 2001; Zerega et al. 2004).
The AFLP data included in this study were generated in the Cullman Laboratory for Molecular Systematics at the New York Botanical Garden, which graciously welcomed A.J.M. as a visiting research scientist in 2003. We used an AFLP plant mapping kit protocol following Zerega et al. (2002, 2004) (Applied Biosystems). In the restriction-ligation step, 3.3 µL (0.3–0.5 µg) of genomic DNA was restricted in 3.3 µL of a reaction mixture that contained 0.66 µL 10×T4 DNA ligase buffer with ATP, 27 mm NaCl, 0.095 mg/mL BSA, MseI (0.6 U = 0.6 µL of 10.000 U/mL), EcoRI (3.0 U = 0.03 µL of 100.000 U/mL), T4 DNA ligase (0.6 U = 0.12 µL of 5 U/µL), 0.6 µL Mse1 adaptor, 0.6 µL EcoRI adaptor, and 0.24 µL autoclaved nanopure water. The product was diluted with 113 µL of 0.1× TE. Preselective amplifications were carried out in 12-µL reactions: 2.4 µL diluted restriction-ligation product, 0.60 µL preselective primer pairs, 9.00 µL AFLP Core Mix (Applied Biosystems). PCR conditions for preselective amplification were 72 °C for 2 min, 94 °C for 1 s, 56 °C for 30 s, 72° for 2 min, for 20 cycles, then 60 °C for 30 min. The product of the preselective amplification was diluted with 114 µL of 0.1 × TE buffer. Selective amplifications were performed initially using 12 primer pairs screened on four samples; of these, four primer pairs were evaluated for an additional 20 samples. Selective amplification reactions included 1.8 µL of diluted preselective amplification product, 0.6 µL MseI primer (5 µm), 0.6 µL EcoRI primer (1 µm), 9.0 µL AFLP Core (Mix). PCR conditions were 94 °C for 2 min, 65 °C for 30 s, 72 °C for 2 min, then eight cycles of 94 °C for 1 s, 64 °C for 30 s, 72 °C for 2 min with a 1 °C decrease in annealing time at each step; then, 23 cycles of 94 °C for 1 s, 56 °C for 30 s, 72 °C for 2 min, and finally 60 °C for 30 min. Initially, three primer pairs were chosen based on their repeatability and the percentage of polymorphic bands (EcoRI-AAG/MseI-CAC, EcoRI-ACA/MseI-CTG, and EcoRI-ACA/MseI–CAC); however, the primer pair EcoRI-ACA/MseI–CAC was eliminated later on because this primer pair failed more detailed repeatability analyses.
The products of the selective amplification were prepared for analysis on an ABI 377 by adding 0.8 µL selective amplification product and 1.6 µL loading buffer (6.0 µL Formamide, 2.3 µL EDTA dextran blue loading dye, 1.7 µL GS ROX-labelled size standard (16 fluorescent-labelled fragments ranging in size from 35 to 500 bp). Samples were run on a 5.0% acrylamide gel. Raw data were collected using ABI genescan software (Applied Biosystems) and genotyper 2.1 (Applied Biosystems) was used to score AFLP data manually for the presence and absence of different sized fragments. Bands of the same size were assumed to be homologous. To test the repeatability of the fragments scored, the complete AFLP procedure (restriction ligation, preselective amplification, selective amplification) was repeated for 5–10% of the samples for each primer pair. Each fragment was scored as a dominant locus with two states: present or absent. Fragments were identified initially using genescan software and then each locus was manually inspected. Only unambiguously detectable fragments were scored.
Data analysis
To estimate population genetic diversity, the percentage of polymorphic sites (PPL), Shannon's diversity index (I), and Nei's (1973) gene diversity (h) were obtained using the program popgene version 1.31 (Yeh et al. 1997). Gene diversity was also estimated using a Bayesian method implemented with the program hickory version 1.0 using all recommended default settings (Holsinger et al. 2002; Holsinger & Lewis 2003; Holsinger & Wallace 2004). hickory calculates a Bayesian estimate of gene diversity, hs (average panmictic heterozygosity), by internally calculating the posterior distribution for allele frequencies at every locus in every population. Hs (the average hs across populations) is calculated for every sample from the posterior distribution, from which the mean, median, and 95% credible intervals are calculated (Holsinger & Wallace 2004; K. Holsinger, personal communication). The Bayesian estimator of genetic diversity is calculated for each of the four models: (i) full model (includes priors for f, πI, and θ); (ii) f = 0 (assumes no inbreeding); (iii) θB = 0 (assumes no population structure); (iv) ƒ-free (allows the incorporation of uncertainty about ƒ into the analysis). The four models were applied to the data and evaluated based on measures of deviance information criterion (DIC, similar to Akaike's information criterion, a measure of both how well a model fits the data and how many parameters are required to fit the model; Akaike 1973), and Dbar (a measure of how well the model fits the data). Significant differences between wild and cultivated populations were quantified using Wilcoxon group tests and Kruskal–Wallis tests as implemented in the statistical package jmp version 5.1 (SAS Institute). Bonferroni corrections were applied to the results of the Wilcoxon two-group tests comparing wild populations and living fences, wild populations and backyard trees, and wild populations and orchards.
Hierarchical structuring of genetic variation and pairwise ΦST distances (analogous to FST statistics at the molecular level; Excoffier et al. 1992) among populations were determined by an analysis of molecular variance (amova) with iwinamova version 1.55 (Excoffier et al. 1992). Significance levels of the variance components were based on 1000 permutations. A pairwise Euclidean distance matrix and all input files needed for the amova were produced using the amova prep program version 1.1 (Miller 1997). An estimator of FST under a random-effects model of population sampling, θB, and GST-B, a Bayesian analogue of Nei's GST, were obtained for all populations and for subsets of the data (wild populations, living fences, backyard trees, orchards) using hickory (Nei 1973; Holsinger 1999; Holsinger & Lewis 2003). The Bayesian approach incorporates the effect of uncertainty about the magnitude of inbreeding (ƒ) in FST estimates obtained with dominant marker data (Holsinger et al. 2002).
To examine the geographic structure of genetic variation, we tested for correlations between genetic distance and geographic distance using a Mantel test based on a pairwise matrix of Nei's (1978) unbiased genetic distances (generated in popgene version 1.31, Yeh et al. 1997) and a pairwise matrix of geographic distances (generated in passage version 1.0, Rosenberg 2001). The AFLP data were analysed using principal components analysis (PCA) on a matrix of correlations using the statistical package jmp 5.1 (JMP). Principle component scores were used in a manova to determine if the AFLP data suggested multiple origins of cultivated populations.
Results
AFLP patterns and polymorphism
The repeatability analysis revealed that two primer combinations, EcoRI-AAG/MseI-CAC and EcoRI-ACA/MseI-CTG, consistently produced the same fragments in individual samples. The two primer pairs produced 200 scorable loci ranging in size from 40 to 400 bp. All fragments produced were polymorphic. AAG-CAC and ACA-CTG differed only slightly in levels of gene diversity (Table 1).
| Primer | N | h (SD) | I (SD) | S/PPL |
|---|---|---|---|---|
| AAG-CAC | 97 | 0.1654 (0.1423) | 0.2812 (0. 1941) | 200/100% |
| ACA-CTG | 103 | 0.1912 (0.1632) | 0.3112 (0.2211) | 200/100% |
| Combined | 200 |
- N, bands scored for each locus.
- h, Nei's (1973) gene diversity.
- I, Shannon's diversity index (Lewontin 1972).
- S, number of polymorphic site; PPL, % polymorphic loci.
Population genetic diversity
The Bayesian approach provided the posterior mean, standard deviation, and 95% credible interval for each of the four available models (Table 2). The full model displayed the lowest DIC and Dbar values (Table 2). Although the full model had a slightly lower (better) DIC value than the ƒ-free model, we chose the ƒ-free model to estimate parameters for the dominant AFLP data. Recent studies have found that estimates of ƒ from dominant markers may be unreliable, particularly in data sets with many loci and few (< 10 samples) per population (Holsinger & Wallace 2004), a situation that pertains to this study. The ƒ-free model chooses ƒ values at random from its prior distribution while estimating other parameters during the MCMC (Markov chain Monte Carlo) run, resulting in estimates of θB which incorporate all of the uncertainty in the prior of ƒ (Holsinger 2003).
| Model | Posterior mean, standard deviation (SD) and 95% credible interval (CI) of ƒ and θB for AFLP data under four alternative models. | Parameters‡ of the posterior distributions under four alternative Bayesian models | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ƒ* | θB† | |||||||||
| Mean | SD | 95% CI | Mean | SD | 95% CI | Dbar§ | Dhat¶ | pD** | DIC†† | |
| Full | 0.9895 | 0.0106 | (0.9600, 0.9997) | 0.3125 | 0.0085 | (0.2961, 0.3289) | 7625.7248 | 5977.1887 | 1648.5361 | 9274.2609 |
| ƒ = 0 | 0.2332 | 0.0077 | (0.2186, 0.2489) | 7627.1783 | 5793.1332 | 1834.0451 | 9461.2233 | |||
| θB = 0 | 0.9861 | 0.0139 | (0.9492, 0.9997) | 16640.6485 | 16448.5931 | 192.0554 | 16832.l7040 | |||
| ƒ free | 0.5057 | 0.2900 | (0.0255, 0.9728) | 0.2854 | 0.0109 | (0.2638, 0.3065) | 7707.2601 | 6004.9786 | 1702.2814 | 9409.5415 |
- * ƒ, Bayesian estimate of FIS, the inbreeding within populations (Holsinger 2003).
- † θB, Bayesian estimate of FST under a random-effects model of population sampling.
- ‡ Models with smaller DIC are generally preferred; the model with a better fit to the data (smaller Dbar) may be preferred when the DIC difference is primarily a result of differences in model dimension, pD.
- § A measure of how well the model fits the data.
- ¶ A measure of how well the best point estimate fits the data.
- ** A measure of model complexity (approximate number of parameters being estimated).
- †† Deviance information criterion, a Bayesian analogoue of Akaike's information criterion (= Dbar + pD).
Nei's (1973) measure of gene diversity (h), Shannon's diversity index (I), and the Bayesian estimate of average panmictic heterozygosity [H(s)] were greater in wild trees than in cultivated individuals (considered as a single group) (Table 3). Cultivated populations exhibited a higher percentage of polymorphic loci (PPL) compared to the wild individuals, although there were no significant differences (Tables 3 and 4). The Wilcoxon two-group test revealed significant differences between wild and all cultivated populations for Nei's (1973) gene diversity, Shannon's diversity index, and Bayesian gene diversity (Table 4). However, the Kruskal–Wallis test failed to reject the null hypothesis, suggesting that cultivated and wild populations do not differ significantly in estimates of genetic variation (Table 4).
| Pop.* | N † | PPL‡ | h § | I¶ | h[s]— Bayesian** |
|---|---|---|---|---|---|
| BY11 | 5 | 17% | 0.0656 ± 0.1489 | 0.0972 ± 0.218 | 0.1113 ± 0.0069 |
| BY13 | 2 | 6.5% | 0.0325 ± 0.1236 | 0.0451 ± 0.1713 | 0.1117 ± 0.0086 |
| BY2 | 7 | 24% | 0.0816 ± 0.1548 | 0.1242 ± 0.2293 | 0.1054 ± 0.0059 |
| BY3 | 7 | 57.5% | 0.1980 ± 0.1865 | 0.3007 ± 0.2728 | 0.1785 ± 0.0070 |
| BY4 | 6 | 28.5% | 0.1022 ± 0.1698 | 0.1539 ± 0.2505 | 0.1207 ± 0.0068 |
| BY5 | 8 | 25.5% | 0.0889 ± 0.1642 | 0.1339 ± 0.2399 | 0.1356 ± 0.0069 |
| BY6 | 9 | 38% | 0.1160 ± 0.1668 | 0.1804 ± 0.2469 | 0.1322 ± 0.0062 |
| BY7 | 5 | 15% | 0.0528 ± 0.1284 | 0.0802 ± 0.1934 | 0.0995 ± 0.0067 |
| BY8 | 5 | 18% | 0.0720 ± 0.1578 | 0.1056 ± 0.2289 | 0.1096 ± 0.0065 |
| BY9 | 5 | 14% | 0.0552 ± 0.1404 | 0.0813 ± 0.2045 | 0.1011 ± 0.0067 |
| LF8 | 6 | 46.5% | 0.1558 ± 0.1772 | 0.2391 ± 0.2649 | 0.1539 ± 0.0072 |
| LF1 | 8 | 24.5% | 0.0877 ± 0.1644 | 0.1314 ± 0.2401 | 0.1077 ± 0.0063 |
| LF11 | 4 | 27% | 0.1119 ± 0.1869 | 0.1629 ± 0.2705 | 0.1396 ± 0.0078 |
| LF3 | 8 | 12.5% | 0.0392 ± 0.1123 | 0.0607 ± 0.1679 | 0.1191 ± 0.0080 |
| LF9 | 4 | 28.5% | 0.1125 ± 0.1803 | 0.1662 ± 0.2651 | 0.1361 ± 0.0076 |
| O1 | 3 | 15% | 0.0667 ± 0.1591 | 0.0955 ± 0.2279 | 0.1176 ± 0.0079 |
| O2 | 3 | 12% | 0.0533 ± 0.1448 | 0.0764 ± 0.2074 | 0.1138 ± 0.0080 |
| O3 | 8 | 21% | 0.0745 ± 0.1547 | 0.1119 ± 0.2261 | 0.1100 ± 0.0061 |
| O4 | 8 | 38.5% | 0.1209 ± 0.1678 | 0.1874 ± 0.25 | 0.1371 ± 0.0064 |
| O5 | 7 | 10% | 0.0306 ± 0.0970 | 0.0479 ± 0.1482 | 0.0873 ± 0.0070 |
| O6 | 13 | 32.5% | 0.0843 ± 0.1376 | 0.1363 ± 0.2115 | 0.1106 ± 0.0061 |
| W1 | 8 | 35.5% | 0.1225 ± 0.1785 | 0.1854 ± 0.2619 | 0.1316 ± 0.0055 |
| W12 | 4 | 8% | 0.0325 ± 0.1116 | 0.0476 ± 0.1626 | 0.0945 ± 0.0072 |
| W10 | 7 | 26% | 0.0833 ± 0.1496 | 0.1288 ± 0.2252 | 0.1145 ± 0.0062 |
| W13 | 7 | 32% | 0.1135 ± 0.1766 | 0.1708 ± 0.2588 | 0.1318 ± 0.0065 |
| W14 | 8 | 43% | 0.1538 ± 0.1907 | 0.231 ± 0.2782 | 0.1546 ± 0.0055 |
| W15 | 7 | 25% | 0.0886 ± 0.1620 | 0.1335 ± 0.2388 | 0.1310 ± 0.0068 |
| W2 | 7 | 36% | 0.1245 ± 0.1785 | 0.1886 ± 0.2623 | 0.1385 ± 0.0069 |
| W4 | 9 | 44.5% | 0.1368 ± 0.1733 | 0.2124 ± 0.2556 | 0.1453 ± 0.0059 |
| W5 | 6 | 28.5% | 0.1078 ± 0.1784 | 0.1601 ± 0.2601 | 0.1304 ± 0.0067 |
| W6 | 4 | 32% | 0.1331 ± 0.1974 | 0.1937 ± 0.2852 | 0.1618 ± 0.0077 |
| W7 | 7 | 38% | 0.1290 ± 0.1771 | 0.1965 ± 0.2617 | 0.1397 ± 0.0060 |
| W8 | 6 | 35.5% | 0.1408 ± 0.1987 | 0.2065 ± 0.2861 | 0.1455 ± 0.0075 |
| W9 | 5 | 17% | 0.0664 ± 0.1507 | 0.0980 ± 0.22 | 0.1265 ± 0.0072 |
| Pop.* | N † | PPL‡ | H § | I¶ | H[s]— Bayesian** |
|---|---|---|---|---|---|
| Wild | 85 (13) | 86.50% | 0.1867 ± 0.1615 | 0.3026 ± 0.2247 | 0.1343 ± 0.0172 |
| Cult. | 131 (21) | 94.00% | 0.1694 ± 0.1559 | 0.2812 ± 0.2140 | 0.1208 ± 0.0208 |
| BY | 59 (10) | 78.50% | 0.1588 ± 0.1587 | 0.2611 ± 0.2238 | 0.1205 ± 0.0238 |
| LF | 30 (5) | 75.50% | 0.1886 ± 0.1762 | 0.2985 ± 0.2456 | 0.1313 ± 0.0181 |
| O | 42 (6) | 64.50% | 0.1422 ± 0.1649 | 0.2303 ± 0.2363 | 0.1127 ± 0.0159 |
- * Population letters correspond to Fig. 1. BY, backyard population; LF, living fence population; O, orchard population; and W, wild population.
- † N, number of individuals per population. The lower part of the table includes the number of individuals per population type, the number of populations in parentheses.
- ‡ PPL, percentage of polymorphic loci.
- § h, Nei's (1973) gene diversity (average) per population; H, average across groups.
- ¶ I, Shannon's diversity index (Lewontin 1972).
- ** h[s], Bayesian gene diversity average per population; H[s], average across groups.
|
Analysis 1: Kruskal–Wallis test for differences between wild populations, living fences, backyard populations, and orchards |
|||
|---|---|---|---|
| Y | χ2 | d.f. | χ2-prob |
| S/PPL* | 7.5063 | 3 | 0.0574 |
| I† | 7.668 | 3 | 0.0534 |
| h (Nei 1973)‡ | 5.1900 | 3 | 0.1584 |
| H[s]§ | 7.1154 | 3 | 0.0683 |
|
Analysis 2: Wilcoxon two-group test — Wild populations vs. all cultivated populations |
|||||
|---|---|---|---|---|---|
| Y | Z | Z-prob | χ2 | d.f. | χ2-prob |
| S/PPL* | 1.773 | 0.0762 | 3.207 | 1 | 0.0733 |
| I† | 2.091 | 0.0365 | 4.446 | 1 | 0.0350 |
| h (Nei 1973)‡ | 2.144 | 0.0320 | 4.6739 | 1 | 0.0306 |
| H[s]§ | 2.12631 | 0.0335 | 4.5969 | 1 | 0.0320 |
|
Analysis 3a: Wilcoxon two-group test — Wild populations vs. living fences |
|||||
|---|---|---|---|---|---|
| Y | Z | Z-prob | χ2 | d.f. | χ2-prob |
| S/PPL* | −0.740 | 0.459 | 0.6238 | 1 | 0.4296 |
| I† | −0.493 | 0.6221 | 0.294 | 1 | 0.5877 |
| h (Nei 1973)‡ | −0.49286 | 0.6221 | 0.2931 | 1 | 0.5877 |
| H[s]§ | −0.29572 | 0.7674 | 0.1190 | 1 | 0.7301 |
|
Analysis 3b: Wilcoxon two-group test — Wild populations vs. backyard trees |
|||||
|---|---|---|---|---|---|
| Y | Z | Z-prob | χ2 | d.f. | χ2-prob |
| S/PPL* | −1.614 | 0.1064 | 2.708 | 1 | 0.0999 |
| I† | −1.892 | 0.0586 | 3.6962 | 1 | 0.0545 |
| h (Nei 1973)‡ | −1.8601 | 0.0627 | 3.5797 | 1 | 0.0585 |
| H[s]§ | −1.82951 | 0.0673 | 3.4615 | 1 | 0.0628 |
|
Analysis 3c: Wilcoxon two-group test — Wild populations vs. orchards |
|||||
|---|---|---|---|---|---|
| Y | Z | Z-prob | χ2 | d.f. | χ2-prob |
| S/PPL* | −1.361 | 0.1736 | 1.973 | 1 | 0.1602 |
| I† | −1.973 | 0.0485 | 4.0692 | 1 | 0.0437 ¶ |
| h (Nei 1973)‡ | −2.14879 | 0.0317 | 4.8077 | 1 | 0.0283 ¶ |
| H[s]§ | −2.32420 | 0.0201 | 5.6077 | 1 | 0.0179 ¶ |
- * S, Number of polymorphic sites; PPL, percentage of polymorphic loci.
- †I, Shannon's information index ( Lewontin 1972).
- ‡ h, Nei's (1973) gene diversity.
- § H[s], average gene diversity (panmictic heterozygosity).
- ¶ Not significant following Bonferroni corrections.
When cultivated populations were partitioned by habitat (living fences, backyards, and orchards), levels of genetic variation were lower for the orchard trees than for trees planted in backyards, in living fences, or growing in native forests (Table 3). Spondias purpurea trees found in living fences and backyards harboured qualitatively intermediate levels of genetic variation that exceeded the variability of the orchards but were generally less than the diversity found in the wild (Table 3). Wilcoxon two-group tests comparing living fences and wild populations (Table 4, Analysis 3a) and backyard trees and wild populations (Table 4, Analysis 3b) revealed no significant differences in any of the genetic diversity measures. In contrast, Wilcoxon two-group tests comparing estimates of genetic variation in orchards and wild populations produced significant results (Table 4, Analysis 3c). However, when the Bonferroni correction (α′ = 0.017) was applied to the tests in Table 4, Analyses 3a–c, none of the results were significant.
Population structure
Analyses of molecular variance indicated that 35.65% of the total molecular variance was attributable to divergence among populations, with 64.35% of the variance housed within populations (Table 5). Overall, wild populations exhibited less population structure (ΦST = 0.302) than cultivated populations (ΦST = 0.398). The percentage of variation partitioned among wild populations (30.19%) was similar to that partitioned among populations of backyard trees (31.08%). Living fences and orchards displayed higher percentages of variation distributed among populations (48.31%, 44.82%, respectively). A Bayesian estimate of FST under a random-effects model of population sampling (θB) and the Bayesian analogue of Nei's GST (GST-B) similarly revealed that wild populations and backyard populations have lower levels of variance distributed among populations than living fences and orchards (Table 5).
| amova | Bayesian estimators | |||||
|---|---|---|---|---|---|---|
| Source of variation | d.f. | Φ-statistic* | % total | P value | θB†± SD | G ST-B‡± SD |
| Analysis 1 — All samples | ||||||
| Among populations | 34 | ΦST = 0.357 | 35.65% | < 0.0010 | 0.3125 ± 0.0085 | 0.3116 ± 0.0064 |
| Within populations | 181 | 64.35% | ||||
| Analysis 2 — Wild populations | ||||||
| Among populations | 12 | ΦST = 0.302 | 30.19% | < 0.0010 | 0.2776 ± 0.0157 | 0.2573 ± 0.0131 |
| Within populations | 72 | 69.81% | ||||
| Analysis 3 — Backyard trees | ||||||
| Among populations | 9 | ΦST = 0.311 | 31.08% | < 0.0010 | 0.2885 ± 0.0194 | 0.2556 ± 0.015 |
| Within populations | 49 | 68.92% | ||||
| Analysis 4 — Living fences | ||||||
| Among populations | 5 | ΦST = 0.483 | 48.31% | < 0.0010 | 0.3947 ± 0.0261 | 0.3291 ± 0.019 |
| Within populations | 24 | 51.69% | ||||
| Analysis 5 — Orchards | ||||||
| Among populations | 5 | ΦST = 0.448 | 44.82% | < 0.0010 | 0.395 ± 0.0262 | 0.3312 ± 0.0201 |
| Within populations | 36 | 55.18% | ||||
- * F ST analogues at the molecular level (Excoffier et al. 1992).
- † F ST analogues under a random-effects model of population sampling (Holsinger 2003).
- ‡Bayesian analogue of Nei's G ST (Nei 1973; Holsinger 1999).
Correlation between genetic distance and geographic distance
Mantel tests detected no significant correlations between geographic distance and genetic distance in all populations taken together (r = –0.0336, P = 0.695, two-tailed), nor in seven subsets of the data: (i) wild populations only (r = 0.0708, P = 0.182), (ii) cultivated populations only (r = –0.1429, P = 0.914), (iii) backyards only (r = –0.1307, P = 0.806), (iv) living fences only (r = –0.2815, P = 0.813), (v) orchards only (r =–0.2710, P = 0.837), (vi) populations from western Central Mexico (r = 0.0236, P = 0.345), and (vii) populations from southern Mexico and Central America (r = –0.0273, P = 0.609).
Principal components analysis
AFLP data were summarized with three principal components that together accounted for 21.74% of the AFLP variation (PC 1 = 10.37%, PC 2 = 6.36%, PC 3 = 4.99%) (2, 3). AFLP variation analysed with principal components in another tropical fruit tree species, breadfruit (Artocarpus altilis), displayed similar values (e.g. Zerega et al. 2004). The PCAs indicate that trees from wild populations cluster in two distinct groups: (i) a northern group: western central Mexico (states of Colima, Jalisco, Nayarit, and Michoacan) (Fig. 3A, B) and (ii) a southern group: southern Mexico (Chiapas, Oaxaca) and Central America (Fig. 3A, B). This pattern is interrupted by three individuals from a roadside population just north of Puerto Vallarta (Jalisco) (Fig. 3A), which fall into the graph space otherwise occupied by wild trees from southern Mexico and Central America (Fig. 3B). Samples found in the portion of the PCA space where the two groups of wild populations intersect represent individuals from the southernmost wild populations from the northern group and the northernmost wild populations (Chiapas) from the southern group. The distinct northern and southern groups identified in wild populations are also apparent in the cultivated populations (Fig. 3C, D). The manova results indicate that the wild populations form two distinct regional groups (F3,81 = 46.125, P < 0.0001), and that the cultivated populations form two distinct regional groups (F3,127 = 9.592, P < 0.0001).
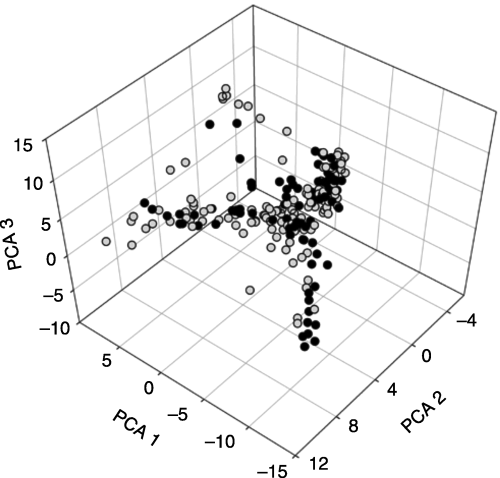
AFLP variation in cultivated and wild Spondias purpurea trees is summarized with principal components analyses (PC1 = 10.37%; PC2 = 6.36%;PC3 = 4.99%). Wild individuals are shown with dark circles, cultivated individuals are represented with light circles.
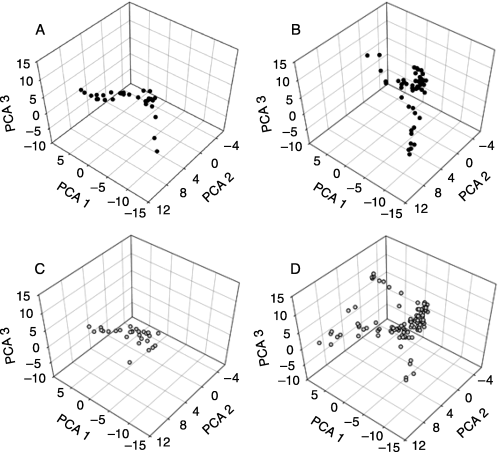
Principal components analyses AFLP variation are used to explore the geographic distribution of AFLP variation in cultivated and wild Spondias purpurea trees. Wild individuals (shown with dark circles) cluster in two regionally distinct geographic areas (F3,81 = 46.125, P < 0.0001): (A) the northern region including western Central Mexico and (B) the southern region, including wild individuals from southern Mexico (Oaxaca, Chiapas) and Central America. Trees from cultivated population (shown with light circles) also cluster in two regional groups (F3,127 = 9.592, P < 0.0001): (C) the northern region including western Central Mexico and (D) the southern region, including wild individuals from southern Mexico (Oaxaca, Chiapas) and Central America.
Discussion
The domestication process in Spondias purpurea resulted in a reduction in genetic variation in the cultivated populations as compared with their wild progenitors. This genetic bottleneck was detected statistically using the Wilcoxon two-group test, but not with the Kruskal–Wallis test.
Numerous studies have shown that cultivated populations harbour a subset of the total genetic variation present in their wild progenitors (e.g. Mimura et al. 2000; Buckler et al. 2001; Lumaret & Ouazzani 2001; Ren & Timko 2001; Sun et al. 2001; Anthony et al. 2002; Papa & Gepts 2003; Tang & Knapp 2003; Birmeta et al. 2004; Cahill 2004; Lumaret et al. 2004; Vigouroux et al. 2005; Wright 2005); however, the relative reduction in variation ranges among species. In annual plants that are propagated from seeds (e.g. corn, rice, common beans, azuki beans, sunflowers), the domesticated populations harbour between 50% and 67% of the variation of the wild progenitors (Wright 2005; Mimura et al. 2000; Sun et al. 2001; Papa & Gepts 2003; Tang & Knapp 2003). In contrast some perennial domesticates retain relatively higher percentages of the variation of their wild ancestors. Cultivated columnar cacti populations (Polaskia chichipe) retained 88–96% of the variation of their ancestors (Otero-Arnaiz et al. 2005) and cultivated populations of the tropical fruit tree Inga edulis and their wild ancestors did not differ in gene diversity (Hollingsworth et al. 2005). Similarly, cultivated S. purpurea populations retain approximately 90% of the variation detected in wild populations, which is consistent with the reduction in variation seen in other long-lived species. The fact that significant differences between cultivated and wild S. purpurea were detected with the Wilcoxon two-group test and not with the Kruskal–Wallis test likely reflects the relatively small reduction in variation that accompanied the domestication of S. purpurea. Additional, independent evidence for a reduction in variation in cultivated S. purpurea populations as compared with their wild relatives has been demonstrated with chloroplast sequence data (Miller & Schaal 2005).
It has been suggested that intense artificial selection during domestication results in a progressive narrowing of the genetic base of the cultivated populations (Tanksley & McCouch 1997; Abbo et al. 2003). In recent times, the genetic base of cultivated populations most likely has been reduced further as modern crop improvement programmes have selectively bred only a small subset of the original cultivated gene pool (Tanksley & McCouch 1997). If domestication occurs as a series of genetic bottlenecks that limit genetic variation in a stepwise manner, then the gene pools of crop populations cultivated in modernized agricultural habitats (e.g. orchards) should reflect more recent genetic bottlenecks, and should contain relatively less genetic variability than the gene pools of crop populations growing in more traditional agricultural habitats (e.g. backyard gardens) that have not yet been subjected to modern breeding programmes. Orchard populations of S. purpurea include one or at most two varieties of jocotes, while trees grown in backyards and living fences have fruits that vary widely in colour, size, shape, and taste. Estimates of genetic variation in backyard and living fence populations do not differ significantly from the wild populations. Estimates of genetic variation in orchards and wild populations differ significantly prior to the application of a Bonferroni correction, which renders these differences not significant. Considering that conservative nonparametric statistical tests were used and produced a statistically significant result in levels of genetic variation between orchard and wild populations, that the study system underwent a relatively small (but statistically detectable) reduction in diversity, and that the results make sense biologically, it appears that the Bonferroni correction may have produced a type II error for these data (see Cabin & Mitchell 2000; Moran 2003; Nakagawa 2004). Consequently, these data suggest that levels of genetic variation in orchard populations are different from levels of variation in wild populations. This difference was not observed in populations growing in more traditional agricultural habitats, highlighting the importance of populations cultivated in informal agricultural habitats in the region of origin as possible reservoirs of genetic variation for the crop species (e.g. Brush 1995, 2000).
Domestication affects the structure of genetic variation in cultivated populations
Domestication impacts not only the amount of genetic variation contained in cultivated populations, but also the structure of this variation. Hamrick & Godt (1997) reported that the mean GST level (analogous to ΦST) for crop species as 0.339, while the mean GST for noncrop species as 0.212. They attributed the higher GST values in cultivated taxa to the higher proportion of selfing in cultivated species as compared with species that are not cultivated (Hamrick & Godt 1996, 1997). Our results are consistent with this trend: crop (cultivated) S. purpurea populations have a greater portion of their variance distributed among populations (ΦST = 0.398) than wild (noncrop) S. purpurea populations (ΦST = 0.302). We infer that increased ΦST values for cultivated S. purpurea populations relative to their wild ancestors reflects the different modes of reproduction in cultivated (clonally propagated) and wild (sexually reproducing) populations. Like selfing, vegetative reproduction results in more homogeneous populations over time, that exhibit a greater proportion of the variance distributed among populations. Sexually reproducing, outcrossing populations, on the other hand, should maintain variation within populations, and as a result display a greater proportion of variance within populations, and smaller proportion of variance among populations, than vegetatively propagated populations.
Of the three cultivated populations included in this study, home gardens (backyards) represent a common and traditional agro-ecosystem in Mexico and Central America (e.g. Anderson 1952; Levasseur & Olivier 2000; Mendez et al. 2001; Zaldivar 2002; Angel-Pérez & Mendoza 2004). AFLP estimates of genetic structure in backyard populations are statistically indistinguishable from wild populations. Interestingly, populations of backyard trees exhibit only slightly more variation among populations (31.08%, ΦST = 0.311) than wild populations (ΦST = 0.302). In contrast, populations cultivated in living fences and orchards contain a greater proportion of variation among populations (48.31%, ΦST = 0.483; 44.82%, ΦST = 0.448, respectively) relative to wild populations and backyard populations. The existence of nearly 10% more variance among populations in orchards and living fences, nearly 1/3 more variance than what was recovered among wild populations and backyards, may reflect differences in the method of reproduction in these populations. Trees grown in orchards and living fences are propagated exclusively vegetatively (Zahawi 2005; A.J.M., personal observation). New backyard trees are planted from stocks of older trees, but many trees found in backyards are so old it is impossible to know if they were propagated vegetatively or if they were grown from seed. Further, relatively low estimates of among-population variation for backyards may reflect ongoing exchange of backyard stocks.
Geographic distribution of genetic variation and the origins of cultivated S. purpurea populations
Two geographic origins of cultivated Mesoamerican S. purpurea individuals were suggested previously based on phylogeographic analyses of chloroplast sequence data (Miller & Schaal 2005). These analyses indicated that cultivated S. purpurea trees were domesticated in two regions within Mesoamerica: western central Mexico and southern Mexico/Central America. The AFLP data are consistent with two geographic origins of cultivated S. purpurea: wild and cultivated S. purpurea populations form two distinct clusters within Mesoamerica: (i) a northern group from western central Mexico and (ii) a southern group from southern Mexico and Central America. This pattern could result from gene flow between sympatric cultivated and wild populations; however, there are two biological reasons why this is not likely in the case of S. purpurea. First, cultivated S. purpurea populations are propagated exclusively vegetatively, and do not produce viable seed. If there was movement of pollen from wild to cultivated populations, it is unlikely that viable seed would result; even if viable seeds were produced, they would not be allowed to germinate in managed environments, where only S. purpurea stocks are used to propagate new individuals. Second, gene flow in the form of pollen from cultivated populations to wild population is not likely because S. purpurea is a polygamo-dioecious species, and the vast majority of trees in cultivation are females (A. Miller, unpublished) because they produce the fruit for which the trees are cultivated.
Conclusions
The domestication process in the Mesoamerican fruit tree S. purpurea reduced levels of genetic variation in cultivated populations as compared to their wild progenitors. Cultivated populations from different types of agricultural habitats contain varying levels of genetic variation: trees cultivated in orchards harbour less genetic variability than trees cultivated in backyard gardens and living fences, which display qualitatively intermediate levels of genetic variation. These populations may function as reservoirs of genetic variation in the species, as large-scale cultivation becomes more common and native populations go extinct. The proportion of genetic variation distributed among populations is greater in cultivated populations than in wild populations, a reflection of relative amounts of vegetative propagation. Living fence and orchard populations display similar levels of variation distributed among populations; both are significantly greater than the degree of population structure observed in backyard and wild populations. Finally, the AFLP data provide additional support for two distinct geographic origins of cultivated S. purpurea trees in Mesoamerica.
Acknowledgements
We thank members of the Schaal laboratory, Tom Ranker, Jenny Ramp, Shannon Fehlberg, two anonymous reviewers, and the subject editor for helpful comments. Yu-Chung Chiang, Jason Knouft, and Jason Kolbe provided valuable assistance with analyses. AFLP data were generated at the Cullman Laboratory for Molecular Systematics at the NewYork Botanical Garden, and was greatly facilitated by the assistance of Lorna Lueck, Tim Motley, Susan Pell, and Nyree Zerega. Thank you to field collaborators: R. Aguilar F., A. Anzueto, G. Borjas, G. Carnevali, J. Castilla Canales, L. Chavez V., I. Diaz, A-C. Gomez, A. Herrera, M. Diaz, A. and C. MacVean, M. Merello, A. Molina R., P. Moreño, A. Muehlenbachs, M. Olson, E. O'Mahoney-Cubbison, A. Paschke, E. Pimienta Barrios, B. Ramirez Hernandez, R. Rueda, R. Ruenes, N. Ventura, and B. Wong. This work was supported by the National Science Foundation (PD 0105134), the Organization for Tropical Studies, the Botanical Society of America, the Andrew W. Mellon Foundation support of Missouri Botanical Garden graduate students, Washington University Division of Biology and Biomedical Sciences Graduate Fellowship, and a Danforth Foundation Grant to support undergraduates in plant biology research at Washington University.
Appendix
Appendix 1
| Habitat | Pop.# | N | Country | State (Locality) | Latitude | Longitude |
|---|---|---|---|---|---|---|
| Wild | W1 | 8 | Mexico | Jalisco (Puerto Vallarta, Cabo Corrientes) | 20.409 | −105.2855 |
| Wild | W15 | 7 | Mexico | Jalisco (Toliman) | 19.58605556 | −104.015638 |
| Wild | W13 | 7 | Mexico | Jalisco (Malaque and La Huerta) | 19.29808333 | −104.78175 |
| Wild | W9 | 5 | Mexico | Colima (Manzanillo) | 19.02011111 | −104.1198611 |
| Wild | W12 | 4 | Mexico | Michoacan (Arteaga) | 18.38769444 | −102.1791389 |
| Wild | W14 | 8 | Mexico | Chiapas (Chiapa del Corzo) | 16.75455556 | −92.97175 |
| Wild | W2 | 7 | Mexico | Chiapas (Ocozocautla) | 16.7055 | −93.53213889 |
| Wild | W6 | 4 | Guatemala | Guatemala (Villa Canales) | 14.43306667 | −90.64451667 |
| Wild | W8 | 6 | El Salvador | Cabañas (Puebla de Cinquera) | 13.88698333 | −88.96195000 |
| Wild | W5 | 6 | Honduras | Choluteca (El plan del jocotes) | 13.47456 | −87.23146 |
| Wild | W4 | 9 | Nicaragua | Boaco | 12.44222222 | −85.68205556 |
| Wild | W10 | 7 | Nicaragua | Managua (San Francisco Libre) | 12.38541667 | −86.09652778 |
| Wild | W7 | 7 | Costa Rica | Guanacaste (Santa Rosa NP) | 10.80397222 | −85.64052778 |
| Backyard | BY6 | 9 | Mexico | Jalisco/Colima border | 19.12313 | −104.3799 |
| Backyard | BY13 | 2 | Mexico | Oaxaca (San Mateo del Mar) | 16.193 | −95.07280556 |
| Backyard | BY5 | 8 | Mexico | Chiapas (Ocozocautla) | 16.76816667 | −93.382 |
| Backyard | BY3 | 7 | Guatemala | Zacapa (Rio Hondo) | 15.017283 | −89.6792 |
| Backyard | BY2 | 7 | El Salvador | Ahuachapán (San Francisco Menendez) | 13.84781667 | −90.00868333 |
| Backyard | BY11 | 5 | Honduras | La Paz (Pueblo Miravalle) | 14.36730556 | −87.65363889 |
| Backyard | BY4 | 6 | Honduras | Choluteca (El Plan del jocotes) | 13.25677 | −87.14374 |
| Backyard | BY7 | 5 | Costa Rica | Guanacaste (Filadelfia) | 10.48061111 | −85.60430556 |
| Backyard | BY8 | 5 | Costa Rica | Puntarenas (Puntarenas) | 9.842888889 | −84.84916667 |
| Backyard | BY9 | 5 | Panama | Panama (El Espavecito) | 8.5613611 | −79.9506111 |
| Living Fence | LF11 | 4 | Mexico | Colima (Manzanillo) | 19.02011111 | −104.1198611 |
| Living Fence | LF1 | 8 | Mexico | Guerrero (San Marcos) | 16.80816667 | −99.36275 |
| Living Fence | LF3 | 8 | Mexico | Chiapas (Ocozocautla) | 16.7457222 | −93.50952778 |
| Living Fence | LF8 | 6 | Nicaragua | Masaya, Boaco (Catarina) | 12.26351 | −86.09695 |
| Living Fence | LF9 | 4 | Costa Rica | Puntarenas (Puntarenas) | 9.978305556 | −85.854124 |
| Orchard | O3 | 8 | Mexico | Nayarit (Tepic) | 21.59408333 | −104.9991667 |
| Orchard | O4 | 8 | Mexico | Nayarit (San Blas) | 21.64663889 | −105.124222 |
| Orchard | O5 | 7 | Mexico | Chiapas (Villa de Acala) | 16.528 | −92.82958333 |
| Orchard | O1 | 2 | Guatemala | Guatemala (Villa Canales) | 14.3568 | −90.53776667 |
| Orchard | O6 | 13 | Guatemala | Solala (Panajachel) | 14.7288 | −91.26325 |
| Orchard | O2 | 4 | Honduras | Choluteca | 13.68938889 | −87.33013889 |
References
Allison Miller is a postdoctoral researcher working in the University of Colorado Museum. Her research interests include evolution of plant populations under domestication. Barbara Schaal is the Spencer T. Olin Professor in Arts and Sciences at Washington University. Her research is on the evolutionary genetics of plants. This work was carried out while A.J.M. was a graduate student with B.A.S. and Peter Raven at the Missouri Botanical Garden and is part of A.J.M.'s dissertation on the origin and evolution of Spondias purpurea.




