Bioavailability and its assessment
Abstract
Bioavailability is a key pharmacokinetic parameter which expresses the proportion of a drug administered by any nonvascular route that gains access to the systemic circulation. Presented in this review are the different approaches to measurement of bioavailability (absolute and relative), including the case in which intravenous administration is impossible. The rate of drug absorption is also discussed with special emphasis on the possible difficulties encountered using Cmax and Tmax or curve fitting to evaluate the rate of drug absorption.
Introduction
Bioavailability (denoted as F and generally expressed as a percentage, F%) quantifies the proportion of a drug which is absorbed and available to produce systemic effects. Bioavailability is a fundamental property of a pharmaceutical product for a given route of administration. It should be known and shown to be reproducible for all drug products intended to produce a systemic effect. Bioavailability assessment may also be of value for substances locally administered and intended to produce only local effect, in order to demonstrate the absence of systemic exposure and to support claims regarding the absence of systemic effect, or possible residues in edible tissues of food producing species.
This review will focus on the bioavailability assessment (rate and extent) and not on the numerous physicochemical, physiological and pathological factors capable of influencing the bioavailability of a drug (see Baggot, 2001). The review by Cutler (1981) on the several approaches to compute bioavailability is still authoritative.
Definition of bioavailability
According to the European Medicines Evaluation Agency (EMEA, human guidelines) ‘bioavailability means the rate and extent to which the active substance or active moiety is absorbed from a pharmaceutical form, and becomes available at the site of action’ (Anonymous, 2001). As the site of action may not be well defined, it is also stated that ‘bioavailability is understood to be the extent and the rate at which a substance or its active moiety is delivered from a pharmaceutical form, and becomes available in the general circulation’.
To become available in the general circulation, drug should gain access to arterial blood. However, as arterial (aortic) blood is seldom sampled, bioavailability is normally referred to the usual site of measurement (venous blood). There are occasions when drugs delivered to venous blood are not systemically available due to an extensive pulmonary first-pass effect (vide infra).
Absorption vs. bioavailability
In a physiological context, the terms absorption and bioavailability are neither synonymous nor interchangeable (Chiou, 2001). Absorption is only one of the steps separating drug administration from its delivery to the site of action. From a mechanistic point of view, it can be helpful to distinguish the two concepts in order to explain the origin of low bioavailability; for example, a drug can be 100% absorbed from a given formulation (therefore no possible improvement) but have nevertheless a low bioavailability due to breakdown after absorption. This is the case for prostaglandin (PgF2α), which undergoes a 90% lung first-pass effect (Bonnin et al., 1999) (see review on clearance in this issue) and for many drugs undergoing variable hepatic first-pass effect after oral or intra-peritoneal administration, for example propranolol in dog (Bai et al., 1985). To ascribe low bioavailability to poor absorption (and expecting to improve it with a new formulation) when the cause is actually a first-pass effect (and not amendable to improvement) can be counterproductive during drug development.
In the context of bioavailability measurement (not interpretation), the terms of absorption and bioavailability are often used interchangeably (e.g. in Gibaldi & Perrier, 1982; Rowland & Tozer, 1995) despite the above considerations. Unless stated otherwise, the word absorption in this review should also be understood to be synonymous with bioavailability.
Absolute vs. relative bioavailability
Absolute bioavailability is the actual percentage of the administered dose (from 0 to 100%), which reaches the general circulation. Estimation involves comparing drug exposure following extravascular (e.v.) administration of the tested dosage form with that of an intravenous administration (i.v.), assumed to be 100% available.
Relative bioavailability involves comparison of two formulations (or two routes of administration of the same formulation) without reference to an i.v. administration. It should be emphasized that interpretation of a relative bioavailability trial can be of limited value if the absolute bioavailability of the reference formulation is not known. Indeed, improving by 100% the bioavailability of a given reference formulation (e.g. either by manipulating the food regimen in the case of oral administration or modifying the formulation) has different meanings if the reference formulation is 5 or 50% bioavailable. In the former case, the improvement lacks interest, whereas in the latter it is very significant!
Bioavailability vs. bioequivalence
Although bioavailability is used as an endpoint in bioequivalence trials, bioavailability and bioequivalence trials are conceptually different. A bioequivalence trial aims to establish the therapeutic equivalence of two formulations (or two routes of administration). It is not concerned with documenting the physiological factors capable of influencing systemic exposure of the drug. In a bioequivalence trial, animals are only biological test-tubes, required for an in vivo quality control for different formulations (Toutain & Koritz, 1997). In contrast, in a bioavailability trial, it is the animal physiology and possibly pathology (age, sex, food intake, disease state and severity, etc.) which are of primary interest.
It is a misconception that a low bioavailability can always be compensated by increasing the recommended dose
It is frequently stated that ‘the absolute bioavailability of this drug/product is of no consequence (e.g. a pour-on for cattle), because the dose has been sufficiently increased to guarantee clinical efficacy’. This statement is questionable in general terms, as it is a primary objective of all rational drug development programmes to market drug products having the highest possible systemic bioavailability.
More specially, a low bioavailability can be a major source of therapeutic variability. If the mean bioavailability in a group of animals is 100%, there is no possibility of inter-individual variability in drug exposure because of the different factors influencing the bioavailability. In contrast, when the mean bioavailability is low (e.g. 10%), a large inter-individual variability will be expected, with some subjects having a very low (e.g. 5%), and with others having a higher bioavailability (e.g. 20%), thus leading to exposures varying from 1 to 4, i.e. by 400% (and consequently, a lack of reproducibility of this formulation in terms of clinical efficacy).
Fig. 1 shows the relationship between absolute bioavailability and inter-individual variability for a set of drugs in man (Hellriegel et al., 1996). In veterinary medicine, similar observations can be made, e.g. in the horse, the bioavailability of rifampicin when the drug is administered 1 h before feeding is 68 ± 26% (coefficient of variation = 38%), whereas when the same drug is administered 1 h after feeding, the bioavailability is 26 ± 17%, i.e. with a coefficient of variation of 67% (Baggot, 2001). In pigs, the mean absolute bioavailability of chlortetracycline administered by the oral route in fasted animals is low (19%) and variable, ranging from 9 to 30% (Kilroy et al., 1990), which is not satisfactory in terms of the prudent use of antibiotics. Indeed, the emergence of resistance is often because of an underexposure of small animal population subgroups despite an appropriate average dose.
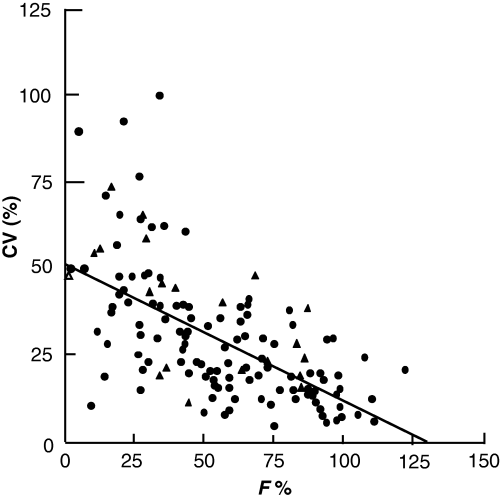
Relationship between bioavailability (F%) and inter-subject variability (CV) in man (Hellriegel et al., 1996). Data correspond to 100 different drugs.
Whenever bioavailability is low, drug companies may attempt to increase the dose to achieve an appropriate drug exposure. However, it may not be recognized that the dose is generally increased more than proportionally to the mean bioavailability factor in order to ensure drug efficacy in animals having the lowest bioavailability. For instance, for a hypothetical drug having a mean bioavailability of 33% (with some subjects having 20% bioavailability, and others 50%) and for which an exposure corresponding to 100% bioavailability is required, the dose should be multiplied by 5 (not by 3) to guarantee that the subjects with the lowest bioavailability are fully exposed. By doing this, the subjects having an initial bioavailability of 50% are unnecessarily overexposed by a factor of 2.5! If such an overexposure is considered to be detrimental on safety or other grounds, the dose can only be doubled. Then, it will be the subjects with the poorest availability who will be underexposed, with a possible reduction of clinical efficacy or worse, by creating a situation favouring the emergence of resistance (antibiotic and antiparasitic drugs). Finally, for a drug having both a narrow therapeutic window and a poor bioavailability, it is possible to encounter a situation for which no dose is able to expose adequately all the animals within a population (Fig. 2).
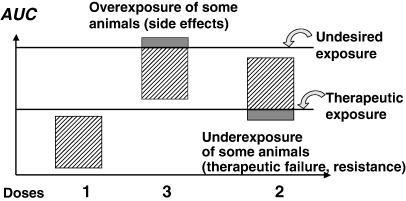
Low bioavailability and the impossibility of establishing a safe and efficacious dosage regimen for all animals. The figure shows, diagrammatically, the circumstance for which a drug formulation having a low and variable bioavailability cannot be administered at the same efficacious dosage in all animals due to a relatively narrow therapeutic window. With dose 1, all animals fail to achieve effective therapeutic exposure. Increasing the dose threefold guarantees that all animals now have an exposure above the therapeutic threshold, but animals with the highest bioavailability are now above the undesired threshold. Finally, increasing the dose by twofold guarantees that no animal undergoes undesired exposure, but the animals having the lowest bioavailability are under-exposed.
A poor (oral) bioavailability is also a risk factor for possible interaction. Indeed, for a drug having a low bioavailability, there is room for increasing exposure and a possibility of leading to over-exposure, as exemplified in man with felodipine. Felodipine is an anti-arrhythmic drug which has a low (approximately 15%) and erratic bioavailability because of a gut first-pass effect (metabolism by intestinal CYP3A4). Ingestion of grapefruit (which inhibits intestinal CYP450) can greatly increase the systemic exposure to felodipine (from 1 to 12 times between individuals) (Bailey et al., 2000). In veterinary medicine, oral bioavailability of endectocides is relatively low, leading to a possible interaction with food components as shown between moxidectin and quercetin, a natural flavonoid occurring in plants, and which is a modulator of P-glycoprotein (Dupuy et al., 2003).
Finally, in order to document exposure variability and to anticipate possible under or over exposure, the measurement of absolute bioavailability is mandatory for any new drug formulation. Thus, that no serious drug development should be performed without intravenous data information.
Rate of bioavailability
Not only extent, but also rate of absorption needs to be known, because both determine the shape of the plasma concentration vs. time curve and may influence the drug effect (e.g. concentration vs. time dependent antibiotic, duration of protection for an avermectin, etc.). Similarly, the toxic- or side-effect can be markedly different when absorption rates for new formulations differ widely (Fig. 3). It is also essential to know the rate of availability when a drug is presented as a specific formulation, intended to precisely control the rate of drug delivery (e.g. modified released products such as rumen retention device, vaginal sponge, etc.).
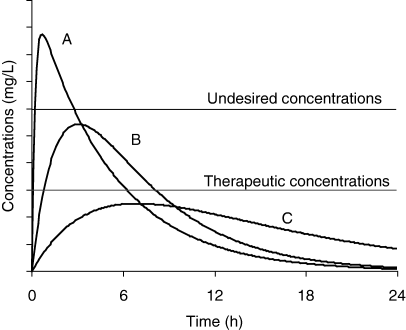
Drug effect and the rate of drug absorption. For three formulations (A, B and C) having the same bioavailability (same AUC), effect (therapeutic and undesired) differs depending on rate of absorption. For formulation A, the rate constant of absorption is high and the peak plasma concentration is above the safe concentration. In contrast, for formulation C, the rate of absorption is too low to allow plasma concentration to reach effective plasma concentrations (e.g. for a time-dependent antibiotic). Only formulation B gives a plasma concentration profile within the therapeutic window.
Absolute bioavailability by the i.v. route is not always 100%
By assumption, a drug administered by the i.v. route has 100% bioavailability. This is true only if the active substance reaches arterial blood without loss. Drugs are generally administered by the i.v. route and have first to cross the pulmonary circulation before gaining access to arterial blood. Lungs can be the site of an extensive first-pass effect and reduce drug availability. This is the case for prostaglandins or some amines (see our companion paper on plasma clearance in this issue, Toutain & Bousquet-Mélou 2004, pp. 415–425).
After the i.v. administration of a pro-drug, bioavailability can be <100%. For example, methylprednisolone (a corticosteroid) is a poorly hydrosoluble drug. In order to administer it by the i.v. route, a hydrosoluble ester has been synthesized (methylprednisolone sodium succinate or Solumedrol®). This is a pro-drug of methylprednisolone, and the ester must be hydrolysed to release its active moiety (i.e. methylprednisolone). In the dog, it was shown that the i.v. bioavailability of methylprednisolone from its succinic ester was only 40% (Toutain et al., 1986) (Fig. 4). Other examples of pro-drugs are inactive esters of macrolides, antibiotics such as pivampicillin and chloramphenicol succinate and antiviral pro-drugs.
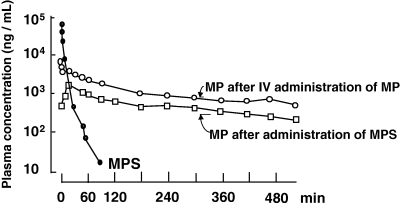
Absolute bioavailability of methylprednisolone in the dog. Methylprednisolone (MP) is a nonhydrosoluble steroid which can be administered by the i.v. route using a hydrosoluble salt of a succinate ester (methylprednisolone sodium succinate, MPS). After i.v. administration of MPS, its concentration decreases rapidly providing the active moiety, i.e. MP. Using this MP plasma concentration profile to estimate the MP bioavailability of another formulation would lead to gross overestimation of the true MP bioavailability, because only 44% of the administered MPS was transformed into MP. The true bioavailability of an MP formulation should be obtained by administering MP itself via the i.v. route (Toutain et al., 1986).
The measurement of absolute bioavailability
There are many methods used to evaluate the extent of systemic availability, the most classical one consisting of comparing plasma exposure (AUC) after an i.v. and an e.v. administration. Classically, the bioavailability factor is obtained by the following equation:
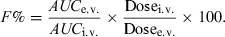 ()
()In Eqn 1, AUC is the area under the plasma (total or free) drug concentration or total blood concentration–time curve and Dosei.v. and Dosee.v. are the doses actually administered to evaluate F%.
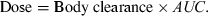 ()
()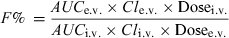 ()
()Generally, bioavailability is measured experimentally using a crossover study design and it is necessary to check for a possible carry-over effect, i.e. a differential residual effect of the first period over the second one. For example, hepatic enzymatic inhibition (or induction) after the first administration can modify the clearance during the second period. Therefore, the washout period should be long enough, not only to guarantee the absence of residual drug plasma concentration but also the lack of residual drug effect on clearance (induction/inhibition). This nonlinearity due to time dependency is also called nonstationarity.
The presence of a significant (differential) carry-over effect can be detected by properly analysing the design (by testing the sequence effect), but if an unbalanced design has been carried out (i.e. by performing i.v. route of administration for all animals in the first period, and e.v. in the second period), an equal carry-over will be obtained, which can be totally confounded with a period effect leading to a possibly large overestimation (or underestimation) of bioavailability. With this type of design, a bioavailability higher than 100% can be computed.
For random inter-occasion clearance variability, it has been suggested to correct the computed bioavailability factor by the terminal half-life (Wagner, 1967) using the following equation:
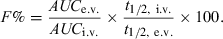 ()
()The logic for the so-called half-life correction is rooted in the relationship between t1/2 and clearance from the following equation:
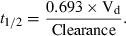 ()
()Assuming that Vd is invariable, t1/2 can be incorporated as a surrogate of clearance in Eqn 3.
This correction should be used cautiously and accepted only if it results in a substantial decrease in the variability of the results, or in order to avoid a mean bioavailability higher than 100%. Indeed, the estimation of terminal half-life (contrary to body clearance) is not very robust. In addition, if the terminal half-life does not represent the drug elimination but rather drug absorption (flip-flop), the correction becomes totally illicit and its unjustified use may lead to markedly underestimated F%. For the same objective, an equation correction can be made using renal clearance, which could be independently evaluated during a bioavailability trial. According to Karlsson and Sheiner (1994), the best way to handle random inter-occasion clearance variability is to analyse all the subjects simultaneously with a nonlinear mixed effect model.
Measurement of absolute bioavailability when plasma drug concentrations are not directly measurable
In some instances, the measurement of plasma concentration of the administered drug is impossible, either because an appropriate analytical technique is not available, or more often because the drug is rapidly transformed into an active metabolite (e.g. 4-methylaminoantipyrine or 4-MMA from dipyrone). In these conditions, the drug absolute bioavailability can be evaluated by measuring the AUC of its metabolite using the following equation:
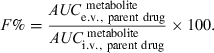 ()
()The condition for using Eqn 6 is that the metabolite must not be formed at the administration site or by a first-pass effect. In the same circumstance (no first-pass effect) a nonspecific assay (e.g. radioactivity), measuring both the drug and its metabolite(s), can be used to determine bioavailability. However, a nonspecific assay cannot be used for nonlinear systems.
If a drug is metabolized solely by the liver and subjected to a significant hepatic first-pass effect, then Eqn 1 will be appropriate to measure the absolute bioavailability of an oral formulation, whereas Eqn 6 will give the fraction of the dose actually absorbed after the oral administration (for more information see Weiss, 1990).
Measurement of bioavailability using urinary concentrations
Absolute bioavailability can be assessed by measuring the amount of drug excreted in urine (or any other biological fluid or excreta) using the following equation:
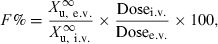 ()
()where 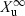 is the total amount of drug eliminated in urine (or other biological fluid).
is the total amount of drug eliminated in urine (or other biological fluid).
The assumption underlying Eqn 7 is that the ratio of renal clearance and total clearance is the same for the i.v. and e.v. administrations. The main limit of the urinary approach is the need to collect urine (or faeces, milk, etc.) until almost all the drug has been excreted. The use of partial urine collection is theoretically possible but requires several assumptions not always easy to check. Urinary metabolite, provided that it is not formed by a first-pass effect, can be used for absolute bioavailability measurement:
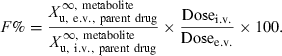 ()
()Equation 8 can be used to assess the relative bioavailability of two formulations administered by the same route regardless of the presence of a first-pass effect.
Evaluation of bioavailability when terminal half-life is very prolonged and limits the use of a cross-over design
For some drugs having a long terminal half-life (e.g. avermectins, moxidectin, salicylanilides, etc.) the absolute bioavailability is seldom measured, because trials involving two (long) periods separated by a washout period of 10 times the terminal half-life are considered as prohibitive. In addition, nothing guarantees the invariance of the plasma clearance over such a prolonged period of time, especially in growing animals, thus making invalid the use of Eqn 1.
A possible solution to this problem is to consider the estimation of bioavailability by a semi-simultaneous drug administration such as that described by Karlsson and Bredberg (1990). The principle of this method comprises administering one of the two doses (i.v. then e.v., or e.v. then i.v.) at an optimal interval and fitting simultaneously the entire curve obtained with an appropriate model, including and estimating the rate constant of absorption, lag, and the bioavailability factor.
It was shown that the precision of the method was influenced by the dose rate, the order of administration, the e.v. vs. i.v. dose ratio, the duration of the sampling, and the interval between the doses. This approach deserves to be encouraged in veterinary medicine as a screening method, when intra-animal variability is expected (e.g. time-dependent variation of clearance during growth), or to reduce the total number of blood samplings. The most appropriate design can be determined by Monte Carlo simulations. The relative bioavailability of two e.v. formulations can also be documented using this approach.
Measurement of an absolute bioavailability when an i.v. administration is not possible
Sometimes, it is difficult or impossible to administer a drug by the i.v. route, but an indirect evaluation of the absolute bioavailability is still possible if a fraction of the dose is eliminated by the kidney (or any other accessible body fluid), and if there is a sufficiently large variability in renal clearance among the different subjects under investigation (Hinderling & Shi, 1995).
The principle of this method is as follows; after an i.v. administration:
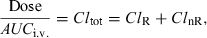 ()
()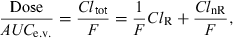 ()
()where F is the bioavailability factor to be estimated. Assuming that ClnR/F is a constant and ClR is a variable, Eqn 10 is the equation of a straight line (y = mx + c) which can be visualized by plotting Dose/AUCe.v. against ClR; the slope is 1/F and the intercept ClnR/F. These two parameters of the line are obtained by curve fitting (Fig. 5). The conditions for this approach are twofold: the drug must be cleared mainly by the renal route (or any other measurable route), and patients under investigation should display a large inter-individual variability in their renal clearance (see Hinderling, 2003 for application of the method).
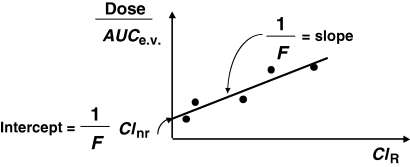
Evaluation of absolute bioavailability when intravenous (i.v.) administration is not possible. When i.v. administration is not possible but urine sample collection is possible (or any other matrix as faeces, etc.), then absolute bioavailability can be measured. The absolute clearance of the excretory pathway should be evaluated and the inter-individual variability of this absolute clearance should be large enough to use a regression approach in order to compute bioavailability. Bioavailability is estimated by the slope of the straight line between the measured absolute (renal) clearance and the apparent extra-vascular (Dose/AUC) clearance (see text for further explanation).
If it is known that a drug is exclusively (or almost exclusively) eliminated by an experimentally accessible route of elimination (urine, faeces), as is the case for eprinomectin, which is almost totally eliminated unchanged by faeces in cattle, absolute bioavailability can be obtained without i.v. administration by collecting all the effluents (mass balance principle). However, for a long acting drug (e.g. avermectins), collecting all the faeces can be cumbersome. An alternative and less demanding method would involve measuring, for some limited periods of time (e.g. 24 h), the faecal clearance (Clfaeces) using the following equation:
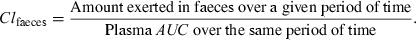 ()
()Simultaneously, the total plasma AUC0--∞ should be evaluated (this is easier to determine than to collect all the faeces over several weeks), and the absolute bioavailability can then be computed using the following equation:
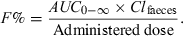 ()
()Here Clfaeces is assumed to be equal to the total body clearance, and consequently the quantity eliminated via faeces(Clfaeces × AUC0--∞) is equal to the bioavailable dose.
Why may a bioavailability higher than 100% be computed?
Bioavailabilities higher than 100% are regularly reported, which is conceptually impossible. The reasons for this are numerous, including experimental errors and nonfulfilment of the assumption for computation of absolute bioavailability (Martinez, 1998). Table 1 gives the main reasons for obtaining a bioavailability higher than 100%.
| 1. Experimental errors during the in-life phase of the experiment |
| Dose administered by the e.v. route is too high (gross error, different salts or esters without correction for the molecular weight, inappropriate scoring of tablets etc.) |
| Dose administered by i.v. route is too low or not available [gross error, physical interaction with the injecting material (e.g. lidocaine), drug is not stable in solution (e.g. peptide during infusion). In vivo precipitation of an extemporaneous solution, a different salt or ester without correction for the molecular weight, incomplete transformation of an ester pro-drug to its active moiety (see Fig. 4)] |
| Exchange of drug between animals raised in groups (licking in cattle, coprophagy in dogs, etc.) |
| 2. Experimental errors during sampling, preparation and conservation of samples |
| Sampling in the jugular vein homolateral to an ear-implant in cattle |
| Contamination of the extra-vascular samples when working with a pour-on formulation |
| Nonstability of the drug in the i.v. samples: photodegradation (carprofen), delay to centrifugation and freezing for longer period compared with e.v. samples |
| Insufficient samples during the initial phase after the i.v. bolus administration or the upswing of the curve after an i.v. infusion (see Fig. 7). |
| 3. Analytical technique |
| For safety reasons, the administered dose using i.v. route is lower than for extra-vascular route, and the LOQ of the analytical phase is too high and fails to detect a part of the i.v. AUC |
| Non-enantioselective analytical technique for a racemate having an enantioselective disposition (e.g. possible presystemic chiral inversion in the digestive tract favouring the enantiomer having the lowest clearance) |
| Enantioselective analytical technique for a racemate having an enantioselective disposition (e.g. presystemic chiral inversion of ibuprofen in the digestive tract of rabbit increases the S(+) from the R(−) ibuprofen (Doki et al., 2003) |
| Bacteriological analytical technique for antibiotics overestimates bioavailability when a fraction of the drug is metabolized into a more potent metabolite during the absorption process (e.g. enrofloxacin transformed into ciprofloxacin) |
| 4. Computation method for AUC |
| Sparse sampling for the e.v. route and the arithmetic trapezoidal rule which overestimates the AUC for concave curves |
| For the e.v. curve, overestimation of the extrapolated part of the AUC, either because the last sample concentration is overestimated or because the slope of the terminal curve is underestimated. Inverse situation for the i.v. curve |
| Modelling approach with some misfits with parameter estimation |
| 5. Assumption to compute bioavailability not fulfilled or not checkable |
| Nonlinearity of clearance |
| Lower clearance for e.v. route due to an enzyme inhibition, and higher clearance for i.v. administration due to an enzyme induction when the experimental design is unbalanced (e.g. all e.v. route administration during the second period of a crossover leading to a period-effect) |
| Different groups of animals for i.v. and e.v. route of administration |
| Inter-occasion variability for clearance with a true bioavailability close to or equal to 100% |
| Inter-occasion variability of clearance in growing animals when there is a long washout period |
Relative bioavailability between two formulations or two e.v. routes of administration
Relative bioavailability can be measured by comparing the AUC of the two tested formulations at the same dose levels using the following equation:
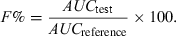 ()
()Relative bioavailability can also be evaluated under steady-state conditions (Fig. 6), because the total AUC over a dosing interval at steady-state (i.e. AUC) is equal to the total AUC0--∞ after a single dose administration.
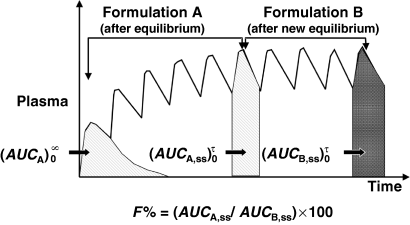
Measurement of bioavailability under steady-state conditions. Relative bioavailability can be measured in steady-state conditions and without any washout period between two formulation administrations (as for a cross-over design). In this type of trial, the formulation A is administered until reaching steady-state conditions. Under these conditions 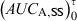 is equal to the
is equal to the 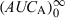 following a single dose administration. Then, the second formulation is immediately administered until the new steady-state condition is reached, and
following a single dose administration. Then, the second formulation is immediately administered until the new steady-state condition is reached, and 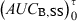 which equals to
which equals to 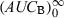 is measured. The ratio AUCA/AUCB in steady-state conditions gives the relative bioavailability. The condition for this approach is that the whole of the administered drug is absorbed over the dosing interval τ.
is measured. The ratio AUCA/AUCB in steady-state conditions gives the relative bioavailability. The condition for this approach is that the whole of the administered drug is absorbed over the dosing interval τ.
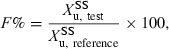 ()
()where 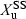 denotes the amount of drug excreted in the urine over a dosing interval at steady-state. Equation 14 is used for the same dosage regimen for both formulations. The advantage of this approach is the duration of the collecting period (corresponding to the dosage interval), which can be much shorter than after a single dose administration. The condition to apply Eqn 14 is to have reached an initial steady-state with the reference formulation and to have measured
denotes the amount of drug excreted in the urine over a dosing interval at steady-state. Equation 14 is used for the same dosage regimen for both formulations. The advantage of this approach is the duration of the collecting period (corresponding to the dosage interval), which can be much shorter than after a single dose administration. The condition to apply Eqn 14 is to have reached an initial steady-state with the reference formulation and to have measured 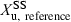 . Then, without washout, to have administered the test formulation and to have measured
. Then, without washout, to have administered the test formulation and to have measured 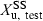 over a dosing interval when the new steady-state is obtained.
over a dosing interval when the new steady-state is obtained.
Accurate evaluation of AUC
Many methods for the computation of AUC have been proposed (Yeh & Kwan, 1978; Purves, 1992). Attention should be paid to the sampling design in order to avoid either an underestimation of AUC (not enough sampling times in the ascending phase of the kinetics) or an overestimation of AUC (not enough sampling times in the descending part of the curve) (Fig. 7). A too sparse sampling strategy may lead to doubling of the bioavailability. When a sparse sampling is used (e.g. for the assessment of drug exposure in toxicological studies), the evaluation of AUC using nonlinear mixed effect modelling may provide more accurate information, not only for the mean value of AUC but also for the estimate of inter-animal variability (Burtin et al., 1996). Furthermore, when the concavity of the curve is pronounced, a log-linear trapezoidal rule is more accurate (see Fig. 7).

Evaluation of area under the curve (AUC) by the trapezoidal rule. The arithmetic trapezoidal rule consists of evaluating the AUC of the entire curve by using the sum of individual trapezoids (S1, S2…); an arithmetic mean of the plasma concentrations being used to evaluate the trapezoid. If the sampling design is too sparse (curve C), the arithmetic trapezoidal rule will overestimate the true area (by the black shaded position of the curve). Under this condition, a log-linear trapezoidal rule is preferred. In contrast, if not enough samples are obtained during the initial phase (curve B), the AUC can be under-estimated (by the shaded portion of the curve).
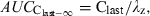 ()
()where λz is the slope of the terminal phase. Any bias in the estimation of λz can lead to estimation of bioavailability higher than 100%. In practice, the extrapolation portion of the AUC should remain as limited as possible and represent no more than 20% of the total AUC.
Finally, it is preferable to use the truncated AUC when the level of quantification of the analytical technique is relatively low. Indeed, the use of partial area in comparative bioavailability studies is theoretically possible because the terminal part of the curve reflects only the elimination phase, which is a drug property and not that of the formulation (Lovering et al., 1975; Martinez & Jackson, 1991). This approach is appropriate for drugs having a long terminal half-life and which are rapidly absorbed. However, the use of this approach cannot be encouraged if the effective end of the absorption phase is unknown (Gibaldi & Perrier, 1982).
Cmax and Tmax are not appropriate measures of the rate of absorption
It is frequently stated that ‘absorption’ is rapid because visual inspection of the curve shows that the time (Tmax) of the maximum plasma concentration (Cmax) is observed rapidly after the drug administration.
This ‘visual evaluation’ can be very misleading. Cmax and Tmax are single point determined, and their precision depends on the sampling schedule. More importantly, an early Tmax can also be associated with a formulation having a very low rate of drug absorption. Indeed, Tmax and Cmax are hybrid variables influenced by both the rate of drug elimination and absorption. In addition, Cmax is influenced by the extent of absorption. For a mono-compartmental model (no distribution), Tmax is given by the relationship:
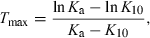 ()
()where Ka and K10 are the first-order rate constants of absorption and elimination, respectively. Inspection of Eqn 16 shows that Ka and K10 play a symmetric role, and exactly the same Tmax can be observed for two drugs having the same Ka and K10, but in a flip-flopped circumstance (Fig. 8).
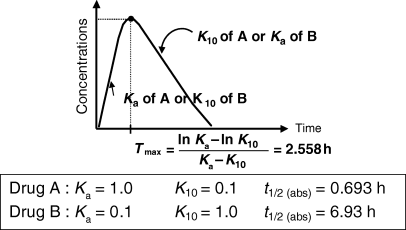
T max and flip-flop situation for a drug obeying a mono-compartmental model. This figure exemplifies the fact that exactly the same Tmax can be obtained with two different drugs (A and B) having very different rate constants of absorption (Ka). This is due to the fact that Tmax is a hybrid parameter reflecting both the rate constant of absorption and the rate constant of elimination (K10).
This kind of situation is frequently encountered with long-acting formulations, for which it is necessary to stress again the invaluable information provided by an i.v. study, which provides the only means of recognizing the drug disposition properties without the risk of confounding it with a formulation effect.
Another point which is not generally well appreciated is that Tmax can also be influenced by the extent of bioavailability. For reasons explained in the companion paper in this issue on the half-life, the so-called half-life of absorption (t1/2Ka) actually reflects the drug disappearance from the site of administration, not the rate of drug absorption per se (Garrett, 1994) (Fig. 9). Ka is the sum of two rate constants: Ka1, which reflects the passage of the drug from the injection site to the plasma, and Ka2, which reflects the irreversible loss of drug at the administration site. Thus, the bioavailability is given by:
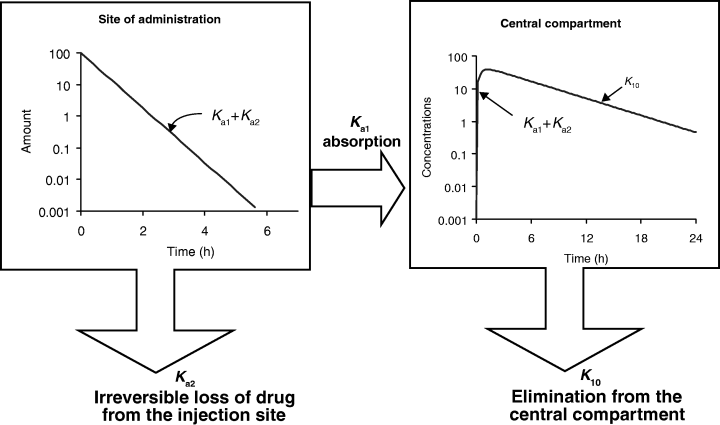
The so-called half-life of absorption vs. the process of drug absorption. This figure corresponds to a drug obeying a mono-compartmental model with a phase of absorption. The reported half-life of absorption (t1/2Ka) does not reflect unequivocally the process of drug absorption (here presented by Ka1, the first-order rate constant of drug transfer from the injection site to the central compartment) but the sum of Ka1 and Ka2, Ka2 being the rate constant reflecting the irreversible loss of drug at the administration site. t1/2Ka reflects unequivocally drug absorption only if Ka2 = 0, i.e. if the bioavailability is total. Here Ka1 + Ka2≫K10.
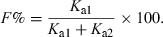 ()
()This relationship predicts that an unchanged rate of absorption (i.e. a fixed value of Ka1) associated with an increase of Ka2 (i.e. a reduction of bioavailability) will lead to a more precocious Tmax (Fig. 10).
T max and absolute bioavailability. The disposition kinetics of two formulations of a given drug having an elimination rate constant (K10) of 0.2 h−1 and the same rate constant of absorption (Ka1 = 1 h−1) but different bioavailability (Ka2 = 0 for formulation A or Ka2 = 1 h−1 for formulation B, i.e. a bioavailability of 100% for formulation A and 50% for formulation B) were simulated. It can be seen that Tmax, B is observed earlier for formulation B (1.27 h) than for formulation A (2.01 h). This is not due to a more rapid absorption of formulation B but to its lower bioavailability.
For all these reasons Tmax cannot be considered as an appropriate metric to judge the rate of drug absorption, especially if the occurrence of a flip-flop situation is not checked.
The fact that Cmax and Tmax are not appropriate to assess the rate of drug absorption does not mean that these two measures have no value when used empirically in order to describe the drug exposure with Tmax for the time of maximum exposure, Cmax for the maximum exposure and AUC for the overall exposure. Such descriptive values of the shape of the disposition curve are the reasons why Cmax and Tmax have been selected as endpoints in bioequivalence trials.
Measurement of the rate of absorption using curve fitting
The rate of drug absorption is classically reported from the results of curve fitting (e.g. t1/2Ka). When the main goal of data analysis is to determine precisely the process of absorption for a physiological interpretation, the simple curve fitting approach can be disappointing or even misleading (Brouwer & McNamara, 1986; Gibson et al., 1987; Murata & Kohno, 1989; Liang & Derendorf, 1998). Indeed, it can be difficult to properly isolate the different rates constants of absorption (Ka), distribution (λ1) and elimination (λ2) if they are not sufficiently different (i.e. Ka/λ1 > 3–5).
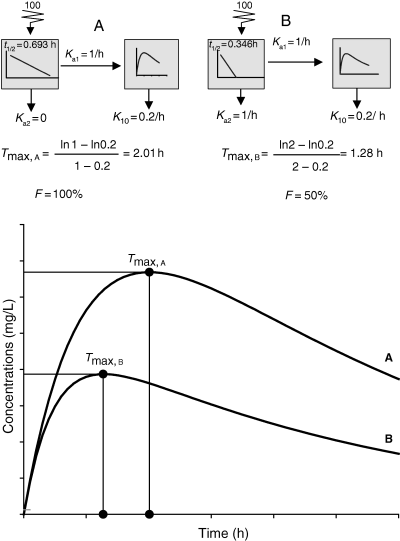
In addition, the proper interpretation of rate constants obtained by curve fitting can be misleading if there are no i.v. data, causing the possible permutation of Ka and λ1 (i.e. to consider the larger rate constant as a rate constant of absorption when it is actually the rate constant of drug distribution). The best solution to this dilemma is to fit simultaneously i.v. and e.v. data. Finally, the process of absorption can be characterized by several rate constants (e.g. parallel or sequential first-order rate constants) or by zero-order input (etc.) making the classical curve fitting of relatively limited interest when the main goal of the study is to qualify the input process. Figure 11 gives an example of an observed curve that could correspond to very different situations with respect to the absorption process.
Curve fitting and evaluation of the rate constants of absorption. Top: A curve displaying the classical three phases (ascending, rapidly and slowly decreasing) can be fitted with a given set of parameters but actually corresponds to different other models (bottom), giving exactly the same quality of fitting but different sets of parameters, and showing that the three models are indistinguishable but identifiable. A: Model with two parallel rate constants of absorption (Ka1, Ka2). About 6.34% of the dose being absorbed with Ka2 = 0.0376 h−1 and 93.66% of the dose with Ka1 = 3.00 h−1 . Other combinations of these parameters exist for this model. B: Classical bi-compartmental model with a single rate constant of absorption (Ka = 3.00 h−1). C: Mono-compartmental model with a volume of 0.0666 L/kg where the administered dose precipitates locally to the site of administration (K23 = 2.00 h−1) and is progressively released (K32 = 0.5 h−1) to gain access to the central compartment with K21 = 3.00 h−1. Then the drug is eliminated with K10 = 3.00 h−1. It should be noted that clearance is the same for the three models (0.2 L/kg/h).
Evaluation of drug absorption rate by deconvolution
The best approach to establish the process of drug absorption is to analyse the plasma concentration–time profile obtained after e.v. administration using a deconvolution technique. Deconvolution is primarily used to obtain the input function (curve), i.e. a rate-time profile reflecting the instantaneous process of drug absorption, which can display the existence of multiple peaks, and can reflect different rates of drug absorption. From this profile, parameters like rate constant of absorption can be estimated by distinguishing first-order or zero-order input, parallel or sequential absorption, etc. Deconvolution can also qualify the rate of drug release from a given formulation (using either in vitro or in vivo experiments).
The so-called Wagner–Nelson (for a mono-compartmental model) and Loo–Riegelman (for 2- or 3-compartmental model) approaches are historical deconvolution methods (Wagner, 1983). Currently, the use of specific software is mandatory to benefit from more advanced mathematical deconvolution technique (Madden et al., 1996) in order to solve a problem which is often ill-conditioned. Figure 11 shows that very different input drug processes can lead to the same plasma concentration profiles. In order to distinguish between each possible situation, it is necessary to know the model of the drug disposition and its corresponding parameters, i.e. to perform an i.v. study.
The inverse of a deconvolution analysis is termed convolution. Convolution involves predicting the drug output profile (plasma concentration–time profile), when both the input process and the disposition model are known. The input process may be known from in vitro dissolution measurements. Convolution and deconvolution are powerful tools to optimize the development of a controlled release drug formulation, because the rate of availability of extravascular formulations, contrary to the other basic pharmacokinetic parameters (clearance, volume of distribution, etc.), is under the control of drug developers.
Investigation of rate of absorption by means of statistical moments
After i.v. drug administration, mean residence time (MRTi.v.) can be computed by statistical moment analysis (Yamaoka et al., 1978). MRTi.v. is the mean time a molecule resides in the system. Similarly, after administration of a drug solution by the e.v. route (e.g. p.o.), an MRTp.o. can be computed by statistical moments, which is actually the sum of a mean absorption time (MATp.o.) and MRTi.v. when using the following equation:
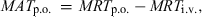 ()
()where MATp.o. is the mean time of drug absorption, MRTp.o. is the value of MRT after the oral drug administration, and MRTi.v., the MRT after the i.v. drug administration.
This approach can be extended to other steps which separate drug administration from the resulting plasma concentration profile (Riegelman & Collier, 1980). For example, the drug can be administered as a tablet (or a slow release bolus into the rumen). The resulting plasma concentration profile reflects the process of dissolution (or release), the process of absorption and the process of drug elimination. If the mean dissolution time (MDT) corresponds to the mean time a drug stays in a solid form in the tablet, the overall measured MRT after a tablet administration (MRTtablet) is:
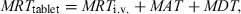 ()
()where MRTi.v. and MAT are as defined above. By difference:
 ()
()Equation 20 indicates that with a 3-period trial, MRTi.v., MAT and MDT can be evaluated and provide information on the input process in a compact and useful unit (namely time).
For example, a short MAT suggests a rapid absorption and an MAT longer than MRTi.v. suggests a flip-flop situation. The attractiveness of the MRT concept is the additivity of time. If the MDTs (or mean release time) of different dosage forms are independently known (e.g. from dissolution tests), then the overall in vivoMRT can be readily predicted, if MRTi.v. and MAT (which are drug properties, not formulation properties) are known from in vivo studies.
In the framework of compartmental model, it can be shown that MAT is related to Ka using the following equation:
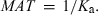 ()
()Equation 21 indicates that MAT is also subjected to the same limits as Ka, to put it in physiological terms. As Ka actually represents the rate of drug disappearance from its administration site, MAT is the stochastic view of this process and a shorter MAT can be because of a poor bioavailability (a high Ka2, see Fig. 10), and not to a rapid transfer of the drug from the administration site to the central compartment (see Veng-Pedersen, 1989a,b).
A limitation of the statistical moment approach relates to the possible lack of precision in the estimation of the different MRT. As for AUC, bias in the estimation can be because of an inappropriate sampling time and to the difficulty of extrapolation, but error is more severe with MRT because the terms in time raised to square are now estimated and negative MAT values can be spuriously computed.
In addition, MAT estimated by Eqn 18 is obtained with low precision when its value is much shorter than the MRTi.v., and, in this circumstance, negative MAT can be estimated due to either a slight over-evaluation of MRTi.v. or to a slight under-evaluation of MRTp.o..
Bioavailability when drug disposition is nonlinear
The evaluation of bioavailability by Eqn 1 requires the assumption of drug linear elimination (i.e. clearance must be a parameter, not a dose or a time-dependent variable). However, bioavailability can still be measured using Eqn 1 if the distribution or the absorption process itself is nonlinear. If the drug elimination process behaves in a nonlinear way (clearance), the situation becomes more complex and several options are possible including use of the mass balance approach. When clearance nonlinearity is due to a nonlinear binding to plasma proteins, another option consists of modelling total drug disposition, and in computing the free concentration which can follow a linear disposition; as shown for inhibitors of angiotensin-converting enzyme (ACEI) (Toutain et al., 2000), i.e. to use a model-dependent approach that recognizes the nonlinearity. For ACEI it was shown that incorrect use of the measured plasma concentration in order to estimate the absolute bioavailability may actually double the true absolute bioavailability as measured using the free plasma ACEI concentration.
Conclusion
Absolute bioavailability is a key pharmacokinetic parameter which must be systematically estimated for a new drug formulation or a new modality of administration. Many possible approaches exist to evaluate both rate and extent of bioavailability, including situations for which intravenous drug administration is not possible. Veterinary pharmacologists should pay special attention to possible misinterpretations when Cmax, Tmax, MAT or t1/2Ka are used to estimate the rate of drug absorption.




