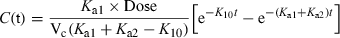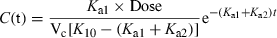Plasma terminal half-life
Abstract
Terminal plasma half-life is the time required to divide the plasma concentration by two after reaching pseudo-equilibrium, and not the time required to eliminate half the administered dose. When the process of absorption is not a limiting factor, half-life is a hybrid parameter controlled by plasma clearance and extent of distribution. In contrast, when the process of absorption is a limiting factor, the terminal half-life reflects rate and extent of absorption and not the elimination process (flip-flop pharmacokinetics). The terminal half-life is especially relevant to multiple dosing regimens, because it controls the degree of drug accumulation, concentration fluctuations and the time taken to reach equilibrium.
Introduction
The plasma half-life (half-life of elimination or half-life of the terminal phase) is the most frequently reported of all pharmacokinetic parameters. It has the apparent advantage of being a familiar term, immediately comprehensible because it is expressed in units of time. This is not the case for body clearance (the most important pharmacokinetic parameter), which is more difficult to conceive because it has the units of flow.
The half-life is (apparently) easy to compute and it is often the only reported pharmacokinetic parameter in some in vitro or in vivo assays. In some circumstances, it is generally the only parameter which can be computed, e.g. for a drug metabolite or any analyte disposition when the dose is unknown.
Actually, plasma half-life is very often wholly misunderstood and many non-kineticists continue to mistakenly believe that it represents the time required to eliminate half the administered dose of a drug.
In this review, we will re-state the definition of terminal half-life and qualify its pharmacokinetic meaning, which can be very different after intravenous (i.v.) and extra-vascular administration. The clinical relevance of terminal half-life will also be discussed together with its value in the rational selection of dosage interval. Finally, some technical issues concerning its estimation (sampling time and level of quantification of the analytical technique) will be addressed.
In this review, the term ‘terminal half-life’ is preferred to ‘elimination half-life’, because it does not prejudge the mechanism controlling plasma concentration decay.
Definition of terminal half-life
Following i.v. administration, the terminal half-life is the time required for plasma/blood concentration to decrease by 50% after pseudo-equilibrium of distribution has been reached; then, terminal half-life is computed when the decrease in drug plasma concentration is due only to drug elimination, and the term ‘elimination half-life’ is applicable. Therefore, it is not the time necessary for the amount of the administered drug to fall by one half.
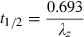 ()
()Figure 1 shows two drugs having the same terminal half-life but with very different clearances. In order to express the overall persistence of a drug in the body using a time parameter, then the mean residence time (MRT), and not the terminal plasma half-life, should be selected.
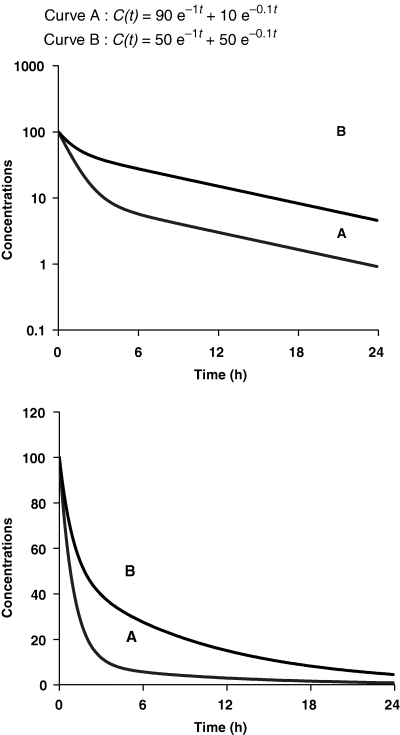
Terminal half-life is the time required for the plasma concentration to fall by 50% during the terminal phase, and not the time required to eliminate half the administered dose. The figure shows two drugs (A and B) having exactly the same terminal half-life (6.93 h) (see top figure semi-logarithmic plot), but for which the time required to eliminate half the administered dose is very different (6 h for drug B and 2 h for drug A) (see bottom figure arithmetic plot). This difference is due to the fact that drug B has a lower clearance than drug A (0.182 mL/kg/h vs. 0.526 mL/kg/h), and a lower Varea (1.82 mL/kg vs. 5.26 mL/kg). It is only when the pseudo-equilibrium state has been reached (e.g. 12 h after drug administration), that the time required to eliminate half the remaining amount of drug in the body becomes equal to the terminal half-life.
The confusion in the definition of half-life is historical. In the early stages of pharmacokinetics, analytical performances were poor and many drug dispositions were described by a single mono-exponential phase. In this situation, and only in this situation, the half-life is also the time it takes to eliminate half the administered dose of the drug. It is also relevant to note that when the pseudo-equilibrium has been reached, the disposition curve becomes mono-exponential and here also, the terminal half-time becomes the time taken to eliminate half the remaining fraction (not half the administered dose).
Pharmacokinetic meaning of half-life
It is sometimes difficult for a non-pharmacokineticist to understand the difference between information conveyed by plasma clearance and terminal half-life. Table 1 gives an example of antibiotics having the same clearance in dog but very different terminal half-lives. The plasma clearance expresses only the ability of the body to eliminate the drug (see Toutain & Bousquet-Mélou, 2004a). In contrast, terminal half-life expresses the overall rate of the actual drug elimination process during the terminal phase; this overall rate of elimination depends not only on drug clearance but also on the extent of drug distribution.
| Parameters | Benzyl penicillin | Gentamicin | Oxytetracycline | Tylosin |
|---|---|---|---|---|
| Plasma clearance (mL/kg/min) | 3.5 | 3.1 | 4.0 | 22 |
| Terminal half-life (min) | 30 | 75 | 360 | 54 |
- Note that for three antibiotics (penicillin, gentamicin and oxytetracycline) the plasma clearances are very similar but the terminal half-lives are very different, indicating that terminal half-life and plasma clearance do not convey the same information. The terminal half-life is also influenced by the extent of drug distribution, so that, for almost the same plasma clearance, oxytetracycline having the largest volume of distribution also has the longest half-life.
 ()
()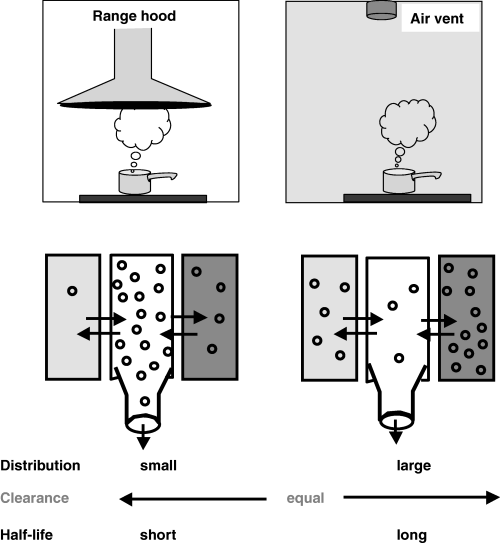
Top: A pictorial explanation of the hybrid characteristic of a half-life. Imagine that we have to boil water (drug) in a kitchen (the body). In a modern kitchen (left), the boiling kettle is placed just under an efficient range hood (high clearance) and the steam produced (the dose) is quickly eliminated from the kitchen (with a short half-life) because the volume in which the steam is scattered (volume of distribution of the steam) is small. In a less ideal situation, there is no kitchen range hood but an air vent having exactly the same intrinsic capacity as the range hood (the same clearance). In this situation, the time required to eliminate the same amount of steam (the same dose) will be longer (longer half-life), because the steam disperses all over the kitchen (has a larger volume of distribution). Bottom: a compartmental view of the preceding system.
Equation 2 indicates that a long terminal half-life can be associated to a large volume of distribution (Vd) or/and attributable to a small plasma clearance. During the terminal phase, the drug will be eliminated only if it is presented to the clearing organs, regardless of the capacity level of these clearing organs to eliminate the drug. In mammals, the two most important clearing organs are the liver and kidney. In the framework of compartmental models, both are located in the central compartment and if the drug is present mainly in a peripheral compartment, the efficiency of the overall clearance process of drug elimination will be low and terminal half-life will be long.
How to use terminal slope to express the efficiency of drug elimination
A simple way to express the efficiency of drug elimination is to consider the numerical value of the slope (λz) of the terminal phase. For instance, the terminal half-life of phenylbutazone in cattle following i.v. administration is about 48 h, which corresponds to a terminal slope of 0.0144/h (Toutain et al., 1980), a figure not easy to conceptualize. However, if this rate constant is multiplied by 100, it will mean that during the terminal phase of elimination, about 1.44% of the residual amount of phenylbutazone is eliminated per hour. This approximation is relatively accurate if λz is expressed with an appropriate time unit in order to obtain a low numerical value of λz (e.g. lower than 0.02).
Plasma half-life and other time parameters used in pharmacokinetics are hybrid parameters
Plasma half-life is a dependent parameter in contrast to plasma clearance and volume of distribution, which are said to be independent parameters, because they have a primary physiological basis and they are not determined by a combination of other basic pharmacokinetic parameters (at least at the macroscopic level). In pharmacokinetics, all time parameters (derived from rate constants) are hybrid (composite) parameters (Fig. 3), and terminal half-life is the most hybrid of all pharmacokinetic parameters, i.e. it is influenced by many other kinetic parameters (Fig. 4). Figure 5 explains the dependence of terminal half-life on the different micro-constants for a bi-compartmental model.
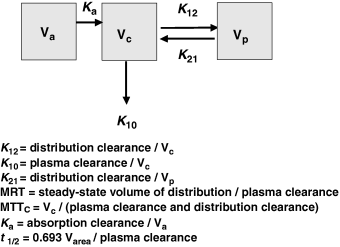
Physiological primary determinants of the main time parameters in pharmacokinetics. The time parameters such as half-life (t1/2), mean residence time (MRT), mean transit time (MTT) in the central compartment, and rate constants (Ka, K12, K21, K10,…) are called hybrid parameters because they are actually a combination of parameters having a direct physiological meaning. All the rate constants can be interpreted in terms of ratio of a solute conductance term (clearance of absorption, clearance of distribution, clearance for elimination, etc.) and as capacitance terms (a volume of distribution) such as Va: volume of the site of administration, Vc: volume of the central compartment, Vp: volume of the peripheral compartment, Vss: steady-state volume of distribution, Varea: volume of distribution by area method. For rate constants like the rate constant of absorption (Ka), it is seldom possible to evaluate separately the two physiological determinants (clearance of absorption and volume of the site of administration), unless it is possible to sample the administration site (e.g. udder after an intra-mammary administration) (see Chiou, 1995 for the application of the clearance concept to absorption). MRT: mean residence time of the system, MTTC: mean transit time in the central compartment, i.e. the average interval of time spent by a drug molecule from its entry into the central compartment to its next exit; t1/2: terminal half-life.
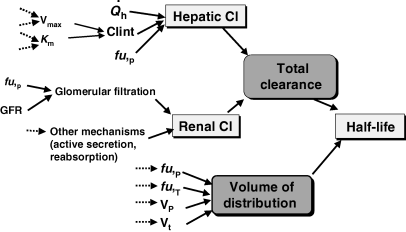
Physiological factors influencing the terminal half-life (t1/2) and giving it the status of a hybrid parameter. The value of t1/2 is linked to that of clearance and volume of distribution. In turn, plasma clearance is the sum of different organs clearances (e.g. hepatic and renal clearances) themselves depending on many factors, including (for hepatic clearance) hepatic blood flow ( ), intrinsic hepatic clearance (Clint), free fraction in plasma (fu,P). Intrinsic hepatic clearance reflects maximum metabolism capacity (Vmax), and the Michaelis Menten constant which is linked to drug affinity for the metabolic enzymatic system (KM). Many factors also influence renal clearance. In addition, t1/2 is influenced by the extent of drug distribution, which in turn depends on the drug affinity for circulating proteins (fu,P), for tissues (fu,T), on the volume of plasma (VP) and tissues (VT) etc.
), intrinsic hepatic clearance (Clint), free fraction in plasma (fu,P). Intrinsic hepatic clearance reflects maximum metabolism capacity (Vmax), and the Michaelis Menten constant which is linked to drug affinity for the metabolic enzymatic system (KM). Many factors also influence renal clearance. In addition, t1/2 is influenced by the extent of drug distribution, which in turn depends on the drug affinity for circulating proteins (fu,P), for tissues (fu,T), on the volume of plasma (VP) and tissues (VT) etc.
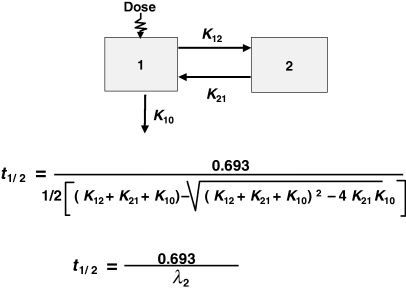
The terminal half-life for a bi-compartmental model. The terminal half-life reflects both capacity of elimination (K10), and processes of distribution (K12) and redistribution (K21). The numerical value of t1/2 is a combination of K10, K12 and K21.
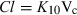 ()
()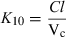 ()
()The consequence of the hybrid character of terminal half-life is that half-life is a poor parameter to evaluate the influence of physiological factors (age, sex, etc.) or of pathology (renal failure, etc.) in drug disposition. For instance, the pharmacokinetics of gentamicin was investigated in horse before and after occurrence of nephrotoxicity. It was shown that body clearance was reduced by 40%, indicating impairment of the body capacity to eliminate gentamicin but with the terminal half-life remaining unchanged (192 min vs. 204 min). This was because of the fact that the volume of distribution was reduced in the same proportion as clearance (Riviere et al., 1983).
Why calculate a terminal half-life
Terminal half-life is an index of drug persistence in the body during the terminal phase. The main clinical application of terminal half-life is to select an appropriate length for the dosing interval in circumstances of multiple dose administration. Indeed, terminal half-life allows prediction of drug accumulation and the time to reach steady-state equilibrium. This explains why the consequence of the value of terminal half-life is not the same for drugs having a short terminal half-life vs. a long terminal half-life. The impact of the value of half-life also differs for drugs requiring only a single dose administration vs. those requiring a multiple dose regimen.
For drugs having a short terminal half-life, it is important to maintain the plasma therapeutic concentration, and this will require dosage forms with a low input rate in order to obtain a flip-flop condition (vide infra). In contrast, if terminal half-life is long and the drug is to be administered repeatedly, questions of drug accumulation and delay in the time to reach steady-state conditions arise.
Terminal half-life and repeated administration
Terminal plasma half-life is an important determinant of drug concentration–time profiles following repeated drug administration, which are characterized by an initial accumulation phase, followed by a steady-state with fluctuations of concentration during the inter-dosing interval. Plasma half-life can be used to predict these different factors (vide infra). For simplification, the calculations presented in the following sections were performed assuming a mono-compartmental disposition of the drug.
Drug accumulation for drugs having a monophasic disposition
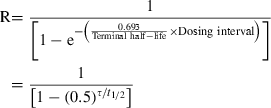 ()
()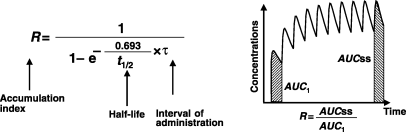
Terminal half-life and drug accumulation during a multiple dosing regimen. After the first drug administration, the entire administered drug is not eliminated at the time of the second administration, and plasma concentration will be higher during the second dosing interval than after the first administration (superposition principle). With the repetition of dosing (at the same dose rate), plasma concentrations increase progressively until reaching a plateau, i.e. steady-state conditions. Under steady-state conditions, the amount of administered drug exactly compensates for the amount of eliminated drug over the dosing interval (noted τ). An accumulation index can be defined as the ratio of the average amount of drug in the body under steady-state conditions to the average amount of drug in the body after the first administration, thus,
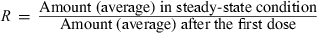 R is estimated by the ratio of the two corresponding areas under the curve (AUC) (hatched area) with R = AUCss/AUC1. For a mono-compartmental model or if drug is administered in the post-absorption phase for a multi-compartmental model, R is given by a simple mathematical expression having two parameters: terminal half-life and τ. Therefore, drug accumulation is not an intrinsic drug property but rather a variable which relies on both the drug property (t1/2) and a clinical decision (the dosing interval).
R is estimated by the ratio of the two corresponding areas under the curve (AUC) (hatched area) with R = AUCss/AUC1. For a mono-compartmental model or if drug is administered in the post-absorption phase for a multi-compartmental model, R is given by a simple mathematical expression having two parameters: terminal half-life and τ. Therefore, drug accumulation is not an intrinsic drug property but rather a variable which relies on both the drug property (t1/2) and a clinical decision (the dosing interval).
| τ/t1/2 | 0.125 | 0.25 | 0.5 | 1 | 2 | 4 |
|---|---|---|---|---|---|---|
| R | 12 | 6 | 3 | 2 | 1.3 | 1.07 |
| P/T ratio | 1.09 | 1.2 | 1.4 | 2 | 4 | 16 |
- R and P/T ratios are defined by Eqns 5 and 6, respectively, in the text. The calculation assumes administration of a fixed dose.
Many veterinary drugs have terminal half-lives shorter than 12 h. When these drugs are given once daily (τ = 24 h), their accumulation ratios are less than 1.3. In consequence, the concentrations at equilibrium will not be more than 30% greater than plasma concentrations obtained following the first administration. From a practical clinical point of view, problems associated with accumulation are likely to be minimal for drugs exhibiting plasma half-lives shorter than 12 h.
The time to reach steady-state conditions
In contrast to the accumulation ratio, the time to reach the steady state is not influenced by the dosing interval but is only a function of terminal half-life. Figure 7 presents plasma concentration–time profiles of the same drug obtained with three different dosage regimens but with the same daily dosage (repeated administration of the dose 100 once daily, τ = 24 h; repeated administration of the dose 50 BID, τ = 12 h; i.v. infusion at the rate of 100/24 h). For the three dosage regimens, the same average concentration (Css) is obtained at steady-state (because Css depends only on drug entry, Dose/τ, and drug clearance), and the time required to reach this concentration is the same. Practically speaking, steady state is obtained after a delay of 3–5 times the half-life. Thus, for any drug having a terminal half-life of 12 h or less, the steady state will be reached after the second or third daily administration. For drugs exhibiting longer half-lives (more than 24 h), the delay before reaching therapeutic concentrations can be so long that initial administration of a loading dose is required.
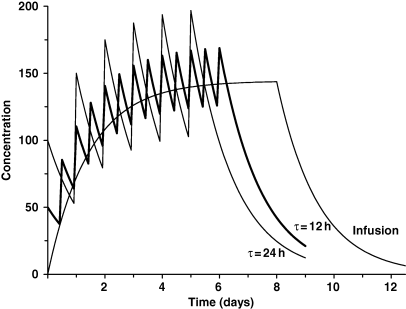
Terminal half-life and the time required to reach steady-state conditions. For a multiple dosing regimen (or for an i.v. infusion), the time required to reach steady state (plateau) is a genuine drug property governed only by the terminal half-life. This figure illustrates two dosing regimens; the same total daily dose is administered but with two dosing intervals (12 and 24 h) for a drug having a terminal half-life of 48 h. Visual inspection shows that the plateau is reached after about 8–10 days regardless of the dosing interval (i.e. 3–5 times the terminal half-life); it should be noted that the accumulation ratios (as defined by Eqn 5 and illustrated in Fig. 6) are however different (3.414 and 6.286 for the dosing intervals of 24 and 12 h, respectively). From a clinical perspective, it should be noted that the average amount of drug at steady state (or the average plasma concentration) is the same for the two dosing strategies, the only relevant difference being the degree of plasma concentration excursion (i.e. the extent of the difference between peak and trough plasma concentrations).
Fluctuations of plasma concentrations at steady-state
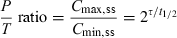 ()
()The influence of modifying the τ/t1/2 ratio on the Peak-Trough ratio is presented in Table 2 and illustrated in Fig. 7. Practically speaking, for a given drug, to divide the daily dose is associated with a reduction of the amplitude of fluctuations at steady state, which usually represents an increase of safety for drugs exhibiting a narrow therapeutic window. However, this is not always the case, particularly when total exposure of the target tissue to the drug relies more closely on toxicity than the peak plasma concentration. This is the case for the nephrotoxicity of aminoglycoside which is lesser for a SID than a BID dosing rate because for a SID dosing rate, the total kidney exposure will be less important than for a BID due to saturation of aminoglycoside kidney capture for high amynoglycoside concentrations.
Accumulation and time to reach steady-state conditions for drugs having a multiphasic disposition
When drug disposition displays a multiphasic profile, the situation becomes more complicated because there are several half-lives corresponding to the different distribution phases preceding the terminal half-life of elimination. Each half-life is, to some degree, a function of distribution, redistribution, and elimination. Practically speaking, terminal t1/2 controls drug accumulation when at least 50% of the drug is eliminated during the terminal decay phase. When this is not the case, the terminal phase can be irrelevant. Figure 8 illustrates the pharmacokinetics of two drugs obeying a bi-compartmental model and also having the same initial and terminal half-lives, but for which the degree of drug accumulation differs because the contribution of the terminal phase to drug elimination is different. To predict the degree of drug accumulation for a drug having a multiphasic disposition, the most straightforward approach involves understanding that, under equilibrium conditions, the AUC over the dosing interval is equal to the total AUC (i.e. from 0 to ∞) after a single dose administration. On the other hand, if doses are administered in the post-distributive phase (i.e. when the decay is again monoexponential), Eqn 5 is also applicable, if most of the drug is eliminated during the elimination phase.
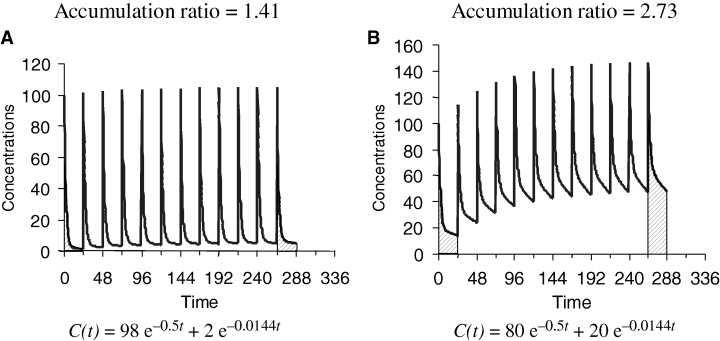
Half-life and time to reach steady-state conditions and the extent of accumulation for two drugs obeying a bi-compartmental model and having the same terminal half-life (48 h), but which differ regarding the fraction of the dose which remains to be eliminated during the terminal phase (low for drug A and high for drug B). Visual inspection shows that apparent steady state is reached more rapidly when most of the drug is eliminated during the distribution phase (drug A) than when most of the drug is eliminated during the terminal phase (drug B). Practically speaking, t1/2λz controls drug accumulation only if at least 50% of the drug is eliminated during the terminal phase. The equations used for simulation are given under the figures.
Accumulation and delay to reach steady state in peripheral compartments
Most drugs display multiphasic pharmacokinetic profiles, which suggests the existence of both a central and several peripheral compartments. For these drugs, it is relevant to examine the degree of drug accumulation, not only in plasma but also in the peripheral compartment (possible location of the biophase, level of drug residues, etc.). Figure 9 illustrates the example of a hypothetical drug obeying a tri-compartmental model and having a terminal half-life of 48 h. The drug is administered once daily. Figure 9 shows that drug accumulation in the shallow and deep compartments is very different. In the deep compartment, drug accumulation is large and progressive. In contrast, in the shallow compartment, a pseudo-plateau is reached much sooner. If the site of action is in rapid equilibrium with plasma, pharmacological (or toxicological) effects can be immediately equivalent to those characterizing the steady-state conditions. In contrast, if the effect site is in the deep compartment, there is a time development of effects, which progressively increases with successive drug administrations. This example illustrates the general rule that delay to reach steady-state conditions in the deepest tissue compartment is controlled by the terminal half-life, and that the rate of accumulation is associated with the rate constant of redistribution from the deep compartment to the central compartment when this rate constant is a major determinant of the terminal half-life.
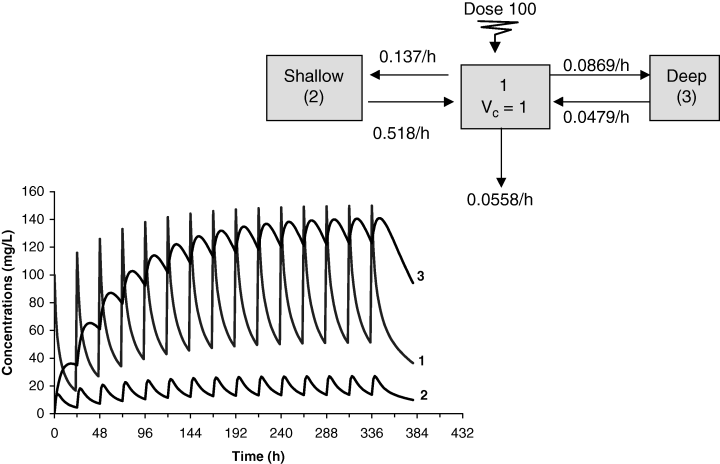
Terminal half-life and accumulation of drug in peripheral compartment vs. central compartment. A tri-compartmental model was simulated to show that the degree of drug accumulation for daily administration of a fixed dose can be very different in central (1), shallow (2) and deep (3) peripheral compartments. This can be of clinical relevance with regard to location of the biophase. If the biophase is located in a shallow (2) compartment, the ‘steady-state’ condition for efficacy is obtained almost immediately, whereas when the biophase is in the deep (3) compartment, the effect would develop progressively over several days. This situation can also apply to residues in edible tissues.
Terminal half-life and the rational selection of a dosing interval
The dosing interval is often selected for practical convenience (SID, BID, etc.). For many drugs and formulations it is necessary to control not only the dose but also the dosing interval, in order to optimize efficacy and/or to minimize side-effects. The relationship between terminal half-life and dosing interval determines the amplitude of fluctuations in drug plasma concentrations during the dosing intervals (Fig. 7). If the dosing interval is large relative to terminal half-life, there will be wide fluctuations in concentrations with possible side-effects (Cmax too high), or lack of efficacy (Cmin too low). The particular drugs for such considerations are those having a narrow therapeutic index (anti-arrhythmic, anti-epileptic, etc.), a poor selectivity (Cox1 vs. Cox2 inhibitory effect for NSAID), or which should be maintained above some threshold value (anti-arrhythmic drugs, time-dependent antibiotics, etc.).
In the case of digoxin in the dog, it has been proposed that plasma concentrations should exceed 2 ng/mL for therapeutic effects and that the probability of adverse effects increase when concentrations exceed 2.5 ng/mL. Therefore, an appropriate dosage regimen must guarantee that digoxin plasma concentrations fluctuate within this narrow therapeutic window. First, the daily dose can be selected to obtain an average steady-state concentration within the therapeutic window [see the relation between dose, clearance and average steady-state concentration (Toutain & Bousquet-Mélou, 2004a)]. Secondly, calculating the ratio of the upper and lower required concentrations (2.5/2) we obtain the value 1.25, which can be compared to the fluctuations of digoxin plasma concentrations at steady-state given by the P/T ratio (Eqn 6). This P/T ratio must be smaller than 1.25, and using Eqn 6 or Table 2, it can be calculated that this fluctuation is obtained for a τ/t1/2 ratio of 0.25. Finally, because digoxin t1/2 in dog being 40–48 h, the corresponding dosing interval is 10–12 h. This is the reason why the dosage regimen of digoxin requires the daily dose to be divided in two (half in the morning and half in the evening).
The extent of fluctuation can be easily predicted using the steady-state volume of distribution (Vss) (Toutain & Bousquet-Mélou, 2004b). It should also be realized that the biophase is generally outside the plasma compartment and the effects can be indirectly related to plasma concentration. In this case, the best strategy for designing an appropriate dosage interval is to simulate the effects using a PK/PD approach.
The terminal half-life and the requirement for a loading dose
 ()
()Terminal half-life for an extra-vascular route of administration and the flip-flop phenomenon
After an extra-vascular (EV) drug administration, the terminal half-life can be more prolonged than after an i.v. administration. This is frequently the case in veterinary medicine where many long-acting formulations, obtained using slow sustained release dosage forms, subdermal implants and vaginal sponges are marketed to provide a prolonged duration of action by maintaining plasma concentration above a minimal therapeutic concentration.
Similarly, some active principles (e.g. penicillin G) are or have been marketed as repository salt preparations (e.g. procaine penicillin G and benzathine penicillin G), or as water insoluble esters (e.g. corticoids) to obtain a prolonged duration of action (Fig. 10). Alternatively, an antibiotic, e.g. oxytetracycline may be solubilized in organic solvents in a series of concentrations (5, 10, 20 and 30%). After intramuscularly injection the active principle precipitates in increasing amounts at the injection site to provide increasing values of the terminal half-life. The route of administration for a given formulation can also be responsible for the flip-flop phenomenon. For instance, methylprednisolone acetate is poorly water soluble and it is a long acting formulation when administered by the i.m. route, but a short acting formulation when administered orally because the acetate ester is hydrolyzed in the digestive tract before intestinal drug absorption.
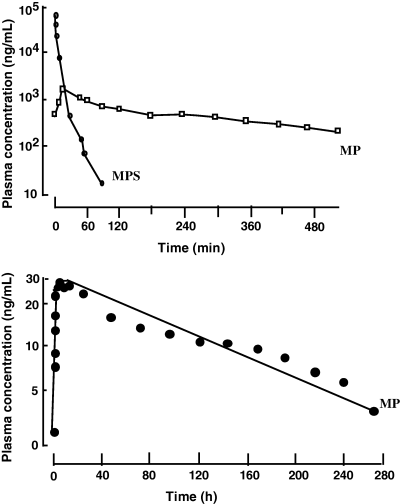
Flip-flop and half-life of methylprednisolone in dogs. Top: methylprednisolone sodium succinate (MPS), a hydrosoluble pro-drug of methylprednisolone (MP), has been administered i.v. to dogs at a dose rate of 4 mg/kg (as MP). MPS was rapidly transformed into MP and the terminal half-life of MP, the active metabolite of MPS was 1.6–2.64 h. Bottom: methylprednisolone acetate, a non-hydrosoluble pro-drug of MP was administered by the intramuscular route at the same dose rate of 4 mg/kg (as MP). Now, the terminal half-life was 70 h, i.e. much longer than after the i.v. MPS administration, reflecting the very slow process of drug absorption from muscle. This example shows that the same active principle may behave very differently according to the selected formulation for administration (Toutain et al., 1986).
For all the aforementioned formulations, dosage forms, etc. the terminal half-life no longer reflects the drug elimination rate (as after an i.v. administration), but rather the absorption rate. The term flip-flop is used to describe this phenomenon, and a flip-flop exists when the rate of absorption is the rate limiting step in the sequential processes of drug absorption and elimination. In other words, a drug cannot be eliminated before it has been absorbed.
The consequence of flip-flop is that the terminal half-life is actually a half-life of absorption (or more exactly, as will be seen later, a half-life of drug disappearance from the administration site).
It is essential to recognize when the flip-flop mechanism occurs in order to avoid erroneous physiological interpretations. In a flip-flop situation, the terminal slope is no longer controlled by clearance and volume of distribution (Eqn 2) but instead by the bioavailability factor (rate and also extent of absorption) (vide infra). Similarly, recognizing the occurrence of flip-flop avoids incorrectly calculation of some parameters such as Varea (Toutain & Bousquet-Mélou, 2004b). The best way to detect a flip-flop situation is to compare with a cross-over design i.v. and EV kinetics (Fig. 11). One of the major requirements for rational drug development is that the pharmacokinetics of any new chemical entity should be investigated by the i.v. route (to determine half-life of the substance itself), regardless of the expected route of administration for the final marketed formulation.
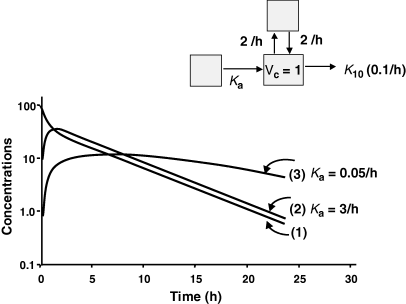
Terminal half-life and the flip-flop phenomenon. The pharmacokinetic disposition of a hypothetical drug having a terminal half-life of 7 h was simulated for an i.v. (1) administration, and for an extra-vascular administration with a rapid rate of absorption (Ka = 3/h) (2) or a slow rate of absorption (Ka = 0.05/h) (3). The parameters used for simulation were K12 = K21 = 2/h and K10 = 0.1/h. For the rapid rate constant of absorption (2) the slope of the terminal phase is parallel to that of the i.v. disposition curve and represents a rate of drug elimination (i.e. it is controlled by drug clearance and extent of distribution). In contrast, for a slow rate constant of absorption (3), the slope of the terminal phase is no longer parallel to that of the i.v. administration, reflecting the actual rate limiting step which is now related to drug absorption.
Ignoring the flip-flop phenomenon is the most frequent mistake in veterinary pharmacological papers, especially for some classes of drugs (avermectins and milbemycins) for which i.v. pharmacokinetic parameters are never (or seldom) reported for comparison with those obtained for the recommended route of administration.
The flip-flop phenomenon and interpretation of the terminal phase in terms of bioavailability factors
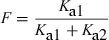 ()
()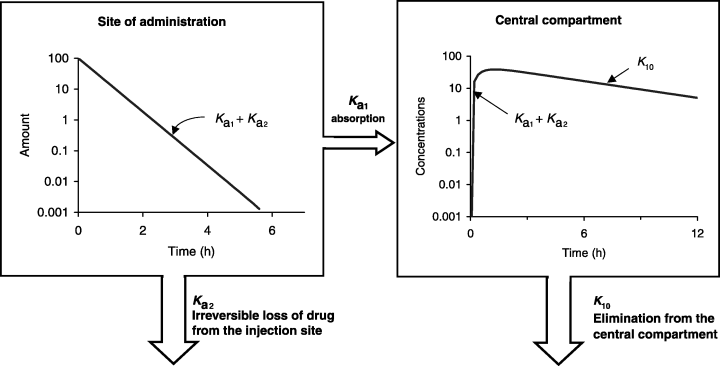
The so-called half-life of absorption vs. the process of drug absorption. This figure corresponds to a drug obeying a mono-compartmental model with a phase of absorption. The reported half-life of absorption (t1/2Ka) does not reflect solely the process of drug absorption (here represented by Ka1, the first-order rate constant of drug transfer from the injection site to the central compartment) but the sum of Ka1 and Ka2, Ka2 being the rate constant reflecting the irreversible loss of drug at the administration site. t1/2Ka reflects simply drug absorption only if Ka2 = 0, i.e. if the bioavailability is total. HereKa1 + Ka2 >> K10 and so no flip-flop phenomenon is observed.
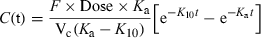 ()
()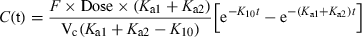 ()
()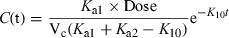 ()
()Here the terminal slope is K10 and it reflects the process of drug elimination, and the initial phase has a slope of Ka1 + Ka2.
Now, the terminal slope reflects Ka1 + Ka2, i.e. both drug absorption (Ka1) and drug leakage (Ka2), whereas the initial phase reflects K10, thus justifying the term flip-flop.
The practical consequence is that for a slowly absorbed drug (low Ka1), some formulations can lead to a flip-flop phenomenon because Ka2 is low or null (good bioavailability), whereas some other formulations do not display a flip-flop phenomenon, not because they are rapidly absorbed but because Ka2 is large, because their bioavailability is low (Fig. 13).

Terminal half-life and the flip-flop case. This figure illustrates the influence of bioavailability on the slope of the terminal phase. Left: a hypothetical drug formulation administered by the extra-vascular route (EV) is absorbed according to a slow process (Ka1), leading to a flip-flop. Right: for the same drug and the same physiological process of absorption (the same Ka1), the slope of the terminal phase can be dramatically decreased if bioavailability becomes low due to a source of drug leakage (represented here by Ka2); if the sum of Ka1 and Ka2 is higher than the terminal slope (λz) following i.v. administration, the terminal phase will represent in fact the process of drug elimination. Without an i.v. study, the interpretation of the left vs. right curves can be totally misleading (i.e. one can consider the right curve as being a formulation having a rapid absorption, whereas it is only a formulation with a low bioavailability).
More generally, interpretation of the terminal slope in presence of a flip-flop system should be undertaken in terms of Ka1 and Ka2, i.e. in terms of bioavailability factors and not in terms of clearance and volume of distribution.
A relevant terminal half-life and the meaning of a very late terminal half-life
Terminal half-life is the parameter most sensitive to performance of the analytical technique, especially the level of quantification (LOQ). Figure 14 shows, for a hypothetical drug, values of terminal half-life for different levels of LOQ. Using the same equation, different kinetic parameters were calculated for a LOQ of 1 or 0.1 ng/mL. It can be seen that the body clearance is the most robust pharmacokinetic parameter, the ratio between the values obtained with LOQ of 1 and 0.1 being of 1.51, whereas the terminal half-life was 10 times longer for a LOQ of 0.1.
Terminal half-life and level of quantification of the analytical technique. The reported terminal half-life (and also the other pharmacokinetic parameters) is influenced by the performance of the analytical technique, and especially by the level of quantification (LOQ). A curve was simulated with the equation given in the figure (time in hours and concentrations in ng/mL), and the pharmacokinetic parameters (clearance, volume of distribution, half-life) were computed from results obtained with analytical techniques having a LOQ of either 1 (LOQ1) or 0.1 ng/mL (LOQ2). It is clear that the calculated terminal half-life is very sensitive to the LOQ (50 h vs. 500 h), whereas clearance is least affected (the most robust) parameter with respect to the LOQ (0.0695 vs. 0.0464 L/kg/h), as indicated by the quoted ratios.
Twenty years ago, we published pharmacokinetic parameters for dexamethasone (DXM) in horses using a HPLC technique with a LOQ of 2–3 ng/mL. We reported a plasma clearance of 12.8 mL/kg/min and a short terminal half-life of 53 min (Toutain et al., 1984). More recently, Cunningham et al. (1996), using an improved analytical technique (LOQ = 200 pg/mL) reported that the plasma clearance of DXM in horse was 8 mL/kg/min, i.e. not markedly different from that in our earlier study, whereas the reported terminal half-life was three times longer (158 min) because a supplementary phase was detected.
The steady improvement in sensitivity of analytical techniques raises the question of relevance of detection of a supplementary very late terminal phase. The importance of any terminal half-life depends on its biological relevance (contribution to clinical efficacy, persistence of residues in food producing species, persistence of doping agents in the horse, required duration of a washout for a cross-over design, etc.). The case of aminoglycosides may be cited. The terminal phase of clinical relevance is relatively short (2 h) but, using a sensitive analytical technique, a supplementary phase can be detected having a half-life of approximately 24 h. This phase does not contribute to the antibiotic efficacy but reflects persistence of drug residues, this terminal phase being controlled by the redistribution rate constant from tissue to plasma. Aminoglycosides achieve particularly high and persistent concentrations in the kidney, so that concentrations in plasma decline with hours or days, whilst concentrations in renal tissue can exceed the MRL (maximum residue limit) for weeks or months. A similar find of binding to kidney has been described for polymyxins.
When estimating an acceptable daily intake (ADI) for a residue, it is assumed that ‘residues’ are ingested daily for life. Therefore, a very late terminal phase without any toxic or even therapeutic significance for the treated animal may become theoretically significant in terms of drug accumulation from the regulatory perspective of whole-life repeated dosing.
The presence of a very late terminal half-life can also create difficulties for a cross-over design when trying to avoid a carry-over effect (residual effect from the first period impacting on the second). The washout period should be long enough to guarantee that most of the drug has been cleared.
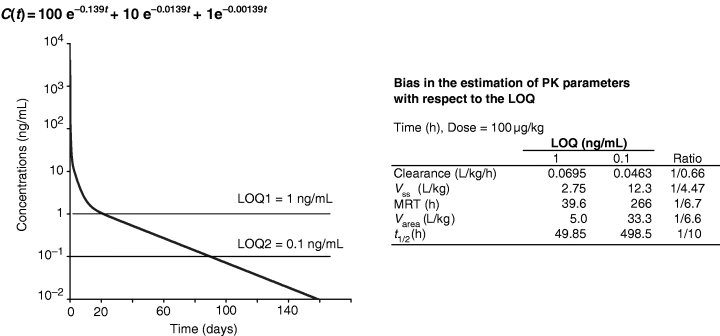
For doping control in relation to equine and canine competitive sports, a very late terminal phase, not detected in plasma, may be easily measured in urine when the urine-to-plasma concentration ratio is large. This may require a long withdrawal period to reach regulatory limits. In addition, this very late phase may be a cause of accumulation during a multiple dosing regimen. In consequence, the withdrawal period for doping control can be much longer after the cessation of a multiple dosing regimen than after a single-dose administration (Fig. 15). A similar phenomenon may occur during withdrawal periods for edible tissues in food producing animals. The time point at which the concentration of residues in all tissues falls below the respective maximum residue limit may be significantly longer after a multiple administration than after a single dose.
Significance of a very late terminal phase for doping control or for withdrawal time. Doping (medication) controls are generally carried out with analytical techniques having a low level of detection (LOD1), i.e. they are able to detect urine or plasma concentrations having no therapeutic impact but requiring a more or less prolonged delay after a drug treatment. This delay, required to achieve a ‘negative’ finding, can be much more prolonged after a multiple dosing regimen (delay 2) than after a single dose administration (delay 1). This is because a very late terminal phase (not detected after a single administration) gives concentrations above the LOD1 after a multiple dose administration due to accumulation specially linked to this very late phase. In contrast, with a higher LOD (LOD2) the delay to become ‘negative’ after a single dose or a multiple dose administration will be similar. The same phenomenon may explain that the withdrawal period, dictated by the time to fall below the MRL can be very different after a single and a multiple dose administration with regard to the value of MRL (MRL1 vs. MRL2). It is noteworthy that in this example, there is no therapeutically relevant accumulation in plasma concentration during the treatment itself but it is only the remnant amount of drug during the terminal phase which is consistently higher after a repeated dosing regimen. This situation is observed with phenylbutazone but not with meloxicam in horse.
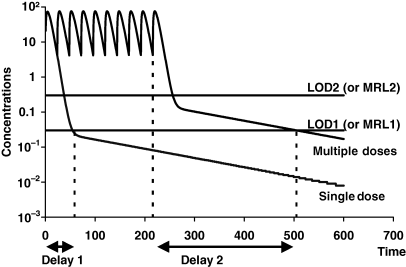
A practical approach to determine (a) if a terminal half-life has a therapeutic meaning and (b) what is the appropriate LOQ for an analytical technique, is to compute the AUC associated with each phase (Fig. 16) by integrating an equation describing the drug pharmacokinetics. For example, for gentamicin, the plasma pharmacokinetics can be described by a tri-exponential equation, the two first phases representing 98% of the total AUC indicating that the last phase (2% of AUC) does not significantly contribute to the overall drug exposure and can be discounted when discussing drug efficacy.
Clinical meaning of a terminal phase. The continual improvement of analytical techniques can lead to the detection of a very late terminal phase (e.g. for ivermectin) without clinical meaning. The questions are (a) when to stop sampling and (b) what is the appropriate level of quantification (LOQ) for an analytical technique. If the pharmacokinetic study is performed to address the question of drug efficacy, the range of efficacious concentrations should be considered. If there is evidence that the total exposure (as evaluated by the area under the plasma concentration time curve or AUC) is relevant in terms of drug efficacy, the different AUC associated with the different phases can be determined by integrating the equation describing drug disposition (i.e. for a tri-exponential curve AUC1 = Y1/λ1, AUC2 = Y2/λ2 and AUC3 = Y3/λ3) with Y1, Y2, Y3: the intercepts, and λ1,λ2, and λ3: the slopes of the different phases. Two curves (drug A and drug B) were simulated with exactly the same terminal slopes (0.01/h) but with different intercepts [low (Y3 = 1) for drug A and high (Y3 = 100) for drug B]. By integrating the equation describing these 2 curves respectively, it can be computed that the terminal phase (half-time of 69.3 h) accounts for only 1.6% of the total exposure (AUC) for drug A, whereas for drug B, the corresponding value is of 62.5%. For drug B, it is likely to be necessary to determine the last terminal phase (i.e. to carry out the study with an analytical technique having a LOQ of about 1), whereas for drug A, the last terminal phase can be considered as a very late terminal phase without clinical meaning, and it is not necessary to improve the analytical technique, i.e. to have a LOQ < 1 to detect the late terminal phase. However, this very late terminal phase may be very significant in terms of residues (e.g. for aminoglycosides).
Some considerations for the estimation of terminal half-life
It is not within the scope of the present article to explain how to effectively estimate pharmacokinetic parameters such as terminal half-life, but some technical points deserve mention. First, the accurate estimation of a slope requires sampling times over at least three times the expected half-life. In other words, it can be very misleading to estimate a half-life of 24 h with sampling data for 12 or 24 h.
Another point which can strongly influence half-life estimation is the use (or not) of an appropriate weighting factor when fitting data using non-linear regression analysis. It is acknowledged that one of the main factors of variation in half-lives reported in the literature derives not from biological factors but from the selection of the weighting scheme. As an example, Fig. 17 provides raw data for which fitting with or without a weighting factor leads to very different terminal half-lives.
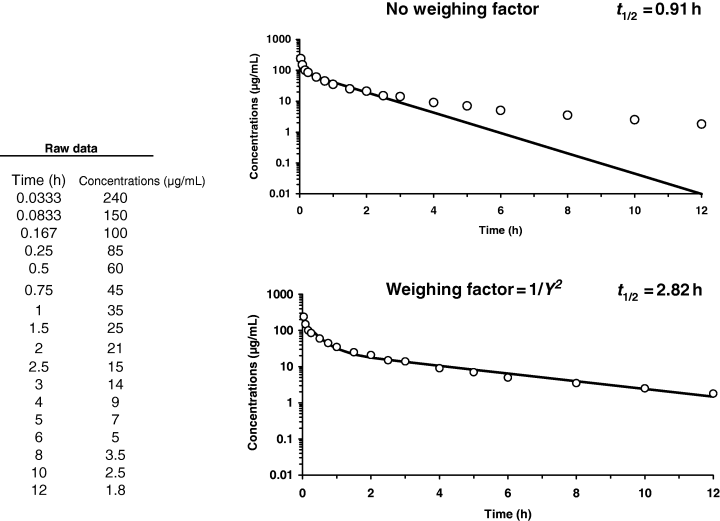
Influence of weighing factor on the calculated values of terminal half-life. Raw data were fitted using a bi-compartmental model (WinNonlin 4.0.1; Pharsight Corp., Mountain View, CA, USA), without (top) or with (bottom) a weighing factor (1/Y2), Y being the observed concentration. Visual inspection reveals a serious misfit when no weighing factor is used.
More generally, if a terminal half-life is first roughly approximated by visual inspection, computer programs using non-linear regression and an appropriate weighting scheme can then improve the isolation and estimation of terminal half-life.
After computation, of half-life for each individual animal, the results are generally reported as mean ± SD or SE. For terminal half-life, it is recommended that harmonic mean is used rather than arithmetic mean, and it is appropriate to compute standard error using a jackknife technique (Lam et al., 1985).
Conclusion
Terminal half-life is the most frequently reported pharmacokinetic parameter, but it is commonly misinterpreted. It is the least robustly estimated and its interpretation can be totally flawed if a flip-flop situation is not recognized. The clinical utility of terminal half-life is mainly to select an appropriate dosage regimen interval.