Methane emissions from soils: synthesis and analysis of a large UK data set
Abstract
Nearly 5000 chamber measurements of CH4 flux were collated from 21 sites across the United Kingdom, covering a range of soil and vegetation types, to derive a parsimonious model that explains as much of the variability as possible, with the least input requirements. Mean fluxes ranged from −0.3 to 27.4 nmol CH4 m−2 s−1, with small emissions or low rates of net uptake in mineral soils (site means of −0.3 to 0.7 nmol m−2 s−1) and much larger emissions from organic soils (site means of −0.3 to 27.4 nmol m−2 s−1). Less than half of the observed variability in instantaneous fluxes could be explained by independent variables measured. The reasons for this include measurement error, stochastic processes and, probably most importantly, poor correspondence between the independent variables measured and the actual variables influencing the processes underlying methane production, transport and oxidation. When temporal variation was accounted for, and the fluxes averaged at larger spatial scales, simple models explained up to ca. 75% of the variance in CH4 fluxes. Soil carbon, peat depth, soil moisture and pH together provided the best sub-set of explanatory variables. However, where plant species composition data were available, this provided the highest explanatory power. Linear and nonlinear models generally fitted the data equally well, with the exception that soil moisture required a power transformation. To estimate the impact of changes in peatland water table on CH4 emissions in the United Kingdom, an emission factor of +0.4 g CH4 m−2 yr−1 per cm increase in water table height was derived from the data.
Introduction
Methane (CH4) is the second most important trace gas contributing to the radiative forcing of the atmosphere. The largest term in the global CH4 budget is the emission from wetland soils, as a product of anaerobic decomposition of soil organic matter by methanogenic micro-organisms (Gorham, 1991; Lelieveld et al., 1993; Denman et al., 2007), although global-scale estimates of this vary widely (13–160 Tg yr−1, Petrescu et al., 2010). Soils can also act as a significant sink for CH4, via oxidation by methanotrophic bacteria, and the net efflux is the balance between production and oxidation (Dalal & Allen, 2008; Lai, 2009). Methane emissions are expected to increase in future in a warmer and wetter climate, and in response to changes in land management, particularly restoration and re-wetting of peatlands (Denman et al., 2007; Waddington & Day, 2007). With emission reduction targets now in place, measures to reduce greenhouse gas emissions through land management are being investigated as a potential means to mitigate climate change. Driven by this, there is a strong demand from policy-makers for simple emission factors, which quantify the effect of land management activities on the net emission of greenhouse gases, but as yet these are poorly developed (Couwenberg et al., 2011; Eggleston et al., 2011). As part of this, we require a better understanding of how the emissions of CH4 (as well as CO2 and N2O) respond to changes in environmental factors (Segers, 1998; Conrad, 2009). Also, given predictions of climatic change, there is a need to know how CH4 fluxes will respond in the long term, and emissions may increase in a warmer and wetter climate. Modelling work has shown the potential for positive feedback with climatic change (Gedney et al., 2004), particularly in arctic and boreal regions (Koven et al., 2011).
Measurements of CH4 flux are most commonly made using static chambers, whereby a small area of the land surface (typically ca. 0.1 m2) is enclosed, and the rate of change in methane concentration measured in a sequence of gas samples, analysed subsequently on a gas chromatograph. It is commonly observed that these small-scale measurements are very variable in space and time, making their interpretation in terms of processes difficult. This is because (i) the balance between CH4 production and oxidation is a complex interaction, influenced by biotic diversity and activity, soil water, oxygen concentrations within the soil, redox potential and transport processes within the soil–water–plant–atmosphere (diffusion, ebullition and transport via aerenchyma and xylem), and (ii) the driving variables are themselves heterogeneous in time and space, and often difficult to measure appropriately. If these chamber measurements are to be used to estimate fluxes at larger scales or over longer time periods, a robust method for scaling up is required which accounts for the key environmental driving variables and their interactions, that can be calibrated over an appropriate range of conditions, and with a suitably large sample size (Baird et al., 2009a). Such a method is needed if CH4 emissions from natural wetlands are to be included appropriately in IPCC greenhouse gas inventories (IPCC, 2003; Eggleston et al., 2011). Models of CH4 flux range from simple empirical or statistical models (e.g. Couwenberg et al., 2011), to detailed mechanistic models which explicitly represent many of the processes involved, including CH4 production, oxidation, transport via diffusion, ebullition and plant stems (Arah & Stephen, 1998; Walter et al., 2001). Because of the computation time and coarse spatial resolution in regional- and global-scale models, relatively simple models of CH4 emissions are better suited in this context.
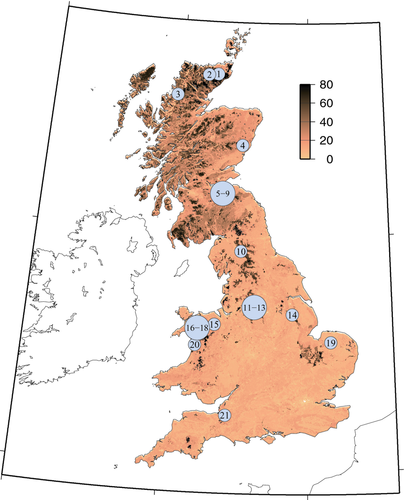
Here, we have collated a large number (4831) of existing chamber measurements of soil CH4 flux made in the United Kingdom, covering a range of vegetation types, and including both mineral and organic soils. The overarching aim of this study was to analyse this data set in terms of a number of co-located measurements of environmental and ecological variables, to assess the appropriate degree of complexity for modelling. Given the explanatory variables that are generally available, we aimed to derive a parsimonious model with the least requirements for environmental inputs, suitable for calculating national-scale CH4 emissions from ecosystems, or inclusion within a regional-scale land surface model (e.g. Clark et al., 2011). As an example application of such a model, we then derived a simple emission factor for peatland restoration based on the modelled responses to water table changes.
Methods
Field sites and measurements
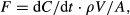 (1)
(1)
| Site | Lat | Lon | Soil class | Sampling method used | Fitting method used | References (to site or data set) |
|---|---|---|---|---|---|---|
| Auchencorth | 55.79 N | 3.24 W | Organic | 1 | 1 | Drewer et al. (2010) |
| Clocaenog | 53.08 N | 3.38 W | Organo-mineral | 2 | 1 | Unpubl. |
| Cow Park | 55.85 N | 3.22 W | Mineral | 1 | 1 | Jones et al. (2005) |
| Easter Bush | 55.86 N | 3.21 W | Mineral | 1 | 1 | Unpubl. |
| Forsinard | 58.37 N | 3.97 W | Organic | 4 | 2 | Gray (2007) |
| Glensaugh | 56.90 N | 2.52 W | Organo-mineral | 1 | 1 | Unpubl. |
| Grenstein | 52.73 N | 0.81 E | Mineral | 1 | 1 | Unpubl. |
| Hafren | 52.63 N | 3.95 W | Mineral | 1 | 1 | Unpubl. |
| House O'Muir | 55.86 N | 3.25 W | Mineral | 1 | 1 | Unpubl. |
| Lincoln | 53.32 N | 0.55 W | Mineral | 1 | 1 | Drewer et al. (submitted) |
| Loch More | 58.39 N | 3.60 W | Organic | 1 | 2 | Macdonald et al. (1998) |
| Migneint A | 52.99 N | 3.80 W | Organic | 2 | 2 | Unpubl. |
| Migneint B | 52.99 N | 3.80 W | Mineral | 2 | 2 | Unpubl. |
| Migneint C | 52.99 N | 3.80 W | Organic | 3 | 1 | Unpubl. |
| Moor House | 54.65 N | 2.45 W | Organic | 5 | 1 | Ward et al. (2007) |
| Peaknaze A | 53.47 N | 1.91 W | Organo-mineral | 2 | 1 | Unpubl. |
| Peaknaze B | 53.47 N | 1.91 W | Organic | 2 | 2 | Unpubl. |
| Peaknaze C | 53.47 N | 1.91 W | Mineral | 2 | 2 | Unpubl. |
| Tadham | 51.16 N | 2.81 W | Organic | 5 | 1 | Lloyd (2006) |
| Ullapool | 57.91 N | 5.17 W | Organic | 1 | 1 | Unpubl. |
| Whim | 55.76 N | 3.27 W | Organic | 1 | 1 | Sheppard et al. (2004) |
- In sampling method 1, the chamber was 38 cm in diameter and 23 cm high, sample volume was 20 mL, two samples were taken over 30–90 min, gas samples were stored in vials or tedlar bags, and analysis was by gas chromatograph (GC, 5890 series II; Hewlett Packard, Santa Clara, CA, USA). In sampling method 2, the chamber was 20 cm in diameter and 10 cm high, sample volume was 20 mL, three samples were taken over 30 min, gas samples were stored in vials, and analysis was by GC (Clarus 500; Perkin Elmer, Cambridge, UK). In sampling method 3, the chamber was 30 cm in diameter and 41 cm high, sample volume was 20 mL, 2–4 samples were taken over 0.5–2 h, gas samples were stored in vials or tedlar bags, and analysis was by GC (Clarus 500; Perkin Elmer). In sampling method 4, the chamber was 63 cm in diameter and 29 cm high, sample volume was 20 mL, four samples were taken over 30 min, gas samples were stored in vials or tedlar bags, and analysis was by GC (5890 series II; Hewlett Packard). In sampling method 5, the chamber was 30 cm in diameter and 35 cm high, sample volume was 20 mL, two samples were taken over 1–2 h, gas samples were stored in Exetainers, and analysis was by GC (Clarus 500; Perkin Elmer). In fitting method 1, the mean values of dC and dt were used to calculate dC/dt in Eqn 1; in fitting method 2, the slope of a linear regression between C and t was used.
Data analysis
The raw concentration data (i.e. C with t) were not generally available, so the analysis here is based on the pre-existing calculated fluxes. The data from all sites were collated into a single data set containing 4831 CH4 flux measurements. As far as possible, we collated a common set of explanatory variables associated with each flux measurement. The explanatory variables obtained were: soil temperature (Tsoil, °C) at the depth deemed most relevant in the original study; soil moisture (θ, volumetric water content as a fraction), water table depth (zwater, cm), soil carbon stock (Csoil, kg C m−2), peat depth (zpeat, m), soil pH, soil bulk density (ρsoil, g dry mass cm−3), and soil CO2 efflux (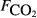 , μmol m−2 s−1).
, μmol m−2 s−1).
As these data were collected under several different measurement programmes and for different purposes, there were missing values for several variables at most sites. Where possible, these gaps were filled by regressing against other explanatory variables. At most sites, some measurements of both soil moisture and water table were available, and where a reasonably clear relationship was present, this relationship was used to fill gaps where there were missing values in either variable. Soil carbon stock was generally calculated from local measurements of soil carbon concentration (g C g−1 dry mass), bulk density (g dry mass cm−3), and soil depth. For the peatland sites, default values for soil carbon concentration and bulk density of 0.5 and 0.12, respectively, were used where local values were not available (i.e. in these cases, soil carbon stock was assumed to be linear with peat depth, assuming 600 kg C m−3). Whilst this is a broad-brush assumption, the results of the analysis are fairly insensitive to the exact value used, and this simply converts peat depth into a measure of soil carbon stock for comparison with soil carbon stock in mineral soils. For sites with mineral soil, peat depth was set to zero; where a clear water table was not apparent, water table depth was given a missing value code.
At three of the sites (containing 70 plots over eight sub-sites), the composition of the vegetation within each chamber was identified to species level, including nonvascular plants, and this was summarized in two ways. First, the percentage cover of species known to possess aerenchyma was calculated (Aer, %). Second, a principal components analysis (PCA) was performed, to find the orthogonal axes of species cover which correlate best with methane flux. The first PCA axis (Spp1, dimensionless) characterized a gradient in soil moisture, and accounted for 46% of the variance in the species cover data.
- Each individual chamber location (or ‘plot’), thereby removing temporal variability but retaining spatial variability.
- Groups of plots (or ‘sub-sites’), where plots were grouped within sites, based on spatial location or experimental treatment.
- Each site, whereby all the data for each site were averaged, thereby removing temporal variability and within-site spatial variability.
Some extreme values were found at several sites, probably resulting from ebullition events (Baird et al., 2004) or measurement error (Christiansen et al., 2011), and arbitrary thresholds for data exclusion were set at −20 and 200 nmol m−2 s−1. Given these extreme values, simple arithmetic means are an imperfect summary statistic. As discussed by (Baird et al., 2009a), the skewed nature of the distributions should be accounted for when extrapolating to larger scales. This might use measurements or simulations of the explanatory variables with high-resolution in time and space to fill the gaps between observations and integrate up to larger scales. This is the subject of on-going work, but is beyond the scope of the present analysis.
The data were first analysed using univariate linear regression to examine how much variation could be accounted for by each explanatory variable considered independently. Multivariate linear and nonlinear regressions were then used to examine how much variation could be accounted for by the complete set of explanatory variables considered together. The data were analysed using the GenStat statistical software (ver 12.1; VSN International Ltd., Hemel Hempstead, UK).
Results
Site means for methane flux and the explanatory variables are shown in Table 2. CH4 fluxes showed strongly left-skewed distributions at all sites, dominated by low, positive (i.e. emission) fluxes (Fig. 2a). Overall, the mean and median fluxes were 6.3 and 0.23 nmol m−2 s−1, with lower and upper quartiles at −0.1 and 4.5 nmol m−2 s−1. Sites with mineral soils tended to have small emissions or low rates of net uptake, with site means between −0.3 and 0.7 nmol m−2 s−1 (Fig. 2). Sites with organic soils had much larger emissions, with means between −0.3 and 27.4 nmol m−2 s−1. Sites with organo-mineral soils were intermediate, though the sample size was much smaller.
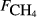 ) and explanatory variables by site
) and explanatory variables by site| Site |
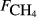
|
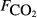
|
z water | θ | T soil | pH | z peat | C soil | ρ soil | A er | S pp1 | n |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Auchencorth | 0.4 | 1.6 | −13.1 | 0.91 | 9.0 | 4.4 | 0.5 | 33.0 | 595 | |||
| Clocaenog | 0.1 | 0.32 | 8.1 | 3.9 | 0.1 | 15.1 | 130 | |||||
| Cow Park | 0.1 | 0.45 | 12.2 | 6.4 | 0.0 | 13.9 | 290 | |||||
| Easter Bush | 0.1 | 0.30 | 10.2 | 5.0 | 0.0 | 12.1 | 704 | |||||
| Forsinard | 15.9 | −8.7 | 0.36 | 9.9 | 4.0 | 2.9 | 189.9 | 28.6 | 0.8 | 615 | ||
| Glensaugh | 2.2 | 2.5 | 0.91 | 7.3 | 4.5 | 0.7 | 0.6 | 18 | ||||
| Grenstein | 0.7 | 1.2 | 0.60 | 3.0 | 0.22 | 69 | ||||||
| Hafren | −1.4 | 2.9 | 0.06 | 8.6 | 4.5 | 0.6 | 0.5 | 29 | ||||
| House O'Muir | −0.3 | 3.5 | 0.73 | 12.0 | 6.0 | 0.0 | 5.0 | 0.27 | 80 | |||
| Lincoln | −0.1 | 1.7 | 0.23 | 0.0 | 8.3 | 229 | ||||||
| Loch More | 27.4 | −5.6 | 0.93 | 14.5 | 4.0 | 264.0 | 188 | |||||
| Migneint A | 16.9 | 0.1 | −10.1 | 8.0 | 4.3 | 2.0 | 130.9 | 251 | ||||
| Migneint B | 0.0 | 0.4 | 8.4 | 4.4 | 0.2 | 14.8 | 261 | |||||
| Migneint C | 12.7 | −5.8 | 12.6 | 4.0 | 2.0 | 132.0 | 160 | |||||
| Moor House | 11.3 | 2.1 | −10.3 | 0.90 | 7.3 | 3.8 | 1.5 | 85.0 | 32.4 | −0.4 | 208 | |
| Peaknaze A | 0.0 | 0.49 | 9.9 | 4.1 | 0.1 | 5.0 | 75 | |||||
| Peaknaze B | 5.5 | 0.3 | −15.0 | 8.3 | 3.9 | 2.3 | 153.0 | 249 | ||||
| Peaknaze C | −0.3 | 0.4 | −1.0 | 8.4 | 4.1 | 0.2 | 13.7 | 239 | ||||
| Tadham | −0.4 | −32.7 | 11.1 | 6.4 | 2.0 | 132.0 | 197 | |||||
| Ullapool | 7.2 | 2.0 | 0.77 | 8.1 | 4.5 | 0.7 | 0.4 | 0.14 | 15 | |||
| Whim | 22.2 | −2.6 | 0.95 | 8.0 | 3.6 | 6.0 | 396.0 | 0.10 | 48.5 | 0.5 | 229 |
-
The explanatory variables are: soil CO2 efflux (
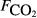 , μmol m−2 s−1), water table depth (zwater, cm), soil moisture (θ, volumetric water content as a fraction), soil temperature (Tsoil, °C); soil pH, peat depth (zpeat, m), soil carbon stock (Csoil, kg C m−2), soil bulk density (ρsoil, g dry mass cm−3), the percentage cover of aerenchymatous species (Aer, %), and the first axis (Spp1, dimensionless) of an ordination of species cover. n is the number of CH4 flux samples.
, μmol m−2 s−1), water table depth (zwater, cm), soil moisture (θ, volumetric water content as a fraction), soil temperature (Tsoil, °C); soil pH, peat depth (zpeat, m), soil carbon stock (Csoil, kg C m−2), soil bulk density (ρsoil, g dry mass cm−3), the percentage cover of aerenchymatous species (Aer, %), and the first axis (Spp1, dimensionless) of an ordination of species cover. n is the number of CH4 flux samples.
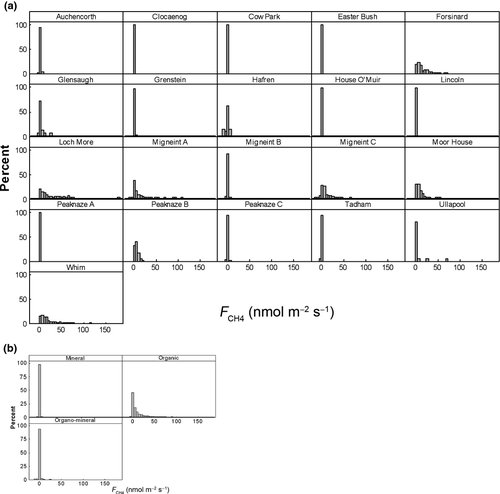
Scatterplots of methane flux against the main explanatory variables are shown in Fig. 3 and Figs S1 and S2. Some pattern is apparent with most variables, and this is clearest when the data are averaged at site and sub-site level. The strongest relationships are with soil carbon, soil moisture and the measures of plant species composition. Where relationships appeared nonlinear, transformations were examined to find a more linear relationship with methane flux. However, only in the case of soil moisture did a transformation give a consistently better fit to the data across all averaging levels, where θ4 had the closest linear relationship with methane flux; this transformation was used in the statistical modelling.
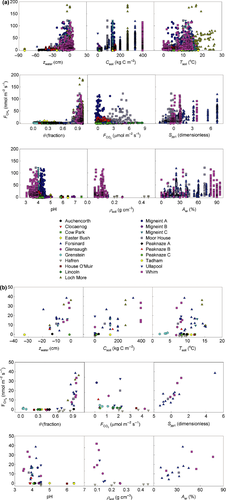
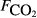 , μmol m−2 s−1), the first axis (Spp1, dimensionless) of an ordination of species cover, soil pH, soil bulk density (ρsoil, g dry mass cm−3), and the percentage cover of aerenchymatous species (Aer,%).
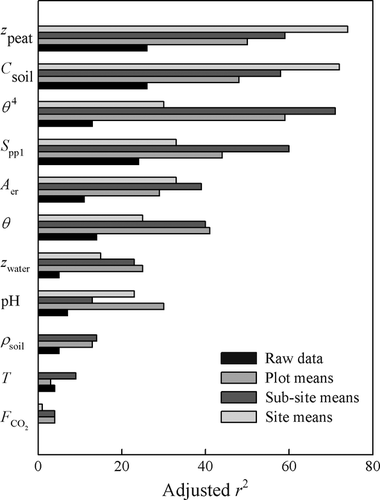
, μmol m−2 s−1), the first axis (Spp1, dimensionless) of an ordination of species cover, soil pH, soil bulk density (ρsoil, g dry mass cm−3), and the percentage cover of aerenchymatous species (Aer,%).Figure 4 and Table 3 show that the adjusted r2, effectively the percentage of variance explained by the regression model, increases with the extent of averaging; the model fit is poorest with the raw data and best when the site means are analysed. Several variables show reasonably close relationships with methane flux, particularly soil carbon, peat depth, soil moisture and plant species composition, though the ranking varies between averaging levels. Table 3 shows that the size of the data set (without missing values) varies widely between variables, so an exact like-for-like comparison is not possible. Also, much of the variation in explanatory variables is confounded, so caution is needed in ascribing cause and effect. Some variables showed surprisingly poor relationships with methane flux when analysed in this simple way, such as water table, soil temperature, CO2 efflux, pH and bulk density.
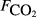 , μmol m−2 s−1).
, μmol m−2 s−1).| Variable | Adjusted r2 | n | ||||||
|---|---|---|---|---|---|---|---|---|
| All data | Plot | Sub-site | Site | All data | Plot | Sub-site | Site | |
| C soil | 26 | 48 | 58 | 72 | 4764 | 279 | 54 | 21 |
| z peat | 26 | 50 | 59 | 74 | 4764 | 279 | 54 | 21 |
| S pp1 | 24 | 44 | 60 | 33 | 1016 | 85 | 17 | 3 |
| θ | 14 | 41 | 40 | 25 | 3000 | 254 | 46 | 21 |
| θ 4 | 13 | 59 | 71 | 30 | 3000 | 254 | 46 | 21 |
| A er | 11 | 29 | 39 | 33 | 1016 | 85 | 17 | 3 |
| pH | 7 | 30 | 13 | 23 | 4171 | 235 | 45 | 21 |
| Bulk density | 5 | 13 | 14 | 0 | 292 | 28 | 16 | 5 |
| z water | 5 | 25 | 23 | 15 | 2517 | 130 | 24 | 10 |
| T soil | 4 | 3 | 9 | 0 | 3950 | 302 | 54 | 21 |
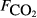
|
0 | 4 | 4 | 1 | 2055 | 173 | 26 | 12 |
-
The explanatory variables are: soil carbon stock (Csoil, kg C m−2), peat depth (zpeat, m), the first axis (Spp1, dimensionless) of an ordination of species cover, soil moisture (θ, volumetric water content as a fraction), the percentage cover of aerenchymatous species (Aer, %), soil pH, soil bulk density (g dry mass cm−3), water table depth (zwater, cm), soil temperature (Tsoil, °C), and soil CO2 efflux (
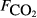 , μmol m−2 s−1).
, μmol m−2 s−1).
All sub-sets of variables were used in a multivariate regression procedure to identify which combinations of variables were most useful in explaining the variation in methane flux. The best-fitting models with each number of terms are shown in Table 4, ranked by their Akaike Information Criterion (AIC; Burnham & Anderson, 2002), a measure which ranks competing models according to goodness-of-fit with a penalty associated with the number of parameters (here, equivalent to the number of explanatory variables used + 1). Other similar measures (Mallow's Cp and Bayesian Information Criterion) were examined but gave essentially the same rankings. Comparisons among models becomes difficult when there are missing values for some variables, so results are presented for each averaging level, with and without a restriction on the data sub-set to those with species composition data.
| Terms | Adjusted r2 | AIC |
|---|---|---|
| Raw data, with species composition data, n = 974 | ||
| Spp1+T+Aer+zpeat+Csoil+pH+θ4 | 43.6 | 982.0 |
| Spp1+T+Aer+zpeat+Csoil+pH | 43.6 | 982.5 |
| Spp1+T+Aer+zpeat+Csoil | 43.4 | 984.5 |
| Spp1+T+Aer+zpeat | 41.9 | 1008.5 |
| Spp1+T+Aer | 40.3 | 1035.1 |
| Spp1+T | 35.4 | 1118.8 |
| S pp1 | 24.3 | 1308.8 |
| Raw data, n = 2095 | ||
| zpeat+T+θ4+Csoil | 38.5 | 2099.5 |
| zpeat+T+θ4+Csoil+pH | 38.5 | 2101.0 |
| zpeat+T+θ4 | 38.3 | 2104.8 |
| zpeat+T | 37.7 | 2126.4 |
| z peat | 32.9 | 2288.1 |
| Plot means, with species composition data, n = 70 | ||
| Spp1+Aer+zpeat | 57.7 | 72.2 |
| Spp1+Aer+zpeat+pH | 57.5 | 73.6 |
| Spp1+Aer+zpeat+pH+Csoil | 57.8 | 74.2 |
| Spp1+Aer+zpeat+pH+Csoil+θ4 | 57.1 | 76.1 |
| Spp1+Aer+zpeat+pH+Csoil+θ4+T | 56.5 | 78.0 |
| Spp1+Aer | 53.2 | 78.1 |
| S pp1 | 45.3 | 89.6 |
| Plot means, n = 188 | ||
| zpeat+θ4 | 58.9 | 190.0 |
| zpeat+θ4+T | 59.1 | 190.2 |
| zpeat+θ4+T+Csoil | 58.9 | 192.0 |
| zpeat+θ4+T+Csoil+pH | 58.7 | 194.0 |
| z peat | 55.9 | 202.5 |
| Sub-site means, with species composition data, n = 8 | ||
| Spp1+θ4 | 69.1 | 10.3 |
| S pp1 | 53.5 | 11.7 |
| Spp1+θ4+Aer | 62.7 | 12.1 |
| Spp1+θ4+Aer+Csoil | 54.4 | 13.8 |
| Spp1+θ4+Aer+Csoil+WT | 63.7 | 14.0 |
| Sub-site means, n = 35 | ||
| θ4+Csoil | 66.8 | 36.5 |
| θ4+zpeat+T | 67.5 | 37.0 |
| θ 4 | 63.4 | 38.7 |
| θ4+zpeat+T+pH | 66.4 | 39.0 |
| θ4+T+zpeat+pH+Csoil | 65.2 | 41.0 |
| Site means, n = 21 | ||
| z peat | 73.8 | 19.9 |
| zpeat+θ4 | 73.1 | 21.5 |
| zpeat+θ4+T | 72.2 | 23.1 |
| zpeat+θ4+T+Csoil | 70.7 | 25.0 |
| zpeat+θ4+T+Csoil+pH | 68.8 | 27.0 |
- The candidate models are ranked by the Akaike Information Criterion (AIC), which identifies the models which explain the most variance in the data with fewest terms in the model.
Where species composition data were available, the first PCA axis, Spp1, came out as the best-fitting univariate model at all averaging levels. The percentage cover of aerenchymatous species, Aer, gave additional information, and was the second or third term to be added to the model. Using these two terms alone could account for up to 53% of the variance in methane flux, although n was always smaller when restricted to samples with species data. Without the restriction of including species data, peat depth was the best single predictor of methane flux, accounting for 74% of the variance at site level, and 33% in the raw data. According to the AIC, the parsimonious models included soil temperature, soil moisture and soil carbon, although the best combinations of these depended on the averaging level. When a unique identifier for each plot was included as an extra term in the model, the adjusted r2 was generally increased by a further 10%. In other words, 10% of the variance was explained by something specific to each unique location, but not captured by the explanatory variables measured here.
Nonlinear regression was used to test some commonly used models, and the goodness-of-fit measures and model parameters are shown in Table 5; for brevity, results are only shown for two averaging levels, but the pattern is similar elsewhere. The results show that the exponential function of temperature alone has little explanatory power for these data. Water table also performs poorly for the raw data, and is less effective than soil moisture at sub-site level. When the exponential response to temperature is combined with a power function for soil moisture and a linear function for soil carbon, the explanatory power is much better, and is similar to or better than that from the best sub-sets linear modelling.
| Model | n | Adj r2 | AIC | B 0 | B 1 | B 2 | B 3 |
|---|---|---|---|---|---|---|---|
| Sub-site means | |||||||
| B0+B1×zwater | 23 | 23.1 | 136 | 22.660 | 0.804 | ||
| B0+B1×exp(B2×Tsoil) | 54 | 7.0 | 328 | −10.400 | 10.100 | 0.064 | |
| B0+B1×Csoil×exp(B2×Tsoil)×(θB3) | 38 | 66.0 | 291 | 2.070 | 0.036 | 0.094 | 4.770 |
| Raw data | |||||||
| B0+B1×zwater | 2516 | 5.1 | 34773 | 15.023 | 0.334 | ||
| B0+B1×exp(B2×Tsoil) | 3940 | 4.8 | 54946 | 2.378 | 1.011 | 0.149 | |
| B0+B1×exp(B2×Tsoil)×(θB3) | 2350 | 36.0 | 30989 | −1.060 | 11.695 | 0.076 | 4.531 |
| B0+B1×Csoil×exp(B2×Tsoil)×(θB3) | 2295 | 41.6 | 30041 | 0.667 | 0.044 | 0.074 | 3.609 |
- The table lists the sample size available (n) in either the sub-site means or the raw data, the adjusted r2 obtained, the Akaike Information Criterion (AIC), and the fitted model parameters (B0…3).
Discussion
Our analyses show that some of the expected relationships are present in these data, and up to ca. 74% of the variance in methane flux can be explained at site level. However, there is a considerable amount of noise in the data, and more than half the variance in the raw data is unexplained. This is similar to other studies which have applied statistical approaches, and the primary relationships with explanatory variables are similar. In peatlands in Canada and Finland, several studies on individual sites have found poor correlations between CH4 flux and temperature, but reasonable relationships with water table depth (r2 typically ca. 0.5 using seasonal means and log transformation, Liblik et al., 1997 and references therein). Bubier (1995a) found that r2 was increased to 0.84 by adding mean temperature at mean water table depth, water chemistry (conductivity, pH, Ca), tree cover and herbaceous plant cover to the regression model. Macdonald et al., 1998 found similar relationships with temperature and water table in mesocosms from Northern Scotland under controlled conditions, and found a clear effect of plant-mediated transport via the stems of bogbean Menyanthes trifoliata L. Greenup et al. (2000) also found a strong relationship between below-ground biomass of an aerenchymatous sedge species and CH4 emission in a UK bog. At sites in Germany, Couwenberg et al. (2011) report a close relationship between the number of leaves of two aerenchymatous species and CH4 emission. Kettunen et al. (2000) found reasonable plot-specific relationships with temperature (0.33 < r2 < 0.72) at a fen site in Finland; water table depth had less explanatory power, probably because its range of variation was small. The fitted model performed poorly when the data were pooled across plots, and did not explain short-term variations well. Laine et al. (2007) found very similar results in a blanket bog in Ireland. In addition, they measured the leaf area of aerenchymatous species, but found little relationship with CH4 flux.
There are several likely causes for the unexplained variation in the raw data. First, there is typically a substantial amount of measurement error in static chamber flux measurements, which adds some random noise to the data (Levy et al., 2011), as well as possible systematic errors (Christiansen et al., 2011). Levy et al. (2011) estimate typical 95% confidence intervals of ±20% for individual flux measurements, using Monte Carlo error propagation. Second, CH4 can be transported by ebullition (i.e. via rising bubbles of gas in soil water), rather than diffusion. This will add a random term to the measured flux, if transport of bubbles is not as a continuous stream of small bubbles, but episodic and largely stochastic, influenced by short-term wind-driven surface pressure fluctuations which are unpredictable (Baird et al., 2004). Third, the net efflux of methane is a complex interaction between several underlying processes, and several of the variables driving the underlying processes are either not measured, or poorly represented by the independent variables which are commonly measured. To give some examples, water table depth or soil moisture are used as surrogate variables for soil O2 concentration, and the extent of the anaerobic zone. However, Askaer et al. (2010) show, using high-resolution measurements using planar O2 optodes, that water table depth can be a poor proxy for anaerobic status at small spatio-temporal scales, as aerobic zones were observed below the water table, and vice versa, especially when the water table was dynamic. The correspondence becomes much better when the water table depth remains more stable, and at larger spatial scales. The rate of methane production is affected by soil redox potential and the availability of terminal electron acceptors (primarily Fe3+, Mn4+, SO42−, NO3−). These are not commonly measured, so variation due to these will be unaccounted for; at best, they may correlate with soil pH or pollutant deposition as a proxy. The availability of carbon substrates and the methanogenic microbial biomass and diversity are generally assumed not to be limiting, but there is some evidence to the contrary (Segers & Kengen, 1998). Furthermore, there are two distinct metabolic pathways which can produce methane, (based on either acetate or hydrogen/CO2 substrates, and associated with different bacterial taxa), and their response to environmental variables and relative abundance may differ (Cadillo-Quiroz et al., 2006; Lai, 2009). Soil carbon stock and peat depth will provide some proxy for the availability of carbon substrates, as well as the extent of anaerobic conditions, but this will not include short-term variations.
Model fit was much improved when the raw data were averaged in time and over increasingly larger spatial scales, and there were a number of probable reasons for this. If there is substantial random measurement error in the flux data, this will tend to cancel out as more measurements are averaged. Similarly, there will be some random measurement error in the independent variables which will again tend to cancel out with averaging. Furthermore, the co-location of measurements of independent and dependent variables is not exact, and some independent variables were only measured at site or sub-site level, so some mis-match at plot level is inevitable. Several of the independent variables vary only on relatively long time scales (e.g. soil carbon, species composition, pH), so cannot account for short-term temporal variation. Only a small number of independent variables vary on short time scales (temperature, soil moisture, CO2 efflux, etc.), and these do not fully account for the variations in methane flux. Averaging removes this unexplained short-term temporal variation.
The results show that plant species composition is the best single predictor of mean CH4 flux, where data are available. This may be because of direct effects of particular plant species (because some species transport CH4 or provide suitable substrates for the production of CH4), as well as indirect effects (because plant species composition is a good indicator of environmental conditions, and effectively integrates past conditions over the long term). For example, Wamelink et al. (2005) showed that plant species composition was a very good predictor of soil pH in a large European data set. Bryophytes are particularly sensitive to water table position, and their use as predictors of CH4 flux has been noted previously (Bubier, 1995b; Dias et al., 2010). The results suggest that there is an effect of plant species composition beyond that of transport via aerenchyma, as the multivariate PCA axis has substantially better explanatory power, and it seems likely that both direct and indirect effects are important. Using plant species composition may be useful in predicting CH4 fluxes at large scales, where vegetation survey data are available. Further validation of this approach is being investigated, and this could form part of a method for obtaining national-scale emissions of CH4 from soils. Plant species composition is hard to include in ecosystem or biogeochemical models, and at best is approximated by some plant functional type classification (e.g. Couwenberg et al., 2011). However, these classifications are relatively crude, and our mechanistic understanding is still incomplete (De Deyn et al., 2008; Kip et al., 2010).
Of the abiotic variables, soil carbon and peat depth have the most explanatory power. Again, a component of this will be a direct effect, as deep peats have a larger pool of carbon substrate for methanogenesis, but indirect effects probably predominate. Deep peats exist because the waterlogged conditions which inhibit decomposition also provide the extensive anaerobic environment which permits methanogenesis. Both soil carbon and peat depth were included in the analyses, even though the two are so closely linked, as the former was generally calculated from the latter at peatland sites. However, their main difference lies in how they represent the transition between mineral and organic soils: soil carbon gives a continuous transition, whereas peat depth (having a zero value in mineral soils) shows a ‘broken stick’ response, with a sharp delineation between mineral and organic soils. The latter commonly fits the CH4 flux data slightly better. Interestingly, there is no apparent influence of decomposition rate, measured as soil CO2 efflux, on CH4 flux. It might be expected that this would provide a measure of the size of the labile carbon pool and substrate availability, and this effect is included in some models (Clark et al., 2011). It may simply be that the measurements here are not sufficient to detect this effect, and more co-located CO2 and CH4 flux measurements would be required to quantify this rigorously.
Whilst there is strong evidence that pH affects soil bacterial communities in wetland soils (Hartman et al., 2008), the net effect on CH4 fluxes is less clear. An increase in CH4 fluxes with declining pH would be expected from most studies on methanogens under controlled conditions; for example, in a study by Taconi et al. (2007) methane production from waste water was increased by 30% when pH was decreased from 7.0 to 4.5. On the other hand, reduced pH in UK semi-natural soils is often associated with (current or historically) elevated inputs of atmospheric sulphate, which has a suppressive effect on methanogenesis (e.g. Gauci et al., 2004), potentially countering a direct pH effect. However, methanotrophs may have a different responses to pH which could complicate the net effect; both methanogens and methanotrophs are likely to have bell-shaped response, but with potentially different optima (Dedysh, 1998). Indeed, the role of methanotrophs in bog systems may have been substantially under-estimated (Kip et al., 2010). Our results suggest a weak but detectable effect of pH, with CH4 fluxes tending to increase with acidity. Partially, this is attributable to the negative correlation between pH and soil carbon, and the regression when this effect is removed is not statistically significant (P = 0.2). A similar effect is present in the relationship between soil bulk density and CH4 flux, which is apparent in Fig. 3. Soil carbon stock is calculated using the bulk density values, and the two closely co-vary. When the correlation with soil carbon is removed, bulk density provides little extra predictive information.
Throughout the analysis we have focussed on the explanatory power of the models, rather than predictive power, as the latter is not tested here. Given the complexity of possible feedbacks and interactions between the driving variables and the issues of extrapolating to the long term (Norby & Luo, 2004; Boardman et al., 2011), prediction of response to long-term global change is much more difficult. However, in the shorter term, there is considerable current interest in the impact of peatland restoration activities on greenhouse gas emissions (Waddington & Price, 2000; Laine et al., 2006; Rochefort & Lode, 2006; Eggleston et al., 2011). In the United Kingdom, there is some debate over the merits of restoring water tables by blocking moorland drains (Wilson et al., 2010), which may promote Sphagnum growth and re-initiate peat accumulation (and presumably, net CO2 uptake), at a potential cost of increased methane emissions (Baird et al., 2009b). There are few pertinent data to quantify these effects (Basiliko et al., 2007; Bussell et al., 2010; Fenner et al., 2011; Urbanova et al., 2011), but the relationships in Fig. 3 could be used as a crude summary of the effect of water table on methane flux, if we assume that the long-term effect of water table manipulation is the same as the relationship observed in natural variations. This indicates an effect of +0.8 (±0.28 SE) nmol CH4 m−2 s−1 (or +0.4 g CH4 m−2 yr−1) per cm increase in water table. To offset this would require an increase in CO2 sequestration of 7.3 nmol CO2 m−2 s−1 (or 10.1 g CO2 m−2 yr−1) per cm increase in water table (assuming that a gramme of CH4 has the global warming potential of 25 grammes of CO2 over a 100-year time span). By comparison, the review of studies in the Netherlands, Germany, Sweden and France by Couwenberg et al. (2011) obtained a value of +1.7 g CH4 m−2 yr−1 per cm increase in water table, around four times larger than our value. However, their value applied only to sites with aerenchymatous vegetation and mean annual water tables <20 cm from the surface. Including all their data points would give a value more similar to ours, and whether the differences reflect real geographic variation, or merely sampling error in a variable parameter, is hard to discern. We note that there are several reasons why the effects of manipulated and natural variations in water table might be different, certainly in the short term, as the dynamics of the system are complex. Also, as Frolking et al. (2006) point out, the relative impacts of CO2 sequestration and CH4 emissions on radiative forcing depend largely on the time scale considered. As the time scale considered increases, the relative importance of CH4 emissions decreases, and the commonly used time horizon of 100 years is essentially arbitrary.
The analysis of this data set has demonstrated the potential and limitations of commonly measured environmental variables as predictors of soil CH4 fluxes. The observed variability in instantaneous fluxes will remain difficult to explain or predict whilst the explanatory variables are weak surrogates for the underlying driving variables. However, longer term and larger-scale averages are much better predicted by environmental variables, and notably by soil carbon stocks and measures of plant species composition. Given that these variables are often available in national vegetation and soil surveys, these could have considerable utility in estimating national-scale CH4 emissions from soils. Detailed vegetation characteristics are generally not represented in land surface models, but given an accurate simulation or prescription of soil carbon stock (or peat depth) and hydrology, these have suitable explanatory power for predicting CH4 fluxes.



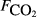 , μmol m−2 s−1), the first axis (Spp1, dimensionless) of an ordination of species cover, soil pH, soil bulk density (ρsoil, g dry mass cm−3), and the percentage cover of aerenchymatous species (Aer, %).
, μmol m−2 s−1), the first axis (Spp1, dimensionless) of an ordination of species cover, soil pH, soil bulk density (ρsoil, g dry mass cm−3), and the percentage cover of aerenchymatous species (Aer, %).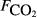 , μmol m−2 s−1), the first axis (Spp1, dimensionless) of an ordination of species cover, soil pH, soil bulk density (ρsoil, g dry mass cm−3), and the percentage cover of aerenchymatous species (Aer, %).
, μmol m−2 s−1), the first axis (Spp1, dimensionless) of an ordination of species cover, soil pH, soil bulk density (ρsoil, g dry mass cm−3), and the percentage cover of aerenchymatous species (Aer, %).
