Genetic maladaptation of coastal Douglas-fir seedlings to future climates
Abstract
Climates are expected to warm considerably over the next century, resulting in expectations that plant populations will not be adapted to future climates. We estimated the risk of maladaptation of current populations of coastal Douglas-fir (Pseudotsuga menziesii var. menziesii) to future climates as the proportion of nonoverlap between two normal distributions where the means and genetic variances of current and future populations are determined from genecological models derived from seedling common garden studies. The risk of maladaptation was large for most traits when compared with the risk associated with current transfers within seed zones, particularly for the more drastic climate change scenario. For example, the proportion of nonoverlap for a composite trait representing bud set, emergence, growth, and root : shoot ratio was as high as 0.90. We recommend augmenting within-population variation by mixing local populations with some proportion of populations from lower elevations and further south. Populations expected to be adapted to climates a century from now come from locations as far down in elevation as 450–1130 m and as far south in latitude as 1.8–4.9°.
Introduction
Plant populations may adjust to climate change by exhibiting phenotypic plasticity (i.e. altering their biochemistry, physiology, and development in response to environmental change), migrating to new habitats, or evolving in place (Davis & Shaw, 2001; Rehfeldt et al., 2001; Westfall & Millar, 2004). The relative roles of these processes will depend on the biological characteristics of the organism and the time frame considered. Most climate change predictions use a time horizon of 100 years or less – a time frame that provides little opportunity for forest trees to migrate or evolve in place. During the next century, there may be ample time for species with short generation times to respond via migration and in situ evolution – but this is not true for forest trees (Rehfeldt et al., 2001, 2002; Savolainen et al., 2004). The forests of the next century will largely consist of trees that are alive today. In coastal Douglas-fir (Pseudotsuga menziesii var. menziesii), for example, stand replacing disturbances typically occur at a frequency of 200 years or more, although they may become more frequent in the future (Bachelet et al., 2001; Westerling et al., 2006). The situation for plantation-grown Douglas-fir, however, is different. Because rotations typically range from 40 to 75 years (e.g. depending on ownership), most plantations will be replanted one or two times during the next 100 years. Furthermore, by using artificial reforestation, silviculturists have the opportunity to mimic long-term natural migration and evolution by planting species in new areas or by choosing new seed sources with adaptive characteristics chosen to match some presumed future climate (Ledig & Kitzmiller, 1992).
Genecological studies are valuable for helping us judge whether existing populations will be adapted to future climates. Genecology is the study of genetic variation in relation to the environment. The genecology of forest trees is typically studied by collecting wind-pollinated seeds from trees in natural stands, growing the progeny in a common garden test, then measuring adaptive traits such as survival, growth, cold hardiness, drought hardiness, and vegetative bud phenology (Campbell, 1979, 1986; Rehfeldt et al., 2001, 2002; St Clair et al., 2005). Models are then developed to predict population phenotypes from location (e.g. latitude, longitude, elevation) or climatic variables (e.g. St Clair et al., 2005). The goals of genecological studies are to identify climatic variables that exert strong selective pressures on natural populations, identify the traits that respond to the selective pressures, and develop models that can be used to predict the phenotype for a given location or climate. Once these models are developed, they can be used to study the potential effects of climate change (Rehfeldt et al., 2001, 2002).
Two kinds of approaches are typically used to study genecology: (1) long-term field tests in native environments (e.g. provenance tests or reciprocal transplant studies) and (2) seedling tests in controlled environments (e.g. controlled environmental chambers, greenhouses, or outdoor nurseries). The advantages and disadvantages of each approach were recently discussed by Howe et al. (2006). In a few species, provenance tests have been used to evaluate the effects of climate change (Schmidtling, 1994; Carter, 1996; Mátyás, 1996; Rehfeldt et al., 1999, 2002; Andalo et al., 2005), and this can be particularly informative when a large, diverse set of provenances has been tested in a wide variety of environments.
Long-term provenance tests of coastal Douglas-fir are being used to study climate change (M. U. Stoehr, http://www.for.gov.bc.ca/hre/forgen/coastal/douglas-fir.htm). In western North America, five provenance tests were planted between 1958 and 1974, each of which contains six to 77 provenances planted on three to 23 sites. Unfortunately, some of these tests suffer from low statistical precision and other limitations (Howe et al., 2006). Therefore, analyses of climate change in North America will also include data from a large series of provenance tests planted throughout Europe (Breidenstein et al., 1990; M. U. Stoehr; http://www.for.gov.bc.ca/hre/forgen/coastal/douglas-fir.htm).
In this paper, we describe an alternative approach that does not involve long-term field testing, and demonstrate this approach using a seedling common garden study of coastal Douglas-fir (St Clair et al., 2005). This approach focuses on (1) seedlings, the stage at which most natural selection occurs (Lawrence & Rediske, 1962; Campbell, 1979), (2) adaptive traits known to be under strong natural selection, and (3) nursery tests in which traits can be measured with little environmental error resulting in high heritabilities. We use a statistic called the relative risk of maladaptation (Campbell, 1986) to compare current populations of Douglas-fir with populations that are predicted to be well adapted to future climates. Relative risk, which quantifies the difference in adaptive phenotypes between two populations, is a function of the means of the two populations and their within-population genetic variation. We also make recommendations for choosing Douglas-fir seed sources in light of predicted climate change, and identify research gaps that limit our ability to predict how Douglas-fir populations will respond to climate change during this century.
We focus on Douglas-fir because it is one of the most economically and ecologically important trees in the world, and has been the focus of ecological genetics research for nearly 100 years (Howe et al., 2006). Douglas-fir grows on over 20 million ha of natural forests and plantations in the United States and Canada, and in extensive plantations in Europe, New Zealand, Australia, and Chile (Hermann & Lavender, 1999; Smith et al., 2001). Douglas-fir has one of the largest breeding programs in the world, with more than 4 million progeny from nearly 34 000 parents growing on almost 1000 test sites in western North America alone (Lipow et al., 2003). The forests of the Pacific Northwest, which are often dominated by Douglas-fir, have total (i.e. above- and belowground) carbon densities higher than any other terrestrial ecosystem (Birdsey, 1992; Smithwick et al., 2002). Furthermore, Pacific Northwest forests can store much more carbon than they currently do – perhaps an additional 338 Mg C ha−1 (Smithwick et al., 2002). Therefore, maintaining the adaptability and productivity of Douglas-fir forests is important for enhancing carbon sequestration, reducing atmospheric CO2, and mitigating the effects of climate change (Schulze et al., 2000; Harmon & Marks, 2002; Smithwick et al., 2002).
Materials and methods
Common garden procedures
This study used the same plant materials that were described by St Clair et al. (2005). Briefly, open-pollinated families (i.e. wind-pollinated seedlots from single trees) were collected from parents located in naturally regenerated stands throughout the range of Douglas-fir in western Oregon and Washington. At approximately one-quarter of the locations, two parents were sampled per location to estimate family-within-location variance. Progeny from the parents were grown for 2 years in raised beds in Corvallis, Oregon, using five-tree family row plots and four blocks. To evaluate a large number of parents, tests were established in three successive years (1994–1996) using different sets of families, but with a common set of families included in all 3 years to allow for adjustment of year effects. Growth, phenology, and biomass partitioning were measured on the progeny of 1256 parents from 985 locations as described by St Clair et al. (2005). Fall cold hardiness was measured on a subset of the progeny of 792 parents from 666 locations as described in St Clair (2006).
Traits considered in this study include bud set (days since December 31), bud burst (days since December 31), rate of emergence (cumulative number of seedlings emerged per day on a probit scale), total weight (dry weight after 2 years in grams), root : shoot ratio (ratio of dry weights after 2 years), taper (ratio of second-year diameter to second-year height in millimeters per centimeter), and fall cold damage (percent tissue damage). We also analyzed two composite traits derived from previous canonical correlation analyses of seedling traits vs. environmental variables (St Clair et al., 2005). These traits, referred to as trait 1 and trait 2, are the first and second canonical variates. They accounted for 30% and 15%, respectively, of the total variation among all traits, and are uncorrelated with each other. Higher values of trait 1 are associated with increased vigor (i.e. later bud set, faster emergence, larger size, and greater partitioning to shoot vs. roots). Trait 1 is most strongly correlated with temperature, particularly minimum temperatures in the late fall and winter months. Higher values of trait 2 are associated with earlier bud burst and greater taper. Trait 2 is most strongly correlated with summer aridity (i.e. lower summer precipitation and higher summer temperature).
Genecological models
We used genecological models to describe the variation we observed in the common garden experiment. That is, we derived models that predict seed source phenotypes (i.e. location means for the seedling quantitative traits) from variables that reflect the environmental characteristics of the seed source locations. General procedures for developing genecological models have been described by St Clair et al. (2005). To study climate change, we derived genecological models from climatic variables for which we have future predictions, namely precipitation and temperature. Family least-square means for the quantitative traits were calculated using sas proc glm, and the resulting family means were used to develop the genecological models using multiple linear regression and sas proc reg (SAS Institute Inc., 1999). We did not include new climatic variables in the model, however, unless they increased the R2 by 1% or more. It is unlikely that our models are overparameterized because of the large number of locations (666 or 985) and the small number of independent variables in the models (i.e. two to four). According to the AIC criterion, we could have used a greater number of independent variables, often twice as many as we used (i.e. six to 10). Although we tested quadratic and interaction terms, they were omitted because they explained little of the trait variation. The climatic data were obtained from GIS coverages generated from PRISM (Parameter-Elevation Regressions on Independent Slopes Model), a statistical–geographical model in which climate parameters are predicted for 4 km × 4 km grid cells using localized regression equations of climate as a function of elevation and topographical position (Daly et al., 1994; see http://www.ocs.orst.edu/prism/prism_new.html). Climate values at specific parent tree locations were determined as distance-weighted averages of the four nearest grid cells using the LATTICESPOT function with the bilinear interpolation option in ARC/INFO. Climate data are based on the averages for the years 1961–1990.
Variance components
We analyzed seedling plot means to estimate variance components for family-within-location (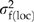
) and plot error (
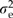) using restricted maximum likelihood (sas proc mixed). Analyses of family means were used to estimate the location variance components (
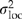), and regression analyses were used to partition 
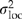into two components: one that describes variation explained by the regression (
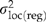) and one that describes deviations from the model (
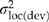). A ratio of location variance components (
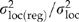) was used to judge the success of the model. Additive genetic variation within locations (
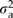) was estimated as 
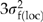, which assumes that open-pollinated progeny are a combination of half-sibs, full-sibs, and selfs (i.e. average coefficient of relationship = 1/3; Campbell, 1979). Qst, which describes the proportion of total genetic variation that occurs among locations, was calculated as 
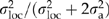(Spitze, 1993). We also calculated Qst(reg) and Qst(dev) by substituting 
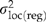and 
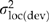for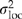 
in numerator of the Qst equation. These latter statistics are also useful for judging the success of the genecological model.
Climate change predictions
Climate change predictions were determined from three widely accepted general circulation models (GCMs), each with two different scenarios of future greenhouse gas emissions (Price et al., 2004). These GCMs were developed by the Canadian Climate Centre (CGCM2), the Hadley Centre of the UK Meteorological Office (HADCM3), and the Australian Climate Center (CSIRO). The emissions scenarios included greenhouse gas increases that were moderately high (A2) and moderately low (B2), and were taken from the range of scenarios considered by the Intergovernmental Panel on Climate Change (Nakicenovic et al., 2000). From GIS coverages of the six climate change scenarios, we determined the average change in monthly temperatures (minimum and maximum) and precipitation for western Oregon and Washington. We used regional averages because the climate change predictions varied little across the region. We then calculated seasonal values for climate change for winter (December, January, and February), spring (March, April, May), summer (June, July, August), and fall (September, October, November). Future temperatures were calculated by adding the climate change predictions to the current temperatures derived from PRISM, and an analogous approach was used for precipitation. These future values were then used in our genecological models to predict the corresponding quantitative trait values for our seed source locations. These trait values represent the mean phenotypes of populations that are presumed to be well adapted to the future climates.
Calculating relative risk
To judge whether current populations will be adapted to future climates, we used the relative risk index proposed by Campbell (1986) for seed transfer. For a quantitative trait, relative risk from climate change is the proportion of nonoverlap between two normal distributions – one distribution representing the current population and the other representing a population that is predicted to be well adapted to the future climate. The means of the two populations (i.e. current and future) were determined from the genecological models, whereas their common variance was set equal to the additive genetic variance within populations (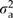
). When relative risk is used, one generally assumes that the current population is optimally adapted to the local environment, but this may not be the case. Empirical studies, for example, often suggest that populations would achieve greater stand-level growth in either warmer or colder environments (Schmidtling, 1994; Rehfeldt et al., 1999, 2002; Andalo et al., 2005), but these studies should be interpreted with caution because short-term growth may be imperfectly correlated with long-term fitness. In any case, relative risk is useful as long as the current populations are ‘well adapted’ to their local environments. In this study, current climates are represented by the climates the populations experienced from 1961 to 1990.
We present results for two climate change scenarios, CGCM2 B2 and CSIRO A2, which represent extremes in predicted warming for the Pacific Northwest. For each seed source location in western Oregon and Washington, we used our genecological models (i.e. regression equations) to predict the mean values for each trait in the current environment and in the future predicted environment. These two trait means, plus our pooled estimate of within-population genetic variation, were then used to calculate relative risk for each location. These estimates of risk were then averaged over all locations. The estimated risks vary slightly over the study area due to differences in absolute amounts of precipitation. Because the climate change models predict absolute changes in temperature, but proportional changes in precipitation, predicted increases in temperature are uniform throughout our study area, but changes in the amount of precipitation are not. Nonetheless, among-location variation in estimated risk is small (e.g. the minimum and maximum values for trait 1 are 0.47 and 0.51 for the CGCM2 B2 model). Therefore, our average risk values across the entire region are considered our best estimates of risk for each location.
Evaluating relative risk
We judged the confidence, magnitude, and implications of our risk values using various approaches. First, we judged the success of our models by evaluating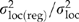 
, Qst(reg), and Qst(dev) (described above). Second, we used the average risk among populations within seed zones as a baseline – (i.e. as a value representing an acceptable level of risk). A seed zone is a geographic area within which seed can be moved (i.e. collected and replanted) with the expectation that the resulting stands will be well adapted. Seed zone boundaries are widely accepted for ensuring productive and healthy forests, and have proven to be empirically valid. We used the most recent seed zones for Douglas-fir in western Oregon and Washington (Randall, 1996; Randall & Berrang, 2002). These 123 seed zones are based on both geographic and elevational delineations. The mean risk for a seed zone was calculated as the mean of all possible within-zone transfers between the seed source locations we sampled. These values were then averaged over all seed zones. The maximum risk of transfer within seed zones was calculated as the maximum risk within a seed zone averaged over all seed zones. Our estimates of maximum risk may be less than the true maximum because we did not always sample at the geographic and elevational boundaries of the seed zones.
For each location, we also determined how far one would need to go in elevation and latitude to find current populations that are adapted to the future climate at that location. This information is useful to managers for determining general guidelines for population movement in the face of climate change. We first determined the values for trait 1, trait 2, and cold damage that correspond to current and future climates using the climate change predictions in Table 1 and the regression equations in Table 2. We then determined the relationships between each trait and elevation and latitude (longitude was not strongly related to any of the traits independent of elevation). We considered polynomial terms in the models, but they increased the R2 little and, thus, were not included in the final models. Using these relationships, we determined how far in elevation or latitude one would need to go to correspond to the differences in trait values. Using this approach, the reported differences in elevation and latitude correspond to the predicted differences between current and future climates shown in Table 1.
| CGCM2 A2 | CGCM2 B2 | CSIRO A2 | CSIRO B2 | HADCM3 A2 | HADCM3 B2 | |
|---|---|---|---|---|---|---|
| Minimum temperature (°C increase) | ||||||
| Winter | 3.5 | 2.5 | 6.2 | 4.9 | 2.6 | 1.7 |
| Spring | 3.2 | 2.2 | 3.8 | 2.3 | 2.9 | 2.2 |
| Summer | 3.3 | 2.3 | 5.0 | 4.2 | 5.3 | 3.7 |
| Fall | 3.2 | 2.1 | 4.7 | 3.5 | 4.0 | 3.0 |
| Maximum temperature (°C increase) | ||||||
| Winter | 4.2 | 3.2 | 3.9 | 3.3 | 2.8 | 2.2 |
| Spring | 3.7 | 2.6 | 2.2 | 1.4 | 3.4 | 3.1 |
| Summer | 3.6 | 2.7 | 4.8 | 4.0 | 7.5 | 5.8 |
| Fall | 3.5 | 2.7 | 4.8 | 3.6 | 5.2 | 3.8 |
| Precipitation (proportion) | ||||||
| Winter | 1.39 | 1.23 | 1.21 | 1.05 | 1.06 | 0.93 |
| Spring | 0.99 | 0.94 | 1.03 | 1.06 | 0.93 | 0.87 |
| Summer | 0.91 | 0.90 | 0.64 | 0.65 | 0.45 | 0.44 |
| Fall | 1.17 | 1.07 | 0.82 | 0.89 | 0.80 | 0.86 |
| Trait | R 2 | Model* |
|---|---|---|
| Trait 1† | 0.53 | Y=− 0.0126 + 0.580 WINMNT − 0.532 FALMNT + 0.262 SUMMNT + 0.00369 SUMPRE |
| Trait 2‡ | 0.40 | Y= 3.182 + 0.00578 SUMPRE − 0.300 SUMMXT + 0.333 SPRMXT − 0.201 WINMXT |
| Fall cold damage (%) | 0.58 | Y= 36.4 + 5.24 WINMXT − 2.87 FALMXT − 0.155 SUMPRE + 0.0387 SPRPRE |
| Bud set (days) | 0.46 | Y= 261 + 1.494 WINMNT + 0.787 SPRMXT + 0.0235 SUMPRE |
| Emergence (probits day−1) | 0.30 | Y= 0.02880–0.00147 SPRMNT–0.000974 WINMNT + 0.00169 FALMNT + 0.000548 SUMMXT |
| Total weight (g) | 0.15 | Y= 6.284 + 0.305 WINMNT + 0.280 SUMMXT |
| Root : shoot ratio | 0.12 | Y= 0.435 − 0.00456 WINMNT − 0.00439 SUMMNT |
| Bud burst (days) | 0.24 | Y= 112 − 0.621 SUMMXT + 0.0289 SUMPRE + 0.420 SPRMXT |
| Taper (mm cm−1) | 0.19 | Y= 0.202 − 0.000170 SUMPRE + 0.0000254 SPRPRE − 0.00203 SPRMNT |
- * In the climatic variable names, SPR, SUM, FAL, and WIN denote spring, summer, fall, and winter, whereas MNT, MXT, and PRE denote minimum annual temperature, maximum annual temperature, and precipitation. Climatic variables in the regression equations are ordered according to their correlations with the predicted trait (i.e. strongest to weakest correlations). In each case, a single environmental variable explains most of the trait variation. All models are significant at the P < 0.01 level of probability.
- † Trait 1 refers to the first canonical variate from previous canonical correlation analysis (St Clair et al., 2005). Higher values are associated with later bud set, faster emergence, larger size, and greater partitioning to shoot vs. roots.
- ‡ Trait 2 refers to the second canonical variate from previous canonical correlation analysis (St Clair et al., 2005). Higher values are associated with earlier bud burst and greater taper.
Results
Temperatures in western Oregon and Washington are projected to increase about 3.5 °C between 1961–1990 and 2070–2099 when averaged over all six climate change scenarios (Table 1). Differences in predicted climate change were found between the three different GCMs and the two greenhouse gas emissions scenarios. Warming for the moderately high emissions scenario (A2) was about 1 °C greater than for the moderately low emissions scenario (B2) (4.1 °C compared with 3.0 °C averaged over GCMs). Furthermore, warming varies about 1 °C among the GCMs. When averaged over the two emission scenarios, warming is projected to be 3.0 °C for the CGCM2 model, 3.9 °C for the CSIRO model, and 3.7 °C for the HADCM3 model. Increases in winter minimum temperature for the two scenarios chosen for further analysis are projected to be 2.5 °C for CGCM2 B2 and 6.2 °C for CSIRO A2. Precipitation is expected to increase about 14% in the winter, but will decrease 33% in the summer when averaged over all six climate change scenarios. Because the Pacific Northwest has little summer rainfall, a decrease in the summer precipitation will have little effect on annual precipitation, but combined with increasing summer temperatures, summer drought should be more severe.
As judged by the regression models in Table 2, each of the traits was significantly related to climate (P < 0.01). As expected from previous analyses, fall cold damage, bud set, emergence, growth and root : shoot ratio, and the composite trait 1 are predominately related to cool-season temperatures, whereas bud burst, taper, and the composite trait 2 are predominately related to summer precipitation and summer maximum temperature (Table 6 in St Clair et al., 2005; Table 4 in St Clair, 2006). The success of the genecological models can be judged by the R2 values in Table 2 and by the ratio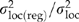 
in Table 3. The R2 values describe how well the model predicts family means, and thus, is strongly influenced by the amount of sampling variation associated with within-population genetic variation (i.e. variation that is not associated with macroclimate). In contrast, 
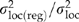reflects how well the models predict location means. Based on both measures, the traits can be divided into two groups – a group that is strongly related to climate (trait 1, trait 2, cold damage, and bud set) and a group that is moderately related to climate (emergence, total weight, root : shoot ratio, bud burst, and taper). For the former traits, our models were particularly effective, with 
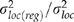ranging from 0.66 to 0.82 (Table 3).
| Trait | Current trait mean | Current risk in seedzones | Trait means expected tobe adapted to futureclimates | Risk in future climates | |||
|---|---|---|---|---|---|---|---|
| Mean | Maximum | CGCM2 B2 | CSIRO A2 | CGCM2 B2 | CSIRO A2 | ||
| Trait 1 | 0.00 | 0.20 | 0.43 | 0.90 | 2.24 | 0.50 | 0.90 |
| Trait 2 | 0.00 | 0.12 | 0.27 | − 0.64 | − 1.74 | 0.30 | 0.70 |
| Fall cold damage (%) | 25.5 | 0.22 | 0.45 | 34.6 | 38.8 | 0.51 | 0.67 |
| Bud set (days) | 273.6 | 0.15 | 0.32 | 279.3 | 283.6 | 0.36 | 0.59 |
| Emergence (probits day−1) | 0.0466 | 0.11 | 0.25 | 0.0458 | 0.0454 | 0.08 | 0.14 |
| Total weight (g) | 12.7 | 0.07 | 0.16 | 14.3 | 15.9 | 0.20 | 0.40 |
| Root : shoot ratio | 0.397 | 0.09 | 0.20 | 0.375 | 0.347 | 0.24 | 0.53 |
| Bud burst (days) | 106.3 | 0.09 | 0.21 | 105.4 | 103.0 | 0.09 | 0.31 |
| Taper (mm cm−1) | 0.188 | 0.14 | 0.29 | 0.184 | 0.187 | 0.12 | 0.10 |
- CGCM2 B2 is the Canadian Climate Centre moderately low emissions scenario, whereas CSIRO A2 is the Australian Climate Center moderately high emissions scenario (Nakicenovic et al., 2000).
| Trait | Plot variation | Withinlocationvariation | Among location variation | Proportion of totalgenetic variation thatoccurs among locations | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
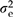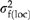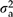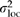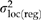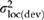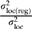Q st | Q st(reg) | Q st(dev) | |
| Trait 1* | 0.48 | 0.15 | 0.45 | 0.79 | 0.56 | 0.23 | 0.71 | 0.46 | 0.33 | 0.14 |
| Trait 2† | 0.81 | 0.23 | 0.69 | 0.64 | 0.42 | 0.22 | 0.66 | 0.32 | 0.21 | 0.11 |
| Fall cold damage (%) | 168.93 | 16.33 | 48.99 | 194.38 | 145.74 | 48.64 | 0.75 | 0.67 | 0.50 | 0.17 |
| Bud set (days) | 40.30 | 11.95 | 35.86 | 30.25 | 24.76 | 5.49 | 0.82 | 0.29 | 0.24 | 0.05 |
| Emergence (probits day−1× 10−5) | 0.52 | 0.36 | 1.09 | 0.83 | 0.39 | 0.45 | 0.46 | 0.28 | 0.13 | 0.15 |
| Total weight (g) | 10.05 | 3.11 | 9.33 | 2.61 | 1.25 | 1.36 | 0.48 | 0.13 | 0.06 | 0.07 |
| Root : shoot ratio (× 10−4) | 52.35 | 4.08 | 12.24 | 5.55 | 2.57 | 2.98 | 0.46 | 0.18 | 0.09 | 0.10 |
| Bud burst (days) | 11.31 | 5.69 | 17.07 | 9.24 | 3.95 | 5.29 | 0.43 | 0.21 | 0.09 | 0.12 |
| Taper (mm cm−1× 10−4) | 4.47 | 0.38 | 1.14 | 0.93 | 0.45 | 0.48 | 0.48 | 0.30 | 0.15 | 0.16 |
- * Trait 1 refers to the first canonical variate from previous canonical correlation analysis (St Clair et al., 2005). Higher values are associated with later bud set, faster emergence, larger size, and greater partitioning to shoot vs. roots.
- † Trait 2 refers to the second canonical variate from previous canonical correlation analysis (St Clair et al., 2005). Higher values are associated with earlier bud burst and greater taper.
Strong natural selection is suggested when Qst is much higher than Fst (reviewed in Howe et al., 2003). Fst is analogous to Qst, but measures the proportion of total variation for neutral genetic markers that is attributed to differences among populations. The traits we measured had Qst values that were 1.8–9.4 times the Fst values reported for allozyme markers in coastal Douglas-fir (= 0.071; Li & Adams, 1989) (Table 3). Furthermore, the Qst for cold damage was particularly high (0.67), which is consistent with results from P. menziesii var. glauca (Qst= 0.47) (reported in Howe et al., 2003 based on data from Rehfeldt, 1978). Although Qst(reg) (i.e. the Qst associated with the regression) was also high for trait 1, trait 2, cold damage, and bud set (0.21–0.50), the variation not explained by the regression yielded Qst(dev) values as high as 0.17 for these traits. This unexplained variation includes true error because our climatic (independent) variables were not measured without error, but were predicted using the PRISM climate model. This unexplained variation may also include real location variation that is not associated with macroclimate, but this variation should be small (i.e. once true error is considered), particularly for trait 1, trait 2, cold damage, and bud set.
Risks of maladaptation from climate change depend upon the climate change scenario, but for all four focal traits (i.e. trait 1, trait 2, cold damage, and bud set), the risks of maladaptation were substantially larger than the corresponding average risks within seed zones. For example, the risk for trait 1 is 0.50 for climate scenario CGCM2 B2 and 0.90 for climate scenario CSIRO A2, compared with a risk of 0.20 for the average risk within a seed zone, and 0.42 for the maximum risk within a seed zone (Table 4; Fig. 1).
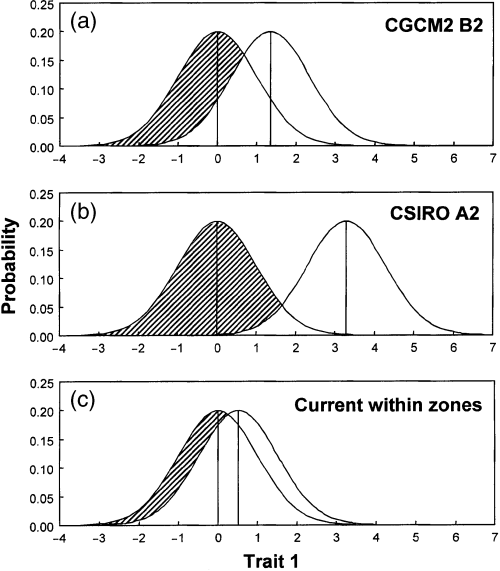
Relative risk of maladaptation associated with current populations in future (2077–2099) climates for trait 1. In each panel, the distribution on the left represents the current population, whereas the distribution on the right represents the population predicted to be well adapted to the future climate. The hatched portion of the left distribution represents the relative risk of maladaptation. (a) Risk assuming a conservative amount of climate change (CGCM2 B2 climate model). (b) Risk assuming a less conservative amount of climate change (CSIRO A2 climate model). (c) The average risk associated with moving populations within current Oregon and Washington seed zones is shown for comparison.
Where can we find populations that are well adapted to future climates? Trait 1 is predominately correlated with elevation (r=− 0.74). The regression of trait 1 on elevation indicates that one would need to go down in elevation 460 m to find populations that are adapted to future climates given the CGCM2 B2 climate change scenario, and 1130 m to find populations that are adapted to future climates given the CSIRO A2 scenario (Fig. 2a). The changes in climate associated with these elevational differences are given in Table 1 (460 m = CGCM2 B2 column and 1130 m = CSIRO A2 column). Trait 2 is predominately correlated with latitude (r=− 0.61). The regression of trait 2 on latitude indicates that one would need to go south in latitude 1.8° (∼200 km) to find populations that are adapted to future climates given the CGCM2 B2 climate change scenario, and 4.9° south in latitude (∼540 km) to find populations that are adapted to future climates given the CSIRO A2 scenario (Fig. 2b). The changes in climate associated with these latitudinal differences are also given in Table 1 (1.8° latitude = CGCM2 B2 column and 4.9° latitude = CSIRO A2 column). Fall cold damage is correlated with both elevation (r=− 0.35) and latitude (r=− 0.49). Thus, to find populations that are adapted to future climates, one could move down in elevation, south in latitude, or some combination of the two (Fig. 3). At a constant elevation, one would need to go south in latitude 1.8–2.5° (∼200–275 km), depending on the climate change scenario. At constant latitude, one would need to go down in elevation 450–660 m, depending on the climate change scenario. Again, the changes in climate associated with these geographical differences are given in Table 1.
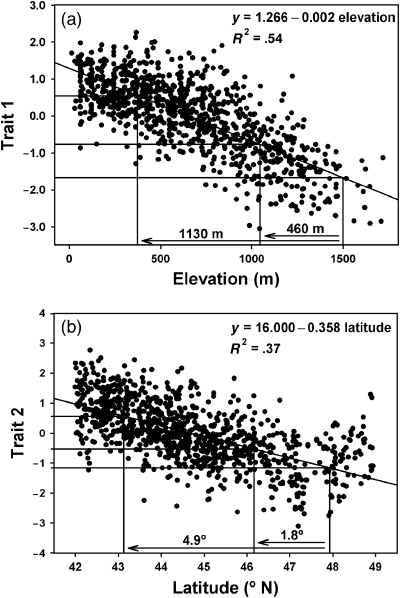
Regressions of (a) trait 1 on elevation and (b) trait 2 on latitude showing the implications of two climate change scenarios. The arrows indicate decreases in elevation (trait 1) or latitude (trait 2) between current populations and populations predicted to be adapted to future climates. The smaller decreases in elevation and latitude were estimated based on the CGCM2 B2 scenario, and the larger decreases were estimated based on the CSIRO A2 scenario.
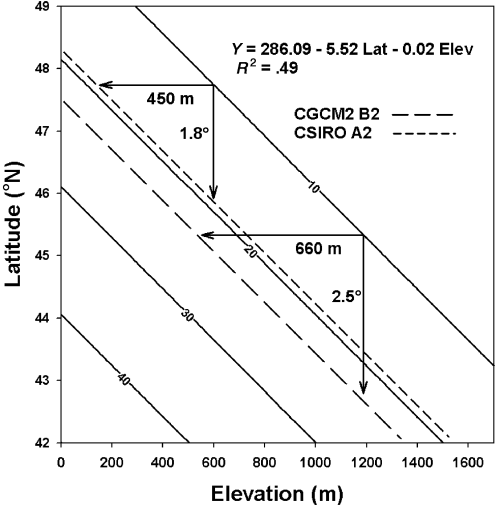
Predicted levels of fall cold damage for specific combinations of latitude and elevation. The solid diagonal contour lines indicate cold damage in percent. The implications of two climate change scenarios are shown for populations currently inhabiting locations where the predicted cold damage is 10%. The arrows indicate differences between current populations and populations predicted to be adapted to future climates – either differences in elevation for a constant latitude, or differences in latitude for a constant elevation. For the CGCM2 B2 scenario, populations 450 m lower in elevation or 1.8° farther south are expected to be well adapted to the future climate (see the arrows pointing to the dashed line showing the locations of adapted populations). For the CSIRO A2 scenario, populations 660 m lower in elevation or 2.5° farther south are expected to be well adapted to the future climate.
Discussion
Two questions are immediately important in judging whether populations of forest trees will be genetically adapted to future climates. The first question is whether current populations are adapted to the climates they will experience during their lifetimes. This is particularly important for forest trees because many species live hundreds of years, and appreciable climate change is expected during their lifetimes. The second question is whether current populations can regenerate new stands that will be even better adapted to future climates – that is, how much genetic change can occur from one generation to the next? The answers to these questions will largely determine the success of natural populations of forest trees during the next 100 years. A third less immediate question is ‘what is the long-term evolutionary potential of forest tree species (e.g. over tens of generations)’? This latter question is much harder to answer because of large uncertainties about the extent of long-term climate change, as well as insufficient information on components of fitness, natural selection intensities, and other quantitative genetic parameters in natural populations of forest trees.
Are current populations adapted to future climates?
We used average and maximum risks of seed transfer within current seed zones as benchmarks for comparing the risks associated with climate change. Seed zones are used to minimize the risk of maladaptation in planting programs, and have proven to be effective based on practical experience. Based on these comparisons, current populations are expected to be poorly adapted to future climates (Table 4; Fig. 1). For the more conservative climate change scenario (CGCM2 B2), risk from climate change is at least two times the average seed zone risk for trait 1, trait 2, cold damage, bud set, total weight, and root : shoot ratio. For the less conservative scenario (CSIRO A2), the risk from climate change is more than five times the average seed zone risk for trait 2, total weight, and root : shoot ratio. Although forest trees have considerable within population variation, differences in trait means between current populations and populations expected to be well adapted to future climates are large enough that the degree of population overlap may be small (e.g. 0.10 for trait 1; Table 4).
Trait 1 and cold damage had the largest risks for transfers within current seed zones (0.20–0.22) and, except for trait 2 under the CSIRO A2 scenario, the largest risks for climate change (0.51–0.90) (Table 4). As expected, these traits also had the largest amounts of variation among populations (i.e. Qst values; Table 3). Risk is a function of differences among populations, and differences among populations are larger for these traits than for other traits. Thus, these traits seem to be under strong natural selection and deserve the most attention when considering risks from seed movement or climate change.
Our results do not explain how current populations are genetically maladapted to future climates, but two possibilities are likely. First, decreased summer moisture will lead to increased drought stress, and increased summer temperatures will exacerbate this effect. Furthermore, genecological patterns of variation suggest that drought hardiness is important. In coastal Douglas-fir, drought hardiness increases from the northern, mesic areas along the coast to the hot, dry areas of southwestern Oregon and California (Pharis & Ferrell, 1966; Heiner & Lavender, 1972; Kung & Wright, 1972; Larsen, 1981), and a similar pattern is associated with a large west to east decrease in precipitation and humidity (Pharis & Ferrell, 1966; Sorensen, 1979). In general, populations that are more drought hardy tend to flush earlier, set bud earlier, and have less annual height growth, which presumably results in seedlings that are better able to complete their annual growth before the onset of drought in summer (Lavender et al., 1968; Heiner & Lavender, 1972; Lavender & Overton, 1972; Kaya et al., 1994). Based on these observations, we do not expect current populations to have optimal drought hardiness in the future.
Second, increased temperatures throughout the fall, winter, and spring may extend the growing season in a way that lowers the fitness of current populations. At the genetic level, there is an important tradeoff between adaptation to cold and annual growth (Saxe et al., 2001; Howe et al., 2003). Seedlings that grow late into the fall are susceptible to early fall frosts, yet trees that stop growing too early are at a competitive disadvantage. Similarly, seedlings that break bud too early in the spring are susceptible to late spring frosts, yet trees that break bud too late may not be able to complete their seasonal growth before the onset of summer drought (discussed above). The existence of these tradeoffs suggests that the direction of change is unimportant when evaluating maladaptation. If a single phenotype could be optimally adapted to all climates, then pronounced local adaptation would not exist (e.g. all populations would exhibit a high degree of cold hardiness). For older trees, the link between the annual growth cycle and adaptation to cold is less clear (Howe et al., 2003), but in Douglas-fir and other conifers, provenances from stressful environments typically grow slower than provenances from mild climates with plenty of moisture (Silen & Mandel, 1983; Monserud & Rehfeldt, 1990; Hernandez et al., 1993; Chuine et al., 2006). In short, the annual growth cycles of current populations are under strong genetic control, and will not be closely synchronized to the annual climatic cycle in the future.
Despite these well-proven relationships, future maladaptation may result from factors other than temperature and precipitation per se. Warmer and drier climates may be associated with changes in fires, storms, snow, the severity of extreme events, and the fitness of other organisms (Saxe et al., 2001), and these selective forces may have contributed to the genecological patterns we observed. Our approach simply uses genetic differences among populations to infer natural selection to particular climatic regimes, without invoking cause and effect. Furthermore, CO2 levels are predicted to increase, but we do not know whether this will affect adaptation to future climates. Therefore, our results assume that future selection regimes will be similar to past selection regimes, despite changes in CO2 concentration.
Our genecological approach has three caveats. First, because we measured seedlings, we do not know whether older (e.g. existing) stands will have the same risks as we predict for seedlings. Nonetheless, most natural selection occurs at the germinant or seedling stage (Lawrence & Rediske, 1962; Campbell, 1979) and our data strongly suggest that the seedlings produced by existing stands may be substantially maladapted to future climates. Second, we do not know what specific physiological and developmental consequences will result from the relative risk values we measured. Third, we did not measure the seedlings in multiple native environments, so we do not know the phenotypic plasticity of the populations we studied. However, the mere existence of climate-associated patterns of genetic variation suggests that long-term adaptation to future climates is not possible via phenotypic plasticity alone. The strength of the genecological approach is that it allows us to predict how populations will perform in complex abiotic and biotic environments without needing to fully characterize or replicate these environments.
Can current populations produce new stands that are adapted to future climates?
In the absence of selection and gene flow, the seedlings derived from current stands will exhibit the same traits and degree of maladaptation as their parents. However, if selection is intense at the seedling stage, the regenerated stands could be better adapted than their parents. The highest selection intensities occur at the germinant or seedling stage, particularly for naturally regenerated populations (Lawrence & Rediske, 1962). A mature Douglas-fir tree, for example, may have survived from more than 2000 established seedlings (Campbell, 1979). Therefore, there is ample opportunity for population means to change within a single generation, even for moderately heritable traits such as the traits we measured (Howe et al., 2003). Nonetheless, problems can be expected under the more extreme CSIRO A2 scenario because (in the worst-case scenario) population overlap between the current population and the adapted future population (i.e. 1 − risk) is only 10% for trait 1. The ecological consequences will also be more severe if natural selection occurs much later in mature stands, which may be likely if most natural selection occurs in response to rare, extreme events (Gutschick & BassiriRad, 2003), or if poor performance results from the slow accumulation of damage. For example, observations from off-site plantings and provenance trials in the Pacific Northwest indicate that the consequences of poor adaptation may not become evident until later ages (Silen, 1963; Silen & Olsen, 1992).
Gene flow will also affect whether the new stands will be better adapted than their parents. In conifers such as Douglas-fir, most gene flow occurs via pollen, and substantial amounts of long-distance, pollen-mediated gene flow (e.g. > 500 m) are not uncommon (Hamrick & Nason, 2000). Furthermore, even low levels of gene flow can have substantial impacts on evolutionary change (Morjan & Rieseberg, 2004). Unfortunately, long-distance gene flow is notoriously difficult to measure and may be biased against gene flow among climatically diverse populations. For example, differences in flowering phenology substantially inhibit gene flow in Douglas-fir (Slavov et al., 2005) and there is a strong relationship between the timing of flowering and elevation in natural populations of Douglas-fir (Silen, 1962). Nonetheless, pollen flow among climatically diverse populations may contribute to the adaptive genetic variation available to regenerating stands of trees. Our analyses, however, show that gene flow would need to occur across very large differences in elevation (450–1130 m) or latitude (1.8–4.9°) to contribute alleles from populations that are well adapted to future climates (2, 3).
What is the long term evolutionary potential of forest trees?
The rate of evolutionary change depends on the additive genetic variation in a population, gene flow, heritability, selection intensity, and generation interval. The longevity of Douglas-fir may be particularly important in preventing populations from adapting to future climates. Slow generation turnover was largely responsible for slow genetic changes in response to climate change in a simulation of Pinus sylvestris (Savolainen et al., 2004). The number of generations required for populations to evolve to new optima for future climates may be considerable. Rehfeldt et al. (2001) estimated that as many as 12 generations and 1200 years would be required for Pinus contorta populations in southern British Columbia, and Rehfeldt et al. (2002) estimated that up to 12 generations and more than 1500 years would be required for Pinus sylvestris populations in Eurasia. In short, many centuries may be required for populations to become adapted to climates that are expected within the next century. Thus, forest trees are expected to exhibit considerable adaptational lag, resulting in populations that are maladapted to their environments and susceptible to population extirpation.
What should be done?
We conclude that human intervention will be required to ensure productive and adapted Douglas-fir forests in the face of climate change. Ledig & Kitzmiller (1992), for example, recommended moving populations from south to north or from lower to higher elevations; planting a more diverse array of genotypes by deploying mixtures of seed sources; using higher planting densities; and breeding for broadly adapted genotypes (i.e. enhancing phenotypic plasticity). Our results suggest that populations should be moved 450–1130 m higher in elevation, and 1.8–4.9° higher in latitude (∼200–540 km northward) to match climates expected by the end of the 21st century, depending on the pace of climate change (Table 1; 2, 3). But what is the appropriate climate for which to select – the climate of the next decade or the next century? Should we be more concerned about adaptation of seedlings and saplings or longer term adaptation of mature trees? And which is the most likely future climate scenario? One way to manage uncertainty is to increase within-stand diversity by planting mixtures of local seed sources and seed sources from lower elevations and farther south. This strategy may be combined with higher planting densities and increased thinning to allow for some natural and artificial selection within stands.
Presently, much of the Douglas-fir planting stock used in reforestation comes from tree improvement programs, particularly for low elevation sites. Because parents in tree improvement programs come from a wide geographic area, planting stock from tree improvement programs may be more diverse than seedlings in naturally regenerated stands (Adams et al., 1998) or from seed collected from a limited geographic area. Thus, seed from breeding programs may be useful for buffering against an uncertain future climate. Selection for broadly adapted genotypes could also contribute to more stable populations across a range of possible future climates, but the feasibility of this approach has not been proven.
Gene conservation approaches need to be redesigned to address climate change. The genecological structure of Douglas-fir has been partly maintained by the large number of seed zones and breeding zones in the Pacific Northwest. Moving populations among zones, however, will begin to erode that structure. Currently, Douglas-fir genetic resources are well-protected both in ex situ collections (Lipow et al., 2003) and in situ reserves (Lipow et al., 2004). As climates change, however, the in situ reserves will become increasingly maladapted. Pollen flow from adjacent planted forests should contribute genetic diversity to in situ reserves, and possibly promote the evolutionary potential for gene conservation populations to become adapted to future climates.
Research needs
Our approach for judging the effects of climate change should be particularly useful for species that lack suitable long-term provenance tests, but questions remain, including (1) what is the relationship between risk measured in seedling tests and long-term field performance? and (2) how are patterns of genecological variation influenced by the temperature environment in which the seeds were produced (Saxe et al., 2001)? This is important because open-pollinated seeds are collected from parents in natural stands that are exposed to the same temperature differences that are included in our genecological models.
A direct approach for judging the effects of climate change is to evaluate long-term growth in provenance tests. Optimally, these tests would include a large and diverse collection of seed sources and many test sites distributed across a diverse set of environments (including ones that mimic a range of climate change scenarios). These kinds of tests provide strong empirical tests of climate change scenarios, but are rare. Most species cannot be studied using this approach because suitable provenance tests do not exist and are unlikely to be established in the near future. Although many trees and shrubs lack provenance tests (i.e. because they are economically unimportant), they may play important ecological roles. Another drawback to provenance tests is that sexual reproduction has been largely ignored. This is because the tests were often too young or stand structure was not conducive to flowering and seed production. In contrast, flowering and seed production could be readily studied in existing seed orchards, which contain trees that were established far from their source locations. Furthermore, it would be enlightening to compare seed stratification, germination, and seedling establishment of a large number of seed sources in an environmentally diverse collection of native stands.
Alternatives to long-term provenance tests are needed because analysis of ecosystem responses will require information on a very large number of species. This is because genetic adaptation to future climates will vary by species. Some species – the adaptive specialists – may be particularly prone to climate-induced maladaptation, whereas other species – the adaptive generalists – may be particularly resilient. Douglas-fir and lodgepole pine are considered specialists because genecological patterns of variation are pronounced, but species such as western white pine and western redcedar are considered generalists because geographic patterns of genetic variation are weak (Rehfeldt, 1994). These differences also point to the need to better understand how phenotypic plasticity will contribute to future adaptation, and the influence of genetic variation on phenotypic plasticity.
The seedling genecological approach can be used to study the effects of climate change quickly and cheaply, but cannot be used to predict the actual physiological and developmental consequences of climate change because relative risk values have never been calibrated empirically. We use the average risk within seed zones as a baseline with which to judge risks associated with climate change, and this approach can be adopted for species for which seed zones have been carefully designed and evaluated via practical experience (i.e. via large-scale planting programs, which has been the case for Douglas-fir). Therefore, it would be particularly desirable to calibrate relative risk values against results from long-term provenance tests. The best way to do this would be to conduct retrospective seedling tests that are directly comparable to existing provenance tests. Existing provenance tests of lodgepole pine (Illingworth, 1978; Rehfeldt et al., 2001) and Scots pine (Rehfeldt et al., 2002) are particularly good candidates. In Douglas-fir, it may soon be possible to compare our seedling results with results from long-term provenance tests in western North America and Europe (Breidenstein et al., 1990; Howe et al., 2006; M. U. Stoehr, http://www.for.gov.bc.ca/hre/forgen/coastal/douglas-fir.htm). If these results validate the use of relative risk, then seedling genecological studies could be extended to many more species – ultimately allowing us to judge whether competitive relationships among species might be altered, and whether large-scale changes in community ecology might be expected in the future.
In trees and other plants, temperature acts as both an environmental constraint and environmental signal. In temperate regions, cold temperatures often cause damage and death from early fall frosts (i.e. before trees are fully acclimated in the fall) and late spring frosts (i.e. after trees have deacclimated in the spring) (reviewed in Howe et al., 2003, 2006). Low temperatures regulate the timing of vegetative and reproductive bud burst via chilling requirements, and a similar process (seed stratification) regulates the timing of seed germination in the spring. If buds or seeds receive too little chilling in the winter, seed germination and vegetative growth may be adversely affected. It is important to address these potentially adverse effects of climate warming directly via appropriate physiological and genetic studies. These kinds of studies shed light directly on the mechanisms of cold adaptation which have been addressed only indirectly via our genecological approach and most analyses of provenance tests.
As with all studies of climate change, our predictions assume that the climate change scenarios are correct and that the GCMs accurately reflect these scenarios. Furthermore, the GCMs must be able to accurately predict precipitation and temperature for our predictions to be reliable. Our genecological models can be used to refine our predictions of relative risk whenever alternative GCMs become available.
Acknowledgements
This research was funded by the USDA Forest Service, Pacific Northwest Research Station. Seed for the common garden study was kindly provided by the USDA Forest Service Region 6, USDA Bureau of Land Management, Oregon Department of Forestry, and Northwest Tree Improvement Cooperative. We thank Jeff Riddle for his care in raising seedlings and data collection, Nancy Mandel for help with the analyses, Ray Drapek and Ron Nielson for providing GIS coverages for different climate change scenarios for the study area, Ken Vance-Borland for determining regional means for climate change using the GIS coverages, and Ron Neilson and Jerry Rehfeldt for helpful reviews.
