Determining spatial heterogeneity in species richness of plant community
Abstract
Species richness (number of species) per small quadrat is an important characteristic of plant communities that, along with cover and biomass, can be readily measured in field surveys. We show that variance in the number of species among quadrats can be used to determine the spatial heterogeneity of plant communities. Comparisons between variance estimated based on the observed number of species among quadrats, and variance calculated based on an assumption that all species are arranged randomly among quadrats, can describe the spatial structure of species richness. We show field examples with different degrees of spatial heterogeneity in species richness to demonstrate how to survey, analyze and interpret: three natural grasslands with low heterogeneity in China, and a weedy grassland community with high heterogeneity in Japan.
Introduction
Species richness in plant communities is determined by various natural and anthropogenic factors, but its precise determinants are difficult to elucidate. Although it is clear that bio- and geo-historical events over the past 10,000 years have played a major role (Rieseberg and Willis 2007; Wilkinson 2012), they do not account for all spatio-temporal variation seen in the present species richness pattern. The stage of biological succession, natural variation in vegetation (caused by climatic and edaphic conditions, saline levels, natural disturbances and so on) and anthropogenic disturbances (e.g. cultivation and modification of land) all cause changes in species richness within given bio- and geo-historical constraints (Pielou 1979; Begon et al. 1996). Furthermore, intra- and inter-specific interactions, and interactions between organisms and their environments, will cause spatio-temporal variation in species richness pattern. More recently, the complex effects of above- and underground environments on vegetation, and especially underground niche structure, have been shown to also affect species richness (Mommer et al. 2010; Hiiesalu et al. 2012). Niche hypothesis indicates that each species in a biological community occupies temporally and spatially inherent habitat which is often mutually exclusive among species (Hutchinson 1957; Begon et al. 1996).
Occurrence frequency, number of individuals (density), cover and biomass per unit area (Bonham 2013), and number of species and species composition per quadrat (Shiyomi et al. 2010) are often censused in vegetation surveys. Since 2000, we have proposed several methods for field surveys and statistical analyses of herbaceous plant populations and communities (Shiyomi et al. 2000; Chen et al. 2006, 2008a,b; Chen and Shiyomi 2014; Gao et al. 2014). However, there are still many unresolved questions, one of which is how to express the spatial characteristics of species richness. The spatial characteristics of species richness are assumed to be divided into the three categories based on the niche hypothesis: (i) Species composition and richness are similar among quadrats; (ii) Species composition varies greatly among quadrats, with many species in some and few in others; (iii) Species are randomly distributed among quadrats.
Here, we propose a method to determine the spatial patterns of species richness for any plant community, present field examples of survey, analysis and interpretation applying the proposed method, and discuss the factors underlying spatial variation in species richness.
Materials and methods
Survey method and analysis
 (1)
(1)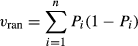 (2)
(2)For example, let the number of quadrats be 10, and seven species, A, B, C, D, E, F and G occur at 5, 2, 3, 4, 3, 10 and 9 quadrats, respectively (i.e. N = 10 and n = 7). Then, each species is assigned to random quadrats as shown in Table 1a, where 1 indicates occurrence and blank indicates absence. The relative frequencies of occurrences to the 10 quadrats (i.e. Pi), are 0.5, 0.2, 0.3, 0.4, 0.3, 1.0 and 0.9 for species A to G, respectively; the mean per-quadrat species richness, m, is 3.6 and the variance among quadrats (vobs) is 1.156, as estimated from “Total 2” in Table 1a. The expected variance is calculated based on Equation 2: vran = 0.5 (1 – 0.5) + 0.2 (1 – 0.2) + … + 0.9 (1 – 0.9) = 1.16, which is very near to the variance estimated for the 10 quadrats in this example (1.156).
| Species name/Quadrat number | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Total 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (a) A case in which species are arranged based on random numbers | |||||||||||
| A | 1 | 1 | 1 | 1 | 1 | 5 | |||||
| B | 1 | 1 | 2 | ||||||||
| C | 1 | 1 | 1 | 3 | |||||||
| D | 1 | 1 | 1 | 1 | 4 | ||||||
| E | 1 | 1 | 1 | 3 | |||||||
| F | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 |
| G | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 9 | |
| Total 2 | 3 | 5 | 4 | 3 | 3 | 3 | 3 | 3 | 3 | 6 | 36 |
| (b) A case in which species are arranged uniformly to obtain the minimum variance among quadrats | |||||||||||
| A | 1 | 1 | 1 | 1 | 1 | 5 | |||||
| B | 1 | 1 | 2 | ||||||||
| C | 1 | 1 | 1 | 3 | |||||||
| D | 1 | 1 | 1 | 1 | 4 | ||||||
| E | 1 | 1 | 1 | 3 | |||||||
| F | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 |
| G | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 9 | ||
| Total 2 | 3 | 4 | 4 | 4 | 4 | 3 | 3 | 4 | 4 | 3 | 36 |
| (c) A case in which species are arranged aggregately to obtain the maximum variance among quadrats | |||||||||||
| A | 1 | 1 | 1 | 1 | 1 | 5 | |||||
| B | 1 | 1 | 2 | ||||||||
| C | 1 | 1 | 1 | 3 | |||||||
| D | 1 | 1 | 1 | 1 | 4 | ||||||
| E | 1 | 1 | 1 | 3 | |||||||
| F | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 10 |
| G | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 9 | |
| Total 2 | 7 | 7 | 6 | 4 | 3 | 2 | 2 | 2 | 2 | 1 | 36 |
| n (1) | n (2) | n (3) | n (4) | n (5) | n (6) | n (7) | n (8) | n (9) | n (10) | ||
- (a) Mean (m) = 3.6; Variance (vobs) = 1.156; True variance (vran) = 1.16 (based on Equation 2).
- (b) Mean (m) = 3.6; Variance (vmin) = 0.24 (based on Equation 3).
- (c) Mean (m) = 3.6; Variance (vmax) = 4.64 (based on Equation 5).
- Total 1: the number of occurrences for each species; Total 2: the number of occurrences at each quadrat.
- n(i): the total number of species occurred at quadrat i.
Due to intra- and inter-specific interactions (density-dependent effects, avoidance and attraction, autocorrelation among sampling units in the vegetation, etc.), species are not always arranged independently. Therefore, vobs, which is estimated from field data, must differ from vran. For example, in the case that a mutual avoidance or exclusion among species levels out the number of species in the area, the variation in species richness among quadrats must be less than in the case where all species are arranged randomly; i.e. vobs < vran. By contrast, where attraction or a high local death rate leads to species aggregation, variation in species richness among quadrats must be larger than where species are arranged randomly; i.e. vobs > vran.
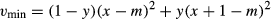 (3)
(3)for the entire community. Even if the number of species follows any distribution, its minimum variance among quadrats is vmin. In the above numerical example, vmin is estimated as 0.4 × (3 − 3.6)2 + 0.6 × (4 − 3.6)2 = 0.24.
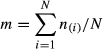 (4)
(4)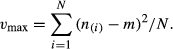 (5)
(5)The variance expressed by Equation 5 takes the maximum value under the constraint of the given mean, m. In Table 1c, vmax = 4.64 for m = 3.6 (as same as in Table 1a,b).
To summarize, (i) vobs and vran are located between vmin and vmax. (ii) When the scale of patch size in a community exceeds quadrat size, and/or species avoid or exclude each other, species richness based on observation may tend to be uniform among quadrats and vran > vobs. (iii) By contrast, where aggregation occurs due to attraction or uneven resource distribution (Pielou 1975), both community structure and species richness will vary widely among quadrats, and vran < vobs. (iv) When species are distributed randomly/independently, vran ≈ vobs. (v) A χ2 test may be used to statistically discriminate among (ii) to (iv).
Examples of field surveys
The first six examples of field survey and analysis are from natural grasslands in China. We conducted three vegetation surveys in natural grasslands near Shenmu village, Shaanxi Province, in 2010 (Lv et al. 2011): Thymus mongolicus grassland, Artemisia scoparia grassland and Artemisia ordosica shrubland. We set 180 25 × 25-cm quadrats on each side of a 45-m transect line (i.e. a total of 360 quadrats) in each of the three surveys. All plant species within the quadrats were carefully recorded. In each of the three surveys, we merged groups of four adjoining 25 × 25-cm quadrats into 90 50 × 50-cm quadrats. Species occurring in >70% of the 360 quadrats were: in T. mongolicus grassland, A. scoparia, Lespedeza davurica, Cleistogenes squarrosa, Setaria viridis and T. mongolicus; in A. scoparia grassland, A. scoparia, L. davurica, Heteropappus altaicus and Polygala tenuifolia; and in A. ordosica shrubland, A. ordosica, P. tenuifolia and Chenopodium glaucum.
The second example is from a weedy grassland in central Japan. We tilled and weeded an abandoned dry field in May 2005, established 100 10 × 10-cm quadrats in a grid, then left the field untreated. All plant species in the quadrats were harvested at ground level in October (the final season of summer annuals), 2005, and censused in the laboratory. Species appearing in >40% of quadrats were: Digitaria adscendens, Erigeron philadelphicus, Cyperus microiria and S. viridis.
The two-tailed χ2 test is used to test “H0: vobs = vran” because vobs × (number of data – 1)/vran follows a χ2 distribution under the condition of random sample. Comparisons of spatial heterogeneity in species richness among communities were made using the coefficient of variation (CV). The seven field surveys shown as examples are statistically tested to the following three possibilities: (i) H0 is accepted; (ii) H0 is rejected because of vobs > vran, and (iii) H0 is rejected because of vobs < vran. The following should be noticed that when quadrats are sequentially arranged on a line or a grid, a correlation may occur among quadrats. Then, there is a possibility that the variance among biological quantities is under- or overestimated although the mean can be properly estimated.
Results and discussion
Table 2 shows seven results from the three surveys in China and one in Japan. In the 25 × 25-cm quadrats in both the A. scoparia grassland and A. ordosica shrubland, vobs < vran (significant at α = 0.05 and 0.001, respectively), but in the 50 × 50-cm quadrats in both communities, H0: vobs = vran was accepted at α = 0.05. Thus, species were distributed somewhat uniformly among the 25 × 25-cm quadrats, and the actual community “unit” size may have been larger than the quadrat size, which suggests that antagonistic interactions may have operated between species or that some species excluded others and occupied a large, patchy area. Conversely, vobs > vran (significant at α = 0.001) in the weedy grassland, indicating aggregation potentially due to the patchy death of some plant species in response to excessive density and resulting in large variation in species richness among quadrats. In the T. mongolicus grassland, vobs was statistically similar to vran for both quadrat sizes (not significant at α = 0.05), which suggests that species were distributed randomly/independently among quadrats and that species interactions were neutral (or non-autocorrelation).
| Quadrat and variance/Community | Quadrat size, cm2 | No. quadrats | Per-quadrat richness | v min | vobs (CV) | vran (CV) | v max | |
|---|---|---|---|---|---|---|---|---|
| Thymus mongolicus | 50 × 50 | 90 | 8.444 | 0.247 | 3.778 (0.230) | ns | 3.791 (0.231) | 48.824 |
| grassland | 25 × 25 | 360 | 5.317 | 0.217 | 2.902 (0.320) | ns | 2.990 (0.325) | 34.327 |
| Artemisia scoparia | 50 × 50 | 90 | 8.622 | 0.235 | 3.766 (0.225) | ns | 3.130 (0.205) | 33.613 |
| grassland | 25 × 25 | 360 | 5.411 | 0.242 | 2.003 (0.262) | <* | 2.295 (0.280) | 22.026 |
| Artemisia ordosica | 50 × 50 | 90 | 7.770 | 0.177 | 3.642 (0.246) | ns | 3.503 (0.241) | 40.645 |
| shrubland | 25 × 25 | 360 | 4.744 | 0.190 | 1.973 (0.296) | <*** | 2.788 (0.352) | 27.851 |
| Weedy grassland | 10 × 10 | 100 | 3.300 | 0.210 | 2.556 (0.484) | >*** | 1.554 (0.378) | 9.850 |
- vmin: Variance when the number of species distributes most uniformly among quadrats.
- vobs: Variance estimated based on the observed number of species per quadrat.
- vran: Variance when the number of species distributes at random quadrats.
- vmax: Variance when the number of species among quadrats distributes most heterogeneously among quadrats.
- CV: coefficient of variation.
- *, ***, ns: In the statistical test for H0: vobs = vran, significant at 5%, 0.1% and not significant, respectively, based on the two-tailed χ2 test.
These results suggest that species richness in each quadrat may depend on the niche hypothesis because vobs ≠ vran in some surveys, although we were unable to find direct evidence for this conclusion. Species distribution is strongly influenced by various natural and anthropogenic factors and depends on both physical, chemical and biological niche requirements and the available species pool (van der Maarel and Sykes 1993; van der Maarel et al. 1995; Duncan et al. 1998). The presence of more niche types means that more species with more diverse niche requirements can live in an area.
If each niche size is so large spatially that several quadrats are contained within it, the plant community would take the form of large uniform patches. Therefore, variation in species richness among quadrats would be relatively small, i.e. vobs < vran. Conversely, if the niche size is spatially small relative to quadrat size, the plant community would consist of many small patches, each with different characteristics. In such cases, the actual variation in observed species richness among quadrats, vobs, might be nearly equal to or greater than the hypothetical random variation, vran. These tendencies are shown in the comparison of two quadrat sizes for A. scoparia grasslands and the A. ordosica shrubland in Table 2; i.e. vobs < vran when we used small quadrats of 25 × 25 cm2, but vobs ≈ vran for larger quadrats of 50 × 50 cm2. As quadrat size is often determined arbitrarily by the investigator, ensuring that an adequate quadrat size is used is important when measuring vegetation characteristics (Auerbach and Shmida 1987; Bonham 2013). Therefore, it should be determined to meet the survey's objective based on our experiences, and there is not any common quadrat size.




