Characterizing the variation of functional traits in nature is a first step towards linking environmental changes to changes in ecosystem function. Here we aim to characterize the spatial variability of major plant functional traits along wide environmental gradients in Mediterranean and temperate forests, and assess to what extent this variability differs between two dominant families in Northern Hemisphere forests: Fagaceae and Pinaceae.

Location

Catalonia (north-east Iberian Peninsula).

Methods

Four functional traits were selected to incorporate information on both the leaf and the wood economic spectra: maximum tree height (H_max), wood density (WD), leaf mass per area (LMA) and nitrogen content of leaves (N_mass). We quantified the variance distribution of each functional trait across three nested ecological scales: population, species and family. Through such scales, we explored the spatial variation of functional traits through climatic and biotic gradients, as well as the covariation among traits.

Results

Functional trait variability was distributed across all the ecological scales considered, but mostly at the family level, with functional traits differing markedly between Fagaceae and Pinaceae. Within families, variation in functional traits was similar or higher within species than between species. The spatial variability in functional traits was related to biotic and abiotic gradients, although this effect was quantitatively small compared with differences between families. Covariation among functional traits was not necessarily conserved across ecological scales. Trait covariation across all species was structured along the H_max−WD and LMA−N_mass axes, but this structure was partially lost within families, where variation was mostly structured along the H_max−LMA and WD−N_mass axes.

Main conclusions

Intraspecific variation emerges as a fundamental component of functional trait structure along wide environmental gradients. Understanding the sources of intraspecific variation, as well as how it contributes to community assembly and ecosystem functioning, thus becomes a primary research question.

Introduction

Determining how individual variation is distributed in nature is a fundamental question in biology, and characterizing its patterns and understanding its causal mechanisms are of major importance for global change ecology (Sutherland et al., 2013). Plant functional traits affect the performance of individual plants (i.e. growth, reproduction and survival) and, ultimately, the structure and dynamics of vegetation (Violle et al., 2007). Functional traits also determine plant community responses to environmental variation, and therefore they can be used to assess the potential impacts of global change on ecosystems (Lavorel & Garnier, 2002). Thus, characterizing the distribution of functional traits in nature and understanding their responses to environmental conditions can be seen as a first step towards linking environmental changes to changes in ecosystem function.

Some key functional traits have been used to define plant ecological strategies across species (Westoby et al., 2002). Maximum height has a fundamental role in the interception of light, and hence taller species have been reported to grow faster (Poorter et al., 2008), but it requires greater investment in mechanical support and water transport structures (Mencuccini, 2003). The close covariation among key leaf functional traits has been used to define the leaf economics spectrum, which illustrates a continuum between species with a fast return on investments of nutrients and dry mass (e.g. high leaf nutrient concentrations, high photosynthetic rates) to species with a lower potential rate of return (Wright et al., 2004). Wood density, the plant's investment in biomass per unit of wood volume, has been used to define the wood economics spectrum (Chave et al., 2009), and it has been consistently linked to species performance in different ecosystem types, although the strength of the relationship is not always high and can vary substantially among studies (Poorter et al., 2008; Chave et al., 2009; Martínez-Vilalta et al., 2010).

Understanding functional trait variation along environmental gradients has been recognized as a central issue in community ecology (McGill et al., 2006). Importantly, this variation is distributed across different ecological scales, including the within-species level (Messier et al., 2010). Both phenotypic plasticity as well as genetic differentiation may generate large functional variation within species, and this variability needs to be accounted for in studies of community ecology (Albert et al., 2010). For instance, intraspecific trait variability may be responsible for up to 40% of the overall variation in some traits at the global scale (Kattge et al., 2011). The challenge we face is to integrate variation at both the inter- and intraspecific levels in order to understand the responses of vegetation to environmental variability, and to assess their impacts on community structuring and ecosystem function (Violle et al., 2014). Although there is plenty of empirical evidence of functional variation within tree species and of the environmental correlates of this variation (e.g. Martínez-Vilalta et al., 2009; Fajardo & Piper, 2011; Laforest-Lapointe et al., 2014), so far little is known about: (1) the importance of the intraspecific contribution versus higher levels of organization in explaining functional variation in forests (but see e.g. Hulshof & Swenson, 2010); (2) differential responses of functional variation across different ecological scales along wide environmental gradients (but see Hulshof et al., 2013); and (3) how trade-offs between functional traits and their overall covariation may differ, or be conserved or linked across ecological scales (Maire et al., 2013; but see Jackson et al., 2013).

Mediterranean, temperate and boreal forests from the Northern Hemisphere represent around 45% of the world's forested area and 42% of the world's forest carbon stocks (Pan et al., 2011). These forests are broadly dominated by tree species in the Fagaceae and Pinaceae families, in both Eurasia (Fang et al., 2001; Shvidenko & Nilsson, 2002; Brus et al., 2012) and North America (Canada's National Forest Inventory, 2006; Smith et al., 2007). The overall response of Northern Hemisphere forests to global change is likely to depend on the balance between species in these two major families and their differential response to environmental drivers. In some areas at least, recent forest dynamics indicate large-scale changes in species composition with a widespread increase of Fagaceae at the expense of Pinaceae (Carnicer et al., 2013a; Vayreda et al., 2013). Thereby, quantifying and assessing sources of ecological variation across these major tree taxa is essential for understanding both the reasons behind their differential responses to global change and the functional implications at the ecosystem level (Brodribb et al., 2012; Carnicer et al., 2013b).

Here, we aim to characterize the spatial variability of major plant functional traits along wide environmental gradients in Mediterranean and temperate forests growing in Catalonia (north-east Iberian Peninsula), and assess to what extent this variability differs between Fagaceae and Pinaceae species. We hypothesize that: (1) given that the phylogenetic distance between Fagaceae and Pinaceae reflects the fundamental angiosperm–gymnosperm divergence, functional trait variability will be associated mostly with the family level, with Fagaceae being characterized by quicker returns on investment of nutrients and dry mass in leaves than Pinaceae; (2) within families, the contribution of intra- (i.e. among populations) and interspecific variability will be similarly important; (3) abiotic and biotic environmental factors explaining functional trait variation will differ markedly between families; and (4) factors shaping trait variability probably differ at different taxonomic and ecological levels of organization and, therefore, trade-offs and covariation among functional traits may differ when assessed at different scales.

Material and Methods

Study system

The study system corresponds to the whole territory of Catalonia (31,900 km²), located in the north-eastern Iberian Peninsula (Fig. 1a and Appendix S1 in Supporting Information).

**Figure 1**
Open in figure viewer PowerPoint

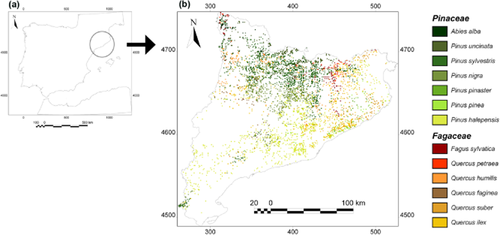
(a) Location of Catalonia in the Iberian Peninsula. (b) Distribution of the sampling plots of the Ecological and Forest Inventory of Catalonia for the 13 species (coloured dots) considered in this study. Green and brown-orange colours represent Pinaceae and Fagaceae species, respectively.

The forested territory of Catalonia encompasses 1.2 × 10⁶ ha, around 38% of its total land area. Catalan forests are mainly covered by conifer and broadleaved (deciduous and evergreen) species. We studied the 13 most abundant species in the region that dominate around 90% of the total forested area in Catalonia (Gracia et al., 2000–2004) and are included in the Pinaceae (seven species) and Fagaceae (six species) families (Appendices S1 & S2). All Pinaceae species studied are evergreen, and all Fagaceae are winter deciduous except Quercus ilex and Quercus suber.

Data sources

Functional trait data were obtained from the Ecological and Forest Inventory of Catalonia (IEFC), collated out by the Centre for Ecological Research and Forestry Applications (CREAF) between 1988 and 1998 (Gracia et al., 2000–2004; see a complete description in Appendix S2). Four functional traits were selected in our study to incorporate information relevant for both the leaf and the wood economics spectra: maximum tree height (H_max, m), wood density (WD, g cm⁻³), leaf mass per area (LMA, mg cm⁻²) and nitrogen content of leaves (N_mass, %mass). We are aware that correlations between LMA and mass- or area-based leaf traits can be problematic on statistical grounds due to lack of independence (Lloyd et al., 2013; Osnas et al., 2013), and that both representations (mass and area based) are complementary for assessing plant function (Westoby et al., 2013). However, in our case we decided to use only N_mass because concurrent measures of N_mass and LMA were missing in about a thousand plots and thus using N_area would have greatly limited our sample size.

Individual plots were selected for our analysis according to the following criteria: (1) total basal area per plot ≥ 4 m² ha⁻¹, to ensure that very sparse woodlands, which can hardly be considered a forest, were excluded; (2) species-specific basal area ≥ 15% of the total plot basal area; and (3) species-specific stand density ≥ 159 individuals ha⁻¹ (n ≥ 5), to ensure that the sampled species was sufficiently representative of the plot; and (4) species-specific maximum diameter at breast height per plot ≥ 15 cm, to avoid young stands. Finally, only species present in more than 10 plots with measures for a given functional trait were considered in the final analyses. Overall, this filtering scheme resulted in a total of 4903 populations being selected, covering the whole territory of Catalonia (Fig. 1b). The number of plots varied by species and depending on the functional trait being considered (Appendix S2). Data for H_max and WD were available for all of the 13 species, while data for N_mass for Quercus faginea and for LMA for Pinus pinaster, Quercus faginea, Quercus petraea and Quercus suber were not included because the available number of plots with measures of these traits for these species was ≤ 10 (Appendix S2).

Forest structure and both inter- and intraspecific competition were characterized with a set of variables also collected within the IEFC framework. Climatic data for each IEFC plot were obtained from the Climatic Digital Atlas of Catalonia (Ninyerola et al., 2000). In both cases (forest structure and climate) the initial set of cross-correlated variables was analysed using principal components analysis to obtain a reduced number of relatively orthogonal variables that were used to characterize each plot (see Appendix S3 for details about the initial set of variables considered in each case and on the selection process). The variables selected to characterize forest structure were: species-specific total aboveground biomass as a measure of population productivity, species-specific stand density as a measure of stand (or population) development, and species abundance (percentage basal area) as a measure of species dominance in the plot. The final set of climate variables included: mean annual temperature (°C), characterizing a first climatic gradient of increasing temperature and declining rainfall; and thermal amplitude (°C) as a measure of continentality.

Data analysis

A variance component analysis was performed for each trait to calculate variance partitioning of functional traits across three nested ecological scales in the following increasing order: population, species and family. We fitted two models for each trait, one with plot and species and the other with plot, species and family. Ninety-five per cent confidence intervals were calculated for the percentage of variance explained at each nested level by bootstrapping (1000 runs with specific trait and sample size n with replacement). Sample size was 4863 for H_max, 4665 for WD, 1783 for N_mass and 754 for LMA. H_max, WD and N_mass were log_e-transformed in all analyses to satisfy normality assumptions, while this was not necessary for LMA.

To explore the relationships between each functional trait and the selected climatic (temperature and thermal amplitude) and forest structure variables (stand density, aboveground biomass and percentage basal area), we fitted linear mixed models (LMMs) using each of the four functional traits as different dependent variables. Correlations between selected explanatory variables for climate and forest structure were always < 0.30. We also included in all models the squared mean annual temperature in order to account for possible nonlinear effects of temperature. Family and its interaction with climatic and forest structural variables were also introduced as fixed effects in order to account for differences in the association of functional traits with forest structure and climate between Pinaceae and Fagaceae. Species was introduced as a random factor. Fixed covariates were centred per species prior to carrying out the analyses in order to remove interspecific variability in environmental factors, and therefore focus on the effects of environmental variation at the within-species level. Starting from the saturated model, we created the fully crossed set of models and ranked them from lowest to highest AIC (Akaike information criterion). All the best models (lowest AIC) within two AIC units were considered to be equivalent in terms of fit. Coefficients of determination were used to assess the percentage contribution of fixed effects alone (R²_marginal) and both fixed and random effects (R²_conditional) in explaining functional trait variability (Nakagawa & Schielzeth, 2013).

As an estimate of the contribution of environmental variables on functional trait variability, R²_marginal was compared between the full best models and the ‘null’ models only containing family as a fixed effect. The relative percentage increase in R²_marginal obtained by adding environmental variables was considered as the contribution of these variables to functional trait variability. Because plots within species may also present spatial autocorrelation we refitted the same models accounting for spatial effects by using an autocorrelation structure. However, spatial autocorrelation was low, so these models were very similar in terms of fit to the equivalent LMMs and, therefore, we only present the results of the latter models. Finally, in order to evaluate differences when interspecific variability in environmental factors is also considered, analyses were repeated by overall centring of fixed covariates.

Pearson correlations were used to test for association between pairs of functional traits, across all plots together, across plots within families and across plots within species. Because all functional traits were subject to measurement error, we used standardized major axis (SMA) regressions to quantify pairwise associations between functional traits, as well as to test for homogeneity of the slopes of these relationships among three groups: all populations, populations within Pinaceae and populations within Fagaceae. The squared correlation coefficient (R²) was used to evaluate the strength of each pairwise association for each group. Because not all functional traits were measured in each population, sample size for each pairwise SMA regression ranged from 683 (LMA−N_mass) to 4651 (H_max−WD) at the ‘all populations’ level, from 150 (WD−LMA) to 1169 (H_max−WD) for Fagaceae and from 518 (LMA−N_mass) to 3482 (H_max−WD) for Pinaceae.

To quantify the extent to which the four functional traits covary in a multidimensional space, and to determine if covariation among traits varies depending on the ecological scale considered, we performed a principal components analysis (PCA) for each of the following groups: across species means, across all populations together and across plots within each family. Because LMA and N_mass were unavailable for some species (see Data sources above) and not all functional traits were measured in each plot, the sample size for each PCA consisted of nine species at the species means level, and 624, 140 and 484 species when ‘all populations’, Fagaceae or Pinaceae were considered, respectively. The sample size available for each species ranged from 11 (Fagus sylvatica) to 175 (Pinus sylvestris).

Variance components and LMMs, Pearson correlations, SMA regressions and PCAs were carried out with R software version 3.1.1 (R Development Core Team, 2014) using the packages ape, boot, MuMIn, nlme, stats and smatr (see the R code used in Appendix S4).

Results

Variance components

Mean values of WD, LMA and N_mass were clearly different between families and among species within families, while H_max did not show contrasted values between families (Appendix S2, Fig. 2). The partitioning of variance in functional traits revealed substantial changes depending on whether the family level was accounted for or not (Table 1). When family was not included, the largest proportion of variance in WD, LMA and N_mass was explained at the species level, but there was also a substantial intraspecific contribution (Table 1a). In contrast, the distribution of variance in H_max was more balanced across scales, although it was slightly higher at the intraspecific level (Table 1). When family was accounted for, the largest proportion of the variance in WD, LMA and N_mass was explained at this level, and the proportion of variance explained at the intraspecific level was always higher than the variance among species. On the other hand, the distribution of variance in H_max between the species and intraspecific scales was similar regardless of whether the family level was considered or not, as this level made very little contribution to the overall variation (Table 1). In all cases, similar results were obtained if different models were fitted for each family (results not shown).

**Figure 2**
Open in figure viewer PowerPoint

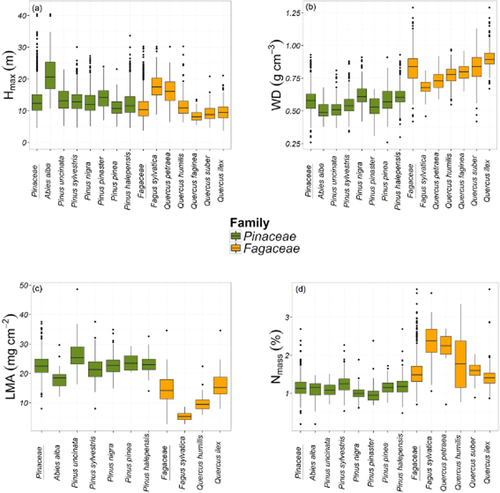
Boxplots of each functional trait as a function of species and family (Pinaceae or Fagaceae): (a) maximum height (H_max), (b) wood density (WD), (c) leaf mass per area (LMA), and (d) nitrogen content of leaves (N_mass). The limits of boxes indicate the first and third quartiles, and the horizontal line within boxes corresponds to the median. The upper whisker extends from the third quartile to the highest value within 1.5 × IQR (interquartile range) of the third quartile. The lower whisker extends from the first quartile to the lowest value within 1.5 × IQR of the first quartile. Black circles are outliers. Box colours indicate the different families (Pinaceae or Fagaceae).

Table 1. Variance partitioning across ecological scales of the nested linear models for H_max, WD, N_mass and LMA: (a) populations nested within species, and (b) populations nested within species nested within family. Sample size was 4863 for H_max, 4665 for WD, 1783 for N_mass and 754 for LMA. H_max, WD and N_mass were log_e-transformed prior to the analyses. Square brackets represent the 95% confidence intervals

Scale	% Variance [95% CI]
Scale	H_max	WD	N_mass	LMA
(a)
Population	53 [49,56]	27 [25,29]	32 [26,38]	23 [20,27]
Species	47 [44,51]	73 [71,75]	68 [62,74]	77 [73,80]
(b)
Population	52 [49,55]	18 [16,19]	22 [18,27]	15 [13,17]
Species	46 [42,50]	9 [8,11]	11 [9,15]	13 [10,17]
Family	2 [0,5]	73 [71,74]	67 [61,70]	72 [67,76]

H_max, maximum height; WD, wood density; N_mass, nitrogen content of leaves; LMA, leaf mass per area; CI, confidence intervals.

Determinants of functional variation

The fitted LMMs explained a large proportion of functional variability through the environmental gradients and the ecological scales considered. Fixed effects (R²_marginal) accounted for 34–52% of the total variance for different functional traits, while both fixed and species (random) effects (R²_conditional) accounted for 65–80% of their total variance (Table 2, Fig. 3). The model for H_max included the fixed effects of family, the interactions of temperature, thermal amplitude, stand density and aboveground biomass with family, as well as the effects of temperature squared and percentage basal area (Table 2). Without very strong differences between families, H_max increased with increasing temperature and stabilized at higher temperatures, increased with thermal amplitude and aboveground biomass, and declined with increasing percentage basal area and stand density (Fig. 3a–e, Table 2). There were eight other candidate models (ΔAIC < 2) for H_max which always included most of the effects contained in the best model (Table 2). The fixed effects included in the WD model were family, the interactions of temperature, thermal amplitude, stand density and aboveground biomass with family, as well as the effect of temperature squared (Table 2). WD reached a maximum at intermediate temperatures and stabilized for populations growing under warmer temperatures, and it was lower for Pinaceae than for Fagaceae (Fig. 3f, Table 2). Thermal amplitude had a negative effect on WD for Fagaceae, while this effect disappeared for Pinaceae (Fig. 3g, Table 2). The effect of stand density on WD was positive but not significant for Fagaceae, while it was significantly negative for Pinaceae (Fig. 3h, Table 2). Aboveground biomass had a positive effect on WD; this effect was only significant for Pinaceae (Fig. 3i, Table 2). There were seven other candidate models (ΔAIC < 2) for WD which always included most of the effects contained in the best model (Table 2). Family, stand density and aboveground biomass were the only fixed effects included in the model of N_mass, with higher N_mass content in Fagaceae, and N_mass decreasing with stand density (Fig. 3j, Table 2) but increasing with aboveground biomass (Fig. 3k, Table 2). There were 14 other candidate models (ΔAIC < 2) for N_mass which always included the effects of family and aboveground biomass, while stand density was present in 11 models (Table 2). Finally, the model for LMA included the fixed effects of family, temperature, thermal amplitude, percentage basal area, aboveground biomass, as well as the interactions of these covariates with family (Table 2). LMA was higher in Pinaceae but the effects of environmental variables were generally stronger for Fagaceae. LMA decreased with temperature (Fig. 3l, Table 2) and increased with thermal amplitude (Fig. 3m, Table 2). Finally, LMA also increased with increasing percentage basal area (Fig. 3n, Table 2) and decreased with increasing aboveground biomass (Fig. 3o, Table 2). There were four other candidate models for LMA (ΔAIC < 2), always maintaining the same fixed effects included in the best model, with the exception of the interaction between temperature and family which was present in three models.

Table 2. Summary of the mixed linear models relating environmental variables with the spatial variability of each functional trait. Sample size was 4863 for H_max, 4665 for WD, 1783 for N_mass and 754 for LMA. H_max, WD, N_mass, stand density and aboveground biomass were log_e-transformed and all fixed covariates were centred for each species prior to the analyses. Model coefficients ± SE and significance levels for each explanatory variable are given

Mixed models	H_max	n_i†	WD	n_i‡	N_mass	n_i§	LMA	n_i¶
Intercept	2.42 ± 0.12***	8	−0.24 ± 0.04***	7	0.56 ± 0.06***	14	10.7 ± 1.97***	4
F[Pi]	0.16 ± 0.15	8	−0.35 ± 0.05***	7	−0.48 ± 0.08***	14	12.2 ± 2.40**	4
T	−0.03 ± 0.00***	8	0.00 ± 0.00	7	n.i.		−0.48 ± 0.17**	4
T²	−0.00 ± 0.00(*)	6	−0.00 ± 0.00*	7	n.i.		n.i.
A	0.02 ± 0.00***	8	−0.01 ± 0.00*	6	n.i.		0.56 ± 0.20**	4
%BA	−0.00 ± 0.00***	8	n.i.		n.i.		0.04 ± 0.01**	4
SD	−0.15 ± 0.01***	8	0.01 ± 0.01	7	−0.02 ± 0.01*	11	n.i.
B	0.32 ± 0.01***	8	0.00 ± 0.00	7	0.03 ± 0.01***	14	−2.04 ± 0.46***	4
F[Pi] × T	−0.01 ± 0.00	5	0.01 ± 0.00***	7	n.i.		0.36 ± 0.21(*)	3
F[Pi] × T²	n.i.		n.i.		n.i.		n.i.
F[Pi] × A	0.01 ± 0.01*	8	0.01 ± 0.00(*)	5	n.i.		−0.63 ± 0.25*	4
F[Pi] × %BA	n.i.		n.i.		n.i.		−0.04 ± 0.02*	4
F[Pi] × SD	−0.02 ± 0.01(*)	6	−0.03 ± 0.01***	7	n.i.		n.i.
F[Pi] × B	0.04 ± 0.01***	8	0.04 ± 0.01***	7	n.i.		1.11 ± 0.52*	4
R² (m/c) (%)	34/80		52/69		47/65		52/74

(*)P < 0.1; *P < 0.05; **P < 0.01; ***P < 0.001.n.i., not included in the final model; R² (m/c), explained variance by fixed effects (R² marginal)/explained variance by fixed and random effects (R² conditional); n_i, number of candidate models in which the fixed effect is included; H_max, maximum height; WD, wood density; N_mass, nitrogen content of leaves; LMA, leaf mass per area; F[Pi], family [Pinaceae]; T, temperature; A, amplitude; %BA, % basal area; SD, stand density; B, biomass. The value and significance of coefficients correspond to the reference family level (Fagaceae), except those including the F[Pi] term, which quantify the differences in relation to the reference family level.†Total number of candidate models = 8.‡Total number of candidate models = 7.§Total number of candidate models = 14.¶Total number of candidate models = 4.

**Figure 3**
Open in figure viewer PowerPoint

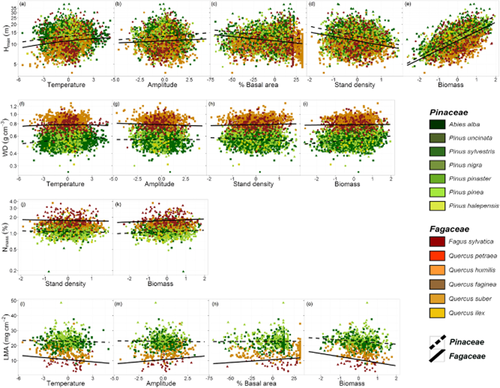
Predicted effects of environmental variables and family on functional trait variability in the fixed part of the mixed linear models: (a) effect of annual temperature on H_max, (b) effect of thermal amplitude on H_max, (c) effect of percentage basal area on H_max, (d) effect of stand density on H_max, (e) effect of aboveground biomass on H_max, (f) effect of annual temperature on WD, (g) effect of thermal amplitude on WD, (h) effect of stand density on WD, (i) effect of aboveground biomass on WD, (j) effect of stand density on N_mass, (k) effect of aboveground biomass on N_mass, (l) effect of annual temperature on LMA, (m) effect of thermal amplitude on LMA, (n) effect of % basal area on LMA, and (o) effect of aboveground biomass on LMA. Regression coefficients are based on the fixed effects of the models shown in Table 2. H_max, maximum height; WD, wood density; N_mass, nitrogen content of leaves; LMA, leaf mass per area. Note the logarithmic scale of the y-axis when the variables are loge-transformed.

The variance explained by fixed effects in the model for H_max (34%, corresponding to the value of R²_marginal) was exclusively due to environmental variables, with R²_marginal increasing by 34% when comparing the ‘null’ model including only family effects with the best full model. However, the overall contribution of environmental variables in the models for WD, N_mass and LMA was low, with R²_marginal increasing by 2%, 1% and 3%, respectively, when comparing the ‘null’ models including only family effects with the best full models. Overall, the contribution of the species level to the overall variability (R²_conditional − R²_marginal) was similar in magnitude to the residual variability not accounted by the model for each functional trait (100 − R²_conditional).

When interspecific variability in environmental factors was considered the models obtained were very similar to the equivalent LMMs presented here, i.e. in terms of fit, variables included and the direction of their effects and significance (Appendix S5).

Covariation among functional traits

SMA regressions between pairs of functional traits showed different relationships across and within families for some traits (Fig. 4, Appendix S6). H_max and WD were negatively associated, albeit weakly, across all populations, while they were more strongly negatively associated across populations within Fagaceae, and were not related within Pinaceae (Fig. 4a). The association between H_max and LMA was strong and negative across populations within Fagaceae, and also negative, but weakly so, within Pinaceae, while this association was not significant across all populations (Fig. 4b). The association between H_max and N_mass was positive across populations within Fagaceae and negative, but only weakly so, across all populations (Fig. 4c). The relationship between WD and LMA was significantly negative for all populations together and positive across populations within Fagaceae (Fig. 4d). The relationship between WD and N_mass was positive for all populations together and negative for Fagaceae and also negative, although weakly so, for Pinaceae (Fig. 4e). Finally, the association between LMA and N_mass was significant and strongly negative for all populations and across populations within families (Fig. 4f). All these associations between pairs of functional traits were also observed by using Pearson correlations (Appendix S7).

**Figure 4**
Open in figure viewer PowerPoint

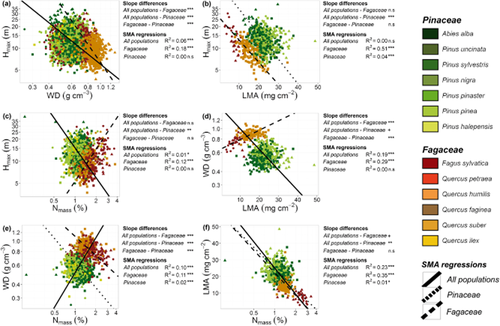
Graphic representation of the standardized major axis (SMA) regressions between pairs of functional traits: (a) H_max−WD, (b) H_max−LMA, (c) H_max−N_mass, (d) WD−LMA, (e) WD−N_mass, and (f) LMA−N_mass. Symbol shape and colour combinations denote different species. Green and brown-orange colours represent Pinaceae and Fagaceae species, respectively. Each line type corresponds to the slope for all populations (solid line), Fagaceae (dashed line) and Pinaceae (dotted line). The significance of slope differences among groups, and the R² for each significant SMA regression are also shown. Note the logarithmic scale of the x- and y-axes when the variables are log_e-transformed.

PCAs were generally consistent with the results presented in the previous paragraph and revealed differential patterns of covariation between functional traits for the ecological scales considered (Fig. 5). Patterns of covariation among functional traits were similar across species means and across all populations (Fig. 5a, b). The first PCA component clearly segregated species and/or populations by family, with Pinaceae being characterized by higher LMA and lower N_mass and WD (Fig. 5a, b). The second component segregated species and populations according to their H_max, Abies alba and Fagus sylvatica being the species reaching the highest values (Fig. 5a, b). Interestingly, the covariation among functional traits changed when assessed across populations within families (Fig. 5c, d). Within both families (considered separately), the dominant trait associations at higher levels (mostly along the H_max−WD and LMA−N_mass axes) were lost and variation was mostly structured along the H_max−LMA and WD−N_mass axes (Fig. 5c, d).

**Figure 5**
Open in figure viewer PowerPoint

Graphic representation of the first and second components of the principal components analysis (PCA) of functional traits at each of the scales considered: (a) across species means, (b) across all populations, (c) across populations within Fagaceae, and (d) across populations within Pinaceae. Symbol shape and colour combinations denote different species. Green and brown-orange colours represent Pinaceae and Fagaceae species, respectively. H_max, maximum height; WD, wood density; N_mass, nitrogen content of leaves; LMA, leaf mass per area.

Discussion

In this study, we have assessed how trait variance is distributed and structured across different ecological scales in Mediterranean and temperate forests from the north-eastern Iberian Peninsula. Overall, our findings agreed with our initial hypotheses: (1) functional variation was distributed across all the ecological scales considered, but mostly at the family level, with functional traits differing markedly between Fagaceae and Pinaceae; (2) within families, variation in functional traits was similar or higher between populations (within species) than between species; (3) the spatial variability in functional traits was related to biotic and abiotic gradients, although this effect was quantitatively small compared with differences between families, except for H_max; and (4) covariation among functional traits was not necessarily conserved across ecological scales.

Functional trait variation occurs mostly within species and between families

The variance distribution of functional traits among the three ecological scales considered in this study (i.e. family, species and population) reflects the significance of studying variation at different levels and suggests that trait variation is determined by processes acting at different scales (Messier et al., 2010). The patterns of variance partitioning were broadly consistent for WD, LMA and N_mass, suggesting that similar processes may determine the structure of variation for these traits. The fact that trait variance occurs mostly at the family level reflects high trait conservatism within angiosperms and gymnosperms and provides further evidence for the known divergence in functional strategies between these two major clades (Brodribb et al., 2012; Carnicer et al., 2013b). In contrast, variance partitioning for H_max shows that differentiation between families is low for this trait. This reflects that H_max is probably under stronger environmental control (biotic and abiotic) than any of the other traits studied here (see Moles et al., 2009, for a global synthesis of patterns of plant heights), at least when only dominant tree species are considered.

Interestingly, however, at the within-family level intraspecific variation was higher than the variation across species for all functional traits studied here. This is particularly noteworthy considering that our study did not account for trait variation within populations, a potentially important source of trait variability within species (Bolnick et al., 2011). This result contrasts with the general assumption that functional variation is higher between than within species (e.g. Hulshof & Swenson, 2010; Jackson et al., 2013). Although the generality of our results remains to be established, because the contribution of within-species variation might have been different if other traits had been considered (e.g. Kattge et al., 2011) or may depend on the biogeographical or phylogenetic context, our results agree with the recent focus on intraspecific variation as an important component of overall variability of functional traits (Albert et al., 2010; Violle et al., 2012).

Variation of functional traits along environmental gradients

The results reported here suggest that the dominant tree species in our study system hold enough variation to exploit a wide variety of ecological conditions. In this context, a directional shift in trait values along environmental gradients is consistent with ecological filtering on the basis of plant function as a deterministic process behind distribution patterns of populations and species (e.g. Hulshof et al., 2013; Sides et al., 2014). In our case, H_max, WD and LMA varied as a function of climate and forest structure, while N_mass was only affected by aboveground biomass and stand density. As reported in previous studies (e.g. Campetella et al., 2011; Laforest-Lapointe et al., 2014) forest structure is an important source of functional variation, which not only reflects the direct effects of biotic interactions but also the influence of stand attributes on microclimatic conditions within populations (Grimmond et al., 2000). Specifically, stand development and interspecific competition appeared as important processes regulating functional trait variability, i.e. populations with high stand densities were characterized by shorter heights and soft woods, while trees were taller and showed a lower LMA with increasing abundance of other species. There was also evidence that functional traits varied along the gradient of aboveground productivity, with resource-acquisitive traits (high H_max and N_mass, and low LMA) dominating in highly productive populations where light is likely to be the key limiting factor (Cavender-Bares et al., 2004). Additionally, high WD was also associated with productive populations (particularly in Pinaceae). This is contrary to observations in tropical forests, and the discrepancy may be related to the relationship between wood density and drought resistance (Hacke et al., 2001; Chave et al., 2009), which is likely to be a key environmental driver in our study system.

Regarding the climatic gradient, populations located in colder sites or experiencing higher thermal amplitudes were characterized by a higher LMA compared with those in sites experiencing warmer and more stable temperatures. This is consistent with studies showing an increase in LMA within species at higher altitudes (Fajardo & Piper, 2011) due to lower cell expansion at lower temperatures (Poorter et al., 2009). Maximum tree height was positively associated with average temperature and thermal amplitude, in agreement with global patterns mostly accounting for variability across species (Moles et al., 2009). Finally, populations located in warmer sites were also characterized by denser woods, which might provide higher resistance to dry conditions (Chave et al., 2009).

Interestingly, however, the patterns reported show that only H_max is clearly under strong environmental control, indicating that other (unaccounted for) sources of variation contribute to the spatial variation of WD, N_mass and LMA. For these functional traits the variability explained by environmental conditions was < 5%. This is consistent with the relatively low association between species-level functional traits and climatic variables (temperature and precipitation) at the global scale (Moles et al., 2014). Clearly, however, this is not due to a lack of trait variation, neither globally nor regionally, and even within species, as clearly shown in our study. Three main reasons may explain this large unexplained variance and, in particular, the relatively low importance of climate and stand structure in our models. Firstly, the abiotic and biotic variables considered here might weakly reflect the availability of water and other key resources at the scale of our study, which may be more controlled by soil type, lithology (e.g. Russo et al., 2008) or micro-environmental conditions (Cornwell & Ackerly, 2009). Secondly, genetic variability and local adaptation, not considered in this study, might be dominant processes shaping trait variability across populations (Kremer et al., 2014). Finally, stand structural variables may not completely capture differences in age and stand development across plots (Laforest-Lapointe et al., 2014).

One of our most intriguing findings is that the dominant dimensions of functional variation are not necessarily equal when they are assessed at different ecological scales. Dominant trait relationships at higher levels (H_max−WD and LMA−N_mass) were mostly conserved at the within-family scale (basically for Fagaceae) when assessed in a bivariate space. In a multivariate space, however, trait covariation at higher levels was partially lost and within-family variation was mostly structured along the H_max−LMA and WD−N_mass axes. These dimensions of variation were also dominant at the species-specific level (Appendix S7), which is consistent with the observed patterns for P. sylvestris in the same region (Laforest-Lapointe et al., 2014). Our results highlight the need to incorporate intraspecific variation in studies of trait relationships, particularly when trying to integrate leaf (LMA and N_mass) and stem traits (H_max and WD) into overall plant resource-use strategies (Poorter et al., 2014). The importance of assessing the leaf economics spectrum within species has recently been addressed by Niinemets (2015) using Q. ilex, one of the species studied here, as a case study.

Large functional differences between Pinaceae and Fagaceae: implications for forest dynamics and function under global change

As expected, functional differences between Fagaceae and Pinaceae were very large, not only in the differences among their trait values but also in their contrasted responses to environmental gradients and their segregation along the functional dimensions of variation. Each family was located at opposite extremes of the leaf- and wood economics spectra (Wright et al., 2004; Chave et al., 2009). In relation to the leaf economics spectrum, Fagaceae were characterized by resource-acquisitive traits (low LMA and high N_mass) and Pinaceae showed resource-conservative traits (high LMA and low N_mass), whereas the opposite was true for wood traits (low WD for Pinaceae versus high WD for Fagaceae). Our results probably reflect patterns of evolutionary divergence in trait covariation between angiosperms and gymnosperms (Ackerly & Reich, 1999). All these patterns are also consistent with the greater shade tolerance of Fagaceae (cf. Valladares & Niinemets, 2008) and have to be interpreted in the context of the contrasted successional dynamics of the two families in the study area, where Pinaceae are mostly early successional whereas Fagaceae tend to be late-successional species.

Recent studies at the regional scale show that the current structure of Iberian forests is, to a large extent, the result of the abandonment of management activities and the corresponding expansion of broadleaves (Fagaceae) over areas formerly dominated by Pinaceae, due to the greater competitive capacity of the former (Carnicer et al., 2013a; Vayreda et al., 2013). To the extent that the studied functional traits can be considered (or are linked to) response traits (sensu Lavorel & Garnier, 2002) these differential patterns through environmental gradients might hold information for understanding the disparity of responses to environmental changes between these two dominant species groups in mediterranean and temperate forests (Carnicer et al., 2013b).

At the same time, the divergent responses between the two studied families may have large implications for ecosystem function (effect traits; Lavorel & Grigulis, 2012). If changes in species composition continue towards increased dominance of late-successional Fagaceae, corresponding shifts in ecosystem function should be expected (Augusto et al., 2015). However, we hypothesize that changes in forest dynamics and ecosystem function will depend on intraspecific variability and its role in shaping population responses (acclimation, adaptation) and community dynamics. Disentangling the sources and consequences of intraspecific variation emerges as an essential step towards linking environmental changes to changes in species distribution and ecosystem function.

Acknowledgements

We thank Jordi Vayreda for his help querying the IEFC database and Maurizio Mencuccini for his insightful comments on an earlier version of the manuscript. Financial support was obtained from the Spanish Ministry of Economy and Competitiveness via competitive grant CGL2013-46808-R (FUN2FUN project).

Supporting Information

References

Ackerly, D.D. & Reich, P.B. (1999) Convergence and correlations among leaf size and function in seed plants: a comparative test using independent contrasts. American Journal of Botany, 86, 1272–1281.
10.2307/2656775
CAS PubMed Web of Science® Google Scholar
Albert, C.H., Thuiller, W., Yoccoz, N.G., Douzet, R., Aubert, S. & Lavorel, S. (2010) A multi-trait approach reveals the structure and the relative importance of intra- vs. interspecific variability in plant traits. Functional Ecology, 24, 1192–1201.
10.1111/j.1365-2435.2010.01727.x
Web of Science® Google Scholar
Augusto, L., De Schrijver, A., Vesterdal, L., Smolander, A., Prescottand, C. & Ranger, J. (2015) Influences of evergreen gymnosperm and deciduous angiosperm tree species on the functioning of temperate and boreal forests. Biological Reviews, 90, 444–466.
10.1111/brv.12119
PubMed Web of Science® Google Scholar
Bolnick, D.I., Amarasekare, P., Araújo, M.S., Bürger, R., Levine, J.M., Novak, M., Rudolf, V.H.W., Schreiber, S.J., Urban, M.C. & Vasseur, D.A. (2011) Why intraspecific trait variation matters in community ecology. Trends in Ecology and Evolution, 26, 183–192.
10.1016/j.tree.2011.01.009
PubMed Web of Science® Google Scholar
Brodribb, T.J., Pittermann, J. & Coomes, D.A. (2012) Elegance versus speed: examining the competition between conifer and angiosperm trees. International Journal of Plant Sciences, 173, 673–694.
10.1086/666005
Web of Science® Google Scholar
Brus, D.J., Hengeveld, G.M., Walvoort, D.J.J., Goedhart, P.W., Heidema, A.H., Nabuurs, G.J. & Gunia, K. (2012) Statistical mapping of tree species over Europe. European Journal of Forest Research, 131, 145–157.
10.1007/s10342-011-0513-5
Web of Science® Google Scholar
Campetella, G., Botta-Dukát, Z., Wellstein, C., Canullo, R., Gatto, S., Chelli, S., Mucina, L. & Bartha, S. (2011) Patterns of plant trait–environment relationships along a forest succession chronosequence. Agriculture, Ecosystems and Environment, 145, 38–48.
10.1016/j.agee.2011.06.025
Web of Science® Google Scholar
Canada's National Forest Inventory. (2006) Canada's National Forest Inventory . Available at: https://nfi.nfis.org/index.php.
Google Scholar
Carnicer, J., Coll, M., Pons, X., Ninyerola, M., Vayreda, J. & Peñuelas, J. (2013a) Large-scale recruitment limitation in Mediterranean pines: the role of Quercus ilex and forest successional advance as key regional drivers. Global Ecology and Biogeography, 23, 371–384.
10.1111/geb.12111
Web of Science® Google Scholar
Carnicer, J., Barbeta, A., Sperlich, D., Coll, M. & Peñuelas, J. (2013b) Contrasting trait syndromes in angiosperms and conifers are associated with different responses of tree growth to temperature on a large scale. Frontiers in Plant Science, 4, 1–19.
10.3389/fpls.2013.00409
PubMed Web of Science® Google Scholar
Cavender-Bares, J., Kitajima, K. & Bazzaz, F.A. (2004) Multiple trait associations in relation to habitat differentiation among 17 Floridian oak species. Ecological Monographs, 74, 635–662.
10.1890/03-4007
Web of Science® Google Scholar
Chave, J., Coomes, D., Jansen, S., Lewis, S.L., Swenson, N.G. & Zanne, A.E. (2009) Towards a worldwide wood economics spectrum. Ecology Letters, 12, 351–366.
10.1111/j.1461-0248.2009.01285.x
CAS PubMed Web of Science® Google Scholar
Cornwell, W.K. & Ackerly, D.D. (2009) Community assembly and shifts in the distribution of functional trait values across an environmental gradient in coastal California. Ecological Monographs, 79, 109–126.
10.1890/07-1134.1
Web of Science® Google Scholar
Fajardo, A. & Piper, F.I. (2011) Intraspecific trait variation and covariation in a widespread tree species (Nothofagus pumilio) in southern Chile. New Phytologist, 189, 259–271.
10.1111/j.1469-8137.2010.03468.x
PubMed Web of Science® Google Scholar
Fang, J., Chen, A., Peng, C., Zhao, S. & Ci, L. (2001) Changes in forest biomass carbon storage in China between 1949 and 1998. Science, 292, 2320–2322.
10.1126/science.1058629
CAS PubMed Web of Science® Google Scholar
Gracia, C., Ibáñez, J.J., Burriel, J.A., Mata, T. & Vayreda, J. (2000–2004) Inventari ecològic i forestal de Catalunya. Catalunya, 10 volumes. CREAF, Bellaterra, Spain.
Google Scholar
Grimmond, C.S.B., Robeson, S.M. & Schoof, J.T. (2000) Spatial variability of micro-climatic conditions within a mid-latitude deciduous forest. Climate Research, 15, 137–149.
10.3354/cr015137
Web of Science® Google Scholar
Hacke, U.G., Sperry, J.S., Pockman, W.T., Davis, S.D. & McCulloh, K.A. (2001) Trends in wood density and structure are linked to prevention of xylem implosion by negative pressure. Oecologia, 126, 457–461.
10.1007/s004420100628
PubMed Web of Science® Google Scholar
Hulshof, C.M. & Swenson, N.G. (2010) Variation in leaf functional trait values within and across individuals and species: an example from a Costa Rican dry forest. Functional Ecology, 24, 217–223.
10.1111/j.1365-2435.2009.01614.x
Web of Science® Google Scholar
Hulshof, C.M., Violle, C., Spasojevic, M.J., McGill, B., Damschen, E., Harrison, S. & Enquist, B.J. (2013) Intra-specific and inter-specific variation in specific leaf area reveal the importance of abiotic and biotic drivers of species diversity across elevation and latitude. Journal of Vegetation Science, 24, 921–931.
10.1111/jvs.12041
Web of Science® Google Scholar
Jackson, B.G., Peltzer, D.A. & Wardle, D.A. (2013) The within-species leaf economic spectrum does not predict leaf litter decomposability at either the within-species or whole community levels. Journal of Ecology, 101, 1409–1419.
10.1111/1365-2745.12155
CAS Web of Science® Google Scholar
Kattge, J., Díaz, S., Lavorel, S. et al. (2011) TRY – a global database of plant traits. Global Change Biology, 17, 2905–2935.
10.1111/j.1365-2486.2011.02451.x
Web of Science® Google Scholar
Kremer, A., Potts, B.M. & Delzon, S. (2014) Genetic divergence in forest trees: understanding the consequences of climate change. Functional Ecology, 28, 22–36.
10.1111/1365-2435.12169
Web of Science® Google Scholar
Laforest-Lapointe, I., Martínez-Vilalta, J. & Retana, J. (2014) Intraspecific variability in functional traits matters: case study of Scots pine. Oecologia, 175, 1337–1348.
10.1007/s00442-014-2967-x
PubMed Web of Science® Google Scholar
Lavorel, S. & Garnier, E. (2002) Predicting changes in community composition and ecosystem functioning from plant traits: revisiting the Holy Grail. Functional Ecology, 16, 545–556.
10.1046/j.1365-2435.2002.00664.x
CAS Web of Science® Google Scholar
Lavorel, S. & Grigulis, K. (2012) How fundamental plant functional trait relationships scale-up to trade-offs and synergies in ecosystem services. Journal of Ecology, 100, 128–140.
10.1111/j.1365-2745.2011.01914.x
Web of Science® Google Scholar
Lloyd, J., Bloomfield, K., Domingues, F. & Farquhar, G.D. (2013) Photosynthetically relevant foliar traits correlating better on a mass vs an area basis: of ecophysiological relevance or just a case of mathematical imperatives and statistical quicksand? New Phytologist, 199, 311–321.
10.1111/nph.12281
CAS PubMed Web of Science® Google Scholar
McGill, B.J., Enquist, B.J., Weiher, E. & Westoby, M. (2006) Rebuilding community ecology from functional traits. Trends in Ecology and Evolution, 21, 178–185.
10.1111/j.1365-2745.2004.00838.x
PubMed Web of Science® Google Scholar
Maire, V., Gross, N., Hill, D., Martin, R., Wirth, C., Wright, I.J. & Soussana, G.S. (2013) Disentangling coordination among functional traits using an individual-centred model: impact on plant performance at intra- and inter-specific levels. PLoS ONE, 8, 1–16.
10.1371/journal.pone.0077372
Web of Science® Google Scholar
Martínez-Vilalta, J., Cochard, H., Mencuccini, M. et al. (2009) Hydraulic adjustment of Scots pine across Europe. New Phytologist, 184, 353–364.
10.1111/j.1469-8137.2009.02954.x
CAS PubMed Web of Science® Google Scholar
Martínez-Vilalta, J., Mencuccini, M., Vayreda, J. & Retana, J. (2010) Interspecific variation in functional traits, not climatic differences among species ranges, determines demographic rates across 44 temperate and Mediterranean tree species. Journal of Ecology, 98, 1462–1475.
10.1111/j.1365-2745.2010.01718.x
Web of Science® Google Scholar
Mencuccini, M. (2003) The ecological significance of long-distance water transport: short-term regulation, long-term acclimation and the hydraulic costs of stature across plant life forms. Plant, Cell and Environment, 26, 163–182.
10.1046/j.1365-3040.2003.00991.x
Web of Science® Google Scholar
Messier, J., McGill, B.J. & Lechowicz, M.J. (2010) How do traits vary across ecological scales? A case for trait-based ecology. Ecology Letters, 13, 838–848.
10.1111/j.1461-0248.2010.01476.x
CAS PubMed Web of Science® Google Scholar
Moles, A.T., Warton, D.L., Warman, L. et al. (2009) Global patterns in plant height. Journal of Ecology, 97, 923–932.
10.1111/j.1365-2745.2009.01526.x
Web of Science® Google Scholar
Moles, A.T., Perkins, S.E., Laffan, S.W. et al. (2014) Which is a better predictor of plant traits: temperature or precipitation? Journal of Vegetation Science, 25, 1167–1180.
10.1111/jvs.12190
Web of Science® Google Scholar
Nakagawa, S. & Schielzeth, H. (2013) A general and simple method for obtaining R² from generalized linear mixed-effects models. Methods in Ecology and Evolution, 4, 133–142.
10.1111/j.2041-210x.2012.00261.x
Web of Science® Google Scholar
Niinemets, Ü. (2015) Is there a species spectrum within the world-wide leaf economics spectrum? Major variations in leaf functional traits in the Mediterranean sclerophyll Quercus ilex. New Phytologist, 205, 79–96.
10.1111/nph.13001
PubMed Web of Science® Google Scholar
Ninyerola, M., Pons, X. & Roure, J.M. (2000) A methodological approach of climatological modelling of air temperature and precipitation through GIS techniques. International Journal of Climatology, 20, 1823–1841.
10.1002/1097-0088(20001130)20:14<1823::AID-JOC566>3.0.CO;2-B
Web of Science® Google Scholar
Osnas, J.L.D., Lichstein, J.W., Reich, P.B. & Pacala, S.W. (2013) Global leaf trait relationships: mass, area, and the leaf economics spectrum. Science, 340, 741–744.
10.1126/science.1231574
CAS PubMed Web of Science® Google Scholar
Pan, Y., Birdsey, R.A., Fang, J. et al. (2011) A large and persistent carbon sink in the world's forests. Science, 333, 988–993.
10.1126/science.1201609
CAS PubMed Web of Science® Google Scholar
Poorter, L., Wright, S.J., Paz, H. et al. (2008) Are functional traits good predictors of demographic rates? Evidence from five Neotropical forests. Ecology, 89, 1908–1920.
10.1890/07-0207.1
CAS PubMed Web of Science® Google Scholar
Poorter, H., Niinemets, Ü., Poorter, L., Wright, I. & Villar, R. (2009) Causes and consequences of variation in leaf mass per area (LMA): a meta-analysis. New Phytologist, 182, 565–588.
10.1111/j.1469-8137.2009.02830.x
CAS PubMed Web of Science® Google Scholar
Poorter, H., Lambers, H. & Evans, J.R. (2014) Trait correlation networks: a whole-plant perspective on the recently criticized leaf economic spectrum. New Phytologist, 201, 378–382.
10.1111/nph.12547
PubMed Web of Science® Google Scholar
R Development Core Team (2014) R: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. Available at: www.r-project.org/.
Google Scholar
Russo, S.E., Brown, P., Tan, S. & Davies, S.J. (2008) Interspecific demographic trade-offs and soil-related habitat associations of tree species along resource gradients. Journal of Ecology, 96, 192–203.
10.1111/j.1365-2745.2007.01330.x
Web of Science® Google Scholar
Shvidenko, A. & Nilsson, S. (2002) Dynamics of Russian forests and the carbon budget in 1961–1998: an assessment based on long-term forest inventory data. Climatic Change, 55, 5–37.
10.1023/A:1020243304744
CAS Web of Science® Google Scholar
Sides, C.B., Enquist, B.J., Ebersole, J.J., Smith, M.N., Henderson, A.N. & Sloat, L.L. (2014) Revisiting Darwin's hypothesis: does greater intraspecific variability increase species' ecological breadth? American Journal of Botany, 101, 56–62.
10.3732/ajb.1300284
PubMed Web of Science® Google Scholar
Smith, W.B., Miles, P.D., Perry, C.H. & Pugh, S.H. (2007) Forest resources of the United States, 2007. General Technical Report WO-78. US Department of Agriculture, Forest Service, Washington Office, Washington, DC.
Google Scholar
Sutherland, W.J., Freckleton, R.P., Godfray, H.C. et al. (2013) Identification of 100 fundamental ecological questions. Journal of Ecology, 101, 58–67.
10.1111/1365-2745.12025
Web of Science® Google Scholar
Valladares, F. & Niinemets, Ü. (2008) Shade tolerance, a key plant feature of complex nature and consequences. Annual Review of Ecology, Evolution, and Systematics, 39, 237257.
10.1146/annurev.ecolsys.39.110707.173506
Web of Science® Google Scholar
Vayreda, J., Gracia, M., Martínez-Vilalta, J. & Retana, J. (2013) Patterns and drivers of regeneration of tree species in forests of peninsular Spain. Journal of Biogeography, 40, 1252–1265.
10.1111/jbi.12105
Web of Science® Google Scholar
Violle, C., Navas, M.L., Vile, D., Kazakou, E., Fortunel, C., Hummel, I. & Garnier, E. (2007) Let the concept of trait be functional! Oikos, 116, 882–892.
10.1111/j.0030-1299.2007.15559.x
Web of Science® Google Scholar
Violle, C., Enquist, B.J., McGill, B.J., Jiang, L., Albert, C.H., Hulshof, C., Jung, V. & Messier, J. (2012) The return of the variance: intraspecific variability in community ecology. Trends in Ecology and Evolution, 27, 244–252.
10.1016/j.tree.2011.11.014
PubMed Web of Science® Google Scholar
Violle, C., Reich, P.B., Pacala, S.W., Enquist, B.J. & Kattge, J. (2014) The emergence and promise of functional biogeography. Proceedings of the National Academy of Sciences USA, 111, 13690–13696.
10.1073/pnas.1415442111
CAS PubMed Web of Science® Google Scholar
Westoby, M., Falster, D.S., Moles, A.T., Vesk, P.A. & Wright, I.J. (2002) Plant ecological strategies: some leading dimensions of variation between species. Annual Review of Ecology and Systematics, 33, 125–159.
10.1146/annurev.ecolsys.33.010802.150452
Web of Science® Google Scholar
Westoby, M., Reich, P.B. & Wright, I.J. (2013) Understanding ecological variation across species: area-based vs mass-based expression of leaf traits. New Phytologist, 199, 322–323.
10.1111/nph.12345
CAS PubMed Web of Science® Google Scholar
Wright, I.J., Reich, P.B., Westoby, M. et al. (2004) The worldwide leaf economics spectrum. Nature, 428, 821–827.
10.1111/j.1469-8137.2005.01349.x
CAS PubMed Web of Science® Google Scholar

Data Accessibility

The data used are available from three different sources: (1) functional trait data are available at the TRY database (https://www.try-db.org/TryWeb/Home.php), (2) forest structure data are available at http://natura.uab.es/mirabosc/, and (3) climatic data are available at http://www.opengis.uab.cat/acdc/en_index.htm.

Albert Vilà-Cabrera is a post-doctoral research at CREAF. His major research interest is the understanding of the structure and functioning of plant populations and communities and their responses to environmental changes.

Jordi Martínez-Vilalta is senior lecturer at Universitat Autònoma Barcelona (UAB) and researcher at CREAF. His work is focused on the study of forest communities and emphasizes drought impacts in the context of climate change.

Javier Retana is a professor at UAB and director of CREAF. His research is focused on forest dynamics and the effects of disturbances on animal and plant communities.

Citing Literature

Volume24, Issue12

December 2015

Pages 1377-1389

Functional trait variation along environmental gradients in temperate and Mediterranean trees

Abstract