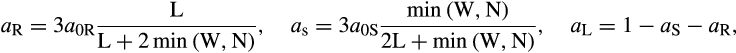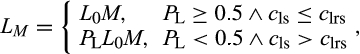Leveraging plant hydraulics to yield predictive and dynamic plant leaf allocation in vegetation models with climate change
Abstract
Plant functional traits provide a link in process-based vegetation models between plant-level physiology and ecosystem-level responses. Recent advances in physiological understanding and computational efficiency have allowed for the incorporation of plant hydraulic processes in large-scale vegetation models. However, a more mechanistic representation of water limitation that determines ecosystem responses to plant water stress necessitates a re-evaluation of trait-based constraints for plant carbon allocation, particularly allocation to leaf area. In this review, we examine model representations of plant allocation to leaves, which is often empirically set by plant functional type-specific allometric relationships. We analyze the evolution of the representation of leaf allocation in models of different scales and complexities. We show the impacts of leaf allocation strategy on plant carbon uptake in the context of recent advancements in modeling hydraulic processes. Finally, we posit that deriving allometry from first principles using mechanistic hydraulic processes is possible and should become standard practice, rather than using prescribed allometries. The representation of allocation as an emergent property of scarce resource constraints is likely to be critical to representing how global change processes impact future ecosystem dynamics and carbon fluxes and may reduce the number of poorly constrained parameters in vegetation models.
1 INTRODUCTION
Forested regions around the globe represent ~363 Pg C (equivalent to ~170 ppm CO2 if released to the atmosphere) and sequester ~2.3 Pg C annually, or approximately 25% of annual anthropogenic carbon emissions (Bonan, 2008; Pan et al., 2011). Tree carbon allocation to leaf biomass, and the resultant ratio of leaf area (AL) relative to sapwood area (area of tree water transport tissue, AS), influences ecosystem carbon drawdown and water loss through the stomata. Leaf allocation is shaped both by intrinsic plant physiological traits (Bartlett, Scoffoni, & Sack, 2012; Choat et al., 2012) and the local environment (Martinez-Vilalta et al., 2009; Mencuccini & Bonosi, 2001; Mencuccini & Grace, 1994). However, due to the elusive nature of the biological mechanisms underlying tree leaf allocation, vegetation models often determine AL using fixed coefficients or scaling laws. Uncertainty in leaf allocation strategy introduced using fixed coefficient or scaling law methods impacts AL projections, the ratio of AL:AS, and the sensitivity of vegetation productivity to environmental drivers.
The objective of this review is to provide an overview of how leaf allocation strategy is represented in current state-of-the-art numerical vegetation models, how allocation impacts internal plant water stress, and ultimately how allocation is tied to predictions for terrestrial productivity. First, we discuss the theory, history, and fundamental limitations of the use of allometric equations, which are a common technique used to standardize leaf biomass allocation estimates among species or plant functional groups. Second, we examine the different representations of plant carbon allocation to leaves in vegetation models ranging in scales and complexities from single plant models to ecosystem models and large-scale vegetation models. Third, we provide context on the role of leaf allocation in the physiology of plant water limitation. Fourth, we propose a way for moving forward with prognostic leaf allocation in large-scale models to improve predictive abilities for plant productivity and water stress. We conclude with a discussion on how the plant hydraulics framework presented here can inform the global optimization problem of understanding allocation broadly in the presence of multiple limiting resources.
2 ALLOMETRIC BIOMASS EQUATIONS: HISTORY AND THEORY
The fields of forestry and ecology rely heavily on allometric regression equations, which relate tree size to plant biomass, to quantify species-specific allocation strategies. Numerous species- and site-specific allometric regression models have been developed over the years, beginning in prevalence the 1960s, that document the relationships between tree size (often diameter at breast height, dbh, or diameter at tree base) and plant biomass components, including total aboveground tree biomass, stem biomass, bark biomass, branch biomass, and leaf biomass (Baskerville, 1972; Chave et al., 2014; Jenkins, Chojnacky, Heath, & Birdsey, 2003; Ploton et al., 2016; Ter-Mikaelian & Korzukhin, 1997; Whittaker & Woodwell, 1968; Zianis, Muukkonen, Mäkipää, & Mencuccini, 2005). These equations are useful for many applications. However, literature-reported single-species allometric regression model performance is often no better at predicting out-of-sample tree allometries than multispecies models because substantial intraspecific variation in allocation exists due to local environmental conditions (Fayolle, Doucet, Gillet, Bourland, & Lejeune, 2013; Lines, Zavala, Purves, & Coomes, 2012). Indeed, it has been documented that the largest source of error in scaling from trees to forests biomass estimates is error associated with allometric model choice, rather than errors in tree measurement or sampling uncertainty associated with plot size or composition (Chave et al., 2004). Furthermore, general allometry equations perform particularly poorly when predicting local leaf or tree crown biomass (Bond-Lamberty, Wang, & Gower, 2002; Ploton et al., 2016), making allometric regression models inaccurate when determining tree allocation strategies to leaves, and consequently increasing tree AL:AS uncertainty in out-of-sample environmental conditions. Indeed, the need to use “local” allometric equations or to validate equations locally has long been emphasized in the forestry literature (Ketterings, Coe, Van Noordwijk, Ambagau, & Palm, 2001).
Thus, a fundamental question arises: how much does leaf allocation (and AL:AS) vary within a species for trees of equivalent size? A recently published Biomass And Allometry Database (BAAD) for woody plants (Falster et al., 2015) provides initial insights and has strong potential for improving our understanding of the complexity underlying biotic and abiotic allocation factors. The BAAD is a compilation of individual-level allocation data from numerous previously published studies that span thousands of individual woody plants, hundreds of species, and different growth environments around the globe. Although the number of observations with concurrent documentation of AL and AS for a given tree within the BAAD is relatively sparse (863 observations), assuming tree trunk basal area (BA) as proportional to AS 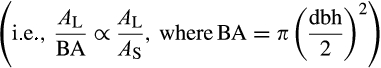 provides enough additional data for us to perform a synthesis of 91 unique studies, comprising 9,585 individuals, 338 species, 192 genera, and 81 families. In addition, BA presumably better reflects the biomechanical and hydraulic limits for AL, making this assumption mechanistically consistent with our framework relating AL:BA to AL:AS.
provides enough additional data for us to perform a synthesis of 91 unique studies, comprising 9,585 individuals, 338 species, 192 genera, and 81 families. In addition, BA presumably better reflects the biomechanical and hydraulic limits for AL, making this assumption mechanistically consistent with our framework relating AL:BA to AL:AS.
We performed variance decomposition to determine the taxonomic scales of variation in AL:BA. We used linear mixed effects models for log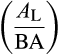 . First, we built a model including a fixed intercept, fixed effect method for calculating AL:AS (directly from measurements of AS at DBH or basal height or indirectly from basal diameter or DBH), and nested random effects for family, genus, and species. We compared the size of the random effects' variance parameters within species (i.e., residual variance), within genus, within family, and between families and found that 50% of the observed variation in AL:BA across the BAAD database occurred within species (Figure 1). We then included a fixed effect for log(tree height) for each plant species (because AS should theoretically increase more rapidly than AL with tree height, as resistance to sap flow increases with tree height). Based on the marginal R2 of the model with and without the species-level height effect, we determined that roughly three-fifths of the within-species variation (29% of the total variation in AL:BA) could be attributed to within-species variation related to tree size (Figure 1, dashed line). Interestingly, within-species patterns of AL:BA versus height, while negative on average, varied enormously across species, both in strength and direction (Figures S1 and S2).
. First, we built a model including a fixed intercept, fixed effect method for calculating AL:AS (directly from measurements of AS at DBH or basal height or indirectly from basal diameter or DBH), and nested random effects for family, genus, and species. We compared the size of the random effects' variance parameters within species (i.e., residual variance), within genus, within family, and between families and found that 50% of the observed variation in AL:BA across the BAAD database occurred within species (Figure 1). We then included a fixed effect for log(tree height) for each plant species (because AS should theoretically increase more rapidly than AL with tree height, as resistance to sap flow increases with tree height). Based on the marginal R2 of the model with and without the species-level height effect, we determined that roughly three-fifths of the within-species variation (29% of the total variation in AL:BA) could be attributed to within-species variation related to tree size (Figure 1, dashed line). Interestingly, within-species patterns of AL:BA versus height, while negative on average, varied enormously across species, both in strength and direction (Figures S1 and S2).
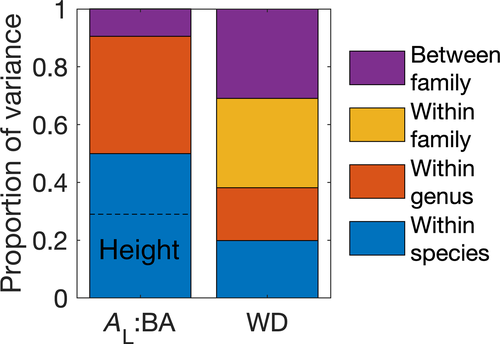
The substantial within-species variation, even when controlling for tree size, stands in contrast to numerous other plant functional traits that are often included in vegetation models (Rosas et al., 2019). As an example, we performed an equivalent analysis on wood density (WD), a widely used plant functional trait. We leveraged the huge within-species variation in WD within the BAAD, combined with cross-species information from the Global Wood Density Database (Zanne et al., 2009). Our synthesis comprised of 217 unique studies, 19,997 measurements, 8,486 species, 1,694 genera, and 211 families. In contrast to AL:BA, the majority of the variation in WD occurred at large taxonomic scales (e.g., across plant families, Figure 1). The strong intraspecific variation that is particularly apparent in AL:BA indicates that environment strongly influences AL:BA (~AL:AS), perhaps more so than many common species-specific functional traits. Thus, while allometric functions relating plant size to plant investment in leaves have existed for over half a century and are ubiquitous, the generality and out-of-sample applicability of these functions tend to be low, posing considerable challenges to the formulation of fixed trait-based allocation algorithms in mechanistic vegetation models. This strong intraspecific variation implies that AL:AS may need to be predicted from first principles, rather than prescribed as a functional trait.
3 LEAF ALLOCATION IN MECHANISTIC VEGETATION MODELS
There are numerous empirical and optimization-based approaches to determining vegetation allocation that often vary with the spatial scope of the model due to computational costs and trade-offs (Tables 1-3; De Kauwe et al., 2014; Franklin et al., 2012; Walker et al., 2014). In many vegetation models that run at large spatial scales and/or over long time periods, vegetation is represented in an aggregated manner analogous to a “big leaf” in each grid cell due to the large computational costs associated with predicting long-term vegetation dynamics across the globe. In this class of vegetation model, allocation often follows an empirical approach where a fixed fraction of net primary productivity (NPP) is allocated to each of leaves, stem, and fine roots (as well as other costs such as reproduction). This includes both models that are coupled to climate models such as the Community Land Model (CLM) family, as well as a number of models that have not been run coupled to climate models and are generally operated at scales smaller than the globe (Tables 1 and 2).
| Model | Type | Dynamic vegetation? | Plant hydraulics? | Leaf allocation | Reference |
|---|---|---|---|---|---|
| ACONITE | Big leaf | N | N | Flexible | Thomas and Williams (2014) |
| aDGVM | Individual | Y | N | Flexible | Scheiter and Higgins (2009) |
| CABLE | Big leaf | N | N | Fixed | Wang et al. (2011) |
| CLM4 | Big leaf | N | N | Fixed (modified) | Oleson et al. (2010) |
| CLM5 | Big leaf | N | Y | Fixed (modified) | Lawrence et al. (2018) |
| CLM-FATES | Cohort | Y | N | Flexible | Lawrence et al. (2018) |
| ED2 | Cohort | Y | N | Fixed | Medvigy et al. (2009) |
| ED2-hydro | Cohort | Y | Y | Fixed | Xu et al. (2016) |
| Hybrid 3.0 | Individual | Y | N | Flexible | Friend, Stevens, Knox, and Cannell (1997) |
| JeDi-DVGM | Big leaf | Y | N | Fixed | Pavlick, Drewry, Bohn, Reu, and Kleidon (2013) |
| LM3-PPA | Cohort | Y | N | Fixed (modified) | Weng et al. (2015) |
| LPJ-DVGM | Cohort | Y | N | Flexible | Sitch et al. (2003) |
| LPJ-Magnani Hybrid | Cohort | Y | N | Flexible | Magnani et al. (2000); Zaehle et al. (2006) |
| ORCHIDEE | Big leaf | Y | N | Flexible | Friedlingstein, Joel, Field, and Fung (1999); Krinner et al. (2005) |
| SEIB-DGVM | Individual | Y | N | Flexible | Sato, Itoh, and Kohyama (2007) |
| TREES | Individual | N | Y | Flexible | Mackay et al. (2015) |
| Model | Detailed description of leaf allocation |
|---|---|
| CABLE | Big leaf model with fixed allocation coefficients. Annual NPP productivity is determined from annual carbon assimilation corrected for respiratory losses. The growth/decay of biomass during the steady state part of the growing season is determined by partitioning of NPP between leaves, roots, and wood according to PFT-specific fixed coefficients. |
| CLM4 |
Big leaf model with a modified version of fixed allocation coefficients. After accounting for the carbon costs of maintenance respiration, remaining photosynthetic carbon can be allocated to new growth. Allocation to new growth is calculated for all of the plant carbon and nitrogen state variables based on specified C:N ratios for each tissue type and allometric parameters that relate allocation between various tissue types. Leaf carbon allocation is a dynamic function of NPP where the ratio of new stem to new leaf growth (a) is
where NPP an annual value summed over the previous year. This results in increased woody allocation in high NPP environments. |
| CLM5 |
Big leaf model with a modified version of fixed allocation coefficients. After accounting for the carbon costs of maintenance respiration, remaining photosynthetic carbon can be allocated to new growth. Allocation to new growth is calculated for all of the plant carbon and nitrogen state variables based on specified C:N ratios for each tissue type and allometric parameters that relate allocation between various tissue types. Leaf carbon allocation is a dynamic function of NPP where the ratio of new stem to new leaf growth (a) is
where NPP is an annual value summed over the previous year. This results in increased woody allocation in high NPP environments. |
| ED2 |
Cohort-based model. After accounting for respiration costs, remaining photosynthetic carbon can be allocated to new growth. During the steady-state part of the growing season, allocation is determined by a functional relationship dependent on cohort dbh and PFT-specific leaf–dbh biomass relationships
where bl is leaf biomass and a and b are fixed PFT-specific constants. |
| ED2-hydro |
Cohort-based model. After accounting for respiration costs, remaining photosynthetic carbon can be allocated to new growth. During the steady-state part of the growing season, allocation is determined by a functional relationship dependent on cohort dbh and PFT-specific leaf–dbh biomass relationships
where bl is leaf biomass and a and b are fixed PFT-specific constants. |
| JeDi-DVGM | Big leaf model where carbon allocation to each tissue pool is proportional to the size of the storage pool. Allocation is determined by fixed coefficients that are PFT-specific, range from 0 to 1, and are mathematically constrained such that they sum to less than 1. The allocation coefficient fraction is designed to represent functional trade-offs in allocation: A higher allocation to fine roots enhances plant water uptake ability, but this comes at the expense of allocation to the above-ground tissues, decreasing the ability to capture light for photosynthesis. |
| LM3-PPA | Cohort-based model where empirical allometric equations that are PFT-specific and dependent on cohort dbh relate woody biomass (including coarse roots, bole, and branches), crown area, and stem diameter. Another set of fixed equations relate leaf mass to crown area and root mass to leaf mass. The target crown LAI is set by PFT-specific equations and cohort light status (e.g., understory vs. overstory). |
- Abbreviations: NPP, net primary productivity; PFT, plant functional type.
| Model | Detailed allocation description |
|---|---|
| ACONITE | Big leaf model. At each daily time step, instantaneous carbon (C) return is calculated (which accounts for gross photosynthesis, growth respiration, and maintenance respiration of additional leaf allocation) to determine whether investing further C and nitrogen (N) in foliage will result in a positive C net uptake (up to some maximum leaf carbon which is set on an annual timescale). If the maximum leaf allocation has been reached or N limits further leaf allocation, C is allocated to fill storage, grow wood, or increase fine roots. Further surplus C is allocated for N fixation. At the end of each annual cycle, integrated annual marginal C return is used to recompute maximum leaf C and N and maximum root C and N. The marginal changes to photosynthesis from added leaf C, added leaf N, and added leaf C and N together are iterated over using to determine the marginal carbon return. |
| aDGVM |
Individual-based model. After covering respiratory costs, carbon is allocated to root, stem, or leaf in response to limiting resources (i.e., light-limited trees preferentially allocate to stem, water-limited trees preferentially allocate to roots, photosynthetically limited trees preferentially allocate to leaves). Thus, allocation is responsive to environmental conditions according to the following relations:
|
| CLM-FATES | Cohort-based model where photosynthetic carbon is allocated according to the following hierarchy: priority is given to maintenance respiration, followed by tissue maintenance and storage, then allocation to live biomass, and then to the expansion of structural and live biomass pools. The maximum carbon allocation to leaf biomass and other tissues is determined using allometric constants, a scheme based on the Ecosystem Demography model. However, target leaf biomass includes an optimization-based “trimming” factor that allows for removal of leaves in negative carbon balance within the canopy due to light limitation. If the annual maintenance cost of the lowest leaf layer is less than the carbon gain, the canopy is trimmed by an increment which is applied up through the next calendar year. |
| Hybrid 3.0 | Individual-based model. If annual net carbon balance is positive (after allowing for carbon required to cover respiration and turnover costs), carbon is allocated to new growth and growth respiration. Allocation occurs assuming (a) a fixed allometric relationship between diameter at breast height and woody carbon mass; (b) that leaf area is linearly proportional to sapwood area at breast height; and (c) that there is a fixed ratio between leaf and fine root masses. Allocation coefficients are PFT specific. The carbon balance of the lowest leaf layer of each tree crown is calculated daily. If, at the end of each year, carbon balance is negative, the leaf area is reduced by the amount present in the bottom leaf layer. This results in the foliage area being optimized on an annual timestep based on carbon gain. |
| LPJ-DVGM | Cohort-based model. After accounting for maintenance and growth respiration and annual reproductive costs, the remaining carbon is available for producing new tissue. Scaling rules constrain allocation among leaves, fine roots, and sapwood. First, leaf area is related to sapwood area through a constant. Second, rooting biomass is related to leaf biomass through a fixed coefficient and a water limitation factor that is an annual average value ranging between 0 and 1 that is used in calculating this year's leaf to fine root mass ratio for the allocation routine. Thus, water-limited environments require plants to allocate relatively more resources to fine root biomass compared to leaves. This results in increased respiration costs associated with roots and a loss of photosynthetic potential as the cost of having to acquire water and nutrients increases. |
| LPJ-Magnani Hybrid | Cohort-based model where allocation of carbon to conductive sapwood and absorbing roots is optimal with respect to achieving minimal whole-plant leaf-specific hydraulic resistance while supporting a maximum of transpiring leaf tissue. Increased allocation to fine roots with tree height decreases below-ground plant hydraulic resistance which compensates for the increase in leaf-specific resistance of the stem with tree height, maintaining a constant whole-plant leaf-specific hydraulic conductance. Increasing respiratory costs relative to carbon gain to maintain whole-plant leaf-specific hydraulic conductance with increasing tree height reduces growth efficiency, resulting in a decline in productivity. |
| ORCHIDEE |
Big leaf model where carbon is allocated to root, stem, and leaf in response to limiting resources (i.e., water, light, nitrogen). No carbon is allocated to leaves when the leaf area index (LAI) is above a PFT-specific annual maximum. Allocation is specified as:
where aR, aS, and aL describe carbon allocated to roots, stems, and leaves, respectively. a0R and a0S describe the fractions of carbon allocated to roots and stems when resources are not limiting. Both a0R and a0S are set to 0.3, giving a leaf allocation of 0.4 under conditions where resources are totally nonlimiting. Resource availabilities of Light (L), water (W), and nitrogen (N) range from 0.1 (severely limited) to 1.0 (readily available) where W is dependent on monthly soil water content, L is dependent on canopy LAI, and N is assumed to be a function of soil temperature and soil moisture. |
| SEIB-DGVM | Individual-based model where growth and allocation occur at three separate timescales. At the daily timescale, after respiratory costs are accounted for, leaf and fine root turnover is replenished according to fixed ratios between leaf and fine root biomass. Leaf biomass is constrained by two functional relationships based on fixed, PFT-specific coefficients and carbon availability. Functional relationships include maximum crown surface area and maximum cross-sectional area of sapwood. Trunk growth and expansion of crown area occur at the monthly timescale according to fixed constants and PFT-specific allometric relationships. At the annual timescale, the height of the lowest branch increases as a result of self-pruning of the bottom of the crown layer. During pruning, a maximum of 10 crown disks can be pruned at one time, each at a depth of 10 cm. Crown disks are purged based on the expected profit (carbon gain) of a particular crown disk. |
| TREES |
Individual-based model. After accounting for respiration costs, remaining photosynthetic carbon can be allocated to new growth. Leaf turnover is dependent on hydraulic impairment of the lateral stem:
where L0 is initial leaf area index, M is unstressed leaf mortality rate, PL is lateral stem proportional loss of conductivity, and cls and clrs are, respectively, the Weibull c parameters for the lateral stem and the lateral shallow root. Allocation to stem is fixed. |
Another class of vegetation model, the “individual”- or “cohort-based” model, resolves individual plants. Cohort-based vegetation models generally use allometric scaling functions from the forestry literature that relate model-predicted cohort dbh to tree stem, leaf, and root biomass using fixed relationships (see Section 2; Tables 1 and 2). Thus, NPP partitioning to different tree tissues in cohort-based vegetation models is determined by fixed plant functional type (PFT)-specific parameters and tree size. Although computationally more intensive than the big leaf approach, cohort-based vegetation models are more skilled at capturing competition for light and vegetation demographic processes. Furthermore, significant progress is being made toward incorporating cohort-based vegetation models in the next generation of coupled climate–vegetation models used for global-scale climate change projections (Fisher et al., 2018).
Despite the fact that allocation to leaves and other organs in the fixed allocation approach is broadly constrained by PFT-specific fixed coefficients, the fixed coefficient representation of allocation does allow for limited allometric perturbations in response to environment. The representation of phenological processes is one such example of environmental responsiveness. In most fixed allocation vegetation models, deciduous PFTs allocate extra carbon resources to leaves at the beginning of the growing season to meet some target leaf biomass, and cease allocating carbon to leaves at the end of the growing season (though exact allocation fractions are model specific). Phenological responsiveness has been incorporated for both temperate and drought deciduous ecosystems in a number of vegetation models. The representation of allocation to leaves in CLM4 and CLM5 is another such example, where the ratio of NPP going to leaves relative to stem is a function of previous year's NPP such that, as vegetation productivity (NPP) increases, more carbon is allocated to wood relative to leaves (Table 2). A third example of environmental responsiveness that is present in numerous fixed allocation models occurs when respiratory costs exceed plant carbon gain. For example, in the Ecosystem Demography (ED) model family, target leaf biomass is fixed based on PFT and dbh. But, when respiration and leaf and root turnover exceed photosynthetic carbon gains, trees cannot allocate to meet target leaf allometries due to environmental stress. Overall, these approaches have begun to incorporate simple environmental feedbacks on plant allometry. However, allocation schemes are generally limited to prescribed tissue ratios that are drawn from the allometric equation literature. Furthermore, allocation is largely rooted in carbon-based allometries, and other ecologically relevant metrics that have been shown to be important in an ecosystem context such as leaf mass per area (Duursma & Falster, 2016; Falster, Duursma, & FitzJohn, 2018) are not often considered.
Because plant hydraulic processes are increasingly represented in both big leaf and cohort-based vegetation models that use a fixed allocation approach (see below), it is important to understand how fixed allocation and sub-hourly variations in water stress impact predictions of carbon and energy fluxes. The widespread fixed allocation approach of “growing the same tree everywhere” for a given model PFT is inconsistent with the huge forestry literature on the influence of site conditions on leaf allocation (Bond-Lamberty et al., 2002; Fayolle et al., 2013; Jenkins et al., 2003; Ketterings et al., 2001; Ter-Mikaelian & Korzukhin, 1997), making it important to consider the impacts on estimates for global terrestrial productivity.
4 THE IMPORTANCE OF LEAF ALLOCATION FOR THE PHYSIOLOGY OF VEGETATION WATER STRESS
Plant allocation to leaves, plant physiological traits, and local environmental conditions interact to affect water supply and demand and determine tree water status, gas exchange, and productivity. While water availability is set by climatic, hydrologic, and edaphic factors, tree water demand is determined in large part by plant morphology and leaf allocation. Water loss through AL must be matched by water flow through AS, giving the plant considerable agency over the flow of water through the soil–plant–atmosphere continuum purely based on its relative allocation to evaporative (AL) versus solely conductive (AS) tissue area. Because water stress is the result of unmet plant water demand, allocation to AL is a major seasonal to multi-annual control over a plant's exposure to water stress under limiting water supply. Furthermore, water stress has important implications for plant productivity: If no other physiological changes occur, an over allocation of leaves, resulting in a large AL:AS, will cause stomatal closure to prevent excessive water loss, decrease intercellular CO2 (Ci), and decrease leaf-level photosynthesis.
We illustrate the underlying plant physiological response to AL-driven changes in water demand with a fixed water supply using a simple tree model (the Hydraulic Optimization Theory for Tree and Ecosystem Resilience or HOTTER model). HOTTER uses a single resistor to represent whole-plant hydraulic transport up to the substomatal cavity and a hydraulic optimization-based stomatal conductance model (Trugman, Detto, et al., 2018; Wolf, Anderegg, & Pacala, 2016; Figure 2). While the model contains some necessary simplifications, it is broadly consistent with the Ohm's law analogy for hydraulic elements in series and the observed responses of gas exchange to changes in leaf-specific hydraulic conductance (Hubbard, Ryan, Stiller, & Sperry, 2001; Sperry et al., 2016; Sperry, 2000).
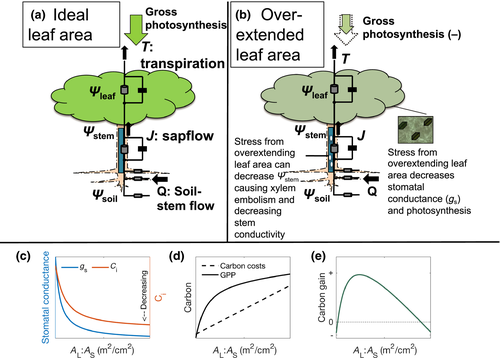
As illustrated by the HOTTER model, when a tree increases water demand via increases in AL, given fixed environmental and physiological conditions, the tree hydraulic conductance (K) per BA increases to a maximum as more leaves are added and the percent whole-tree resistance in leaves declines. Consequently, AL increases faster than K, leading to a monotonic decline in tree hydraulic conductance per AL and hence transpiration per AL. Stomatal closure reduces transpiration per AL in step with the reduction in hydraulic conductance per AL, thus maintaining an approximate homeostasis in leaf water potential. The stomatal control on leaf pressure helps avoid the costs of physiological damage due to water stress (Anderegg et al., 2018; Wolf et al., 2016), but drives down leaf-level photosynthesis by limiting Ci (Figure 2c). Additionally, at higher AL, self-shading further limits water and carbon fluxes. The reduction in photosynthesis per AL results in total tree photosynthesis (photosynthesis per leaf times AL) increasing less rapidly than the linear increase in the cost of leaf canopy construction and maintenance (respiration). Thus, there is an optimal AL:AS that maximizes the benefit of increased tree photosynthesis relative to canopy construction and respiratory cost (Figure 2d,e). Critically, the optimal AL:AS is not fixed for a given set of plant hydraulic traits. Rather AL:AS depends on how local environmental conditions influence the cost–benefit ratio of growing AL: In drier climate conditions, there are lower carbon benefits, resulting in a lower optimal AL compared to wetter conditions where a higher AL is optimal (Westoby, Cornwell, & Falster, 2012). Given that trees within an individual species can grow along relatively broad environmental gradients, significant intraspecific allocational changes to AL can result depending on local environmental conditions (Anderegg & HilleRisLambers, 2016; DeLucia, Maherali, & Carey, 2000; Martinez-Vilalta et al., 2009; Mencuccini & Bonosi, 2001; Mencuccini & Grace, 1994; Pinol & Sala, 2000; Rosas et al., 2019), and are likely a driver behind the large intraspecific variation in AL:BA observed across in the BAAD (Figure 1).
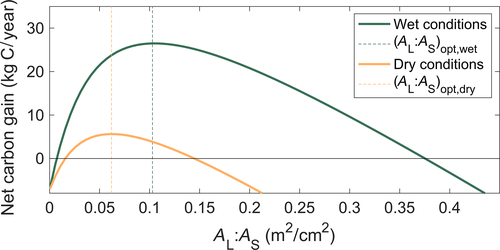
To demonstrate the impact of allocation to leaves on tree-level productivity, we used the HOTTER model with input atmospheric vapor pressure deficit (VPD, a metric of atmospheric dryness), soil water content, and atmospheric CO2 concentration. We ran simulations varying AL:AS under two environmental regimes: a drier environment (VPD = 1,500 Pa and soil water potential (Ψsoil) = −0.6 MPa) and a wetter environment (VPD = 1,000 Pa and Ψsoil = −0.3 MPa). All other traits, tree size, and atmospheric CO2 were kept constant. In the case where AL:AS determined based on the “optimal” AL:AS for the wetter environment (i.e., the AL:AS that maximized instantaneous tree carbon gain per respiratory and turnover costs given the wetter environment), but the tree was experiencing the drier environment, such as might be the case if the allocation functional relationship were derived from trees in a wet environment and applied to modeling tree allocation in a drier environment, the tree overallocated to AL by almost twofold relative to the optimum, resulting in a potential ~35% loss of plant carbon gain due to extra respiratory costs and stomatal closure (Figure 3).
Critically, tree-level responses in productivity resulting from AL:AS and local environmental conditions significantly affect total ecosystem water fluxes and carbon gain. As an illustrative example of the consequences of fixed allometries in hydraulically enabled models for ecosystem-level carbon predictions, we used site-specific allometry to constrain the leaf allocation strategy of aspen trees growing across a resource gradient between central Alaska and central Canada. We used the ED2 model (Trugman et al., 2016), a cohort-based vegetation model with an explicit representation of plant hydraulic processes designed to run at spatial scales ranging from a flux tower footprint to regional scales (Medvigy, Wofsy, Munger, Hollinger, & Moorcroft, 2009; Medvigy & Moorcroft, 2012). We performed two separate simulations forced with identical climate over a 200 year spin-up, but we varied the allometric relationship between dbh and leaf biomass according to two different allometries, one derived from trees sampled in a drier location in central Alaska (Yarie, Kane, & Hall, 2007) and one derived from trees sampled in a wetter location in central Canada (Bond-Lamberty et al., 2002). Depending on the allometric constraints used, ED2 predicted either rapid biomass accumulation within the first 50 years to a stable forest BA (a metric of forest density) of ~27 cm2/m2, compared to a much slower biomass accumulation rate over the multi-century period with a maximum accumulated BA of 20 cm2/m2 (~30% lower) at the end of the simulation (Figure 4). While particularly important in models that include plant hydraulics, this central role of allometric equations in influencing carbon pools and fluxes is visible in a wide range of models and ecosystems and has been identified as a major source of model uncertainty in response to elevated CO2 concentrations (De Kauwe et al., 2014; Walker et al., 2014).

5 PLANT HYDRAULICS IN MECHANISTIC VEGETATION MODELS
As illustrated by the HOTTER and ED2 vegetation models above, plant water transport links the carbon costs and benefits of plant allocation strategy. Thus, the representation of water transport in mechanistic models is the scaffolding upon which allometric schemes feedback to influence modeled plant water stress. Many large-scale vegetation models represent the plant physiological response to supply- and demand-driven water stress using two distinct pathways rather than explicitly representing plant hydraulic transport along the soil–plant–atmosphere continuum (see, Sperry & Love, 2015; Fatichi, Pappas, & Ivanov, 2016; Mencuccini, Manzoni, & Christoffersen, 2018 for detailed reviews of the representation of plant water stress and water transport). Physiological responses to supply-driven soil moisture stress are represented in many vegetation models using an empirical factor based on soil moisture and root biomass that downregulates either photosynthesis or stomatal conductance as soil water decreases below field capacity (Trugman, Medvigy, Mankin, & Anderegg, 2018). Demand-driven water stress responses are represented through an empirical equation that captures the observed relationships between stomatal conductance and environmental drivers, typically humidity or VPD, CO2 concentrations, and photosynthesis (Ball, Woodrow, & Berry, 1987; Leuning, 1995). Importantly, the treatment of supply- and demand-driven limitations as separate pathways influencing water use is unlikely to capture the complex and nonlinear joint influence on stomatal conductance through leaf water potential (Sperry et al., 2017).
Vegetation models that do resolve the plant physiological response to water stress use several tissue-level plant hydraulic traits of roots, stems, and leaves, including saturated xylem hydraulic conductivity and the water potential at 50% loss of conductivity. With a resistor-based representation of water transport and a connection between leaf water stress and stomatal conductance (Figure 2), hydraulically enabled vegetation models mechanistically link tissue-level stresses to ecosystem-level carbon and water fluxes (Christoffersen et al., 2016; Kennedy et al., 2019; Xu, Medvigy, Powers, Becknell, & Guan, 2016). Coupling of plant hydraulic transport to gas exchange at the stomata can be done either using an empirical function where stomatal conductance is parameterized as a function of leaf water potential, in a manner similar to that of the empirical soil moisture stress function above, or via optimization approaches. A recently proposed “carbon maximization” or “gain-risk” optimization that explicitly balances the benefit of additional photosynthesis against the risk of hydraulic dysfunction from falling water potentials (Eller et al., 2018; Sperry et al., 2017; Wolf et al., 2016) has yielded predictive improvements of water and carbon fluxes at leaf and whole-tree scales, particularly during drought. The gain-risk approach, coupled with tissue-level hydraulic traits to explicitly predict internal plant moisture stress (water potential), exceeds the accuracy of standard empirical models and other optimization approaches (Anderegg et al., 2018; Venturas et al., 2018; Wang et al., 2019), suggesting that optimization approaches based on hydraulic risk provide a rigorous predictive method for improving predictions of carbon, water, and energy fluxes.
Despite recent improvements, current state-of-the-art representations of plant hydraulic processes in vegetation models have yet to widely consider how the empirical constraint of fixed allometric traits further affects water relations and productivity. These allometric constraints on AL:AS are particularly important when considering that the new representation of plant water relations results in plant water stress varying on sub-hourly scales with leaf water potential (Xu et al., 2016), rather than monthly timescales with soil moisture (Powell et al., 2013; Trugman, Medvigy, et al., 2018). Short temporal variations in water stress impact predictions of sub-hourly carbon fluxes. Thus, because allocation to AL:AS is integral in determining leaf-level gas exchange and Ci, a flexible allocation strategy to AL:AS that considers local water availability is of critical importance to capturing vegetation dynamics and terrestrial carbon, water, and energy fluxes.
6 FLEXIBLE ALLOCATION APPROACHES
A number of vegetation models of varying scales have made progress toward allocation strategies that are flexible in response to resource limitation, some even in the context of plant hydraulics. In general, there are two main methodologies for representing flexible allocation in mechanistic models. One method adjusts allocation coefficients depending on the strongest resource limitation. The second type of approach, optimization-based approaches, seeks to maximize some proxy of fitness, such as productivity (e.g., Figure 3) or reproductive success (Farrior, Dybzinski, Levine, & Pacala, 2013) given different key resource limitation axes. Within the two broad categories of flexible allocation approaches, individual vegetation model implementations vary significantly. In this section, we highlight a few key examples of flexible allocation from both resource-seeking and optimization-based models along different limitation axes including light, water, and nutrients. We include further analyses of flexible allocation schemes in Table 3.
The Adaptive Dynamic Global Vegetation Model (aDGVM) is one example of a large-scale vegetation model that represents allocation such that tissue biomass partitioning is responsive to environmental conditions. In aDGVM, light-limited trees preferentially allocate to stem (King, 1994), water-limited trees preferentially allocate to roots, and photosynthetically limited trees preferentially allocate to leaves (Table 3). Flexible allocation is achieved using empirical light and water limitation factors based on the relative height of a plant and its surrounding competitors and weighted soil moisture within the rooting zone, respectively (Scheiter & Higgins, 2009). Unstressed allocation (when light and water are not limiting) is defined using fixed coefficients dependent on PFT-specific photosynthetic pathway (e.g., C3 or C4).
The Terrestrial Regional Ecosystem Exchange Simulator (TREES) is a stand-scale vegetation model that integrates carbon uptake and allocation with plant hydraulic limitations (Table 3). TREES uses the soil–plant water transport model first described in Sperry, Adler, Campbell, and Comstock (1998) and explicitly couples plant hydraulics to photosynthesis and leaf carbon allocation through its leaf turnover function, which relates leaf mortality rate to lateral stem proportional loss of conductivity (Mackay et al., 2015). Given that a fixed amount of total available carbon is allocated to stem, and that leaf turnover rate varies depending on plant hydraulic stress, this allocation scheme decreases AL from a predetermined initial value that is dependent on site-specific allometries in response to hydraulic impairment. Using a leaf turnover scheme that is responsive to hydraulic stress, TREES was able to accurately captured AL dynamics and species-specific differences in semiarid piñon pine and juniper forests in the southwestern United States (Mackay et al., 2015).
Although computationally more intensive, optimization-based approaches that account for both the morphological and physiological facets of plant above- and belowground allocation responses to resource stress provide a promising alternative to fixed allometric approaches because the optimization allows for allocation to be predicted from plant functional traits and environment (Sperry et al., 2012). In the context of light limitation, the CLM Functionally Assembled Terrestrial Ecosystem Simulator (CLM-FATES) model utilizes an annualized optimization-based “trimming” factor that allows for removal of leaves in negative carbon balance within the canopy if the annual maintenance cost of the lowest leaf layer is less than the carbon gain (Lawrence et al., 2018). This trimming approach is present in a number of vegetation models (Table 3).
In the context of water limitation, Magnani, Mencuccini, and Grace (2000) developed one of the first tree-level models that integrates plant hydraulics to test the hypothesis that age-related declines in forest productivity are driven by allocational shifts to leaves, stem, and fine roots associated with tree height changes. In their model, Magnani et al. (2000) optimize allocation of carbon to conductive sapwood and absorbing root tissues to minimize whole-plant leaf-specific hydraulic resistance while maximizing leaf tissue. Thus, to avoid negative water potentials as a tree grows taller, plant allocation shifts from leaves to transport tissues because resistance to water transport through the tree stem is proportional to tree height, so transport tissue must increase more rapidly than leaf tissue with height. This size-dependent allocation scheme based on plant hydraulic constraints has been implemented in a version of Lund–Potsdam–Jena (LPJ) vegetation model (Hickler, Prentice, Smith, Sykes, & Zaehle, 2006; Zaehle et al., 2006; Table 3). A number of other optimization studies have used the concept of ecohydrological equilibrium, where allocation to leaves and roots is assumed to be in equilibrium with water availability (Eagleson, 1982; Westoby et al., 2012). The ecohydrological equilibrium framework has successfully reproduced observed trends in AL and root distributions across environmental gradients (Cabon, Martínez-Vilalta, Martínez de Aragón, Poyatos, & De Cáceres, 2018; Schymanski, Sivapalan, Roderick, Beringer, & Hutley, 2008; Yang, Medlyn, De Kauwe, & Duursma, 2018).
Furthermore, optimization approaches that account for multiple resource limitations have been implemented, particularly in the context of nutrient and light limitation (Dewar, Franklin, Mäkelä, McMurtrie, & Valentine, 2009; Rastetter & Shaver, 1992). For example, in the simple vegetation model ACONITE (Analyze Carbon and Nitrogen Interactions in Terrestrial Ecosystems), Thomas and Williams (2014) account for the productivity trade-offs associated with allocating carbon and nitrogen to different tissues (Table 3). The ACONITE allocation scheme is executed through a relatively complex multi-timescale optimization: At each daily time step, instantaneous carbon return is calculated to determine whether investing further carbon and nitrogen in foliage will result in a positive net carbon uptake (up to some maximum leaf carbon which is set on an annual timescale). If the maximum leaf allocation has been reached or nitrogen limits further leaf allocation, carbon is allocated to fill storage, grow wood, or increase fine roots. Further surplus carbon is allocated for nitrogen fixation. At the end of each annual cycle, integrated annual marginal carbon return is used to recompute maximum leaf carbon and nitrogen and maximum root carbon and nitrogen. Thus, at each timestep, ACONITE computes the marginal changes to photosynthesis from added leaf carbon, added leaf nitrogen, and added leaf carbon and nitrogen together, to determine an appropriate allocation strategy.
7 FRONTIERS IN ALLOCATION PREDICTION
In this section, we expand the understanding of allocation drawn from the vegetation hydraulic framework to comment broadly on the global optimization problem of allocation to plant tissues in the presence of multiple resource constraints. Specifically, we highlight current questions arising from flexible allocation schemes, including limitations of both resource-seeking approaches and optimization-based approaches. Concomitantly, we suggest several ways forward to improve the representation of allocation in vegetation models.
Current resource-seeking implementations of flexible allocation still face challenges associated with (a) quantifying the degree and costs of light, water, and nutrient limitation; and (b) uncertainty associated with physiological parameters such as root hydraulic resistance, which can be treated as model calibration factors rather than an observationally constrained biological traits. As a result, a number of vegetation models with resource-seeking allocation effectively trade empirical allometric allocation factors (based on site-specific, but field-measured allometric relationships) for empirical cost factors that may be loosely rooted in limitation mechanisms, such as soil water/nutrient availability or relative tree height of competitors (Table 3). Such trade-offs should be undertaken with caution because the empirical cost factors are difficult to validate using field measurements and are unlikely to capture any nonlinear changes in allocation responses to resource scarcity, as might be expected in out of sample environmental conditions. Furthermore, most resource limitation schemes still rely on fixed coefficients to define allocational strategies under unstressed conditions (Krinner et al., 2005; Lawrence et al., 2018; Mackay et al., 2015; Scheiter & Higgins, 2009).
Key challenges to address in advancing flexible allocational schemes in vegetation models will be to: (a) limit additional free parameters; (b) tie the mechanisms underlying flexible allocation to known aspects of plant physiology such as plant functional traits; (c) assess whether any increases in model complexity toward a more physiological accurate representation of biomass allocation are justified based on model performance. In particular, the universal problem of equifinality (many parameter choices yielding similar model behavior) in vegetation models with many unconstrained or poorly constrained parameters emphasizes the need to implement parsimonious allocation schemes driven by parameters that can be constrained by observations (Tang & Zhuang, 2008). Otherwise, flexible allocation schemes may fit training data well, yet not beat simplistic but empirically constrained fixed allocation schemes when considering multiple measures of model predictive skill.
Recent advances in the field of plant hydraulics provide several examples of methods to mechanistically quantify costs of scarce resource limitation that are informative to the flexible allocation problem. For example, Mackay et al. (2015) accelerated leaf shedding in response to water limitation as a function of lateral stem proportional loss of conductivity and Sperry et al. (2017) defined a hydraulic damage risk function based on the fractional loss of plant hydraulic conductance. Although these approaches are not fully mechanistic, they offer potential improvements that connect hydraulic mechanisms to allocation and damage costs experienced by plants. Additionally, the cost functions associated with hydraulic conductivity or conductance have performed well when tested against diverse allocational and physiological observational datasets (Eller et al., 2018; Mackay et al., 2015; Sperry et al., 2017; Venturas et al., 2018).
Optimality approaches show significant promise for predicting the interaction between plant biophysics and environment and have been implemented in the context of plant hydraulics, as illustrated by the HOTTER model example (Trugman et al., 2019), and for multiple resource limitations (i.e., Dybzinski, Farrior, & Pacala, 2015; Farrior et al., 2013; Rastetter & Shaver, 1992; Thomas & Williams, 2014) in simple models. However, the calculation of the marginal costs and benefits associated with allocation trade-offs can be extremely computationally expensive. Furthermore, the implementation of optimized allocation brings up a number of plant physiological questions that are currently unknown (Dewar et al., 2009). Particularly, how rapidly can plants adjust allocation? How does environmental variability factor into plant allocation strategy? How does competition impact allocation strategy (i.e., Dybzinski et al., 2015; Falster & Westoby, 2003; Farrior et al., 2013)? How do plants reconcile short-term and long-term trade-offs such as sacrificing height growth, which increases short-term carbon gain but ultimately leads to a long-term competitive disadvantage (Buckley & Roberts, 2006; King, 1981)?
Given the significant advantages of optimality principles, but substantial computational trade-offs, hybrid approaches that utilize carbon balance optimization techniques to define resource cost functions associated with allocation to different tissues under varying resource constraints could prove to be computationally more feasible and avoid drawbacks associated with determining the appropriate optimization timescale. For example, allocation routines could calculate marginal changes in plant fitness (such as carbon gain) in response to increased allocation to leaf, root, and stem tissue given a fixed resource availability, similar to the size-based approach (Zaehle et al., 2006), as illustrated in Figure 5.

8 CONCLUSIONS
Overall, we now have the tools to tackle allocation broadly in the presence of multiple limiting resources. In particular, cohort-based vegetation models allow us to tackle the impacts of light limitation on allocation (Fisher et al., 2018; Lawrence et al., 2018). Vegetation models that incorporate plant hydraulics (Christoffersen et al., 2016; Kennedy et al., 2019; Xu et al., 2016) give us an increased ability to understand how water limitation impacts allocation. Models that include microbe-mediated biogeochemistry and competition for nitrogen and phosphorus allow us to predict nutrient limitations on allocation and growth (Medvigy et al., 2019). Although these connections are not yet fully realized, they represent a promising area of future development.
ACKNOWLEDGEMENTS
A.T.T. acknowledges support from the USDA National Institute of Food and Agriculture Postdoctoral Research Fellowship Grant No. 2018-67012-28020. W.R.L.A was supported by the David and Lucille Packard Foundation, National Science Foundation grants 1714972 and 1802880, and the USDA National Institute of Food and Agriculture, Agricultural and Food Research Initiative Competitive Programme, Ecosystem Services and Agro-Ecosystem Management, grant no. 2018-67019-27850. L.D.L.A was supported by the National Science Foundation (DBI-1711243) and the National Oceanic and Atmospheric Administration (Climate and Global Change Fellowship).



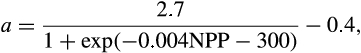
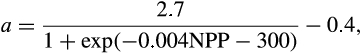
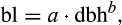
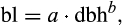
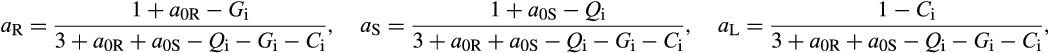 where aR, aS, and aL describe carbon allocated to roots, stems, and leaves, respectively. a0R, a0S, and a0L describe the fractions of carbon allocated to roots, stems, and leaves when resources are not limiting. Qi ranges from 0 to 1 (where 1 is no light limitation) and describes the light status of the plant and is based on the relative height of a given plant and its competitor. Gi is the weighted mean soil moisture index of all soil layers that a plant's roots have access to. Ci describes the deviance of leaf biomass from the fraction of leaf biomass in the nonlimiting case.
where aR, aS, and aL describe carbon allocated to roots, stems, and leaves, respectively. a0R, a0S, and a0L describe the fractions of carbon allocated to roots, stems, and leaves when resources are not limiting. Qi ranges from 0 to 1 (where 1 is no light limitation) and describes the light status of the plant and is based on the relative height of a given plant and its competitor. Gi is the weighted mean soil moisture index of all soil layers that a plant's roots have access to. Ci describes the deviance of leaf biomass from the fraction of leaf biomass in the nonlimiting case.