Legacies of La Niña: North American monsoon can rescue trees from winter drought
Abstract
While we often assume tree growth–climate relationships are time-invariant, impacts of climate phenomena such as the El Niño Southern Oscillation (ENSO) and the North American Monsoon (NAM) may challenge this assumption. To test this assumption, we grouped ring widths (1900-present) in three southwestern US conifers into La Niña periods (LNP) and other years (OY). The 4 years following each La Niña year are included in LNP, and despite 1–2 year growth declines, compensatory adjustments in tree growth responses result in essentially equal mean growth in LNP and OY, as average growth exceeds OY means 2–4 years after La Niña events. We found this arises because growth responses in the two periods are not interchangeable: Due to differences in growth–climate sensitivities and climatic memory, parameters representing LNP growth fail to predict OY growth and vice versa (decreases in R2 up to 0.63; lowest R2 = 0.06). Temporal relationships between growth and antecedent climate (memory) show warmer springs and longer growing seasons negatively impact growth following dry La Niña winters, but that NAM moisture can rescue trees after these events. Increased importance of monsoonal precipitation during LNP is key, as the largest La Niña-related precipitation deficits and monsoonal precipitation contributions both occur in the southern part of the region. Decreases in first order autocorrelation during LNP were largest in the heart of the monsoon region, reflecting both the greatest initial growth declines and the largest recovery. Understanding the unique climatic controls on growth in Southwest conifers requires consideration of both the influences and interactions of drought, ENSO, and NAM, each of which is likely to change with continued warming. While plasticity of growth sensitivity and memory has allowed relatively quick recovery in the tree-ring record, recent widespread mortality events suggest conditions may soon exceed the capacity for adjustment in current populations.
1 INTRODUCTION
Large-scale climate phenomena such as the El Niño Southern Oscillation (ENSO) and the North American Monsoon (NAM) affect ecosystem function, including forest and woodland dynamics and tree growth across the western United States (US), primarily via associated drought impacts (Cole, Overpeck, & Cook, 2002; Kitzberger, Swetnam, & Veblen, 2001). ENSO, an intensively studied global climate pattern, influences large-scale weather patterns in the western United States (D'Arrigo & Jacoby, 1991; Dettinger, Cayan, Diaz, & Meko, 1998). While ENSO also influences weather worldwide (Philander, 1990; Rasmusson & Wallace, 1983; Walker, 1924; Wyrtki, 1965), impacts on winter precipitation in the western United States are particularly well-documented. South of approximately 40°latitude, El Niño years are associated with above average winter precipitation, while La Niña years are associated with winter precipitation deficits (Brown & Comrie, 2004; Dettinger et al., 1998). The effects of ENSO on ecological processes have been extensively studied (Stenseth et al., 2002), including a subset of studies evaluating the impacts of ENSO on forest productivity and tree growth.
In the southwestern United States (“Southwest”), the negative phase (La Niña) and its effects on drought probability are key drivers of regional forest health and growth (Brown & Wu, 2005; Swetnam & Betancourt, 1990, 1998). Multi-year La Niña events are implicated in the majority of major regional droughts in the instrumental record in this region (Cole et al., 2002), with clear implications for tree growth (Touchan, Woodhouse, Meko, & Allen, 2011). Recent work, however, indicates that understanding growth responses to climate requires recognition of multi-year legacy effects of drought on tree growth (Anderegg, Schwalm et al., 2015; Peltier, Fell, & Ogle, 2016) and terrestrial productivity more generally (Schwalm et al., 2017), particularly as multi-year droughts occur more frequently (Seager et al., 2007). However, the impacts of annual drought legacy effects on monthly to seasonal growth–climate sensitivities have not been quantified. Exceedance of species climatic limits may lead to strongly altered growth–climate sensitivities preceding mortality (Cailleret et al., 2017); however, within species tolerances, variability in sensitivities could occur regularly. If the combination of ENSO-related winter drought and variation in summer monsoon patterns associated with the NAM are driving plasticity (i.e., climatic context dependent variability) in tree growth–climate responses, this could have significant effects on tree, woodland, and forest productivity.
The NAM, a pattern of strong convective summer thunderstorms, typically initiates in early July and continues through September in the Southwest (Higgins, Chen, & Douglas, 1999). The NAM creates a summer precipitation gradient across the region, with southeastern Arizona and southwestern New Mexico receiving comparatively high monsoonal precipitation (Douglas, Maddox, Howard, & Reyes, 1993). Variation in NAM onset date and strength affect tree-ring development and growth patterns, including latewood density and width, occurrence of false latewood bands, and latewood 13C (Babst et al., 2016; Griffin et al., 2013; Leavitt, Wright, & Long, 2002). Additionally, the NAM contribution to annual precipitation totals varies strongly in the Southwest, and oxygen and carbon isotopes show differential use of winter vs summer moisture sources across this gradient in precipitation seasonality (Szejner et al., 2016). To better predict carbon fluxes in Southwest forests, tree growth responses to NAM-driven summer precipitation and ENSO-driven winter precipitation anomalies must be studied simultaneously. Importantly, although strong NAM years and strong La Niña years tend to occur out of phase (Stahle et al., 2009), this correlation likely varies in the record (Griffin et al., 2013), with no clear mechanistic linkage.
To better understand how ENSO-related winter droughts and their legacies control tree growth in the context of summer precipitation variability related to the NAM, we apply the stochastic antecedent modeling (SAM) framework (Ogle et al., 2015) to tree-ring data from 364 sites across the Southwest, for three dominant conifers (Pinus edulis, Pinus ponderosa, and Pseudotsuga menziesii), obtained from the International Tree-Ring Data Bank (ITRDB). We subset site-years according to either “La Niña periods” (the year of and 4 years following a La Niña event) or “other years” (all other years in the record) and evaluated the response of tree growth (ring widths) to antecedent (past) climate up to 57 months prior to growth cessation. We address the following questions: (Q1) How do the climatic sensitivities of three conifers representing three widespread Southwest forest types (pinyon-juniper woodland, ponderosa pine forest, mixed conifer forest) change during La Niña periods compared to other years? (Q2) Do the timescales of influence (or “memory”) of monthly or seasonal climate variables (e.g., July or monsoon precipitation) differ during La Niña periods? And (Q3) how do these differences vary across space in relation to the NAM gradient? We hypothesize that tree growth sensitivity to climate and the importance of monthly and seasonal climate variables will reflect legacies of La Niña events (winter drought), but that species will respond differently, as duration of legacy effects (i.e., recovery time) varies between these species (Peltier et al., 2016). We also hypothesize that spatial variation related to Q3 will correlate with relative monsoon contribution to annual precipitation totals (Peltier, Barber, & Ogle, 2017). By applying the model to century-long time-series of tree-ring widths and monthly climate data, there is potential to gain simultaneous understanding of how intra-annual variability in climate can influence tree growth and climatic memory in the context of large-scale climate patterns.
2 MATERIALS AND METHODS
2.1 Data sources and preparation
Ring width data from the ITRDB were incorporated into a relational database (Microsoft Access) in early 2016. We used Pinus edulis Engelm. (pinyon pine), P. ponderosa Dougl. Ex. Laws. (ponderosa pine), and Pseudotsuga menziesii (Mirb.) Franco (Douglas fir) ring widths. We extracted data from sites occurring in states (California, Nevada, Utah, Arizona, Colorado, and New Mexico) that experience precipitation deficits during La Niña winters (Brown & Comrie, 2004; Dettinger et al., 1998; Douglas et al., 1993). Observations prior to 1899 (888,948 ring widths) were used in detrending but discarded prior to analysis given the lack of climate data prior to 1900. The last ring width year available was 2012, resulting in a-114 year record (877,397 ring widths and 9,769 cores after filtering). Monthly precipitation and mean monthly temperature (0.5° resolution) are from the PRISM Climate Group (http://prism.oregonstate.edu, 2017). Self-calibrating Palmer drought severity index (hereafter, “PDSI,” 0.5° resolution) was obtained from the West Wide Drought Tracker (Abatzoglou, McEvoy, & Redmond, 2017).
We detrended raw ring widths for age effects using standard methods (Fritts, 1976; Fritts & Swetnam, 1989) via the R package dplR (Bunn, 2008). Detrending was accomplished by dividing ring widths by a fitted curve—either modified negative exponential curves or, when this failed, flat lines—to remove age effects (and adjust the core-level mean to be equal to 1, approximately). We constructed a single “growth” chronology per site (unique to species) as the average of all ring width indices (i.e., across cores) in a given year, producing 365 age-detrended chronologies (P. edulis: 101, P. ponderosa: 143, P. menziesii: 121) containing a total of 31,585 annual ring width indices.
2.2 Model description
Our application of the SAM model to tree growth chronologies is modified from Peltier et al. (2017). Here, annual growth—chronology-level annual ring width index—is modeled as a linear response to antecedent climate variables, which are constructed as weighted averages of monthly climate over the current and preceding 4 years. The unknown “antecedent weights” are estimated, allowing inference on climatic memory (Ogle et al., 2015)—operationally defined here as the temporal pattern of the response of tree growth to past climate—in addition to the growth sensitivities to climate (regression coefficients). Previously, our application of this model documented strong spatial variation in climatic sensitivities, first order autocorrelation, and baseline growth, which we suggested was driven in part by the NAM gradient (Peltier et al., 2017). Here, we expand upon this previous analysis to understand how La Niña drought may alter growth–climate sensitivities and memory, and how these differences may vary across species and space.
We binned growth years and associated climate covariates into two categories: “La Niña periods” (hereafter, LNP) and “other years” (hereafter, OY). La Niña years (Appendix S1, ~17% of record, 20 La Niña events) were selected according to agreement between an ENSO reconstruction (Li et al., 2013; <−1), NINO 3.4 sea surface temperature anomalies (SSTA < −0.6), and the Oceanic Niño Index (ONI < −0.5, NOAA). When ONI was the only record available (2000-present), ONI had to be <−0.75 to be considered a La Niña year. We define LNP as the year of and 4 years following La Niña years (LNP: 75 years of the 114-year record considered, or 66%); OY are defined as all other years in the record (OY: 39 years, or 34%). We note that successive La Niña years were sometimes separated by fewer than 4 years (e.g., 1999 and 2000, Appendix S1), such that the number of years demarked as LNP is not 100 (100 = 20 La Niña events × 5 years per LNP). We include the 4 years following the La Niña events within the LNP because these periods are (on average) drier and associated with major Southwest 20th century droughts, which often persist after the cessation of specific La Niña events (Cole et al., 2002). Particularly for Southwest conifers, 5th–10th percentile droughts are associated with a 4-year recovery time on average (“legacy effects,” Anderegg, Flint et al., 2015; Anderegg, Schwalm et al., 2015; Peltier et al., 2016). Within our statistical model (Equations 1 and 2), we center each climate covariate (monthly precipitation, temperature, and PDSI) about their time period specific (LNP or OY) means to aid interpretation of intercepts and increase computational efficiency of the numerical methods (see below).
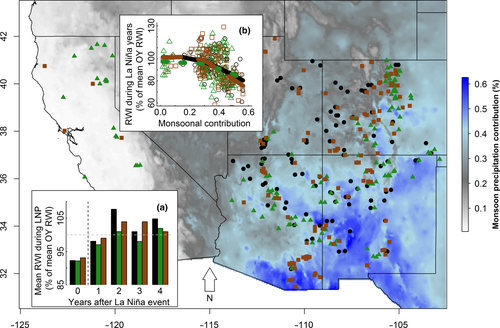
We note that in this dataset, within LNP, mean growth was 7%–8% lower during, but up to 7% higher 2 years after, La Niña years compared to mean growth in OY (Figure 1a), thus mean growth across the whole LNP is essentially equal to that in OY. Growth decreases were greatest in sites with high monsoonal precipitation contribution (Figure 1b). Thus, the model is designed to understand how plasticity in growth responses to climate underlies these patterns in the three study species, and how responses may vary across the NAM gradient.
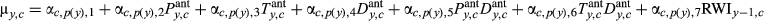 (1)
(1)the α's (coefficients), each allowed to vary by time period p (LNP or OY), include the intercept (baseline growth under average, time period specific climate condition), and the effects of the antecedent climate covariates of precipitation (Pant), temperature (Tant), and PDSI (Dant), in addition to a prior RWI term (RWIy–1,c), equivalent to an AR(1) effect, plus the two-way interactions Pant × Dant and Tant × Dant. We note that PDSI represents an interaction between precipitation and (negative) temperature (Supporting information Figure S1), and thus, we do not include a Pant × Tant interaction. Equation 1 is essentially an autoregressive, random coefficients linear regression, conditional on the antecedent covariates.
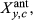 are calculated as follows:
are calculated as follows:
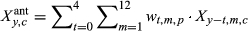 (2)
(2)Equation 2 is applied to each site-specific climate variable (where Xant = Pant, Tant, or Dant, for precipitation, temperature, or PDSI).
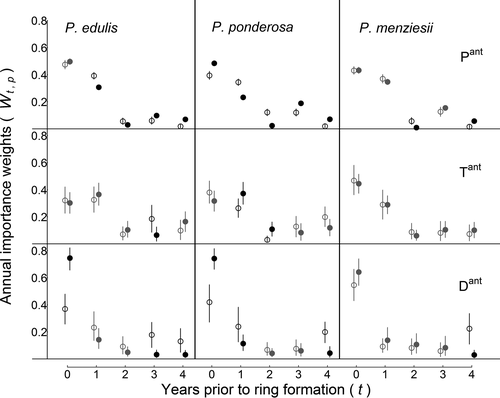
This framework allows the data to inform the weights (w terms), which describe the importance of past conditions on growth. As in Peltier et al. (2017), we assume the model detection skill declines with time into the past (i.e., t index in Equation 2), and estimate weights of increasingly “coarse” time blocks (blocks of months) further into the past. Thus, only 35 “free” weight parameters are estimated for each species and period; the remaining 25 weights are either set equal to zero (post ring formation in t = 0, m = 10, 11, 12; 3 weights) or all monthly weights within a coarse block are assumed equal (Peltier et al., 2017). Monthly weights are constrained to sum to one across lag year t and month m for each species s, period p, and climate variable. Annual weights, Wt,p, are also computed by summing all 12 monthly weights within each lag year t for a given species and climate variable.
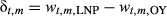 (3)
(3)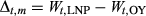 (4)
(4)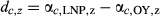 (5)
(5)Calculation of these quantities allowed explicit evaluation of differences in the timescales of influence of climate (Equations 3 and 4) between the two time periods, as well as baseline growth, climate sensitivities, and AR1 effects (Equation 5).
2.3 Prior specification
For each species, the model defined in Equations 1-5 was implemented in a hierarchical Bayesian framework, with normal hierarchical priors for site-level regression parameters assumed to vary around species-level means and variances, which are allowed to vary by period (LNP or OY) and climate variable. The antecedent importance weights were assigned Dirichlet priors to constrain their interpretation as relative importance of climate during each time lag. See Peltier et al. (2017) for more details.
2.4 Implementation
The model was implemented using JAGS 4.0.0 (Plummer, 2003) via the R (Team, 2015) package rjags (Plummer, 2013) according to standard methodology (three chains, thinning to obtain ≥3,000 relatively independent samples, chains assessed for convergence). Chains were run in parallel on high performance computing cluster.
Because the statistical comparisons (Equations 3 and 5) have large group sizes (δ's: 35, and d's: 101, 143, or 121 for P. edulis, P. ponderosa, P. menziesii, respectively), we used a significance (“alpha”) level of 0.01 rather than a more traditional 0.05 level. We did not use formal Bonferroni corrections as these are overly conservative, and partial pooling in a hierarchical Bayesian model reduces risk of erroneous difference detection, such as for the site-level effects (d's) (Gelman, Hill, & Yajima, 2012). Thus, to sufficiently sample the tails of the posterior distributions of the pairwise differences (δ's and d's), we used at least 100,000 posterior samples (≥30 times more samples than would be used for a 0.05 significant level) to estimate the 99% credible intervals of these comparisons.
2.5 Posterior analyses
To address Q3, we only considered the effects of covariates (e.g., prior RWI and AR1 effect) for which species-level effects differed significantly between LNP and OY, and for which we found numerous significant site-level pairwise differences (d's). In these cases, we regressed the posterior means of the d's against site-level relative monsoon contribution (Jul-Aug-Sep summed % of annual) using regression tools in R. We restricted these analyses to the NAM region (i.e., excluded CA and NV sites for P. ponderosa and P. menziesii).
2.6 Model evaluations
We also evaluated model fit (as coefficients of determination, R2, between predicted and observed annual RWI) of the full, correctly applied model described by Equations 1 and 2; we evaluated fit for all years (LNP and OY), and separately for LNP and OY years. We then used the full model and its associated posterior distributions of parameters to evaluate the fit of a series of flipped or partially applied predictive “models” (described in Table 1). The flipped scenarios predicted RWI only during OY using the parameters (α's and w's) estimated for LNP (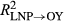 ) and vice versa (OY parameters used to predict RWI during LNP;
) and vice versa (OY parameters used to predict RWI during LNP; 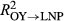 ). We also estimated the contribution of baseline growth or the intercept (
). We also estimated the contribution of baseline growth or the intercept (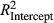 ), climate effects (
), climate effects (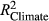 ), and AR1 (
), and AR1 (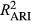 ) terms to the overall R2, using combinations of partially applied models (see Table 1). We emphasize that these model formulations were not fit to data, but rather utilize the parameter estimates from the full model to predict RWI under different scenarios. Thus, R2 values from these “models” are useful for evaluating the importance of period-specific parameters (flipped scenarios) and the relatively contribution of different components affecting growth (partially applied scenarios).
) terms to the overall R2, using combinations of partially applied models (see Table 1). We emphasize that these model formulations were not fit to data, but rather utilize the parameter estimates from the full model to predict RWI under different scenarios. Thus, R2 values from these “models” are useful for evaluating the importance of period-specific parameters (flipped scenarios) and the relatively contribution of different components affecting growth (partially applied scenarios).
| Scenario | Equation | Description |
|---|---|---|
| Correctly applied model | ||
| Full model |
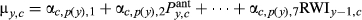
|
See Equation 1 |
| Flipped models | ||
| LNP→OY |
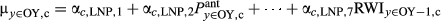
|
LNP parameters predict OY growth |
| OY→LNP |
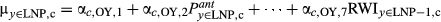
|
OY parameters predict LNP growth |
| Partially applied models | ||
| Climate |
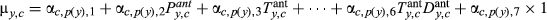
|
Intercept and climate effects; no AR1 term |
| AR1 |
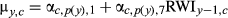
|
Intercept and AR1 term; no climate effects |
| Baseline |
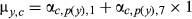
|
Intercept only; no AR1 term or climate effects |
- Only the correctly applied model was fit to data, separately for each species, and the results (parameter estimates) were used to compute predicted growth (μ) based on the flipped and partially applied model scenarios. Model performance was evaluated from coefficients of determination (R2) between observed and predicted RWI. The relative contribution of the climate and AR1 components are estimated from differences in R2 obtained from the partially applied “climate” and “AR1” scenarios relative to the “baseline” scenario, respectively. The R2 for the baseline scenario gives the relative importance of only the intercept (baseline growth). Because RWI (the response variable) is a detrended, unitless index with mean 1, the contribution of AR1 at mean RWIy–1,c is αc,p(y),7 × 1.
3 RESULTS
3.1 Model performance
Model goodness of fit (R2 of predicted vs. observed growth) was relatively high (R2 = 0.67, 0.65, and 0.65 for P. edulis, P. ponderosa, and P. menziesii, respectively) given the coarse climate data (Figure 2, Supporting information Figure S2). Applying “flipped” models with other year (OY) parameters used to predict growth in La Niña periods (LNP) yielded much poorer model fits (R2 = 0.35, 0.47, and 0.49, for P. edulis, P. ponderosa, and P. menziesii, respectively). Even worse fits were obtained using LNP parameters to predict OY growth (R2 = 0.06, 0.46, and 0.30 for P. edulis, P. ponderosa, and P. menziesii, respectively). Poor flipped model performance results from differences in both effects (α's; Figure 3) and importance weights (Wt,p and wt,m,p's; Figure 4) between the two time periods.
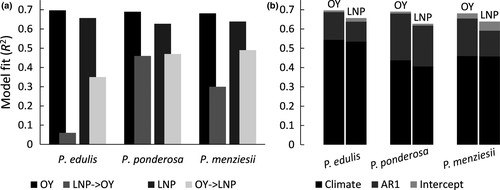
Based on the correctly applied model described by Equations 1 and 2, model fit (R2) was 0.04 (P. edulis), 0.06 (P. ponderosa), and 0.04 (P. menziesii) lower during LNP (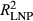 ) compared to OY (
) compared to OY (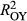 ) (Figure 2). Partially applied models can help to understand how differences in fit for different sub-components of the mean model may explain differences in overall model fit between the two time periods. For P. edulis, this decrease in fit during LNP was driven by decreases in R2 (~0.04 drop) associated with the AR1 component. For P. ponderosa and P. menziesii, decreases in both R2 associated with the AR1 (~0.03–0.06 drop) and climate (~0.03–0.04 drop) contributions drove the overall decreases in LNP.
) (Figure 2). Partially applied models can help to understand how differences in fit for different sub-components of the mean model may explain differences in overall model fit between the two time periods. For P. edulis, this decrease in fit during LNP was driven by decreases in R2 (~0.04 drop) associated with the AR1 component. For P. ponderosa and P. menziesii, decreases in both R2 associated with the AR1 (~0.03–0.06 drop) and climate (~0.03–0.04 drop) contributions drove the overall decreases in LNP.
3.2 La Niña-related changes are species dependent
Posterior means, 95% credible intervals, and standard deviations of all model parameters are presented in Table S2. We focus on species-level effects (i.e., α's), their differences between the two periods (LNP vs. OY), and spatial variability in site-level differences (d's) between the two periods.
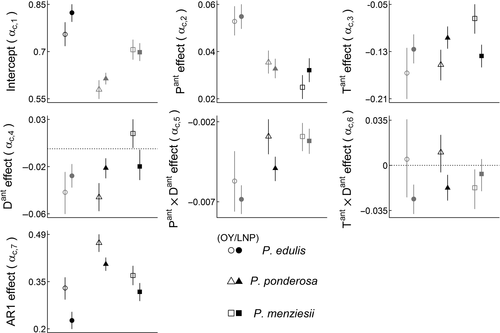
In addition to reduced model performance during LNP, many (11 of 21) species-level effect parameters also differed between LNP and OY. Across species, the AR1 effects decreased by 0.03–0.08 units (reduction of 11%–36%) during LNP (Figure 3). We note that the AR1 effect (αc,7) is generally expected to be between 0 and 1, with 0 indicating the RWI is uncorrelated from 1 year to the next, and 1 indicating extremely high autocorrelation. The effects of climate on growth in P. edulis did not differ between periods; though, the Tant × Dant interaction term was only significant (and negative) and baseline growth (intercept) was higher during LNP (Figure 3). P. ponderosa showed decreased sensitivity (less negative effect) to Tant and Dant, and increased sensitivity (significant negative effect) to the Tant × Dant interaction during LNP (Figure 3). Pseudotsuga menziesii showed increased sensitivity to Pant and Tant (more negative effect), and the Dant effect switched from positive to negative during LNP (Figure 3).
3.3 Changes in the annual importance of climate
Annual weights (Wt,p) indicate that recent climate (current year and year prior to ring formation) is most important to growth during both periods, though the OY weights for P. edulis are comparatively large for temperature and PDSI 3 years prior to ring formation (Figure 4). Relative to OY, there was increased importance of current year PDSI (P. edulis and P. ponderosa) and precipitation (P. ponderosa) during LNP (Figure 4). All three species also show shifts in importance of precipitation from 1 to 2 years prior (decreased weight) to 3 to 4 years prior (increased weight) in LNP, that is, they are relatively less reliant on recent precipitation, and more reliant on less recent precipitation than during OY (Figure 4). Increased importance of temperature 1–2 years prior to ring formation (P. ponderosa) and decreased importance of PDSI 4 years prior (all species) also characterize LNP (Figure 4).
3.4 Changes in importance of recent climate
Differences (δt,m terms) in monthly weights for precipitation, which had a uniformly positive effect on growth (Figure 3), show increased importance of current March (all three species) and current (P. ponderosa) or previous (P. menziesii) July precipitation during LNP compared to OY (p < 0.01, Figure 5). July precipitation δ's (current and previous year) for P. edulis are marginally significantly greater than zero (0.01 < p < 0.05). Decreased importance of previous fall through winter (August-January) precipitation in LNP is also apparent for all species, though specific months with significant δ's vary among species (Figure 5). Differences in monthly weights for temperature, which had a uniformly negative effect on growth (Figure 3), were variable among species (Figure 5). During LNP, there was increased importance compared to OY of temperature during the previous February (P. edulis), previous October (all species), and current July (P. ponderosa and P. menziesii), accompanied by decreased importance of temperature in the previous March (P. ponderosa), previous August (P. edulis), current May (P. ponderosa and P. menziesii), and current September (P. edulis and P. ponderosa) (Figure 5). Current May PDSI is notably more important during LNP for P. ponderosa, with similar (but nonsignificant) patterns in other species (Figure 5).
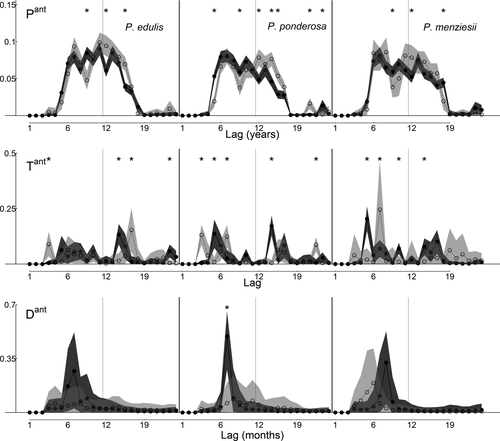
3.5 Increased variability during LNP in the NAM region
Across species, few site-level effect differences (d's) were significant (at p < 0.01); however, the AR1 effect (αc,7) was significantly lower at 15 of 101 sites for P. edulis and 17 of 143 sites for P. ponderosa during LNP (Supporting information Figure S3). For P. ponderosa, linear regression of dc,7 (AR1 effect difference) on average monsoon (Jul-Aug-Sep) contribution (proportion of mean annual precipitation) within the NAM region shows greater reductions in the AR1 effect during LNP relative to OY at sites with higher monsoon contribution (adj. R2 = 0.24, p < 0.0001). While P. menziesii responded similarly to P. ponderosa, few site-level dc,7 terms were significant (3 of 120). Pinus edulis AR1 strength also decreased with monsoon contribution, and this relationship was more robust when a squared term for monsoon contribution was included (linear: adj. R2 = 0.10, p < 0.001; quadratic: adj. R2 = 0.21, p < 0.0001). Accordingly, the AR1 effect decreased with monsoon contribution at P. edulis sites where monsoon contribution exceeds 30% of annual precipitation total, suggesting a threshold response (Supporting information Figure S3).
4 DISCUSSION
This study revealed that periodic drought conditions created by large-scale climate phenomena such as ENSO affect growth–climate sensitivities of dominant conifer species in the Southwest. Failure of flipped models to predict growth demonstrates that plastic growth sensitivities and climatic memory are driving previously unquantified variability in tree growth during La Niña periods (LNP) relative to other years (OY) (Figure 2). Even the best performing flipped model explains ~15% less variation ( vs.
vs. 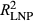 for P. menziesii) in annual growth than the correctly applied model for the same observations. Moreover, growth–climate relationships for P. edulis during LNP notably fail to capture growth during OY (
for P. menziesii) in annual growth than the correctly applied model for the same observations. Moreover, growth–climate relationships for P. edulis during LNP notably fail to capture growth during OY (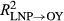 = 0.06; Figure 2). Across species, La Niña periods are associated with a reduced ability to predict growth (
= 0.06; Figure 2). Across species, La Niña periods are associated with a reduced ability to predict growth (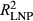 <
<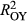 ) and a weaker correlation with prior ring widths (decreased
) and a weaker correlation with prior ring widths (decreased 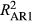 in LNP). Accompanying these decreases in predictive ability during LNP are increased importance of monthly climate preceding the pre-monsoon arid period and during monsoon onset, suggesting a key role for monsoonal precipitation to “rescue” trees following winter drought. However, larger decreases in AR1 effects during LNP at more NAM-driven sites suggest monsoonal precipitation cannot compensate for winter precipitation deficits during the La Niña year, but rather aids recovery and subsequent growth. Taken together, these results suggest ignoring plasticity in tree growth–climate conditions, especially in the unique climate conditions driving tree growth in the Southwest, may limit predictive inference at broader scales under future climate change.
in LNP). Accompanying these decreases in predictive ability during LNP are increased importance of monthly climate preceding the pre-monsoon arid period and during monsoon onset, suggesting a key role for monsoonal precipitation to “rescue” trees following winter drought. However, larger decreases in AR1 effects during LNP at more NAM-driven sites suggest monsoonal precipitation cannot compensate for winter precipitation deficits during the La Niña year, but rather aids recovery and subsequent growth. Taken together, these results suggest ignoring plasticity in tree growth–climate conditions, especially in the unique climate conditions driving tree growth in the Southwest, may limit predictive inference at broader scales under future climate change.
4.1 Q1: Changes in climate sensitivities during La Niña periods
La Niña-related differences in climate sensitivities demonstrate significant legacies of La Niña events (i.e., winter droughts). During La Niña periods—year of and 4 years following La Niña events—climate sensitivities are unchanged in P. edulis, while P. menziesii shows shifts in all three climate main effects, with increased sensitivity to precipitation and temperature, and positive sensitivity to PDSI. Shifts in temperature-related—but not precipitation—effects also occurred for P. ponderosa, and changes in temperature effects on growth of P. ponderosa are consistent with previous analyses showing shorter recovery times of precipitation sensitivity, while temperature sensitivity recovery times can be as long as ~5 years for this species (Peltier et al., 2016). Given recovery times for Pinyon spp. are also ~5 years (Peltier et al., 2016), we speculate that decreases in AR1 effects, but not climate sensitivities, could suggest climate legacies in this species are related to physiological traits such as non-structural carbohydrate (NSC) dynamics, rather than changes in precipitation sensitivity. There is a continuing need for experimental approaches to understanding the physiology of drought legacies and to disentangle the processes integrating physiological and climatic effects into whole ring width over a growing season (e.g., Szejner et al., 2018). Many studies focus on the physiological mechanisms underpinning tree death during drought (Anderegg, Flint et al., 2015; Bigler, Gavin, Gunning, & Veblen, 2007), but few address the physiological mechanisms underlying recovery of mature trees following severe drought.
While the La Niña years defined in this study generally received less precipitation than other years, La Niña events are not always associated with drought (Cole et al., 2002). Other characteristics of La Niña climate could underlie changes in the climatic sensitivities of growth, such as differences in timing of rainfall or the occurrence of warm springs (Ault, Schwartz, Zurita-Milla, Weltzin, & Betancourt, 2015; McCabe, Ault, Cook, Betancourt, & Schwartz, 2012). However, our model accounts for differences in sub-annual climate by allowing the antecedent importance weights to differ among periods (LNP vs. OY; see Timing of climatic events). Regardless, if La Niña period changes in climate sensitivity are similar in the future, incorporation of periodic growth depressions, and associated changes in growth sensitivities could improve predictive ability of the terrestrial carbon cycle in Southwest forest biomes (e.g., pinyon-juniper, ponderosa pine, and mixed conifer forests) under global climate change. However, the ENSO has been amplifying for at least the last three decades (Lee & McPhaden, 2010), and the most recent 2016 El Niño suggests warming may be influencing predictability of associated climate effects, perhaps via changes in atmospheric circulation (Seager, Naik, & Vecchi, 2010; Singh et al., 2016; Wanders et al., 2017).
4.2 Q2: Changes in memory of monthly and seasonal climate during La Niña periods
Differences in monthly importance weights suggest the legacy of La Niña events is a shift to greater importance of monsoon precipitation and its related effects on climate (Figure 5). In the NAM region, precipitation begins to decline in March, while temperatures rapidly rise by June. This “pre-monsoon arid period” is a defining characteristic of NAM climate, terminating with monsoon arrival around early July. These NAM dynamics are key drivers of tree-ring widths across the NAM region (Babst et al., 2016; Peltier et al., 2017; Szejner et al., 2016). Here, increased importance of March and July precipitation (Figure 5) suggests rainfall received during the pre-monsoon arid period, and monsoon onset date (as July precipitation) are both key drivers of growth during the years following a dry La Niña winter. Increased importance of current July temperature during La Niña periods also illustrates the impacts of monsoon arrival, not only through precipitation, but also via temperature conditions during this critical phase. In particular, warmer July temperatures (or later monsoon arrival) have a stronger negative effect on tree growth during La Niña periods compared to other years. Furthermore, May marks the middle of this pre-monsoon arid period, and May PDSI is associated with the largest monthly importance weights that we detected (P. edulis and P. ponderosa, Figure 4); this pattern was strongest during La Niña periods. Thus, following La Niña winters, the drought conditions during the middle of this typically dry period are particularly important to growth, particularly for P. ponderosa.
Recall that PDSI was derived from the same PRISM data used to define antecedent precipitation (Pant) and temperature (Tan), and PDSI represents an interaction of precipitation and (negative) temperature (Supporting information Figure S1). Hence, high (positive) PDSI values correspond to cool, wet conditions, and low (negative) values generally reflect hot, dry conditions. Other studies find positive effects of PDSI as a sole predictor of ring width (Adams & Kolb, 2005) or when using independently derived PDSI (Peltier et al., 2017). Here, responses to antecedent drought conditions (Dant) during La Niña periods were uniformly negative, suggesting growth is more sensitive to precipitation when it is warm (“negative” temperature is low). Given temporal lags inherent in the PDSI calculation (Dai, Trenberth, & Qian, 2004; Palmer, 1965; Wells, Goddard, & Hayes, 2004), high May PDSI importance may also reflect the importance of precipitation during the warm springs (February-March) that are characteristic of La Niña years (Ault et al., 2015; McCabe et al., 2012). Given increased importance of February temperature weights, warm springs likely decrease growth during La Niña phases. Higher October temperature weights further suggest longer growing seasons (as warmer temperatures during the shoulder seasons) are also detrimental to growth during drier La Niña periods (Figure 5). While P. menziesii has the lone positive response to PDSI during other years, this may reflect a less negative or even slightly positive response to temperature, as it also has the least negative response to the main temperature effect during this period (Figure 2), and in the Southwest, it typically grows at or above elevations of 1,800 m or in cool microclimates (e.g., cold-air drainages).
Differences in annual weights (Δ's, Equation 4 and Figure 3) suggest while greater importance of current conditions is a key feature (particularly for PDSI), there is likely a role for long-term NSC storage in enduring stress during La Niña periods. Increased sensitivity to 3–4 years prior precipitation across species suggests increased reliance on older, less-frequently accessed pools of stored carbohydrates (Carbone et al., 2013; Peltier et al., 2016; Richardson et al., 2013) or deeper water sources (Rempe & Dietrich, 2018) during La Niña periods. Reliance on carbon or water reserves is expected if La Niña conditions create dry surface and subsurface soils and/or reduced photosynthesis in response to water stress. Decreases in living root biomass or increases in rhizosphere investment could also underlie drought legacies (Hagedorn et al., 2016). This dual strategy, reliance on older conditions with heightened sensitivity to current climate, seems highly adaptive in the Southwest where drought is a semi-regular climate component (Cook & Krusic, 2004). While longer term (3–4 years prior to growth) climate memory is fairly weak, differences between climate periods are important in the context of changing climate, as droughts are expected to become more frequent (Dai, 2013; Trenberth et al., 2014; but see Sheffield, Wood, & Roderick, 2012). Tree physiological acclimation to stress, such as the ability to draw upon older NSC pools, will be increasingly important.
4.3 Q3: Variation in growth responses during La Niña periods across the NAM region
Changes in memory discussed above suggest strong monsoon precipitation can rescue trees following winter drought during La Niña periods. However, large decreases in AR1 effects at NAM-driven sites (monsoon precipitation > 30% of annual total; southern part of the region) reflect that La Niña winter precipitation deficits (and thus initial growth declines) are the largest at these sites, but that recovery is also the strongest (Supporting information Figures S3 and S4). This suggests that these southern sites may exhibit the greatest plasticity in growth–climate sensitivities and are perhaps the most drought resilient. Southern populations of P. menziesii have been shown to be more resilient to climate change, with the smallest modeled growth reductions under predicted climate change scenarios (Chen, Welsh, & Hamann, 2010). Based on our results, use of late season monsoonal precipitation, perhaps to accumulate additional NSC late in the growing season, may underlie this resilience.
Changes in memory and effects could also be due to non-physiological mechanisms, namely variation in temperature or vapor pressure deficit associated with monsoon arrival leading to decreased total growing season moisture stress during La Niña years with early monsoon arrival. We note that monsoonal precipitation is notoriously variable (particularly in onset date) and spatially heterogeneous, which could increase both spatial and temporal variability in growth across La Niña periods. This variability as well as the key role of the monsoon in drought recovery is further evident in dendrochronological reconstructions of monsoonal and winter precipitation in the southwest, where the most severe decadal droughts are often associated with monsoon failure (low summer precipitation) in combination with prior winter drought (Griffin et al., 2013). In the dataset used here, abnormally wet Julys tended to follow dry winters, which could underlie NAM effects on growth during La Niña periods due to likely incidental (Griffin et al., 2013) correlations between winter and monsoonal precipitation extremes (Stahle et al., 2009). Given our results, monsoon failure following a La Niña winter could have particularly severe impacts on southern populations, and in-phase cool and warm-season precipitation anomalies are associated with major long-term drought events in the tree-ring record over the last four centuries (Carrillo, Castro, Woodhouse, & Griffin, 2016).
Changes in climate sensitivities during La Niña periods compared to other generally wetter years could also be an artifact of the coarse resolution of the climate data. The gridded climate data that we used do not necessarily reflect actual site-level variability, and they certainly do not capture the microclimates experienced at the site or tree level. These results could also be a consequence of our modeling assumptions, which assume linear relationships between growth (RWI) and antecedent precipitation, temperature, and drought conditions (PDSI). However, the inclusion of PDSI is meant to account for non-linear, interactive effects of temperature and precipitation on growth, and two-way interactions between PDSI and temperature and/or precipitation account for potentially important interactive effects. Experimental approaches to evaluating growth responses to climate and their legacies would also help to rule out these potential data and modeling artifacts.
Our results show prediction of tree growth in the Southwest requires consideration of the effects of both the ENSO and NAM on variability in winter and summer precipitation, as they simultaneously drive tree growth sensitivities, growth characteristics, drought legacies, and physiology (e.g., NSC storage). Failure of flipped models to predict growth during distinctly different time periods (LNP vs OY) demonstrates that models parameterized for different ENSO phases are not interchangeable, and capture distinct growth responses to climate. The northwestern United States also experiences significant fluctuations in winter precipitation associated with ENSO (Dettinger et al., 1998), which could affect tree growth parameters, though we did not evaluate this. In the NAM region, winter precipitation deficits associated with La Niña years result in drought legacies and increased reliance on monsoonal precipitation, particularly for species growing at low and mid-elevations (e.g., P. edulis and P. ponderosa). Delayed NAM onset is predicted with climate change, which could further reduce growth during La Niña periods (Cook & Seager, 2013). Though southern populations in the Southwest may exhibit the most variable growth responses, delayed monsoon arrival would likely have particularly severe consequences for these populations following La Niña winters, as monsoonal precipitation plays a key role in drought recovery. Changes in ENSO influences on winter precipitation could also arise with warming and changes in global or regional atmospheric circulation (Singh et al., 2016; Wanders et al., 2017). Widespread mortality events suggest conditions may already be exceeding the resilience capacity in these systems (Allen et al., 2010).
Here, we take a statistical approach to understand how fine-scale (monthly) climate affects variability in annual growth (ring widths) under different climate conditions. Recent studies are also implementing a more direct approach to understanding sub-annual controls on sub-annual ring width processes in this region (Belmecheri, Wright, Szejner, Morino, & Monson, 2018; Szejner et al., 2018). These different approaches are, together, greatly improving our understanding of tree growth in the NAM region. Our results provide a lens through which to understand the unique interaction of climatic factors controlling tree growth in the Southwest, and emphasize a continuing need for experimental and/or physiological studies that explore factors controlling the plasticity of growth at sub-annual timescales, especially in the context of responses to and recovery from drought.
ACKNOWLEDGEMENTS
This work was funded by a National Science Foundation Advances in Biological Informatics award (DBI#1458867). The authors thank George Koch for early inspiration, the Ogle lab for comments on earlier versions, and Bruce Hungate for insightful feedback. We also thank the ITRDB and all authors who contributed tree-ring data to this extremely valuable resource. DMPP also thanks Kevin Hultine and Jarrett Barber for input on a dissertation chapter that lead to this manuscript. We also thank the Monsoon high performance computing cluster (https://nau.edu/hpc), on which model runs were performed.
AUTHOR CONTRIBUTIONS
DP and KO conceived the study. DP wrote and implemented the model. DP and KO analyzed the output. DP wrote the first draft of the manuscript, and KO contributed substantially to revisions.
DATA ACCESSIBILITY
All data used are publicly and freely available online, and sources are noted in the text. Tree-ring data are freely available through the International Tree-Ring Data Bank. If accepted and deemed necessary, data selected for use in this study will be archived on Dryad. Model code would be archived on GitHub.




