In the present paper, the fracture toughness of a polyurethane (PUR) foam (manufactured by Necumer GmbH, Germany, under the commercial designation Necuron 651) is experimentally and numerically investigated in order to examine its dependence on the specimen sizes. As a matter fact, to the best knowledge of the present authors, such an analysis is still missing in the technical literature. To perform the experimental campaign, notched PUR foam beams, with different geometrical sizes, are tested under three-point bending loading, and the Modified Two-Parameter Model (recently proposed by some of the present authors) is employed to measure the fracture toughness. Subsequently, such an experimental campaign is numerically simulated by applying a micromechanical model, implemented in a non-linear finite element homemade code. Finally, the results obtained are compared with some experimental data available in the literature, related to the same PUR foam.

Highlights

The fracture toughness of a polyurethane foam is experimentally investigated.
Notched PUR foam beams, with different sizes, are tested under three-point bending.
The Modified Two-Parameter Model is employed to measure the fracture toughness.
A numerical simulation is performed with a non-linear finite element model.
The results are compared with some experimental data available in the literature.

1 INTRODUCTION

Cellular materials are nowadays very popular materials due to lightweight, efficient, and superior design for engineering structures,¹ with applications in different fields such as defense, healthcare, automotive, construction, and aerospace,² and used both as a stand-alone material and in combination to other ones to form composites.³

They can be classified into natural and man-made (manufactured) cellular materials.^4-6 Cork, bamboo, wood, and human bones are examples of natural cellular materials, whereas polymeric, metallic, and ceramic foams, honeycomb and auxetic structures are examples of man-made ones.

As far as polymeric foams are concerned, their market has significantly increased over the last three decades, such foams being generally employed in building and aircraft/aerospace industries for both thermal and/or acoustic insulation, in automotive industry for energy absorption, thermal insulation, packaging, electronics, and other sectors.^{4, 7}

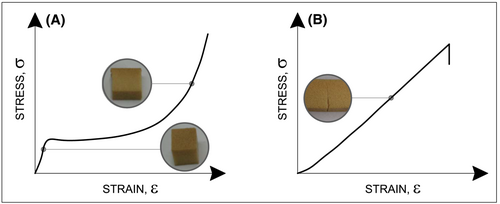
Failure of a polymeric foam is characterized by a crushing behavior under compression, reaching the full densification (Figure 1A), whereas it is characterized by the propagation of a single crack under tension (Figure 1B). Moreover, under tension and in the presence of a stress concentrator (such as a notch and/or a crack), such a foam has a linear-elastic behavior up to failure, highlighting a brittle fracture.⁴ Therefore, in the structural integrity analysis, the fracture toughness of the material represents a key parameter, which has to be examined in order to avoid sudden and catastrophic brittle fracture initiating from existing cracks.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Stress against strain curves for a polymeric foam up to failure, being the failure due to: (A) crushing under compression; (B) propagation of a single crack under tension. [Colour figure can be viewed at wileyonlinelibrary.com]

The investigation on the fracture toughness of a polyurethane (PUR) foam, belonging to the category of polymeric foams, is the object of the present paper. The effort for determining the fracture toughness of PUR foams can be traced back to more than three decades ago.^{4, 8} More precisely, Fowlkes⁹ determined the fracture toughness of a low density rigid PUR foam (density equal to 88 kg/m³) by testing specimens of different types, that is, center cracked specimen, single- and double-edge cracked specimens, and double cantilever beam specimen. By using single-edge crack specimens, McIntyre and Anderton¹⁰ analyzed the fracture behavior of rigid PUR foams characterized by different density, founding a linear correlation between fracture toughness and density.

More recently, Marsavina and Linul⁴ have presented a review on the different approaches to determine the fracture toughness of polymeric foams, including PUR foams, that is, analytical models, numerical micromechanical models, and experimental investigations.

Many research works have been published on fracture behavior of PUR foams. For example, Aliha et al.¹¹ performed Mixed-Mode I/II and I/III fracture tests on rigid PUR foams, with a density ranging from 100 to 300 kg/m³. Under Mixed-Mode I/II loading, such tests were conducted by using asymmetric semi-circular bend (ASCB) and compact tension-shear (CTS) specimens, whereas edge notch disc bend (ENDB) specimens were employed under Mixed-Mode I/III loading. The mode mixity parameter, $M^{e}$ , was made to vary from 0 (that is, the case of pure Mode I loading) to 1 (that is, the case of pure Mode II loading). The corresponding values of the Mixed-Mode fracture toughness and fracture growth direction (or fracture trajectory) were determined. It was found that fracture toughness significantly depended on the density, whereas fracture trajectory did not show any dependence. Moreover, it was observed that the fracture trajectory was curved under Mixed-Mode I/II loading, whereas it was curved and twisted under Mixed-Mode I/III loading, reaching the grater deviation from the pre-crack direction under pure Mode II and pure Mode III, respectively. Linul et al.¹² carried out Mode I fracture tests on three PUR foams, having a density equal to 100, 145, and 300 kg/m³, respectively. The specimens, each of them consisting in a single-edge notched bend (SENB) specimen, were cut along either the foam rise direction (also named out-of-plane loading direction) or the foam flow direction (also named in-plane loading direction) and subjected to either quasi-static or dynamic three-point bending loading. More precisely, quasi-static tests were performed according to the ASTM D-5045-99 standard,¹³ whereas dynamic tests were performed according to the EN ISO 179–2 standard¹⁴ and the procedure presented by Kalthoff.¹⁵ The specimens were tested at both room temperature (25°C) and cryogenic temperature (−196°C). It was found that the Mode I fracture toughness of the examined foams depended on density and significantly increased at cryogenic temperature. The fracture toughness determined for out-of-plane specimens was slightly higher than that for in-plane specimens. Moreover, the dynamic values were higher than the quasi-static ones (up to three times higher). Empirical relationships were proposed for the estimation of quasi-static fracture toughness at −196°C and dynamic fracture toughness at room temperature. Imani et al.¹⁶ performed Mixed-Mode I/II fracture tests on three PUR foams (density 100 ÷ 300 kg/m³). The specimens, each of them consisting in an asymmetric edge notched disc bend (AENDB) specimen, were subjected to asymmetric three-point bending, by varying $M^{e}$ from 0 to 1. For each value of $M^{e}$ , three AENDB specimens were tested. It was found that the Mode I fracture toughness ranged between 0.08 and 0.31 MPa·m^0.5, whereas the Mode II one ranged between 0.09 and 0.34 MPa·m^0.5. It was also observed that, for each value of $M^{e}$ examined, the fracture toughness increased by increasing density. Some experimental results were assessed by employing analytical failure criteria available in the literature.^{17, 18} Further, Shahbazian et al.¹⁹ carried out Mixed-Mode I/II and I/III fracture tests on a rigid PUR foam with a density of 40 kg/m³. Forty ENDB specimens were tested under the above loading conditions. The fracture angle and the fracture toughness were determined, being the experimental results also assessed by using some analytical failure criteria available in the literature.^20-22

In the present paper, the fracture toughness of a PUR foam with a density equal to 708 kg/m³, manufactured by Necumer GmbH (Germany) under the commercial designation Necuron 651, is experimentally and numerically investigated in order to examine its dependence from specimen sizes, being such an analysis missing in the literature to the best knowledge of the present authors. It is worth noticing that, with respect to the research works,^{23, 24, 4} where the thickness is taken as a constant, all the specimen sizes are herein made to vary proportionally.

To perform the experimental campaign, notched PUR foam beams, with different geometrical sizes, are tested under three-point bending loading, and the Modified Two-Parameter Model (MTPM), recently proposed by some of the present authors,^25-29 is applied to measure the fracture toughness. Moreover, such an experimental campaign is numerically simulated by using a micromechanical model, proposed by some of the present authors in the past.^30-32 The results obtained are compared with the experimental data reported by Negru et al.,^{33, 34} which are related to the same PUR foam.

The paper is structured as follows: the material examined is described in Section 2, whereas the experimental campaign performed, the MTPM, and the results obtained are presented in Section 3. Section 4 is devoted to both the description of the micromechanical model used for the numerical simulations and the results obtained. Section 5 is dedicated to the comparison of the present results with the literature data, whereas the main conclusions are summarized in Section 6.

2 MATERIAL EXAMINED

The PUR foam herein examined is manufactured by Necumer GmbH under the commercial designation Necuron 651.³⁵ Being its density equal to 708.00 ± 3.45 kg/m³,^{33, 34, 36, 37} it can be classified as a PUR material with a porous solid structure, as is shown in Figure 2, which represents the material microstructure obtained by using a Quanta™ 250 FEG SEM, at a magnification of 500×.

From the statistical analysis of the microstructure shown in Figure 2, the cell diameter is equal to 49.1 ± 30.2 μm, and the cell wall thickness ranges from 4.7 to 37.6 μm.

The elastic modulus and the Poisson coefficient, determined according to the ASTM E-1876-01 standard,³⁸ are equal to 1250 ± 15 MPa and 0.302,^{33, 34, 37} respectively, whereas the ultimate tensile strength, evaluated according to the EN ISO 527 standard,³⁹ is equal to 17.40 ± 0.32 MPa.^{33, 34, 36, 37}

3 FRACTURE TOUGHNESS: EXPERIMENTAL CAMPAIGN

3.1 Specimen geometries

The tested specimens are made by cutting prismatic samples from Necuron 651 panels in flow direction (Figure 3). According to the MTPM,^25-29 the specimen sizes are function of the panel width, $B$ , as follows: depth $W = 2 B$ , span $S = 8 B$ , and notch depth $a_{0} = 2 / 3 B$ , being the notch width $< 1.45$ mm (see Figure 3). Such a notch is realized by using a circular saw, thus obtaining a blunt notch.

In order to experimentally analyze the fracture toughness dependence on the specimen sizes, three groups of specimens, each of them consisting of six samples, have been cut:

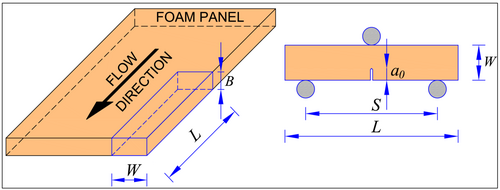
six specimens (named N10-X, where X identifies the specimen No.) with a nominal width, $B$ , equal to $10$ mm;
six specimens (named N25-X) with $B = 25$ mm;
six specimens (named N50-X) with $B = 50$ mm.

For each group, the measured mean values of both width $B$ , depth $W$ , span $S$ , length $L$ , and notch depth $a_{0}$ are listed in Table 1. The average value of the notch width among all the specimens is equal to $1.40$ mm.

TABLE 1. Average specimen sizes for the three groups of specimens examined: width

B

, depth

W

, span

S

, length

L

, and notch depth

a_{0}

Group name	$B [mm]$	$W [mm]$	$S [mm]$	$L [mm]$	$a_{0} [mm]$
N10	10.293	20.862	80	120	6.058
N25	25.394	48.942	200	300	16.710
N50	50.094	99.049	400	500	33.366

Before testing, all specimens are stored in laboratory at 20°C and 65% of relative humidity.

3.2 Testing setup

Three-point bending tests on the above specimens are performed by using a universal testing machine Instron 8862 (Figure 4) at the “Testing Laboratory of Material and Structures” of the University of Parma, Italy, according to both the MTPM^25-29 and the Rilem Recommendations,^{40, 41} under crack mouth opening displacement (CMOD) control by employing a clip gauge. The CMOD rate is equal to 0.15 mm/h.

The applied load $P$ is measured through a load cell of 100 kN, with an accuracy up to 0.02%. Each specimen is monotonically loaded under CMOD control up to the peak load $P_{\max}$ , being the specimen behavior characterized by an initial compliance $C_{i}$ . After $P_{\max}$ is reached, the post-peak stage follows and, when the load is equal to about 95% of $P_{\max}$ , the specimen is fully unloaded under load control in 3 min, being the specimen characterized by an unloading compliance $C_{u}$ . The specimen is then reloaded under CMOD control up to failure.

3.3 Calculation

The fracture toughness, named $K_{(I + II) C}^{S}$ , is evaluated according to the MTPM,^25-29 recently proposed by some of the present authors to compute such a parameter for brittle and quasi-brittle materials. The method consists of the following steps.

Firstly, by means of

C_{i}

deduced from a load-CMOD curve, the elastic modulus is determined as follows:

E = \frac{6 S a_{0} V (α_{0})}{C_{i} W^{2} B}

(1)

where

α_{0} = a_{0} / W

, and the parameter

V (α_{0})

is given by

V (α_{0}) = 0.76 - 2.28 α_{0} + 3.87 α_{0}^{2} - 2.04 α_{0}^{3} + \frac{0.66}{{(1 - α_{0})}^{2}} .

(2)

Then, due to stable crack propagation, two cases can be experimentally observed (see Figure 5):

the kinking angle, $θ$ , is quite constant along the crack path (Figure 5A);
the crack path consists of branches with different orientations (Figure 5B).

In the first case, the effective critical crack length

\underline{a} = a_{0} + (a_{1} + a_{2}) \cos θ

is computed by exploiting the following equation to obtain the unknown quantity

a_{2}

, being

a_{1} = 0.3 a_{0}

E = \begin{array}{l} \frac{6 S}{C_{u} W^{2} B} {a_{0} V (\frac{a_{0}}{W}) + [\cos^{6} \frac{θ}{2} + \sin^{2} \frac{θ}{2} \cos^{4} \frac{θ}{2}] [(a_{0} + a_{1} \cos θ) V (\frac{a_{0} + a_{1} \cos θ}{W}) \\ - a_{0} V (\frac{a_{0}}{W})] + [\cos^{3} θ + \sin^{2} θ \cos θ] [(a_{0} + a_{1} \cos θ + a_{2} \cos θ) V (\frac{a_{0} + a_{1} \cos θ + a_{2} \cos θ}{W}) \\ - (a_{0} + a_{1} \cos θ) V (\frac{a_{0} + a_{1} \cos θ}{W})]} \end{array}

(3)

where

C_{u}

is deduced from the load-CMOD curve. It is worth noticing that, if fracture failure occurs just after the peak load

P_{\max}

, the unloading compliance

C_{u}

is approximately computed as the inverse slope of the line connecting the point at

P_{\max}

with the origin in the P-CMOD graph. When the value of

a_{2}

is negative, it means that

\underline{a} = a_{0} + a_{1} \cos θ

, and the following equation is exploited to obtain the unknown quantity

a_{1}

E = \begin{array}{l} \frac{6 S}{C_{u} W^{2} B} {a_{0} V (\frac{a_{0}}{W}) + [\cos^{6} \frac{θ}{2} + \sin^{2} \frac{θ}{2} \cos^{4} \frac{θ}{2}] [(a_{0} + a_{1} \cos θ) V (\frac{a_{0} + a_{1} \cos θ}{W}) \\ - a_{0} V (\frac{a_{0}}{W})]} . \end{array}

(4)

When

a_{1} = 0.3 a_{0}

, the fracture toughness

K_{(I + II) C}^{S}

is computed as follows:

K_{(I + II) C}^{S} = \frac{3 P_{\max} S}{2 W^{2} B} \sqrt{π [a_{0} + (a_{1} + a_{2}) \cos θ]} f (α) α = \frac{a_{0} + (a_{1} + a_{2}) \cos θ}{W}

(5)

whereas, when

a_{1} < 0.3 a_{0}

, it is computed as follows:

K_{(I + II) C}^{S} = \frac{3 P_{\max} S}{2 W^{2} B} \sqrt{π [a_{0} + a_{1} \cos θ]} f (α) α = \frac{a_{0} + a_{1} \cos θ}{W}

(6)

being

f (α) = \frac{1}{\sqrt{π}} \frac{1.99 - α (1 - α) (2.15 - 3.93 α + 2.70 α^{2})}{(1 + 2 α) {(1 - α)}^{3 / 2}} .

(7)

In the second case, when the crack path is characterized by multiple branches, the above equations are still valid taking into account that the kinking angle

θ_{i}

is that corresponding to:

the orientation of the second branch (that is, $θ_{2}$ in Figure 5B), when the length of the second branch, $l_{2}$ , is greater than that of the first one, $l_{1}$ ;
the orientation of the first branch (that is, $θ_{1}$ in Figure 5B), when $l_{1} > l_{2}$ .

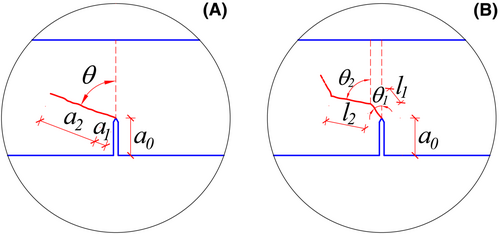
It is worth noticing that, when the fracture surface is not plane, $θ$ is determined as the mean value of the kinking angles related to the front and the back side of the specimen.

3.4 Results

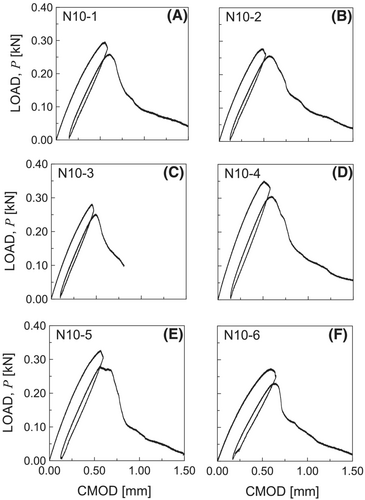
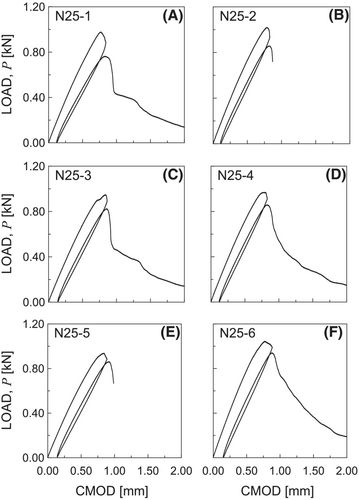
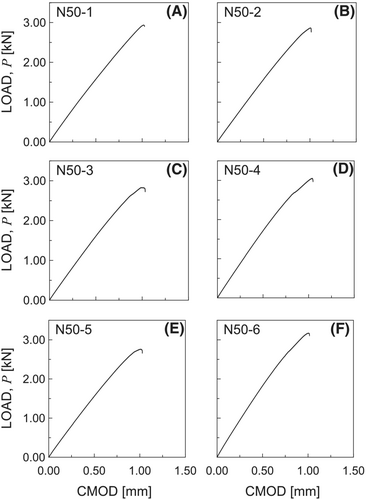
For each specimen group detailed in Section 3.1, the load against CMOD curves are reported in Figures 6-8, whereas the registered values of $C_{i}$ , $C_{u}$ , and $P_{\max}$ are listed in Table 2. The crack paths are shown in Figures 9-11, highlighting a typical Mode I crack path. Therefore, to compute $K_{(I + II) C}^{S}$ , the kinking angle $θ$ is assumed equal to zero for all cases examined.

TABLE 2. Experimental results: initial compliance

C_{i}

, unloading compliance

C_{u}

, peak load

P_{\max}

, fracture toughness

K_{(I + II) C}^{S}

, and average fracture toughness

{\bar{K}}_{(I + II) C}^{S}

Specimen No.	$C_{i} [mm / kN]$	$C_{u} [mm / kN]$	$P_{\max} [kN]$	$K_{(I + II) C}^{S} [MPa \sqrt{m}]$	${\bar{K}}_{(I + II) C}^{S} [MPa \sqrt{m}]$
N10-1	1.442	1.655	0.296	1.430	1.258 ± 0.143
N10-2	1.366	1.613	0.278	1.285
N10-3	1.304	1.471	0.281	1.061
N10-4	1.168	1.378	0.351	1.383
N10-5	1.327	1.499	0.327	1.263
N10-6	1.556	1.906	0.274	1.128
N25-1	0.665	0.884	0.978	1.365	1.334 ± 0.038
N25-2	0.644	0.792	1.020	1.352
N25-3	0.704	0.839	0.949	1.302
N25-4	0.658	0.791	0.970	1.303
N25-5	0.711	0.820	0.937	1.296
N25-6	0.723	0.750	1.046	1.384
N50-1	0.309	0.346	2.937	1.322	1.352 ± 0.066
N50-2	0.316	0.351	2.865	1.301
N50-3	0.307	0.349	2.829	1.316
N50-4	0.289	0.340	3.053	1.390
N50-5	0.317	0.365	2.760	1.314
N50-6	0.259	0.317	3.172	1.469

It can be observed that, for the specimens of the N50 group (Figure 8), fracture failure is reached just after the $P_{\max}$ is achieved. Therefore, the unloading and reloading is not performed, contrary to what occurs for the specimens of N10 and N25 groups (Figures 6 and 7).

For each specimen examined, the corresponding value of $K_{(I + II) C}^{S}$ is reported in Table 2, together with the mean value ${\bar{K}}_{(I + II) C}^{S}$ and standard deviation related to each specimen group. By comparing the ${\bar{K}}_{(I + II) C}^{S}$ values with each other, it can be stated that, according to the MTPM, the fracture toughness of Necuron 651 is a size-independent parameter, being the maximum relative difference in absolute value equal to 0.094, which is lower than the maximum standard deviation related to the fracture toughness results. Consequently, the fracture toughness of the present Necuron can be assumed to be equal to 1.315 ± 0.097 MPa·m^0.5 (computed as the mean value of $K_{(I + II) C}^{S}$ values related to all specimens, reported in Table 2).

4 NUMERICAL SIMULATIONS

4.1 Model description

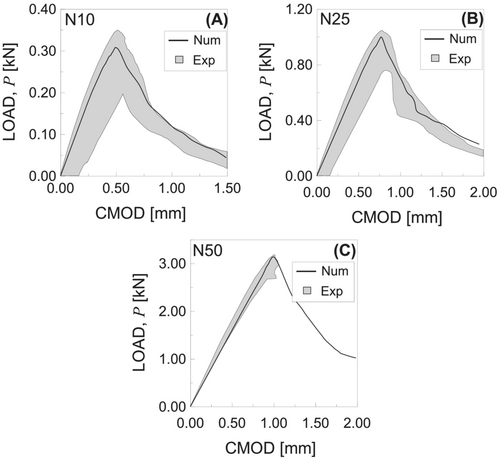
The experimental campaign described in Section 3 is numerically simulated by employing a micromechanical model, implemented in a non-linear Finite Element (FE) homemade code in Fortran language, proposed by some of the present authors in the past.^30-32 More precisely, the P-CMOD curves are numerically simulated, and the fracture toughness is determined according to Equations (1)–(7).

In the present model, the matrix is assumed to have a brittle behavior, and the discontinuities due to the fracture process are simulated by using a suitable modification of the material properties. More precisely, the nucleation of one or more cracks in the finite elements is related to the reduction of the current matrix stiffness in correspondence of the integration points. In order to describe such a process, a cohesive law is employed to simulate the cracked zone, whereas an elastic law is adopted for the uncracked (i.e., continuous) region. The crack faces, hence, transmit a non-zero stress, described by an exponential function of the relative crack opening displacement.

Due to the nature of the simulated tests, a plain strain FE analysis is performed. To such an aim, three notched prismatic models subjected to three-point bending loading are created, whose geometrical sizes are listed in Table 1. According to the specimen geometries (Section 3.1), the notch is schematized as a blunt notch in the numerical model.

The mesh discretization is composed by four-node quadrilateral plane elements, and the model is characterized by a number of finite elements equal to 639 for the N10 model and 630 for both N25 and N50 models. Such discretizations derive from both convergence analyses, performed on the von Mises stress, and a mesh refinement near the notch in order to better simulate the fracture behavior. Consequently, the minimum size of the used four-node quadrilateral element is equal to 0.33 mm.

The input data are represented by: the elastic modulus equal to 915.45 MPa, computed as the average value of the $E$ experimental results; the Poisson ratio and the ultimate tensile strength equal to 0.302 and 17.40 MPa, respectively, according to the experimental values provided by Negru et al.^{33, 34, 37}; and the energy release rate computed as 1715 N/m, by exploiting the well-known relationship related to the fracture toughness under plane strain assumption (the used fracture toughness value is the experimental mean one, that is, 1.315 MPa·m^0.5).

The analyses have been performed under displacement control, by imposing a vertical displacement increment at the top central loading point.

It is worth noticing that, since the unloading branch has not been numerically reproduced, the unloading compliance is computed as the slope of the straight line passing through the origin and $P_{\max}$ of each numerical load against CMOD curve.

4.2 Results

The load against CMOD curves are plotted in Figure 12 together with the experimental scatter bands (drawn by retracing the external contour of the plot containing all the experimental curves for a given group of specimens), showing a quite satisfactory agreement. More precisely, according to the results reported in Table 3, the maximum errors with respect to the experimental data are equal to:

+3.51% on $C_{i}$ , +1.20% on $C_{u}$ , and +9.16% on $P_{\max}$ for the N10 model;
+5.89% on $C_{i}$ , −5.67% on $C_{u}$ , and +1.29% on $P_{\max}$ for the N25 model;
+5.05% on $C_{i}$ , −9.08% on $C_{u}$ , and +6.27% on $P_{\max}$ for the N50 model.

TABLE 3. Numerical results: initial compliance

C_{i, num}

, unloading compliance

C_{u, num}

, peak load

P_{\max, num}

, and fracture toughness

K_{(I + II) C, num}^{S}

Model name	$C_{i, num} [mm / kN]$	$C_{u, num} [mm / kN]$	$P_{\max, num} [kN]$	$K_{(I + II) C, num}^{S} [MPa \sqrt{m}]$
N10	1.408	1.606	0.308	1.257
N25	0.724	0.767	0.996	1.263
N50	0.312	0.313	3.120	1.339

By using the numerical values of $C_{i, num}$ , $C_{u, num}$ , and $P_{\max, num}$ , listed in Table 3, the corresponding values $K_{(I + II) C, num}^{S}$ of fracture toughness are computed by using Equations (1)–(7), assuming $θ = 0 °$ . The maximum error in terms of fracture toughness with respect to ${\bar{K}}_{(I + II) C}^{S}$ is equal to −0.09% for the N10 model, −5.29% for the N25 model, and −0.93% for the N50 model.

5 COMPARISON WITH LITERATURE DATA

The Mixed-Mode I/II fracture toughness evaluation for Necuron 651, performed by using different methods available in the literature,^{33, 34} is discussed in this section, and the comparison with the present results is made.

5.1 Method by using an ASCB specimen

The tested sample employed by Negru et al.³³ was an ASCB specimen with a radius of 40 mm and thickness of 10 mm, containing an edge crack with a length of 20 mm, perpendicular to the specimen edge. The specimen was loaded under three-point bending, and a wide range of Mixed-Mode loading was produced by varying the position of one of the two supports. More precisely, such a distance was made to vary from 30 mm (pure Mode I loading) to 2.66 mm (pure Mode II loading). The tests were carried out by means of a Zwick/Roell Z005 testing machine (maximum load 5 kN), under displacement control with a loading rate of 1 mm/min.

It was found that the Mixed-Mode fracture toughness ranged between 1.073 MPa·m^0.5 (pure Mode II loading) and 1.286 MPa·m^0.5 (pure Mode I loading). Such results are in agreement with both the present experimental and numerical results, equal to 1.315 and 1.286 MPa·m^0.5, respectively, being the maximum relative difference lower than the experimental standard deviation.

5.2 Method by using a SENB specimen

The tested sample employed by Negru et al.³⁴ was a SENB specimen with a depth ( $W$ ) of 20 mm and a thickness of 10 mm, containing an edge crack with a length equal to $0.5 W$ . The specimen was loaded under three-point bending, being the span equal to $4 W$ . The tests were carried out according to the ASTM D 5045-14 standard,⁴² by means of a Zwick/Roell Z005 testing machine (maximum load 5 kN), under displacement control with a loading rate of 1 mm/min.

It was found that the Mode I fracture toughness was equal to 0.996 MPa·m^0.5, being the relative difference with respect to the value obtained using the ASCB specimen³³ equal to about 23%, whereas the difference with respect to the present experimental and numerical results is equal to about 24% and 23%, respectively.

5.3 Method by using a DCR specimen

The tested sample employed by Negru et al.³⁴ was a diametrically compressed ring (DCR) with an inner diameter of 40 mm, an outer diameter of 80 mm, and a thickness of 5 mm, containing a U-shaped notch with a depth equal to 5 mm. Different values of the notch root radius ranging from 0.5 to 1.5 mm were examined. The specimen was loaded under compression, and a wide range of Mixed-Mode loading was produced by varying the notch orientation. More precisely, such an orientation was made to vary from 0° (pure Mode I loading) to 25° (nearly pure Mode II loading). The tests were carried out by means of a Zwick/Roell Z005 testing machine (maximum load 5kN), under displacement control with a loading rate of 1 mm/min.

It was found that, when the notch root radius was equal to 0.5 mm, the generalized notch stress intensity factor ranged between 1.097 MPa·m^0.5 (nearly pure Mode II loading) and 1.147 MPa·m^0.5 (pure Mode I loading). The comparison with the present results can be only qualitative since the DCR specimen is characterized by a notch root radius of 0.5 mm (sharp notch). The above results related to the DCR specimens are of the same order of magnitude as the present ones (both experimental and numerical).

6 CONCLUSIONS

In the present paper, the fracture toughness of the Necuron 651 has been investigated by varying the specimen sizes. From an experimental point of view, the MTPM has been employed, whereas a micromechanical model has been used from a numerical point of view. The results obtained show that:

fracture toughness is a size-independent material parameter;
the numerical model employed is able to estimate the parameters used to compute fracture toughness with a quite good accuracy, providing results characterized by errors, with respect to the experimental ones, lower than the standard deviation values;
the present results are in quite satisfactory agreement with some results available in the literature, experimentally obtained with alternative methods.

This research work also highlights that the present micromechanical model is a good alternative to compute the fracture toughness of brittle materials.

AUTHOR CONTRIBUTIONS

Sabrina Vantadori: Conceptualization; supervision; funding acquisition; investigation; review and editing. Andrea Carpinteri: funding acquisition; Review and editing. Roberto Cerioni: Review and editing. Camilla Ronchei: Formal analysis; investigation; writing. Daniela Scorza: Formal analysis; investigation; writing. Andrea Zanichelli: Formal analysis; investigation; review and editing. Liviu Marsavina: Supervision; review and editing.

ACKNOWLEDGMENTS

The work of Andrea Carpinteri, Roberto Cerioni, Sabrina Vantadori, and Andrea Zanichelli is supported by the Italian Ministry of University and Research (P.R.I.N. National Grant 2017, Project code 2017HFPKZY; University of Parma Research Unit).

Open Research

DATA AVAILABILITY STATEMENT

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

REFERENCES

1Mirsayar M. On brittle fracture of two-dimensional lattices with material anisotropies. Fatigue Fract Eng Mater Struct. 2022; 45(7): 1929-1941.
10.1111/ffe.13711
Web of Science® Google Scholar
2Raghavendra S, Molinari A, Cao A, et al. Quasi-static compression and compression–compression fatigue behavior of regular and irregular cellular biomaterials. Fatigue Fract Eng Mater Struct. 2021; 44(5): 1178-1194.
10.1111/ffe.13422
Web of Science® Google Scholar
3Shamsul BM, Abdullah S, Md NN, Muhamad Paudzi MKF, Arifin A, Karam Singh SS. Observing the simulation behaviour of magnesium alloy metal sandwich panel under cyclic loadings. Frat Ed Integrità Strutt. 2022; 16(61): 230-243.
10.3221/IGF-ESIS.61.15
Google Scholar
4Marșavina L, Linul E. Fracture toughness of rigid polymeric foams: a review. Fatigue Fract Eng Mater Struct. 2020; 43(11): 2483-2514.
10.1111/ffe.13327
Web of Science® Google Scholar
5Guedaoura H, Hadidane Y. Web post-buckling strength of thin-webbed cellular beams using carbon PFRP profiles. Frattura Ed Integrità Strutturale. 2022; 16(60): 43-61. doi:10.3221/IGF-ESIS.60.04
10.3221/IGF-ESIS.60.04
Google Scholar
6Huzni S, Oktianda F, Fonna S, Rahiem F, Angriani L. The use of frictional and bonded contact models in finite element analysis for internal fixation of tibia fracture. Frattura Ed Integrità Strutturale. 2022; 16(61): 130-139.
10.3221/IGF-ESIS.61.09
Google Scholar
7Eremin A, Burkov M, Lyubutin P. Evaluation of tensile fatigue behavior of carbon fiber reinforced polymer modified by single-wall carbon nanotubes. Fatigue Fract Eng Mater Struct. 2023; 46(2): 501-513.
10.1111/ffe.13880
CAS Web of Science® Google Scholar
8Pugna A, Negrea R, Linul E, Marsavina L. Is fracture toughness of PUR foams a material property? A statistical approach. Materials. 2020; 13(21): 1-13.
10.3390/ma13214868
Web of Science® Google Scholar
9Fowlkes CW. Fracture toughness tests of a rigid polyurethane foam. Int J Fract. 1974; 10(1): 99-108.
10.1007/BF00955084
CAS Web of Science® Google Scholar
10McIntyre A, Anderton GE. Fracture properties of a rigid polyurethane foam over a range of densities. Polymer. 1979; 20(2): 247-253.
10.1016/0032-3861(79)90229-5
CAS Web of Science® Google Scholar
11Aliha MRM, Mousavi SS, Bahmani A, Linul E, Marsavina L. Crack initiation angles and propagation paths in polyurethane foams under mixed modes I/II and I/III loading. Theor Appl Fract Mech. 2019; 101: 152-161.
10.1016/j.tafmec.2019.02.016
CAS Web of Science® Google Scholar
12Linul E, Marşavina L, Vălean C, Bănică R. Static and dynamic mode I fracture toughness of rigid PUR foams under room and cryogenic temperatures. Eng Fract Mech. 2020; 225:106274.
10.1016/j.engfracmech.2018.12.007
Web of Science® Google Scholar
13 ASTM D-5045-99. Standard test methods for plane-strain fracture toughness and strain energy release rate of plastic materials; 1999.
Google Scholar
14 EN ISO 179-2. Plastics—determination of Charpy impact properties. Part 2: instrumented impact test; 2000.
Google Scholar
15Kalthoff JF. Characterization of the dynamic failure behaviour of a glass-fiber/vinyl-seter at different temperatures by means of instrumented Charpy impact testing. Compos Part B-Eng. 2004; 35(6-8): 657-663.
10.1016/j.compositesb.2003.11.008
Web of Science® Google Scholar
16Imani DM, Aliha MRM, Linul E, Marsavina L. A suitable mixed mode I/II test specimen for fracture toughness study of polyurethane foam with different cell densities. Theor Appl Fract Mech. 2022; 117:103171.
10.1016/j.tafmec.2021.103171
CAS Web of Science® Google Scholar
17Aliha MRM, Ayatollah MR, Smith DJ, Pavier MJ. Geometry and size effects on fracture trajectory in a limestone rock under mixed mode loading. Eng Fract Mech. 2010; 77(11): 2200-2212.
10.1016/j.engfracmech.2010.03.009
Web of Science® Google Scholar
18Mirsayar MM. Mixed mode fracture analysis using extended maximum tangential strain criterion. Mater Des. 2015; 86: 941-947.
10.1016/j.matdes.2015.07.135
CAS Web of Science® Google Scholar
19Shahbazian B, Mirsayar MM, Aliha MRM, Ghahramani Darvish M, Asadi MM, Jafari Haghighatpour P. Experimental and theoretical investigation of mixed-mode I/II and I/III fracture behavior of PUR foams using a novel strain-based criterion. Int J Solids Struct. 2022; 258:111996.
10.1016/j.ijsolstr.2022.111996
CAS Web of Science® Google Scholar
20Sih GC. Strain-energy-density factor applied to mixed mode crack problems. Int J Fract. 1974; 10(3): 305-321.
10.1007/BF00035493
Web of Science® Google Scholar
21Schöllmann M, Richard HA, Kullmer G, Fulland M. A new criterion for the prediction of crack development in multiaxially loaded structures. Int J Fract. 2002; 117(2): 129-141.
10.1023/A:1020980311611
Web of Science® Google Scholar
22Mirsayar MM, Shahbazian B. An energy-based criterion for mixed-mode I/II/III fracture considering effective critical distances. Eng Fract Mech. 2022; 272:108674.
10.1016/j.engfracmech.2022.108674
Google Scholar
23Linul E, Marşavina L, Sadowski T, Kneć M. Size effect on fracture toughness of rigid polyurethane foams. Solid State Phenom. 2012; 188: 205-210.
10.4028/www.scientific.net/SSP.188.205
CAS Google Scholar
24Marsavina L, Constantinescu DM, Linul E, Apostol DA, Voiconi T, Sadowski T. Refinements on fracture toughness of PUR foams. Eng Fract Mech. 2014; 129: 54-66.
10.1016/j.engfracmech.2013.12.006
Web of Science® Google Scholar
25Benaimeche O, Carpinteri A, Mellas M, Ronchei C, Scorza D, Vantadori S. The influence of date palm mesh fibre reinforcement on flexural and fracture behaviour of a cement-based mortar. Compos Part B-Eng. 2018; 152: 292-299.
10.1016/j.compositesb.2018.07.017
CAS Web of Science® Google Scholar
26Vantadori S, Carpinteri A, Guo LP, Ronchei C, Zanichelli A. Synergy assessment of hybrid reinforcements in concrete. Compos Part B-Eng. 2018; 147: 197-206.
10.1016/j.compositesb.2018.04.020
CAS Web of Science® Google Scholar
27Scorza D, Marsavina L, Carpinteri A, Ronchei C, Vantadori S. Size-effect independence of particleboard fracture toughness. Compos Struct. 2019; 229:111374.
10.1016/j.compstruct.2019.111374
Web of Science® Google Scholar
28Scorza D, Luciano R, Mousa S, Vantadori S. Fracture behaviour of hybrid fibre-reinforced roller-compacted concrete used in pavements. Construct Build Mater. 2021; 271:121554.
10.1016/j.conbuildmat.2020.121554
Web of Science® Google Scholar
29Vantadori S, Ronchei C, Scorza D, Zanichelli A. Experimental tests and FE simulations to compute the mechanical and fracture properties of the shot-earth 772. Fatigue Fract Eng Mater Struct. 2023; 46(1): 49-62.
10.1111/ffe.13846
Web of Science® Google Scholar
30Scorza D.. Mechanical Modelling of Short-Fibre-Reinforced Materials Under Static or Cyclic Loading. ESIS Publishing House; 2021, ISBN: 978-88-31482-00-4.
Google Scholar
31Brighenti R, Scorza D. A micro-mechanical model for statistically unidirectional and randomly distributed fibre-reinforced solids. Math Mech Solids. 2012; 17(8): 876-893.
10.1177/1081286512454447
Web of Science® Google Scholar
32Brighenti R, Carpinteri A, Scorza D. Micromechanical crack growth-based fatigue damage in fibrous composites. Int J Fatigue. 2016; 82: 98-109.
10.1016/j.ijfatigue.2015.04.007
Web of Science® Google Scholar
33Negru R, Marsavina L, Filipescu H, Căplescu C, Voiconi T. Assessment of brittle fracture for PUR materials using local strain energy density and theory of critical distances. Theor Appl Fract Mech. 2015; 79:1604.
10.1016/j.tafmec.2015.07.011
Web of Science® Google Scholar
34Negru R, Serban DA, Pop C, Marsavina L. Notch effect assessment in a PUR material using a ring shaped specimen. Theor Appl Fract Mech. 2018; 97: 500-506.
10.1016/j.tafmec.2018.01.016
CAS Web of Science® Google Scholar
35 Necumer. Accessed March 9, 2023. https://www.necumer.de/index.php/en/produkte-2/board-materials.html
Google Scholar
36Voiconi T, Negru R, Linul E, Marsavina L, Filipescu H. The notch effect on fracture of polyurethane materials. Frat Ed Integrità Strutt. 2014; 30: 101-108.
10.3221/IGF-ESIS.30.14
Google Scholar
37Negru R, Marsavina L, Voiconi T, Linul E, Filipescu H, Belgiu G. Application of TCD for brittle fracture of notched PUR materials. Theor Appl Fract Mech. 2015; 80: 87-95.
10.1016/j.tafmec.2015.05.005
CAS Web of Science® Google Scholar
38 ASTM E-1876-01. Standard test method for dynamic Young's modulus, shear modulus, and Poisson's ratio by impulse excitation technique of vibration, 2001.
Google Scholar
39 EN ISO 527:2012. Plastics-determination of tensile properties, 2012.
Google Scholar
40 RILEM Technical Committee. 50-FMC, determination of the fracture energy of mortar and concrete by means of three-point bend test on notched beams, proposed RILEM draft recommendations. Mater Struct. 1985; 18: 285-290.
Google Scholar
41 RILEM Technical Committee. 89-FMT, determination of fracture parameters (KsIC and CTODc) of plain concrete using three-point bend tests, proposed RILEM draft recommendations. Mater Struct. 1990; 23(6): 457-460.
10.1007/BF02472029
Google Scholar
42 ASTM D 5045-14. Standard test method for plain-strain fracture toughness and strain energy release rate of plastic materials.
Google Scholar

Volume46, Issue10

October 2023

Pages 3654-3666

Fracture toughness of a rigid polyurethane foam: experimental and numerical investigation by varying the specimen sizes

Abstract

Highlights

1 INTRODUCTION

2 MATERIAL EXAMINED