INTRODUCTION

Recruitment is the part of the plant life cycle that spans from the seed to juvenile stages, involving different demographic processes (germination, emergence, seedling survival and sapling growth and survival) (Herrera et al., 1994; Merges et al., 2020). These processes are modulated by direct or indirect plant–plant interactions where the success of a recruiting plant may depend on the identity of the established plants around it (Alcántara et al., 2018; Gómez-Aparicio et al., 2004; Landero & Valiente-Banuet, 2010; Rey & Alcántara, 2000). Understanding the mechanisms that condition the specificity of such plant–plant interactions is of major importance in the study of species coexistence (Alcántara et al., 2019). Among these mechanisms, plant–soil feedbacks have garnered increasing interest (Crawford et al., 2019; Lekberg et al., 2018). Plant–soil feedback (PSF, hereafter) is the process by which plants exert an influence on soil properties that affect the performance of individuals of their own or other plant species (Bever et al., 1997). In the last decade, it is being widely recognized that feedbacks operate in structuring the composition and dynamics of plant communities (Eppinga et al., 2018; Klironomos, 2002; Miller et al., 2022). A decrease of conspecific relative to heterospecific performance (i.e., a negative PSF) can prevent dominance and drive species coexistence in forests (Jiang et al., 2022; Mangan et al., 2010) and grasslands (Petermann et al., 2008) but it can also favour invasiveness of alien species not affected by such feedback (Klironomos, 2002). Conversely, positive PSFs may lead to the destabilization of diverse communities by enhancing the performance of conspecifics, thus increasing their dominance (Kulmatiski et al., 2011; Suding et al., 2013). However, some studies have found contrasting results, such as dominance dynamics or invader species success in spite of the existence of negative PSFs (Heinze et al., 2016; Nijjer et al., 2007), or the absence of relationship between the species abundance and positive PSFs (Reinhart et al., 2021). This suggests that there are knowledge gaps in the factors influencing plant–plant interaction outcomes (Lekberg et al., 2018), so determining the impact of PSFs on plant species diversity and dynamics in natural communities still remains a challenge (Kandlikar et al., 2019).

The mathematical models of PSFs by Bever and colleagues (Bever, 1994, 2003; Bever et al., 1997) provided the basis for the theoretical framework that has guided most empirical research in the field (Miller et al., 2022). The pairwise feedback metric (I_s) proposed by Bever can be quantified experimentally and informs on the strength of stabilization or destabilization of species coexistence (Bever et al., 1997; Crawford et al., 2019). However, it does not take into account the importance of interspecific fitness differences when analysing plant coexistence (Ke & Wan, 2020). To disentangle the role of PSFs in the outcome of plant–plant interactions, recent studies (Kandlikar et al., 2019; Ke & Wan, 2020; Yan et al., 2022) have applied modern coexistence theory (Chesson, 2000). This approach dissects the competitive outcome between a pair of species into stabilizing niche differences that favour the recovery of rare species, and fitness differences that determine the relative competitive ability of plant species (Ke & Wan, 2020). This allows determining whether PSFs, when isolated from other plant–plant interaction mechanisms, promote or prevent coexistence between species pairs, and whether this is mediated by niche differences, fitness differences or both (Kandlikar et al., 2019). The balance between both parameters indicates whether the interaction between two species would allow their coexistence or would lead one of them to extinction through competitive exclusion or priority effects. Kandlikar et al. (2021) and Yan et al. (2022) found that PSFs tend to generate stronger fitness differences than stabilizing or destabilizing effects, consequently predicting a preponderance of species exclusion if competition were driven exclusively by PSFs.

In natural communities, plant species interact with many others, so analysing coexistence through pairwise interactions in isolation may not suffice to discern the actual role of interactions between competing species in the maintenance of diversity (Barabás et al., 2016; Miller et al., 2022). For example, Kandlikar et al. (2021) predict a prevalence of competitive exclusion among six plant species which, however, are known to co-occur in Southern California grasslands. To address these problems, we need to scale the study of PSFs from pairwise to community-level (Eppinga et al., 2018; Eppstein & Molofsky, 2007; Miller & Allesina, 2021). The model proposed by Eppinga et al. (2018) is a community-level extension of the classic PSF model of Bever et al. (1997) and is particularly well suited to explore the role of complex interaction network structures on species coexistence.

When considering competition between more than two species, several studies have shown that intransitivity can promote coexistence (Barabás et al., 2016; Kandlikar et al., 2019; Levine et al., 2017). Intransitive interactions imply that none of the species is able to outcompete all the others, as in the popular game of ‘rock-paper-scissors’, so all species can coexist (Gilpin, 1975; May & Leonard, 1975). Nevertheless, it is still controversial to what extent intransitive interactions actually contribute to coexistence in natural plant communities. While Soliveres et al. (2015) suggested intransitive interactions are widespread, Godoy et al. (2017) and Kinlock (2019) concluded that intransitive competition is infrequent. In the context of multispecies PSFs, the network approach has been proposed (Eppinga et al., 2018; Kandlikar et al., 2019; Mack et al., 2019) but it has not been applied to experimental results yet, so we lack evidence on whether intransitive PSFs may contribute to coexistence. To advance in this direction, we apply to the model of Eppinga et al. (2018) the approach proposed by Alcántara and Rey (2012) that makes it possible to qualitatively infer the potential persistence of species through the analysis of strongly connected components in the network structure.

The main aim of this study is to understand how PSFs influence coexistence in woody plant communities. We experimentally studied the PSFs among 10 species co-occurring in Mediterranean-mixed forests and compared the results with data on recruitment interactions in natural communities. We estimated the stabilization and fitness differences generated by PSFs and predicted their outcome in terms of competitive exclusion, priority effects or coexistence. We used our experimental results to parameterize the community dynamics model of Eppinga et al. (2018) and estimate the persistence of all the possible assemblages obtained by combining the 10 studied species. Finally, we evaluated the effect of intransitivity on species persistence through the topological analysis of the model's interactions matrix. Specifically, we aimed to assess the following questions: (1) Is recruitment success influenced by the canopy species conditioning the soil? (2) what is the frequency of predicted coexistence, competitive exclusion or priority effects across species pairs driven by PSFs? and (3) what is the role of intransitivity in species coexistence in multispecies plant assemblages driven by PSFs?

MATERIALS AND METHODS

Data analyses

Testing for species-specific PSF

The existence of species-specific PSFs can be determined by comparing the success of a plant in soil from conspecifics against its success in soil from a different species (Brinkman et al., 2010; Lekberg et al., 2018). We tested species-specific PSFs for each species separately. We used generalized linear mixed models (GLMMs) with the mean recruitment success of each ISEs of species i averaged across the ISOs of species j as dependent variable, and the soil-source species as predictor variable. All models were fitted assuming beta family distribution. We also added the ISE as random effect. Significant terms indicate that PSFs are species-specific.

To assess whether the experimental results reflect the efficiency of canopy-recruit interactions occurring in the field, we used data from Alcántara et al. (2018) obtained in the same study site as the experimental seeds and soils. We estimated the efficiency of recruitment for the 10 studied species under the canopy of the soil-source species (Eij) as the number of saplings of species i recruiting under species j divided by the cover of the canopy and recruit species. We fitted a GLMM with Eij as dependent variable and the experimental recruitment success of each canopy-recruit pair as the predictor variable, and the recruit and canopy species as random effects. Note that many field estimates were zero, so we fitted the model using Tweedie distribution. Further details are provided in Supplementary methods S1.

Pairwise-level feedback

We estimated recruitment success (s_ij) as the proportion of experimental cells with soil of species j containing a seedling of species i at the end of the experiment. Although biomass is most frequently used as a performance measure in PSF studies (Kandlikar et al., 2021), using biomass in our experiment would discard information from all the replicates that lacked seedling at the end of the experiment (52%). s_ij can differ between recruit species due to intrinsic differences in seed viability not related to PSFs. To account for these differences, we rescaled s_ij to remove the effect of seed viability. We divided the recruitment success of species i in soil from species j (s_ij) by its success in reference soil (s′_ij). As a reference, we used the average recruitment success of species i in soils from species other than j:

$$$$ {s}_{\mathrm{ij}}^{\prime }=\frac{1}{n-1}\sum \limits_{k\ne j}{s}_{ik} $$$$(1)

In this way, we obtained rescaled recruitment success values, σ_ij, which can be more appropriately compared across species. Values of σ_ij between 0 and 1 indicate a negative effect of species j soil on species i performance, while values >1 indicate a positive effect. By relativizing to the reference soil, our estimate of σ_ij controls for the confounding effect of seed viability. From an ecological point of view, this represents the relative advantage or disadvantage in recruitment that species i obtains by dispersing seeds to soils conditioned by species j or to soils conditioned by any of the other species present in the community.

To evaluate the possibility of coexistence of pairs of species, we followed Kandlikar et al. (2019) and Yan et al. (2022). This approach calculates the (de)stabilizing niche difference effects and fitness differences (SD and FD, hereafter) between each species pair as follows:

$$$$ \mathrm{SD}=-\frac{1}{2}\left[{\upsigma}_{11}-{\upsigma}_{12}-{\upsigma}_{21}+{\upsigma}_{22}\right] $$$$(2)

$$$$ \mathrm{FD}=\frac{1}{2}\left[{\upsigma}_{11}+{\upsigma}_{12}-{\upsigma}_{21}-{\upsigma}_{22}\right] $$$$(3)

We compared the absolute magnitude of SD and FD by fitting a GLMM with the difference in the absolute values of SD and FD as a predictor variable, and the recruit and soil-source species as random variables.

Comparing the values of SD and FD for a given pair of species allows for determining whether they could coexist or one of them would exclude the other through competitive exclusion or priority effects. Specifically, the following relationships can be assessed for each species pair:

$$$$ \mathrm{SD}>0\ \mathrm{and}\ \mathrm{SD}>\mathrm{abs}\ \left(\mathrm{FD}\right):\mathrm{Coexistence} $$$$

$$$$ \mathrm{SD}<0\ \mathrm{and}\ \mathrm{abs}\ \left(\mathrm{SD}\right)>\mathrm{abs}\ \left(\mathrm{FD}\right):\mathrm{Priority}\ \mathrm{effects} $$$$

$$$$ \mathrm{abs}\ \left(\mathrm{SD}\right)<\mathrm{abs}\ \left(\mathrm{FD}\right):\mathrm{Competitive}\ \mathrm{exclusion} $$$$

To assess the robustness of these comparisons, we obtained 1000 matrices of randomized s_ij values from a binomial distribution with probability equal to s_ij (see details in Supplementary methods S1). From these matrices we obtained the SD and FD and the frequency of each outcome for each randomization.

Community-level effects of plant–soil feedback

To explore the consequences of PSFs on coexistence at community level, we parameterized the model of Eppinga et al. (2018) using our experimental results (E-model, hereafter). The E-model is an example of the replicator equation originating from evolutionary game theory (Hofbauer & Sigmund, 1998) and describes the dynamics of species under the influence of frequency-dependent PSFs assuming that the plants are equally competitive in any other respects. These assumptions allow exploring the potential effects of PSFs if these were the only drivers of community dynamics, disregarding other properties of the species (e.g., life span, dispersal and competitive ability). The dynamics of the E-model are described by the following system of equations:

$$$$ \frac{d{P}_i}{dt}={P}_i\left({w}_i-\sum \limits_{j=1}^n{w}_j{P}_j\right) $$$$(4)

where P_i is the vector of relative frequencies of the n species in the community (i, j: 1 … n) and w_i is:

$$$$ {w}_i=\sum \limits_{j=1}^n{\sigma}_{ij}{P}_j $$$$(5)

The only parameters needed in the model are σ_ij. The set of all σ_ij form the matrix A (Figure 1a). The relative abundance of each species at equilibrium can be estimated as:

$$$$ {P}_i^{\ast }=\frac{\mathit{\det}\left({\boldsymbol{A}}_{\boldsymbol{i}}\right)}{\sum \limits_{j=1}^n\mathit{\det}\left({\boldsymbol{A}}_{\boldsymbol{j}}\right)} $$$$(6)

where A_i is the A matrix with the column corresponding to species i replaced by a column of ones, and det indicates the determinant of the matrix. The community has a feasible equilibrium if 0 < P_i* < 1 for all species. If a feasible equilibrium does not exist, at least one of the species will become extinct. Even if a feasible equilibrium exists, it may not be stable so some species may become extinct. Stability can be estimated through standard eigenvalue analysis of the system's Jacobian matrix at equilibrium. If the largest real part across all eigenvalues (λ) is negative, then the equilibrium is stable. If a community is feasible and stable according to the E-model, then we will say that the community is E-persistent. The E-model can allow unstable coexistence through cyclic dynamics when λ is positive but sufficiently small and there is negative community-level feedback (I_c):

$$$$ {I}_c={\left(-1\right)}^n\ \sum \limits_{j=1}^n\det {A}_j $$$$(7)

Negative I_c is also a necessary but not sufficient condition for E-persistence. It is not possible to determine which values of I_c and λ would lead to such cyclic dynamics, so it must be determined through simulations of the community dynamics. We conducted such simulations using Runge–Kutta 4th and 5th order integration implemented in R-package deSolve (Soetaert et al., 2010).

To assess the robustness of the results, we parameterized the E-model with 1000 random A matrices obtained as described in the pairwise analyses. Moreover, our experiment allows to parameterize the E-model for any combination of the 10 species. This provides the opportunity to explore which subcommunities would be able to persist. Thus, we recalculated the A matrix and applied the E-model to each of the 1013 subcommunities that can result from combining between 2 and 10 species. The A matrix of each subcommunity was built by rescaling the corresponding σ_ij values considering in Equation 1 only the species in the subcommunity.

Topological analysis of intransitivity

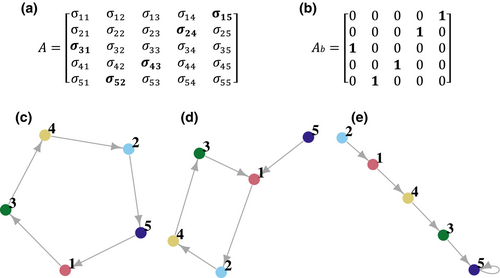
We used matrix A to extract the network of interactions between species caused by PSFs following the approach of Eppinga et al. (2018). The largest value in a column of matrix A indicates the species that would be most benefited in this type of soil. The adjacency matrix corresponding to A is constructed by transforming these largest values into ones and the rest into zeroes (Figure 1a,b). The corresponding networks (Figure 1c–e) have species as nodes and arrows pointing from the soil conditioning species to the species that is most benefited in this soil.

We used this binary adjacency matrix for the qualitative estimate of persistence following the approach of Alcántara and Rey (2012). This approach is based on the analysis of strongly connected components (SCCs) in the network structure (Figure 1c,d). An SCC can consist of a single species (in which case it is called a trivial SCC) or by more than one species (a non-trivial SCC). The largest SCC is named the core. Multiple trivial and/or non-trivial SCCs may form chains of network elements connected transitively (Figure 1d,e). Thus, a complex network may contain simultaneously sets of species interacting transitively and intransitively (Alcántara et al., 2017). A network is fully intransitive when all the nodes belong to the core (Figure 1c).

Assuming linear time-invariant dynamics, Alcántara and Rey (2012) showed that species in the core SCC and those benefited by some core species (called satellite species) can persist in the long term, while species that are not benefited by any core or satellite species will become extinct (called transient species). In the case of non-linear time invariant models (like the E-model) these relationships between network structure and species persistence are not mathematically guaranteed, but simulations showed that core and satellite species are less likely to become extinct and have longer time to extinction than transient species (Alcántara et al., 2017). As defined in Eppinga et al. (2018), the network derived from the A matrix cannot contain satellite species, so we will say that an assemblage is SCC-persistent under the E-model if all the species belong to the same non-trivial SCC, what amounts to say that it is fully intransitive.

Our objective by comparing the E-persistence and SCC persistence is to demonstrate the influence of the subjacent topology of the A matrix on the feasibility and stability properties of the E-model. This influence is one of the basic tenets of ecological network studies (Poisot et al., 2016), but has not been previously demonstrated in the context of PSF theory. To assess the agreement between subcommunities’ persistence according to the E-model and the SCC analysis, we used a confusion matrix that synthetises the number of subcommunities in which both approaches agree or disagree. From this matrix, one can use a Chi-Square test to determine whether both approaches agree more often than expected by chance. It is important to note that the agreement between E-persistence and SCC-persistence can depend on the way A matrix is binarized. We performed these analyses using another two binarization methods and found that the one proposed by Eppinga et al. (2018) provided a better agreement according to Cohens' kappa statistic (Cohen, 1960) (Supplementary Methods S1).

The list of software used in this study is provided in Supplementary methods S1.

RESULTS

Testing for species-specific PSF

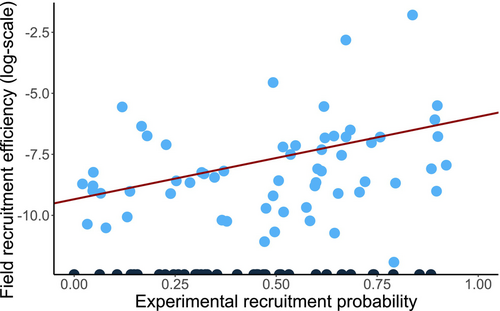
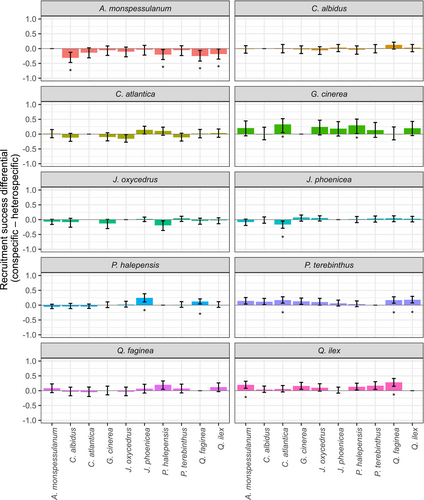
The estimated recruitment success in the experiment for each species pair was positively related to the efficiency of recruitment observed for the same species pairs in the field (slope ± SE: 3.375 ± 1.548, p = 0.029; Figure 2). Experimental estimates explained 16% of the variance in field estimates. We found evidence that recruitment success in heterospecific soil differed from success in conspecific soil across plant species (Figure 3; Table S1). Overall, 14 of 89 species pairs (15.7%) produced statistically significant species-specific PSFs. There were 35 species pairs with negative species-specific PSF and 54 with positive species-specific PSFs with an average close to 0 (log-ratio between conspecific and heterospecific soil effects: 0.016 ± 0.117; range −0.302 to 0.298).

Pairwise-level feedback

The absolute magnitude of FD did not differ from the absolute value of SD (estimate ± SE: −0.006 ± 0.044, p = 0.895). Competitive exclusion was the most frequently predicted outcome of pairwise competition, followed by priority effects and coexistence (40%, 35.56% and 24.4% respectively). Specifically, coexistence was predicted in 11 out of 45 species pairs, 6 of which included A. monspessulanum and 4 included J. oxycedrus (Table S2). The randomization of the outcome for each species pair verified the robustness of our results, indicating pairwise competitive exclusion as the dominant outcome (Figure 4).

Community-level dynamics

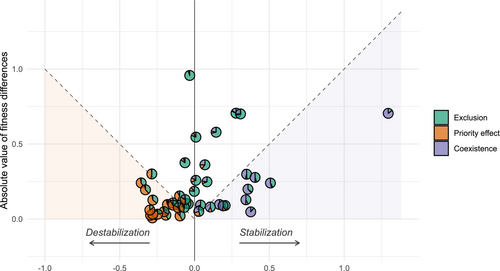
The 10-species assemblage has a feasible but unstable equilibrium, with a positive I_c, so it is not E-persistent. This conclusion was repeated in all of the 1000 simulated plausible matrices (λ > 0.01 in all cases). Although many simulations (47.1%) had a negative I_c, none showed stable cyclic dynamics. The 10-species network had very low intransitivity, with just one non-trivial (core) SCC formed by the pair C. albidus-G. cinerea, and the rest of the species as transients relative to this small core (Figure 5a). In addition, P. terebinthus was disconnected from the rest of the network. The very small core with many transient species and a disconnected SCC makes this assemblage not SCC-persistent.

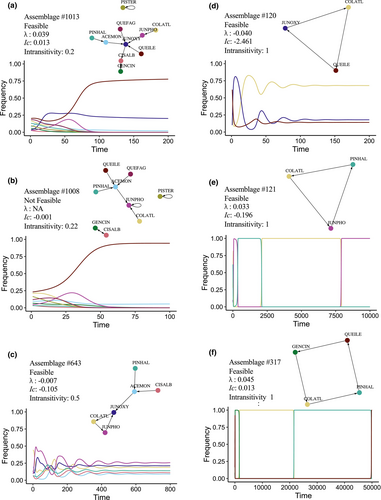
The analysis of the 1013 subcommunities (Table S3; Figure S1) shows that only 157 were not feasible, thus leading some species to extinction (Figure 5b). However, only 54 of the 856 feasible assemblages were E-persistent, many of them (20 out of 54) with just two species and the largest one consisting of 6 species (Figure 5c). In total 959 assemblages (94.66%) were not E-persistent.

Most assemblages (68.11%) contained some intransitive group (i.e., at least one non-trivial SCC) which involved on average 52.21% of the species. The largest intransitive groups were formed by up to five species. The probability that an assemblage contained at least one transient species (and thus, some level of transitivity) increased sharply with the number of species (binomial regression: intercept = 9.91 ± 1.77, slope = 3.55 ± 0.58, p < 0.001, df = 688), to the point that transients occurred in all assemblages with five or more species. The qualitative analysis indicates that 41 assemblages are SCC-persistent.

The association between the predictions of E-persistence and SCC-persistence is highly significant (Chi square = 447.73, p < 0.001; Table S4). The SCC approach classifies correctly as not-persistent 950 of the 959 assemblages identified as such by the E-model. Thus, the SCC approach has a specificity of 99.06%. On the other hand, the SCC approach classifies correctly as persistent 32 out of the 54 assemblages identified as E-persistent (Figure 5d), so the SCC approach has a sensitivity of 59.26%. When the SCC approach predicts that an assemblage is not E-persistent, it succeeds in 950 out of 972 cases (97.74%), and it succeeds 32 out of 41 times (78.05%) when predicting that an assemblage is E-persistent. All nine assemblages classified as persistent by the SCC approach but as unstable by the E-model allow non-equilibrium coexistence through heteroclinic cycles (Figure 5e,f). Thus, all of the 41 assemblages with full intransitivity allow species coexistence, even the one that combines full intransitivity with positive I_c (Figure 5f). Since the SCC approach applied to the E-model predicts persistence only when the community is fully intransitive, our results indicate that full intransitivity always allows species coexistence, and the lack of full intransitivity is almost always associated with the lack of persistence of at least one species.

DISCUSSION

Basic evidence for the role of PSF on plant community dynamics involves demonstrating that plants perform differently in soil conditioned by conspecifics than in soil conditioned by other species (Bever et al., 1997; Van der Putten et al., 2013). Our results show that recruitment success varied depending on the soil-conditioning species, reflecting the existence of species-specific PSFs in the studied community. Nevertheless, we found species-specific PSFs of moderate strength between the 10 studied species, with an average strength close to zero. This agrees with the findings of weaker PSFs in woody than in herb species in Kulmatiski et al. (2008) and Lekberg et al. (2018). Moreover, experiments conducted with naturally conditioned soils tend to obtain weaker PSFs than those using experimentally trained soils (Brandt et al., 2013; Klinerová & Dostál, 2020; Lekberg et al., 2018). In any case, it is not known how large, small or variable PSFs must be to actually have an impact on real plant communities. One way to discern the participation of PSFs in the dynamics of natural plant communities consists of contrasting experimental results against patterns observed in the field. A correspondence between experimental estimates of PSFs and observed demographic properties has been found in several studies (Bennett et al., 2017; Klironomos, 2002; Mangan et al., 2010). In woody plants, Mangan et al. (2010) found a negative correlation between their experimental estimates of PSFs and the observed abundance of tree species in a tropical forest; similarly, Bennett et al. (2017) found that their experimental estimates of PSFs were positively related with the strength of negative density-dependent effects in temperate trees. We found that recruitment success in pairwise experiments was positively related to the recruitment efficiency of the same pairs of woody species observed in the field, clearly suggesting that recruitment in Mediterranean forests is influenced by species-specific PSFs. Thus, our study provides further evidence that PSFs measured under controlled experimental conditions contribute to explaining demographic processes that occur under natural conditions in forest ecosystems.

Studies on coexistence mediated by PSFs have focused on the stabilizing effect of negative PSFs that prevent dominance of abundant species while favouring rare ones (Bever et al., 1997; Crawford et al., 2019). However, modern coexistence theory applied to PSFs (Kandlikar et al., 2019) indicates the need to check the magnitude of SD against FD to predict how PSFs would affect the outcome of competition between pairs of species in the absence of other interaction mechanisms (e.g., facilitation). We found similar magnitudes of SD and FD, consistent with a predominance of competitive exclusion, followed by priority effects and coexistence. Similar magnitude of FD and SD was found in the meta-analysis of Yan et al. (2022) for those studies that, like ours, used a live reference soil and field-trained soil sources. Moreover, a predominance of pairwise competitive exclusion was predicted in empirical studies with co-occurring annual plants in central European grasslands (Klinerová & Dostál, 2020) and southern California grasslands (Kandlikar et al., 2021). This suggests that the fitness advantages generated by PSFs should most often overcome their (de)stabilizing effect, preventing species coexistence and thus, decreasing diversity (Chu & Adler, 2015).

However, predictions at pairwise-level do not necessarily explain the coexistence of species in natural ecosystems (Barabás et al., 2016). Recently, Miller et al. (2022) showed that coexistence in the classic PSF model becomes unstable in systems including more than two species. Eppinga et al. (2018) developed a community-level extension of Bever's model that allows the stable coexistence of multiple species. Moreover, even when the coexistence equilibrium is unstable, negative community-level feedback may enable the persistence of all species through persistent cycles (e.g., their SI Figure S4). However, although the E-model allows for the existence of stable cycles, the parameter space of σ values that lead to such cycles is likely very restricted, and our results show that coexistence in our study system more likely involves heteroclinic than stable cycles (May & Leonard, 1975). Our results add evidence to this possibility since we found that some fully intransitive subcommunities may coexist through heteroclinic cycles, even when the eigenvalue analysis deemed them as unstable, and even when the community-level feedback was positive. Still, the proportion of subcommunities that could persist in this way was small and most often involved a small number of species. This suggests that PSFs may impede the building up of highly diverse communities due to the high probability that newcoming species will join the network as transients. In this way, it is possible that PSFs could act as strong filters against the invasion of local assemblages by new species (Inderjit & Cahill, 2015).

In any case, our results indicate that, although dynamics driven exclusively by PSFs have the potential to reach feasible equilibrium (84% assemblages are feasible), this would seldom happen because such equilibrium is most often unstable. The final state in most assemblages would involve some extinctions depending on the initial state, in a multispecies version of priority effects. This general conclusion is at odds with the observation that the 10 studied species actually co-occur very often in natural habitats. Therefore, although PSFs are at play in determining the outcome of plant–plant interactions during recruitment, other mechanisms must be considered to understand species coexistence, like trade-offs between colonization and competition (Kisdi & Geritz, 2003), facilitation between competitors (Gross, 2008) or the action of specialist aerial antagonists (Janzen, 1970). Nevertheless, the role of PSFs could still be important in combination with some of these mechanisms. For example, facilitation between plants can result in a positive PSF between them (Ashton et al., 2008). On the other hand, since PSFs seem to favour priority effects, a strong spatial structuring of the communities in the landscape could allow the persistence of diverse species if different patches were colonized by different sets of species, or if these arrived in different sequences (Fukami, 2015; Song et al., 2021). Studies are needed to explore the spatial environmental gradients and landscape-scale patterns structuring the biotic communities involved in PSFs, and addressing the possibility that PSFs could give rise to multiple alternative states, thus favouring the persistence of plant species diversity at the ecosystem level (Senthilnathan & D'Andrea, 2023; Van Nuland et al., 2017).

Besides exploring the possible roles of PSFs on multispecies coexistence, our study provides an example of how an approach to network topology can help to understand species persistence in dynamic models. By applying this approach to the results of the E-model, we found that PSFs would often give rise to moderate levels of intransitivity. Full intransitivity was rare in the studied community and would occur mainly in the smallest subcommunities. Nevertheless, full intransitivity is not a necessary condition for persistence in this community since 2.26% (22 out of 972) of subcommunities that were not fully intransitive were persistent. On the other hand, all fully intransitive subcommunities were persistent through either stable or heteroclinic dynamics. Therefore, although PSFs do not seem to promote it, full intransitivity is a sufficient condition for species coexistence.

AUTHOR CONTRIBUTIONS

JLG, JMA and ALG designed the experiment. JMA and MPM conceived the analyses, conducted the simulations and wrote the final draft of the manuscript. All authors collected seeds and soil samples and set up the shade-house experiment. MPM, JMB and ALG monitored germination and seedling survival throughout the experiment. SL and JP processed the plants at the end of the experiment. JLG, JMA and MPM conducted the statistical analyses. All authors provided comments to the final version of the manuscript.