On bootstrap validity for specification tests with weak instruments
Summary
We study the asymptotic validity of the bootstrap for Durbin–Wu–Hausman tests of exogeneity, with or without identification. We provide an analysis of the limiting distributions of the proposed bootstrap statistics under both the null hypothesis of exogeneity (size) and the alternative hypothesis of endogeneity (power). We show that when identification is strong, the bootstrap provides a high-order approximation of the null limiting distributions of the statistics and is consistent under the alternative hypothesis if the endogeneity parameter is fixed. However, the bootstrap only provides a first-order approximation when instruments are weak. Moreover, we provide the necessary and sufficient condition under which the proposed bootstrap tests exhibit power under (fixed) endogeneity and weak instruments. The latter condition may still hold over a wide range of cases as long as at least one instrument is relevant. Nevertheless, all bootstrap tests have low power when all instruments are irrelevant, a case of little interest in empirical work. We present a Monte Carlo experiment that confirms our theoretical findings.
1. INTRODUCTION
Exogeneity tests of the type proposed by Durbin (1954), Wu (1973) and Hausman (1978), henceforth DWH tests, are widely used in applied work to determine whether the ordinary least-squares (OLS) or the instrumental variable (IV) method is appropriate. There is now a considerable body of research on this topic, and most studies often impose identifying assumptions on model coefficients, thus leaving out issues associated with weak instruments. It is well known that IV estimators can be imprecise and that inference procedures (such as tests and confidence sets) can be highly unreliable in the presence of weak instruments. In recent years, concerns have been raised about the reliability of DWH procedures in the presence of weak instruments because they mainly rely on IV estimators; see Staiger and Stock (1997), Guggenberger (2010), Hahn et al. (2010), Doko Tchatoka and Dufour (2011) and Kiviet and Niemczyk (2007), among others.
Staiger and Stock (1997) show that the limiting distributions of Hausman (1978) type statistics depend on the concentration matrix, which usually determines the strength of the identification. Doko Tchatoka and Dufour (2011) show that all DWH exogeneity statistics, including Wu (1973) T3 and alternative Hausman (1978) type statistics, are identification-robust even in a finite sample with or without Gaussian errors. However, applying the usual χ2 critical values to the T3 and Hausman (1978) statistic can lead to overly conservative procedures when identification is weak. Size correction can be achieved by resorting to the method of exact Monte Carlo tests, such as in Dufour (2006). However, the exact Monte Carlo method requires that the conditional distribution of the structural disturbance, given the instruments, be specified. In practice, researchers usually do not know the distribution of the errors even conditionally on available instruments. So, implementing the exact Monte Carlo tests can be difficult.
In this paper, we examine whether a distribution-free method, such as a bootstrap method, can improve the properties of the DWH statistics, especially when identification is not very strong. To be more specific, we exploit the score interpretation of these statistics (see Engle, 1982, and Smith, 1983) to suggest a bootstrap method similar to those of Moreira et al. (2009) for the score test of the null hypothesis in the structural parameters. Our results provide some new insights and extensions of earlier studies.
We show that when identification is strong, the bootstrap method offers a high-order approximation of the null limiting distributions of the DWH statistics. Furthermore, the bootstrap test consistency holds under fixed alternative hypotheses (i.e. when endogeneity is present and does not depend on the sample size). However, the bootstrap only provides a first-order approximation when identification is weak. Moreover, we provide the necessary and sufficient condition under which the proposed bootstrap tests exhibit power under fixed endogeneity and weak instruments. The latter condition may still hold over a wide range of cases, provided that at least one instrument is not irrelevant. However, all the proposed bootstrap DWH tests have low power when all instruments are irrelevant or close to irrelevant.
This paper is organized as follows. In Section 2, the model and assumptions are formulated, and the studied statistics are presented. In Section 3, the proposed bootstrap method is discussed and the limiting distributions of the corresponding DWH statistics are characterized. In Section 4, the Monte Carlo experiment is presented, and the auxiliary theorem and proofs are provided in the Appendix. Throughout the paper, 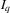 stands for the identity matrix of order q. For any full-column rank
stands for the identity matrix of order q. For any full-column rank 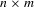 matrix A,
matrix A, 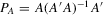 is the projection matrix on the space of A, and
is the projection matrix on the space of A, and 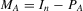 . The notation vec(A) is the
. The notation vec(A) is the 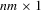 dimensional column vectorization of A.
dimensional column vectorization of A. 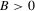 for a squared matrix B means that B is positive definite. Convergence almost surely is symbolized by
for a squared matrix B means that B is positive definite. Convergence almost surely is symbolized by  ,
, 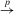 stands for convergence in probability, while
stands for convergence in probability, while 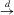 means convergence in distribution. The usual orders of magnitude are denoted by
means convergence in distribution. The usual orders of magnitude are denoted by 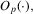
 O(1) and o(1).
O(1) and o(1). 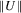 denotes the usual Euclidian or Frobenius norm for a matrix U, while rank(U) is the rank of U. For any set
denotes the usual Euclidian or Frobenius norm for a matrix U, while rank(U) is the rank of U. For any set 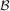 ,
, 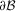 is the boundary of
is the boundary of  and
and  is the ε-neighbourhood of
is the ε-neighbourhood of  . Finally,
. Finally,  is the supremum norm on the space of bounded continuous real functions, with topological space Ω.
is the supremum norm on the space of bounded continuous real functions, with topological space Ω.
2. FRAMEWORK
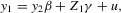 (2.1)
(2.1)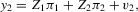 (2.2)
(2.2)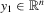 is a vector of observations on a dependent variable,
is a vector of observations on a dependent variable, 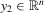 is a vector of observations on a (possibly) endogenous explanatory variable,
is a vector of observations on a (possibly) endogenous explanatory variable, 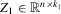 is a matrix of observations on strictly exogenous variables,
is a matrix of observations on strictly exogenous variables, 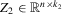 is a matrix of excluded exogenous variables from 2.1 (instruments),
is a matrix of excluded exogenous variables from 2.1 (instruments), 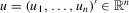 is a vector of structural disturbances,
is a vector of structural disturbances,  is a vector of reduced-form disturbances, β and γ are unknown fixed coefficients (structural parameters) and
is a vector of reduced-form disturbances, β and γ are unknown fixed coefficients (structural parameters) and 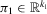 and
and 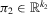 are vectors of reduced-form coefficients.
are vectors of reduced-form coefficients.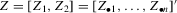 ,
, 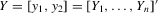 and
and 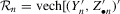
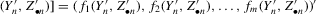 , where
, where 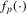 [
[ and
and 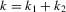 ] are elements of
] are elements of 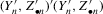 . The sample mean of the first n observations of any random variable X is denoted by
. The sample mean of the first n observations of any random variable X is denoted by 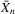 . We suppose that Z has full-column rank k with probability one and
. We suppose that Z has full-column rank k with probability one and 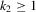 . The full-column rank condition of Z ensures the existence of unique least-squares estimates in 2.2 when y2 is regressed on each column of Z. As long as Z has full-column rank with probability one and the conditional distribution of y2 given Z is absolutely continuous (with respect to the Lebesgue measure),
. The full-column rank condition of Z ensures the existence of unique least-squares estimates in 2.2 when y2 is regressed on each column of Z. As long as Z has full-column rank with probability one and the conditional distribution of y2 given Z is absolutely continuous (with respect to the Lebesgue measure), 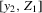 also has full-column rank with probability one. So, the least-squares estimates of β and γ in 2.1 are also unique. From 2.1 and 2.2, we can express the reduced forms for y1 and y2 as
also has full-column rank with probability one. So, the least-squares estimates of β and γ in 2.1 are also unique. From 2.1 and 2.2, we can express the reduced forms for y1 and y2 as
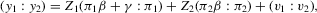 (2.3)
(2.3)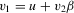 . If u and v2 have zero means and if Z has full-column rank with probability one, then the usual necessary and sufficient condition for the identification of model 2.1–2.2 is
. If u and v2 have zero means and if Z has full-column rank with probability one, then the usual necessary and sufficient condition for the identification of model 2.1–2.2 is 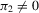 .1 If
.1 If  , then Z2 is irrelevant, and β and γ are completely unidentified. If π2 is close to zero, then β and γ are ill-determined by the data, a situation often called weak identification in the literature; see Dufour (2003).
, then Z2 is irrelevant, and β and γ are completely unidentified. If π2 is close to zero, then β and γ are ill-determined by the data, a situation often called weak identification in the literature; see Dufour (2003). (2.4)
(2.4)Assumption 2.1. for some
for some 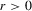 and
and 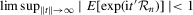 .
.
Assumption 2.2.For sample size 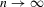 ,
, 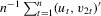
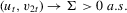 ,
, 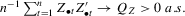 and
and 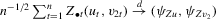 , where
, where 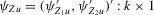 ,
, 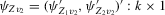 and
and 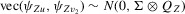 .
.
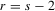 and
and 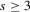 . It requires that
. It requires that 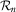 has second moments or greater, and that its characteristic function be bounded above by 1. In particular, the second moments of
has second moments or greater, and that its characteristic function be bounded above by 1. In particular, the second moments of 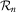 exist if
exist if 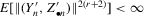 for some
for some 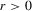 . The bound on the characteristic function of
. The bound on the characteristic function of 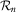 is the commonly used Cramér condition; see Bhattacharya and Ghosh (1978). The first two convergences in Assumption 2.2 are the strong law of large numbers (SLLN) property of
is the commonly used Cramér condition; see Bhattacharya and Ghosh (1978). The first two convergences in Assumption 2.2 are the strong law of large numbers (SLLN) property of 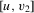 and Z, respectively, while the last one is the central limit theorem (CLT) property. In the remainder of the paper, we use the following additional definitions and notations:
and Z, respectively, while the last one is the central limit theorem (CLT) property. In the remainder of the paper, we use the following additional definitions and notations:
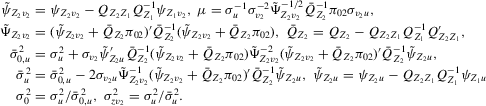 (2.5)
(2.5)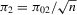 .
.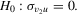 (2.6)
(2.6)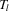 (
(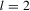 , 3, 4) by Wu (1973) and three alternative Durbin–Hausman statistics (
, 3, 4) by Wu (1973) and three alternative Durbin–Hausman statistics ( ,
, 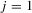 , 2, 3). All statistics can be expressed in a unified way as
, 2, 3). All statistics can be expressed in a unified way as
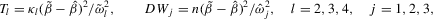 (2.7)
(2.7)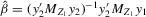 and
and 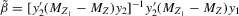 are the OLS and IV estimators of β, respectively,
are the OLS and IV estimators of β, respectively,  ,
, 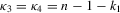 ,
, 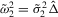 ,
, 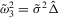 ,
, 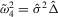 ,
, 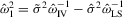 ,
, 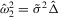 ,
, 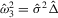 ,
, 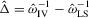 ,
, 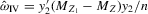 ,
, 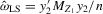 ,
, 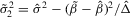 ,
, 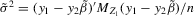 and
and 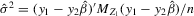 .
.Engle (1982) and Smith (1983) show that T2, T4 and 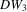 in 2.7 are score (LM) statistics, while T3,
in 2.7 are score (LM) statistics, while T3, 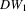 and
and 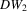 are quasi-Wald statistics.2 Staiger and Stock (1997) and Doko Tchatoka and Dufour (2011), among others, show that the quasi-Wald statistics can be overly conservative when IVs are weak. We investigate whether the bootstrap can improve the size and power of these tests, especially when identification is not very strong.
are quasi-Wald statistics.2 Staiger and Stock (1997) and Doko Tchatoka and Dufour (2011), among others, show that the quasi-Wald statistics can be overly conservative when IVs are weak. We investigate whether the bootstrap can improve the size and power of these tests, especially when identification is not very strong.
It is worth noting that the exogeneity tests in 2.7 also have their own shortcomings. Indeed, Moreira (2009, footnote 1) shows that testing 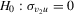 is equivalent to test
is equivalent to test 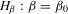 in model 2.1–2.2, where
in model 2.1–2.2, where 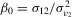 ,
, 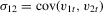 ,
, 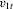 and
and 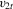 are given in 2.3. This means that doing a pre-test on
are given in 2.3. This means that doing a pre-test on 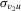 may imply important size distortions when making inference on β using a t-type test after the pre-test. Guggenberger (2010) shows that the asymptotic size of the two-stage t-test where a DWH pre-test is used equals 1 for some choices of the parameter space. Despite this issue, the DWH tests are widely used in many empirical works. This paper studies only the asymptotic validity of the bootstrap for the DWH statistics and does not address the issues of pre-testing.
may imply important size distortions when making inference on β using a t-type test after the pre-test. Guggenberger (2010) shows that the asymptotic size of the two-stage t-test where a DWH pre-test is used equals 1 for some choices of the parameter space. Despite this issue, the DWH tests are widely used in many empirical works. This paper studies only the asymptotic validity of the bootstrap for the DWH statistics and does not address the issues of pre-testing.
3. BOOTSTRAP VALIDITY FOR THE DURBIN–WU–HAUSMAN TESTS
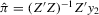 denote the first-stage OLS estimate of
denote the first-stage OLS estimate of 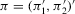 in 2.2 and let
in 2.2 and let 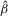 and
and 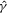 be the OLS estimates of β and γ from the structural equation 2.1. We adapt the bootstrap procedure by Moreira et al. (2009) to DWH exogeneity statistics as follows.
be the OLS estimates of β and γ from the structural equation 2.1. We adapt the bootstrap procedure by Moreira et al. (2009) to DWH exogeneity statistics as follows.
- Step 1. From the observed data, compute
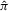 and
and 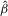 along with all other things necessary to obtain the realizations of the statistics
along with all other things necessary to obtain the realizations of the statistics 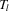 ,
, 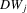 , and the residuals from the reduced-form equation 2.3:
, and the residuals from the reduced-form equation 2.3: 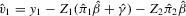 ,
, 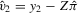 . These residuals are then re-centred by subtracting sample means to yield
. These residuals are then re-centred by subtracting sample means to yield 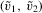 .
. - Step 2. For each bootstrap sample
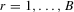 , the data are generated following
where
, the data are generated following
where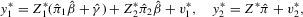 (3.1.)
(3.1.)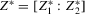 and
and 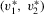 are drawn independently from the joint empirical distribution of Z and
are drawn independently from the joint empirical distribution of Z and 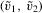 . The corresponding bootstrap statistics
. The corresponding bootstrap statistics 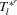 and
and 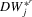 are then computed for each bootstrap sample
are then computed for each bootstrap sample 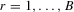 .
. - Step 3. The simulated bootstrap p-value of each statistic is obtained as the proportion of bootstrap statistics that are more extreme than the computed statistic from the observed data.
- Step 4. The corresponding bootstrap test rejects exogeneity at level α if its p-value is less than α.
Although the above bootstrap steps are similar to those in Moreira et al. (2009), it is worth noting that there is a substantial difference. In contrast to Moreira et al. (2009), where the two-stage least-squares (2SLS) or the limited information maximum likelihood (LIML) estimators are suggested as the pseudo-true value of β under the bootstrap data-generating process (DGP), our algorithm uses the OLS estimator of β in 2.1. Indeed, Moreira et al. (2009) show that the validity of their bootstrap requires using an estimator 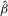 that satisfies
that satisfies 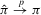 and
and 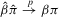 (i.e.
(i.e. 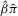 is a (strong) consistent estimator of
is a (strong) consistent estimator of 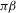 ). In a linear classical setting of this paper, both the 2SLS and LIML estimators satisfy the sufficient conditions for strong consistency; see footnote 3 of Moreira et al. (2009, p. 55). The OLS estimator
). In a linear classical setting of this paper, both the 2SLS and LIML estimators satisfy the sufficient conditions for strong consistency; see footnote 3 of Moreira et al. (2009, p. 55). The OLS estimator 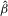 is not qualified for strong consistency when
is not qualified for strong consistency when 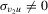 (endogeneity). However, when
(endogeneity). However, when 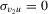 (exogeneity),
(exogeneity), 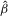 is consistent and efficient even when IVs are weak. Based on this fact,
is consistent and efficient even when IVs are weak. Based on this fact, 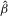 is preferred to an alternative 2SLS or LIML estimator because the choice of the latter should imply a sizable efficiency loss under H0. Moreover, choosing
is preferred to an alternative 2SLS or LIML estimator because the choice of the latter should imply a sizable efficiency loss under H0. Moreover, choosing 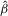 as the pseudo-true value of β when H0 is false is suggested in Horowitz (2001) to approximate the bootstrap power.3
as the pseudo-true value of β when H0 is false is suggested in Horowitz (2001) to approximate the bootstrap power.3
In the remainder of the paper, 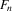 denotes the empirical distribution of
denotes the empirical distribution of 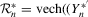 ,
, 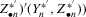 given
given 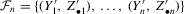 ,
, 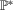 is the probability under the empirical distribution function (given
is the probability under the empirical distribution function (given 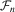 ) and
) and 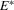 is its corresponding expectation operator. Also, let
is its corresponding expectation operator. Also, let  and
and 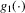 be the cumulative density function (cdf) and the probability density function (pdf) of a χ2-distributed random variable with one degree of freedom. To ease the exposition of our results, we shall deal separately with the case where identification is strong and the case where it is weak.
be the cumulative density function (cdf) and the probability density function (pdf) of a χ2-distributed random variable with one degree of freedom. To ease the exposition of our results, we shall deal separately with the case where identification is strong and the case where it is weak.
3.1. Strong identification
We focus here on the case where identification is strong and we study the limiting distributions of the bootstrap DWH statistics under both the null and alternative hypotheses. Let 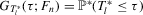 and
and 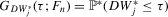 (
(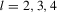 and
and 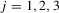 ) denote the empirical cumulative distributions of
) denote the empirical cumulative distributions of 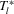 and
and 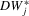 , respectively, evaluated at τ. Theorem 3.1 states the bootstrap validity for the DWH statistics under strong instruments.
, respectively, evaluated at τ. Theorem 3.1 states the bootstrap validity for the DWH statistics under strong instruments.
Theorem 3.1.Suppose that Assumptions 2.1 and 2.2 are satisfied and that 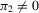 is fixed. Then for some integer
is fixed. Then for some integer  , we have (a)
, we have (a) 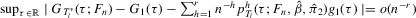 ,
, 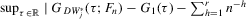
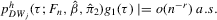 if
if  ; (b)
; (b) 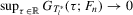 ,
, 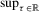
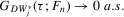 as
as 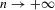 if
if  is fixed. Here,
is fixed. Here, 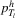 ,
, 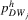 are polynomials in τ with coefficients depending on
are polynomials in τ with coefficients depending on 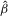 ,
, 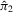 and the moments of
and the moments of 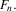
The proof of Theorem 3.1(a) follows the same steps as Theorem 3 in Moreira et al. (2009) and is therefore omitted. The proof of Theorem 3.1(b) follows similar steps to those of Lemma A.1(b) of the online Appendix, and thus it is omitted. Theorem 3.1(a) shows that the bootstrap estimates and the 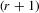 -term empirical Edgeworth expansion in Theorem A.1(a) (see the Appendix) for all statistics are asymptotically equivalent up to the
-term empirical Edgeworth expansion in Theorem A.1(a) (see the Appendix) for all statistics are asymptotically equivalent up to the 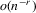 order under H0. Furthermore, the bootstrap makes an error of size
order under H0. Furthermore, the bootstrap makes an error of size 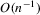 under H0, which is smaller as
under H0, which is smaller as 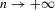 than both
than both 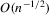 and the error made by the first-order asymptotic approximations. The bootstrap provides a greater accuracy than the
and the error made by the first-order asymptotic approximations. The bootstrap provides a greater accuracy than the 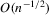 order because all the DWH statistics are quadratic functions of symmetric pivotal statistics (see Horowitz, 2001, Chapter 52, equation (3.13)) under exogeneity (
order because all the DWH statistics are quadratic functions of symmetric pivotal statistics (see Horowitz, 2001, Chapter 52, equation (3.13)) under exogeneity (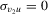 ) and strong identification (
) and strong identification (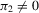 ). Theorem 3.1(b) implies that all bootstrap tests are consistent when endogeneity is fixed and model identification is strong. Note that the bootstrap DWH test consistency holds under fixed endogeneity and strong identification no matter which critical value τ is used in the bootstrap procedure. In particular, this would be the case if the bootstrap critical value or the empirical size-corrected critical value were used in the bootstrap procedure, as suggested by Horowitz (2001). Although Theorem 3.1(b) only considers fixed alternative hypotheses, there is no impediment to expanding it to local to zero alternatives of the form
). Theorem 3.1(b) implies that all bootstrap tests are consistent when endogeneity is fixed and model identification is strong. Note that the bootstrap DWH test consistency holds under fixed endogeneity and strong identification no matter which critical value τ is used in the bootstrap procedure. In particular, this would be the case if the bootstrap critical value or the empirical size-corrected critical value were used in the bootstrap procedure, as suggested by Horowitz (2001). Although Theorem 3.1(b) only considers fixed alternative hypotheses, there is no impediment to expanding it to local to zero alternatives of the form 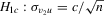 (
(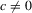 ). This proof is omitted in order to shorten the exposition.
). This proof is omitted in order to shorten the exposition.
3.2. Local to zero weak instruments
We now analyse the Staiger and Stock (1997) local to zero weak instruments framework. To be more specific, we assume that 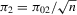 , where
, where 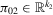 is a fixed vector (possibly zero). Because of the lack of identification, an Edgeworth expansion, such as in Theorem 3.1(a), is no longer valid. Indeed, we can express
is a fixed vector (possibly zero). Because of the lack of identification, an Edgeworth expansion, such as in Theorem 3.1(a), is no longer valid. Indeed, we can express 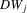 , for example, as a quadratic function in
, for example, as a quadratic function in 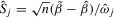 , where
, where 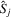 itself is a function
itself is a function 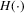 of the sample.4 However, this function
of the sample.4 However, this function 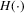 is not differentiable when IVs are weak.5 Nonetheless, we can prove the first-order validity of the bootstrap under both H0 and the alternative hypothesis (endogeneity).
is not differentiable when IVs are weak.5 Nonetheless, we can prove the first-order validity of the bootstrap under both H0 and the alternative hypothesis (endogeneity).
Theorem 3.2.Suppose that Assumption 2.2 holds and 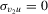 (exogeneity). Let
(exogeneity). Let 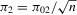 , where
, where 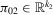 is fixed. If, for some
is fixed. If, for some 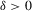 ,
, 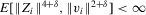 , then
, then 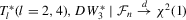 ,
, 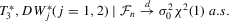 , conditional on
, conditional on 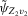 , where
, where 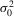 and
and 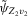 are given in 2.5.
are given in 2.5.
Theorem 3.3.Suppose that Assumption 2.2 is satisfied and 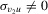 is fixed (endogeneity). Let
is fixed (endogeneity). Let 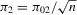 , where
, where 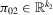 is fixed. If, for some
is fixed. If, for some 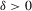 ,
, 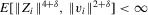 , then the necessary and sufficient condition under which
, then the necessary and sufficient condition under which  and
and 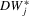 exhibit power is that
exhibit power is that 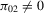 . More precisely, we have (a)
. More precisely, we have (a) 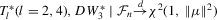 ;
; 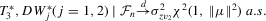 conditional on
conditional on 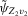 , if
, if  , where
, where 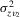 and
and 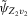 are given in 2.5; (b)
are given in 2.5; (b) 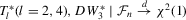 ;
; 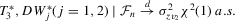 , conditional on
, conditional on 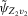 , if
, if 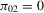 .
.
The proofs of Theorems 3.2 and 3.3 follow directly from those of Lemmata A.5 and A.6 in the online Appendix, and thus are omitted. Theorem 3.2 shows that the bootstrap provides a first-order approximation of the empirical distributions of all DWH statistics. Therefore, the bootstrap DWH tests almost surely have the correct size, despite the lack of identification. Because of the score nature of T2, T4 and 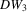 , the validity of the bootstrap for these statistics can be viewed as an extension of Moreira et al. (2009) to LM tests for exogeneity. However, the bootstrap validity for the Wald-type tests T3,
, the validity of the bootstrap for these statistics can be viewed as an extension of Moreira et al. (2009) to LM tests for exogeneity. However, the bootstrap validity for the Wald-type tests T3, 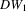 and
and 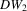 is not intuitive. In general, the bootstrap often fails for Wald-type statistics when instruments are weak because their limiting distributions often involve nuisance parameters; see Moreira et al. (2009), among others. The validity of the bootstrap for the DWH statistics is mainly justified by the fact that they do not directly depend on the unidentified structural coefficient β, even when endogeneity is present; see Section 3 of Wu (1973). So, the lack of identification of β has no impact on the size of the bootstrap tests. This is not, however, the case for the power of the bootstrap tests. Indeed, Theorem 3.3(b) shows that the power of the bootstrap tests cannot exceed the nominal level if IVs are irrelevant (
is not intuitive. In general, the bootstrap often fails for Wald-type statistics when instruments are weak because their limiting distributions often involve nuisance parameters; see Moreira et al. (2009), among others. The validity of the bootstrap for the DWH statistics is mainly justified by the fact that they do not directly depend on the unidentified structural coefficient β, even when endogeneity is present; see Section 3 of Wu (1973). So, the lack of identification of β has no impact on the size of the bootstrap tests. This is not, however, the case for the power of the bootstrap tests. Indeed, Theorem 3.3(b) shows that the power of the bootstrap tests cannot exceed the nominal level if IVs are irrelevant (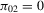 ), no matter which critical value is used in the bootstrap procedure. This is because the limiting distributions of all bootstrap statistics are the same as when H0 holds, although
), no matter which critical value is used in the bootstrap procedure. This is because the limiting distributions of all bootstrap statistics are the same as when H0 holds, although 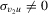 is fixed. This result is intuitive because
is fixed. This result is intuitive because 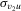 is not identifiable if β is not identifiable (see Doko Tchatoka and Dufour, 2014), which is the case when
is not identifiable if β is not identifiable (see Doko Tchatoka and Dufour, 2014), which is the case when 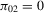 . Clearly, all values of
. Clearly, all values of 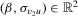 are observationally equivalent when
are observationally equivalent when 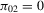 so that the bootstrap tests fail to discriminate between
so that the bootstrap tests fail to discriminate between  and
and 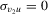 . However, the bootstrap tests exhibit power, provided that at least one instrument is not irrelevant (
. However, the bootstrap tests exhibit power, provided that at least one instrument is not irrelevant (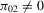 ).
).
4. MONTE CARLO EXPERIMENT
 (no exogenous instruments in 2.1), Z2 contains
(no exogenous instruments in 2.1), Z2 contains  instruments, each generated i.i.d.
instruments, each generated i.i.d.  and independent of
and independent of 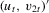 for all
for all 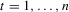 . The true value of β is set at 2 and the reduced-form coefficient π2 is chosen as
. The true value of β is set at 2 and the reduced-form coefficient π2 is chosen as 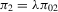 , where
, where 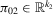 is a vector of ones and
is a vector of ones and  characterizes the strength of the instruments. More precisely,
characterizes the strength of the instruments. More precisely, 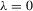 is a design of complete non-identification (irrelevant instruments),
is a design of complete non-identification (irrelevant instruments), 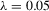 designs weak identification,
designs weak identification, 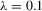 is the set-up of moderate identification, and finally
is the set-up of moderate identification, and finally 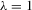 symbolizes strong identification. The errors
symbolizes strong identification. The errors 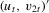 are generated as
are generated as 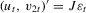 , where
, where 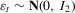 ,
,
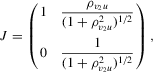
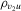 measures the endogeneity of y2. The exogeneity of y2 is then expressed as
measures the endogeneity of y2. The exogeneity of y2 is then expressed as 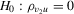 . In this experiment, we vary
. In this experiment, we vary 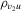 in
in 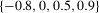 , but the results do not change qualitatively for alternative values of
, but the results do not change qualitatively for alternative values of 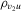 . The rejection frequencies are computed using 1000 replications for the standard DWH tests, while those of the bootstrap tests are obtained with
. The rejection frequencies are computed using 1000 replications for the standard DWH tests, while those of the bootstrap tests are obtained with 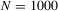 replications and
replications and 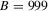 bootstrap pseudo-samples of size
bootstrap pseudo-samples of size 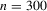 . Table 1 presents the empirical rejection frequencies of both the bootstrap and standard DWH tests. First, we observe that the empirical rejections are close to the 5% nominal level for all bootstrap tests when
. Table 1 presents the empirical rejection frequencies of both the bootstrap and standard DWH tests. First, we observe that the empirical rejections are close to the 5% nominal level for all bootstrap tests when  (exogeneity), irrespective of the value of λ (quality of the IVs). Meanwhile, only the LM versions of the standard DWH tests have correct size when
(exogeneity), irrespective of the value of λ (quality of the IVs). Meanwhile, only the LM versions of the standard DWH tests have correct size when 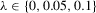 (weak or moderate IVs). The quasi-Wald versions of the standard DWH tests are overly conservative under weak IVs. As expected, the rejections under exogeneity of the standard DWH tests are similar to those of the bootstrap tests and are close to the 5% nominal level with strong identification (
(weak or moderate IVs). The quasi-Wald versions of the standard DWH tests are overly conservative under weak IVs. As expected, the rejections under exogeneity of the standard DWH tests are similar to those of the bootstrap tests and are close to the 5% nominal level with strong identification (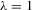 ). Second, when identification is strong and endogeneity is large (
). Second, when identification is strong and endogeneity is large ( and
and 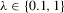 ), both the bootstrap and standard tests have rejections approaching or equal to 100%. However, all tests have low power when identification is very weak. Nevertheless, even the quasi-Wald bootstrap DWH tests exhibit power with weak IVs and large endogeneity. For example, the rejections of
), both the bootstrap and standard tests have rejections approaching or equal to 100%. However, all tests have low power when identification is very weak. Nevertheless, even the quasi-Wald bootstrap DWH tests exhibit power with weak IVs and large endogeneity. For example, the rejections of 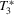 ,
, 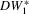 and
and 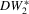 when
when 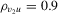 and
and 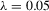 are around 24%, which nearly triple those of T3,
are around 24%, which nearly triple those of T3, 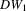 and
and 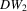 .
.| Bootstrap DWH tests | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
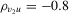 |
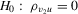 |
 |
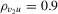 |
|||||||||||||
Statistics↓  |
0 | 0.05 | 0.1 | 1 | 0 | 0.05 | 0.1 | 1 | 0 | 0.05 | 0.1 | 1 | 0 | 0.05 | 0.1 | 1 |
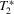 |
6.8 | 17.9 | 73.4 | 100 | 5.2 | 6.6 | 5.8 | 4.5 | 4.6 | 11.2 | 35.7 | 100 | 6.2 | 24.1 | 82.2 | 100 |
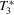 |
5.5 | 21.0 | 71.7 | 100 | 4.4 | 4.4 | 6.6 | 4.4 | 4.1 | 5.9 | 35.5 | 100 | 4.0 | 24.4 | 77.1 | 100 |
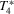 |
6.8 | 17.9 | 73.4 | 100 | 5.2 | 6.6 | 5.8 | 4.5 | 4.6 | 11.2 | 35.7 | 100 | 6.2 | 24.1 | 82.2 | 100 |
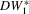 |
5.5 | 21.0 | 71.7 | 100 | 4.4 | 4.4 | 6.6 | 4.4 | 4.1 | 5.9 | 35.5 | 100 | 4.0 | 24.4 | 77.1 | 100 |
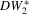 |
5.5 | 21.0 | 71.7 | 100 | 4.4 | 4.4 | 6.6 | 4.4 | 4.1 | 5.9 | 35.5 | 100 | 4.0 | 24.4 | 77.1 | 100 |
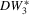 |
6.8 | 17.9 | 73.4 | 100 | 5.2 | 6.6 | 5.8 | 4.5 | 4.6 | 11.2 | 35.7 | 100 | 6.2 | 24.1 | 82.2 | 100 |
| Standard DWH test | ||||||||||||||||
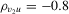 |
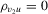 |
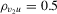 |
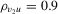 |
|||||||||||||
Statistics↓  |
0 | 0.05 | 0.1 | 1 | 0 | 0.05 | 0.1 | 1 | 0 | 0.05 | 0.1 | 1 | 0 | 0.05 | 0.1 | 1 |
| T2 | 5.0 | 19.3 | 74.8 | 100 | 4.8 | 6.2 | 6.0 | 4.9 | 3.8 | 12.0 | 38.4 | 100 | 5.1 | 25.6 | 82.8 | 100 |
| T3 | 0.2 | 6.7 | 64.3 | 100 | 0.2 | 0.9 | 3.0 | 4.9 | 0.4 | 2.1 | 26.9 | 100 | 0.4 | 8.0 | 74.4 | 100 |
| T4 | 4.9 | 19.0 | 74.7 | 100 | 4.8 | 6.2 | 5.9 | 4.9 | 3.8 | 11.4 | 38.2 | 100 | 4.9 | 25.3 | 82.7 | 100 |
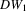 |
0.2 | 6.6 | 64.0 | 100 | 0.2 | 0.8 | 3.0 | 4.8 | 0.4 | 2.0 | 26.7 | 100 | 0.4 | 7.7 | 73.7 | 100 |
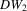 |
0.2 | 6.7 | 64.4 | 100 | 0.2 | 0.9 | 3.0 | 4.9 | 0.4 | 2.3 | 27.2 | 100 | 0.4 | 8.1 | 74.8 | 100 |
 |
5.0 | 19.0 | 74.7 | 100 | 4.8 | 6.2 | 5.9 | 4.9 | 3.8 | 11.7 | 38.3 | 100 | 4.9 | 25.3 | 82.7 | 100 |
ACKNOWLEDGEMENTS
We are grateful to Professor Richard J. Smith, Managing Editor of the Econometrics Journal and to two anonymous referees for their constructive comments and suggestions. We also thank Jean-Marie Dufour, Mardi Dungey, Ngoc Thien Ahn Pham and Robert Garrard for several useful comments. This project is supported by a School of Economics and Finance (University of Tasmania) research grant, and I am grateful for the support.
Appendix A: AUXILIARY THEOREM
Let 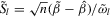 and
and 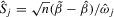 , where
, where 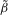 ,
, 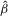 ,
, 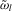 and
and 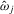 are given in 2.7.
are given in 2.7.
Theorem A.1.Suppose that Assumptions 2.1 and 2.2 are satisfied and that 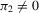 is fixed. Then for some integer
is fixed. Then for some integer 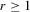 , we have (a)
, we have (a) 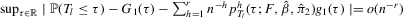 ,
, 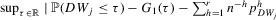
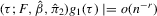 if
if  ; (b)
; (b) 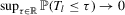 ,
, 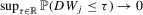 as
as 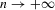 if
if 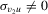 is fixed, where
is fixed, where 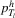 and
and 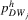 depend on
depend on 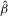 ,
, 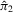 , and the moments of the distribution F of
, and the moments of the distribution F of  .
.
Proof.First, we can write 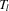 and
and 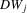 as
as 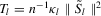 (with
(with 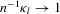 as
as 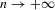 ) and
) and 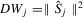 . (a) Suppose that H0 is satisfied. We want to approximate
. (a) Suppose that H0 is satisfied. We want to approximate 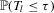 and
and 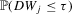 uniformly in τ. First, we can write both
uniformly in τ. First, we can write both 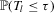 and
and 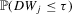 as
as 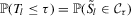 and
and 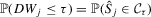 , where
, where  are convex sets. From Bhattacharya and Rao (1976, Corollary 3.2), we have
are convex sets. From Bhattacharya and Rao (1976, Corollary 3.2), we have 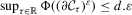 for some constant d and
for some constant d and 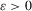 . So, Theorem 1 of Bhattacharya and Ghosh (1978) holds with
. So, Theorem 1 of Bhattacharya and Ghosh (1978) holds with  and
and 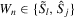 . By using the approximation of
. By using the approximation of 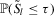 and
and 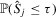 in Lemma A.1(a) of the online Appendix and the definition of
in Lemma A.1(a) of the online Appendix and the definition of 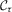 , Theorem A.1(a) follows directly from the fact that the odd terms of the quadratic expansion are even. (b) When
, Theorem A.1(a) follows directly from the fact that the odd terms of the quadratic expansion are even. (b) When 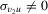 is fixed, the proof follows similar steps to those of Lemma A.1(b) of the online Appendix.
is fixed, the proof follows similar steps to those of Lemma A.1(b) of the online Appendix.
REFERENCES
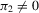 is fixed, the limit of the derivative of H with respect to the argument of
is fixed, the limit of the derivative of H with respect to the argument of 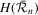 corresponding to
corresponding to 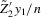 (where
(where 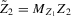 ) takes the form:
) takes the form: 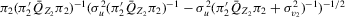 . It is easy to see that this derivative is not well defined at
. It is easy to see that this derivative is not well defined at  . In addition, the limits of this derivative at
. In addition, the limits of this derivative at 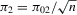 and
and 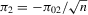 ,
, 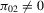 , are given by
, are given by 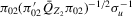 and
and 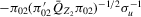 , respectively. These expressions are also equal to directional derivatives at
, respectively. These expressions are also equal to directional derivatives at 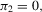 establishing that no limit exists at
establishing that no limit exists at 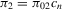 for any sequence
for any sequence 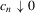 (similar to Moreira et al., 2009).
(similar to Moreira et al., 2009).



