First-differencing in panel data models with incidental functions
Summary
This note discusses a class of models for panel data that accommodate between-group heterogeneity that is allowed to exhibit positive within-group variance. Such a set-up generalizes the traditional fixed-effect paradigm in which between-group heterogeneity is limited to univariate factors that act like constants within groups. Notable members of the class of models considered are non-linear regression models with additive heterogeneity and multiplicative-error models suitable for non-negative limited dependent variables. The heterogeneity is modelled as a non-parametric nuisance function of covariates whose functional form is fixed within groups but is allowed to vary freely across groups. A simple approach to perform inference in such situations is based on local first-differencing of observations within a given group. This leads to moment conditions that, asymptotically, are free of nuisance functions. Conventional generalized method of moments procedures can then be readily applied. In particular, under suitable regularity conditions, such estimators are consistent and asymptotically normal, and asymptotically valid inference can be performed using a plug-in estimator of the asymptotic variance.
1. INTRODUCTION
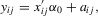
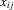 represents log-input factors such as capital and labour, α0 is the corresponding vector of elasticities, and
represents log-input factors such as capital and labour, α0 is the corresponding vector of elasticities, and 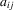 is total factor productivity, which will typically be correlated with the inputs, rendering the ordinary least-squares estimator of α0 inconsistent. To estimate the elasticities from within-group variation, total factor productivity is decomposed as
is total factor productivity, which will typically be correlated with the inputs, rendering the ordinary least-squares estimator of α0 inconsistent. To estimate the elasticities from within-group variation, total factor productivity is decomposed as  , where
, where 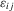 is assumed to be orthogonal to the production inputs but
is assumed to be orthogonal to the production inputs but  can be correlated with the
can be correlated with the 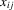 . In this case, a within-group transformation will sweep out
. In this case, a within-group transformation will sweep out 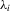 , after which least-squares can be applied to estimate α0. The inclusion of fixed effects in this manner has become standard practice in applied work.
, after which least-squares can be applied to estimate α0. The inclusion of fixed effects in this manner has become standard practice in applied work.However, there are good reasons to believe that unobserved heterogeneity goes beyond what can be captured by such location parameters. In the production-function example, it seems natural that managerial ability depends on such things as experience, education and sector-specific characteristics. As such, ability itself is the outcome of a production process, and it can be difficult to justify that it remains constant over the sampling period. A more appropriate way to control for managerial ability then could have 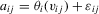 for some latent function
for some latent function 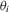 that maps drivers
that maps drivers 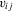 , such as experience and schooling, into ability. Similarly, in matching models,
, such as experience and schooling, into ability. Similarly, in matching models, 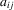 could represent the match-efficiency parameter. In the context of the labour market, Sedláček (2014) finds empirical evidence that matching efficiency is procyclical and is, at least partially, driven by the hiring standards of firms. Moreover, the matching literature has argued that the efficiency parameter should be endogenous to the agents' optimization behaviour, rather than exogenously determined.
could represent the match-efficiency parameter. In the context of the labour market, Sedláček (2014) finds empirical evidence that matching efficiency is procyclical and is, at least partially, driven by the hiring standards of firms. Moreover, the matching literature has argued that the efficiency parameter should be endogenous to the agents' optimization behaviour, rather than exogenously determined.
This note suggests a simple way to conduct inference on common parameters in panel-data models with non-parametric incidental functions. Besides the linear set-up just described, the approach can equally be used for models with multiplicative errors, such as models for count data, and for logit models, for example. In either case, staying true to the fixed-effect paradigm, the aim is to estimate a finite-dimensional parameter while controlling for between-group heterogeneity in a non-parametric manner. The difference with the traditional fixed-effect view, however, is that the heterogeneity is allowed to vary both within and between groups. This view on unobserved heterogeneity is different from the one taken in recent work on the linear random-coefficient model (Arellano and Bonhomme, 2012, and Graham and Powell, 2012) and, as such, can serve as a useful complement.
2. LOCAL FIRST-DIFFERENCING
2.1. Incidental Functions
Consider a panel dataset consisting of two observations on n units. Restricting attention to two observations is without loss of generality. We let 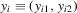 denote the outcome variables for unit i, and let
denote the outcome variables for unit i, and let 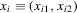 and
and 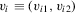 denote observable covariates. The distinction between the variables
denote observable covariates. The distinction between the variables 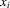 and
and  will become clear below.
will become clear below.
 (2.1)
(2.1)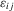 and vector of slope coefficients α0. Applications of this model are widespread. When
and vector of slope coefficients α0. Applications of this model are widespread. When 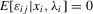 , an ordinary least-squares regression of
, an ordinary least-squares regression of 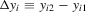 on
on 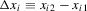 is known to yield a consistent point estimator of α0 as
is known to yield a consistent point estimator of α0 as 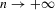 . Indeed,
. Indeed,

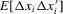 has full rank. When the covariates are not strictly exogenous, the above moment condition can be replaced by
has full rank. When the covariates are not strictly exogenous, the above moment condition can be replaced by 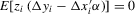 for a vector of instrumental variables
for a vector of instrumental variables  . A leading case would be a dynamic model where
. A leading case would be a dynamic model where 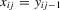 and
and  contains further lags of the outcome variable; see, e.g., Arellano and Bond (1991).
contains further lags of the outcome variable; see, e.g., Arellano and Bond (1991).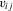 , as additional regressors. This delivers a specification of the form
, as additional regressors. This delivers a specification of the form
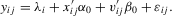 (2.2)
(2.2)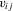 can be flexible polynomials specifications or other non-linear transformations of the controls and, of course, can include interactions with
can be flexible polynomials specifications or other non-linear transformations of the controls and, of course, can include interactions with  . The choice of functional form is up to the researcher, and linearity is popular because of the resulting ease of computation via multiple regression. An approach that would prevent functional-form misspecification in the effect of the control variables would be to work with the partially linear model
. The choice of functional form is up to the researcher, and linearity is popular because of the resulting ease of computation via multiple regression. An approach that would prevent functional-form misspecification in the effect of the control variables would be to work with the partially linear model
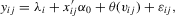 (2.3)
(2.3)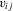 to be non-parametric, it is restricted to be identical across i. Recent empirical work has stressed the presence of excess heterogeneity across agents in microeconometric models. Guvenen (2009), Browning et al. (2010) and Browning and Carro (2010, 2014), for example, provide extensive discussions and empirical evidence on this. An alternative extension of the Robinson framework that stays true to the fixed-effect tradition would be
to be non-parametric, it is restricted to be identical across i. Recent empirical work has stressed the presence of excess heterogeneity across agents in microeconometric models. Guvenen (2009), Browning et al. (2010) and Browning and Carro (2010, 2014), for example, provide extensive discussions and empirical evidence on this. An alternative extension of the Robinson framework that stays true to the fixed-effect tradition would be
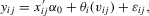 (2.4)
(2.4)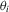 are unit-specific non-parametric functions, and the usual location parameter
are unit-specific non-parametric functions, and the usual location parameter 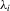 has been absorbed into it. A special case of 2.4 that has received some attention recently is the standard linear random-coefficient model (Swamy, 1970, Chamberlain, 1992b, and Arellano and Bonhomme, 2012). Another is the varying-coefficient model (Hastie and Tibshirani, 1993). None the less, the motivation for allowing for excess heterogeneity is clearly different in these cases.
has been absorbed into it. A special case of 2.4 that has received some attention recently is the standard linear random-coefficient model (Swamy, 1970, Chamberlain, 1992b, and Arellano and Bonhomme, 2012). Another is the varying-coefficient model (Hastie and Tibshirani, 1993). None the less, the motivation for allowing for excess heterogeneity is clearly different in these cases.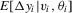 and
and 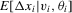 can be consistently estimated. Clearly, this is not possible under asymptotics where the number of observations per unit is held fixed. Suppose that
can be consistently estimated. Clearly, this is not possible under asymptotics where the number of observations per unit is held fixed. Suppose that 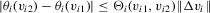 for some function
for some function 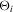 for which the expectation
for which the expectation 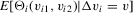 exists for all v in a neighbourhood of zero. Then, provided that
exists for all v in a neighbourhood of zero. Then, provided that 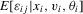 is a constant,
is a constant,
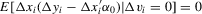
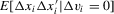 has full rank. Indeed,
has full rank. Indeed,
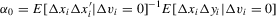
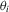 is fairly weak. Suppose that
is fairly weak. Suppose that 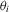 is continuously differentiable. Then, its derivative, say
is continuously differentiable. Then, its derivative, say 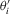 , is locally bounded. Hence,
, is locally bounded. Hence, 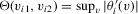 , with v restricted to the neighbourhood
, with v restricted to the neighbourhood 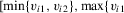 ,
, 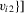 , satisfies the required Lipschitz-type smoothness condition. When the support of
, satisfies the required Lipschitz-type smoothness condition. When the support of 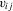 is discrete, we require that
is discrete, we require that 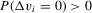 . An estimator of α0 would be
. An estimator of α0 would be
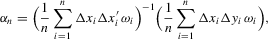
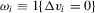 . This estimator is
. This estimator is 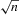 -consistent and asymptotically normal under standard moment assumptions. When
-consistent and asymptotically normal under standard moment assumptions. When 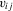 is continuous, the event
is continuous, the event 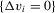 has probability zero and
has probability zero and 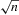 -consistent estimation will not be possible. However, under suitable regularity conditions, we can still perform asymptotically valid inference on α0 via
-consistent estimation will not be possible. However, under suitable regularity conditions, we can still perform asymptotically valid inference on α0 via 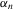 on redefining
on redefining  as
as
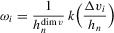
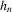 .1,2 Here, the convergence rate of
.1,2 Here, the convergence rate of 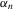 will be reduced to
will be reduced to 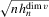 . We provide regularity conditions and more detailed asymptotic theory below. In either case, the approach consists of simply constructing
. We provide regularity conditions and more detailed asymptotic theory below. In either case, the approach consists of simply constructing 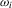 for each i and then performing a weighted least-squares regression of
for each i and then performing a weighted least-squares regression of 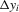 on
on 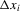 with weight
with weight  . This estimator is similar in spirit to the one considered for sample-selection models by Kyriazidou (1997, 2001).
. This estimator is similar in spirit to the one considered for sample-selection models by Kyriazidou (1997, 2001).The  can be seen as incidental functions, as opposed to the incidental parameters
can be seen as incidental functions, as opposed to the incidental parameters 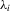 in the conventional set-up in 2.1. Furthermore, the
in the conventional set-up in 2.1. Furthermore, the 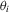 can be seen as draws from a distribution that depends on
can be seen as draws from a distribution that depends on 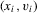 but which is left unspecified. The approach just described does not estimate these functions but, rather, differences them out by focusing on the population of “stayers” (Chamberlain, 1984), that is, on units for which
but which is left unspecified. The approach just described does not estimate these functions but, rather, differences them out by focusing on the population of “stayers” (Chamberlain, 1984), that is, on units for which 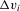 lies in a shrinking neighbourhood of zero. As such, this approach could be called local first-differencing. Of course, a prerequisite to identification is that the support of
lies in a shrinking neighbourhood of zero. As such, this approach could be called local first-differencing. Of course, a prerequisite to identification is that the support of 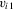 and the support of
and the support of 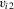 are not disjoint. The leading example where this requirement would be violated is when the
are not disjoint. The leading example where this requirement would be violated is when the 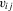 include time dummies or time trends. Such aggregate time effects are commonly used in applied work. Of course, they can easily be included in the traditional way, that is, by including them in a linear fashion and assigning them homogeneous coefficients.
include time dummies or time trends. Such aggregate time effects are commonly used in applied work. Of course, they can easily be included in the traditional way, that is, by including them in a linear fashion and assigning them homogeneous coefficients.
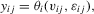
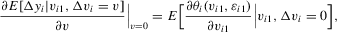
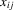 to be predetermined as opposed to strictly exogenous, and can accommodate discrete components in both
to be predetermined as opposed to strictly exogenous, and can accommodate discrete components in both  and
and  . None the less, as in Hoderlein and White (2012) and Arellano and Bonhomme (2012), allowing for feedback toward the
. None the less, as in Hoderlein and White (2012) and Arellano and Bonhomme (2012), allowing for feedback toward the 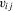 is complicated, because the distribution of the transitory shocks,
is complicated, because the distribution of the transitory shocks, 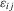 , can change after conditioning on the event
, can change after conditioning on the event 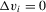 .
.2.2. Non-linear Specifications
The applicability of local first-differencing is not limited to the linear model. Indeed, any fixed-effect model where heterogeneous intercepts can be accommodated can be extended to allow for incidental functions. The literature on panel data models is large, and we do not attempt to give a complete overview here. A survey is provided by Arellano and Honoré (2001).
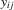 and
and 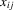 but to maintain additivity of the incidental function, as in
but to maintain additivity of the incidental function, as in
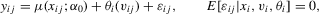
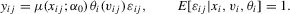
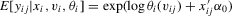 . Here,
. Here,

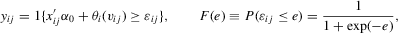
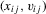 independent of
independent of 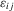 . An application of the conditional-likelihood argument shows that
. An application of the conditional-likelihood argument shows that
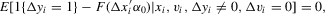
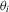 . The optimal unconditional moment condition in the sense of Chamberlain (1987) equals
. The optimal unconditional moment condition in the sense of Chamberlain (1987) equals
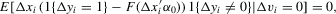
In each of the examples just mentioned, it is easy to construct a generalized method of moments (GMM) estimator in which the usual moment condition is complemented with the kernel weight 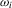 as described above. We provide asymptotic theory in the next section.
as described above. We provide asymptotic theory in the next section.
There are several other models that could be extended to allow for incidental functions. Some interesting examples are truncated and censored regression models (Honoré, 1992), as well as general transformation models and generalized regression models (Abrevaya, 1999, 2000). The resulting estimators would have similar asymptotic properties. However, they are M-estimators rather than GMM estimators, and the associated criterion functions are characterized by a certain degree of non-smoothness. As such, they will not fit exactly the generic set-up entertained below.
3. ASYMPTOTIC THEORY
 is identified through the moment condition
is identified through the moment condition

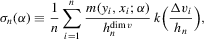
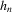 is a non-negative bandwidth sequence that is o(1) and k is a kernel function. Regularity conditions on
is a non-negative bandwidth sequence that is o(1) and k is a kernel function. Regularity conditions on 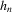 and k are collected in Assumption 3.3. A GMM estimator of α0 based on
and k are collected in Assumption 3.3. A GMM estimator of α0 based on 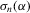 is then given by
is then given by
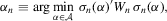
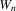 denotes a given positive-definite weight matrix. This section provides distribution theory for
denotes a given positive-definite weight matrix. This section provides distribution theory for  in the form of a consistency result and an asymptotic-normality result. The proofs are given in the Appendix.
in the form of a consistency result and an asymptotic-normality result. The proofs are given in the Appendix.Some elementary regularity conditions are collected in Assumption 3.1.
Assumption 3.1.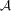 is a compact set and α0 is interior to it. m is twice continuously differentiable in α with derivatives
is a compact set and α0 is interior to it. m is twice continuously differentiable in α with derivatives 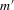 and
and 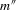 . The distribution of
. The distribution of 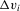 is absolutely continuous and the associated density function is strictly positive in a neighbourhood of zero.
is absolutely continuous and the associated density function is strictly positive in a neighbourhood of zero.
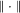 denote the Euclidean and Frobenius norms. To state sufficient conditions for consistency, let
denote the Euclidean and Frobenius norms. To state sufficient conditions for consistency, let
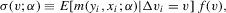
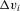 .
.
Assumption 3.2.For all  ,
, 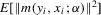 and
and 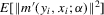 are finite,
are finite, 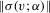 is bounded in v, and
is bounded in v, and 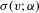 is continuous in v in a neighbourhood of zero.
is continuous in v in a neighbourhood of zero.
Assumption 3.3.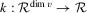 is a bounded and symmetric sth-order kernel function.
is a bounded and symmetric sth-order kernel function.
The conditions in Assumptions 3.2 and 3.3 are conventional. We refer to Li and Racine (2007) for a definition, examples and a discussion of kernel functions that satisfy Assumption 3.3.
The consistency result is stated in Theorem 3.1.
Theorem 3.1.Let Assumptions 3.1–3.3 hold. Suppose that 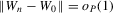 for W0 non-stochastic and positive definite. Then
for W0 non-stochastic and positive definite. Then 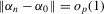 .
.
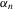 , we need an additional set of conditions. We let
, we need an additional set of conditions. We let
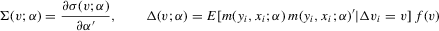
Assumption 3.4.For all 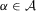 ,
, 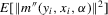 is finite,
is finite, 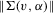 is bounded in v, and
is bounded in v, and 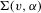 is continuous in v in a neighbourhood of zero.
is continuous in v in a neighbourhood of zero. 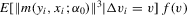 is bounded.
is bounded. 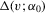 is continuous in v in a neighbourhood of zero and
is continuous in v in a neighbourhood of zero and 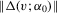 is bounded.
is bounded. 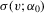 is s-times continuously differentiable with bounded derivatives.
is s-times continuously differentiable with bounded derivatives.
Let 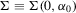 and
and 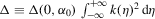 . Theorem 3.2 gives the asymptotic distribution of
. Theorem 3.2 gives the asymptotic distribution of 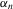 .
.
Theorem 3.2.Let Assumptions 3.1–3.4 hold. Suppose that Σ has maximal column rank, that Δ is positive definite, and that 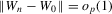 for W0 non-stochastic and positive definite. Then
for W0 non-stochastic and positive definite. Then
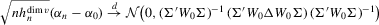
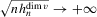 and
and 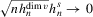 .
.
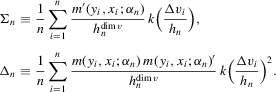
ACKNOWLEDGMENTS
I am grateful to Jaap Abbring, Manuel Arellano, Stefan Hoderlein and three referees.
APPENDIX A
PROOFS OF THEOREMS
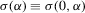 . Given identification, the regularity conditions in Assumption 3.1, and the fact that
. Given identification, the regularity conditions in Assumption 3.1, and the fact that 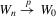 , we only need to verify
, we only need to verify
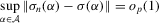
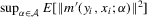 is finite, and k is bounded, Lemma 2.9 in Newey and McFadden (1994) further states that it suffices to prove that
is finite, and k is bounded, Lemma 2.9 in Newey and McFadden (1994) further states that it suffices to prove that 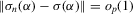 for all
for all 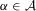 . Fix
. Fix 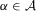 . By the triangle inequality,
. By the triangle inequality,
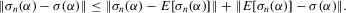
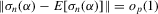 by the law of large numbers. Dominated convergence implies that
by the law of large numbers. Dominated convergence implies that
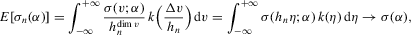
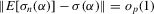 . Thus,
. Thus, 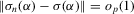 . This holds for any
. This holds for any 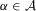 , and so consistency has been shown.
, and so consistency has been shown. 
 and (b)
and (b) 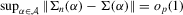 . The asymptotic distribution of the estimator then follows from the linearization
. The asymptotic distribution of the estimator then follows from the linearization
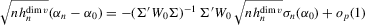
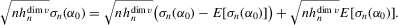
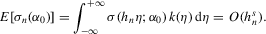
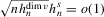 ,
, 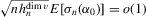 and the bias term is asymptotically negligible. The leading term satisfies the conditions of Lyapunov's central limit theorem. To see this, write
and the bias term is asymptotically negligible. The leading term satisfies the conditions of Lyapunov's central limit theorem. To see this, write
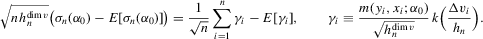
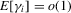 and
and
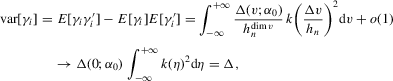
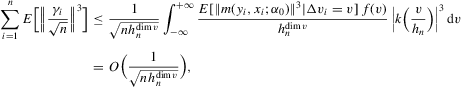
 . This establishes (a). To verify (b), we can proceed as in the proof of Theorem 3.1. In particular, Lemma 2.9 of Newey and McFadden (1994) can again be applied. By the moment conditions in Assumption 3.4, we have that
. This establishes (a). To verify (b), we can proceed as in the proof of Theorem 3.1. In particular, Lemma 2.9 of Newey and McFadden (1994) can again be applied. By the moment conditions in Assumption 3.4, we have that 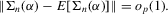 An application of the bounded convergence theorem similarly shows that
An application of the bounded convergence theorem similarly shows that 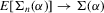 . Uniform convergence of the Jacobian matrix follows and the proof is complete.
. Uniform convergence of the Jacobian matrix follows and the proof is complete. 
REFERENCES
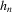 . An automated approach to selecting the bandwidth is to estimate it jointly with α0, as in Härdle et al. (1993). See the Online Appendix for details and simulation experiments.
. An automated approach to selecting the bandwidth is to estimate it jointly with α0, as in Härdle et al. (1993). See the Online Appendix for details and simulation experiments.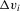 and indicator functions for the discrete elements.
and indicator functions for the discrete elements.



