A social interaction model with an extreme order statistic
Summary
In this paper, we introduce a social interaction econometric model with an extreme order statistic to model peer effects. We show that the model is a well-defined system of equations and that it is a static game with complete information. The social interaction model can include exogenous regressors and group effects. Instrumental variables estimators are proposed for the general model that includes exogenous regressors. We also consider distribution-free methods that use recurrence relations to generate moment conditions for estimation. For a model without exogenous regressors, the maximum likelihood approach is computationally feasible.
1. INTRODUCTION
There is a growing body of literature in which the influence of social peers in economics and other social sciences is addressed; see Durlauf (2004) for a recent survey. Conventional social interaction models, including the spatial autoregressive model and the linear-in-means model, assume that an individual's outcome depends linearly on the mean of the outcomes of the individual's peers; see, e.g. Anselin (1988), Manski (1993), Moffitt (2001), Lee (2007) and Bramoulle et al. (2009). For instance, a student's test score would be affected linearly by the mean test score of their classmates. In certain situations, we believe that a better specified model might involve the full distribution or other distributional characteristics, such as order statistics, rather than the mean (e.g. Ioannides and Soetevent, 2007).
In this paper, we introduce a social interaction econometric model with an extreme order statistic to allow non-linearity in modelling endogenous peer effects.1 Let 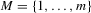 be a finite set of players in a social network (group) and let
be a finite set of players in a social network (group) and let 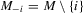 be the set of players, except the ith player, who are i's neighbours. For example, a simple social interaction model with the maximum statistic for the ith player is specified as
be the set of players, except the ith player, who are i's neighbours. For example, a simple social interaction model with the maximum statistic for the ith player is specified as 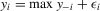 , where
, where 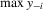 denotes
denotes 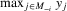 and
and  is a random element. The social interaction model with the minimum statistic can be defined in a similar way.
is a random element. The social interaction model with the minimum statistic can be defined in a similar way.
Empirical studies have found evidence regarding peer effects on educational outcomes; see, e.g. Hanushek (1992), Hanushek et al. (2003) and Hoxby (2000). It is plausible that peers affect educational outcomes by aiding learning through questions and answers or by hindering learning through disruptive behaviour. Lazear (2001) has suggested that disruptive students could interfere with the educational outcomes of their peers. For instance, a student who has bad grades in class might hinder learning by asking poor questions. This disruptive behaviour might have large negative effects on the academic achievements of this student's peers, and thus might generate strong endogenous peer effects. Figlio (2007) has found empirical evidence of the effects of disruptive students on the performance of their peers, which indicates that students suffer academically from the presence of classroom disruption. Thus, our social interaction model with an extreme order statistic might be useful to explore such ‘bad apple’ effects in some empirical studies.
In many real-world situations, rewards are based on relative performance rather than absolute performance, and competition in terms of extreme outcomes may occur. Holmstrom (1982) has suggested that a relative performance scheme provides a better evaluation than an absolute performance scheme in the presence of costly monitoring of the agent's effort. Lazear and Rosen (1981) have suggested that there is a convex relation between pay and performance level in tournament schemes.2 Frank and Cook (1995) have attributed much of this phenomenon to winner-take-all markets, which compete fiercely for the best. Examples of such schemes include companies offering bonuses to the ‘salesperson of the year’, universities rewarding researchers for writing the ‘best paper’ and athletes being rewarded for having the best Olympic performances. Main et al. (1993) have conducted a detailed survey of executive compensations and have found some support for a relative performance scheme. Ehrenberg and Bognanno (1990a,b) have found that the performances of professional golf players are influenced by the level and structure of prizes in major golf tournaments.
In contrast to the situation where individuals are competitors in the labor market, individuals can benefit from their peers in a social group. The benefit might take the form of the sharing of know-how between individuals. This is an efficient way for individuals to obtain valuable experiences from their peers and especially from those who are most capable.3 Therefore, individuals might react to the performance of their best peers in a strategic model of social network.
The paper is organized as follows. In Section 2., we provide some theoretical justifications for the social interaction model with the minimum or maximum statistic on economic grounds. In Section 3., we introduce a general model specification with an extreme order statistic. We show that the social interaction model with an extreme order statistic is a well-defined system of equations. The solution to the system exists and is unique. Our model has the essential features of a static game with complete information for a finite number of players. In particular, this game is asymmetric and has a unique pure-strategy Nash equilibrium. In Section 4., we provide a simple instrumental variables (IV) approach for a general model where exogenous regressors are relevant. In Section 5., we consider the generalized method of moments (GMM), which uses IV moments and recurrence relations for moments of order statistics. Our asymptotic analysis of estimation methods (IV and GMM) is based on a sample consisting of a large number of groups where group sizes remain fixed and bounded (as the number of groups tends to infinity). In Section 6., we give a brief introduction of an extended social interaction model with mixed mean and maximum. In Section 7., we provide some Monte Carlo results and in Section 8., we provide an empirical example. To illustrate the practical use of this model, we apply it to the National Collegiate Athletic Association (NCAA) men's basketball data and we obtain some interesting results. In Section 9., we draw our conclusions. In Appendix A, we list some useful notations and some moments of ordered normal random variables. In Appendix B, we give detailed proofs of the theorems provided in Sections 3., 4. and 6.. In Appendix C, we provide a brief description of the maximum likelihood estimation (MLE) of simple model specifications and some Monte Carlo results. In Appendix D, we give a useful lemma and some technical details about the GMM estimation with recurrence moments discussed in Section 5..
2. THEORETICAL ECONOMIC CONSIDERATIONS
Our model specification can be derived from a simultaneous move game with perfect information.4 The sample can be viewed as repetitions of a game played among individuals with possibly varying finite numbers of players. We give three theoretical examples to illustrate the model specification within the game-theoretic framework. These theoretical models are for illustrative purposes and are not exclusive for possible economic applications of the proposed econometric model.
2.1. A synergistic relationship
A game has m players involved in a synergistic relationship (Osborne, 2004). It is a static game with complete information, in which each player knows the pay-offs and strategies available to other players. Each player's set of actions is the set of performance levels. Denote by 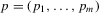 a performance profile chosen by players and by
a performance profile chosen by players and by 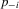 , which is a subvector of p with dimension
, which is a subvector of p with dimension  , the performance profile of all players except the ith player in the game. Player i's preference is represented by the pay-off function
, the performance profile of all players except the ith player in the game. Player i's preference is represented by the pay-off function 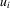 , which depends on p in the following way. First,
, which depends on p in the following way. First, 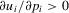 and
and 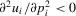 capture the concave relationship between pay-offs and performance levels. Secondly,
capture the concave relationship between pay-offs and performance levels. Secondly, 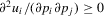 ,
, 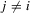 , captures the synergistic relationship between player i and player i's peer j.
, captures the synergistic relationship between player i and player i's peer j.
 for all i). The social capital can only be used to establish social connections between players. If player i spends an amount
for all i). The social capital can only be used to establish social connections between players. If player i spends an amount 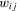 on j, then player i's pay-off can increase proportionally by
on j, then player i's pay-off can increase proportionally by 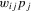 . Intuitively, the player will spend all their social capital in establishing connections with their peers such that
. Intuitively, the player will spend all their social capital in establishing connections with their peers such that 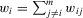 . Formally, we have the pay-off function
. Formally, we have the pay-off function
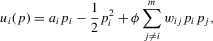 (2.1)
(2.1)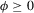 . Note that
. Note that 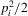 represents the cost of performance, which is similar to the moral cost in the crime network study of Liu et al. (2011). It should be stressed that
represents the cost of performance, which is similar to the moral cost in the crime network study of Liu et al. (2011). It should be stressed that 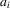 , which is a function of characteristics of the individual i, varies across individuals. In other words, 2.1 depends on which player chooses the action. So, the game is asymmetric. To maximize the pay-off, the player will spend all their capital on their best peer who has the highest performance level in the synergistic relationship.5 So, we have that
, which is a function of characteristics of the individual i, varies across individuals. In other words, 2.1 depends on which player chooses the action. So, the game is asymmetric. To maximize the pay-off, the player will spend all their capital on their best peer who has the highest performance level in the synergistic relationship.5 So, we have that
 (2.2)
(2.2)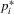 to maximize (2.2), which gives the reaction function of player i as
to maximize (2.2), which gives the reaction function of player i as
 (2.3)
(2.3)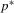 , the performance profile, is observable, and the index
, the performance profile, is observable, and the index 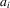 will be specified as
will be specified as 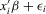 , where
, where 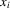 is a vector of observed characteristics of individual i and
is a vector of observed characteristics of individual i and  represents the characteristics that are unobservable by econometricians. Here, ϕ and β are unknown parameters for estimation.
represents the characteristics that are unobservable by econometricians. Here, ϕ and β are unknown parameters for estimation.As an alternative specification, it is possible to justify the game in terms of choosing effort instead of performance level directly, as long as the response of an individual to their peers is on their maximum performance level. Suppose that an individual chooses their effort to respond to the best performance of their peers. Then, we have  . Suppose that the performance of individual i is the sum of their effort and unobserved disturbance
. Suppose that the performance of individual i is the sum of their effort and unobserved disturbance  (i.e.
(i.e. 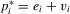 ). Then, the model with the measurement relation becomes
). Then, the model with the measurement relation becomes 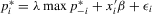 , which is similar to 2.3, where
, which is similar to 2.3, where 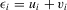 is the overall disturbance.
is the overall disturbance.
2.2. A tournament scheme
 depends on p in the following way. First,
depends on p in the following way. First, 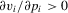 and
and 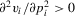 capture the convex relationship between pay and performance. Secondly,
capture the convex relationship between pay and performance. Secondly, 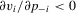 reflects the competition among players (Calvo-Armengol and Zenou, 2004). Formally, we have the gross pay-off function in a tournament game
reflects the competition among players (Calvo-Armengol and Zenou, 2004). Formally, we have the gross pay-off function in a tournament game
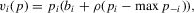 (2.4)
(2.4)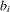 varies across individuals. With
varies across individuals. With 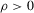 , player i will be rewarded for winning the tournament, and penalized for losing. Suppose that player i's cost is a convex function of performance with
, player i will be rewarded for winning the tournament, and penalized for losing. Suppose that player i's cost is a convex function of performance with 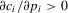 and
and 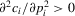 . Formally,
. Formally,
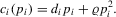 (2.5)
(2.5)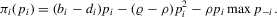 (2.6)
(2.6)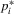 in order to maximize the net pay-off according to the first-order condition
in order to maximize the net pay-off according to the first-order condition
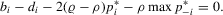 (2.7)
(2.7)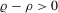 , which is sufficient for a maximum at
, which is sufficient for a maximum at 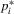 . It follows that the reaction function is
. It follows that the reaction function is
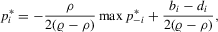 (2.8)
(2.8)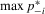 is negative. For estimation,
is negative. For estimation, 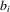 and
and 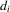 would be functions of the observable and unobserved characteristics of individual i by econometricians. Here, ρ and ϱ would be unknown parameters. Because
would be functions of the observable and unobserved characteristics of individual i by econometricians. Here, ρ and ϱ would be unknown parameters. Because 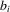 and
and 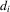 would also involve unknown coefficients of individual characteristics, only the composite parameter
would also involve unknown coefficients of individual characteristics, only the composite parameter 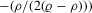 can be identifiable in this model if only
can be identifiable in this model if only 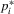 are observed but not the costs
are observed but not the costs  .
.2.3. A game that combines the tournament scheme and the synergistic relationship
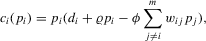 (2.9)
(2.9)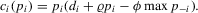 (2.10)
(2.10)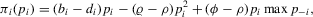 (2.11)
(2.11)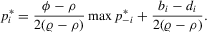 (2.12)
(2.12)Note that the coefficients of 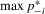 in (2.3) and (2.8) are positive and negative, respectively. We can interpret the former as the social effect and the latter as the competition effect. The net pay-off function (2.11) combines the tournament scheme and the synergistic relation into a single game. In this situation, the coefficient of
in (2.3) and (2.8) are positive and negative, respectively. We can interpret the former as the social effect and the latter as the competition effect. The net pay-off function (2.11) combines the tournament scheme and the synergistic relation into a single game. In this situation, the coefficient of 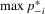 in (2.12 ) would represent the difference between the social effect and the competition effect, so that it can take either a negative or a positive value. Its sign indicates the domination of one effect over the other. They cannot be separately identified from (2.12) alone. These effects would be separately identified if the cost or pay-off of a player could be observed. In the next section, we shall see that the best response function (2.3), (2.8) or (2.12) has a unique Nash equilibrium under some general conditions.
in (2.12 ) would represent the difference between the social effect and the competition effect, so that it can take either a negative or a positive value. Its sign indicates the domination of one effect over the other. They cannot be separately identified from (2.12) alone. These effects would be separately identified if the cost or pay-off of a player could be observed. In the next section, we shall see that the best response function (2.3), (2.8) or (2.12) has a unique Nash equilibrium under some general conditions.
3. THE SOCIAL INTERACTION MODEL WITH MAXIMUM AND REGRESSORS
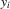 and the outcome profile of the individual's peers being
and the outcome profile of the individual's peers being 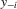 . The individual's observed characteristics will be represented by a vector of regressors
. The individual's observed characteristics will be represented by a vector of regressors 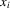 and unobserved characteristics involved will be summarized as
and unobserved characteristics involved will be summarized as  . So, in general, we consider the social interaction model with maximum and regressors:
. So, in general, we consider the social interaction model with maximum and regressors:
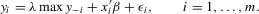 (3.1)
(3.1)Here, m is the total number of players in a game, 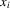 is a vector of observed individual characteristics and
is a vector of observed individual characteristics and  is an individual disturbance, which is known to the agent but unobservable to econometricians. Thus, the reaction functions 2.3, 2.8 and 2.12 can all be included in this framework. For example, λ will be
is an individual disturbance, which is known to the agent but unobservable to econometricians. Thus, the reaction functions 2.3, 2.8 and 2.12 can all be included in this framework. For example, λ will be 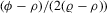 for 2.12, and
for 2.12, and 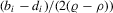 will become
will become 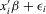 in this general formulation. Because
in this general formulation. Because  and possibly
and possibly 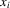 vary across individuals, 3.1 can be interpreted as the reaction function for an asymmetric game with perfect information. With given individual characteristics
vary across individuals, 3.1 can be interpreted as the reaction function for an asymmetric game with perfect information. With given individual characteristics  and
and  , 3.1 can have a unique Nash equilibrium when
, 3.1 can have a unique Nash equilibrium when 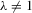 . The following theorem summarizes the solution of 3.1 as the unique Nash equilibrium.
. The following theorem summarizes the solution of 3.1 as the unique Nash equilibrium.
Theorem 3.1.Denote 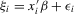 for simplicity. The system 3.1 with
for simplicity. The system 3.1 with  but
but 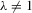 is equivalent to the following system with order statistics:
is equivalent to the following system with order statistics:
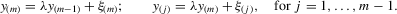 (3.2)
(3.2)Here, 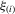 and
and 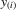 are the corresponding order statistics of
are the corresponding order statistics of 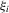 and
and 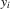 in ascending order. The system 3.2 has the unique solution:
in ascending order. The system 3.2 has the unique solution:
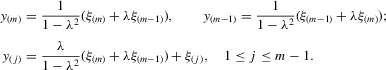 (3.3)
(3.3)Analogously, for the social interaction model with minimum, 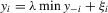 , the solution exists and is unique as
, the solution exists and is unique as 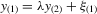 and
and 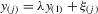 for
for 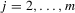 given
given 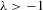 but
but 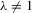 . We note that the existence and uniqueness of the solution are valid without any distributional assumption on
. We note that the existence and uniqueness of the solution are valid without any distributional assumption on 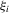 .
.
We see that, from the arguments of the proof for Theorem 3.1, as long as 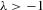 but
but 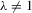 , the order statistics
, the order statistics  have the same ascending order as
have the same ascending order as  . In this case, the solution (Nash equilibrium) of the system exists and is unique. The restriction
. In this case, the solution (Nash equilibrium) of the system exists and is unique. The restriction 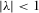 provides the stability of the system. However, the system is unstable or divergent when
provides the stability of the system. However, the system is unstable or divergent when 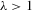 .
.
It is apparent that the system has many possible solutions when λ is 1 or −1. This is also the case with 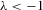 . For any
. For any  , consider the quantities defined by
, consider the quantities defined by 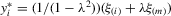 , and
, and 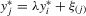 with
with 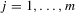 but
but 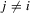 . The quantities of these elements have the order
. The quantities of these elements have the order 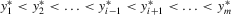 . They also imply
. They also imply 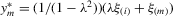 and
and 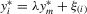 . When
. When 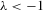 ,
, 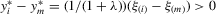 ; hence, these
; hence, these 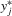 for
for 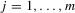 satisfy the structure
satisfy the structure 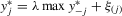 and form a solution set. For
and form a solution set. For 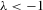 , because i can be any individual of
, because i can be any individual of 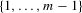 , there are multiple solutions for the system.
, there are multiple solutions for the system.
For certain estimation methods, such as the method of maximum likelihood (ML), a unique solution of the system is essential, because it requires a well-defined mapping of the disturbance vector  to the sample vector
to the sample vector  conditional on observed exogenous variables in order to set up the likelihood function. However, for certain estimation methods, such as IV or the two-stage least-squares (2SLS) estimation, even though the system might have multiple solutions, asymptotic analysis of such estimation methods could still be valid as long as proper instrumental variables are available for the endogenous explanatory variables of the structural equation and the rank condition is satisfied, under the scenario that the number of groups R tends to infinity but the group sizes remain finite and bounded.6
conditional on observed exogenous variables in order to set up the likelihood function. However, for certain estimation methods, such as IV or the two-stage least-squares (2SLS) estimation, even though the system might have multiple solutions, asymptotic analysis of such estimation methods could still be valid as long as proper instrumental variables are available for the endogenous explanatory variables of the structural equation and the rank condition is satisfied, under the scenario that the number of groups R tends to infinity but the group sizes remain finite and bounded.6
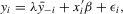 (3.4)
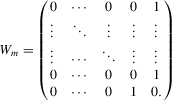
(3.4)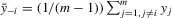 . This group interaction model allows individuals to interact with each other within a group, and peer effects are reciprocal in the model. The social interaction model in 3.2 implicitly assumes that every player except the best player depends on the first-order statistic (i.e. the group maximum). There are no reciprocal effects between players except for the first- and second-order statistics in 3.2. The conventional group interaction model is a special case of spatial autoregressive models, which assume exogenous interaction structures. In contrast, the interaction structure of the model with an extreme order statistic is endogenously determined. It resembles an extension of a star network but the star is endogenously determined with the adjacency matrix of the form7
. This group interaction model allows individuals to interact with each other within a group, and peer effects are reciprocal in the model. The social interaction model in 3.2 implicitly assumes that every player except the best player depends on the first-order statistic (i.e. the group maximum). There are no reciprocal effects between players except for the first- and second-order statistics in 3.2. The conventional group interaction model is a special case of spatial autoregressive models, which assume exogenous interaction structures. In contrast, the interaction structure of the model with an extreme order statistic is endogenously determined. It resembles an extension of a star network but the star is endogenously determined with the adjacency matrix of the form7
4. ESTIMATION
Suppose that the economy has a well-defined group structure. Each player belongs to a social group. The players can interact with each other within a group but not with members in another group. The sample consists of R groups with 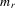 players in the rth group. The total sample size is
players in the rth group. The total sample size is 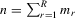 . For empirical relevance, we allow variable group sizes in the model but group sizes remain finite and bounded as the number of groups increases.8
. For empirical relevance, we allow variable group sizes in the model but group sizes remain finite and bounded as the number of groups increases.8
Assumption 4.1.Assume that 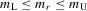 for all r, where the lower bound
for all r, where the lower bound  and the upper bound mU is finite.
and the upper bound mU is finite.
For the estimation, we make the distinction whether exogenous regressors are present or not in the model. Because the model with exogenous regressors might be more relevant for practical use, we focus on the estimation of this general case in the main text, whereas the estimation of the model without regressors is given in Appendix C.
4.1 The model with exogenous regressors
Here, 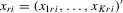 and
and 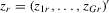 denote
denote 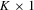 and
and 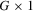 vectors of exogenous variables. If
vectors of exogenous variables. If 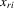 and
and 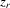 are relevant regressors, the IV approach is possible and is distribution-free.
are relevant regressors, the IV approach is possible and is distribution-free.
Assumption 4.2.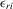 are i.i.d. random variables with zero mean and a finite variance
are i.i.d. random variables with zero mean and a finite variance 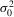 , and are independent of
, and are independent of 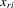 and
and 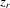 .
.
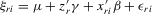 , in terms of order statistics in Theorem 3.1, the system 4.1 is equivalent to
, in terms of order statistics in Theorem 3.1, the system 4.1 is equivalent to
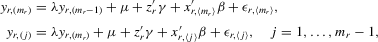 (4.2)
(4.2)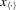 and
and 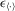 are the transformed variables of x and ε, respectively, under the permutation of y into an ascending order. The
are the transformed variables of x and ε, respectively, under the permutation of y into an ascending order. The  and
and 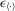 are not necessarily in ascending order, even though
are not necessarily in ascending order, even though 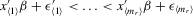 .
. and
and 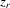 being constants,
being constants, 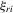 are independent but not identically distributed, so the likelihood function for
are independent but not identically distributed, so the likelihood function for 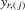 can be complicated. Under normality, the density of
can be complicated. Under normality, the density of 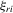 conditional on
conditional on 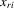 and
and 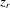 is
is  , where
, where 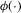 is the standard normal density function. Conditional on
is the standard normal density function. Conditional on 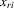 and
and 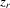 , the joint density of the order statistics
, the joint density of the order statistics  is
is
 (4.3)
(4.3) of
of 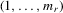 (David, 1981, p. 22). The density function for
(David, 1981, p. 22). The density function for  is
is
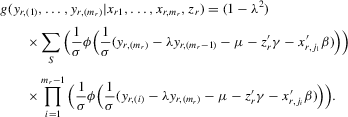 (4.4)
(4.4)Because the possible number of permutations is large in general, the ML approach will be computationally demanding unless the number of players in a game is very small. Furthermore, a parametric ML approach will not be distribution-free. For tractable estimation, we consider an IV approach.
 and
and  are exogenous, important moment restrictions of 4.1 are
are exogenous, important moment restrictions of 4.1 are 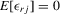 ,
, 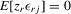 and
and 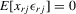 for all
for all 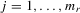 . The number of such IV moments is
. The number of such IV moments is 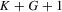 . In order to distinguish possible parameter values from those of the true values that generate the sample observations, a subscript 0 on parameters is added to indicate their true values. Because
. In order to distinguish possible parameter values from those of the true values that generate the sample observations, a subscript 0 on parameters is added to indicate their true values. Because 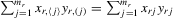 and
and 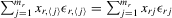 , the model via (4.2) implies that
, the model via (4.2) implies that
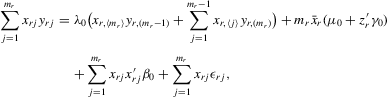 (4.5)
(4.5)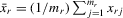 . Because
. Because 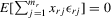 ,
,
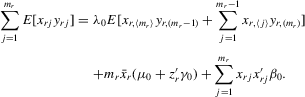 (4.6)
(4.6)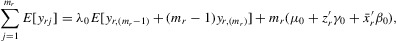 (4.7)
(4.7) (4.8)
(4.8)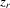 ,
, 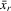 can also have
can also have
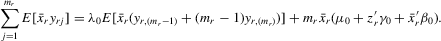 (4.9)
(4.9)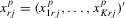 and
and 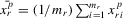 for
for 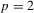 or 3. Then,
or 3. Then, 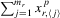
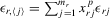 , which has zero mean by mutual independence of x and ε. It follows that
, which has zero mean by mutual independence of x and ε. It follows that 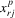 provides a set of valid instruments,
provides a set of valid instruments,
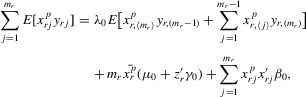 (4.10)
(4.10) does not collapse into any of its lower-order power variables for
does not collapse into any of its lower-order power variables for 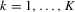 .9
.9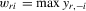 and
and 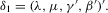 Writing 4.1 in vector form, we have
Writing 4.1 in vector form, we have
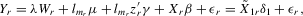 (4.11)
(4.11)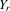 ,
, 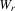 ,
, 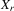 and
and 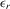 are the corresponding vectors and matrices in the rth group,
are the corresponding vectors and matrices in the rth group,  is the
is the 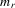 -dimensional vector consisting of ones in its entries,
-dimensional vector consisting of ones in its entries, 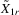 collects all these explanatory variables in a single matrix and δ1 is the complete vector of coefficients. Let
collects all these explanatory variables in a single matrix and δ1 is the complete vector of coefficients. Let 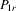 be a generic IV matrix for
be a generic IV matrix for 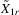 , which satisfies the following assumption.
, which satisfies the following assumption.
Assumption 4.3.The probability limits of 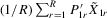 and
and 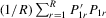 exist and are non-singular. Furthermore,
exist and are non-singular. Furthermore, 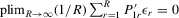 and
and
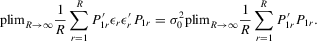
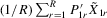 has full rank asymptotically, which is a sufficient condition for the identification of δ1. The IV estimator with
has full rank asymptotically, which is a sufficient condition for the identification of δ1. The IV estimator with 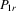 for 4.11 is
for 4.11 is
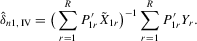 (4.12)
(4.12)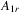 denote a matrix consisting of
denote a matrix consisting of 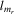 ,
, 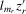 ,
, 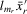 ,
, 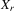 and some powers of
and some powers of 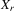 .10 The 2SLS estimator with
.10 The 2SLS estimator with 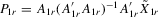 is
is
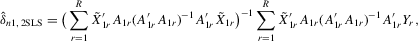 (4.13)
(4.13)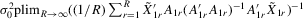 . For the estimation of σ2, the moment
. For the estimation of σ2, the moment 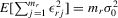 implies that a variance estimator can be
implies that a variance estimator can be
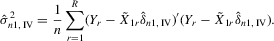 (4.14)
(4.14)4.2. The model with exogenous regressors and group effects
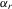
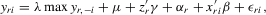 (4.15)
(4.15)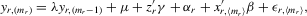 (4.16)
(4.16)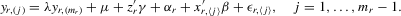
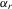 to correlate with
to correlate with 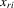 or
or 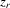 . Hence, it is desirable to treat
. Hence, it is desirable to treat 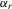 as fixed effects. However, there is a need to eliminate the incidental parameter's problem as R tends to infinity, for which purpose, we consider the deviation from a group mean operation. Denote
as fixed effects. However, there is a need to eliminate the incidental parameter's problem as R tends to infinity, for which purpose, we consider the deviation from a group mean operation. Denote 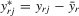 ,
, 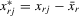 and
and 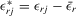 , where
, where 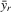 ,
, 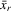 and
and 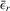 are the corresponding group means. Pre-multiplying 4.16 by the transformation matrix
are the corresponding group means. Pre-multiplying 4.16 by the transformation matrix 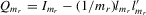 , individual observations are measured as deviations from group means
, individual observations are measured as deviations from group means
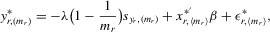 (4.17)
(4.17)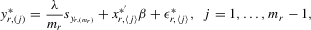
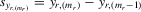 .
.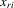 are exogenous, important moments of 4.15 are
are exogenous, important moments of 4.15 are 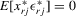 for all
for all 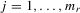 . By multiplying each equation in 4.17 by the corresponding
. By multiplying each equation in 4.17 by the corresponding 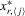 ,
, 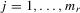 , and taking their summation, the model via 4.17 implies that
, and taking their summation, the model via 4.17 implies that
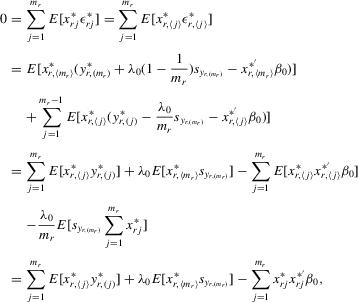
 . Hence,
. Hence,
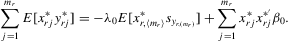 (4.18)
(4.18) on the right-hand side of 4.17. Denote
on the right-hand side of 4.17. Denote 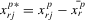 for
for 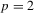 or 3. Because
or 3. Because 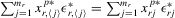 , which has zero mean,
, which has zero mean,
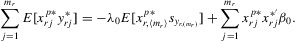 (4.19)
(4.19)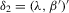 . The within-group equation of 4.15 is
. The within-group equation of 4.15 is
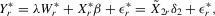 (4.20)
(4.20)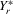 ,
, 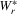 ,
, 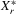 ,
, 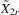 and
and 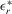 are the corresponding vectors and matrices in the rth group. Let
are the corresponding vectors and matrices in the rth group. Let 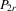 be a generic IV matrix for
be a generic IV matrix for 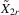 , which satisfies the following assumption.
, which satisfies the following assumption.
Assumption 4.4.The probability limits of 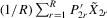 and
and 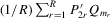
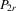 exist and are non-singular. Furthermore,
exist and are non-singular. Furthermore,  and
and
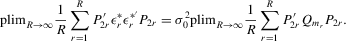
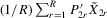 has full rank asymptotically, which is a sufficient condition for the identification of δ2. The IV estimator with
has full rank asymptotically, which is a sufficient condition for the identification of δ2. The IV estimator with 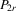 for 4.20 is
for 4.20 is
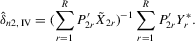 (4.21)
(4.21)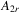 denote a matrix consisting of
denote a matrix consisting of 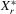 and some of its powers. The 2SLS estimator with
and some of its powers. The 2SLS estimator with 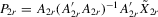 is
is
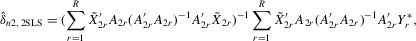 (4.22)
(4.22)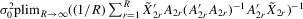 . For the estimation of σ2, the moment
. For the estimation of σ2, the moment  implies that a variance estimator can be
implies that a variance estimator can be
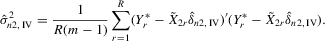 (4.23)
(4.23)5. THE GMM APPROACH
If all the exogenous regressors were irrelevant, the above IV methods would no longer be applicable. In other words, if β0 and γ0 were zero, IV moments alone would not identify the model parameters. Furthermore, it is impossible to test the joint significance of all the exogenous regressors based on those IV estimators. To remedy such a possible but unknown scenario, we suggest a combination of IV moments with some recurrence relations for moments of order statistics. The resulting estimation method is distribution-free. However, when regressors are really relevant, the validity of the recurrence relations would require that the regressors 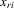 are i.i.d. for all i and r, which is a strong assumption of this estimation strategy for the model.
are i.i.d. for all i and r, which is a strong assumption of this estimation strategy for the model.
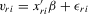 , which has the same ascending order as
, which has the same ascending order as 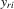 in terms of order statistics. We can eliminate the common group effect of 4.15 by the differencing method, and we obtain the following system
in terms of order statistics. We can eliminate the common group effect of 4.15 by the differencing method, and we obtain the following system
 (5.1)
(5.1)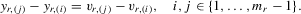 (5.2)
(5.2)Assumption 5.1.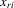 and
and 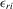 are i.i.d. for all members in a group as well as across groups.
are i.i.d. for all members in a group as well as across groups.
 and
and 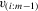 be the ith-order statistics in random samples of size m and
be the ith-order statistics in random samples of size m and 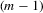 , respectively. We have a useful recurrence relation
, respectively. We have a useful recurrence relation
 (5.3)
(5.3)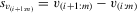 for
for 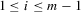 . Equation 5.3 implies
. Equation 5.3 implies
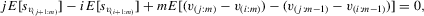 (5.4)
(5.4)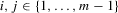 . By taking
. By taking 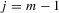 , 5.4 implies that
, 5.4 implies that
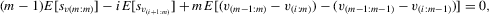 (5.5)
(5.5) . Denote
. Denote 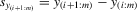 and
and 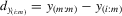 for
for  . For a generic group of size m, the system of equations 5.1 and 5.2 implies that
. For a generic group of size m, the system of equations 5.1 and 5.2 implies that
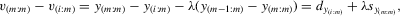 (5.6)
(5.6)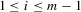 , and
, and
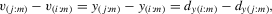 (5.7)
(5.7)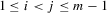 . It follows that
. It follows that 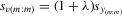 and
and 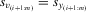 for
for 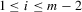 . The corresponding moment in terms of dependent variables of 5.1 and 5.2 is
. The corresponding moment in terms of dependent variables of 5.1 and 5.2 is
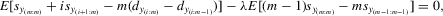 (5.8)
(5.8)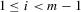 . As in the general GMM estimation framework, let
. As in the general GMM estimation framework, let 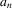 be some weighting matrix such that
be some weighting matrix such that 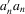 is non-negative definite. The GMM estimator with weights
is non-negative definite. The GMM estimator with weights 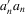 is
is 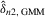 , which minimizes
, which minimizes 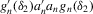 , where
, where 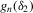 is an empirical moment vector consisting of the recurrence moment 5.8 and the IV moments for the model 4.15. The GMM estimator satisfies the first-order condition
is an empirical moment vector consisting of the recurrence moment 5.8 and the IV moments for the model 4.15. The GMM estimator satisfies the first-order condition

Assumption 5.2.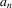 converges in probability to a constant weighting matrix a0 with a rank no less than
converges in probability to a constant weighting matrix a0 with a rank no less than 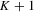 , and
, and 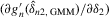 converges in probability to D0 that exists and is finite.
converges in probability to D0 that exists and is finite.
By the generalized Schwartz inequality, the optimal choice of a0 is 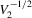 . It follows that the optimal GMM estimator minimizes
. It follows that the optimal GMM estimator minimizes 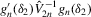 , where
, where 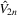 is a consistent estimate of V2 (see Appendix D for details on the Proof of Theorem 5.1).
is a consistent estimate of V2 (see Appendix D for details on the Proof of Theorem 5.1).
6. THE MODEL WITH MIXED MEAN AND MAXIMUM
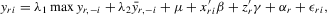 (6.1)
(6.1)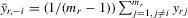 , or, equivalently,
, or, equivalently,
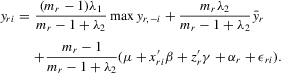 (6.2)
(6.2)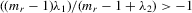 but
but 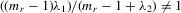 is a well-defined system and has a unique solution. It includes the social interaction with the mean or maximum of peers as a special case. For empirical application, we provide a simple IV estimator under the fixed-effects specification.
is a well-defined system and has a unique solution. It includes the social interaction with the mean or maximum of peers as a special case. For empirical application, we provide a simple IV estimator under the fixed-effects specification.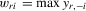 . As
. As  , it implies that
, it implies that 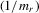
 and
and 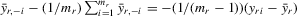 . The within-group equation of 6.1 is
. The within-group equation of 6.1 is
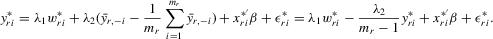
 (6.3)
(6.3)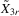 collects all explanatory variables in a single matrix, and
collects all explanatory variables in a single matrix, and 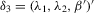 is the corresponding parameter vector. Let
is the corresponding parameter vector. Let 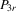 be a generic IV matrix for
be a generic IV matrix for 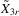 , which satisfies the following assumptions.
, which satisfies the following assumptions.
Assumption 6.1.Assume that 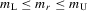 for all r where the lower bound
for all r where the lower bound  and the upper bound mU are finite. Furthermore, either
and the upper bound mU are finite. Furthermore, either  or there are sufficient number of groups with
or there are sufficient number of groups with 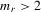 .
.
Assumption 6.2.The probability limits of 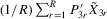 and
and 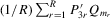
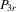 exist and are non-singular. Furthermore,
exist and are non-singular. Furthermore, 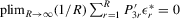 and
and
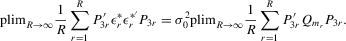
7. MONTE CARLO RESULTS
We randomly draw 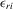 from the standardized χ2(5) distribution to investigate finite sample properties of distribution-free estimators under this non-normal distribution. The two regressors
from the standardized χ2(5) distribution to investigate finite sample properties of distribution-free estimators under this non-normal distribution. The two regressors 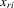 and
and 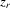 are i.i.d. N(0, 1) for all r and i, and are independent of
are i.i.d. N(0, 1) for all r and i, and are independent of  . The group effect
. The group effect 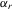 is generated as
is generated as 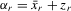 . The true parameters are
. The true parameters are 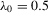 ,
, 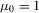 ,
, 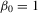 and
and 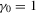 . We allow group sizes to vary from three to five. We design the same number of groups for each group size. The average group size is four by design. In the simulation, we experiment with different numbers of groups R from 60 to 1920. The number of Monte Carlo repetitions is 300.
. We allow group sizes to vary from three to five. We design the same number of groups for each group size. The average group size is four by design. In the simulation, we experiment with different numbers of groups R from 60 to 1920. The number of Monte Carlo repetitions is 300.
We try two different IV estimators. IV1 uses the group average 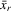 of 4.9 as instruments, and IV2 uses
of 4.9 as instruments, and IV2 uses 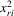 and
and 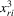 of 4.10 in the first model. Because
of 4.10 in the first model. Because 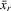 is invariant within the group, only IV2 is relevant to the second model. We also consider the GMM and the two-step procedure (TSP). The GMM uses IV1 and recurrence relation 5.3 for the first model, and uses IV2 and 5.8 for the second model. For computational simplicity, we use the identity matrix as a weighting matrix in a GMM objective function.11 The TSP uses the moments of 5.3 or 5.8 to estimate λ in the first step, and then regresses fitted residuals on exogenous variables to estimate their coefficients by the ordinary least-squares method in the second step.
is invariant within the group, only IV2 is relevant to the second model. We also consider the GMM and the two-step procedure (TSP). The GMM uses IV1 and recurrence relation 5.3 for the first model, and uses IV2 and 5.8 for the second model. For computational simplicity, we use the identity matrix as a weighting matrix in a GMM objective function.11 The TSP uses the moments of 5.3 or 5.8 to estimate λ in the first step, and then regresses fitted residuals on exogenous variables to estimate their coefficients by the ordinary least-squares method in the second step.
Table 1 presents the bias (Bias) and standard deviation (SD) of IV1, IV2, GMM and TSP estimates of Model 1. The IV1 and IV2 estimates of λ are unbiased for all R. The GMM estimate of λ is biased upward when  or 120, and this bias decreases as R increases. The TSP estimate of λ has a large upward or downward bias when
or 120, and this bias decreases as R increases. The TSP estimate of λ has a large upward or downward bias when  or 120, but this bias decreases sharply when
or 120, but this bias decreases sharply when 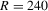 or more. All the estimates of λ have smaller SDs as R increases. The IV1 estimate of λ has much smaller SDs than those of the other estimates. The IV2 estimate of λ has larger SDs than those of the GMM estimates for all R, and has smaller SDs than that of the TSP estimate when
or more. All the estimates of λ have smaller SDs as R increases. The IV1 estimate of λ has much smaller SDs than those of the other estimates. The IV2 estimate of λ has larger SDs than those of the GMM estimates for all R, and has smaller SDs than that of the TSP estimate when 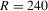 or less. However, it has larger SDs than that of the TSP estimate when
or less. However, it has larger SDs than that of the TSP estimate when 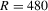 or more. These estimates of β, γ, μ and σ have similar properties in bias and standard deviation. Table 2 presents finite sample results of IV2, GMM and TSP estimates of Model 2. The IV2 estimate of λ is unbiased for all R. The GMM estimate of λ is biased downward when
or more. These estimates of β, γ, μ and σ have similar properties in bias and standard deviation. Table 2 presents finite sample results of IV2, GMM and TSP estimates of Model 2. The IV2 estimate of λ is unbiased for all R. The GMM estimate of λ is biased downward when 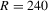 or less, and this bias decreases as R increases. The TSP estimate of λ has large upward bias when
or less, and this bias decreases as R increases. The TSP estimate of λ has large upward bias when  or 120, but this bias decreases sharply when
or 120, but this bias decreases sharply when 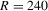 or more. The GMM estimate of λ has smaller SDs than those of the IV2 and TSP estimates. These estimates of β and σ have similar properties in bias and standard deviation.
or more. The GMM estimate of λ has smaller SDs than those of the IV2 and TSP estimates. These estimates of β and σ have similar properties in bias and standard deviation.
| R | IV1 | IV2 | GMM | TSP | R | IV1 | IV2 | GMM | TSP | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| λ | Bias | 60 | −0.0040 | 0.0737 | 0.1958 | 0.8023 | 480 | −0.0004 | 0.0026 | 0.0484 | −0.0421 |
| SD | 0.0743 | 0.9290 | 0.2477 | 11.1507 | 0.0227 | 0.2368 | 0.1325 | 0.2097 | |||
| β | Bias | −0.0065 | −0.0373 | −0.0856 | −0.2203 | 0.0005 | −0.0017 | −0.0217 | 0.0142 | ||
| SD | 0.0687 | 0.2474 | 0.1403 | 3.2108 | 0.0235 | 0.0807 | 0.0650 | 0.0750 | |||
| γ | Bias | 0.0048 | −0.1467 | −0.3810 | −1.7597 | 0.0012 | −0.0039 | −0.0981 | 0.0804 | ||
| SD | 0.1669 | 1.8454 | 0.4833 | 24.1389 | 0.0519 | 0.4807 | 0.2612 | 0.4082 | |||
| μ | Bias | −0.0013 | 0.0097 | −0.0185 | 0.0289 | 0.0014 | 0.0024 | −0.0030 | −0.0011 | ||
| SD | 0.0659 | 0.1450 | 0.0978 | 1.4228 | 0.0236 | 0.0274 | 0.0250 | 0.0318 | |||
| σ | Bias | 0.0075 | 0.3261 | 0.0727 | 2.1491 | 0.0012 | 0.0588 | 0.0117 | 0.0516 | ||
| SD | 0.0701 | 1.0161 | 0.1516 | 15.5359 | 0.0247 | 0.1256 | 0.0567 | 0.1660 | |||
| λ | Bias | 120 | 0.0013 | 0.0129 | 0.1451 | −0.2968 | 960 | −0.0013 | −0.0122 | 0.0273 | −0.0138 |
| SD | 0.0464 | 0.5421 | 0.2495 | 3.3297 | 0.0181 | 0.1603 | 0.0890 | 0.1065 | |||
| β | Bias | −0.0020 | −0.0051 | −0.0609 | 0.1065 | −0.0002 | 0.0033 | −0.0135 | 0.0037 | ||
| SD | 0.0502 | 0.1934 | 0.1261 | 1.1990 | 0.0170 | 0.0548 | 0.0438 | 0.0402 | |||
| γ | Bias | 0.0014 | −0.0296 | −0.2809 | 0.6019 | 0.0028 | 0.0239 | −0.0549 | 0.0272 | ||
| SD | 0.1028 | 1.0825 | 0.4884 | 6.8572 | 0.0414 | 0.3201 | 0.1803 | 0.2147 | |||
| μ | Bias | −0.0030 | −0.0027 | −0.0218 | 0.0182 | −0.0001 | 0.0003 | −0.0025 | −0.0003 | ||
| SD | 0.0441 | 0.0812 | 0.0624 | 0.2489 | 0.0176 | 0.0188 | 0.0190 | 0.0187 | |||
| σ | Bias | 0.0007 | 0.2169 | 0.0541 | 0.9507 | 0.0003 | 0.0313 | 0.0034 | 0.0155 | ||
| SD | 0.0515 | 0.4537 | 0.1307 | 5.2488 | 0.0187 | 0.0692 | 0.0300 | 0.0535 | |||
| λ | Bias | 240 | −0.0025 | −0.0043 | 0.0863 | −0.0016 | 1920 | −0.0014 | 0.0008 | 0.0085 | −0.0141 |
| SD | 0.0349 | 0.4986 | 0.1721 | 1.7710 | 0.0124 | 0.1097 | 0.0638 | 0.0722 | |||
| β | Bias | 0.0016 | −0.0021 | −0.0360 | 0.0045 | 0.0013 | 0.0003 | −0.0032 | 0.0054 | ||
| SD | 0.0354 | 0.1546 | 0.0835 | 0.5087 | 0.0122 | 0.0376 | 0.0310 | 0.0266 | |||
| γ | Bias | 0.0051 | 0.0085 | −0.1759 | 0.0102 | 0.0018 | −0.0029 | −0.0188 | 0.0262 | ||
| SD | 0.0792 | 1.0067 | 0.3481 | 3.3791 | 0.0287 | 0.2190 | 0.1253 | 0.1424 | |||
| μ | Bias | −0.0037 | −0.0048 | −0.0091 | −0.0056 | −0.0004 | −0.0001 | −0.0010 | −0.0006 | ||
| SD | 0.0345 | 0.0557 | 0.0363 | 0.1201 | 0.0121 | 0.0128 | 0.0125 | 0.0125 | |||
| σ | Bias | −0.0009 | 0.1600 | 0.0200 | 0.3584 | 0.0003 | 0.0137 | 0.0026 | 0.0094 | ||
| SD | 0.0340 | 0.4625 | 0.0676 | 2.5571 | 0.0126 | 0.0369 | 0.0221 | 0.0270 |
| R | IV2 | GMM | TSP | R | IV2 | GMM | TSP | ||
|---|---|---|---|---|---|---|---|---|---|
| λ | Bias | 60 | 0.0282 | −0.2355 | 4.2695 | 480 | 0.0068 | −0.0457 | 0.0188 |
| SD | 0.9543 | 0.5486 | 71.3090 | 0.2629 | 0.2407 | 0.2746 | |||
| β | Bias | −0.0073 | −0.0661 | 1.1213 | 0.0014 | −0.0122 | 0.0041 | ||
| SD | 0.2071 | 0.1582 | 19.1270 | 0.0640 | 0.0646 | 0.0661 | |||
| σ | Bias | 0.0403 | 0.0106 | 1.5919 | 0.0046 | −0.0038 | 0.0061 | ||
| SD | 0.1949 | 0.0966 | 23.2660 | 0.0467 | 0.0461 | 0.0529 | |||
| λ | Bias | 120 | 0.0279 | −0.1006 | 0.2327 | 960 | 0.0119 | −0.0073 | 0.0239 |
| SD | 0.6435 | 0.4291 | 1.3350 | 0.1861 | 0.1848 | 0.1962 | |||
| β | Bias | −0.0006 | −0.0308 | 0.0465 | 0.0021 | −0.0006 | 0.0051 | ||
| SD | 0.1453 | 0.1235 | 0.2943 | 0.0443 | 0.0508 | 0.0484 | |||
| σ | Bias | 0.0183 | −0.0067 | 0.0591 | 0.0030 | 0.0001 | 0.0048 | ||
| SD | 0.1193 | 0.0793 | 0.3586 | 0.0355 | 0.0342 | 0.0364 | |||
| λ | Bias | 240 | 0.0000 | −0.1326 | 0.0057 | 1920 | 0.0006 | −0.0141 | 0.0017 |
| SD | 0.3751 | 0.3166 | 0.4717 | 0.1394 | 0.1320 | 0.1426 | |||
| β | Bias | 0.0002 | −0.0324 | 0.0024 | 0.0014 | −0.0021 | 0.0018 | ||
| SD | 0.0894 | 0.0867 | 0.1090 | 0.0330 | 0.0352 | 0.0356 | |||
| σ | Bias | 0.0049 | −0.0156 | 0.0074 | 0.0008 | −0.0016 | 0.0008 | ||
| SD | 0.0671 | 0.0560 | 0.0948 | 0.0242 | 0.0231 | 0.0248 |
If exogenous regressors are irrelevant to the model, the IV method is inconsistent. However, GMM and TSP, which use recurrence relations for moments of order statistics, remain valid. For illustration, we present finite sample results of the IV, GMM and TSP estimates of the models when β0 and γ0 are zero. The IV1 estimate of λ has significant upward or downward bias for all R in Table 3, and the IV2 estimate of λ has significant downward bias for all R in Table 4. In contrast, the GMM and TSP estimates of λ have smaller biases and these biases decrease as the number of groups increases.
| R | IV1 | GMM | TSP | R | IV1 | GMM | TSP | ||
|---|---|---|---|---|---|---|---|---|---|
| λ | Bias | 60 | 1.1676 | 0.0801 | −0.1009 | 480 | −1.67 × 102 | 0.0190 | −0.0041 |
| SD | 11.0140 | 0.2450 | 0.7187 | 2.82 × 103 | 0.0819 | 0.0938 | |||
| β | Bias | −0.0004 | −0.0026 | −0.0055 | −2.31 × 10−2 | 0.0010 | 0.0008 | ||
| SD | 0.1408 | 0.0826 | 0.0733 | 3.03 × 10−1 | 0.0232 | 0.0225 | |||
| γ | Bias | −0.0860 | −0.0021 | −0.0018 | 6.20 × 100 | 0.0004 | 0.0000 | ||
| SD | 1.0608 | 0.0797 | 0.0845 | 1.06 × 102 | 0.0224 | 0.0223 | |||
| μ | Bias | −0.7194 | −0.0583 | 0.0660 | 1.13 × 102 | −0.0129 | 0.0037 | ||
| SD | 6.5073 | 0.1760 | 0.4654 | 1.92 × 103 | 0.0602 | 0.0664 | |||
| σ | Bias | 1.5278 | 0.0073 | 0.0917 | 1.38 × 102 | −0.0011 | 0.0040 | ||
| SD | 8.2338 | 0.0877 | 0.3772 | 2.33 × 103 | 0.0314 | 0.0330 | |||
| λ | Bias | 120 | 17.5350 | 0.0367 | −0.0860 | 960 | −0.8384 | 0.0071 | −0.0056 |
| SD | 225.1000 | 0.1828 | 0.3066 | 65.9200 | 0.0571 | 0.0665 | |||
| β | Bias | −0.2452 | 0.0047 | −0.0007 | 0.0037 | −0.0007 | −0.0005 | ||
| SD | 3.5708 | 0.0774 | 0.0492 | 0.0868 | 0.0157 | 0.0158 | |||
| γ | Bias | 0.3809 | 0.0099 | 0.0035 | 0.2426 | 0.0001 | 0.0002 | ||
| SD | 9.5496 | 0.0782 | 0.0508 | 3.1064 | 0.0169 | 0.0167 | |||
| μ | Bias | −12.7630 | −0.0318 | 0.0523 | 0.5270 | −0.0054 | 0.0038 | ||
| SD | 165.9500 | 0.1275 | 0.2043 | 43.4560 | 0.0424 | 0.0497 | |||
| σ | Bias | 16.3410 | 0.0053 | 0.0374 | 6.3651 | −0.0007 | 0.0022 | ||
| SD | 178.1700 | 0.0731 | 0.1335 | 55.7460 | 0.0218 | 0.0241 | |||
| λ | Bias | 240 | 0.6479 | 0.0365 | −0.0171 | 1920 | 0.7953 | 0.0068 | 0.0007 |
| SD | 11.7950 | 0.1213 | 0.1576 | 6.8995 | 0.0402 | 0.0472 | |||
| β | Bias | 0.0113 | 0.0020 | 0.0013 | 0.0017 | 0.0009 | 0.0009 | ||
| SD | 0.0927 | 0.0330 | 0.0332 | 0.0192 | 0.0114 | 0.0113 | |||
| γ | Bias | −0.0418 | 0.0004 | 0.0002 | −0.0002 | −0.0014 | −0.0013 | ||
| SD | 0.4317 | 0.0348 | 0.0369 | 0.1063 | 0.0115 | 0.0113 | |||
| μ | Bias | −0.4100 | −0.0298 | 0.0084 | −0.5260 | −0.0052 | −0.0008 | ||
| SD | 8.2165 | 0.0865 | 0.1098 | 4.5290 | 0.0295 | 0.0345 | |||
| σ | Bias | 1.6218 | −0.0052 | 0.0079 | 1.3726 | −0.0011 | 0.0003 | ||
| SD | 9.5404 | 0.0398 | 0.0536 | 5.4796 | 0.0146 | 0.0158 |
| R | IV2 | GMM | TSP | R | IV2 | GMM | TSP | ||
|---|---|---|---|---|---|---|---|---|---|
| λ | Bias | 60 | −2.7994 | −0.2025 | 0.2221 | 480 | −2.3605 | −0.0198 | 0.0133 |
| SD | 11.1320 | 0.5884 | 1.1072 | 5.2979 | 0.2540 | 0.2783 | |||
| β | Bias | 0.0024 | −0.0033 | −0.0050 | 0.0014 | 0.0000 | 0.0007 | ||
| SD | 0.1454 | 0.0972 | 0.0791 | 0.0371 | 0.0317 | 0.0256 | |||
| σ | Bias | 0.3681 | −0.0106 | 0.0422 | 0.0732 | −0.0010 | 0.0026 | ||
| SD | 1.6721 | 0.0926 | 0.1724 | 0.6112 | 0.0428 | 0.0444 | |||
| λ | Bias | 120 | −2.0023 | −0.0949 | 0.1380 | 960 | −2.6978 | −0.0080 | 0.0126 |
| SD | 6.6691 | 0.4514 | 0.6714 | 4.7140 | 0.1734 | 0.1889 | |||
| β | Bias | 0.0001 | −0.0052 | −0.0026 | −0.0019 | 0.0017 | 0.0002 | ||
| SD | 0.0728 | 0.0664 | 0.0554 | 0.0235 | 0.0237 | 0.0189 | |||
| σ | Bias | 0.1047 | −0.0092 | 0.0189 | 0.0297 | −0.0007 | 0.0016 | ||
| SD | 0.9480 | 0.0743 | 0.1002 | 0.5201 | 0.0289 | 0.0305 | |||
| λ | Bias | 240 | −2.5636 | −0.0647 | 0.0074 | 1920 | −1.4783 | −0.0102 | −0.0022 |
| SD | 6.2293 | 0.3319 | 0.3822 | 10.8100 | 0.1250 | 0.1332 | |||
| β | Bias | 0.0012 | 0.0026 | 0.0023 | −0.0011 | 0.0017 | 0.0016 | ||
| SD | 0.0597 | 0.0467 | 0.0391 | 0.0278 | 0.0165 | 0.0135 | |||
| σ | Bias | 0.0767 | −0.0070 | 0.0007 | 0.2684 | −0.0011 | −0.0002 | ||
| SD | 0.8438 | 0.0521 | 0.0573 | 1.7928 | 0.0199 | 0.0208 |
8. AN EMPIRICAL EXAMPLE
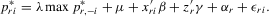 (8.1)
(8.1)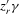 and
and 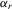 capture observed and unobserved common group factors (e.g. coach effects), respectively, which are eliminated by the covariance transformation in our fixed-effects estimation framework. As a comparison, we estimate the group interaction model with the mean specification as well as the generalized model 6.1.
capture observed and unobserved common group factors (e.g. coach effects), respectively, which are eliminated by the covariance transformation in our fixed-effects estimation framework. As a comparison, we estimate the group interaction model with the mean specification as well as the generalized model 6.1.There are over 10,000 men's basketball players competing in three divisions at about 1,000 colleges and universities within the NCAA. Division I (D-I) has the most prestigious basketball programmes, which have the greatest financial resources and attract the most athletically talented students. We collect men's basketball player statistics of D-I teams during the period 2005–2010 from web sites including ncaa.org, espn.com and statsheet.com. The total number of teams (groups) is 1,673 in the five seasons.12 The total number of observations is 22,122. The average team size is 13, with a minimum of eight and a maximum of 20.
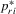 ) as the dependent variables of our regression models. There are five
) as the dependent variables of our regression models. There are five 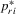 measures that are different combinations of points, assists, rebounds, blocks and steals. Estimated results of each of these are reported separately in Tables 6–10. Specifically, we have the following measures for the dependent variable
measures that are different combinations of points, assists, rebounds, blocks and steals. Estimated results of each of these are reported separately in Tables 6–10. Specifically, we have the following measures for the dependent variable 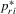 for a player:
for a player:
- the dependent variable in Table 6 is the points per game of a player;
- the dependent variable in Table 7 is the sum of points and assists per game;
- the dependent variable in Table 8 is the sum of points, assists and rebounds per game;
- the dependent variable in Table 9 is the sum of points, assists, rebounds, and steals per game;
- the dependent variable in Table 10 is the sum of points, assists, rebounds, steals and blocks per game.
| Variable | Obs. | Mean | SD | Min | Max |
|---|---|---|---|---|---|
| Points per game | 22,122 | 5.71 | 4.90 | 0.00 | 28.65 |
| Assists per game | 22,122 | 1.10 | 1.17 | 0.00 | 11.69 |
| Rebounds per game | 22,122 | 2.65 | 2.06 | 0.00 | 14.80 |
| Steals per game | 22,122 | 0.57 | 0.50 | 0.00 | 4.77 |
| Blocks per game | 22,122 | 0.28 | 0.43 | 0.00 | 6.53 |
| Height (inches) | 22,122 | 76.69 | 3.58 | 63.00 | 91.00 |
| Weight (pounds) | 22,122 | 203.76 | 26.27 | 80.00 | 380.00 |
| Minutes per game | 22,122 | 17.02 | 10.51 | 0.30 | 40.00 |
| Freshman | 22,122 | 0.32 | 0.47 | 0.00 | 1.00 |
| Sophomore | 22,122 | 0.26 | 0.44 | 0.00 | 1.00 |
| Junior | 22,122 | 0.23 | 0.42 | 0.00 | 1.00 |
| Senior | 22,122 | 0.19 | 0.39 | 0.00 | 1.00 |
| IV | IV | IV | IV | GMM | |
|---|---|---|---|---|---|
| Regressor | (1) | (2) | (3) | (4) | (5) |
| Best performance of peers | −1.359** | −1.253** | −1.355** | ||
| (0.218) | (0.220) | (0.217) | |||
| Average performance of peers | −2.173** | −0.884 | |||
| (0.477) | (0.556) | ||||
| Height | 0.012** | 0.015** | 0.010** | 0.015** | 0.015** |
| (0.007) | (0.006) | (0.006) | (0.005) | (0.006) | |
| Weight | 0.047** | 0.045** | 0.038** | 0.042** | 0.045** |
| (0.001) | (0.008) | (0.008) | (0.007) | (0.008) | |
| Minutes per game | 4.379** | 3.729** | 3.594** | 3.460** | 3.731** |
| (0.038) | (0.109) | (0.199) | (0.186) | (0.109) |
Note
- Number of observations is 22,122. Individual coefficients are statistically significant at the
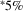 or
or 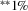 levels. Standard errors are given in parentheses under coefficients.
levels. Standard errors are given in parentheses under coefficients.
| IV | IV | IV | IV | GMM | |
|---|---|---|---|---|---|
| Regressor | (1) | (2) | (3) | (4) | (5) |
| Best performance of peers | −1.057** | −0.948** | −1.056** | ||
| (0.139) | (0.1318) | (0.139) | |||
| Average performance of peers | −2.173** | −1.241** | |||
| (0.477) | (0.413) | ||||
| Height | −0.094** | −0.073** | −0.078** | −0.065** | −0.073** |
| (0.007) | (0.006) | (0.007) | (0.006) | (0.006) | |
| Weight | 0.027** | 0.032** | 0.022** | 0.029** | 0.032** |
| (0.010) | (0.008) | (0.008) | (0.007) | (0.008) | |
| Minutes per game | 5.176** | 4.611** | 4.355** | 4.141** | 4.612** |
| (0.038) | (0.081) | (0.199) | (0.170) | (0.080) |
Note
- Number of observations is 22,122. Individual coefficients are statistically significant at the
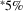 or
or  levels. Standard errors are given in parentheses under coefficients.
levels. Standard errors are given in parentheses under coefficients.
| IV | IV | IV | IV | GMM | |
|---|---|---|---|---|---|
| Regressor | (1) | (2) | (3) | (4) | (5) |
| Best performance of peers | −1.174** | −1.092** | −1.169** | ||
| (0.205) | (0.212) | (0.204) | |||
| Average performance of peers | −1.983** | −0.766 | |||
| (0.477) | (0.458) | ||||
| Height | 0.053** | 0.047** | 0.046** | 0.045** | 0.047** |
| (0.008) | (0.007) | (0.007) | (0.006) | (0.007) | |
| Weight | 0.161** | 0.138** | 0.135** | 0.130** | 0.139** |
| (0.011) | (0.010) | (0.011) | (0.010) | (0.010) | |
| Minutes per game | 6.714** | 6.017** | 5.619** | 5.642** | 6.020** |
| (0.044) | (0.127) | (0.236) | (0.218) | (0.127) |
Note
- Number of observations is 22,122. Individual coefficients are statistically significant at the
 or
or  levels. Standard errors are given in parentheses under coefficients.
levels. Standard errors are given in parentheses under coefficients.
| IV | IV | IV | IV | GMM | |
|---|---|---|---|---|---|
| Regressor | (1) | (2) | (3) | (4) | (5) |
| Best performance of peers | −1.131** | −1.067** | −1.126** | ||
| (0.204) | (0.214) | (0.204) | |||
| Average performance of peers | −1.777** | −0.579 | |||
| (0.425) | (0.462) | ||||
| Height | 0.031** | 0.030** | 0.028** | 0.029** | 0.030** |
| (0.008) | (0.007) | (0.007) | (0.007) | (0.007) | |
| Weight | 0.152** | 0.132** | 0.129** | 0.126** | 0.133** |
| (0.011) | (0.010) | (0.011) | (0.010) | (0.010) | |
| Minutes per game | 7.086** | 6.391** | 6.045** | 6.093** | 6.393** |
| (0.046) | (0.131) | (0.252) | (0.232) | (0.131) |
Note
- Number of observations is 22,122. Individual coefficients are statistically significant at the
 or
or  levels. Standard errors are given in parentheses under coefficients.
levels. Standard errors are given in parentheses under coefficients.
| IV | IV | IV | IV | GMM | |
|---|---|---|---|---|---|
| Regressor | (1) | (2) | (3) | (4) | (5) |
| Best performance of peers | −1.121** | −1.051** | −1.118** | ||
| (0.205) | (0.211) | (0.204) | |||
| Average performance of peers | −1.814** | −0.698 | |||
| (0.426) | (0.456) | ||||
| Height | 0.090** | 0.080** | 0.078** | 0.076** | 0.081** |
| (0.009) | (0.007) | (0.008) | (0.007) | (0.007) | |
| Weight | 0.155** | 0.133** | 0.132** | 0.125** | 0.133** |
| (0.012) | (0.010) | (0.011) | (0.010) | (0.010) | |
| Minutes per game | 7.233** | 6.534** | 6.154** | 6.673** | 6.536** |
| (0.047) | (0.134) | (0.258) | (0.119) | (0.133) |
Note
- Number of observations is 22,122. Individual coefficients are statistically significant at the
 or
or  levels. Standard errors are given in parentheses under coefficients.
levels. Standard errors are given in parentheses under coefficients.
The explanatory variables  for each of the Tables 6–10 are the same, and include height, weight and minutes per game. Height gives a major advantage in professional basketball, because taller players generally achieve more rebounds, block more shots and make more dunks than shorter players. Weight might also give a college player some advantages, because strength is an important factor in many aspects of the game. Both height and weight will have a positive effect on a player's performance. Minutes per game is defined as the total minutes played in one season divided by the number of games played, and this is expected to have a positive coefficient. For reasons of scale, we divide weight and minutes per game by ten in the actual regressions.
for each of the Tables 6–10 are the same, and include height, weight and minutes per game. Height gives a major advantage in professional basketball, because taller players generally achieve more rebounds, block more shots and make more dunks than shorter players. Weight might also give a college player some advantages, because strength is an important factor in many aspects of the game. Both height and weight will have a positive effect on a player's performance. Minutes per game is defined as the total minutes played in one season divided by the number of games played, and this is expected to have a positive coefficient. For reasons of scale, we divide weight and minutes per game by ten in the actual regressions.
Tables 6–10 report the regression estimates under the fixed-effects specification. Column (1) presents the within-group IV estimates of 6.1, for which there are no endogenous interaction regressors. We find that the coefficients of these regressors (i.e. the elements of the vector 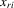 discussed above) are statistically significant. Physical characteristics (with an exception in Table 7) have positive estimates, which indicate that taller and stronger athletes play better basketball. Table 7 uses the sum of points and assists as the performance measure, and finds that height has a negative effect. The point guard is one of the most important positions on a basketball team, and players at this position are shorter and are awarded more assists, which might explain the unexpected sign of height. Minutes per game is potentially endogenous because coaches generally give better players more time on the court. Hence, we use the years of college education (freshman, sophomore and junior) as the instruments for this endogenous regressor, and the IV estimates are statistically significant and positive.
discussed above) are statistically significant. Physical characteristics (with an exception in Table 7) have positive estimates, which indicate that taller and stronger athletes play better basketball. Table 7 uses the sum of points and assists as the performance measure, and finds that height has a negative effect. The point guard is one of the most important positions on a basketball team, and players at this position are shorter and are awarded more assists, which might explain the unexpected sign of height. Minutes per game is potentially endogenous because coaches generally give better players more time on the court. Hence, we use the years of college education (freshman, sophomore and junior) as the instruments for this endogenous regressor, and the IV estimates are statistically significant and positive.
Because interaction regressors are endogenous, we use the instruments proposed in Section 4.2 for the best performance of peers and the instruments proposed by Lee (2007) for the average performance of peers. Columns (2) and (3) show that the interaction regressor has a negative and statistically significant effect in the respective model.14 Column (4) shows that both interaction regressors remain negative in the generalized model 6.1. The best performance of peers is statistically significant, whereas the average performance of peers is statistically insignificant, except for the case that uses the sum of points and assists as a performance measure. Column (5) presents the GMM estimates of the model 8.1, which are similar to the IV estimates.15 We conclude that a college basketball player reacts negatively and statistically significantly to the best performance of his teammates, which suggests that there exist important competition effects among basketball players in an NCAA D-I team.
9. CONCLUSION
In this paper, we introduce a social interaction econometric model with an extreme order statistic, which differs from conventional social interaction models in that an individual's outcome is affected by the extreme outcome of peers. Our model represents one of the possible extensions to allow non-linearity in modelling endogenous social peer effects.
We show that the social interaction model with an extreme order statistic is a well-defined system of equations. The solution to the system exists and can be unique. We provide a simple IV method for model estimation if exogenous regressors are relevant. A distribution-free method that uses recurrence relations is applicable, even when regressors might be irrelevant. It should be noted that ML estimation would be infeasible for the model including exogenous regressors (unless the number of players is very small), even if one were willing to make a distributional assumption of the disturbances, because the likelihood function of order statistics for independent but not identically distributed variates is rather complicated.
We apply the social interaction models with peer's maximum, peer's average and a mixed specification to the NCAA D-I men's basketball data. We find that a college player performs negatively and statistically significantly in response to the best performance of his peers, which suggests the existence of competition effects in the basketball game. For future research, we can apply this model to explore the possible ‘bad apple’ effect in an empirical study of education. We can also consider a model with reaction to certain quantiles of the outcome distribution.
ACKNOWLEDGEMENTS
We thank two referees and the co-editor, Jaap Abbring, for their valuable comments and suggestions, which have improved the presentation of this paper.
 with a unique solution, there would be some technical difficulty for the MLE method because the parameter space of λ is not a connected set due to the need to rule out
with a unique solution, there would be some technical difficulty for the MLE method because the parameter space of λ is not a connected set due to the need to rule out 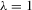 . When the parameter space is not connected, the use of the mean value theorem for analysis of asymptotic distribution of the ML estimator might not be justifiable. Furthermore, the determinant of the Jacobian transformation
. When the parameter space is not connected, the use of the mean value theorem for analysis of asymptotic distribution of the ML estimator might not be justifiable. Furthermore, the determinant of the Jacobian transformation 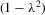 would have its sign changed. All of the above would have created technical difficulties for estimation using the ML method. So, for the ML estimation method, it would be desirable to limit attention to the stable model with the restriction
would have its sign changed. All of the above would have created technical difficulties for estimation using the ML method. So, for the ML estimation method, it would be desirable to limit attention to the stable model with the restriction  . However, because there is no specific constraint imposed on λ, the IV or 2SLS methods do not have such technical difficulties. We are grateful to a referee who has directed our attention to the tractability of the IV and 2SLS methods for the estimation of the structural equation.
. However, because there is no specific constraint imposed on λ, the IV or 2SLS methods do not have such technical difficulties. We are grateful to a referee who has directed our attention to the tractability of the IV and 2SLS methods for the estimation of the structural equation. , which could be a restrictive assumption. If necessary, we might extend the model with its parameters to depend on its group size as additional interactive components.
, which could be a restrictive assumption. If necessary, we might extend the model with its parameters to depend on its group size as additional interactive components.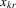 is a dichotomous variable, then its power is the same as
is a dichotomous variable, then its power is the same as 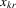 itself.
itself.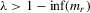 for
for 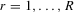 (Lee, 2007). In our case,
(Lee, 2007). In our case, 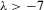 , because the minimum size is 8.
, because the minimum size is 8. are continuously distributed, the probability that
are continuously distributed, the probability that 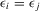 for
for 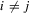 is zero. Hence, it is appropriate to assume that
is zero. Hence, it is appropriate to assume that  are distinct.
are distinct.APPENDIX A: NOTATION LIST AND MOMENTS OF ORDERED NORMAL VARIABLES
Table A.1 summarizes some frequently used notations in the text.
| Notation | Description |
|---|---|
| R | total number of groups |
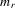 |
member size of the rth group |
| n | total number of observations |
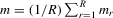 |
empirical mean of group size |
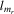 |
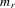 -dimensional column vector of ones -dimensional column vector of ones |
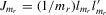 |
orthogonal projector to the linear space spanned by the vector 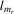 |
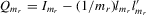 |
covariance transformation matrix |
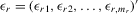 |
column vector of disturbances in the rth group |
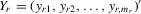 |
column vector of dependent variables in the rth group |
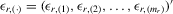 |
column vector of order statistics of 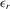 in ascending order in ascending order |
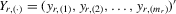 |
column vector of order statistics of 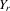 in ascending order in ascending order |
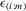 |
ith-order statistic of ε in a group of size m |
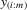 |
ith-order statistic of y in a group of size m |
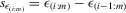 |
spacing statistic between 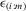 and and 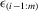 |
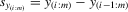 |
spacing statistic between 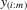 and and 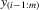 |
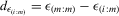 |
difference between largest and ith-order statistics of ε |
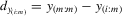 |
difference between largest and ith-order statistics of y |
The following properties for normal-order statistics are useful.
Lemma A.1.Suppose that  are i.i.d. N(0, 1). Let the corresponding
are i.i.d. N(0, 1). Let the corresponding 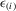 be order statistics of standard normal variables in the ascending order. Then, (a)
be order statistics of standard normal variables in the ascending order. Then, (a) 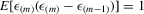 , and (b)
, and (b) 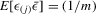 , where
, where  is the sample mean of
is the sample mean of  .
.
The first result is a special case of the recurrence relation for the standard normal distribution (Balakrishnan and Sultan, 1998, p. 174).
Lemma A.2.Let 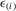 denote order statistics of standard normal variables of a random sample with size m in the ascending order. Then, (a)
denote order statistics of standard normal variables of a random sample with size m in the ascending order. Then, (a) 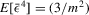 ; (b)
; (b) 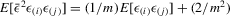 for
for 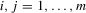 ; (c)
; (c) 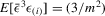 for
for 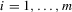 ; (d)
; (d) 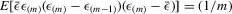 ; (e)
; (e) 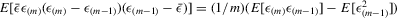 ; (f)
; (f) 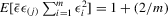 for
for 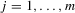 ; (g)
; (g) 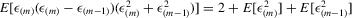 ; (h)
; (h) 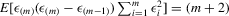 .
.
The property that 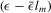 is independent of
is independent of  under normality is useful for the preceding properties. In addition, the technique of the integration by parts can be used to derive some of the above results. Detailed proofs of these results are available upon request.
under normality is useful for the preceding properties. In addition, the technique of the integration by parts can be used to derive some of the above results. Detailed proofs of these results are available upon request.
APPENDIX B: PROOFS OF RESULTS IN THE MAIN TEXT
Proof of Theorem 3.1.Given  , without loss of generality, assume that values of ξ are distinct.16 They can be permuted into the order statistics with an ascending order
, without loss of generality, assume that values of ξ are distinct.16 They can be permuted into the order statistics with an ascending order  , i.e.
, i.e.  . Because
. Because 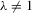 , define
, define
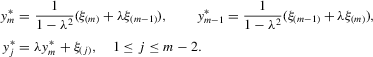 (B.1)
(B.1)When 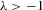 (and
(and 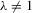 ), the solution vector
), the solution vector 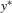 in B.1 satisfying the system 3.1 can be seen as follows. First, the values of
in B.1 satisfying the system 3.1 can be seen as follows. First, the values of 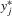 also have an ascending order like those of
also have an ascending order like those of 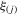 , i.e.,
, i.e.,  if
if  . This is so, because
. This is so, because 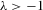 by assumption,
by assumption,
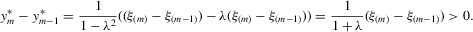
 ,
, 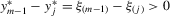 , and
, and 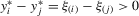 . Second, the system B.1 implies that
. Second, the system B.1 implies that 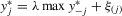 . From
. From 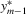 , it implies that
, it implies that 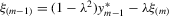 . By substitution,
. By substitution,

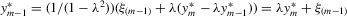 . Therefore, the system of
. Therefore, the system of 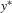 follows. By permuting the indices back to the original ones in terms of ξ, the system consisting of
follows. By permuting the indices back to the original ones in terms of ξ, the system consisting of 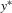 implies the existence of a solution to the original system 3.1.
implies the existence of a solution to the original system 3.1.It remains to show that 3.1 has a unique solution for given  . We can show that the inverse mapping theorem from y to ξ has an order preserving property. If
. We can show that the inverse mapping theorem from y to ξ has an order preserving property. If 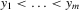 in 3.1 with
in 3.1 with 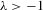 , then it is necessary that
, then it is necessary that  . This is so, because
. This is so, because 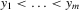 , and 3.1 becomes
, and 3.1 becomes 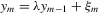 and
and 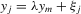 for
for  . Hence,
. Hence, 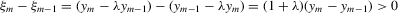 and
and 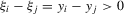 for
for 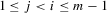 . This property is used to guarantee the unique solution of the system 3.1 for given ξ.
. This property is used to guarantee the unique solution of the system 3.1 for given ξ.
Finally, we can show that the system 3.1 has a unique solution for given ξ. Without loss of generality, assume that  . From the preceding arguments, there exists a vector
. From the preceding arguments, there exists a vector 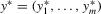 such that
such that  satisfying 3.1. In particular, it has
satisfying 3.1. In particular, it has
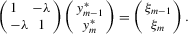
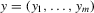 is another solution of 3.1 with an ascending order
is another solution of 3.1 with an ascending order 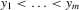 . Then
. Then
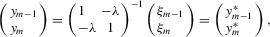
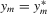 and
and 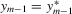 ). Because both
). Because both 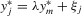 and
and 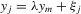 for
for 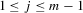 , it follows that
, it follows that 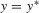 . Next, suppose that there exists y such that its components are not in ascending order. In that case, there exists a permutation such that
. Next, suppose that there exists y such that its components are not in ascending order. In that case, there exists a permutation such that 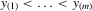 . Previous arguments will imply that the inverse vector of
. Previous arguments will imply that the inverse vector of  from 3.1 must have an ascending order. This is a contradiction because the original elements of the vector ξ are in ascending order.
from 3.1 must have an ascending order. This is a contradiction because the original elements of the vector ξ are in ascending order.From the above results, given any  , there exists a unique solution vector y to the system 3.1. By reordering ξ into ascending order, 3.1 can be conveniently rewritten as the equivalent explicit expression 3.2.
, there exists a unique solution vector y to the system 3.1. By reordering ξ into ascending order, 3.1 can be conveniently rewritten as the equivalent explicit expression 3.2. 
APPENDIX C: LIKELIHOOD FUNCTIONS OF MODELS
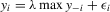 , if a specific parametric distribution is specified for the disturbances. Let
, if a specific parametric distribution is specified for the disturbances. Let 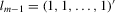 ,
,  and
and
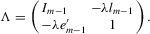
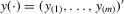 and
and 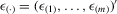 be column vectors of order statistics. The structural equation system is
be column vectors of order statistics. The structural equation system is 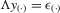 , and the reduced-form system is
, and the reduced-form system is 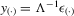 , with
, with
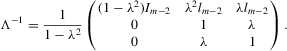
 are i.i.d. with a density function
are i.i.d. with a density function 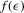 . The implied density function of
. The implied density function of 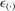 is
is 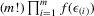 (David, 1981, p. 10). Because the determinant of Λ is
(David, 1981, p. 10). Because the determinant of Λ is 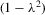 by the partition matrix formulae (see Proposition 30 of Dhrymes, 1978), the density function of
by the partition matrix formulae (see Proposition 30 of Dhrymes, 1978), the density function of 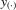 is
is
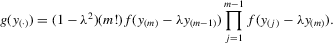
 are normally distributed with zero mean and a finite variance σ2. The model equation in the rth group can be written as
are normally distributed with zero mean and a finite variance σ2. The model equation in the rth group can be written as
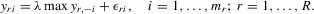 (C.1)
(C.1)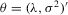 . The log likelihood function is
. The log likelihood function is
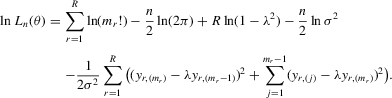 (C.2)
(C.2)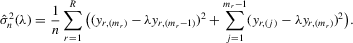
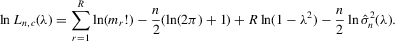 (C.3)
(C.3)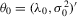 be the true parameter vector. To investigate the asymptotic properties of the MLE of (C.2), the following basic regularity conditions are assumed.
be the true parameter vector. To investigate the asymptotic properties of the MLE of (C.2), the following basic regularity conditions are assumed.
Assumption C.1.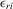 are i.i.d.
are i.i.d. 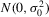 .
.
Assumption C.2.The parameter space Θ is a compact convex subset of 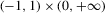 , and the true λ0 is in the interior of Λ, a connected compact subset of the interval ( − 1, 1).
, and the true λ0 is in the interior of Λ, a connected compact subset of the interval ( − 1, 1).
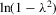 is well defined and that
is well defined and that 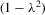 is bounded away from zero for all
is bounded away from zero for all 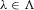 . Assumption C.2 also requires σ2 to be bounded away from zero. The first-order derivatives of the log likelihood function C.2 are
. Assumption C.2 also requires σ2 to be bounded away from zero. The first-order derivatives of the log likelihood function C.2 are
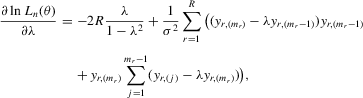
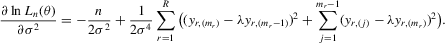
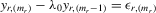 and
and 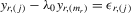 for
for  . Hence,
. Hence,
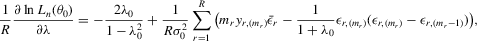
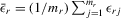 , because
, because  . From the moments for the normal-order statistics,
. From the moments for the normal-order statistics,
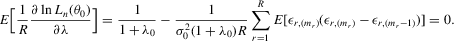
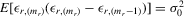 of the normal-order statistics from Lemma A.1. Because these moment properties would not necessarily hold for other distributions, this illustrates that the consistency of the MLE depends on the distributional assumption. In this case, it is the normality in Assumption C.1. In other words, the MLE assuming normality would not be robust to other distributions.
of the normal-order statistics from Lemma A.1. Because these moment properties would not necessarily hold for other distributions, this illustrates that the consistency of the MLE depends on the distributional assumption. In this case, it is the normality in Assumption C.1. In other words, the MLE assuming normality would not be robust to other distributions.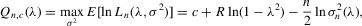
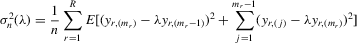
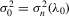 . Following Lemma A.1, we have
. Following Lemma A.1, we have
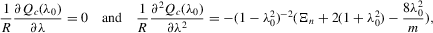

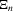 is bounded from above because group sizes are finite and bounded, and that it is bounded below by Lemma A.1, because
is bounded from above because group sizes are finite and bounded, and that it is bounded below by Lemma A.1, because
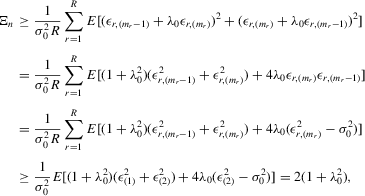
 in a group of size two. Therefore, such positiveness would not vanish in the limit, which guarantees the non-singularity of the information matrix. It follows that
in a group of size two. Therefore, such positiveness would not vanish in the limit, which guarantees the non-singularity of the information matrix. It follows that 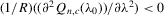 for
for  and
and  .
.
Theorem C.1.Under Assumptions 4.1, C.1 and C.2, θ0 is globally identifiable and  is a consistent estimator of θ0.
is a consistent estimator of θ0.
Proof.The consistency of 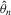 will follow from the uniform convergence of
will follow from the uniform convergence of 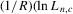
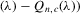 to zero on Λ and the uniqueness identification condition that, for any
to zero on Λ and the uniqueness identification condition that, for any 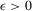 ,
,
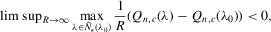
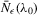 is the complement of an open neighbourhood of λ0 in Λ of diameter ε; see Theorem 3.4 of White (1994). Note that
is the complement of an open neighbourhood of λ0 in Λ of diameter ε; see Theorem 3.4 of White (1994). Note that 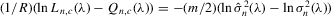 , where
, where
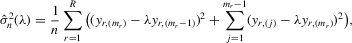
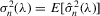 .
.By Kolmogorov's strong law of large numbers or Chebyshev's weak law of large numbers for independent random variables, 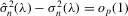 uniformly on Λ, where
uniformly on Λ, where 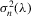 is bounded away from zero on Λ. Therefore,
is bounded away from zero on Λ. Therefore, 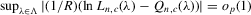 .
.
A third-order Taylor series expansion of the function 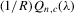 at λ0 can be written as
at λ0 can be written as
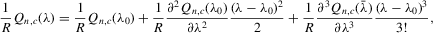
 lies between λ and λ0, and
lies between λ and λ0, and
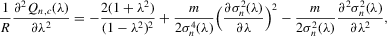
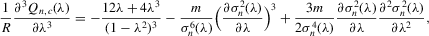
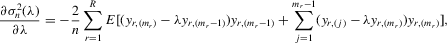
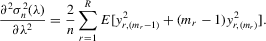
For 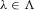 ,
,
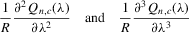
 such that, for large enough R,
such that, for large enough R,
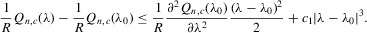
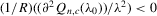 for
for  and
and  . Hence,
. Hence, 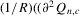
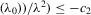 for some
for some 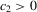 for large R. Let
for large R. Let  . For
. For 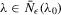 , we have
, we have 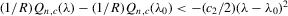 . Therefore, the consistency of
. Therefore, the consistency of 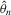 follows from the uniform convergence of
follows from the uniform convergence of 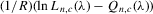 to zero on Λ and the identification uniqueness condition that holds on
to zero on Λ and the identification uniqueness condition that holds on 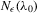 .
. 
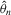 can be derived from the Taylor series expansion of
can be derived from the Taylor series expansion of 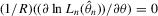 at θ0. The variance matrix of
at θ0. The variance matrix of 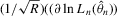
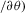 is
is
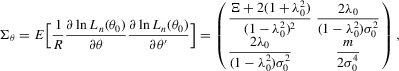
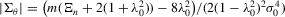 is strictly positive for
is strictly positive for  and
and  .
.
Proof.Applying the mean-value theorem to 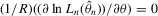 at θ0, we obtain
at θ0, we obtain
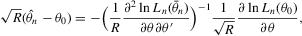
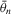 lies between
lies between 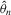 and θ0. The asymptotic distribution of
and θ0. The asymptotic distribution of 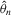 follows by the application of a uniform law of large numbers of independent observations to the Hessian matrix and Lyapunov's central limit theorem to the score vector.
follows by the application of a uniform law of large numbers of independent observations to the Hessian matrix and Lyapunov's central limit theorem to the score vector.The second-order derivatives of the log likelihood function are
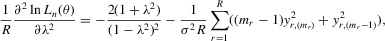
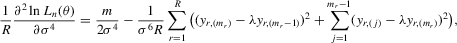
Denote 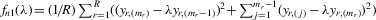 . Then,
. Then, 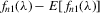 can be expanded in terms of a polynomial of λ as follows:
can be expanded in terms of a polynomial of λ as follows:

 by Chebyshev's law of large numbers of independent observations and because Λ is a bounded set, it follows that
by Chebyshev's law of large numbers of independent observations and because Λ is a bounded set, it follows that
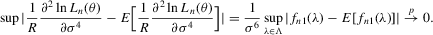
Similarly, denote 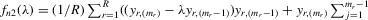
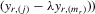 . We have
. We have 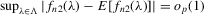 . It follows that
. It follows that
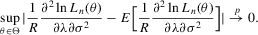
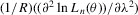 in θ follows directly from Assumptions 4.1, C.1 and C.2.
in θ follows directly from Assumptions 4.1, C.1 and C.2.The first-order derivatives of the log likelihood function at θ0 are

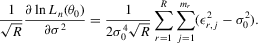
Let k be an even integer and let  denote the kth moment of a normal variate. Note that
denote the kth moment of a normal variate. Note that

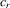 inequality, the third inequality is from the Cauchy–Schwarz inequality and C is a finite constant. Then
inequality, the third inequality is from the Cauchy–Schwarz inequality and C is a finite constant. Then
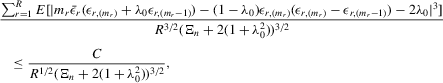
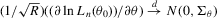 .
. 
 (C.4)
(C.4)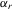 and
and 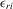 are mutually independent and can be characterized by i.i.d. random variables with zero mean and finite variances,
are mutually independent and can be characterized by i.i.d. random variables with zero mean and finite variances, 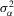 and σ2, respectively.
and σ2, respectively.It is revealing to decompose C.4 into two parts, 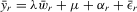 , which can be called a between-group (BG) equation, and
, which can be called a between-group (BG) equation, and  , which is a within-group (WG) equation, because they bear some similarity to the parts of a panel data regression model (Hsiao, 1986).
, which is a within-group (WG) equation, because they bear some similarity to the parts of a panel data regression model (Hsiao, 1986).
Ignoring potential group effects, the MLE would be inconsistent, because the above likelihood function is misspecified. In panel data models, it often makes a difference in estimation whether researchers treat 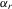 as fixed or random. In the fixed-effects model, we encounter an incidental parameters problem when m is finite but R is large. We can eliminate the group effects (by either the first-differencing method or WG transformation) or we can use the random-effects approach to obtain consistent estimates under the normality assumption. Note that the mutual independence between
as fixed or random. In the fixed-effects model, we encounter an incidental parameters problem when m is finite but R is large. We can eliminate the group effects (by either the first-differencing method or WG transformation) or we can use the random-effects approach to obtain consistent estimates under the normality assumption. Note that the mutual independence between 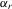 and
and 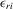 is not necessary for the consistency of the first-differencing or WG MLE.
is not necessary for the consistency of the first-differencing or WG MLE.
1 Derivation of the score equation that ignores common group factors
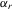 , C.4 reduces to
, C.4 reduces to 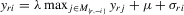 . The misspecified log likelihood function is
. The misspecified log likelihood function is

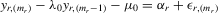 and
and 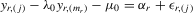 for
for  . Denote
. Denote 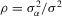 , the ratio of
, the ratio of 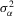 to σ2. Let ρ0 be the true parameter of ρ. From the moments relations of the normal-order statistics in Lemma A.1,
to σ2. Let ρ0 be the true parameter of ρ. From the moments relations of the normal-order statistics in Lemma A.1,
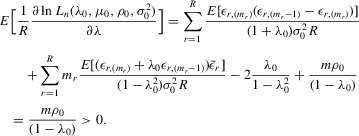
2 Derivation of the likelihood function of fixed-effects specification
 for
for  , and
, and  . Under the condition that ε are i.i.d.
. Under the condition that ε are i.i.d. 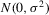 , the likelihood function of the fixed-effects specification of C.4 is
, the likelihood function of the fixed-effects specification of C.4 is

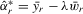 , for all r at any given value of λ, into the above likelihood function, the concentrated fixed-effects log likelihood function,
, for all r at any given value of λ, into the above likelihood function, the concentrated fixed-effects log likelihood function, 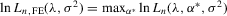 , follows:
, follows:
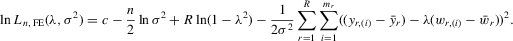
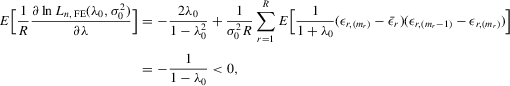
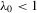 . Thus, the fixed-effects MLE is inconsistent.
. Thus, the fixed-effects MLE is inconsistent.3 Derivation of the likelihood function for first-differenced samples
 ,
,  , in ascending order, spacing random variables
, in ascending order, spacing random variables  , for
, for  , are defined as the order statistics via
, are defined as the order statistics via 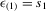 ,
, 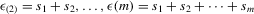 . The relation between the vector
. The relation between the vector 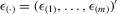 and
and 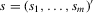 is
is 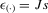 , where
, where
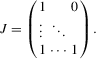
 is
is  , the density of spacings s is
, the density of spacings s is  . When ε are i.i.d.
. When ε are i.i.d. 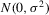 , the density of
, the density of  is
is

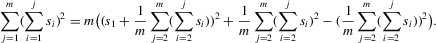
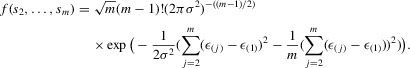
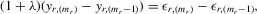
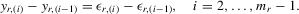
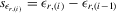 and
and 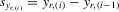 represent the spacings between the order statistics of ε and y for the rth group. Because the joint density of
represent the spacings between the order statistics of ε and y for the rth group. Because the joint density of 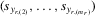 is
is 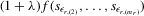 , it follows that
, it follows that
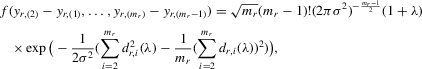
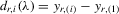 for
for  and
and 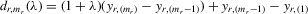 . The log likelihood function of a first-differenced sample with R groups is
. The log likelihood function of a first-differenced sample with R groups is
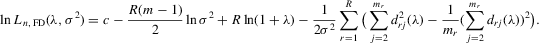
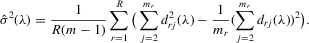
4 Derivation of the partial likelihood function of the within-group equation
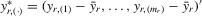 and
and 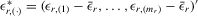 be column vectors of demeaned order statistics. The WG equation is
be column vectors of demeaned order statistics. The WG equation is 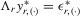 , where
, where
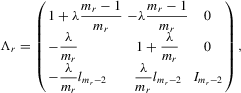
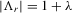 .
.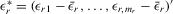 is
is
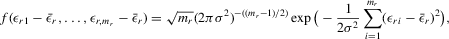
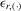 is
is 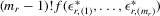 . The partial likelihood function of the WG equation follows because the Jacobian is
. The partial likelihood function of the WG equation follows because the Jacobian is 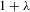 .
.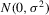 , the log likelihood function of the WG equation is
, the log likelihood function of the WG equation is
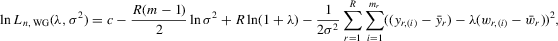
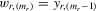 and
and 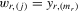 for
for  . The MLE of σ2 is
. The MLE of σ2 is
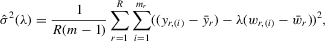
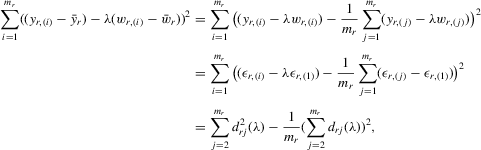
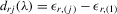 for
for  . Thus, the first-differencing and WG transformations lead to the numerically exact likelihood function.
. Thus, the first-differencing and WG transformations lead to the numerically exact likelihood function.5 Derivation of the likelihood function of the random-effects approach
 is
is 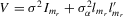 , which has the determinant
, which has the determinant 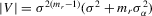 and the inverse
and the inverse 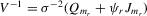 with
with 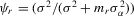 ,
, 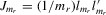 and
and 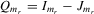 . The likelihood function of the random effects (RE) specification follows. When
. The likelihood function of the random effects (RE) specification follows. When 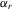 and
and 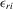 are mutually independent and normally distributed, the log likelihood function under the RE specification is
are mutually independent and normally distributed, the log likelihood function under the RE specification is
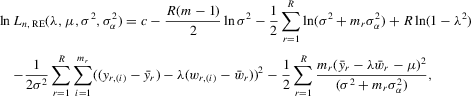
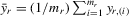 and
and 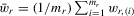 .
.6 Derivation of the conditional likelihood function of the between-group equation
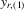 conditional on
conditional on 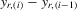 for
for  . It is a partial likelihood function:
. It is a partial likelihood function:

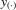 , the BG equation becomes
, the BG equation becomes
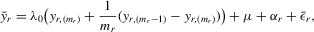
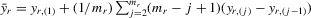 . Thus, the BG equation can be rewritten as
. Thus, the BG equation can be rewritten as
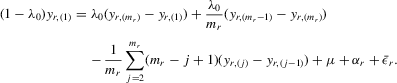
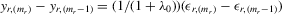 and
and 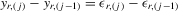 for
for  , and
, and  for all i under normality. Hence, we can regard all the variables
for all i under normality. Hence, we can regard all the variables 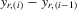 for
for  as exogenous variables and the dependent variable is
as exogenous variables and the dependent variable is 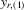 . The likelihood function of the BG equation is simply the conditional likelihood function of
. The likelihood function of the BG equation is simply the conditional likelihood function of 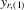 conditional on
conditional on 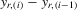 for
for  . The likelihood function of the WG equation is thus a partial likelihood function.
. The likelihood function of the WG equation is thus a partial likelihood function.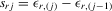 for
for  , the conditional density of
, the conditional density of 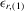 given
given 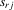 and
and 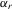 is
is
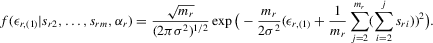
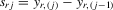 for
for  ,
, 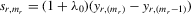 , and
, and

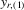 given
given 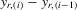 for
for  is
is
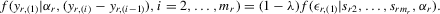
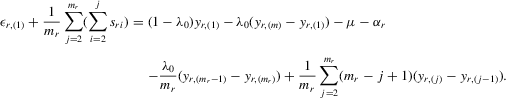
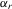 as the extra source of variation, we see that the density function of the BG equation is related to the density of
as the extra source of variation, we see that the density function of the BG equation is related to the density of 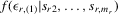 .
.The likelihood functions of all the proposed approaches (i.e. the first-differencing approach, RE specification, WG equation and BG equation) are well defined and depend on a fixed number of parameters. Similar to Theorem C.2, under the i.i.d. normality assumption, these estimators can be consistent and asymptotically normal as R goes to infinity. Among these consistent estimators, the RE MLE will be asymptotically efficient.
7 Monte Carlo results
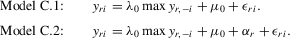
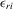 from N(0, 1) to investigate the asymptotic property of the MLE and we also draw
from N(0, 1) to investigate the asymptotic property of the MLE and we also draw  from the standardized χ2(5) distribution in order to investigate its sensitivity against non-normality. The group effect
from the standardized χ2(5) distribution in order to investigate its sensitivity against non-normality. The group effect 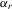 is randomly drawn from N(0, 1). The true parameters are
is randomly drawn from N(0, 1). The true parameters are 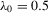 and
and  .
.Table C.1 presents the bias (Bias) and standard deviation (SD) of the MLE and MOMEs of Model C.1 under the normal distribution. The MLEs of λ have very small biases for all R, and its SDs tend to decrease as R increases. The MOMEs of λ have large biases for small R and its biases become small when R is 240 or larger. When R increases, the MOMEs have smaller standard errors. In general, the MLE has smaller SDs than the MOME. The estimates of μ and σ have similar properties as those of λ under the normal distribution. Table C.2 presents finite sample results of Model C.1 under the χ2 distribution. The MLE of λ has significant downward biases. The MOME of λ has large biases for small R, but small biases when R is 240 or larger. These results reveal that the MLE is sensitive to distributional assumptions, and that the MOME is distribution-free and has satisfactory performance for reasonably large R. Table C.3 presents finite sample results of various MLEs and MOMEs of Model C.2 under the normal distribution. As expected, the inconsistent MLEs that ignore group effects (IGE) or treat them as fixed effects (FEs) are biased in different directions, and the consistent MLEs (WG, BG and RE) have small biases for all R. The MOMEs of Model C.2 perform similar to those of Model C.1. The RE-MLE approach performs best in terms of SDs among the consistent estimators, and all the consistent MLEs perform better than the MOMEs.
| R | MLE | MOM | R | MLE | MOM | ||
| λ | Bias | 60 | −0.0043 | 14.9160 | 480 | −0.0006 | −0.0112 |
| SD | 0.0432 | 263.4300 | 0.0144 | 0.0802 | |||
| μ | Bias | 0.0048 | −6.1766 | 0.0008 | 0.0070 | ||
| SD | 0.0659 | 109.8200 | 0.0245 | 0.0502 | |||
| σ | Bias | 0.0029 | 4.6755 | 0.0000 | −0.0023 | ||
| SD | 0.0481 | 79.8610 | 0.0192 | 0.0300 | |||
| λ | Bias | 120 | −0.0023 | −0.0717 | 960 | −0.0001 | −0.0020 |
| SD | 0.0273 | 0.2855 | 0.0101 | 0.0559 | |||
| μ | Bias | −0.0008 | 0.0394 | −0.0001 | 0.0009 | ||
| SD | 0.0464 | 0.1767 | 0.0157 | 0.0339 | |||
| σ | Bias | −0.0021 | −0.0135 | −0.0002 | −0.0003 | ||
| SD | 0.0340 | 0.0665 | 0.0135 | 0.0194 | |||
| λ | Bias | 240 | −0.0008 | −0.0375 | 1920 | −0.0007 | −0.0059 |
| SD | 0.0213 | 0.1685 | 0.0070 | 0.0390 | |||
| μ | Bias | 0.0016 | 0.0264 | 0.0004 | 0.0032 | ||
| SD | 0.0361 | 0.1178 | 0.0114 | 0.0238 | |||
| σ | Bias | −0.0027 | −0.0120 | 0.0001 | −0.0012 | ||
| SD | 0.0553 | 0.0693 | 0.0091 | 0.0135 |
| R | MLE | MOM | R | MLE | MOM | ||
|---|---|---|---|---|---|---|---|
| λ | Bias | 60 | −0.0898 | −0.1833 | 480 | −0.0815 | −0.0228 |
| SD | 0.0589 | 0.9894 | 0.0201 | 0.1039 | |||
| μ | Bias | 0.0537 | 0.1203 | 0.0546 | 0.0157 | ||
| SD | 0.0777 | 0.6868 | 0.0269 | 0.0729 | |||
| σ | Bias | 0.0177 | −0.0018 | 0.0206 | −0.0028 | ||
| SD | 0.0703 | 0.1270 | 0.0256 | 0.0315 | |||
| λ | Bias | 120 | −0.0856 | −0.0398 | 960 | −0.0809 | −0.0125 |
| SD | 0.0407 | 0.3414 | 0.0142 | 0.0768 | |||
| μ | Bias | 0.0537 | 0.0254 | 0.0533 | 0.0079 | ||
| SD | 0.0517 | 0.2451 | 0.0194 | 0.0537 | |||
| σ | Bias | 0.0188 | −0.0013 | 0.0191 | −0.0024 | ||
| SD | 0.0501 | 0.0635 | 0.0170 | 0.0212 | |||
| λ | Bias | 240 | −0.0826 | −0.0177 | 1920 | −0.0810 | −0.0026 |
| SD | 0.0283 | 0.1764 | 0.0097 | 0.0497 | |||
| μ | Bias | 0.0546 | 0.0118 | 0.0548 | 0.0026 | ||
| SD | 0.0386 | 0.1229 | 0.0135 | 0.0340 | |||
| σ | Bias | −0.0208 | −0.0002 | 0.0204 | −0.0002 | ||
| SD | 0.0350 | 0.0449 | 0.0128 | 0.0159 |
| R | IGE | FE | WG | BG | RE | MOM | ||
|---|---|---|---|---|---|---|---|---|
| λ | Bias | 120 | 0.2385 | −0.7780 | 0.0057 | −0.0309 | −0.0085 | 0.3536 |
| SD | 0.0199 | 0.0247 | 0.1367 | 0.1951 | 0.0935 | 3.2983 | ||
| μ | Bias | −0.1249 | 0.4874 | 0.0049 | 0.0260 | 0.0131 | −0.1810 | |
| SD | 0.0579 | 0.2626 | 0.1377 | 0.1694 | 0.1251 | 2.0278 | ||
| σ | Bias | 0.0942 | −0.1673 | −0.0010 | −0.0641 | −0.0030 | 0.1069 | |
| SD | 0.0380 | 0.0357 | 0.0471 | 1.0738 | 0.0424 | 1.0339 | ||
 |
Bias | −0.1088 | 0.0011 | 0.8097 | ||||
| SD | 0.4993 | 0.2508 | 7.3440 | |||||
| λ | Bias | 240 | 0.2391 | −0.7753 | 0.0143 | −0.0101 | 0.0015 | 0.0698 |
| SD | 0.0135 | 0.0167 | 0.0955 | 0.1136 | 0.0666 | 0.4111 | ||
| μ | Bias | −0.1270 | 0.4676 | −0.0083 | 0.0052 | −0.0013 | −0.0336 | |
| SD | 0.0399 | 0.1958 | 0.0925 | 0.0974 | 0.0809 | 0.2270 | ||
| σ | Bias | 0.0956 | −0.1641 | 0.0051 | −0.1537 | 0.0027 | 0.0216 | |
| SD | 0.0300 | 0.0279 | 0.0357 | 0.8178 | 0.0314 | 0.1052 | ||
 |
Bias | −0.0630 | −0.0162 | 0.0258 | ||||
| SD | 0.3402 | 0.1794 | 0.7527 | |||||
| λ | Bias | 480 | 0.2418 | −0.7765 | 0.0049 | −0.0036 | −0.0016 | 0.0211 |
| SD | 0.0096 | 0.0116 | 0.0647 | 0.0808 | 0.0483 | 0.3042 | ||
| μ | Bias | −0.1314 | 0.4669 | −0.0047 | −0.0001 | −0.0011 | −0.0133 | |
| SD | 0.0308 | 0.1407 | 0.0687 | 0.0755 | 0.0633 | 0.1745 | ||
| σ | Bias | 0.0925 | −0.1668 | −0.0010 | −0.1795 | −0.0022 | 0.0055 | |
| SD | 0.0199 | 0.0174 | 0.0227 | 0.7383 | 0.0206 | 0.0716 | ||
 |
Bias | −0.0331 | 0.0034 | 0.0085 | ||||
| SD | 0.2455 | 0.1304 | 0.6488 | |||||
| λ | Bias | 960 | 0.2408 | −0.7776 | −0.0029 | 0.0037 | −0.0043 | 0.0062 |
| SD | 0.0064 | 0.0088 | 0.0480 | 0.0498 | 0.0331 | 0.1844 | ||
| μ | Bias | −0.1287 | 0.4765 | 0.0033 | −0.0009 | 0.0040 | −0.0011 | |
| SD | 0.0209 | 0.0986 | 0.0488 | 0.0485 | 0.0433 | 0.1059 | ||
| σ | Bias | 0.0928 | −0.1679 | −0.0017 | −0.1993 | −0.0019 | 0.0013 | |
| SD | 0.0136 | 0.0131 | 0.0177 | 0.6127 | 0.0152 | 0.0444 | ||
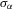 |
Bias | −0.0190 | 0.0083 | −0.0206 | ||||
| SD | 0.1521 | 0.0924 | 0.4518 | |||||
| λ | Bias | 1920 | 0.2412 | −0.7769 | 0.0014 | 0.0045 | −0.0005 | −0.0021 |
| SD | 0.0048 | 0.0059 | 0.0326 | 0.0362 | 0.0230 | 0.1223 | ||
| μ | Bias | −0.1296 | 0.4685 | −0.0017 | −0.0035 | −0.0006 | 0.0004 | |
| SD | 0.0145 | 0.0677 | 0.0335 | 0.0337 | 0.0296 | 0.0706 | ||
| σ | Bias | 0.0936 | −0.1662 | 0.0006 | −0.2441 | 0.0003 | 0.0002 | |
| SD | 0.0099 | 0.0089 | 0.0113 | 0.5209 | 0.0104 | 0.0284 | ||
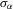 |
Bias | 0.0052 | 0.0012 | −0.0061 | ||||
| SD | 0.1167 | 0.0645 | 0.3297 |
APPENDIX D: RECURRENCE MOMENTS
Lemma D.1.Let  be a random sample of size m and let
be a random sample of size m and let  be the corresponding order statistics in the ascending order. Assume that the first moment of any one order statistics in a sample of size m exists. Then,
be the corresponding order statistics in the ascending order. Assume that the first moment of any one order statistics in a sample of size m exists. Then,
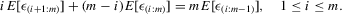
This lemma follows directly from Balakrishnan and Sultan (1998, p. 155).
Proof of Theorem 5.1.For analytical convenience, we assume that there are 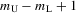 different group sizes. Each group size has the same number of groups T, and R and T have the same order of magnitude, because
different group sizes. Each group size has the same number of groups T, and R and T have the same order of magnitude, because 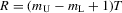 and mU is bounded. Denote
and mU is bounded. Denote 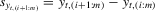 and
and 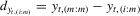 , where
, where 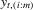 is the ith-order statistics in the tth subgroup with group size m for
is the ith-order statistics in the tth subgroup with group size m for  and
and  . The GMM estimation vector for the model 4.15 is
. The GMM estimation vector for the model 4.15 is
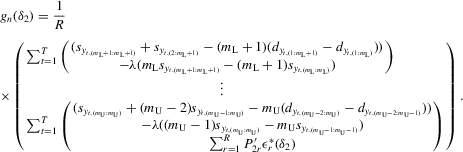
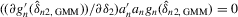 at δ20,
at δ20,
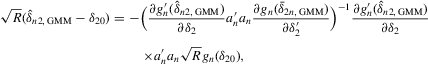
 is between
is between 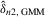 and δ20, and
and δ20, and
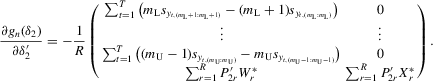
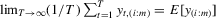 for bounded m. It follows that
for bounded m. It follows that 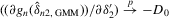 , where
, where
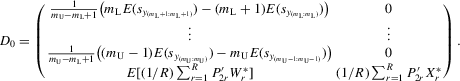
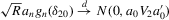 , and
, and
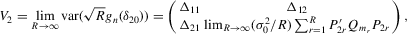
 exists and has full column rank
exists and has full column rank 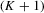 , it follows that
, it follows that
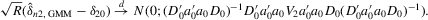

1 Consistent estimation of Δ11 and Δ12
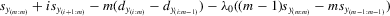 , can be estimated by
, can be estimated by
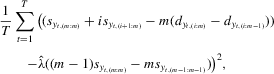
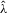 is an initial estimate of λ0. If two different recurrence moments have common group size, their covariance is non-zero and can be estimated with cross moments in a similar way.
is an initial estimate of λ0. If two different recurrence moments have common group size, their covariance is non-zero and can be estimated with cross moments in a similar way.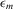 be a generic disturbance vector of m rows and let
be a generic disturbance vector of m rows and let 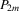 be the corresponding IV matrix. Under Assumption 5.1, the covariance of the linear IV moment
be the corresponding IV matrix. Under Assumption 5.1, the covariance of the linear IV moment 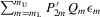 and a generic recurrence moment
and a generic recurrence moment 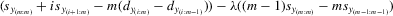 for
for 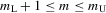 is
is 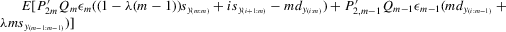 . Let
. Let 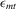 be the disturbance vector of the tth group of size m, and let
be the disturbance vector of the tth group of size m, and let 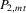 be the corresponding IV matrix. The above expectation can be estimated by
be the corresponding IV matrix. The above expectation can be estimated by
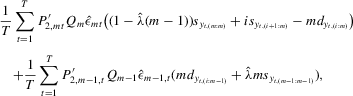
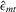 is the residual of an IV regression.
is the residual of an IV regression.


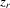 as well as individual characteristics
as well as individual characteristics 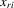 :
:
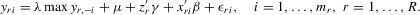
 with
with  is consistent and
is consistent and
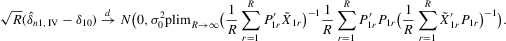
 with
with  is consistent and
is consistent and
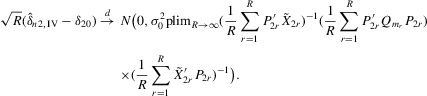
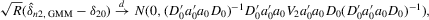
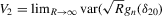 .
.
 and
and  are identical for
are identical for  . Assumption
. Assumption 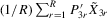 has full rank asymptotically, which is a sufficient condition for the identification of δ3. The IV estimator with
has full rank asymptotically, which is a sufficient condition for the identification of δ3. The IV estimator with 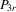 for
for 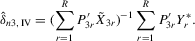
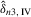 with
with 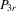 is consistent and
is consistent and
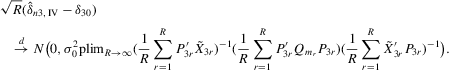
 as an IV for
as an IV for  . Let
. Let  denote a matrix consisting of
denote a matrix consisting of 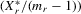 and
and 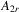 in
in 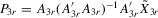 is
is
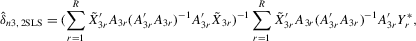
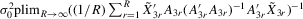 . Similarly to
. Similarly to 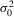 is
is
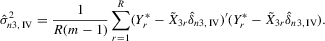
 are given by
are given by 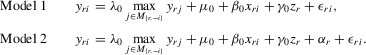
 implies that
implies that
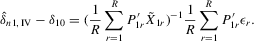
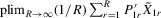 is non-singular, and
is non-singular, and 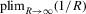
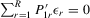 . Hence,
. Hence,  is consistent. For the limiting distribution,
is consistent. For the limiting distribution,
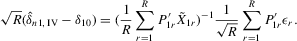
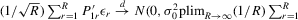
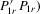 , it follows that
, it follows that
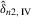 and
and 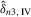 are consistent and are asymptotically normal.
are consistent and are asymptotically normal. 
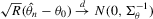 .
.
