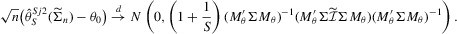Indirect inference based on the score
Summary
The efficient method of moments (EMM) estimator is an indirect inference estimator based on the simulated auxiliary score evaluated at the sample estimate of the auxiliary parameters. We study an alternative estimator that uses the sample auxiliary score evaluated at the simulated binding function, which maps the structural parameters of interest to the auxiliary parameters. We show that the alternative estimator has the same asymptotic properties as the EMM estimator but in finite samples behaves more like the distance-based indirect inference estimator of Gouriéroux et al.
1. INTRODUCTION
Indirect inference estimators take advantage of a simplified auxiliary model that is easier to estimate than a proposed structural model. The estimation consists of two stages. First, an auxiliary statistic is calculated from the observed data. Then, an analytical or simulated mapping of the structural parameters to the auxiliary statistic is used to calibrate an estimate of the structural parameters. The simulation-based indirect inference estimators are typically placed into one of two categories: score-based estimators made popular by Gallant and Tauchen (1996b), or distance-based estimators proposed by Smith (1993) and refined by Gouriéroux et al. (1993). However, many studies have shown (e.g. Michaelides and Ng, 2000, Ghysels et al., 2003, and Duffee and Stanton, 2008) that score-based estimators often have poor finite sample properties relative to distance-based estimators. In this paper, we study an alternative score-based estimator that utilizes the sample auxiliary score evaluated with the auxiliary parameters estimated from simulated data. We show that this alternative estimator is asymptotically equivalent to the Gallant and Tauchen (1996b) score-based estimator but has finite sample properties that are very close to those of distance-based estimators.
2. REVIEW OF INDIRECT INFERENCE
Indirect inference techniques have been introduced into the econometrics literature by Smith (1993), Gouriéroux et al. (1993), Bansal et al. (1994, 1995), and Gallant and Tauchen (1996b), and have been surveyed by Gouriéroux and Monfort (1996) and Jiang and Turnbull (2004). There are four components present in simulation-based indirect inference: (a) a true structural model whose parameters θ are of ultimate interest but are difficult to directly estimate; (b) simulated observations from the structural model for a given θ; (c) an auxiliary approximation to the structural model whose parameters μ are easy to estimate; (d) the binding function, a mapping from μ to θ uniquely connecting the parameters of these two models.
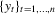 are generated from a strictly stationary and ergodic probability model
are generated from a strictly stationary and ergodic probability model  ,
, 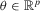 , with density
, with density 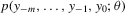 that is difficult or impossible to evaluate analytically.1 Typical examples are continuous time diffusion models and dynamic stochastic general equilibrium models. Define an auxiliary model
that is difficult or impossible to evaluate analytically.1 Typical examples are continuous time diffusion models and dynamic stochastic general equilibrium models. Define an auxiliary model 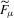 in which the parameter
in which the parameter 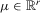 , with
, with 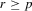 , is easier to estimate than θ. For ease of exposition, the auxiliary estimator of μ is defined as the quasi-maximum likelihood estimator (QMLE) of the model
, is easier to estimate than θ. For ease of exposition, the auxiliary estimator of μ is defined as the quasi-maximum likelihood estimator (QMLE) of the model 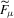 ,
,
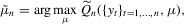 (2.1)
(2.1)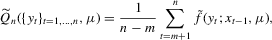 (2.2)
(2.2)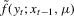 is the log density of
is the log density of 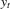 for the model
for the model 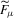 conditioned on
conditioned on 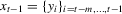 ,
, 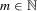 . We define
. We define
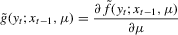
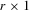 auxiliary score vector. For more general
auxiliary score vector. For more general 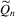 , we refer the reader to Gouriéroux and Monfort (1996).
, we refer the reader to Gouriéroux and Monfort (1996).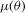 , which is the functional solution of the asymptotic optimization problem
, which is the functional solution of the asymptotic optimization problem
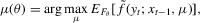 (2.3)
(2.3)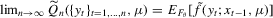 , and
, and 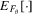 means that the expectation is taken with respect to
means that the expectation is taken with respect to 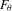 . In order for
. In order for 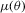 to define a unique mapping, it is assumed that
to define a unique mapping, it is assumed that 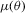 is one-to-one and that
is one-to-one and that  has full column rank.
has full column rank.Indirect inference estimators differ in how they use 2.3 to define an estimating equation. The distance-based indirect inference estimator finds θ to minimize the (weighted) distance between 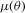 and
and 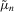 . The score-based indirect inference estimator finds θ by solving
. The score-based indirect inference estimator finds θ by solving 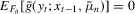 , the first-order condition (FOC) associated with 2.3.2 Typically, the analytical forms of
, the first-order condition (FOC) associated with 2.3.2 Typically, the analytical forms of 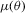 and
and 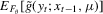 are not known and simulation-based techniques are used to compute the two types of indirect inference estimators.
are not known and simulation-based techniques are used to compute the two types of indirect inference estimators.
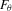 for a given θ. These simulated observations are typically drawn in two ways. First, a long pseudo-data series of size
for a given θ. These simulated observations are typically drawn in two ways. First, a long pseudo-data series of size 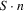 is simulated, giving
is simulated, giving
 (2.4)
(2.4)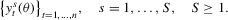 (2.5)
(2.5)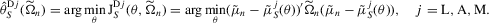 (2.6)
(2.6)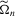 is a positive definite and symmetric weight matrix, which can depend on the data through the auxiliary model, and the simulated binding functions are given by
is a positive definite and symmetric weight matrix, which can depend on the data through the auxiliary model, and the simulated binding functions are given by
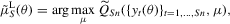 (2.7)
(2.7)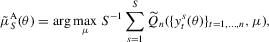 (2.8)
(2.8)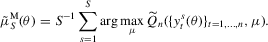 (2.9)
(2.9)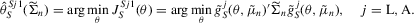 (2.10)
(2.10)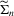 is a positive definite and symmetric weight matrix, which can depend on the data through the auxiliary model, and the simulated scores are given by
is a positive definite and symmetric weight matrix, which can depend on the data through the auxiliary model, and the simulated scores are given by
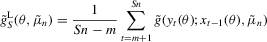 (2.11)
(2.11)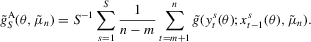 (2.12)
(2.12)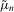 , no M-type estimator is available.
, no M-type estimator is available.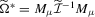 and
and  , where
, where
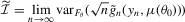
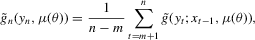
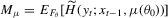
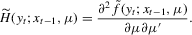
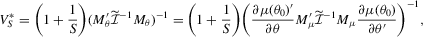 (2.13)
(2.13)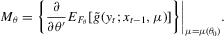
3. ALTERNATIVE SCORE-BASED INDIRECT INFERENCE ESTIMATOR
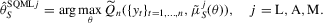 (3.1)
(3.1)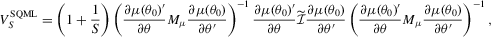 (3.2)
(3.2)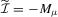 .
.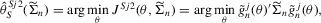 (3.3)
(3.3)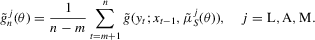 (3.4)
(3.4)The proof is given in Appendix A of the Supporting Information. We make the following remarks.
Remark 3.1.When 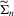 is a consistent estimator of
is a consistent estimator of 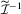 , the asymptotic variance of
, the asymptotic variance of 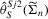 in 3.5 is equivalent to the asymptotic variance of Gallant and Tauchen's score-based estimator
in 3.5 is equivalent to the asymptotic variance of Gallant and Tauchen's score-based estimator 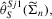 and is equivalent to 2.13. Contrary to the claim of Gouriéroux and Monfort (1996), for a given auxiliary model the alternative score-based indirect inference estimator is not less efficient than the optimal traditional indirect inference estimators.
and is equivalent to 2.13. Contrary to the claim of Gouriéroux and Monfort (1996), for a given auxiliary model the alternative score-based indirect inference estimator is not less efficient than the optimal traditional indirect inference estimators.
Remark 3.2.To see the relationship between the two score-based estimators, 2.10 and 3.3, note that the FOCs of the optimization problem 2.3 defining 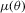 are
are
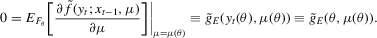 (3.6)
(3.6)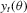 and
and 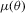 , and both score-based indirect inference estimators make use of this population moment condition. The S1 and S2 estimators differ in how sample information and simulations are used. For the S1 estimator,
, and both score-based indirect inference estimators make use of this population moment condition. The S1 and S2 estimators differ in how sample information and simulations are used. For the S1 estimator, 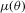 is estimated from the sample and simulated values of
is estimated from the sample and simulated values of 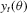 are used to approximate
are used to approximate 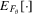 . For the S2 estimator,
. For the S2 estimator, 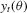 is obtained from the sample, and simulated values of
is obtained from the sample, and simulated values of 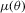 are used for calibration to minimize the objective function. Because the S2 estimator 3.3 evaluates the sample auxiliary score with a simulated binding function, it has certain properties that make it similar to the distance-based indirect inference estimator 2.6.
are used for calibration to minimize the objective function. Because the S2 estimator 3.3 evaluates the sample auxiliary score with a simulated binding function, it has certain properties that make it similar to the distance-based indirect inference estimator 2.6.
Remark 3.3.To see why the S1 and S2 estimators are asymptotically equivalent and efficient, and why the SQML estimator is generally inefficient, consider the FOCs defining these estimators. From 2.10, the FOCs for the optimal S1 estimator are
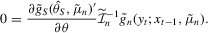 (3.7)
(3.7)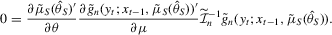 (3.8)
(3.8) is a consistent estimate of
is a consistent estimate of  . When n and S are large enough,
. When n and S are large enough, 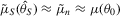 ,
, 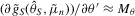 ,
, 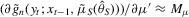 and
and 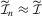 . It follows that 3.7 and 3.8 can be re-expressed as
. It follows that 3.7 and 3.8 can be re-expressed as
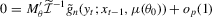 (3.9)
(3.9)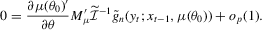 (3.10)
(3.10)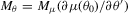 , it follows that the FOCs for the S1 and S2 estimators pick out the optimal linear combinations of the over-identified auxiliary score and produce efficient indirect inference estimators. In contrast, from 3.1, the FOCs for the SQML are
, it follows that the FOCs for the S1 and S2 estimators pick out the optimal linear combinations of the over-identified auxiliary score and produce efficient indirect inference estimators. In contrast, from 3.1, the FOCs for the SQML are
 (3.11)
(3.11)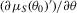 does not pick out the optimal linear combinations of the auxiliary score unless
does not pick out the optimal linear combinations of the auxiliary score unless 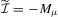 .
.
4. FINITE SAMPLE COMPARISON OF INDIRECT INFERENCE ESTIMATORS
We compare the finite sample performance of the alternative score-based S2 estimator to the traditional S1 and D estimators using an Ornstein–Uhlenbeck (OU) process. Our analysis is motivated by Duffee and Stanton (2008), who compared the finite sample properties of traditional indirect estimators using highly persistent AR(1) models. They found that the S1 estimator is severely biased, has wide confidence intervals, and performs poorly in coefficient and over-identification tests. We show that the alternative formulation of the score-based estimator leads to a remarkable improvement in its finite sample performance.
4.1. Model set-up
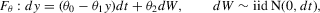 (4.1)
(4.1)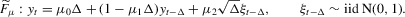 (4.2)
(4.2)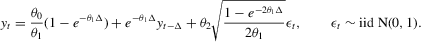 (4.3)
(4.3)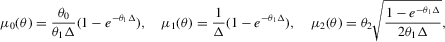 (4.4)
(4.4)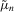 =
= 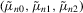 is an asymptotically biased estimator of
is an asymptotically biased estimator of  ; see Lo (1988). Without loss of generality, we set
; see Lo (1988). Without loss of generality, we set  in 4.2–4.4; see Fuleky (2012). The analytically tractable OU process gives us the opportunity to compute non-simulation-based analogues (SN1, SN2 and DN) of the simulation-based estimators.
in 4.2–4.4; see Fuleky (2012). The analytically tractable OU process gives us the opportunity to compute non-simulation-based analogues (SN1, SN2 and DN) of the simulation-based estimators.Because the finite sample performance of the estimators is mostly influenced by the speed of mean reversion, in our data-generating process we vary θ1 and consider the following two sets of true parameter values: 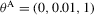 and
and 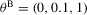 . The values
. The values 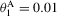 and
and 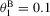 correspond to autoregressive coefficients equal to
correspond to autoregressive coefficients equal to 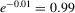 and
and 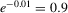 , respectively, in 4.3. In addition to estimating θ0, θ1 and θ2, we also consider the case when θ0 and θ2 are assumed to be known, and the indirect estimators of θ1 are over-identified (
, respectively, in 4.3. In addition to estimating θ0, θ1 and θ2, we also consider the case when θ0 and θ2 are assumed to be known, and the indirect estimators of θ1 are over-identified (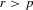 ). For the simulations 2.4 and 2.5, we set
). For the simulations 2.4 and 2.5, we set 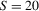 , so that the simulation-based estimators have a 95% asymptotic efficiency relative to the non-simulation-based estimators; see 2.13. We analyse samples of size
, so that the simulation-based estimators have a 95% asymptotic efficiency relative to the non-simulation-based estimators; see 2.13. We analyse samples of size 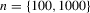 , and our results are based on 1000 Monte Carlo simulations.
, and our results are based on 1000 Monte Carlo simulations.
4.2. Results
In line with the proposition of Gouriéroux and Monfort (1996, p. 66), the score-based and distance-based indirect inference estimators of a particular type (N, L, A or M) produce equivalent results in a just-identified setting. The bias and root-mean-squared error of the just-identified estimators is summarized in Table B.1 in Appendix B of the Supporting Information. Notably, each indirect inference estimator of θ1 is biased upward, but in comparison to the others, the M-type estimators are more accurate with a tighter distribution around the true value.
Despite their equivalent distributional characteristics, the just-identified indirect inference estimators do not have equal test performance. Table 1 summarizes the rejection rates of likelihood ratio tests of the hypotheses, 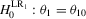 and
and 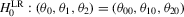 , where
, where  denotes the true value of the parameter vector. In both tests, the S1 estimator is much more oversized than the S2 and D estimators. The large improvement in the performance of the S2 estimator over the S1 estimator can be attributed to using the simulated binding function instead of the simulated score for calibration. The shape of the S1 objective function is determined by the simulated score,
denotes the true value of the parameter vector. In both tests, the S1 estimator is much more oversized than the S2 and D estimators. The large improvement in the performance of the S2 estimator over the S1 estimator can be attributed to using the simulated binding function instead of the simulated score for calibration. The shape of the S1 objective function is determined by the simulated score, 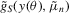 , which depends on the variance of the simulated sample. Consequently, the S1 objective function quickly steepens as θ1 approaches the non-stable region of the parameter space below
, which depends on the variance of the simulated sample. Consequently, the S1 objective function quickly steepens as θ1 approaches the non-stable region of the parameter space below 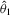 . As a result, the confidence sets around the S1 estimates, which are upward biased in the θ1 dimension, frequently exclude the true θ1 parameter value. In contrast, the shape of the S2 and D objective functions is determined by the simulated binding function,
. As a result, the confidence sets around the S1 estimates, which are upward biased in the θ1 dimension, frequently exclude the true θ1 parameter value. In contrast, the shape of the S2 and D objective functions is determined by the simulated binding function, 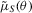 , which is approximately linear around
, which is approximately linear around 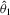 , and the roughly symmetric confidence sets around the estimates contain the true parameter value with higher frequency. As
, and the roughly symmetric confidence sets around the estimates contain the true parameter value with higher frequency. As  , the binding function slightly steepens and the confidence set tightens, which affects the rejection rate of the least-upward-biased M-type estimators. In joint tests, the shrinkage of the confidence sets dominates the bias reduction of the M-type estimators and leads to higher rejection rates.
, the binding function slightly steepens and the confidence set tightens, which affects the rejection rate of the least-upward-biased M-type estimators. In joint tests, the shrinkage of the confidence sets dominates the bias reduction of the M-type estimators and leads to higher rejection rates.
| n | SN1 | SN2 | DN | SL1 | SL2 | DL | SA1 | SA2 | DA | SM2 | DM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
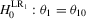 |
||||||||||||
| θA | 100 | 0.869 | 0.206 | 0.285 | 0.800 | 0.162 | 0.251 | 0.724 | 0.171 | 0.252 | 0.063 | 0.098 |
| 1000 | 0.321 | 0.082 | 0.083 | 0.314 | 0.076 | 0.080 | 0.288 | 0.078 | 0.082 | 0.058 | 0.060 | |
| θB | 100 | 0.286 | 0.068 | 0.106 | 0.265 | 0.064 | 0.088 | 0.248 | 0.061 | 0.088 | 0.061 | 0.085 |
| 1000 | 0.090 | 0.053 | 0.057 | 0.097 | 0.051 | 0.052 | 0.095 | 0.051 | 0.055 | 0.047 | 0.048 | |
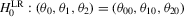 |
||||||||||||
| θA | 100 | 0.911 | 0.146 | 0.189 | 0.868 | 0.131 | 0.174 | 0.821 | 0.131 | 0.179 | 0.416 | 0.383 |
| 1000 | 0.401 | 0.070 | 0.067 | 0.396 | 0.073 | 0.069 | 0.381 | 0.070 | 0.070 | 0.140 | 0.128 | |
| θB | 100 | 0.404 | 0.088 | 0.112 | 0.379 | 0.087 | 0.104 | 0.375 | 0.083 | 0.104 | 0.176 | 0.164 |
| 1000 | 0.128 | 0.058 | 0.057 | 0.117 | 0.063 | 0.057 | 0.117 | 0.064 | 0.057 | 0.068 | 0.055 | |
Note
- Empirical size of likelihood ratio tests for a nominal size
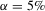 and true value of the parameter vector
and true value of the parameter vector 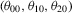 . Results reported for just-identified estimation of the OU process 4.1 with true parameter values:
. Results reported for just-identified estimation of the OU process 4.1 with true parameter values: 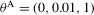 and
and 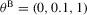 .
.
Table 2 shows that the S2 estimator retains its superiority over the S1 estimator in an over-identified setting.3 The S1 estimator is up to ten times more biased than the S2 estimator (N-, L- and A-type), which itself exhibits some bias reduction compared to the D estimator. Here, θ0 and θ2 are held fixed at the true values, which in general are different from the values that minimize the just-identified objective function for a given set of observations, and θ1 has to compensate for those restrictions when minimizing the over-identified objective function. In conjunction with the relatively mild penalty when θ1 moves away from the non-stable region of the parameter space, this will cause the over-identified S1 estimator to have a larger upward bias than the just-identified S1 estimator. In contrast, because of the approximate linearity of the binding function and near symmetry of the S2 and D objective functions, the S2 and D estimators do not suffer from this excessive bias. However, because of the interaction between the weighting matrix and the moment conditions, the over-identified M-type estimators lose their bias correcting properties; see also Altonji and Segal (1996). Finally, the over-identified S1 estimators have the highest rejection rates in both J and LR tests. The high rejection rate of these tests is caused by the finite sample bias of the S1 estimators combined with the asymmetry of the S1 objective functions. Figure 1 shows plots of LR-type statistics for 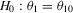 as functions of θ10 in the over-identified OU model with θ0 and θ2 being held fixed at their true values. The left and right panels display plots based on representative samples of size
as functions of θ10 in the over-identified OU model with θ0 and θ2 being held fixed at their true values. The left and right panels display plots based on representative samples of size 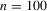 , and parametrizations
, and parametrizations 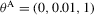 and
and 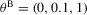 , respectively. The horizontal grey line and the vertical red line represent the 95% χ2(1) critical value and the true value of θ1, respectively. The shape of the objective function is equivalent to the shape of the LR statistic except for a level shift.
, respectively. The horizontal grey line and the vertical red line represent the 95% χ2(1) critical value and the true value of θ1, respectively. The shape of the objective function is equivalent to the shape of the LR statistic except for a level shift.
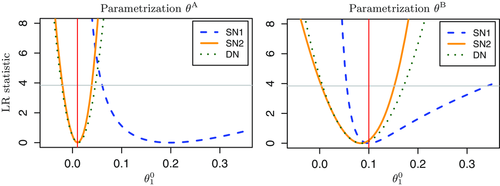
 .
.| n | SN1 | SN2 | DN | SL1 | SL2 | DL | SA1 | SA2 | DA | SM2 | DM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Bias and [root-mean-squared error] of  |
||||||||||||
| θA | 100 | 0.2637 | 0.0254 | 0.0281 | 0.2509 | 0.0241 | 0.0268 | 0.2531 | 0.0242 | 0.0269 | −0.0094 | −0.0086 |
| [0.3624] | [0.0415] | [0.0444] | [0.3524] | [0.0406] | [0.0437] | [0.3544] | [0.0408] | [0.0438] | [0.0296] | [0.0311] | ||
| 1000 | 0.0154 | 0.0022 | 0.0023 | 0.0151 | 0.0021 | 0.0021 | 0.0152 | 0.0021 | 0.0021 | −0.0023 | −0.0022 | |
| [0.0268] | [0.0057] | [0.0057] | [0.0264] | [0.0057] | [0.0057] | [0.0265] | [0.0057] | [0.0058] | [0.0060] | [0.0060] | ||
| θB | 100 | 0.1409 | 0.0175 | 0.0242 | 0.1430 | 0.0149 | 0.0218 | 0.1430 | 0.0149 | 0.0219 | −0.0285 | −0.0214 |
| [0.2339] | [0.0569] | [0.0607] | [0.2395] | [0.0566] | [0.0602] | [0.2391] | [0.0566] | [0.0602] | [0.0634] | [0.0622] | ||
| 1000 | 0.0075 | 0.0024 | 0.0029 | 0.0075 | 0.0021 | 0.0026 | 0.0075 | 0.0021 | 0.0026 | −0.0017 | −0.0012 | |
| [0.0179] | [0.0149] | [0.0151] | [0.0182] | [0.0152] | [0.0154] | [0.0182] | [0.0153] | [0.0154] | [0.0152] | [0.0153] | ||
| Empirical size of over-identification tests | ||||||||||||
| θA | 100 | 0.394 | 0.160 | 0.181 | 0.382 | 0.165 | 0.165 | 0.383 | 0.167 | 0.164 | 0.194 | 0.160 |
| 1000 | 0.149 | 0.085 | 0.089 | 0.148 | 0.082 | 0.076 | 0.147 | 0.080 | 0.076 | 0.091 | 0.088 | |
| θB | 100 | 0.132 | 0.100 | 0.099 | 0.125 | 0.094 | 0.091 | 0.125 | 0.092 | 0.088 | 0.083 | 0.099 |
| 1000 | 0.058 | 0.054 | 0.052 | 0.060 | 0.055 | 0.051 | 0.060 | 0.056 | 0.052 | 0.059 | 0.051 | |
| Empirical size of likelihood ratio tests | ||||||||||||
| θA | 100 | 0.933 | 0.048 | 0.105 | 0.884 | 0.041 | 0.092 | 0.846 | 0.040 | 0.091 | 0.404 | 0.383 |
| 1000 | 0.451 | 0.039 | 0.038 | 0.432 | 0.045 | 0.041 | 0.418 | 0.045 | 0.042 | 0.132 | 0.127 | |
| θB | 100 | 0.437 | 0.040 | 0.080 | 0.418 | 0.040 | 0.075 | 0.411 | 0.042 | 0.073 | 0.186 | 0.148 |
| 1000 | 0.133 | 0.052 | 0.056 | 0.118 | 0.053 | 0.063 | 0.118 | 0.053 | 0.064 | 0.057 | 0.061 | |
Note
- Results for the
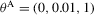 and
and 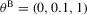 parametrizations of the OU process 4.1 when only the mean reversion parameter, θ1, is estimated, and θ0 and θ2 are held fixed at their true values. Empirical size of tests for a nominal size
parametrizations of the OU process 4.1 when only the mean reversion parameter, θ1, is estimated, and θ0 and θ2 are held fixed at their true values. Empirical size of tests for a nominal size 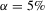 .
.
5. CONCLUSION
We study the asymptotic and finite sample properties of a score-based indirect inference estimator that uses the sample auxiliary score evaluated at the simulated binding function. This estimator is asymptotically equivalent to the original score-based indirect inference estimator of Gallant and Tauchen (1996), but in finite samples behaves much more like the distance-based indirect inference estimator of Gouriéroux et al. (1993). In our Monte Carlo study of a continuous time OU process, the alternative score-based estimator exhibits greatly improved finite sample properties compared to the original. Our results indicate that estimators operating through the simulated binding function are more suitable for highly persistent time series models than estimators operating through the simulated score.
ACKNOWLEDGEMENTS
In this paper, we summarize the main results in P. Fuleky's PhD dissertation, written at the University of Washington. E. Zivot greatly appreciates support from the Robert Richards chair. We are grateful to the editor and two anonymous referees for helpful suggestions.
 .
.


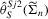 (j = L, A, M) defined in
(j = L, A, M) defined in 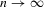 :
: