Biological effectiveness and relative biological effectiveness of ion beams for in-vitro cell irradiation
Abstract
Biological effectiveness and relative biological effectiveness are critical for proton and ion beam radiotherapy. However, the relationship between the two quantities and physical character of ion beams is not well established. By analyzing 1188 sets of in-vitro cell irradiation experiments using ion beams ranging from protons to 238U, compiled by the Particle Irradiation Data Ensemble (PIDE) project, the biological effectiveness of the ion beams, with cell survival fractionation (SF) as the endpoint, was found to be dependent on the fluence and linear energy transfer (LET) of the ion beam. Consequently, the relative biological effectiveness of the ion beam to photon beam was also established as a function of LET. A common form of relationship among SF, fluence, and LET was found to be valid for all ion beam experiments. The close form relationship could be used for proton and ion beam radiotherapy applications.
Abbreviations
-
- DSB
-
- double strand break
-
- LET
-
- linear energy transfer
-
- LQ
-
- linear quadratic
-
- PIDE
-
- Particle Irradiation Data Ensemble
-
- RBE
-
- relative biological effectiveness
-
- SF
-
- survival fractionation
1 INTRODUCTION
Biological effects of ionization radiation include cell killing, carcinogenesis, and mutation.1 The principal target of ionization radiation for these biological effects is DNA.2 Extensive in-vivo experiments have been performed to investigate the relationship between ionizing radiation and cell death, among other biological endpoints.3-7
The absorbed dose of ionizing radiation has been used to relate the imparted radiation energy to biological effects, specifically for in-vitro cell experiments, cell death, and survival fractionations. The widely accepted linear quadratic (LQ) model establishes the relationship between absorbed dose and cell survival fractionation and has been extensively used to analyze and predict ionizing radiation response both in vitro and in vivo.8 Ions, or charged particles, could have physical and radiobiological advantages over photon irradiation for radiation therapy.9 The radiobiological advantage of ion beam irradiation manifests in the form of more effective cell killing with the same absorbed dose for in-vitro cell irradiation experiments.10 Different ion beams and beams with the same ion but with different kinetic energies (and, thus, different linear energy transfer, LET) have different biological effectiveness, which is not reflected in the dose-survival model; that is, the same absorbed dose delivered by different ion beams or the same ion beam with different LET would yield different survival fractionation for the same cell line.11 The difference in biological effect between low and high LET radiation could affect human exploration of outer space as the space radiation has high LET components that need to be accounted for.12
Because of the observed difference of dose needed to achieve the same biological endpoint for ion beams, relative biological effectiveness (RBE), defined as the ratio of the doses required by two different types of radiation beams to cause the same level of biological effect, was introduced to account for the difference.13-15 Although considerable research, including both experiment and modeling efforts, has been undertaken, the relationship between the (relative) biological effectiveness of ion beam and dose, or other descriptors of the ion beam characteristic, remains unclear.16
Defined as the amount of energy absorbed by matter per unit mass,17 the absorbed dose could be represented as the product of fluence and LET.18 By definition, LET is the energy loss per unit length and could be considered a measurement of the density of ionization events around ion tracks, whereas fluence represents the number of ion tracks per unit area. Ionization events, induced by ionizing radiation, cause DNA damage, including double stand breaks (DSB) and cluster damage, which in turn leads to cell death. In this context, it became clear that, unlike photon irradiation, for which the spatial distribution of ionization events could be in general considered uniform, the spatial distribution of the energy deposition and ionization events plays an essential role in the biological effectiveness of the ion beam. This is because more ionization events near DNA in the cell nucleus, in general, would be more damaging to the cell. Therefore, dose is not adequate for use as the sole parameter to quantify the biological effects of ion beams because of the lack of spatial information.
Models have been proposed to describe the relative biological effects of ion beams. The most notable models are the local effect model (LEM),19-22 the (modified) microdosimetric kinetic model (MKM),23-25 and the repair–misrepair–fixation (RMF) model.26, 27 In general, to establish the relationship between the reference photon irradiation and the ion beam irradiation, specific and unvalidated assumptions were made for each of these models. For example, Scholz and Kraft stated in a commentary that “the fundamental assumption of the LEM is that the local biological effect is determined by the local dose, but is independent of the particular radiation type leading to a given local dose” (Radiation Research 161, Page 612).28 The direct comparison among these models for the same beam condition found large discrepancies in their predictions, indicating that the underlying assumptions in these models might not be valid.29
In this study, it was hypothesized that as opposed to dose and RBE, a different function of fluence and LET could describe the biological effectiveness of ion beam radiation. The description of biological effectiveness could subsequently be used for comparison with the reference photon irradiation to determine RBE, thereby avoid making any assumptions on the relationship between the photon and ion beam irradiation. By analyzing 1118 sets of in-vitro cell experiments with ion beams, complied by the Particle Irradiation Data Ensemble (PIDE) project,16 a common form was established to describe the survival fractionation of all cell experiments.
2 MATERIALS AND METHODS
Absorbed dose is defined as the amount of energy imparted to matter by ionizing radiation per unit mass of the matter and could be represented as a product of and . In this equation, is the fluence of the ion beam, is the density of the medium, and is the unrestricted LET, defined as the energy loss per unit distance, and is the same as stopping power.18
As mentioned above, the dose could be represented by the product of fluence and LET. Although the effect of LET in ion beam radiation has been extensively studied, the role of fluence has not been investigated. It is well established that the RBE of ion beam irradiation rises with LET up to a certain point and then declines. In other words, using the same ion type beam with varying LETs, the dose required to achieve the same biological endpoint declines with LET up to a certain point; then the required dose to reach the said biological endpoint increases.30 The so called “overkill” effect has different “turning point” for different ions but is usually considered to be approximately 100 to 200 keV/μm.31 In this LET range, the average separation of ionization events introduced by a single ion is thought to coincide with the diameter of the DNA helix. Therefore, it is effective in introducing DNA DSB or clustered damage that leads to cell death. For ions with even higher LET, the denser ionization event may cause more localized damage but not result in more cell death.
where parameters a and b vary with cell type and ion type; c varies with , , cell type, and ion type and is a bijective function of SF; and is also a bijective function of SF. In this formalism, D1 numerically equals the dose required to achieve SF for a particular ion beam with LET of 1 keV/μm.
- For each cell line, and
- For each ion type, the sets of experiments performed with the given cell line and ion type were identified with LET, α, and β.
- For each set of experiments, a series of SF was chosen, and the corresponding dose D to achieve each of the SF was calculated by solving Equation (1) with known α, β.
- Fluence was calculated with D and LET using Equation (2)
- For each SF, D1 and were determined with the linear fit for data points with LET <=150 keV/μm
- Separately, for each SF, D1 and were determined with linear fit with all ion beam data with LET >150 keV/μm
Since , , and c are all bijective functions of SF, LET becomes the only variable for RBE for any given SF, which is consistent with the previous “widespread assumption that the RBE for the same cell line and the same biologic endpoint may be assumed to be dependent on LET alone.”31 However, this is the first time a general model of RBE as a function of LET was formulated for all ion beams, and this RBE model could be called the LET power model.
For PIDE data, each set of ion beam irradiation experiments has a corresponding set of photon irradiation, where α, β, and the energy of the photon beam are reported. Thus, Dref for each SF could be easily calculated. However, it should be emphasized that, in determining a, b, c, and D1 for Equations (5) and (6), photon irradiation was not part of the equation and was only used in Equation (9) for calculating RBE. In other words, Equations (5) and (6) describe the biological effectiveness of ion beams instead of the RBE of ion beams described in previous investigations.
To validate the results, the coefficient of determination (R2) between the RBE determined using Equation (9) and from the measured data was calculated for different ions.
3 RESULTS
Table 1 summarizes all cell irradiation experiments included in PIDE. Based on the reported α and β dose versus SF or (D, SF), all experiments were recreated in Figure 1A, where each curve corresponds to one experiment set. Fluence could then be calculated from D using the reported LET and Equation (1), where the (D, SF) data could now be rewritten as (, , SF). Thus, the and required to achieve a specific SF for each experiment sets could be plotted. Figure 1B shows the and required to achieve an SF of 0.8 for all experiments, with experiments reported by Weyrather et al.32 highlighted. Weyrather et al. studied three cell lines, V79, CHO-K1 and xrs5. As shown in the figure, the results from each of the cell lines form two distinctive lines, above and below 150 keV/μm, and each of them deviates from the dose line, indicating that the dose is not a good predictor for biological response. The separation among the lines for the three cell types and the difference in slopes indicate different parameters, D1 and c. Figure 1C shows the and required to achieve an SF of 0.5 for different ions and all experiments. Figure 1D shows the and required to achieve an SF of 0.1 for different ions and V79 cells in asynchronous cell cycle phases. Figures 1A–C show all 1118 sets of experiments, whereas Figure 1D shows 278 sets of V79 experiments, as detailed in Table 1.
| Total | V79 | V79 asynchronous cell phase | T1 | HSG | NB1RGB | C3H10T1/2 | CHO | B14FAF28 | R-1 | HF19 | AG01522 | SQ20B | Other cell lines | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X-ray | 261 | 49 | 37 | 6 | 1 | 5 | 17 | 6 | 1 | 1 | 5 | 6 | 4 | 160 |
| 1H | 180 | 52 | 50 | 8 | 3 | 14 | 3 | 100 | ||||||
| 2H | 17 | 10 | 4 | 5 | 2 | |||||||||
| 3He | 44 | 31 | 23 | 12 | 1 | |||||||||
| 4He | 107 | 36 | 26 | 7 | 7 | 10 | 3 | 44 | ||||||
| 12C | 385 | 70 | 61 | 22 | 21 | 24 | 2 | 14 | 11 | 4 | 3 | 11 | 203 | |
| 20Ne | 131 | 23 | 20 | 23 | 21 | 15 | 1 | 9 | 11 | 2 | 26 | |||
| 40Ar | 57 | 21 | 17 | 11 | 1 | 1 | 6 | 6 | 1 | 1 | 9 | |||
| Other ions | 197 | 77 | 77 | 6 | 12 | 9 | 10 | 24 | 8 | 5 | 46 | |||
| Ions total | 1118 | 320 | 278 | 69 | 54 | 51 | 34 | 34 | 30 | 28 | 25 | 28 | 15 | 430 |
- Note: 1H: hydrogen ion with a mass number of 1 (proton). Empty cells represent that no experiments were performed using the combination of ion and cell line.
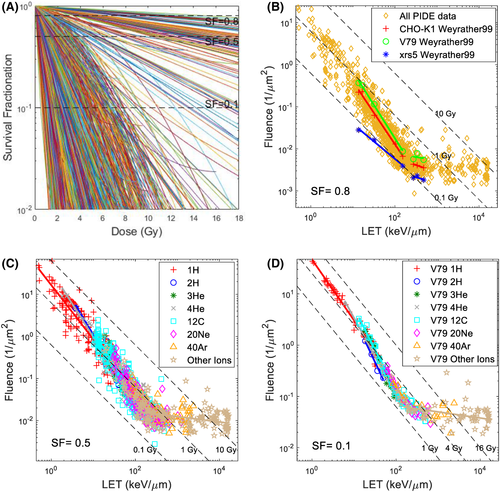
Table 2 summarizes the linear fitting results for a, b, c, and D1 for the V79 cell line in asynchronous cell cycle phases, as shown in Figure 1D, with proton, carbon, and high LET (>150 keV/μm) irradiation. Table 2 also shows the calculated Dref using the reported α and β of photon experiments paired with PIDE ion beam experiments.
| SF | a | b | c | D 1 | Dref (Gy) | |
|---|---|---|---|---|---|---|
| 1H | 0.8 | −0.041 ± 0.0028 | 2.01 ± 0.029 | 1.48 ± 0.11 | 2.54 ± 0.75 | 1.35 ± 0.40 |
| 0.5 | 1.33 ± 0.07 | 4.23 ± 0.76 | 3.17 ± 0.62 | |||
| 0.1 | 1.17 ± 0.06 | 7.33 ± 0.99 | 7.20 ± 1.05 | |||
| 12C (<150 keV/μm) | 0.8 | −2.2e-3 ± 3.3e-4 | 2.22 ± 0.04 | 1.72 ± 0.14 | 8.04 ± 5.99 | 1.35 ± 0.40 |
| 0.5 | 1.60 ± 0.10 | 13.00 ± 6.38 | 3.17 ± 0.62 | |||
| 0.1 | 1.51 ± 0.07 | 23.33 ± 7.73 | 7.20 ± 1.05 | |||
| High LET ion beam (>150 keV/μm) | 0.8 | −221.9 ± 2.4 | 1.12 ± 0.003 | 0.134 ± 0.04 | 2.0e-3 ± 0.7e-3 | 1.35 ± 0.40 |
| 0.5 | 0.124 ± 0.04 | 5.8e-3 ± 1.8e-3 | 3.17 ± 0.62 | |||
| 0.1 | 0.111 ± 0.03 | 1.7e-2 ± 4.6e-3 | 7.20 ± 1.05 |
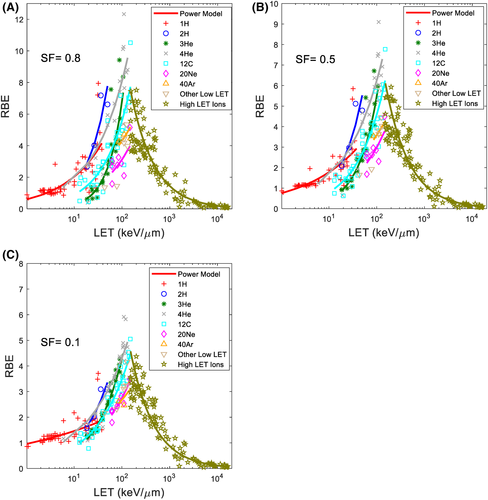
Using the linear fitting results of c, D1 and Dref, RBE for various ion beams at different SF can then be calculated with Equation (9). Figure 2 shows the calculated RBE using the LET power model (Equation 9) compared against the calculated RBE with experimental data (Equation 8) at SF of 0.8, 0.5, and 0.1 for various ions. The coefficient of determination (R2) between RBE determined using the model and the experimental data for different ions at different SF were calculated and are tabulated in Table 3.
| Ion type | Number of experiments | SF | ||
|---|---|---|---|---|
| 0.8 | 0.5 | 0.1 | ||
| 1H | 50 | 0.454 | 0.437 | 0.432 |
| 2H | 4 | 0.900 | 0.923 | 0.959 |
| 3He | 23 | 0.765 | 0.823 | 0.833 |
| 4H | 22 | 0.552 | 0.768 | 0.870 |
| 12Ca | 34 | 0.755 | 0.849 | 0.870 |
| 20Nea | 8 | 0.770 | 0.770 | 0.770 |
| 40Ara | 3 | 0.612 | 0.632 | 0.664 |
| High LET ions | 128 | 0.543 | 0.727 | 0.820 |
- a LET<=150 keV/μm only.
4 DISCUSSION
The absorbed dose has been used to relate the imparted radiation energy to biological effects, specifically for in-vitro cell experiments, cell death, and survival fractionations. In the form of the product of fluence and LET, the implicit assumptions of the dose are that the relative contribution from fluence and LET are equal and that spatial distribution of ionization events is not relevant. This study demonstrated overwhelming evidence that while both are important to cell survival, fluence and LET have different contributions at different LET and fluence ranges. The relative importance of the two is described by a new parameter c, as shown in Equation (6). As a result, both fluence and LET could be viewed as variables of SF, which is, in essence, a unitless cumulative probability distribution function.
In the LET–fluence–SF plots, as shown in Figures 1B–D, each data point represents the intersection between the specific SF line and the dose–SF curve, as shown in Figure 1A. It is worth pointing out that, according to Equation (2), with varying LET, one would need different fluence to achieve the same dose, and these points also form an “iso-dose” line on the log–log scale, where each point on the line represents the same dose. Several iso-dose lines were plotted as dotted lines in the figures and intersected with the fluence–LET line, which was described by parameters c and D1, to achieve the specific SF. The observation that the experimental data does not follow an iso-dose line again highlights that the same dose does not correspond to the same response for ion beams with varying LET. Instead, the relationship between fluence and LET follows a line with slope c, where c varies for different SF, as shown in Table 2. D1 represents the intersection point between the fluence–LET line and LET of 1 keV/μm and numerically equals the dose needed to achieve the specific SF using an ion beam with 1 keV/μm.
Equations (5) and (6) represent a general formalism of biological effectiveness of ion beams. As shown above, the derivation of the equations and parameters was completely independent from the photons, which separates the current study from previous investigations. Figure 1B shows how the same equations could be applied to different cell types (CHO-K1, V79, and xrs5), only with different parameters D1 and c. As shown in Table 2, as LET increase with heavier ions, the biological effectiveness drifts further from photon. For heavier ions, such as carbon ions, there is a LET threshold, above which increasing LET no longer increases the biological effectiveness of the ion beam, or the curves “flatten out.” The same fluence of high LET beams yields similar cell killing.13 To increase cell killing, one must increase the fluence or increase the number of ions. However, the same Equations (5) and (6) could still be used to describe the biological effectiveness for these high LET ion beams. This fundamental yet critical observation was overlooked in previous investigations of the RBE of ion beams, where assumptions that directly contradict the observation were made in some cases. Once the biological effectiveness of the ion beam was found, it was straightforward to calculate the RBE. As mentioned above, since the relationship between the biological effect of ion beams and beam characteristics were derived independently of the reference irradiation, unlike other RBE models, no additional assumptions were made in the current study. LET versus RBE data similar to Figure 2 has been shown in prior literature,16, 31, 33, 34 but the current study is the first to derive a generic closed-form expression for all ion beams. The coefficient of determination (R2) of RBE determined using the model and experimental data is calculated and tabulated in Table 3 for various ions and SF. The relatively low R2 values of the proton data are due to the high uncertainty in the experimental dataset, as previously explored, and had in part justified the use of a constant RBE value of 1.1.35 To further validate the model in the proton domain, high quality experimental data with precise LET and fluence data would be necessary.
Other factors, such as the oxygen level (the oxygen enhancement ratio)36 and the cell cycle37 also have significant impacts on the biological endpoints and have also been studied extensively. The same method could be expanded and applied to these investigations but is outside the scope of the current study. Uncertainties are inherently large with cell experiments because of the complexity of such investigations and the statistical nature of cell killing. For example, it is impossible to directly measure the dose required to achieve a specific SF for a particular cell line and ion beam, as SF could only be measured days after the cell irradiation. Thus, such data could only be acquired through modeling and interpolation of raw data. Nevertheless, comparable confidence intervals for D1 and Dref for various SF, between proton and photon irradiation, were shown in Table 2, noting that both photon and proton beams could be in the 1 keV/μm range. In contrast, for heavier ions, the LET ranges move further away from photons as the atomic number increases (there were no 1 keV/μm beams for heavier ions), thus making the direct comparison with photons more challenging. Another notable source of uncertainty arises from the reported LET. Different variants of LET, including dose averaged LET, track averaged LET, in addition to LET∞, were reported in the literature, which could also lead to uncertainties in the determination of fluence using Equation (2). The rationale for using different LET variations is outside the scope of the current study and will not be further discussed.
Cell survival fractionation could be written as a function of fluence and LET for all ion beam irradiations. The close form relationship could be used for proton and ion beam radiotherapy applications.
ACKNOWLEDGMENTS
I acknowledge the PIDE project for compiling available ion beam in-vitro cell irradiation data.
CONFLICT OF INTEREST
Author declares no competing interests.
Open Research
DATA AVAILABILITY STATEMENT
All data are available through PIDE. https://www.gsi.de/work/forschung/biophysik/forschungsfelder/radiobiological_modelling/pide_project




